1 Introduction

Indeed, image encrypthion is a method for making illegible information, which transfer through a network like the authorisezd person for the special information. In addition, they can get the basic information (encrypted key). Designs of image encryption methods caused many researchers attend to introducing a safe method for transferring images straightway through internet or Wi-Fi networks. Because of basic difference between images and texts in volume and redundant bits, traditional cryptography methods are not efficient [3, 4]. In the 1989, for the first time the effective method of chaotic had introduced based on the cryptograpgy algoritms. As has been noted, many researchers have done on chaos-based image cryptography [7, 11]. Sensitivity to primary conditions, non-periodic, non-convergence, and controlling parameters are unique properties of chaotic cryptography compared to traditional ones. Other advantages of this type of cryptography are their high speed and having no computational overhead [13]. Real difference and several techniques have been introduced for image cryptography that are stated briefly as followings. (Space domain) and (frequency domain) are two major methods used in most papers. In space domain all pixels forming the image are considered and various methods are implemented directly on these pixels. In the second method, frequency domain is a space such that every proportion of image in image position F, shows the intense amount in image I, vary over a specific distance dependent on F. In fact, in this method we turn to the image as it is. Huang and Nein [9] presented a method for pixel shuffling along with multi-chaos system for image encryption. In 2010, Solac et al. [20] by analyzing a method which introduced earlier at this year find its shortcomings and prove that the scheme was vulnerable against two kind of attacks, then they present a solution for encountering it. During that year, Zhang et al. [26] introduced a method base on Arnold Cat map and coupled chaos for image encryption. Rejinder et al.[12] proposed a method for image cryptography based on improving DES and chaos. Zhu et al. [29] proposed a symmetric chaos based image encryption scheme by using of bit-level permutation. They use a simple chaotic map, which named Arnold cat map for bit-level permutation and Logistic map used in diffusion stage. Changing the position and values of pixels are the advantageous of bit-level permutation. Indeed, in bit-level permutation Arnold Cat map and Logistic map has used for determining parameters of the Arnold cat map. Congxu Zhu in [28] proposed a novel image encryption scheme based on hyperchaotic sequences. The hyperchaotic sequences are changed in a way to produce chaotic key streams, which is more suitable for image encryption. The author, in order to improve key sensitivity and plain text sensitivity made final encryption key stream dependent on both of the chaotic key stream and plaintext and this lead to high key sensitivity and plain text sensitivity, which are two important metrics in proving security of the scheme [1, 2]. Wang et al. [21] proposed a fast image encryption method with the help of chaotic maps. In fact, they merged diffusion and permutation phase, which result to acceleration of image encryption scheme. First, image portioned into blocks of pixel, then with help of spatiotemporal chaos, pixel value shuffling and diffusion can run simultaneously. Zhang and Cao in [24] presented an image encryption scheme by using a created chaotic map whose maximal Lyapunov exponent was reached beyond 1 and it was equal to 1.0742. In addition, they used Arnold cat map for permutation phase. Their method has two shortcomings. First, there is no relation between the secret keys and the original image. Indeed, the secret key is not sensitive to the original image, which causes two side effects. First, the secret key may not be changed for various images and it directs a hostile to get a set of basic information to decrypt the encrypted image. Second, using the same sequence for changing all of three-color components of an image decrease the security. Because of any reason, hostile access to the initial value, at the same time he will be able to recover all the color component values. In this paper, we improve presented scheme in [24] and resolve those shortcomings. As it’s obvious, Lyapunov exponent is the main characteristic of chaotic maps. Therefore, the increasing of the Lyapunov exponent, causes to increase the dispersion of output sequence values and better chaotic behavior. Hence, we have made one-dimensional chaotic maps with the Lyapunov exponents 1.38 and 1.518, respectively. These novel chaotic maps in comparison with conventional maps and the ones introduced by Zhang and Cao in [24], have stronger chaotic behaviour. We utilized effective coupled chaotic map to create three Chaotic Matrixes for changing the pixel amounts in each color component, distinctly. In order to improve security of the proposed scheme and key sensitivity, initial state of each color component should be dependant to each other and plain image. By utilizing this procedure, even if an intruder guesses one of the initial state condition values, he wouldn’t be able to rebuild part of secret plain image. Regardless of the dependency on the initial values, if hostail guesses one of the initial values corresponding to one of the color components, he/she can retrive the shadow of the plain image. We provide a test to show this concept, which shown in Fig. 8. We use Cosinus-Arcsinus (CA) map with these initial states to generate three chaotic sequences as inputs for the coupled map in diffusion phase. Moreover, a new permutation scheme, chaotic-diagonal permutation, proposed the intense dependency on the original image. Indeed, after applying chaotic interception steps we will have new plain. By arranging diagonal layers next to each other, we obtain a vector of pixel values with length M × N to fill a matrix in rows. This process will be iterated P times with differing interception indices that obtained from SPL map to make final permuted matrix (Fig. 9). Simulations and performance evaluations show that this permutation algorithm is more efficient and need less iteration compared with other available permutation methods (Fig. 10). The execution time comparison between our proposed method and other available methods has shown in Table 4, which proved our proposed permutation algorithm speed is satisfying. The output of permutation stage, bitxored with Chaotic Matrixes which are result of coupled chaotic map and make encrypted image. Furthermore, two kinds of keys, cutting key (CK R, G, B ) and averaging key (AK R, G, B ) for each color components used to create dependencies between the encryption algorithm and the original image. Therefore, the proposed method will be resistant to the chosen-plain text and known-plain text attacks. The total time of encryption algorithm is almost 0.11 second. Briefly, beside presenting two high level chaotic map novels (CA, SPL), an encryption algorithm which has novelty in both diffusion and permutation phases is proposed. Indeed, in diffusion phase among the presentation of a chaos-based random selection technique, a large key space and high key sensitivity is provided. The overmentioned features cause that the proposed algorithm resistants against brute-force and differential attacks. Moreover, lower computational over head, intenses confusion with lower iterations and high dependency on plain image in chaotic diagonal permutation; and it can also gurantee the performance and security of proposed method. Exprimental results implies that our method has superiority in key space size and convincied results in another part of experimental results such as NPCR about 99.67 and UACI about 33.45.

The paper structure is as follows: in Section 2, necessary, mathematical basics will be presented. After that proposed method will be described in Section 3. Then we provided experimental results and security analysis in Section 4. Finally, in Section 5, we come into conclusions.

2 High level chaotic maps

2.1 The Cosinus-Arcsinus system

We introduce a new chaotic map on interval [0, 1], with high positive Lyapunov exponent by combination of Cosinus and Arc sinus (CA). The mathematical formula of this new chaotic map is as below:

$$ {X}_{n+1}=CA\left(r,{X}_n\right)={ \cos}^2\left(r\; \arcsin \left(\sqrt{\left|{X}_n\right|}\right)\right) $$
(1)

Where r, is a control parameter in a range (0, 4) and X n is initial state condition, which is in the interval [0, 1]. Moreover, in parameter value r = 3.976 Lyapunov exponent has maximum value = λ = 1.38. The Lyapunov exponent bifurcation and spatiotemporal diagram are shown in Figs. 1, 2 and 3, respectively.

Fig. 1
figure 1

The Lyapunov exponent of Cosinus-Arcsinus system

Full size image
Fig. 2
figure 2

The bifurcation diagram of Cosinus-Arcsinus system

Full size image
Fig. 3
figure 3

The spatiotemporal diagram of Cosinus-Arcsinus system

Full size image

2.2 The Sinus-power logistic system

48, 0.48]. This map is a combination of Sinus and PowerLogistic that first introduced in [24]. Based on the Lyapunov exponent diagram, this map has positive Lyapunov exponent for rϵ (0,3.5). Moreover, in parameter value r = 3.465 Lyapunov exponent has maximum value λ = 1.518. The Lyapunov exponent, bifurcation and spatiotemporal diagrams which represented chaotic behaviour of SPL map, shown in Figs. 4, 5 and 6, respectively. The mathematical formula of this new chaotic map is as below:

$$ {X}_{n+1}=SPL\left(r,{X}_n\right)={ \sin}^2\left(r \arcsin \left(\sqrt{\left|{X}_n\right|}\right)\right)+\left(1-r\right)2\left(\left|{X}_n\right|\right)\left(1-2\left|{X}_n\right|\right) $$
(2)
Fig. 4
figure 4

The Lyapunov exponent of Sinus-Power Logistic System

Full size image
Fig. 5
figure 5

Bifurcation diagram of Sinus-Power Logistic System

Full size image
Fig. 6
figure 6

Spatiotemporal diagram of Sinus-Power Logistic System

Full size image

Where r is control parameter in the range (0, 3.5), and X n is initial state condition with a range (−0.48, 0.48). We provide a comparison between the Lyapunov exponent of new proposed chaotic maps and some available maps in Table 1.

Table 1 Comparison between Lyapunov exponents of proposed method with others available chaotic maps
Full size table

2.3 New coupled chaotic map

For having chaotic dynamics in a spatially extended system, we need to use coupled map. Indeed, a coupled map consists of an ensemble of elements of given (“map”) that interact (“couple”) with other elements from a suitably chosen set. The dynamic of each element is given by a map. As a consequence, the coupled map is a discrete time multi-dimensional dynamical systems. An important type of coupled map is the coupled map lattice (CML), in which each element is set on a lattice of a given dimension, resulting in a (“map”), discrete space (“lattice”), and continuous state. The mathematical formula of this map is as below:

$$ {X}_{n+1}(j)=\left(1-\varepsilon \right)f\left({X}_n(j)\right)\Big)+\frac{\varepsilon }{N-1}{\displaystyle \sum_{i\ne j,i\in \left\{1,\dots, N\right\}}f\left({X}_n(i)\right)} $$
(3)

Where X n as the initial state condition is a vector of length N and ε is coupling coefficient, which is in range [0, 1]. The mapping function f (x) is a chaotic map and we use Sinus-Power Logistic in this case, which is defined before in equation (2).

3 Proposed method

3.1 Encryption process

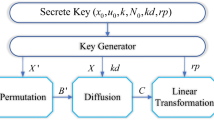
The overall view of encryption process has shown in Fig. 7. At first, we read the plain image and calculate cutting keys (CK R, G, B ) and averaging keys (AK R, G, B ) values for each color component distinctly. Then, multiply selected initial values by AK R, G, B to obtain three desired initial states in order to generate three chaotic sequences by using the CA map. After that, final eligible sequences with length N for each color component obtained by using a random selection method from previously generated sequences. Next, three Chaotic Matrix C R , C G and C B are built by applying coupled map over to intercept sequences of previous step as initial sequences. Finally, the plain image permuted P times and each color component of the resulting matrix bitxored by its corresponding Chaotic Matrixes C R , C G and C B to obtain an encrypted image.

Fig. 7
figure 7

Image encryption proposed method

Full size image

It should be noted that the number of iterations, P, can be fixed when the desired permutation obtained and in our algorithm this number is not too big. Parameters and notation, which are used in this scheme has shown respectively in Tables 2 and 3.

Table 2 Parameters used in the encryption phase
Full size table
Table 3 Notation definition
Full size table

The detailed steps of the proposed image cipher algorithm are as follows:

  1. Step 1

    Read plain image with size of M × N, and create the plain matrix from it. Plain ij define the pixel value in the ith row and jth column of Plain, where 1 ≤ i ≤ M, 1 ≤ j ≤ N.

  2. Step 2

    Initial values and parameters of chaotic maps are set in this step, which are consisting of: x r0 , x g0 , x b0 , r, for CA map, a big integer key K which used for producing cutting and averaging keys (CK, AK), and finally, r,ε values for Coupled map.

  3. Step 3

    Cutting and averaging key values calculated by below equations for each color component separately (three cutting keys and three averaging keys):

$$ C{K}_{R,G,B}=\left({\displaystyle \sum_{i=1}^M{\displaystyle \sum_{j=1}^N plain{\left(i,j\right)}_{R,G,B} \mod\;K}}\right) $$
(4)
$$ A{K}_{R,G,B}=\frac{C{K}_{R,G,B}}{K} $$
(5)

Where plain (i, j) is the pixel value in the ith row and jth column of plain. M and N are the size of plain image and K is a big integer number. As it’s obvious in the above equations, cutting keys (CK R,G,B ), calculated based on whole pixels of the plain image, therefore it is dependent on the plain image. Hence if the image changed slightly, the values of these keys and consequently, the values of averaging keys also changed. This fact, made our scheme highly sensitive to its keys and plain image.

  1. Step 4

    In order to make initial state conditions dependent on each other and make new modulated initial state conditions we use equations (6) to (8). Where X R0 , X G0 and X B0 are modulated initial state conditions and x r0 , x g0 , x b0 are initial values for each colour component of the image. AK R , AK G , AK B are Averaging keys that are produced in pervious step by using equation (5).

$$ {X}_{R0}=\left(\left(\left({x}_{b0}\times {x}_{g0}\right)+{x}_{r0}\right)/2\right)\times A{K}_R $$
(6)
$$ {K}_{GO}=\left(\left(\left({x}_{ro}\times {x}_{bo}\right)+{x}_{go}\right)/2\right)\times A{K}_G $$
(7)
$$ {X}_{BO}=\left(\left(\left({x}_{ro}\times {x}_{go}\right)+{x}_{bo}\right)/2\right)\times A{K}_B $$
(8)

Remark: As mentioned before, a key point is that our scheme highly sensitive to its keys and plain image. Indeed, we make initial state conditions dependent on plain image and each other, in order to prevent adversary from obtaining a partial image. Otherwise, if an adversary guess one of the initial state condition correctly, he can rebuild partial of plain image and see what is behind of encrypted image, but in this way, because of dependency between initial state conditions he/she wouldn’t gain any useful information. (Fig. 8).

  1. Step 5

    In this step, initial state conditions which produced from the previous step use as an input for a CA map which iterate CK R, G, B  + N times to produce three chaotic sequences entitled: Z R , Z G and Z B . After that, N elements randomly select from each sequence by using pseudo-code which is provided below:

$$ Start\ inde{x}_{R,\ G,\ B} = \left(C{K}_{R,G,B}\right)/2 $$
Fig. 8
figure 8

Effect of no-dependency of initial states to each other and plain image. a: Intruder guess value of red component initial state, b: Intruder guess value of blue component initial state, c: Intruder guess value of red component initial state, d: Intruder guess value of red component initial state in proposed method, e: Intruder guess value of blue component initial state in proposed method, f: Intruder guess value of green component initial state in proposed method

Full size image

With the help of above pseudo-code, we define the interception index of each color component sequence and start from determining position to select N consecutive elements \( \left({\tilde{Z}}_R,\;{\tilde{Z}}_G,\;{\tilde{Z}}_B\right) \). Finally, we multiply the intercepted sequences for each color component (\( {\tilde{Z}}_{R,\;G,\;B} \)) by 0.48 to be in the appropriate domain of SPL map, which used in coupled map.

$$ {\widehat{Z}}_{R,G,B}=\left({\tilde{Z}}_{R,G,B}\right)\times 0.48 $$

Then these sequences use as initial state to build M × N Chaotic Matrix C R , C G and C B by using coupled map in a similar way and briefly denote with C R, G, B (eq. 3). Now, we build Chaotic Matrix C, row by row. First, The elements of Ẑ R,G,B use as zero rows C (0) (initial state conditions) that finally removed. Each row of chaotic matrix, for example C (n + 1) obtains from previous row, C (n), with below formula:

$$ {C}_{n+1}(j)=\left(1-\varepsilon \right)SPL\left({C}_n(j)\right)+\frac{\varepsilon }{N-1}{\displaystyle \sum_{i\ne j,i\in \left\{1,\dots, N\right\}}SPL\left({C}_n(i)\right)} $$
(9)

Where ϵ is coupling coefficient.

  1. Step 6

    The plain image permuted P times. Overall overview of the proposed method for permutation is shown in Fig. 9. In the following, detailed procedure is explained. This method has dependency on plain image based on CK R, G, B values, which produced in the third step. Based on Fig. 9a, at first, we scroll down plain image row by row from left to right and put the elements in an array. Then we find the position of the first interception index, I 1 , as below:

$$ {I}_1= \mod \left(SPL\left( \mod \right)\left(AK,0.48\right)\right)\times {10}^9,M\times N $$
(10)
Fig. 9
figure 9

A sample of permutation algorithm for a matrix 8 × 8, (a) elements in plain image, (b) Substituting position of elements based on value of I 1 and I 2 , (c) Segmentation of new plain matrix into main diagonal (VD), upper triangular (VT U ) and lower triangular (VT L ) vector, (d) Result of first round permutation, (e) Result of second round permutation

Full size image

So we put the elements of this position,I 1 , to end of this array into the first positions of a new matrix and the remaining elements put over them as shown in Fig. 9b, and build new plain. After that, new plain matrix divided into 3 segments. The first one is the main diagonal of the matrix (D), second part is an upper triangular matrix (T U ) and the last one is a lower triangular matrix (T L ). The first segment puts in VD vector, then, the upper triangular matrix scrolling down diagonally from left to right and put the elements into the vector respectively, which is called VT U . After doing the same process for the lower triangular matrix VT L vector obtained as shown in Fig. 9c. Finally, V vector is accomplished by equation (11):

$$ V=VD\left|\left|V{T}_U\right|\right|V{T}_L $$
(11)

After that, V vector fill a matrix row by row and rebuild a matrix with a size of original image, as it shown in Fig. 9d for a 8x8 case. This process repeats P times with consider interception indices.

$$ {I}_{j+1}= \mod \left(SPL\left( \mod \left({I}_j\times CK,0.48\right)\right)\times {10}^9,M\times N\right)j=1,\dots, P $$
(12)

In Fig. 9e, the second round permutation result is shown. Where P is the number of iterations of the process which can be fixed when the best result obtained. According to the results, this number is not too large. Indeed, the advantage of this method is high transmogrification with lower iteration and satisfactory speed. The result of permuting Lena gray image with the proposed method, Arnold cat map, Baker map and Standard map with 3 iterations displayed in Fig. 10 and these result show this fact that the power of proposed method is much more than other available algorithms and with only 3 iterations it permutes the Lena image better than overmentioned schemes. Furthermore, we provide execution time and correlation comparisons between proposed method permutation algorithm and other available permutation methods for Lena gray level image that indicated in below (Table 4).

Fig. 10
figure 10

Compression between proposed permutation method and Arnold cat map, Baker map and Standrad map: (a): Lena plain image, (b): 3 times iteration with proposed permutation algorithm (c): 3 times iteration with Arnold cat map, (d): 3 times iteration with Baker map, (e): 3 times iteration with Standard map

Full size image
Table 4 Execution time comparison between proposed permutation method and other available permutation methods
Full size table

As it’s obvious in the above table, our proposed algorithm has a better correlation results among other methods that proved high transmogrification with lower iteration. Indeed, the proposed algorithm disturbs pixel positions in such a way that minimize the correlation between adjacent pixels in horizontal, vertical and diagonal orientation. Although, the speed of Arnold Cat is a little better versus proposed algorithm, but as shown in Fig. 10, with 3 round permutation the result of Arnold Cat map is disappointing, Therefore our algorithm overcome Arnold cat map.

$$ Chaotic\ Matrix=\left(\mathrm{round}\ \left(1{0}^{14}\times \left({C}_{R,\ G,\ B}\right)\right)\right)\ \mod\ 256 $$
(13)
  1. Step 7

    Reform the Chaotic Matrixes by (13), in order to put elements in range [0–255].

Where C R, G, B are chaotic matrixes which produces in step 5, round (x) is a function which gives nearest integer number to x.

  1. Step 8

    Finally, Chaotic Matrixes based on Fig. 7b, bitxored by permuted image to obtain the Encrypted Image.

3.2 Decryption process

Decryption phase is the reverse of encryption phase. The reciever party by having appropriate keys (x r0 , x g0 , x b0 , CK R , CK G , CK B , r (CA), r (SPL), K, P and ε) can re-calculate AK R, G, B based on equation (5). After that, modulated initial state conditions re-build by multiply AK R, G, B with initial states (x r0 , x g0 , x b0 ). We use them as an input for CA map, which iterate CK R, G, B  + N times, this lead to production of chaotic sequences (Z R , Z G , Z B ). After that, the third party must use interception process for randomly selection of N elements based on predeterminded methodology that discussed before in step 5 of section 3.1. Finally, distinct Chaotic Matrixes (C R , C G , C B ) will be produced. Then, encrypted image de-permuted P times and bitxored with Chaotic Matrixes to achieve plain image.

4 Experimental results and security analysis

In our experiment, we use standard images to test, which consist of Lena, Baboon, Barbara, Peppers, Tree and etc. We use a notebook with windows 7 OS, Intel core i5, 2.40 GHZ CPU, using Matlab R2013b. The initial secret keys are selected without any restriction from predetermind intervals. We use (x r0  = 0.3, x g0  = 0.1 , x b0  = 0.5, K = 10001, r = 3.976, r = 3.465 ε = 0.12 and p = 3) values in our experiment as stated in Table 2. Moreover, cutting and averaging keys are calculated based on each plain image.

4.1 Key sensitivity

A secure encryption algorithm should be sensitive to all its keys. In order to evaluate this matter for our proposed method, we utilize two concepts, which are called, a number of pixel changing rate (NPCR) and unified average changing intensity (UACI). In order to calculate these concepts we use equations 14, 15 respectively:

$$ NPCR=\frac{{\displaystyle {\sum}_{i=1}^M{\displaystyle {\sum}_{j=1}^ND\left(M,N\right)}}}{M\times N}\times 100\% $$
(14)
$$ UACI=\frac{1}{M\times N}\left[{\displaystyle \sum_{i=1}^M{\displaystyle \sum_{j=1}^N\frac{\left|{E}_1\left(M,N\right)\right.-{E}_2\left(M,N\right)}{255}}}\right]\times 100\% $$
(15)

Parameters M, N denotes the size of encrypted image E 1 or E 2 . The pixel values in position (m, n) are shown with E 1 (m, n) and E 2 (m, n). The amounts of D (m, n) are determined by the values E 1 (m, n) and E 2 (m, n), such that if E 1 (m, n) = E 2 (m, n) then D (m, n) = 0, otherwise it’s equal to 1. We do this test for some standard images and the result for them displayed in Table 5. In order to do this test, we should slightly change the values of key, which is equal to 10−14 for initial state conditions and for integers K this tiny change equal to 1 [8]. That’s clear based on the above table, if we do very trivial change in each key, the result of encryption changed and this can be deduced based on NPCR and UACI values. Therefor this shows sensitivity to all keys of the proposed method. Moreover, in this part we show the dependency of permutation algorithm on the CK R, G, B values, as you can see on the below table, if we change a bit CK R, G, B values, the result of permutation phase will be changed and its effect can be observed from NPCR and UACI (Table 6).

Table 5 Quantified Key Sensitivity: NPCR and UACI test
Full size table
Table 6 Permutation algorithm sensitivity based on CK R, G, B , just one value (±1) increase/decrease to CK R, G, B
Full size table

4.2 Key space

Calculating key space has a vital role in determining the security of the proposed method. Indeed, if the key space is large, the method will be resistant against brute-force attack. In the proposed method, 11 hidden parameters are considered as keys. In software implementation, this parameters utilizes in double format 52 bits [5]. In Table 7, we do a compression between our method and some other methods.

Table 7 Quantified key space size
Full size table

4.3 Plain text sensitivity and differential attack analysis

The proposed method in order to be resistant against differential attack should be intensely dependent to plain image, in other words, it means a very vital change in plain image cause big changes in the ciphered image [22]. Two equations (14), (15) are used for this analysis. The results of this analysis have been shown in Table 8.

Table 8 NPCR, UACI of test images
Full size table

As you see in Table 8, the average of NPCR is more than 99.67 and the average of UACI is greater than 33.45. We provide a comparison between some available and our proposed methods for NPCR and UACI values of Lena image which shown in Table 9. As obvious based on Chart 1, our proposed method has better values alongside all of availabale methods. Another test which is shown plain-text sensitivity shown in Fig. 11.

Table 9 Comparison of NPCR R, G, B and UACI R, G, B on Lena image
Full size table
Fig. 11
figure 11

Plain-text sensitivity: (a), (b) Couple plain and with one pixel different image, (d), (e) corresponding encrypted image of (a), (b). (c), (f) differential of corresponding plain and encrypted images

Full size image
Fig. 12
figure 12

Image histogram: (a) Lena image, (b) Lena ciphered, (c), (d), (e): Histogram of the plain image for red, green and blue component, (f), (g), (h): Histogram of ciphered image for red, green and blue component

Full size image

Figure 11a is a plain image of couple and Fig. 11b is its corresponding image with one pixel different from the original image (128,128). As it’s obvious in Fig. 11c, when we subtract two images, we have a black plane with one white pixel, which is because of differences on plain image, but in Fig. 11f, when we subtract two encrypted images it does not lead to black plane, which is the result of plain text sensitivity.

4.4 Information entropy analysis

In information theory, entropy is a scale for showing randomness in information. This scale can be calculated by using equation (16):

$$ H(s)=-{\displaystyle \sum_{i=0}^{2^{Q_{-1}}}P\left({s}_i\right){ \log}_2P\left({s}_i\right)} $$
(16)

In above equation, P (s i ) is likelihood frequency of symbol s i° \( \in \) s, Q is the number of bits which used for display symbol s i and log 2 is base 2 logarithm. The ideal value of entropy is 24. So when the entropy value is less than ideal amount, a degree of predictability may be exist and it will violate security. The Result of this test for Lena image depicted in Table 10.

Table 10 The information entropy of plain/cipher for Lena image
Full size table

4.5 Known-and chosen plaintext analysis

Due to the fact that in proposed method cutting and averaging keys build from plain image, then for each image, the value of these keys will be changed. Hence, we have generated different sequences for each color component distinctly to resist agianst Known and Chosen plaintext attacks.

As it is clear based on chart 2, the average of the information entropy for our proposed scheme is the best alongside other proposed methods.

Chart 1
figure 13

Comparision of NPCR and UACI on Lena image

Full size image

4.6 Image histogram

The encrypted image resistant against statistical attack when the color histogram of image distributed uniformly. The image histogram of Lena plain image and its ciphered are depicted in Fig. 12.

Chart 2
figure 14

Comparision of the information entropy on lena image

Full size image

4.7 Correlations of two adjacent pixels

Each pixel in the image is intensely correlated with its adjacent pixels either in horizontal, vertical or diagonal direction. Hence, the proposed method should remove this correlation between adjacent pixels in order to be resistant against statistical attack. In an ideal condition, there should be no correlation between adjacent pixels, and its value (correlation coefficient) should be almost 0. In order to calculate CC (correlation coefficient) we use the following equations:

$$ {r}_{xy}=\operatorname{cov}\left(x,y\right)/\sqrt{D(x)D(y)} $$
(17)
$$ E(x)=\frac{1}{N}{\displaystyle \sum_{i=1}^N{x}_i} $$
(18)
$$ D(x)=\frac{1}{N}{\displaystyle {\sum}_{i=1}^N{\left({x}_i-E(x)\right)}^2} $$
(19)
$$ \operatorname{cov}\left(x,y\right)=\frac{1}{N}{\displaystyle \sum_{i=1}\left({x}_i-E(x)\right)\left({y}_i-E(y)\right)} $$
(20)

Where x and y are the gray value of two adjacent pixels in the image, cov (x, y) is covariance, D (x) is variance and E (x) is mean. The result of this test for Lena image is shown in Table 11. As it is obvious in chart 3, the calculated correlation coeffeicient values for proposed method are −0.0030859, 0.0025108 and −0.0000938 for horizontal, vertical and diagonal orientation, respectively.

Table 11 Average correlation of two adjacent pixels in horizontal, vertical, diagonal of Lena
Full size table
Chart 3
figure 15

Comparison of correlation coefficient for Lena image

Full size image

5 Conclusion

To conclude, we proposed a new scheme for image encryption based on two new chaotic maps with high Lyapunov exponents and the new introduced permutation scheme. The advantages of the new permutation scheme is low computational overhead, because its procedure is so simple, and achieve top transmogification in fewer steps versus available permutation algorithms. Furthermore, our permutation algorithm has a convincing speed that is 18.6 ms, although its speed is a little higher than Arnold Cat map, but as it’s obvious in Fig. 10, our proposed algorithm disturbs pixels more effectively than Arnold cat map. We use two strong chaotic mappings alongside coupled map for the initial seed production and pixel diffusion. The proposed permutation algorithm used to permute pixels. We use cutting and averaging key to make our approach resistant against known and chosen plain text attack, because they are built from plain images and these are dependant to each other. As it’s obvious from experimental results and security analysis, our method has a good performance and good resistant against statistical and differential attack.