1 Introduction

In recent years, and with the fast progress of mathematics, computer science, and technological development of digital cameras, almost of the images are chromatic. Indeed, to transmit or stock more information, the digital color images have more potential than a gray level or binary image. Moreover, the values associated of three colors such as green, blue, and red for each level of the pixel or and as well its hue, brightness, and saturation, can be successful when used in many images processing tasks such as reconstruction, object classification, recognition, registration, and segmentation.

The traditional approach to treatment with digital color images has each level separate while processing, employing a gray level method, and to combining the individual output results. As a consequently, this method misses the inherent correlation between the entities of three colors level. The main problem is therefore to handle three values of each pixel level in entirety.

To solve this problem, recently, algebra quaternion color image analysis to represent digital color images by encoding three levels into the imaginary parts by B. J. Chen et al. [4]. The performance of this quaternion algebra is widely seen when a digital color image is treated as a vector space. Firstly, the quaternion algebra is exploited in digital color image processing for the continuous moments by Chen et al. [3], as well as, [5] using the color image representations by the quaternion type moment functions. Moreover, and to ensure the rotation invariance in the problems of classification; researchers introduced continuous radial moments. Indeed, Xiao [25] came up with the radial moments of Legendre, and extended them in 3D case by El Mallahi et al. [16]. The quaternion pseudo-Zernike moments their RST invariants are defined by Chen et al. [6]. They used these continuous moments in color image recognition. The quaternion radial Fourier moments for digital color image processing are defined by Xiang-Yang et al. [23]. The quaternion polar complex moments of TRS invariants for digital color image representation defined by Wang et al. [22]. Unfortunately, their methods for computing quaternion continuous moments are limited by the discretization error, the high computational cost and the propagation of a numerical error in the computation of continuous polynomials values [7, 8].

These methods result problems of redundancy, and discretization due to finding out errors caused by numerical estimation of integrals in the computation of continuous moments. Indeed, the computation of orthogonal continuous moments requires appropriate transformations of the coordinates of image representation in the interval of definition of the continuous polynomials along with, the calculation of the integral using the finite summations. But, this transformation causes an error of discretization. So as to solve that issue for the gray level images, scientists suggested some methods based on the discrete moments using a discrete polynomials such as the ones of Krawtchouk [2, 9, 11,12,13, 26] Tchebitchef’s [14,15,16, 24], Meixner’s [14], Charlier’s [1, 15], Hahn’s [10, 19,20,21], dual Hahn’s [17, 20], and Racah’s [18] for image processing. The calculation of discrete moments eliminates the need for numerical approximation and satisfies exactly the orthogonality property in discrete space coordinates of the image.

For conserving the color image, no work has been suggested to solve the problem. In this work, and in order to solve this problem of the color image, we opt for an exact method to eliminate the discretization errors and preserve the invariant to the rotation. This method is based on discrete radial moments and classification using multilayer perceptron [1]. We them, we suggest two contributions.

We first introduce a new method for computing an exact, stable and fast computation of higher order QDRKMs in circular coordinates. In this contribution, the use of a discrete form of the Radial Tchebichef polynomials has removed the discretization error granting a height stabilization of the aforementioned method.

Second, we put a new method for extracting translation, scaling and rotation invariants of QDRKMs. The experimental results show highly accurate color image reconstruction of the proposed approach.

These new discrete moments are represented over a disk by using discrete orthogonal radial Krawtchouk moments. The use of discrete moments eliminates the discretization errors produced when continuous moments are used. Furthermore, the method is suggested for highly exact calculation of QDRKMs in polar coordinates where the kernel is thoroughly calculated by over circular color pixels. The translation, scaling, and rotation (TSR) invariances for QDRKMs are demonstrated. Theoretical analysis and numerical experiments investigation were shown in terms of the description performance of TSR invariances, classification, robustness to different noises, and computational times CPU of the QDRKMs compared with continuous quaternion Legendre–Fourier moments using COIL 100 data base.

This work is organized as follows: Section 2 introduces Quaternion Radial Krawtchouk moments (QRKMs). In Sec. 3, the computations of the Quaternion Radial Krawtchouk Moments are calculated. In Sec. 4, a color image reconstruction uses QRKMs. Section 5 takes into account Quaternion Radial Krawtchouk Moments Invariants (QRKMIs) of a test color image for different orders of reconstruction. Section 6 describes the training multilayer perceptron. Some experimental results are presented in Sec. 7, where an evaluation of accurate and computation through some color images have been used. Finally, the conclusions of this research are seen in Sec. 8.

2 Computation of the quaternion radial Krawtchouk moments

2.1 Recurrence relation of Krawtchouk polynomials

The Hyper geometric Krawtchouk polynomial is defined as.

$$ {k}_n\left(r,p|N\right){=}_2{F}_1\left(\begin{array}{c}-n,-r\\ {}-N\end{array}|\frac{1}{p}\right);n=0,1,2\dots N-1;r=N\mid 2;N>0;p\in \left(0,1\right) $$
(1)

Where the orthogonal property of normalized orthogonal polynomial can be rewritten as.

$$ \sum \limits_{r=0}^{v-1}{\overline{k}}_n\left(r,p|N\right){\overline{k}}_m\left(r,p|N\right)=\sum \limits_{k=0}^{\infty}\frac{{\left(-n\right)}_k{\left(-x\right)}_k{\left(\frac{1}{p}\right)}^k}{{\left(1-N\right)}_{k^{k!}}}={\delta}_{nm};\kern1.25em {(a)}_k=a\left(a+1\right)\left(a+2\right)\dots .\left(a+k-1\right) $$
(2)

with (a)k is the Pochhammer symbol and δnm denote the Dirac function; therefore, the three term recursive relation for the weighted Krawtchouk polynomials is given by.

$$ {\overline{k}}_{n+1}\left(r,p|N\right)=\frac{A\times \left(p\times N+2 pn+n-r\right)}{p\times \left(N-n\right)}{\overline{k}}_n\left(r,p|N\right)-\frac{B\times n\left(1-p\right)}{p\times \left(N-n\right)}\times {\overline{k}}_{n-1}\left(r,p|N\right); $$
(3)
$$ for\ n=0,1,2,\dots, N-1 $$

Where.

$$ A=\sqrt{\frac{p\left(N-n\right)}{\left(n+1\right)\left(1-p\right)},\kern0.5em }\kern1.25em B=\sqrt{\frac{p^2\left(N-n\right)\left(N+1-n\right)}{{\left(1-p\right)}^2{\left(n+1\right)}_n}} $$

with n ≥ 2 and the first orders of discrete weighted Krawtchouk polynomials are defined as.

$$ {\displaystyle \begin{array}{c}{\overline{k}}_0\left(r,p|N\right)=\sqrt{w\left(0;p,N\right),}\kern0.75em {\overline{k}}_1\left(r,p|N\right)=\left(1-\frac{r}{pN}\right)\sqrt{w\left(0;p,N\right)}\\ {}w\left(r+1;p,N\right)=\left(\frac{N-r}{r+1}\right)\frac{p}{1-p}w\left(r;p,N\right),w\left(0;p,N\right)={\left(1-p\right)}^N={e}^{N1n\left(1-p\right)}\end{array}} $$
(4)

where

2.2 Proposed computations of quaternion radial Krawtchouk moments

The radial Krawtchouk Moments can be rewritten as.

$$ {\displaystyle \begin{array}{c}{K}_{nm}=\frac{1}{6N}\sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}{\overline{k}}_n\left(r,p|N\right)f\left(r,\theta \right){e}^{\mu m\theta}\\ {}\kern1.08em =\frac{1}{6N}\sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}{\overline{k}}_n\left(r,p|N\right)\left({f}_R\left(r,\theta \right)i+{f}_G\Big(r,\theta \left)j+{f}_B\right(r,\theta \Big)k\right){e}^{\mu m\theta}\kern9.719993em \\ {}\kern1.08em =\frac{1}{6N}\left[i\sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}{f}_R\left(r,\theta \right){\overline{k}}_n\Big(r,p|N\Big){e}^{\mu m\theta}\right.+j\sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}{f}_G\left(r,\theta \right){\overline{k}}_n\left(r,p|N\right){e}^{\mu m\theta}\;\left.+k\sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}{f}_B\left(r,\theta \right){\overline{k}}_n\left(r,p|N\right){e}^{\mu m\theta}\right]\kern0.24em \end{array}} $$
(5)

Where

$$ \sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}f\left(r,\theta \right){\overline{k}}_n\left(r,p|N\right){e}^{\mu m\theta}=\sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}f\left(r,\theta \right){\overline{k}}_n\left(r,p|N\right)\left(\cos \left( m\theta \right)+\frac{i+j+k}{\sqrt{3}}\sin \left( m\theta \right)\right) $$

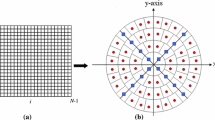
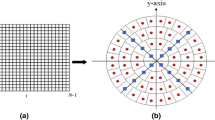
Taking into consideration the proposed value for the quaternion μ, The QRKMs of an RGB image in polar pixels are given by

$$ {\displaystyle \begin{array}{c}{\hat{K}}_{nm}=\frac{1}{6N}\left[i\left\{\operatorname{Re}\left[{K}_{nm}\left({f}_R\right)\right]+\frac{i+j+k}{\sqrt{3}}\operatorname{Im}\left[{K}_{nm}\left({f}_R\right)\right]\right\}+j\left\{\operatorname{Re}\left[{K}_{nm}\left({f}_G\right)\right]+\frac{i+j+k}{\sqrt{3}}\operatorname{Im}\left[{K}_{nm}\left({f}_G\right)\right]\right\}\right.\;\\ {}\kern0.72em +k\left.\left\{\operatorname{Re}\left[{K}_{nm}\left({f}_B\right)\right]+\frac{i+j+k}{\sqrt{3}}\operatorname{Im}\left[{K}_{nm}\left({f}_B\right)\right]\right\}\right]\end{array}} $$
(6)

Finally,

$$ {\hat{K}}_{nm}={A}_{nm}+i\ {B}_{nm}+{C}_{nm}+k{D}_{nm} $$
(7)

Where,

$$ {\displaystyle \begin{array}{c}{A}_{nm}=-\frac{1}{\sqrt{3}}\left\{\operatorname{Im}\left[{K}_{nm}\left({f}_R\right)\right]+\operatorname{Im}\left[{K}_{nm}\left({f}_G\right)\right]+\operatorname{Im}\left[{K}_{nm}\left({f}_B\right)\right]\right\}\\ {}{B}_{nm}=\operatorname{Re}\left[{K}_{nm}\left({f}_R\right)\right]+\frac{1}{\sqrt{3}}\left\{\operatorname{Im}\left[{K}_{nm}\left({f}_G\right)\right]-\operatorname{Im}\left[{K}_{nm}\left({f}_B\right)\right]\right\}\\ {}{C}_{nm}=\operatorname{Re}\left[{K}_{nm}\left({f}_G\right)\right]+\frac{1}{\sqrt{3}}\left\{\operatorname{Im}\left[{K}_{nm}\left({f}_B\right)\right]-\operatorname{Im}\left[{K}_{nm}\left({f}_R\right)\right]\right\}\\ {}{D}_{nm}=\operatorname{Re}\left[{K}_{nm}\left({f}_B\right)\right]+\frac{1}{\sqrt{3}}\left\{\operatorname{Im}\left[{K}_{nm}\left({f}_R\right)\right]-\operatorname{Im}\left[{K}_{nm}\left({f}_G\right)\right]\right\}\end{array}} $$
(8)

3 Color image reconstruction using QRKMs

The color image f(r,θ) can be reconstructed using the inverse transformation of QRKMs is given by

$$ \hat{f}\left(r,\theta \right)={\hat{f}}_A\left(r,\theta \right)+{\hat{f}}_B\left(r,\theta \right)i+{\hat{f}}_C\left(r,\theta \right)j+{\hat{f}}_D\left(r,\theta \right)k $$
(9)

With

$$ {\displaystyle \begin{array}{c}{\hat{f}}_A\left(r,\theta \right)=\operatorname{Re}\left[\hat{A}\left(r,\theta \right)\right]-\frac{1}{\sqrt{3}}\left\{\mathit{\operatorname{Im}}\left[\hat{B}\left(r,\theta \right)\right]\right.+\operatorname{Im}\left[\hat{C}\left(r,\theta \right)\right]+\left.\mathit{\operatorname{Im}}\left[\hat{D}\left(r,\theta \right)\right]\right\}\\ {}{\hat{f}}_B\left(r,\theta \right)=\operatorname{Re}\left[\hat{B}\left(r,\theta \right)\right]+\frac{1}{\sqrt{3}}\left\{\mathit{\operatorname{Im}}\left[\hat{A}\left(r,\theta \right)\right]\right.+\operatorname{Im}\left[\hat{C}\left(r,\theta \right)\right]-\left.\mathit{\operatorname{Im}}\left[\hat{D}\left(r,\theta \right)\right]\right\}\\ {}{\hat{f}}_C\left(r,\theta \right)=\operatorname{Re}\left[\hat{C}\left(r,\theta \right)\right]+\frac{1}{\sqrt{3}}\left\{\mathit{\operatorname{Im}}\left[\hat{A}\left(r,\theta \right)\right]\right.-\operatorname{Im}\left[\hat{B}\left(r,\theta \right)\right]+\left.\mathit{\operatorname{Im}}\left[\hat{D}\left(r,\theta \right)\right]\right\}\\ {}{\hat{f}}_D\left(r,\theta \right)=\operatorname{Re}\left[\hat{D}\left(r,\theta \right)\right]+\frac{1}{\sqrt{3}}\left\{\mathit{\operatorname{Im}}\left[\hat{A}\left(r,\theta \right)\right]\right.+\operatorname{Im}\left[\hat{B}\left(r,\theta \right)\right]-\left.\mathit{\operatorname{Im}}\left[\hat{C}\left(r,\theta \right)\right]\right\}\end{array}} $$
(10)

With

$$ {\displaystyle \begin{array}{c}\hat{A}\left(r,\theta \right)=\sum \limits_{n=0}^{N/2}\sum \limits_m^{6N}{A}_{nm}\;{\overline{k}}_n\left(r,p|N\right)\;{e}^{\mu m\theta},\kern0.36em \hat{B}\left(r,\theta \right)=\sum \limits_{n=0}^{N/2}\sum \limits_m^{6N}{B}_{nm}\;{\overline{k}}_n\left(r,p|N\right)\;{e}^{\mu m\theta}\\ {}\hat{C}\left(r,\theta \right)=\sum \limits_{n=0}^{N/2}\sum \limits_m^{6N}{C}_{nm}\;{\overline{k}}_n\left(r,p|N\right)\;{e}^{\mu m\theta},\hat{D}\left(r,\theta \right)=\sum \limits_{n=0}^{N/2}\sum \limits_m^{6N}{D}_{nm}\;{\overline{k}}_n\left(r,p|N\right){e}^{\mu m\theta}\end{array}} $$
(11)

Note that \( {\hat{f}}_B\left(r,\theta \right) \), \( {\hat{f}}_C\left(r,\theta \right) \) and \( {\hat{f}}_D\left(r,\theta \right) \) represent the red, green, and blue color of the reconstructed image, respectively, and L is the maximum order of QRKMIs used in the reconstruction. Typically, the reconstruction formula has been used to recover the image information up to a certain level of approximation.

The difference between the original image and the reconstructed image is measured using the mean squared error (MSE).Which is defined as follows:

$$ MSE=\sum \limits_{r=0}^{N/2}\sum \limits_{\theta =0}^{6N}\left|f\left(r,\theta \right)-\hat{f}\Big(r,\theta \Big)\right| $$
(12)

Where f(r, θ) represents the original color image vector and \( \hat{f}\left(r,\theta \right) \) the reconstructed color image.

4 Quaternion radial Krawtchouk moments invariants

In this section, we show a rotation, scaling and translation invariance of Quaternion Radial Krawtchouk Moments invariants (QRKMIs) from [2].

For this, we will them show the invariant moment to be linear combination as well as radial complex moment.

The translation invariance of QRKMs can be easily achieved by transforming the 2D color image to the geometric centre before the calculation of QRKMs. In spite of the scaling and rotation invariance which can be achieved then replacing complex moments, with the 2D complex moment invariants due to Quaternion Radial Krawtchouk moments invariants can be expressed as linear combination of 2D complex moments. In this subsection, we introduce a new and direct method to derive the scaling and rotation invariance of quaternion radial Krawtchouk moments invariants.

Let frs(r, θ) be the scaled, and rotated version of image function f(r, θ) with the scale factor λ and rotation angle θ0 we have

$$ {f}^{sr}\left(r,\theta \right)=f\left(\frac{r}{\lambda },\theta +{\theta}_0\right) $$

According to Eq. (5), the QRKMs of scaled and rotated color image is:

$$ \kern2em {K}_{nm}^{\prime }=\frac{1}{6N}\sum \limits_{r^{\prime }=0}^{\frac{N}{2}}\sum \limits_{\theta^{\prime }=0}^{6N}f\left(\frac{r}{\uplambda},\theta +{\theta}_0\right){\overline{k}}_n\left(r,p|N\right){e}^{m\upmu \theta } $$
(13)

By letting \( {r}^{\prime }=\frac{r}{\lambda }{\theta}^{\prime }=\theta +{\theta}_0 \).

Eq. (13) can be written as

$$ {K}_{nm}^{\prime }=\frac{1}{6N}\sum \limits_{r^{\prime }=0}^{N/2}\sum \limits_{\theta^{\prime }=0}^{6N}f\left({r}^{\prime },{\theta}^{\prime}\right){\overline{k}}_n\left(\lambda r^{\prime },p|N\right){e}^{m\upmu \left({\theta}^{\prime }-{\theta}_0\right)} $$
(14)

Where the polynomial of Krawtchouk is defined [38]

$$ {\overline{k}}_n\left(\lambda r,p|N\right)=\sum \limits_{i=0}^nC\left(n,i\right){\lambda}^i{r}^i $$

and

$$ C\left(n,i\right)=\sum \limits_{k=0}^{n-i}{\overline{B}}_{n,n-k}s\left(n-k,i\right) $$
$$ {\overline{B}}_{n,n-k}=w\left(r;p,N\right){B}_{n,n-k} $$
$$ {B}_{n,k}=\frac{-{1}^kn!\left(N-k\right)!}{\left(N-k\right)!N!k!{p}^k} $$

and s(n-k,i) is the stirling numbers of the first kind, with s(k, 0) = s (0, i = 0, k ≥ 1, i ≥ 1) and s(0,0)=1.

Therefore, the relationship between the original and rotation scaled QRKMs can be formed as

$$ {\varphi}_{nm}=\sum \limits_{k=0}^n\sum \limits_{l=0}^m{\eta}_{n,k}{\eta}_{m,l}{K}_{kl}^{\prime }={\lambda}^n{e}^{m\upmu {\theta}_0}\sum \limits_{k=0}^n\sum \limits_{l=0}^m{\eta}_{n,k}{\eta}_{m,l}{K}_{kl} $$

where

$$ {\eta}_{n,k}=1\;\left(n=k\right),{\eta}_{n,k}=\sum \limits_{r=0}^{n-k-1}\frac{-C\left(n-r,k\right){\eta}_{n,n-r}}{C\left(k,k\right)} $$

To eliminate the scale factor, we construct the normalized rotation and scale invariants of QRKMIs

$$ {\psi}_{nm}=\frac{\varphi_{nm}{\varphi}_{00}^{\gamma +1}}{\varphi_{n+\gamma, 0}{\varphi}_{0,m+\gamma }},n,m=0,1,2,\dots, \gamma =1,2,3,\dots $$
(15)

Then, 훹nm is scaling and rotation invariance of QRKMs for any orders n, m.

5 Pattern classification of multi-layer perceptron

5.1 Descriptor vector of color image

These QRKMIs can be used to form the descriptor vector of each color image. Specially that the latter composed of QRKMs up to order S, where S is experimentally selected.

The characteristic vectors V2D is represented as

$$ {V}_{2D\_ Color\_\operatorname{Im} age}=\left[{\psi}_{nm}|n+m\in \left[0,1,\dots S\right]\right] $$
(16)

To perform the recognition of color image to its appropriate classes. We use multi-layer perceptron from Vquery and Vtest where V represent the characteristic vectors V2D_Color_Image.

where the T-dimensional feature Vquery is represented as

$$ {V}_{query}=\left[{V}_{query}^1,{V}_{query}^2,\dots, {V}_{query}^T\right] $$
(17)

and the T-dimensional training vector of class K is shown as

$$ {V}_{test}^K=\left[{V}_{test}^1,{V}_{test}^2,\dots, {V}_{test}^T\right] $$
(18)

5.2 Classification of 2D color object using a multi-layer perceptron

The Learning of Multilayer Perceptron MLP is the process to adapt the connection weights. in order to obtain a minimal difference between the network output and the desired output. For this reason in the literature some algorithms are used as an Ant colony, but the most used called Back-propagation which is based on descent gradient techniques. Assuming that we used an input Layer with n0 neurons V2D _ Color _ Image = (r0,r1, …, rn) and a sigmoid activation function f(x) where

$$ f(r)=\frac{1}{1+{e}^{-r}} $$
(19)

To get the network output, we need to compute the output of each unit in each layer. Now, consider a set of the hidden layers (h1, h2, …, hN), assuming that Ni is the neurons number in each hidden layer hi .

For the output of first hidden layer

$$ {h}_1^i=f\left(\sum \limits_{k=1}^{n_0}{w}_{kj}^0{x}_k\right);j=1,2,\dots, n $$
(20)

Let’s admit a set of hidden layers (h1, ℎ 2, …, hN), assuming that ni is the neurons number in each hidden layer hi. For the outputs \( {h}_i^j \) of neurons in the hidden layers are calculated as follows:

$$ {h}_i^j=f\left(\sum \limits_{k=0}^{n_{i-1}}{w}_{kj}^{i-1}{h}_{i-1}^k\right);i=2,\dots, N;j=1,\dots, {n}_i $$
(21)

Where \( {w}_{kj}^i \) is the weight between the neuron k in the hidden layer i and the neuron j in the hidden layer i+ 1, ni is the number of the neurons in the ith hidden layer, The output of the ith layers can be formulated by.

$$ {h}_i=t\left({h}_i^1,{h}_i^2,\dots \dots .{h}_i^{n_i}\right) $$
(22)

The network outputs are computed by

$$ {y}_i=f\left(\sum \limits_{k=1}^{n_N}{w}_{kj}^N{h}_n^k\right);Y=\left(y1,..\dots, yi,..\dots, {y}_{N+1}\right)=F\left(W,X\right) $$
(23)

Where \( {w}_{kj}^N \) is the weight between the neuron k of the Nth hidden layer and the neuron j of the output layer, n is the number of the neurons in the Nth hidden layer, Y is the vector of the output layer, F is the transfer function and W is the weights matrix, it’s defined as follows

(24)

Where X is the input of neural network and f is the activation function and Wi is the matrix of weights between the ith hidden layer and the (i + 1)ℎ hidden layer for i= 1, …, N− 1, W0 is the matrix of weights between the input layer and the first hidden layer, and WN is the matrix of weights between the N th hidden layer and the output layer.

The Fig. 1 represent the Quaternion Discrete Radial Krawtchouk convolutional neural networks architecture.

Fig. 1
figure 1

Quaternion Discrete Radial Krawtchouk convolutional neural networks architecture

Full size image

6 Numerical experiments

In this section, we show the reconstruction results obtained using some color test images. These RGB test images are shown in Fig. 2 using Eq. (12), we have reconstructed the three cases of test images.

Fig. 2:
figure 2

Reconstructed color image using the proposed method compared with QLFMs. Color test image from (a) diabetic retina and (b) normal retina, dataset benchmarking diabetic (http://www.it.lut.fi/project/imageret/diaretdb1/).

Full size image

6.1 Reconstruction results using QRKMs for color images

In this experiment result, the color image reconstruction capability of QRKMs is shown for Lena in Fig. 2 and diabetic retina in Fig.3. Several comparisons of means square error for different parameters of QRKMs in Figs.4 and 5 and the comparison with QLFMs is also given in this part. We use the statistical computation of normalization image reconstruction error to measure the performance of the color image reconstruction, we deduce that the QRKMs are more convenient instead of QLFMs .

Fig. 3:
figure 3

Reconstructed color image of retina of size 128 × 128 using the proposed method.

Full size image
Fig. 4
figure 4

MSE for Objects (a, b) with p = 0.3,0.5,0.8

Full size image
Fig. 5
figure 5

MSE for objects (a, b) with different values of p.

Full size image

The means square Error (MSE) (Fig. 5) for color image has been usually used to describe how well a color image can be retrieved by a small and big set of QRKMs.

6.2 Invariability for QRKMs

To validate the invariability for QRKMs of the QRKMIs, we use some objects from Coil-100 Database Fig. 6.

Fig. 6.
figure 6

color image Database Coil-100 (http://www.cs.columbia.edu/CAVE/software/softlib/coil-100.php).

Full size image

The selected order of the invariants (QRKMIs00; QRKMIs12; QRKMIs22; QRKMIs23, QRKMIs32) are computed for each image. The results of simulation the scaling invariances of color image Fig.7 are shown in Table 1, the translation invariances of color image Fig.8 are shown in Table 2, the rotation invariances of color image Fig. 9 are shown in Table 3. Finally, the ratio σ/μ can use to measure the capability of the proposed QRKMIs under different image transformation, where σ represents the standard deviation of QRKMs the different factors of each rotation, and μ is the equivalent mean value. The Table 1, 2 and 3 show that the ratio σ/μ is very low and consequently the QRKMIs are very stable under different types of color image Figs. 7, 8 and 9. Hence, the property of invariability of QRKMIs will be used to pattern classification.

Fig 7
figure 7

Scaled color images of the obj6 (Coil - 100)

Full size image
Table 1 Scaling invariances of the scaled images using the proposed method
Full size table
Fig. 8
figure 8

Translated color object from Coil – 100 database.

Full size image
Table 2 Translation invariances of the translated images using the proposed method
Full size table
Fig. 9
figure 9

Rotated color object from Coil – 100 database.

Full size image
Table 3 Rotation invariances of the rotated images using the proposed method
Full size table
Fig. 10:
figure 10

Computation of Salt and Pepper Noise & Gaussian Noise for color image.

Full size image

7 Classification the color image using QRKMs

In this subsection, we will discuss the classification the color image using QRKMs.

To validate the proposed approach for classification, we have taken the color image from the benchmarking diabetic dataset [32]. The total number of color images is 2 distributed as 89 images for each object. All color images of this database have the size 128 × 128 (after adaptation). The test set also degraded by Gaussian and salt and pepper noise with noise densities 1%, 2%, 3%, and 4%. Figure 10 show the densities of Salt and Pepper Noise & Gaussian Noise for color image. The feature vector based on QRKMIs is use to classify these images and its recognition accuracy is compared with that of quaternion Legendre–Fourier momentsThe results of the classification using all features are presented in Table 4.

Table 4 Classification results of Princeton Shape Benchmark (PSB) using Multi-Layer Perceptron
Full size table

8 Conclusion

In this paper, we suggested a new method to calculate the Quaternion Radial Krawtchouk moments, we have also proposed a classification of multi-layer perceptron of Quaternion Radial Krawtchouk moments. The performances of the proposed Quaternion Radial Krawtchouk moments invariants have been tested under different color images. The results obtained show that the representation capability is compared with different color of the same image. This proposed approach has been significantly improved by using the multi-layer perceptron for classification of Quaternion Radial Krawtchouk moments and can highly be useful in the field of color image analysis, and the test of color images are clearly classified from a set of images that are available in benchmarking diabetic dataset for color image.