New Set of Quaternion Moments for Color Images Representation and Recognition

Abstract

In this paper, a new set of quaternion radial-substituted Chebyshev moments (QRSCMs) is proposed for color image representation and recognition. These new moments are circular moments defined over a unit disk by using a new set of orthogonal basis functions called radial-substituted Chebyshev functions. A new hybrid method is proposed for highly accurate computation of QRSCMs in polar coordinates. In this method, the angular kernel is exactly computed by analytical integration of Fourier function over circular pixels. The radial kernel is computed using a recurrence relation which completely eliminates the coefficient matrix associated with the radial-substituted Chebyshev functions. Rotation, scaling, and translation (RST) invariances for QRSCMs are proved. Numerical experiments were conducted where the results of these experiments show better performance of QRSCMs over existing quaternion moments in terms of image reconstruction capabilities, RST invariances, robust to different noises, and CPU elapsed times.

1 Introduction

Moment functions play an essential role in representing digital images. Orthogonal moment functions are preferable in representing digital images due to their minimum information redundancy. Orthogonal moment functions are defined either in polar or Cartesian coordinate systems [1]. Circular orthogonal moments are defined over a unit circle and rotationally invariants by nature. This characteristic is a very attractive in pattern recognition applications. Orthogonal Zernike moments (ZMs) are the first set of circular orthogonal moment defined by Teague [2]. During the last four decades, many circular orthogonal moments were defined and widely used. Bailey and Srinath [3] defined circular pseudo-Zernike moments (PZMs) for image analysis and representation. Sheng and Shen [4] defined the circular orthogonal Fourier–Mellin moments (OFMMs). Ping et al. [5] defined the circular Chebyshev–Fourier moments (CFMs) for image description. Ren et al. [6] defined radial-harmonic-Fourier Moments (RHFMs) for invariant image description. Ping et al. [7] defined the generic circular orthogonal Jacobi–Fourier moments for invariant image description. Yap et al. [8] defined the circular orthogonal polar harmonic transform moments (PHTs) for invariant image representation. Xiao et al. [9] defined the circular orthogonal radial-shifted Legendre moments (RSLMs) for image analysis and invariant image recognition. Recently, Guo et al. [10] defined a new set of circular orthogonal moments based on Chebyshev rational functions.

The interest in color images analysis steadily increased. Color image representation and processing using quaternion moments attract many research groups around the world during the last few years. Chen et al. [11] derived the quaternion Zernike moments (QZMs) from their corresponding ZMs for the three separate RGB channels. Also, they derived the rotation, scaling, and translation (RST) moment invariants of the QZMS. In a similar fashion, Chen et al. [12] derived the quaternion pseudo-Zernike moments (QPZMs) and their RST invariants and then applied these quaternion moments in color face recognition. Guo and Zhu [13] derived the quaternion Fourier–Mellin moments (QFMMs) and their invariants to RST transformations. Xiang-yang et al. [14] derived the quaternion radial-harmonic-Fourier moments (QRHFMs) for color image representation. Wang et al. [15] derived the quaternion polar harmonic transforms (QPHTs) and their RST invariants for color image representation and recognition. Yang et al. [16] derived the quaternion exponent moments (QEMs) and their invariant to similarity transformations for invariant color image representation.

Conventional computation of Chebyshev rational moments as discussed in [10] encountered by three major problems:

• First is the low accuracy due to the approximated evaluation of both angular and radial functions.

• Second is the extremely low speed computational process due to the evaluation of the coefficient matrix for each order. This process is very time-consuming process due to the hug number of factorial terms.

• Third is numerical instabilities due to accumulation of errors and the highly dynamic change in the values of the coefficient matrix.

Recursive computing of the radial kernel, by using recurrence formula overcome these three problems. Highly accurate computation is achieved through accurate computation of the initial terms. Fast computation and numerical stability are achieved by eliminating the coefficient matrix entirely from the computational process.

In this paper, a new set of quaternion radial-substituted Chebyshev moments (QRSCMs) is proposed for color image representation. The QRSCMs are computed in polar coordinates using new accurate method. In this method, the radial kernel is computed recursively where fast computation is achieved through avoiding the hug computational demands encountered in the direct conventional computational methods.

The rest of the paper is organized as follows. Preliminaries about the Chebyshev rational moments for grayscale images. The definition of QRSCMs for RGB color images is presented in Sect. 2. In Sect. 3, the detailed description of the proposed method is presented. Numerical experiments and the obtained results are presented in Sect. 4. Conclusion is presented in Sect. 5.

2 Quaternion Radial-Substituted Chebyshev Moments

This section is divided into three subsections. In the first one, a brief description of the Chebyshev rational moments (CRMs) [10] for grayscale images is presented. In the second subsection, a new set of basis functions called radial-substituted Chebyshev functions is defined in polar coordinates over a unit circle. The quaternion radial-substituted Chebyshev moments (QRSCMs) for color image representation is presented in the third subsection.

2.1 Chebyshev Rational Moments for Gray-Level Images

Chebyshev rational moments (CRMs) are defined as follows [10]:

$$\begin{aligned} M_{n\, m}=\frac{1}{2\, \pi \, a_{n}}\int \limits _0^{2\pi } \int \limits _0^1 {f\left( r,\theta \right) \, R_{n}\left( r \right) \, W\left( r \right) \exp \left( -\hat{i}\, m\theta \right) r\mathrm{d}r\mathrm{d}\theta \,},\nonumber \\ \end{aligned}$$

(1)

where $\hat{i}=\sqrt{-1};n=0,1,2,\ldots$ and $m=0,\,\pm \, 1, \pm \,2,\ldots \ldots$. are the moment orders. The $f\left( r,\theta \right)$ represents the image function in polar coordinates. The normalization constant is defined as:

$$\begin{aligned} a_{n}=\frac{C_{n}\pi }{2}, \end{aligned}$$

(2)

where

$$\begin{aligned} C_{n}=\left\{ {\begin{array}{ll} 2,&{} \mathrm{for}\, n=0 \\ 1,&{} \mathrm{for}\, n\ge 1 \\ \end{array}} \right. \end{aligned}$$

(3)

The weight function, $W\left( r \right)$, and the Chebyshev rational function, $R_{n}\left( r \right)$, are defined as follows:

$$\begin{aligned}&W\left( r \right) =\frac{1}{\left( 1+r \right) \, \sqrt{r} }\,, \end{aligned}$$

(4)

$$\begin{aligned}&R_{n}\left( r \right) =\sum \limits _{k=0}^n {\alpha _{nk}\, \frac{1}{\left( 1+r \right) ^{k}}}, \end{aligned}$$

(5)

where the coefficient matrix is:

$$\begin{aligned} \alpha _{nk}=\frac{\left( k! \right) ^{2}}{\left( 2k \right) !}\left( {\begin{array}{l} n+k-1 \\ k \\ \end{array}} \right) \, \left( {\begin{array}{l} n \\ k \\ \end{array}} \right) \left( -4 \right) ^{k}. \end{aligned}$$

(6)

The first five terms of the Chebyshev rational function, $R_{n}\left( r \right)$ are:

$$\begin{aligned}&R_{0}\left( r \right) =1,\nonumber \\&R_{1}\left( r \right) =\frac{r-1}{r+1},\nonumber \\&R_{2}\left( r \right) =\frac{r^{2}-6r+1}{\left( r+1 \right) ^{2}},\nonumber \\&R_{3}\left( r \right) =\frac{{r^{3}-15\, r}^{2}+15\, r-1}{\left( r+1 \right) ^{3}},\nonumber \\&R_{4}\left( r \right) =\frac{r^{4}-28\, {r^{3}+70\, r}^{2}-28\, r+1}{\left( r+1 \right) ^{4}}. \end{aligned}$$

(7)

The orthogonality of the Chebyshev rational functions is expressed using the following form:

$$\begin{aligned} \int \limits _0^\infty {R_{n}\left( r \right) \, R_{m}\left( r \right) \, W\left( r \right) \, \mathrm{d}r=\frac{C_{n}\pi }{2}\, \delta _{n\, m}}. \end{aligned}$$

(8)

In order to derive the quaternion version of these moments to represent the RGB color images, we encounter a major problem. Chebyshev rational functions as defined in [10] are orthogonal in the infinite domain. They are not orthogonal over the unit disk.

This can be verified by the following:

Let

$$\begin{aligned} I_{nm}\mathrm {=}\int _\mathrm {0}^\mathrm {1} {R_{n}\left( r \right) R_{m}\left( r \right) W\left( r \right) \mathrm{d}r} \end{aligned}$$

(9)

Then

$$\begin{aligned} I_{\mathrm {01}}\mathrm {=}\int \limits _\mathrm {0}^\mathrm {1} {R_{\mathrm {0}}\left( r \right) R_{\mathrm {1}}\left( r \right) W\left( r \right) \mathrm {=}} \left[ \frac{\mathrm {-2}\sqrt{r} }{r\mathrm {+1}} \right] _{\mathrm {0}}^{\mathrm {1}}, \end{aligned}$$

(10)

which is not zero. Therefore, $R_{nm}\mathrm {\ne 0}$, when $n\,\mathrm {\ne }\,m$. This motivate the authors to define the radial-substituted Chebyshev functions as orthogonal functions over a unit disk.

2.2 Radial-Substituted Chebyshev Rational Moments for Gray-Level Images

Based on the definition of Chebyshev rational functions, we can derive the radial-substituted Chebyshev functions $\bar{R}_{{n}}\left( {r} \right)$ by assuming

$$\begin{aligned} \hat{r}=\frac{r}{1+r}\, ,\, r=\frac{\hat{r}}{1-\hat{r}}\, ,\, \mathrm{d}r=\frac{1}{\left( 1-\hat{r} \right) ^{2}}\mathrm{d}\hat{r}. \end{aligned}$$

(11)

Substituting Eq. (11) into (4) and (5), the radial-substituted Chebyshev functions, $\bar{R}_{{n}}\left( {r} \right)$, and the substituted weight function, $\bar{W}\left( r \right)$, are defined as follows:

$$\begin{aligned} \bar{R}_{n+1}\left( \hat{r} \right) =2\, \left( 2\hat{r}-1 \right) \, \bar{R}_{n}\left( \hat{r} \right) -\bar{R}_{n-1}\left( \hat{r} \right) , \end{aligned}$$

(12)

where

$$\begin{aligned}&\bar{R}_{0}\left( \hat{r} \right) =1,\\&\bar{R}_{1}\left( \hat{r} \right) =2\hat{r}-1. \end{aligned}$$

The radial-substituted Chebyshev functions,${\, \bar{R}}_{{n}}\left( {r} \right)$, are defined by using the explicit form as follows:

$$\begin{aligned} \bar{R}_{n}\left( \hat{r} \right) =\sum \limits _{k=0}^n \frac{\left( k! \right) ^{2}}{\left( 2k \right) !} \, \left( {\begin{array}{l} n+k-1 \\ k \\ \end{array}} \right) \, \left( {\begin{array}{l} n \\ k \\ \end{array}} \right) \, \left( -4 \right) ^{k}\left( 1-\hat{r} \right) ^{k}.\nonumber \\ \end{aligned}$$

(13)

For $n\ge 1.$

The substituted weighted function is defined as follows:

$$\begin{aligned} \bar{W}\left( \hat{r} \right) =\frac{\left( 1-\hat{r} \right) ^{3/2}}{\left( 1-\hat{r} \right) ^{2}\, \sqrt{\hat{r}} } = \left( \hat{r}-\hat{r}^{2} \right) ^{-1/2}=\, \frac{1}{\sqrt{\left( \hat{r}-\hat{r}^{2} \right) } }.\nonumber \\ \end{aligned}$$

(14)

The real-valued substituted functions, $\bar{R}_{n}(\hat{r})$, are orthogonal over the unit disk (in the interval $0<\hat{r}<1\, )$ and satisfy the following orthogonally relation:

$$\begin{aligned} \int \limits _0^1 {\bar{R}_{n}\left( \hat{r} \right) \, \bar{R}_{m}\left( \hat{r} \right) \, \bar{W}\left( \hat{r} \right) \, \mathrm{d}\hat{r}=\frac{C_{n}\pi }{2}\, \delta _{n\, m}}. \end{aligned}$$

(15)

Based on orthogonality of the radial-substituted Chebyshev functions, the image function $f(r,\theta )$ could be reconstructed as follows:

$$\begin{aligned} f\left( r,\theta \right) =\sum \limits _{n=0}^\infty \sum \limits _{m=-\infty }^\infty M_{nm} \bar{R}_{n}(r){{\, e}}^{\hat{i}m\theta }. \end{aligned}$$

(16)

Since the summation to infinity is impossible in computing environment, a finite summation to max be replaced where max refers to a user predefined maximum order of the computed radial-substituted Chebyshev moments (RSCMs). Therefore, Eq. (16) is rewritten as follows:

$$\begin{aligned} f\left( r,\theta \right) \approx \sum \limits _{n=0}^{\mathrm{max}} \sum \limits _{m=-\mathrm{max}}^{\mathrm{max}} M_{nm} \bar{R}_{n}\left( r \right) {e}^{\hat{i}m\theta }. \end{aligned}$$

(17)

2.3 Quaternion Radial-Substituted Chebyshev Moments for Color Images

Hamilton [17] defined the quaternion, q, as a generalization of the complex number where this quaternion has one real and three imaginary components:

$$\begin{aligned} q=a+b{\varvec{i}}+c{\varvec{j}}+\mathrm{d}{\varvec{k}}, \end{aligned}$$

(18)

where a, b, c, and d are real numbers, and ${\varvec{i}}$, ${\varvec{j}}$, and ${\varvec{k}}$ are three imaginary units obeying the following rules:

$$\begin{aligned} \mathbf {i}^{\mathbf {2}}= & {} \mathbf {j}^{\mathbf {2}}=\mathbf {k}^{\mathbf {2}}=\mathbf {ijk}=-1,\nonumber \\ \mathbf {ij}=-\,\mathbf {ji}= & {} \mathbf {k},\mathbf {jk}=-\,\mathbf {kj}=\mathbf {i},\mathbf {ki}=-\,\mathbf {ik}=\mathbf {j}. \end{aligned}$$

(19)

The quaternion q is called a pure quaternion when the component $a\, =\, 0$. The modulus and the conjugate of q are defined as follows:

$$\begin{aligned} q^{*}= & {} a-b{\varvec{i}}-c{\varvec{j}}-\mathrm{d}{\varvec{k}}, \end{aligned}$$

(20)

$$\begin{aligned} \left| q \right|= & {} \sqrt{a^{2}+b^{2}+c^{2}+d^{2}}. \end{aligned}$$

(21)

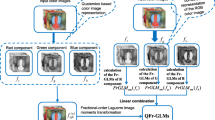
A color image, $f(r,\theta )$, can be represented using a pure quaternion as follows:

$$\begin{aligned} f\left( r,\theta \right) =f_{R}\left( r,\theta \right) \, {\varvec{i}}+f_{G}\left( r,\theta \right) \, {\varvec{j}}+f_{B}\left( r,\theta \right) {\varvec{k}}, \end{aligned}$$

(22)

where $f_{R}\left( r,\theta \right) , f_{G}\left( r,\theta \right)$, and $f_{B}\left( r,\theta \right)$ represent the red, green, and blue channel components, respectively. Based on the definition of the quaternion, the right-side quaternion radial-substituted Chebyshev moments (QRSCMs) are defined as:

$$\begin{aligned} M_{nm}^{R}=\frac{1}{2\, \pi \, a_{n}}\int \limits _0^{2\pi } \int \limits _0^1 {f\left( \hat{r},\theta \right) \, \bar{R}_{n}\left( \hat{r} \right) \, \bar{W}\left( \hat{r} \right) \exp \left( -\mu \, m\theta \right) \hat{r}\mathrm{d}\hat{r}\mathrm{d}\theta }.\nonumber \\ \end{aligned}$$

(23)

The unit pure quaternion ${\mu }$ has the value $\mu {=}\left( {\varvec{i}}+{\varvec{j}}+{\varvec{k}} \right) /\sqrt{3}$. Based on the properties of quaternion algebra, and using Eq. (22) in (23), the right side (QRSCMs) could be represented using the RGB channels as follows:

$$\begin{aligned} M_{nm}^{R}=A_{nm}^{R}+{{\varvec{i}}B}_{nm}^{R}+{\varvec{j}}C_{nm}^{R}+{{\varvec{k}}D}_{nm\, }^{R}\, \end{aligned}$$

(24)

where

$$\begin{aligned} A_{nm}^{R}= & {} -\frac{1}{\sqrt{3} }\left[ \mathrm{imag}\left( M_{nm}\left( f_{R} \right) \right) +\mathrm{imag}\left( M_{nm}\left( f_{G} \right) \right) \right. \nonumber \\&\left. +\,\mathrm{imag}\left( M_{nm}\left( f_{B}\right) \right) \right] \nonumber \\ B_{nm}^R= & {} real\left( M_{nm}\left( f_R \right) \right) +\frac{1}{\sqrt{3}}\left[ \mathrm{imag}\left( M_{nm}\left( f_B\right) \right) \right. \nonumber \\&\left. -\,\mathrm{imag}\left( M_{nm}\left( f_G\right) \right) \right] \nonumber \\ C_{nm}^{R}= & {} \mathrm{real}\left( M_{nm}\left( f_{G} \right) \right) +\frac{1}{\sqrt{3} }\left[ \mathrm{imag}\left( M_{nm}\left( f_{R} \right) \right) \right. \nonumber \\&\left. -\,\mathrm{imag}\left( M_{nm}\left( f_{B}\right) \right) \right] \nonumber \\ D_{nm}^{R}= & {} \mathrm{real}\left( M_{nm}\left( f_{B} \right) \right) +\frac{1}{\sqrt{3} }\left[ \mathrm{imag}\left( M_{nm}\left( f_{G}\right) \right) \right. \nonumber \\&\left. -\,\mathrm{imag}\left( M_{nm} \left( f_{R} \right) \right) \right] \, \end{aligned}$$

(25)

$M_{pq} \left( f_{R} \right)$ , $M_{pq}\left( f_{G} \right)$, and$\, M_{pq} \left( f_{B} \right)$ represent RSCMs for the red, green, and blue channel, respectively. Based on Eq. (25), the computational process of QRSCMs depends on the computational process of the conventional RSCMs for the three single-channel images. Consequently, exact computation of RSCMs results in exact QRSCMs.

Fig. 1

a Cartesian image pixels, b polar image pixels

The input color image could be reconstructed by a finite number of QRSCMs using the following form:

$$\begin{aligned} f^{\mathrm{reco.}}\left( r,\theta \right)= & {} \hat{f}_{A}\left( r,\theta \right) +\hat{f}_{{\varvec{B}}}\left( r,\theta \right) {\varvec{i}}+\hat{f}_{C}\left( r,\theta \right) {\varvec{j}}\nonumber \\&+\hat{f}_{D}\left( r,\theta \right) {\varvec{k}}, \end{aligned}$$

(26)

where

$$\begin{aligned} \hat{f}_{A}\left( r,\theta \right)= & {} \mathrm{real}\left( \acute{A}_{nm}^{R} \right) -\frac{1}{\sqrt{3} }[\mathrm{imag}\left( \acute{B}_{nm}^{R} \right) \nonumber \\&+\,\mathrm{imag}\left( \acute{C}_{nm}^{R} \right) +\mathrm{imag}(\acute{D}_{nm}^{R})]\nonumber \\ \hat{f}_{\mathbf {B}}\left( r,\theta \right)= & {} \mathrm{real}\left( \acute{B}_{nm}^{R} \right) +\frac{1}{\sqrt{3} }[\mathrm{imag}\left( \acute{A}_{nm}^{R} \right) \nonumber \\&+\,\mathrm{imag}\left( \acute{C}_{nm}^{R} \right) -\mathrm{imag}(\acute{D}_{nm}^{R})]\nonumber \\ \hat{f}_{C}\left( r,\theta \right)= & {} \mathrm{real}\left( \acute{C}_{nm}^{R} \right) +\frac{1}{\sqrt{3} }[\mathrm{imag}\left( \acute{A}_{nm}^{R} \right) \nonumber \\&-\,\mathrm{imag}\left( \acute{B}_{nm}^{R} \right) +\mathrm{imag}(\acute{D}_{nm}^{R})]\nonumber \\ \hat{f}_{D}\left( r,\theta \right)= & {} \mathrm{real}\left( \acute{D}_{nm}^{R} \right) +\frac{1}{\sqrt{3} }\left[ \mathrm{imag}\left( \acute{A}_{nm}^{R} \right) \right. \nonumber \\&\left. +\,\mathrm{imag}\left( \acute{B}_{nm}^{R} \right) -\mathrm{imag}\left( \acute{C}_{nm}^{R} \right) \right] \end{aligned}$$

(27)

The value of $\hat{f}_{A}\left( r,\theta \right)$ is very close to 0; and $\hat{f}_{B}\left( r,\theta \right) , \hat{f}_{C}\left( r,\theta \right)$ and $\hat{f}_{D}\left( r,\theta \right)$ are the red, green and blue components of the reconstructed color image. The terms $\acute{A}_{nm}^{R}\, , \acute{B}_{nm}^{R}$, $\acute{C}_{nm}^{R}$ and $\acute{D}_{nm}^{R}$ represent the reconstruction matrix of ${A}_{{nm}}^{{R}},$ ${B}_{{nm}}^{{R}}$ , $C_{nm}^{R}{\, }$and $D_{nm}^{R}$, respectively.

$$\begin{aligned} \acute{A}_{nm}^{R}= & {} \sum \limits _{n=0}^\infty \sum \limits _{m=-\infty }^\infty {A_{nm}^{R}{R}_{n}\left( r \right) } {e}^{\mu m\theta }\approx \sum \limits _{n=0}^{\mathrm{max}} \sum \limits _{m=-\mathrm{max}}^{\mathrm{max}} {A_{nm}^{R}{R}_{n}\left( r \right) } {e}^{\mu m\theta },\nonumber \\ \acute{B}_{nm}^{R}= & {} \sum \limits _{n=0}^\infty \sum \limits _{m=-\infty }^\infty {B_{nm}^{R}{R}_{n}\left( r \right) } {e}^{\mu m\theta }\approx \sum \limits _{n=0}^{\mathrm{max}} \sum \limits _{m=-\mathrm{max}}^{\mathrm{max}} {B_{nm}^{R}{R}_{n}\left( r \right) } {e}^{\mu m\theta },\nonumber \\ \acute{C}_{nm}^{R}= & {} \sum \limits _{n=0}^\infty \sum \limits _{m=-\infty }^\infty {C_{nm}^{R}{R}_{n}\left( r \right) } {e}^{\mu m\theta }\approx \sum \limits _{n=0}^{\mathrm{max}} \sum \limits _{m=-\mathrm{max}}^{\mathrm{max}} {C_{nm}^{R}{R}_{n}\left( r \right) } {e}^{\mu m\theta },\nonumber \\ \acute{D}_{nm}^{R}= & {} \sum \limits _{n=0}^\infty \sum \limits _{m=-\infty }^\infty {D_{nm}^{R}{R}_{n}\left( r \right) }{e}^{\mu m\theta }\approx \sum \limits _{n=0}^{\mathrm{max}} \sum \limits _{m=-\mathrm{max}}^{\mathrm{max}} {D_{nm}^{R}{R}_{n}\left( r \right) } {e}^{\mu m\theta },\nonumber \\ \end{aligned}$$

(28)

Based on Eq. (19), the right- and the left-side QRSCMs are not identical. These moments are related by the form:

$$\begin{aligned} M_{pq}^{L}=-M_{p-q}^{R}, \end{aligned}$$

(29)

where

$$\begin{aligned} M_{nm}^{L}=\frac{1}{2\, \pi \, a_{n}}\int \limits _0^{2\pi } \int \limits _0^1 {f\left( \hat{r},\theta \right) \, \bar{R}_{n}\left( \hat{r} \right) \, \bar{W}\left( \hat{r} \right) \exp \left( -\mu \, m\theta \right) \hat{r}\mathrm{d}\hat{r}\mathrm{d}\theta \, .}\nonumber \\ \end{aligned}$$

(30)

3 The Proposed Computational Method

Radial-substituted Chebyshev functions are defined in polar coordinates. Therefore, computation of these functions in Cartesian coordinate system required a circle-to-square mapping which results in geometric errors. These errors could be avoided through computation in polar coordinates. All details of this approach are found in [18,19,20] where the polar raster is displayed in Fig. 1. Radial-substituted Chebyshev moments could be computed in polar coordinates as following:

$$\begin{aligned} M_{n\, m} =\frac{1}{2\, \pi \, a_{n}}\, \sum \limits _i \sum \limits _j {I_{n}\left( \hat{r}_{i} \right) \, I_{m}\left( \theta _{ij} \right) \, \hat{f}\left( \hat{r}_{i},\theta _{i,j} \right) }. \end{aligned}$$

(31)

The image intensity function $\hat{f}(r_{i},\theta _{i,j})$ is deduced from the input one using the cubic interpolation [21]. The angular and radial kernels are defined as:

$$\begin{aligned} I_{m}\left( \theta _{ij} \right)= & {} \int \limits _{V_{ij}}^{V_{i,j+1}} {e}^{-\hat{i}\, m\, \theta }\mathrm{d}\theta , \end{aligned}$$

(32)

$$\begin{aligned} I_{n}\left( \hat{r}_{i} \right)= & {} \int \limits _{U_{i}}^{U_{i+1}} {\bar{W}\left( \hat{r} \right) {{\, }\bar{R}}_{n}\left( \hat{r} \right) \, \hat{r}\mathrm{d}\hat{r}}. \end{aligned}$$

(33)

The lower and upper limits of the definite integrals in Eqs. (32) and (33) are expressed as follows:

$$\begin{aligned} U_{i+1}= & {} R_{i}+\Delta R_{i}/2\, ; \quad U_{i}=R_{i}-\Delta R_{i}/2, \end{aligned}$$

(34)

$$\begin{aligned} V_{i,j+1}= & {} \theta _{i,j}+\Delta \theta _{i,j}/2\, ; \, V_{i,j}=\theta _{i,j}-\Delta \theta _{i,j}/2\,. \end{aligned}$$

(35)

Based on the principles of calculus, exact computation of the angular kernel, $I_{m}\left( \theta _{ij} \right)$, is achieved by using the analytical integration as follows:

$$\begin{aligned} I_{m}\left( \theta _{i,j} \right) =\frac{\hat{i}}{m}\left( e^{-\hat{i}\, m{\, V}_{i,j+1}}-e^{-\hat{i}\, m{\, V}_{i,j}} \right) . \end{aligned}$$

(36)

For $q\ge 1$, where:

$$\begin{aligned} I_{0}\left( \theta _{i,j} \right) =\left( V_{i,\, j+1}-V_{i,\, j} \right) . \end{aligned}$$

(37)

Now, we looking for accurate computation of the radial kernel$\, I_{n}\left( \hat{r}_{i} \right)$. Equation (12) could be rewritten as follows:

$$\begin{aligned} \bar{R}_{n}\left( \hat{r} \right) =2\, \left( 2\hat{r}-1 \right) \, \bar{R}_{n-1}\left( \hat{r} \right) -\bar{R}_{n-2}\left( \hat{r} \right) . \end{aligned}$$

(38)

For $n\ge 2.$

Using Eq. (38) in (35) yields:

$$\begin{aligned} I_{n}\left( \hat{r}_{i} \right) =\int \limits _{U_{i}}^{U_{i+1}} {\bar{W}(\hat{r})\left[ 2\, \left( 2\hat{r}-1 \right) \, \bar{R}_{n-1}\left( \hat{r} \right) -\bar{R}_{n-2}\left( \hat{r} \right) \right] \, \hat{r}\mathrm{d}\hat{r}}.\nonumber \\ \end{aligned}$$

(39)

Equation (39) is rewritten in the following compact form:

$$\begin{aligned} I_{n}\left( \hat{r}_{i} \right) =\, A_{n-1}\left( \hat{r}_{i} \right) -I_{n-2}\left( \hat{r}_{i} \right) \,. \end{aligned}$$

(40)

For $n\ge 2$, where the first term is defined as follows:

$$\begin{aligned} I_{0}\left( \hat{r}_{i} \right) =\int \limits _{U_{i}}^{U_{i+1}} {\, \frac{\sqrt{\hat{r}}}{\sqrt{1-\hat{r}} }\mathrm{d}\hat{r}\, }. \end{aligned}$$

(41)

This integration, $I_{0}\left( r_{i} \right) \, ,$ is evaluated analytically as follows [22]:

$$\begin{aligned} I_{0}\left( r_{i} \right)= & {} 2\mathrm {arctan}\left( \frac{\sqrt{U}_{i+1} }{\sqrt{1-U}_{i+1} -1} \right) -\sqrt{U}_{i+1} \sqrt{1-U}_{i+1} \nonumber \\&-\,2\mathrm {arctan}\left( \frac{\sqrt{U}_{i} }{\sqrt{1-U}_{i} -1} \right) +\sqrt{U}_{i} \sqrt{1-U}_{i} \, \end{aligned}$$

(42)

$$\begin{aligned} I_{1}\left( \hat{r}_{i} \right)= & {} \int \limits _{U_{i}}^{U_{i+1}} \, \frac{\left( 2\hat{r}-1 \right) \sqrt{\hat{r}}}{\sqrt{1-\hat{r}} }\, \mathrm{d}\hat{r}=\int \limits _{U_{i}}^{U_{i+1}} \, \frac{2\hat{r}\sqrt{\hat{r}}}{\sqrt{1-\hat{r}} }\, \mathrm{d}\hat{r}\nonumber \\&-\int \limits _{U_{i}}^{U_{i+1}} {\, \frac{\sqrt{\hat{r}} }{\sqrt{1-\hat{r}} }\, \mathrm{d}\hat{r}} \, \,\nonumber \\= & {} \int \limits _{U_{i}}^{U_{i+1}} {\, \frac{2\hat{r}\, \sqrt{\hat{r}} }{\sqrt{1-\hat{r}} }\, \mathrm{d}\hat{r}-} I_{0}\left( \hat{r}_{i} \right) , \end{aligned}$$

(43)

where

$$\begin{aligned} A_{n-1}\left( \hat{r}_{i} \right) =\int \limits _{U_{i}}^{U_{i+1}} {2\, \bar{W}(\hat{r})\left( 2\hat{r}-1 \right) \, \bar{R}_{n-1}\left( \hat{r} \right) \, \hat{r}\mathrm{d}\hat{r}}. \end{aligned}$$

(44)

Substituting Eq. (14) in (44) yields:

$$\begin{aligned} A_{n-1}\left( \hat{r}_{i} \right) =\int \limits _{U_{i}}^{U_{i+1}} {2\, \frac{\left( 2\hat{r}-1 \right) \, }{\sqrt{\hat{r}-\hat{r}^{2}} }\, \bar{R}_{n-1}\left( \hat{r} \right) \, \hat{r}\mathrm{d}\hat{r}\,}. \end{aligned}$$

(45)

It is obvious that analytical evaluation of the definite integration in Eq. (45) is impossible. The Gaussian numerical integration method is a highly accurate numerical integration method [23] used to evaluate $A_{n-1}\left( \hat{r}_{i} \right)$. This method was successfully used in [24, 25]. The Gaussian numerical integration method is defined as follows:

$$\begin{aligned} \, \int \limits _a^b {g\left( z \right) dz\approx \frac{\left( b-a \right) }{2}\sum \limits _{l=0}^{c-1} w_{l} } g\left( \frac{a+b}{2},\frac{b-a}{2}t_{l} \right) , \end{aligned}$$

(46)

where $w_{i}$ and $t_{i}$ refer to weights and the location of sampling points and cis the order of the numerical integration with $i=0,1,2,\ldots c-1$. The values of $w_{i}$ are fixed and $\sum \limits _{i=0}^{c-1} w_{i} =2$. The values of $t_{i}$ can be expressed in terms of the limits of the integration aand b.

Fig. 2

A set of color images

4 Numerical Experiments

Numerical experiments are performed in order to achieve two goals. First goal is concerned with the validation of the proposed method. The second goal is concerned with comparing the performance of the QRSCMs with the other quaternion moments. In The first subsection, experiments were performed to reconstruct different RGB color images by using the computed QRSCMs. Evaluation of the reconstructed images ensure the accuracy of the proposed method. Invariances of the QRSCMs with respect to similarity transformations (rotation, scaling, and translation) of RGB color images is presented in the second subsection. Robustness against different kinds of noises discussed in the third subsection.

Evaluation of the classification color images ensure the accuracy of the proposed method with respect to (rotation, scaling, and translation) RST transformations of RGB color images is presented in the fourth subsection. The CPU-speed estimation for the proposed method is discussed in the fifth subsection.

4.1 Color Image Reconstruction

Accurate reconstruction of color images required accurate moments where the reconstruction accuracy increased as the order of moments increased. Accurate computation of higher-order moments represents a challenge for most common numerical methods. Therefore, reconstruction of RGB color images is a very relevant way to assess the accuracy of the proposed method. Numerical experiments were performed where the accuracy of the reconstructed images is evaluated quantitatively and qualitatively. The normalized image reconstruction error (NIRE) [13] is used as a quantitative measure of the reconstruction capability of QRSCMs. The NIRE is defined as follows:

$$\begin{aligned} \mathrm{NIRE}=\frac{\sum \nolimits _{i=0}^{N-1} \sum \nolimits _{j=0}^{N-1} \left| f\left( i,j \right) -f^{\mathrm{recons.}}\left( i,j \right) \right| ^{2} }{\sum \nolimits _{i=0}^{N-1} \sum \nolimits _{j=0}^{N-1} \left| f\left( i,j \right) \right| ^{2} }, \end{aligned}$$

(47)

where $f\left( i,j \right)$ and $f^{\mathrm{recons.}}(i,j)$ represent the original and the reconstructed RGB color images, respectively. A computation method is said to be highly accurate when the values of the NIRE approach zero. The visual inspection of the reconstructed images by human eyes is used in qualitative evaluation of the reconstructed images. Normal human eye could easily measure the degree of similarity between the original and the reconstructed images.

Five color images are displayed in Fig. 2. These images are used in five different numerical experiments. In the first experiment, the QRSCMs of different orders ranging from 0 to 120 are computed for the color image of “Lena” with size $64\times 64$ by using the proposed hybrid method and the QZMs [11], QPZM [12], QFMMs [13], QRHFMs [14], QPCETs [15], and QEMs [16]. The values of NIRE are evaluated and plotted in Fig. 3. It is observed that the values of NIRE for QRHFMs [14], QPCETs [15], QEMs [16] decreased as the moment order increased up to moment orders 20, 15, 15, respectively. Furthermore, the computation of QFMMs [13] is highly instable with moment orders $>20$. The numerical instability of the QPZMs [12] and QZMs [11] comes with moment order $\ge 25$, and 45, respectively. It is also observed that the proposed hybrid method is highly accurate and stable where the values of the NIRE are much smaller and continuously decreased as the moment orders increased.

Fig. 3

NIRE for the image of the Lena of size ${64\times 64}$ using the proposed QRSCMs and the existing quaternion moments [11,12,13,14,15,16]

Fig. 4

NIRE for a color image of b of size pills $128\times 128$ using the proposed QRSCMs and the existing quaternion moments [11,12,13,14,15,16]

The second numerical experiment is performed using the color image of “pills” with size $128\times 128$. The computed values of the NIRE for different methods are displayed in Fig. 4. It is clear that the values of the NIRE of QRHFMs [14], QPCETs [15], and the QEMs [16] are dramatically increased where the accumulation of the approximation errors make this method instable. The values of the NIRE of QFMMs [13], QPZMs [12], and the QZMs [11] keeps its stability for orders up to 20, 25, and 40, respectively, and suddenly becomes highly instable due to the accumulation of errors. The proposed method is stable for all moment orders where the values of NIRE continuously decreased as the moment order increased.

The qualitative quality of the reconstructed color images is evaluated by using a visual perception where the original color image is reconstructed using different orders and the reconstructed color images are displayed for eye observation. To evaluate the effect of geometric error and numerical integration which is reflected in the quality of reconstructed images. In the third experiment, the standard color image of “Peppers” with size $64 \times 64$ is reconstructed by using the proposed method and the other six quaternion moments, QZMs [11], QPZM [12], QFMMs [13], QRHFMs [14], QPCETs [15], and QEMs [16]. The reconstructed images are displayed in Fig. 5. This figure clearly shows that the reconstructed images using the (QZMs) [11], (QPZMs) [12], (QOFMMs) [13], (QRHFM) [14], (QPCET) [15], (QEMs) [16], are significantly damaged due to the low accuracy and highly numerical instability. The reconstructed color images by using the proposed method are very close to the original color image especially with higher-order moments. This observation ensures highly accurate and stable computation of QRSCMs. Visual comparison and quantitative measurements show great results which ensure the accuracy of the proposed method compared with other quaternion moments.

Fig. 5

Reconstructed color image of Pepper with size $64 \times 64$ using selected order of using the proposed QRSCMs and the existing quaternion moments [11,12,13,14,15,16]

Fig. 6

Reconstructed color image of Baboon of size ${128\times 128}$ using selected order of using the proposed QRSCMs and the existing quaternion moments [11,12,13,14,15,16]

Fig. 7

Reconstructed color image of flower of size ${256\times 256}$ using the proposed QRSCMs

In the fourth experiment, the color image of the “Baboon” with size $128\times 128$ is reconstructed by using the proposed method and all aforementioned quaternion moments. The reconstructed color images are displayed in Fig. 6. The fifth experiment is performed using the color image of flower. This image of size $256\times 256$ is reconstructed by using QRSCMs. The reconstructed color images are displayed in Fig. 7. Similar conclusion is reached where the obtained results are similar to the corresponding results of the previous experiments.

Smaller reconstructed errors may be considered due to the accurate computation method of QRSCMs using hybrid exact and Gaussian numerical integration. In order to remove any ambiguity, additional numerical experiment is performed where the conventional ZOA computational method is used for computing QRSCMs and the other existing quaternion moments QZMs [11], QPZMs [12], QOFMMs [13], QRHFMs [14], QPCETs [15], and QEMs [16]. The normalized image reconstruction errors (NIRE) for all mentioned quaternion moments are computed and displayed in Fig. 8. It is clear that the proposed new set of QRSCMs moments show the best performance either with accurate computational method or the conventional ZOA computational method.

The existing quaternion methods could be classified into two groups. The first group contains QZMs [11], QPZMs [12], and QOFMMs [13]. The accurate method is not suitable for these moments. Two major problems are associated with these moments. The first one is concerned with nature of these polynomials while the second one is concerned the coefficients of the radial polynomials. The performance of these moments would not improve, even with the utilization of the accurate computational method.

For the second group which contains QRHFMs [14], QPCETs [15], and QEMs [16], the accurate method could be adapted to be suitable for these moments. The performance of these moments would be improved. Even after this possible improvement, the performance of the proposed QRSCMs is still better due to the nature of the Chebyshev radial polynomials [10].

In the recent published paper, [26], a novel recurrence formula is proposed to remove the errors associated with the computation of QPCETs in polar coordinates. The authors could say, now the door is opened for similar works to improve the accuracy of QRHFMs and QEMs by find hybrid proper exact formula and recurrence relations.

4.2 Similarity Transformations

4.2.1 Rotation Invariance

Invariance to the similarity transformations such as rotation and scaling, are very important in pattern recognition applications. However, QRSCMs moment invariants are negatively affected by the accumulated errors. The original image is rotated with an angle $\alpha$. The image intensity function of rotated image is related to its corresponding one for original image as:

$$\begin{aligned} f^{\mathrm{rot}}\left( r,\theta \right) =f(r,\theta +\alpha ). \end{aligned}$$

(48)

Let $\hat{\theta }=\theta +\alpha$, then $\theta =\hat{\theta }-\alpha$ and $\mathrm{d}\theta =\mathrm{d}\hat{\theta }$

The QCRMs of the two images $f^{\mathrm{rot}}$ and f have the following relations

$$\begin{aligned} M_{pq}^{R}\left( f^{\mathrm{rot}} \right) \,= & {} \frac{1}{2\pi \, a_{n}}\int _0^{2\pi } \int _0^1 {f\left( r,\theta +\alpha \right) } \bar{R}_{p}\left( r \right) \, \bar{W}\left( r \right) \nonumber \\&\qquad e^{-\mu q\theta }r\mathrm{d}r\mathrm{d}\theta \, \nonumber \\= & {} \frac{1}{2\pi \, a_{n}}\int _0^{2\pi } \int _0^1 {f\left( r,\hat{\theta } \right) } \bar{R}_{p}\left( r \right) \, \bar{W}\left( r \right) \nonumber \\&\qquad e^{-\mu q(\hat{\theta }-\alpha )}r\mathrm{d}r\mathrm{d}\hat{\theta }\nonumber \\= & {} \frac{1}{2\pi \, a_{n}}\int _0^{2\pi } \int _0^1 {f\left( r,\hat{\theta } \right) } \bar{R}_{p}\left( r \right) \, \bar{W}\left( r \right) \nonumber \\&\qquad e^{-\mu q\hat{\theta }}e^{\mu q\alpha }{r\mathrm{d}r\mathrm{d}\hat{\theta }}\nonumber \\= & {} \, M_{pq}^{R}(f)e^{\mu q\alpha } \end{aligned}$$

(49)

where ${M}_{\mathrm {pq}}^{{R}}\left( {f}^{\mathrm{rot}} \right)$ and ${M}_{\mathrm {pq}}^{{R}}\mathrm {(}{f}^{\mathrm {\, }}\mathrm {)}$ are the QCRMs of $f^{\mathrm{rot}}$ and f, respectively. Similarly, we can obtain the following relationship for the left-side QCRMs s as follows:

$$\begin{aligned} M_{pq}^{L}\left( f^{\mathrm{rot}} \right) ={e^{\mu q\alpha }M}_{pq}^{L}\left( f \right) . \end{aligned}$$

(50)

Since $\left| {e}^{\mu {q}\alpha } \right| =1$, then:

$$\begin{aligned} {\vert M}_{pq}^{R}\left( f^{\mathrm{rot}} \right) \vert= & {} {\vert M}_{pq}^{R}\left( f^{\mathrm{rot}} \right) e^{\mu q\alpha }\vert ={\vert M}_{pq}^{R}\left( f^{\mathrm{rot}} \right) \vert \vert e^{\mu q\alpha }\vert \\= & {} \vert M_{pq}^{R}\left( f \right) \vert . \end{aligned}$$

The magnitude values of the QRSCMs are rotation invariants. In other words, ${\varphi }_{{pq}}={\vert M}_{pq}^{R}\left( f \right) \vert$ are invariant with respect to rotation transform.

Fig. 8

NIRE for the image of the Lena of size ${64\times 64}$ using the conventional ZOA for computing QRSCMs and the existing quaternion moments [11,12,13,14,15,16]

Fig. 9

Color images of the dataset Coil-100 [27]

In order to evaluate the effectiveness of the proposed QRSCMs invariants under the rotation transform, a set of numerical experiments are performed. The well-known Columbia Object Image Library (COIL-100) [27] of color objects is used in the upcoming numerical experiments. A collection of the 100 objects is displayed in Fig. 9. The color image for the obj_74 of size $128 \times 128$ is rotated by different angles ranging from $0^{\circ }$ to $180^{\circ }$. The rotated images are displayed in Fig. 10. The magnitude values of the first few QRSCMs for various angles of rotation are presented in Table 1. The magnitude values are very similar and almost unchanged with different rotation angles which ensure the accuracy of the rotation invariance of the QRSCMs.

Fig. 10

Original and rotated color images of the obj_74 [27]

Additional experiment is performed where the rotational invariance of the proposed method is compared with other existing quaternion moments [11,12,13,14,15,16]. The mean square error (MSE) is a quantitative measure that reflects the accuracy of rotation which is defined as follows:

$$\begin{aligned} \mathrm{MSE}=\frac{1}{L_{\mathrm{Total}}}\sum \limits _{p=0}^{\mathrm{max}} \sum \limits _{q=0}^{\mathrm{max}} {{({{\vert M}_{pq}^{R}\left( f \right) \vert -\vert M}_{pq}^{R}\left( f^{\mathrm{rot}} \right) \vert \, )}^{2\, }},\qquad \end{aligned}$$

(51)

where $L_{\mathrm{total}}$ is total number of independent QRSCMs and ${\vert M}_{pq}^{R}\left( f \right) \vert$ , ${\vert M}_{pq}^{R}\left( f^{\mathrm{rot}} \right) \vert$ are the magnitudes of QRSCMs before and after the rotation. The MSE are computed using the eight methods with a maximum order 20. The rotation angles, the rotated images, and the values of MSE are presented in Table 2. The MSEs of the proposed method are much smaller than their corresponding ones [11,12,13,14,15,16].

Table 1 Rotation invariance of the rotated images using the proposed QRSCMs

Table 2 MSE for the rotated images using the proposed QRSCMs and the other quaternion moments [11,12,13,14,15,16]

4.2.2 Scaling Invariance

The modulus of QRSCMs moments for RGB color images are invariant to scaling if the computation area can be made to cover the same content [15]. In the proposed method, this condition is met because the QRSCMs are defined and computed on the unit circle. Also, the input RGB color images are mapped into the unit circle as displayed in Fig. 1. Let $f^{S}$ be the scaled version of an image f. The right-side QRSCM moments of $f\, \mathrm {and\, }f^{S}$ are $M_{pq}^R \left( f\right)$ and $M_{pq}^R \left( f^s\right)$ respectively. The mean square error (MSE) is a quantitative measure that reflects the accuracy of scaling which is defined as follows:

$$\begin{aligned} \mathrm{MSE}=\frac{1}{L_{\mathrm{Total}}}\sum \limits _{p=0}^{\mathrm{max}} \sum \limits _{q=0}^{\mathrm{max}} {{({{\vert M}_{pq}^{R}\left( f \right) \vert -\vert M}_{pq}^{R}\left( f^{s} \right) \vert \, )}^{2\, }\,} \end{aligned}$$

(52)

where $L_{\mathrm{total}}$ is total number of independent QRSCMs and ${\vert M}_{pq}^{R}\left( f \right) \vert$ , ${\vert M}_{pq}^{R}\left( f^{s} \right) \vert$ are the magnitudes of QRSCMs before and after the scaling.

In order to test the scaling invariance, an experiment is performed using the color image of obj_52 of the size $128\times 128$. This color test image is uniformly scaled with different scaling factors where both original and scaled images are displayed in Fig. 11. Both $M_{pq}^{R}\left( f^{s} \right)$ and $M_{pq}^{R}\left( f \right)$ are computed with a maximum order 20 by using the proposed hybrid method and the compared methods where the MSE of are showed in Table 3. It is clear that the scaling invariance of the proposed method is outperformed all other methods.

Fig. 11

Original and scaled color images of the obj_52 [27]

4.2.3 Translation Invariance

Translation invariance is achieved when the color image centroid is coinciding with the origin of coordinates. Suk and Flusser [28] defined the centroid $\left( x_{c},y_{c} \right)$ of RGB color images as follows:

$$\begin{aligned} x_{c}= & {} \left( m_{10}\left( f_{R} \right) +m_{10}\left( f_{G} \right) +m_{10}\left( f_{B} \right) \right) / m_{00}\, ,\nonumber \\ y_{c}= & {} \left( m_{01}\left( f_{R} \right) +m_{01}\left( f_{G} \right) +m_{01}\left( f_{B} \right) \right) / m_{00},\nonumber \\ m_{00}= & {} m_{00}\left( f_{R} \right) +m_{00}\left( f_{G} \right) +m_{00}\left( f_{B} \right) . \end{aligned}$$

(53)

where $m_{00}\left( f_{R} \right)$, $m_{10}\left( f_{R} \right)$ and $m_{01}\left( f_{R} \right)$, are the zero-order and first-order geometric moment for red color channel, respectively. Similarly, $m_{00}\left( f_{G} \right)$, $m_{10}\left( f_{G} \right)$ and $m_{01}\left( f_{G} \right)$, and, $m_{00}\left( f_{B} \right)$, $m_{10}\left( f_{B} \right)$ and $m_{01}\left( f_{B} \right)$ are the zero-order and the first-order geometric moment for green and blue color channels, respectively.

By locating the coordinate origin at centroid $\left( x_{c}\, ,y_{c} \right)$, the central QCRMs, which are invariant to translation, are defined as follows:

$$\begin{aligned} \overline{M}_{nm}^{R}=\frac{1}{2\pi \, a_{n}}\int _0^{2\pi } \int _0^1 {f(\overline{r} ,\overline{\theta })} \bar{R}_{p}\left( \bar{r} \right) \, \bar{W}\left( \bar{r} \right) \, {e}^{-\mu q\overline{r} }\overline{r} \mathrm{d}\overline{r} \mathrm{d}\overline{\theta }\, \end{aligned}$$

(54)

The translation invariance of the proposed QRSCMs is evaluated using the color image of the obj_43 [27]. The tested image is translated with different translation factors in both x-, and y-axes. The translated images are displayed in Fig. 12. The low order translated right-side QRSCMs, $\overline{M}_{nm}^{R}$, are computed for the original and the translated objects where the computed moments are showed in Table 4. The computed moments are very similar for different translated objects which ensure the accuracy of the proposed method to translation invariance.

Table 3 MSE for the scaled images using the proposed QRSCMs and the other quaternion moments [11,12,13,14,15,16]

Table 4 Translation invariance of the translated images using the proposed QRSCMs

Fig. 12

Original and translated color images of the obj_43 [27]

4.3 Robustness to Noises

Robustness to different kinds of noise is an attractive characteristic. The noise-free color images of obj_10 [27] is used in this experiment. This color image is contaminated by different levels of the ‘salt and pepper’, the ‘white Gaussian’, the ‘speckle,’ and the ‘Poisson’ noises. The noise-free and contaminated color images are displayed in Fig. 13a–e, respectively. Noisy color images are reconstructed using the proposed method with moment order up to 100. The values of NIRE for the noise-free and noisy color images are plotted and displayed in Fig. 14. Despite of the presence of noises in the contaminated images, the values of the NIRE are decreased as the moment order increased which show numerical stability. The plotted values of the NIRE ensure the robustness of the proposed method against the different kind of noises.

Fig. 13

a Noise-free color image. Noisy images: b white Gaussian, c salt and peppers, d speckle, e poisson

4.4 Classification Performance Using Color Images

In this subsection, we conduct experiments to evaluate the classification performance of the QRSCMs invariants under the RST transforms of color images. A collection of the 100 color objects as displayed in Fig. 9 is used in the numerical experiments. The classification problem is decomposed into two main steps: the first on is feature extraction, and the second is the classification. In this experiment, we construct the feature vecto using the magnitudes of the quaternion radial-substituted Chebyshev moment invariants. We used randomly 40 images from COIL dataset as a training set. The testing set is then constructed as follows: Each sample image was scaled with the factor 0.5 and 1.5, and rotated from $30^{\circ }, 60^{\circ }, 90^{\circ },120^{\circ }$, $180^{\circ }$, and then each image was translated by $\left( \Delta \mathbf {x},\Delta \mathbf {y} \right) =(\mathbf {2},\mathbf {5})$ in both direction.

In the first numerical experiment, the k-nearest neighbor classifier based on minimum Euclidean-distance and the SVM classifier-Weka software are used to measure the correct classification percentage (CCP) with the classification results using different orders, 2, 8 and 20, of the quaternion radial-substituted Chebyshev moment invariants. The obtained results as displayed in Table 5 show that, the CCP of the SVM classifier-Weka software is much better than the k-nearest neighbor classifier.

In the second numerical experiment, the QRSCMs invariants in addition to the other quaternion moment invariants, QZMs [11], QPZMs [12], QFMMs [13], QRHFMs [14], QPCET [15] and QEMs [16] are used to extract the features of the color images, and then the SVM classifier-Weka software is utilized. The corresponding correct classification percentages are computed and shown in Table 6. Based on the tabulated results, we can see that the QSCRMs invariants provide higher classification accuracy than other quaternion moment invariants [11,12,13,14,15,16] for all orders. The CCP of the quaternion moment invariants [11,12,13,14,15,16] decreased as the moment’s order increased while the CCP of QSCRM invariants remains the same even the moment’s order increased. Generally, the results show clearly that the proposed QSCRMs could be useful as a new feature descriptor for object classification.

4.5 Computational CPU Times

Computational CPU times is an essential issue in evaluating new computational methods. These times are used as an indicator that reflects the efficiency of the proposed computational methods by comparing their performances with the existing methods in a quantitative fashion. Fast computation of QRSCMs moments is desirable in real-time applications and processing of big size images. In order to ensure the efficiency of the proposed method, a number of numerical experiments are performed with three different datasets of color images.

The first dataset is the dataset of birds [29] which contains 600 images (100 samples each) of six different classes of birds. The images are color JPEG with different sizes. The second dataset is the dataset of butterflies [30] which contains 619 images of seven different classes of butterflies. The images are color JPEG with different sizes. These classes are “Admiral: 111 images”, “Black Swallowtail: 42 images”, “Machaon: 83 images”, “Monarch 1 (wings closed): 74 images”, “Monarch 2 (wings open): 84 images”, “Peacock: 134 images”, and “Zebra: 91 images”. Selected images of these datasets are displayed in Figs. 15 and 16.

Fig. 14

NIRE curves for noise-free and noisy color images of Obj_10 [27] computed using the proposed QRSCMs

The QRSCMs of orders 0–50 with increment 10 are computed for all color images of birds and butterflies. Due to the difference in size of the color images of the first and the second datasets, the elapsed CPU times for all images is accumulated and individual average CPU time for each dataset is computed. Additional experiments are performed to compute the QZMs [11], QPZM [12], QFMMs [13], QRHFMs [14], QPCETs [15], and QEMs [16] of the same orders. The average CPU times are showed in Tables 7 and 8, respectively.

The third dataset is the colored Brodatz texture (CBT) dataset which is a colored version of the original 112 Brodatz grayscale texture images [31]. These color images have a unified size of $640\times 640$. Selected images of this dataset are displayed in a Fig. 17. The proposed QRSCMs and the QZMs [11], QPZM [12], QFMMs [13], QRHFMs [14], QPCETs [15], and QEMs [16] are computed for order ranging from 0 to 50. Since all images have the same size, each computational process is repeated five times and the average CPU time for the entire dataset is shown in Table 9. A quick comparison of the average CPU times in seconds for the moment order 50 is displayed in Fig. 18. The obtained results clearly show that the proposed method is very fast and much faster than the other quaternion moments [11,12,13,14,15,16].

Table 5 Correct classification percentages (CCP%) for the color image COIL dataset using the proposed method

Table 6 Correct classification percentages (CCP%) of the proposed method and The different quaternion moments [11,12,13,14,15,16] using SVM-Weka

Fig. 15

Selected color images of the dataset of Birds [29]

Fig. 16

Selected color images of the dataset of butterflies [30]

Table 7 Average CPU times for the dataset of color images of Birds [29]

Table 8 Average CPU times for the dataset of color images of butterflies [30]

Fig. 17

Selected color images of the dataset of colored Brodatz texture [31]

Table 9 Average CPU times for the dataset of color images of (CBT) [31]

Fig. 18

Average CPU times the three datasets at moment order 50

5 Conclusion

In this paper, a new set of quaternion radial-substituted Chebyshev moments for color image representation is presented. A highly accurate and stable method of computing the QRSCMs is proposed. The new set of quaternion moments show a significant improvement in color image reconstruction capabilities for high orders. Numerical experiments obviously show that, highly accurate computation of the QRSCMs results in highly accurate rotation, scaling, and translation invariances of these moments. Based on its simplicity, the proposed method is very fast which make suitable for real-time image processing applications. The comparison with existing quaternion moments ensure the superiority of the new set of QRSCMs.