A plaintext-related image encryption algorithm based on chaos

Abstract

A symmetric key image cryptosystem based on the piecewise linear map is presented in this paper. In this cryptosystem, the encryption process and the decryption process are exactly same. They both include the same operations of plaintext-related scrambling once, diffusion twice and matrix rotating of 180 degrees four times. The length of secret key in the system is 64d where d is a positive integer. The proposed system can fight against the chosen/known plaintext attacks due to the using of plaintext-related scrambling. The simulate results and comparison analysis show that the proposed system has many merits such as high encryption/decryption speed, large key space, strong key sensitivity, strong plaintext sensitivity, strong cipher-text sensitivity, good statistical properties of cipher images, and large cipher-text information entropy. So the proposed system can be applied to actual communications.

1 Introduction

With the rapid development of communication technology, the security of image information has drawn increasingly extensive attention, and the image encryption is the most effective means to ensure the confidential image transmission in public information channel. However, the classic text-based encryption methods, such as DES and AES, are no longer suitable for image encryption because the image possesses the characteristics of huge volume, high data redundancy and strong adjacent correlation. Meantime, the chaotic systems firstly discovered in the 1970s by E. N. Lorenz have the intrinsic properties of sensitivity to initial conditions and parameters, non-periodicity and ergodicity, and these properties correspond in a way to the properties of image encryption system such as secret key sensitivity, plaintext/cipher-text sensitivity, cipher-text balance, confusion and so on. Hence, chaotic systems are widely employed in digital image encryption systems to generate secret code streams for encryption [2, 5, 9, 10, 12, 16, 17, 25, 30].

Some of the existing chaotic-system-based image encryption systems use chaotic systems to produce pseudo-random numbers with excellent statistical properties to be used as the secret code streams, but their image encryption algorithms [11, 14, 15, 20, 32, 34] essentially employ the same secret code streams to encrypt the different plain images. Therefore, these image encryption systems cannot resist the chosen/known plaintext attacks [4, 19, 22, 26, 29, 31]. However, as a frequently used attack method, chosen/known plaintext attacks can be used by eavesdroppers to crack some not well-designed image encryption systems in a short time. In order to secure plain images against these types of attack methods, the scholars suggested the plaintext-related image encryption algorithms [1, 24, 27, 28, 33, 30].

The main features of the plaintext-related image encryption algorithm are that the plaintext information is directly or indirectly employed to change the secret code streams during the encryption process, which makes different plain images encrypted with different secret code streams even when their secret key or equivalent keys are same. In [1], an image encryption algorithm named BES-w/r/b was proposed, where BES means a block encryption scheme, w represents the number of bits per pixel, r represents the number of rounds, and b represents the length of secret key (in bytes). This scheme used the initial secret key and the extension of previous cipher block to produce the secret key of encrypting the current image block, and to make the diffusion plaintext-related. However, this scheme is poor on security when r = 1 while slow on encryption speed when r ≥ 2.

In [24], the generalized Logistic map is used to produce three groups of secret code streams for encrypting. In order to fight against the chosen plaintext attack, the value of current pixel in plain image is positively diffused then oppositively diffused to influence the encryption of next pixel in the plain image. In [33], an image encryption scheme based on feedback method was proposed, which used the plaintext information as feedback in the confusion process so that different plain images have different confusion results. In [27], random pixels in the intermediate cipher images generated in the first round were selected to produce the new secret key (named by the second level key), and in this manner, the scheme indirectly realized the plaintext-related image encryption. But the encryption speed of the scheme is relatively slow.

In 2016, we proposed a method which added plaintext information in the confusion process, and the structure of the encryption scheme is ‘diffusion - plaintext related confusion- diffusion’. Its encryption speed is much faster than those schemes with plaintext related diffusion algorithms [28, 30]. However, this scheme requires three secret code matrices with the same size as the plain image. Due to the huge volume of image data, the scheme has high performance requirements for pseudo-random number generator.

In the foresaid plaintext-related image encryption schemes based on chaotic systems, the encryption algorithms are different from the decryption algorithms, and the latter are the reverse of the former. So the communication parties both need two sets of equipment, for encryption and decryption algorithms respectively. This paper attempts to study an image cryptosystem whose encryption and decryption algorithms are the same, which makes the communication parties possess only one set of equipment and one algorithm to achieve encryption and decryption. Meanwhile, the proposed image cryptosystem needs only one secret code matrix and adopt the plaintext-related scrambling algorithm to resist the chosen/known plaintext attacks effectively. The remains of the paper are organized as follows: Section 2 details the structure and algorithms of the proposed image encryption scheme; Section 3 presents some simulation results of encryption and decryption applications; Section 4 analyzes the security performance of the scheme from various aspects, such as encryption/decryption speed, key space, statistical properties of the cipher-text, key sensitivity, plaintext sensitivity, cipher-text sensitivity, information entropy and so on; Section 5 summarizes the paper.

2 Image encryption scheme

2.1 Used chaotic system

The piecewise linear chaotic map (PWLCM) is used in this paper, and its equation is as follows [3]:

$$ {x}_{i+1}= F\left({x}_i, p\right)=\left\{\begin{array}{c}\hfill \frac{x_i}{p},0\le {x}_i< p\hfill \\ {}\hfill \frac{x_i- p}{0.5- p}, p\le {x}_i<0.5\hfill \\ {}\hfill F\left(1-{x}_i, p\right),0.5\le {x}_i<1\hfill \end{array}\right. $$

(1)

Where, x _i ∈(0,1), and p∈(0,0.5).

In [13], the chaotic characteristics of PWLCM were studied thoroughly, and also the PWLCM used to generate pseudo-random sequences with good statistical properties was verified. The PWLCM is widely used in variety of image encryption systems [8, 21].

2.2 Typical image cryptosystem

The typical image encryption system based on chaotic system includes both confusion module and diffusion module, and it converts plain image into noise-like cipher image through executing the two modules for multiple rounds, as shown in Fig. 1. In this image encryption system, chaotic system is used to generate the pseudo-random secret code stream for encryption. The number of rounds is not less than 2. And the decryption process is different from the encryption process, it is the reverse of the encryption process [5, 17].

Fig. 1

Typical image cryptosystem

On the basis of traditional chaotic image cryptosystem, we try to explore a new image cryptosystem, in which the pseudo-random secret code streams are still produced by the chaotic system, but the encryption process and the decryption process are exactly the same, and no round operation is needed in the two processes. Also, it uses the plaintext-related confusion to frustrate the chosen/known plaintext attacks.

2.3 Proposed encryption scheme

The proposed image encryption scheme is as shown in Fig. 2. In the proposed scheme, the encryption process and the decryption process are exactly the same. They both consist of the operations of secret code streams generation, forward diffusions once, plaintext-related scrambling once, backward diffusion once and matrix rotating 180 degrees for four times. The algorithms will be discussed in detail in the following subsections.

Fig. 2

Proposed encryption scheme

Assume that the plain image is denoted by P with size of M × N, where M and N are the height and width of image, respectively. Note that N must be an even number in the proposed scheme, i.e. N mod 2 = 0. Otherwise, a zero-column vector of length M need to be added to the image P as its last column to make P a matrix of size M×(N + 1).

2.3.1 Secret code stream generating algorithm

The secret key of the proposed scheme is denoted by K with length of 64 × d, where, d is a natural number. And the secret key K can be represented in hexadecimal format as ‘k ₁ k ₂ k ₃ k ₄ k ₅…k _16d-3 k _16d-2 k _16d-1 k _16d ’, where, each k _i , i = 1,2,…,16d, is a decimal integer in range of 0 to 15.

Generating the initial value x ₀ and the parameter p of PWLCM with the secret key K using the following algorithms:

• Step 1. Fetch ‘k ₁ k ₂ k ₃ k ₄ k ₅ k ₆ k ₇ k ₈’ from the secret key K, and calculate the value of x ₀₀ according to the following formula:

$$ {x}_{00}=0.8\times {\sum}_{i=1}^8\frac{k_i}{2^{4 i}}+0.1 $$

(2)

Here, the calculated x ₀₀ is in the range (0.1,0.9).

• Step 2. Fetch ‘k ₉ k ₁₀ k ₁₁ k ₁₂ k ₁₃ k ₁₄ k ₁₅ k ₁₆’ from the secret key K, and calculate the value of p ₀ with the following formula:

$$ {p}_0=0.4\times {\sum}_{i=1}^8\frac{k_{8+ i}}{2^{4 i}}+0.1 $$

(3)

Here, the calculated p ₀ is in the range(0.1,0.5).

• Step 3. Substitute x ₀₀ and p ₀ into Eq. (1) as its initial value and parameter, respectively. Then iterate Eq. (1) for 64 times to get the state variable denoted by x ₆₄. Renew x ₀₀ with x ₆₄, i.e. new x ₀₀ = x ₆₄. If d = 1, then let x ₀ = x ₀₀, p = p ₀, and end.

• Step 4. If d > 1, then execute Steps. 5–9 in a loop for d-1 times. Denote the loop variable by j, and let j = 1.

• Step 5. If j > d-1, then jump to Step 10; Else, continue to Step 6.

• Step 6. Fetch ‘k _16j+1 k _16j+2 k _16j+3 k _16j+4 k _16j+5 k _16j+6 k _16j+7 k _16j+8’ from K, and assign them to ‘k ₁ k ₂ k ₃ k ₄ k ₅ k ₆ k ₇ k ₈’. And use Eq. (2) to calculate a value named by x _0j . Then renew the value x _0j with the following formula:

$$ {x}_{0 j}=0.382\times {x}_{0 j}+0.618\times {x}_{0, j-1} $$

(4)

• Step 7. Fetch ‘k _16j+9 k _16j+10 k _16j+11 k _16j+12 k _16j+13 k _16j+14 k _16j+15 k _16j+16’ from K and assign them to ‘k ₉ k ₁₀ k ₁₁ k ₁₂ k ₁₃ k ₁₄ k ₁₅ k ₁₆’. And use Eq. (3) to calculate a value named by p _j . Then update the value of p _j with the following formula:

$$ {p}_j=0.382\times {p}_j+0.618\times {p}_{j-1} $$

(5)

• Step 8. Substitute x _0j and p _j into Eq. (1) as the initial value and parameter, respectively. Iterate Eq. (1) for 64 times to get the new state variable denoted by x ₆₄. Then renew x _0j with x ₆₄, i.e. new x _0j  = x ₆₄.

• Step 9. j = j + 1 and go to Step 5.

• Step 10. Let x ₀ = x _0,j-1, and p = p _j-1. And x ₀ and p are the initial value and parameter of Eq. (1), respectively.

In the above algorithm, the bigger the value of d is, the longer the length of the secret key K is. For example, when d = 4, the length of K is 256 bits; and when d = 8, the length of K is 512 bits. Consequently, the longer the secret key is, the longer the time consumed for generating x ₀ and p is. Now, substitute the obtained x ₀ and p into Eq. (1) and iterate Eq. (1) for M × N times to get a float matrix named by Y with size of M × N. Then generate the secret code matrix X from Y by converting each element of Y(i,j) into X(i,j) using the following formula:

$$ \boldsymbol{X}\left( i, j\right)=\mathrm{floor}\left(\boldsymbol{Y}\left( i, j\right)\times {10}^{14}\right) \mod 256, i=1,2,\dots, M, j=1,2,\dots, N $$

(6)

Rotate matrix X by 180 degrees to generate another matrix named by Z.

2.3.2 Forward diffusion

The forward diffusion operation is used to convert plain image P into a new matrix named by A, with the secret code matrix X. The steps of this operation are as follows:

• Step 1. Let i = 1,j = 1.

• Step 2. Let A(i,j) = P(i,j) + X(i,j) (mod 256).

• Step 3. j = j + 1. If j > N, then go to Step 5; Else, continue to Step 4.

• Step 4. A(i,j) = P(i,j) + A(i,j-1) + X(i,j) (mod 256), then go to Step 3.

• Step 5. Let j = 1, i = i + 1.

• Step 6. A(i,j) = P(i,j) + A(i-1,j) + A(i-1,N) + X(i,j) (mod 256).

• Step 7. j = j + 1. If j > N, then go to Step 5; otherwise, continue to Step 8.

• Step 8. A(i,j) = P(i,j) + A(i-1,j) + A(i,j-1) + X(i,j) (mod 256).

• Step 9. If i = M and j = N, then stop; otherwise, go to Step 7.

The obtained matrix A is rotated by 180 degrees to get an image matrix named by B, which is the input of the plaintext-related scrambling. The scrambling operation will be discussed in the next subsection.

2.3.3 Plaintext-related scrambling

The plaintext-related scrambling operation is used to transform matrix B into a new matrix named by D. The steps of this operation are as follows:

• Step 1. For each coordinate point (i,j) of matrix B, i = 1,2,…,M, j = 1,2,…,N, calculate the sum of the i-th row (except B(i,j)) and then calculate the sum of the j-th column (except B(i,j)), denoted by R _i and H _j , respectively. After that, calculate a new coordinate point (m,n) with the following methods:

• If j mod 2=1, then m=(H _j mod M)+1, n=(R _i mod N)+1.

• If j mod 2=0, then m=M-(H _j mod M), n=N-(R _i mod N).

• If the calculated m=i or n=j, then do nothing; otherwise, swap B(i,j) and B(m,n).

• Step 2. Scramble matrix B by looping the Step 1 for each pixel in B from the left to right and then top to bottom, to get a matrix named by D.

The above steps are shown in Fig. 3. Matrix E is generated by rotating matrix D by 180 degrees, and it will be used in backward diffusion described in the next subsection.

Fig. 3

Flowchart of plaintext-related scrambling

2.3.4 Backward diffusion

The backward diffusion operation is used to convert the matrix E into a new matrix named by F, with the help of pseudo-random secret code matrix Z. The steps of this operation are as follows:

• Step 1. Let i = 1, j = 1.

• Step 2. Calculate F(i,j) = (256 × 3 + E(i,j)-E(i,j + 1)-E(i + 1,j)-Z(i,j)) (mod 256).

• Step 3. Let j = j + 1. If j = N, then continue to Step 4; otherwise, go to Step 2.

• Step 4. Calculate F(i,j) = (256 × 3 + E(i,j)-E(i + 1,N)-E(i + 1,1)-Z(i,j)) (mod 256).

• Step 5. Let j = 1,i = i + 1. If i = M, then continue to Step 6; otherwise, go to Step 2.

• Step 6. Calculate F(i,j) = (256 × 2 + E(i,j)-E(M,j + 1)-Z(i,j)) (mod 256).

• Step 7. j = j + 1. If j = N, continue to Step 8; otherwise, go to Step 6.

• Step 8. Calculate F(i,j) = (256 + E(i,j)-Z(i,j)) (mod 256).

• Step 9. End

Rotating the obtained matrix F by 180 degrees, we get a matrix named by C, and it is the expected cipher image.

3 Simulation results

In our proposed scheme, the encryption algorithm and the decryption algorithm share the same function. Based on C language, we programmed the encryption/decryption function ‘[I ₂] = EncDecAlg(K,I ₁)’. For the encryption process, the inputs of the function ‘EncDecAlg’ are the secret key K and the plain image P, while the output is the cipher image C, i.e. C = EncDecAlg(K,P); while for the decryption process, the inputs are K and C, while the output is the recovered image P, i.e. P = EncDecAlg(K,C).

The computer used is configured with Intel Core I7-6700 k@4.00GHz CPU, 8GB DDR4 Memory, Windows 10 (64-bit) and Eclipse C/C++ with MinGW GCC Build Tool Chain. Without loss of generality, with the help of encryption/decryption function ‘EncDecAlg’ and the secret key of length 256-bit (d = 4) K = ‘FEDCBA98765432100123456789ABCDEF02468ACE13579BDFF0 E1D2C3B4A59687’ (in hexadecimal), we encrypted the plain images Lena, Baboon, Pepper and Plane (all of size 353 × 398, as shown in Fig. 4a–d, respectively) to obtain the cipher images as shown in Fig. 4e–h, respectively. Then we used the same function ‘EncDecAlg’ and the same key K to decrypt the Fig. 4e–h, and the recovered images are as shown in Fig. 4i–l. The histograms of the plain images Lena, Baboon, Pepper and Plane are as shown in Fig. 4m–p, respectively. The histograms of the cipher images (as shown in Fig. 4e–h respectively) are as shown in Fig. 4q–t, respectively.

Fig. 4

Simulation results-I. a–d Plain images of Lena, Baboon, Pepper and Plane, respectively; e–h Cipher images of (a–d), respectively; i–l Recovered images of (e–h), respectively; (m–p) Histograms of (a–d), respectively; q–t Histograms of (e–h), respectively

As can be seen from Fig. 4, (i) the proposed scheme encrypted the plain images (as shown in Fig. 4a–d, respectively) into the noise-like cipher images (as shown in Fig. 4e–h, respectively) with no visual information leakage; (ii) the decrypted images (as shown in Fig. 4i–l, respectively) are identical to the original plain images (as shown in Fig. 4a–d, respectively); (iii) the histograms of cipher images (as shown in Fig. 4q–t, respectively) are fairly flat and largely different from those of plain images (as shown in Fig. 4m–p, respectively).

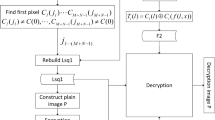
With the key K = ‘4E176D626DDBA9D65247F262F49FFF9BAF3A518EE31D4B89FE955 D51C7B52B61’ (in hexadecimal), we encrypted all-0 s image and all-255 s image (both of size 353 × 398, as shown in Fig. 5a–b, respectively) into cipher images (as shown in Fig. 5c–d, respectively). The histograms of cipher images are as shown in Fig. 5e–f, respectively. Meanwhile, when the all-black image is used as P in Fig. 2a, the intermediate cipher images A, B, D, E and F are as shown in Fig. 6a–e, respectively; when the image of Fig. 5c is used as the cipher image C in Fig. 2b, the decrypted intermediate images A _d , B _d , D _d , E _d and F _d are as shown in Fig. 6f–j, respectively. Where, A _d  = D, and E _d  = B. This indicates that one forward diffusion is equivalent to the combination of one 180-degree matrix rotation, one backward diffusion and another 180-degree matrix rotation, and the combination of one 180-degree matrix rotation and the scrambling operation is equivalent to the combination of the same scrambling operation and one 180-degree matrix rotation.

Fig. 5

Simulation results-II. a All-0 s image; b All-255 s image; c Cipher image of (a); d Cipher image of (b); e–f Histograms of (c–d), respectively

Fig. 6

The intermediate cipher images

It can be seen from Fig. 5 that the proposed cryptosystem can encrypt the all-0 s image and all-255 s image into noise-like images without any visual information leakage, and the histograms of cipher images are fairly flat.

4 Security analysis

This section will discuss the security performance of the proposed scheme from various aspects, such as encryption/decryption speed, key space, statistical properties of the cipher-text, key sensitivity, plaintext sensitivity, cipher-text sensitivity, information entropy, and so on.

4.1 Encryption and decryption speed

In the proposed scheme, the encryption and decryption processes share the same function, so the encryption speed and the decryption speed are the same. The encryption/decryption speed is related to the length of secret key and the size of image. The larger the image size and the longer the secret key length are, the longer the encryption/decryption time is. Table 1 lists the encryption/decryption time under the condition of different secret key lengths and different image sizes, where the length of the secret key is 64d bits, d = 1, 2, 4, 8, 16, and 32, the size of image is 128 × 128, 256 × 256, 353 × 398, 384 × 384 and 512 × 512, and the unit of encryption/decryption time is second.

Table 1 Encryption/decryption time for different image sizes and secret key lengths (unit:s)

As can be seen from Table 1, for the same image, the encryption/decryption time with key length of 2048 bits (d = 32) is almost equal to the encryption/decryption time with key length of 64 bits (d = 1). These demonstrate that the length of secret key imposes fairly small impact on the encryption/decryption time. Therefore, the proposed scheme can use longer secret key to enhance the security.

Take the key length of 256 bits (d = 4) as an example, the relationship between the image size and the encryption/decryption time is as shown in Fig. 7.

Fig. 7

Relationship between the encryption/decryption time and the image size

It can be seen from Fig. 7 that the encryption/decryption time is approximately linear with the image size by the fitting curve of y = (1.0149 × 10⁻⁷)x + 2.7907 × 10⁻⁴. When the image size is x = 353 × 398, the calculated encryption/decryption time is about y = 0.0145 s which is close to value 0.0140 s in Table 1, and their relative error is about 3.45%.

4.2 Key space

With the development of computer, it’s required for the security system that the length of secret key is at least 128 bits [18]. In the proposed scheme, the length of secret key is 64d bits, where d is a positive integer. As for the image of size 256 × 256, according to the encryption/decryption time as shown in Table 1, the consumed time for cracking the system with the brute-force attack method is listed in Table 2 while the used computer is the same as mentioned in Section 3. The unit of time is year in Table 2.

Table 2 Consumed time for cracking the proposed encryption system

As can be seen from Table 2, exhaustively attacking the image of size 256 × 256 in the proposed scheme, the consumed time is about 7.5532 × 10²⁸ years for the key length of 128 bits (d = 2) and about 2.5702 × 10⁶⁷ years for the key length of 256 bits (d = 4). In fact when the key length is growing to 2048 bits (d = 32), the exhaustive attack time is about 7.1734 × 10⁶⁰⁶ years. And for most applications, key of 128 bits (d = 2) or 256 bits (d = 4) is enough, and then the size of key space is 2¹²⁸ or 2²⁵⁶.

4.3 Statistical characters of cipher images

Without loss of generality, we consider the statistical properties of cipher images as shown in Fig. 4e–h. These cipher images have extremely flat histograms as shown in Fig. 4q–t, indicating that the occurrence probability of each gray scale value is approximately equal, which is the reason that the cipher image is noise-like. The relationship between adjacent pixels in the cipher images will be discussed in the following.

Select N pairs of adjacent pixels randomly from the image, and denote the values of the i-th pair by (x _i ,y _i ), i = 1,2,…,N (Labeling x = {x _i }, y = {y _i }). Then the correlation coefficient r _xy between x and y can be calculated by the following formulas:

$$ {r}_{xy}=\frac{cov\left(\boldsymbol{x},\boldsymbol{y}\right)}{\sqrt{D\left(\boldsymbol{x}\right)}\sqrt{D\left(\boldsymbol{y}\right)}} $$

(7)

$$ \mathrm{cov}\left(\boldsymbol{x},\boldsymbol{y}\right)=\frac{1}{N}{\sum}_{i=1}^N\left({x}_i- E\left(\boldsymbol{x}\right)\right)\left({y}_i- E\left(\boldsymbol{y}\right)\right) $$

(8)

$$ D\left(\boldsymbol{x}\right)=\frac{1}{N}{\sum}_{i=1}^N{\left({x}_i- E\left(\boldsymbol{x}\right)\right)}^2 $$

(9)

$$ E\left(\boldsymbol{x}\right)=\frac{1}{N}{\sum}_{i=1}^N{x}_i $$

(10)

Where, cov(x,y) represents the covariance between x and y, D(x) represents the variance of x, E(x) returns the mean value of x, and N is the length of vector x.

Here, let N = 2000, and then calculate the correlation coefficients of the plain images (as shown in Fig. 4a–d) and their corresponding cipher images (as shown in Fig. 4e–h) in the horizontal, vertical and diagonal directions, respectively. List the calculated results in Table 3. Meanwhile, illustrate the correlation of each image in the horizontal direction in Fig. 8.

Table 3 Correlation coefficients of the plain and cipher images

Fig. 8

Results of correlation analysis. a–d Correlations in horizontal direction for the plain images of Lena, Baboon, Pepper and Plane, respectively; e–h Correlations in horizontal direction for the cipher images of Lena, Baboon, Pepper and Plane, respectively

As can be seen from Table 3 and Fig. 8, the plain images have strong correlation between adjacent pixels with the correlation coefficient being close to 1; while the cipher images hardly have correlation between adjacent pixels due to their correlation coefficients being close to 0. These indicate that the proposed scheme can frustrate the attacks based on statistical properties.

4.4 Sensitivity analysis

The indicators of NPCR (number of pixels change rate) and UACI (unified average changing rate) are usually used to quantitatively measure the system sensitivity [5]. Assume that the images C ₁ and C ₂ are both of size M × N. Then define NPCR and UACI as follows:

$$ \mathrm{NPCR}=\frac{1}{ M N}{\sum}_{i=1}^M{\sum}_{j=1}^N\left|\mathrm{Sign}\left({\boldsymbol{C}}_1\left( i, j\right)-{\boldsymbol{C}}_2\left( i, j\right)\right)\left|\times 100\%\right.\right. $$

(11)

$$ \mathrm{UACI}=\frac{1}{ M N}{\sum}_{i=1}^M{\sum}_{j=1}^N\frac{\left|{C}_1\left( i, j\right)-{C}_2\left( i, j\right)\right|}{255}\times 100\% $$

(12)

For two random images, the theoretical values of NPCR and UACI are 255/256 ≈ 99.6094% and 257/768 ≈ 33.4635%, respectively [27].

4.4.1 Key sensitivity analysis

Assume the secret keys K ₁ and K ₂ are only 1-bit different, the key sensitivity can be checked from the following two cases:

• Case 1: Encrypt the plain image P by the proposed scheme with secret keys K ₁ and K ₂ to obtain two cipher images, denoted by C ₁ and C ₂ respectively. Then calculate the values of NPCR and UACI between C ₁ and C ₂.

• Case 2: Encrypt the plain image P ₁ by the proposed scheme with the secret key K ₁ to get the cipher image, denoted by C. Then decrypt the cipher image C by the proposed scheme with the secret key K ₂ to get the recovered image, denoted by P ₂. Then calculate the values of NPCR and UACI between P ₁ and P ₂.

When P ₁ takes Lena, Baboon, Pepper and Plane (as shown in Fig. 4a–d, respectively) in turn and P ₂ is a random image, the theoretical values of NPCR are all 255/256 ≈ 99.6094%, while the theoretical values of UACI are approximately 28.6181, 27.5702, 29.5959 and 32.4698%, respectively [27].

Without loss of generality, we take the plain images as shown in Fig. 4a–d (all of size 353 × 398) as examples to check the key sensitivity with the key length of 64 bits (d = 1), 128 bits (d = 2), 256 bits (d = 4), 512 bits (d = 8), 1028 bits (d = 16) and 2048 bits (d = 32). For the each selected image and key length, we do 100 trials to calculate the average values of NPCR and UACI, respectively. The calculated results are listed in Tables 4, 5, 6, 7, 8 and 9, where the values in brackets are the theoretical values of corresponding indicators. In each test, the secret keys K ₁ and K ₂ are only different on the k-th bit and are randomly generated by the following formulas:

$$ {\boldsymbol{K}}_1=\mathrm{floor}\left(\mathrm{rand}\left(1,16\times d\right)\times 1000\right) \mod 16 $$

(13)

$$ {\boldsymbol{K}}_2={\boldsymbol{K}}_1 $$

(14)

$$ k=\mathrm{floor}\left(\mathrm{rand}\times 1000\right) \mod \left(64\times d\right)+1 $$

(15)

$$ {\boldsymbol{K}}_2\left(\mathrm{floor}\left(\left( k-1\right)/4\right)+1\right)=\mathrm{bitxor}\Big({\boldsymbol{K}}_2\left(\mathrm{floor}\left(\left( k-1\right)/4\right)+1\right),\mathrm{pow}2\left(\left( k-1\right) \mod 4\right) $$

(16)

Table 4 Results of key sensitivity tests (d = 1)

Table 5 Results of key sensitivity tests (d = 2)

Table 6 Results of key sensitivity tests (d = 4)

Table 7 Results of key sensitivity tests (d = 8)

Table 8 Results of key sensitivity tests (d = 16)

Table 9 Results of key sensitivity tests (d = 32)

Where, rand(a,b) produces a 0–1 uniformly distributed random number matrix with size of a × b, floor(x) returns the largest integer less than or equal to x, pow2(x) means 2^×, and bitxor(x,y) means x bitwise XOR y.

The results in Tables 4, 5, 6, 7, 8 and 9 show that the calculated values of NPCR and UACI are very close to their corresponding theoretical values. This indicates that one bit change of any secret key with length of 64 bits (d = 1), 128 bits (d = 2), 256 bits (d = 4), 512 bits (d = 8), 1024 bits (d = 16) or 2048 bits (d = 32) will lead to dramatic changes in cipher images or recovered images, which demonstrates that the proposed scheme has strong key sensitivity, and each secret key in key space is valid.

4.4.2 Plaintext sensitivity analysis

Assume that the plain images P ₁ and P ₂ are only one pixel different. Encrypt them by the proposed scheme with the same key K to get two cipher images, denoted by C ₁ and C ₂, respectively. Then calculate the values of NPCR and UACI between C ₁ and C ₂.

Here taking the plain images Lena, Baboon, Pepper and Plane with size of 128 × 128, 256 × 256, 353 × 398, 384 × 384 and 512 × 512 as examples to explore the proposed scheme with key length of 256 bits (d = 4) and 2048 bits (d = 32). For each image we do 100 trials to calculate the average values of NPCR and UACI, respectively. The results are listed in Tables 10 and 11. Note that for each test, the secret key is randomly produced by the Eq. (13).

Table 10 Results of plaintext sensitivity tests (d = 4, unit: %)

Table 11 Results of plaintext sensitivity tests (d = 32, unit: %)

As can be seen from Tables 10 and 11, the calculated values of NPCR and UACI are very close to their corresponding theoretical values, which indicates that the slight change in plain images will lead to the dramatic changes in cipher images even with the same secret key. So, the proposed scheme possesses strong plaintext sensitivity. Hence, the proposed scheme can in a way frustrate the differential attack base on the plain images.

4.4.3 Cipher-text sensitivity analysis

Assume that the plain image P ₁ was encrypted by the proposed scheme with secret key K ₁ to generate the cipher image, denoted by C ₁. Change C ₁ by only one pixel to get the image named by C ₂, i.e. C ₂ = C ₁ except that C ₂(i,j) = C ₁(i,j) + 1 (mod 256) on a certain pixel position (i,j). Assume that K ₁ is changed by only one bit to get another key named K ₂. We will check the cipher image sensitivity from the following two cases:

• Case 1: Decrypt cipher image C ₂ by the proposed scheme with secret key K ₁ to get the recovered image named P ₂. Then use indicators of NPCR and UACI to analyze the level of difference between P ₁ and P ₂. When P ₁ takes the plain images as shown in Fig. 4a–d in turn and P ₂ is a random image, the theoretical values of NPCR are all 255/256 ≈ 99.6094%, while the theoretical values of UACI are 28.6181, 27.5702, 29.5959 and 32.4698%, respectively [27].

• Case 2: Decrypt C ₁ and C ₂ by the proposed scheme with the slightly changed key K ₂ to get the recovered images, denoted by P ₃ and P ₄, respectively. Then use indicators of NPCR and UACI to analyze the degree of difference between P ₃ and P ₄. The theoretical values of NPCR and UACI are 255/256 ≈ 99.6094% and 257/768 ≈ 33.4635%, respectively [27].

Without loss of generality, take the plain images Lena, Baboon, Pepper and Plane (as shown in Fig. 4a–d all of size 353 × 398) as examples to test the cipher-text sensitivity of proposed scheme with the key length of 256 bits (d = 4) and 2048 bits (d = 32). For given plain image P ₁, firstly, randomly generate two secret keys K ₁ and K ₂ with Eqs. (13)–(16). Secondly, encrypt P ₁ by the proposed scheme with the secret key K ₁ to get the cipher image C ₁. Thirdly, randomly change one pixel of C ₁ by one bit to get the image C ₂, and then decrypt C ₂ by the proposed scheme with the secret key K ₁ to get P ₂. Fourthly, decrypt C ₁ and C ₂ by the proposed scheme with the secret key K ₂ to get their corresponding P ₃ and P ₄. Finally, calculate the values of NPCR and UACI with Eqs. (11)–(12). Repeat the above trails for 100 times, and calculate the average values of NPCR and UACI, respectively. The results are listed in Tables 12 and 13, where, the values in brackets are theoretical values of corresponding indicators. In Table 12 the length of secret key is 256 bits (d = 4), while in Table 13 the length of secret key is 2048 bits (d = 32).

Table 12 Results of cipher image sensitivity tests (d = 4)

Table 13 Results of cipher image sensitivity tests (d = 32)

As can be seen from Tables 12 and 13, the test value of NPCR and UACI are very close to their corresponding theoretical values, indicating that the proposed scheme is extremely sensitive to the tiny change of cipher images, which is helpful for the scheme to resist the differential attack based on cipher images.

4.5 Information entropy

Information entropy reflects the uncertainty of the image information. For a grey image of L-level, when the occurrence probability of grey value i is p(m _i ), the information entropy of this image is formulated as follows:

$$ H(m)=-{\sum}_{i=0}^{L-1} p\left({m}_i\right){log}_2\left( p\left({m}_i\right)\right) $$

(17)

The larger the information entropy is, the more uncertainty the image information is, and the less intelligible the image is. For an 8-bit random image, the theoretical value of information entropy is 8.

Here, L = 256. We used the plain images all-zeros (pure black), all-255 s (pure white), Lena, Baboon, Pepper and Plane (all with size of 128 × 128, 256 × 256, 353 × 398, 384 × 384 and 512 × 512) and their corresponding cipher images. The secret keys used in each test are randomly generated by Eq. (13) with the length of 128 bits (d = 2) and 256 bits (d = 4). The calculated values of information entropy for these plain and cipher images are listed in Tables 14, 15 and 16.

Table 14 Results of information entropy tests for all-white and all-black images (d = 2 and d = 4)

Table 15 Results of information entropy tests (d = 2)

Table 16 Results of information entropy tests (d = 4)

According to the results in Tables 14, 15 and 16, we can see that the values of information entropy for plain images are largely different from the theoretical value of noise image (i.e. 8), while the values of information entropy for cipher images are very close to 8. For the plain images of all-black and all-white whose information entropies are 0, their corresponding cipher images still have excellent information entropies (see Table 14). These demonstrate that the proposed scheme can resist the attacks based on information entropy.

4.6 Comparison analysis

Without losing generality, take image Lena of size 512 × 512 as an example. Compare the proposed scheme with the AES in CBC mode and the schemes in [6, 7, 23] in aspects of encryption/decryption speed and system sensitivity. The computer used has the same configuration as the one in Section 3. The system sensitivities of AES and the schemes in [6, 7, 23] are listed in Table 17. Here, AES uses a key of 128-bit length. In [23], the initial value and parameter of Logistic map are directly used as the secret key, so the key length is about 96 bits. The scheme in [7] uses the initial value and parameter of Tent map as the secret key, so its key length is about 100 bits. In [6], the initial values and parameters of two Tent map are directly used as the secret key in the encryption scheme, so the key length is about 200 bits. Here, our proposed system with the key of length 512 bits is used to make the comparison.

Table 17 Sensitivity analysis results of several cryptosystems (Unit: %)

According to Table 17, and the security analyses of our proposed system and the systems in [6, 7, 23], the results of the performance comparison are listed in Table 18.

Table 18 Performance comparison analysis results

From Table 18, the encryption/decryption speed of AES is about 7.5709Mbps, and this speed can be used as a threshold to measure the speed of newly proposed image encryption algorithms. The image encryption algorithms having higher processing speed than AES are considered to be practically significant. The scheme in [23] is slower in encryption/decryption speed than AES. The system sensitivities of AES and the schemes in [7, 23] are not good. However, both our proposed scheme and the scheme in [6] possess fast encryption/decryption speed and excellent system sensitivities. Furthermore, our proposed scheme is the fastest one. So, our scheme is superior to the above schemes.

5 Conclusion

This paper presents a new plaintext-related image encryption system. In the proposed system, the encryption algorithm and the decryption algorithm are exactly the same. They both include the operations of plaintext-related scrambling once, diffusion twice, and matrix rotating 180 degrees four times. The key length of proposed system can be extended to support 64d–bit length, where d is a positive integer. Since the encryption and decryption procedures are identical, the proposed scheme can use one device to fulfill both encryption and decryption to save hardware resources. And due to the usage of plaintext-related scrambling algorithm, the proposed scheme can frustrate the chosen/known plaintext attacks.

For the 512-bit long key, the encryption/decryption speed is up to 77.6723Mbps in the used computer. Since the secret code matrix (i.e. X in Fig. 2) can be generated separately from the confusion and diffusion process, the average encryption/decryption speed will be far higher than the speed of processing one single image when encrypting/decrypting multiple images. The simulation results and comparison analysis show that the proposed scheme has some merits, such as fast encryption speed, large key space, strong key sensitivity, strong plaintext sensitivity, good statistical properties of cipher images, strong cipher-text sensitivity, large information entropy and so on. Therefore, the proposed encryption system can be used in actual communications.

In the future, on the basis of the image cryptosystem with identical encryption and decryption process, further researches on new confusion and diffusion algorithms based on the finite field integer operations will be carried out to improve the processing speed without loss of security. Also, the scheme’s application to color images and videos will be studied.