1 Introduction

In recent years, there has been an increasing interest at multimedia data security because of the wide-spread transmission over all kinds of communication and social networks. Considering the inherent features of image, such as bulk data capacity and strong correlation among adjacent pixels, traditional data encryption schemes cannot meet the requirements of multimedia security. The intrinsic relationship between chaos and cryptography inspired researchers and a variety of encryption schemes have been proposed [1, 2, 5, 6]. For example, Chen et al. [1] designed a three dimensional Arnold cat map, and used it in a symmetrical image encryption algorithm. Guan et al. [2] proposed a fast image encryption design according to the character of hyper-chaos. Unfortunately, many cryptanalysis works [4, 9, 11, 12, 14] have revealed that some of those chaos-based cryptosystems have serious security problems due to their improper use of chaos pseudo-random sequences. Rhouma et al. [9] gives a way that just demands three couples of plaintext/ cipher text to break totally the crypt-system.

In 1994, Adleman first introduced DNA computing into the encryption field, which created a new stage of information security. Due to massive parallelism and extraordinary information density exclusive characteristic of DNA molecule, DNA cryptography emerged as a new frontier and is presently at the forefront of international cryptography research [8, 13]. DNA encryption is a subject of study how to utilize DNA bases as an information carrier, and it uses modern biological technology to achieve encryption. Many symmetric encryption schemes have been proposed, in which the DNA-based image encryption is generally categorized into two phases: firstly, using DNA theory to encode plain image pixels into DNA sequence, and each gray pixel value is decomposed into four DNA elements, which can increase the efficiency of image substitution and permutation. Secondly, the encoded DNA sequence is substituted and permuted to generate a key image based on DNA operation rules and form the cipher image [3, 7, 10].

Recently, a novel image encryption algorithm [15] was designed based on chaos system and combined with DNA coding and information entropy. It mainly consists of two stages of process: substitution and permutation process. Encryption is operated on the domain of DNA encoding matrix, and entropy is introduced to generate various permutation matrix which is expected to enhance security against known/chosen plaintext attacks.

However, we notice that two vulnerabilities exist in this algorithm. First, the introduced entropy fails to protect permutation indexes under chosen-plaintext attack, because we can rebuild the entropy from cipher image directly rather than by breaking encrypted entropy in cipher. And second, the substitution of elements in the last column leaks patterns of the encoding rule, and which permit us to recover the encoding rule and cover matrix after breaking the permutation. Then a complete attack algorithm is presented in this paper based on these two vulnerabilities, and our analysis and experiments demonstrate that this algorithm can break the encryption algorithm under chosen-plaintext attack. Further, some improvements are proposed to make up these vulnerabilities and enhance encryption algorithm’s security.

The remaining of this paper is organized as follows. The next section gives a brief introduction of the original encryption algorithm. The vulnerabilities and the presented chosen-plaintext attack is discussed detailedly in Section 3. In Section 4, some improvement are proposed to enhance the security. And finally, the last section gives a brief conclusion.

2 The original encryption algorithm

2.1 Process of the encryption

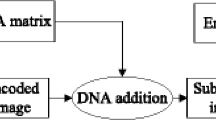
The block diagram of the original image encryption algorithm [15] is shown in Fig. 1.

Fig. 1
figure 1

Block diagram of the image encryption algorithm [15]

Full size image

To perform the encryption, the plain image I input of size m × n is firstly converted into an m × 4n matrix I d by decomposing each pixel into four two-bit numbers. Then the matrix I d is encrypted with the following two main stages:

  1. (1)

    Substitution stage

    Iterate the logistic chaotic map (1) with the initial state \(({x_{0}^{l}},{u_{0}^{l}})\) to get a real number sequence L 1 = {x 1, x 2, ⋯ , x 4n × m }.

    $$ f(x,u) = ux(1-x) $$
    (1)

    Let ⌊x⌋ denote the largest integer less than or equal to x. Compute terms L(i, j) = ⌊x (i − 1) × 4n + j × 28⌋ mod 4(1 ≤ i ≤ m, 1 ≤ j ≤ 4n) to get the integer matrix L, and encode L to cover matrix L′ according to rule (2). At the same time, compute encoding modes e(i) = ⌊x i × 4n × 28⌋ mod 8 and encode I d to matrix I′ (the i-th row is encoded following DNA encoding rule e(i)).

    $$ L^{\prime}(i,j) = \left\{\begin{array}{ll} A & if \ L(i,j) = 0 \\ C & if \ L(i,j) = 1 \\ G & if \ L(i,j) = 2 \\ T & if \ L(i,j) = 3 \end{array}\right. $$
    (2)

    Then perform the DNA addition to get the DNA matrix I DNA by I DNA = I′ + L′. The eight encoding rules for the DNA sequence are listed in Tables 1 and 2 describes DNA addition operation.

  2. (2)

    Permutation stage

    $$ x_{n+1}(i) = (1-\varepsilon)f(x_{n}(i),u)+\frac{\varepsilon}{2}[f(x_{n}(i+1),u)+f(x_{n}(i-1),u)] $$
    (3)

    A 3-dimensional spatiotemporal chaotic system (3), with parameter u s, ε and initial values \({x_{0}^{s}} (1),{x_{0}^{s}} (2),{x_{0}^{s}} (3)\), is adopted to generate two sequences R = {x i (1), 1 ≤ i ≤ m} and C = {x j (3),1 ≤ j ≤ 4n}. Then the DNA matrix is permutated as \(I_{DNA}^{\prime } (i,j) = I_{DNA} (Ind_{R} (i),Ind_{C} (j))\), in which the Ind R and Ind C are the sorting indexes of sequences R and C respectively. To avoid chosen-plaintext attack, entropy H of I DNA is introduced to modify u s thus different plain image will have different permutation indexes. First, the decimal part of entropy H is used as \({x_{0}^{H}}\) (if H is an integer, then \({x_{0}^{H}}={x_{0}^{l}}\)), and generate \(x_{20}^{H}\) with the logistic map (1). Keep the first 64 bits of \(x_{20}^{H}\) as H decimal , and u s = 3.75 + 0.25H decimal .

Table 1 The DNA encoding and decoding rules
Full size table
Table 2 The DNA addition operation
Full size table

Finally, the \(I_{DNA}^{\prime }\) is DNA decoded with the first rule in Table 1 and composed back into an 8-bit cipher image I cipher . The encrypted H decimal and I cipher are sent as cipher text.

2.2 Encryption examples

Here we give a simple example to show the process of encryption. It is also an attack target for our cryptanalysis example in Section 3.

The plain image I is first decomposed into a matrix I d .

For \(key=\{{x_{0}^{l}}=0.437,u^{l}=3.785,{x_{0}^{s}}=(0.364,0.785,0.293),\varepsilon =0.2582\}\), the cover matrix L′ and the encoding mode e are

$$e=(1,7,2,2).$$

and I d is encoded as

Then the substituted matrix

Count the numbers of C, A, T, G, they are #(C) = 10, #(A) = 14, #(T) = 11, #(G) = 13. Then the entropy H ≈ 1.9874, and u s ≈ 3.9321. Run the spatiotemporal system, and sort the generated sequences R and C, we get

$$Ind_{R}=(2,3,4,1),\ and\ Ind_{C}=(1,2,10,7,3,11,8,5,4,12,6,9).$$

Then the permutated matrix

Decode \(I_{DNA}^{\prime }\) and compose the matrix, we get the final cipher image I cipher .

For another example, the gray image Lena is encrypted with the same key, and the result is shown in Fig. 2.

Fig. 2
figure 2

Image Lena and its cipher image

Full size image

3 Chosen-plaintext cryptanalysis

Since the first step “decomposition” and the last step “DNA decoding & composing” in encryption algorithm are independent with the key, we will bypass them in following discussion for simplicity. The to-be-broken cipher matrix is denoted by \(I_{DNA\_t}^{\prime }\).

Although entropy has been introduced to affect the parameter of the spatiotemporal system, and thus the permutation indexes may differ for different images, we found it is still possible to create an image which has the same permutation index as special cipher image used. We name this image a ”good-entropy” image. In the following, the method of creating good-entropy images will be described firstly, and it will be used to rebuild the permutation indexes Ind R and Ind C ; then a further method is given to recover the e and L′. Finally, the target plain image can be decrypted with the e, L′, Ind R and Ind C .

3.1 Method to generate a good-entropy plain image

Notice that the spatiotemporal system is driven by the key and the entropy of I DNA , so a plain image who generates the same I DNA entropy will have the same spatiotemporal system intput and also have the same permutation indexes. Therefore the focus is how to create a plain image with a specific I DNA entropy.

There is a clue for the I DNA entropy: The numbers of C, A, T, G are the same before and after permutation because permutation changes positions but leaves values unchanged. So the entropy of I DNA is equal to the entropy of I cipher . In fact, we do not need to send the encrypted H decimal in the encryption algorithm, it can be calculated from the cipher image with the key.

Based on this clue, we can design a greedy algorithm which tunes elements one by one in the decomposed plain matrix I d , while observe the numbers of C, A, T, G in the cipher image, until they are all equal to those in the target cipher image. The input of this algorithm is a random image, and the output image has the same permutation indexes as the target cipher image has. The detail of the greedy algorithm GA() is given in Table 3.

Table 3 ᅟ
Full size table

Note elements in the last column in I d0 are kept unchanged, because this column will be used to recover the modes e. This is discussed in Section 3.3.

3.2 Rebuild the permutation indexes Ind R and Ind C

Once we make a good-entropy image matrix, denoted I d0, it is possible to rebuild the permutation indexes.

Suppose we have another image matrix I d1 that is equal to I d0, except two elements (at position a and b) are different: I d0(a) ≠ I d1(a) and I d0(b) ≠ I d1(b). If the two elements’ substitution results are swapped, i.e. S(I d0(a)) = S(I d1(b)) and S(I d0(b)) = S(I d1(a)), the numbers of C,A,T,G in cipher matrixes for I d0 and I d1 will be equal, then we know I d1 is also a good-entropy image matrix. Here we define function f(I(a), e) represents element I(a) being DNA encoded by rule e, and function S(I(a)) = f(I(a), e) + L′(a) represents the substituted element at position a (Fig. 3).

Fig. 3
figure 3

Construct plain image with equal entropy by changing two elements

Full size image

If we limit the two elements in the same row i (1 ≤ i ≤ m), they will be permuted to a same row j (1 ≤ j ≤ m). By observing the difference between their cipher matrixes Enc(I d0) and Enc(I d1), only two different elements exist in one row, we can find where the j is. Repeat the work for each row, and the permutation index Ind R is rebuilt. We name this process PI_R() and details are given in Table 4.

Table 4 ᅟ
Full size table

Similar algorithm PI_C() is performed to rebuild the column permutation index Ind C , in which all works on rows are changed to columns.

It is also worth to mention that since there are only four possible values for each elements in plain matrix and cipher matrix, it is easy to find two proper elements and their modifications.

3.3 Recover the encoding modes e and cover matrix L′

The next work is to recover the encoding modes e.

We noticed that the encoding modes and cover matrix for the last column are both from logistic sequence x 4n × i . For example, element I d (1,4n) is encoded with rule e(1) = ⌊x 4n × 28⌋ mod 8 and added with cover L′(1,4n), which is mapped from L(1,4n) = ⌊x 4n × 28⌋ mod 4 = e(1) mod 4. The substitution results f(I(∗,4n), e) + L′(∗,4n) for element value I(∗,4n) = 0 and 3 are listed in Table 5.

Table 5 ᅟ
Full size table

It can be seen that the pairs (f(0, e) + L′, f(3, e) + L′) uniquely decide the encoding rule e, and the mapping is given in Table 6.

Table 6 Encoding rule e uniquely decided by substituted elements of two cases
Full size table

To perform the recovery, we first prepare two plain images I df0 (a matrix in which all elements are 0) and I df3 (a matrix in which all elements are 3), tune them with algorithm \(I_{d0}=GA(I_{df0}, I_{DNA\_t}^{\prime })\) and \(I_{d3}=GA(I_{df3}, I_{DNA\_t}^{\prime })\), so that they are both good-entropy image matrixes. Note the last column will not be changed in GA(), i.e. elements in the last column of I d0 are all 0 and that of I d3 are all 3. Encrypt them, and inverse-permute the cipher matrixes, so that we can get the substitution results of the last columns. Then the encoding rule e can be obtained by looking up Table 6 according to the last columns.

To recover the cover matrix L′ is easy. A simple DNA subtraction between substitution result and encoded I d0 can make it.

3.4 The entire attack process

The entire attack process is given in Table 7, which includes:

  1. Step 1:

    Generate two good-entropy image matrixes I d0 and I d3 with the greedy algorithm GA(), in which elements in the last columns are 0 or 3 respectively. Then they are encrypted as \(I_{DNA0}^{\prime }\) and \(I_{DNA3}^{\prime }\).

  2. Step 2:

    I d0 is used to rebuild the permutation indexes Ind R and Ind C with algorithm PI_R() and PI_C().

  3. Step 3:

    The cipher matrixes of \(I_{DNA0}^{\prime }\) and \(I_{DNA3}^{\prime }\) are inverse permuted. The last columns of them are used to recover the DNA encoding rule e according to Table 6.

  4. Step 4:

    I d0 is DNA encoded with rule e, then DNA subtracted from the inverse permuted cipher matrixes of I d0. The result recovers the cover matrix L′.

  5. Step 5:

    Use the Ind R , Ind C , e and L′ to decrypt the cipher image with normal decryption algorithm.

Table 7 The attack algorithm
Full size table

3.5 Attacks on examples in Section 2.2

As an example, we will attack the matrix I cipher in Section 2.2 first.

In step 1, two good-entropy image matrixes I 0 and I 3 are generated according to the matrix \(I_{DNA\_t}^{\prime }\).

The cipher matrixes are:

Count the numbers of C, A, T, G in both matrixes, they are #(C) = 10, #(A) = 14, #(T) = 11, #(G) = 13, equal to the result of \(I_{DNA}^{\prime }\).

In step 2, permutation indexes Ind R and Ind C are rebuilt and equal to those shown in Section 2.2.

In step 3, I e0 and I e3 are inverse permuted, and we get:

Take the last column to look up Table 6, we get the encode rule e. This is shown in Table 8.

Table 8 Recover of rule e for matrix example in Section 2.2
Full size table

In step 4, I d0 is DNA encoded with rule e,

Compute \(L^{\prime }=I_{DNA0}-I_{0}^{\prime }\), we can get the same cover matrix as given in Section 2.2.

Finally in step 5, we use the Ind R , Ind C , e and L′ to decrypt the cipher image with normal decryption algorithm, and the decryption result is equal to original input matrix I.

For the example of encrypted Lena, the attack result is shown in Fig. 4.

Fig. 4
figure 4

Revealed image Lena

Full size image

4 Improvement on encryption algorithm

There are two vulnerabilities in the original encryption algorithm: one is the entropy fails to play the role in protecting permutation indexes; and the other is the encoding rule and cover matrix for elements in last column are based on a same number, which leaves a pattern in cipher and cause the rule be recovered. Therefore, our improvement aims at these two vulnerabilities.

  1. (1)

    To protect the permutation indexes

    Instead of using entropy of I DNA , a hash function is much better to generate a finger print of I DNA . For example, we can DNA decode I DNA using rule 0, and reform all elements into a 0-1 sequence. Then standard SHA algorithm can be applied to hash the sequence, and the hash value is used to replace the entropy value.

    We know hash value can be viewed as a fingerprint of data. No matter what changes in numbers or positions of C,A,T,G, it will lead to a different hash value. So, although I DNA and \(I_{DNA}^{\prime }\) have same numbers of C,A,T,G, they don’t have same hash value, and attackers can’t guess I DNA from \(I_{DNA}^{\prime }\).

    Also, the hash value needs to be encrypted and sent.

  2. (2)

    To improve the substitution process

    To separate the source of encoding rule and cover matrix, we can assign a private value to e by generating longer chaos sequences. Namely,

    $$L_{1}=\{x_{1},x_{2},\cdots,x_{4n}\},\ \ \ e_{1}=\lfloor x_{4n+1}\times2^{8} \rfloor\mod8,$$
    $$L_{2}=\{x_{4n+2},x_{4n+3},\cdots,x_{8n+1}\},\ \ \ e_{2}=\lfloor x_{8n+2}\times2^{8} \rfloor\mod8.$$

    and so on.

    Such, the relation between encoding rule and cover matrix will be protected by the property of chaos system.

Further, if we use another logistic sequence driven by appending key \(({x_{0}^{e}},{u_{0}^{e}})\) to calculate encoding rule e, and use original logistic sequence driven by \(({x_{0}^{l}},{u_{0}^{l}})\) to calculate cover matrix L′, the relation between encoding rule and cover matrix can be protected more safely.

5 Conclusion

In this paper, we present a cryptanalysis on an encryption algorithm which based on chaos system and combined with DNA coding and information entropy. Two vulnerabilities are found, and they make the substitution based on DNA coding and operation fail to cover plain data, and introduced entropy fails to protect permutation indexes under chosen-plaintext attack. A complete attack algorithm is given, and our analysis and experiments demonstrate its effectiveness. Finally, some advices are proposed to make up these vulnerabilities and enhance encryption algorithm’s security.