1 Introduction

3D deformed meshes are commonly used in computer games, computer generated movies, and many scientific applications. In these applications, they are often complex and nonlinearly generated. Deformed objects contain large geometric datasets. Indeed, the deformations are computed by a minimization method. We develop a new mesh deformation method applied in the domain of ROI (region of interest) based on Multi Library Wavelet Neural Network structure relying on several mother wavelets families (MLWNN) to optimize and align the mesh features.

Actually, 3D deformed models require even larger memory and transmission bandwidth since a sequence consists of a large number of frames and every frame is a large static 3D object. Therefore, it is important to develop compact representations that significantly reduce the storage space of the deformed models and facilitate their transmission over networks.

Our approach generated smaller encoded file size to encode the current frame and get higher compression rates while maintaining reasonable quality. The main objective of compression algorithms is to eliminate the redundancy present in the original data and to obtain progressive representations targeting the best trade-off between data size and approximation accuracy [18]. Moreover, these compression algorithms allow smaller compressed representations guaranteeing good visual fidelity. For our 3D deformed mesh, we propose a multi-layer compression method based on the geometric and connectivity data of the 3D object applied in each layer of deformation process. This compression was applied to facilitate transmission of the vertex of a deformed object to another. It can eliminate the passage of a deformed object since compression removes not important vertices when deformation is not performed in the region of interest. The object becomes less complex, making easier the whole deformation process.

Our compression was performed using the spherical geometrical image obtained by our spherical parameterization based on trust region method [21]. A spherical projection method was applied to transform meshes into geometrical image.

The best compression algorithms in literature generally use remeshing as the preliminary step; since they are not applicable to irregular meshes. In these algorithms, much smaller errors reside while making predictions on the vertices of these models. Thus, their compression bit rates are very low compared to those of algorithms that are compressing irregular meshes. For this surface, mesh should be represented as a semi-regular one obtained by regular 1:4 subdivision of a base mesh. A wavelet transform can be used to compress surface connectivities based on adaptive wavelet transformation (WT) scheme that can be embedded into a known image coder. The WT scheme is used in the coding of the image objects.

2 Related work

Many existing compression schemes are restricted to animated and deformed meshes that do not change the topological information from one frame to another in order to be compressed once. In these schemes, only the vertex positions need to be compressed for the individual frames. Here, we distinguish between four methods:

Predictive-based methods [10, 33], PCA-based representations [1, 12, 29], wavelet-based techniques [7, 25] and and clustering-based approaches [15, 35]. Recently, research has started to focus on animated meshes with fixed connectivity. Lengyel [15] introduced the first work on animated geometry compression. He partitioned the mesh into sub-meshes and described the motion of the sub-meshes by rigid body transformations.

Jinghua et al [35] used an octree to spatially cluster the vertices and represent their motion from the previous frame to the current one with a very few number of motion vectors. Their algorithm predicts the motion of the vertices enclosed in each cell by tri-linear interpolation in the form of weighted sum of eight motion vectors associated with the cell corners. The octree approach was later used by K. Mueller et al [19] to cluster the difference vectors between the predicted position and the original one. Alexa et al [1] applied PCA to achieve a compact representation of animation sequences. Afterwards Karni and Gotsman [12] improved this method by using second-order Linear Prediction Coding (LPC) to the PCA coefficients such that the large temporal coherence present in the sequence would be further exploited. Sattler et al [29] introduced the clustered PCA. According to this approach, mesh is segmented into meaningful clusters which are then compressed independently using a few PCA components only. Prediction techniques can also be used to efficiently compress animated meshes. Assuming that the connectivity of the meshes is stable, the neighborhood in the current and previous frame(s) of the compressed vertex is exploited to predict its location or its displacement [10, 33]. The residuals are compressed up to a user-defined error. Guskov et al [7] used wavelets for a multi-resolution analysis and exploited the parametric coherence in animated sequences. The wavelet detail coefficients are progressively encoded. Payan et al. [25] developed the lifting scheme to exploit the temporal coherence. The wavelet coefficients were thereby optimally quantized.

Kammoun et al [11] proposed to optimize the prediction scheme of lifting-based wavelet transforms (Butterfly and Loop). For each detail level, the best parameters of the predictor were computed to minimize the set of detail coefficients. Experimental results show that, compared to classic wavelet decomposition, the root mean square distortion is slightly reduced (2 %) at similar rate. Chourou et al [4] resorted to mesh segmentation in order to optimize the wavelet operators for each of the generated clusters. The parameters of lifting scheme prediction step were chosen to minimize the variance of the detail coefficients. The compression scheme of Zhao et al [36] based on matrix-valued Loop is subdivision for better shape control. The encoder of Denis et al [5] exploited the statistical dependencies between the intraband and composite wavelet coefficients to determine the best quantizers. Chen et al [3] suggested compressing an input surface by regularly remeshing it with quads. The quadrilateral subdivision splits each face into 4 new faces by inserting one vertex. The wavelet decomposition was formulated through a lifting scheme. Zerotree coding was also used to encode the coefficients. Other mesh methods using wavelet transforms focused on mobile decompression [17] and the lossy transmission support [16]. The objectives of this approach are to reduce the number of computations needed for the decompression and to use error protection techniques to fit mobile computational capabilities and lossy networks. Nevertheless, in general, wavelet-based algorithms generally provide a significantly better rate-distortion performance despite their lossless counterparts. Recently, Tang [31] proposed 3D triangle mesh compression based on vector quantization with k-ring vector prediction which optimally employs the correlation between the vertex to be encoded and its adjacent encoded vertices. Rabab M. Ramadan and Rehab F. Abdel-Kader [27] developed 3D Face Compression and Recognition using Spherical Wavelet Parametrization. They also introduced a fully automatic process for the preprocessing and the registration of facial information in the 3D space. Next, the spherical wavelet features were extracted, which provided a compact descriptive biometric signature. Indeed, spherical representation of faces permits effective dimensionality reduction through simultaneous approximations.

3 Our proposed mesh deformation based on MLWNN architecture and Multi-layer compression algorithm

3.1 Mesh deformation based on MLWNN architecture

Geometric modeling focuses particularly on the geometrical representation and spatial relationships between real objects. For mesh deformation, it is important to apply an effective method to align the features between the original object and the target one to have good deformation technique with low rate deformation of fixed features. Wavelet neural networks, using wavelets as basic function, have various interesting properties including fast training and good generalization performance. In fact, various methods have been proposed for structure selection and wavelet neural networks training.

The wavelet network structure with one output,f, can be expressed by the following equation:

$$ f(x)=\sum\limits_{j=1}^{M}\sum\limits_{i=1}^{N_{l}}{\omega_{i}^{j}}{{\Psi}_{i}^{j}}(x)+ \sum\limits_{k=0}^{N_{i}}a_{k}x_{k}+b $$
(1)

\(x=[x_{1},x_{2},...,x_{N_{i}}]^{T}\) is the input vector. Functions \({\omega _{i}^{j}}\) are dilated and translated versions of the several mother wavelets Ψj. N l is the selected wavelet number for the mother wavelet family. The index l depends on the wavelet family and the choice of the mother wavelet. The wavelet network architecture proposed in [2, 22, 23] can be viewed as a network with an input vector of N i components, a hidden layer that is constituted of N M w wavelets of M mother wavelets; each belongs to a wavelet family of the size N i and a linear output neuron. Such a network is shown in Fig. 1.

Fig. 1
figure 1

Multi-Mother Wavelet Network Structure

Full size image

We introduce, in this work, a new 3D deformed approach based on MLWNN structure. It was realized in two steps:

  • Network initialization: this step consists in developing a wavelet library made up of translated, dilated and rotated versions of a mother wavelet.

  • Optimization of network parameters: was performed by combining a selection method OLS (Orthogonal Least Squares) and an optimization algorithm Levenberg-Marquardt. This algorithm determines the linear parameters of the network and iteratively optimizes the number and the parameters of wavelets by minimizing the rate deformation between the two objects.

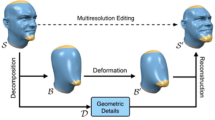
Figure 2 represents our proposed algorithm as follows:

Fig. 2
figure 2

Deformation processes based spherical parametrization and MWNN

Full size image

We applied an effective spherical mapping algorithm using trust region optimization scheme minimizing angle and area distortions. It generally guarantees a bijective spherical parameterization [21] as a common domain of the source and target objects. Spherical parameterization, which consists in establishing a correspondence between the two source and target meshes, is a mandatory and important step in the deformation process. In order to define a geometric mesh object, we concentrated on the use of feature points. We assumed that the shape of the object is defined by the locations of the predefined feature points on the surface of the mesh. Moreover, the mesh deformation can be completely determined by the movements of these feature points (alternatively referred as control points) from their neutral positions either in absolute or in normalized units. We used a Wavelet network approximation to optimize the align feature for mesh and minimize distortion with fixed features.

The general process of our proposed mesh deformation based on Multi Library Wavelet Neural Network architecture is presented in Fig. 3.

Fig. 3
figure 3

Overview of the feature-based MLWNN algorithm

Full size image

The objective of our algorithm is to achieve a feature alignment process that reduces the distances between features without modifying the local vertex positions on the spherical maps. Indeed, our method is based on the Laplacian representation designed for large rotations. Laplacian mesh editing allows deforming 3D objects while their surface details are preserved because it allows the simulation of realistic deformations [20, 30]. This representation permits direct detail-preserving reconstruction of the modified mesh by solving a linear least squares system.

3.2 Progressive compression algorithm for MLWNN mesh deformation

Geometry image is an original method that compresses manifold meshes, and remesh an arbitrary surface onto a semi regular structure . It can be encoded using traditional image compression and decompression algorithms, such as wavelet-based coders. The mesh-based spherical scheme is more natural for coding geometry. The sphere is a natural and seamless parametric domain for closed genus-0 surfaces. It provides good reconstruction of shape details at very low bit budgets. The spherical wavelet transformation is used to decompose the object into multi-resolution sub-images. Besides, the geometry of meshes is often very dense (over-sampling) and their connectivity is arbitrary (irregular neighborhood of vertices). It is often necessary to remesh them to reduce their complexity (simplification), improve the quality of triangles products and optimize the sampling geometry or connectivity as regular as possible.

3.2.1 Trust region spherical parameterization

Trust region spherical parameterization algorithm [21] was integrated to obtain good geometry images. Besides, a spherical parameterization method was applied to convert meshes into geometrical image. Our approach reduced the computation distortion required for the procedure of mesh parameterization in a sphere since all calculations were performed in the sphere space to reduce the distortion angle and region at mapping each of the triangles.

We propose an effective optimization scheme to compute such parameterization and have an algorithm exposing a property of global convergence, which is the case of Trust Region Spherical Parameterization (TRSP) algorithm. Thus, faces will have the correct orientation, creating a good 3D spherical geometrical image. Simulation results show that it is possible to achieve a considerable correspondence between the angle and area perspective distortion. Our method overcame the limitation of parameterization for shapes containing many extremities. In fact, parameterization onto the sphere suffers from distortions which give rise to rippling effects under lossy reconstruction.

The main objective of our trust region method is to transform the original optimization problem by a series of sub-optimization problems easier to solve. In each sub-problem, the objective function was transformed by a model function into a current iterate. A trust region was inspired as the region within which trust was given to the model function about its quality to give a good approximation (low distortion) of the objective function. Consequently, the rate of the inverted triangle was reduced. Obviously, our approach ensures effective and bijective parameterization.

We started by creating a smoothing operator:

  1. 1.

    First load and display the mesh.

  2. 2.

    Compute the weights; the weights should be positive for the method to work.

  3. 3.

    Compute the normalized weight matrix such that its rows sums to 1.

  4. 4.

    Find a convergent sequence of points by iteratively solving the trust-region sub-problems.

  5. 5.

    New vertex location: The final convergent point.

  6. 6.

    Spherical Relaxation was obtained by: Smoothing the positions of the mesh on the sphere and projecting back on the sphere and check which faces have the correct orientation.

To perform side-by-side comparisons, we implemented the harmonic spherical mapping [6], curvilinear spherical parameterization [34], the progressive spherical parameterization [26]. We obtained mapping results from the Spherical Parameterization using progressive optimization [32]. We also parameterized various input models using our algorithm under different weights. Our algorithm can be robustly applied on large geometric models with complex geometry and overcame the limitation of parameterization for shapes containing many extremities (Fig. 4).

Fig. 4
figure 4

Description of the Trust region method

Full size image

3.2.2 Spherical geometry image

Using our spherical parameterization, mapping the surface on a sphere created a geometry image. We notice that the faces had the correct orientation in comparison with the object proposed by Hope et al in [26]. These geometry images offer numerous advantages for object compression. First, simple extension rules extended the square image domain to cover the infinite plane. Then, providing a globally smooth surface parameterization. Geometrical images also facilitate compression and level-of-detail control. The 2D grid structure permits using ordinary image wavelets, including higher-order ones with polynomial precision. The coarsest wavelets span the entire surface and thus encode the lowest frequencies of the shape.

Geometrical image is an original method that compresses manifold meshes with a wavelet image compression scheme. To resample the input mesh over a regular 2D grid, the mesh was first cut in order to be homeomorphic to a disc. Then a parametrization function, mapping the points of the cut mesh to the points of a unit square, allowed computing x y z values for each pixel of the image. During the decompression, the geometry image pixels were used to build a triangle mesh approximation of the original mesh. However, the lossy compression led to cracks along the surface cuts. Hoppe and Praum [9] proposed to create the geometry image applying a spherical approach. To describe the sphere on to geometry image, they proposed a structure based on a regular octahedron domain and another scheme based on flattened octahedron domain. The geometry of these domains fits nicely with the use of spherical wavelet, avoiding boundary reconstruction issues.

Indeed, geometry images are regularly-sampled 2D images that have three channels encoding geometric information (x, y and z) and components of a vertex in R 3. Each channel of the geometry image is treated as a separate image for the wavelet analysis. To be able to construct spherical wavelets on an arbitrary mesh, this surface mesh, obtained by regular 1:4 subdivision of a base mesh, should be represented as a multi-resolution mesh.

3.2.3 semi-regular remeshing and wavelet transform

3D meshes are often dense and full of redundant vertices and irregular sampling. Thus, to reduce the complexity, the mesh quality (connectivity regularity) must be ameliorated. Geometry compression techniques proceeding by semi-regular remeshing are among the best reported ones to date. The main idea behind semi-regular remeshing methods [8, 13, 14, 24] is to consider a mesh representation to have three components: geometry, connectivity and parameterization. It is also necessary to assume that the last two components (connectivity and parameterization) are not efficient for the geometrical representation. We computed a semi-regular mesh from our trust region spherical geometry image (TRSGIM).

First, the 3D mesh was mapped to the spherical parameterization domain. Second, the geometry image was obtained as a color image and a surface image. Third, the trust region spherical-based wavelet coefficients were computed for efficient representation of the 3D mesh. Two different approaches were used to obtain the wavelet coefficients. In the initial approach, the geometry image was transformed to a semi-regular mesh where the spherical wavelet transform was applied. Alternatively, the wavelet transform can be applied directly to the geometry image. Connectivity-based adaptive wavelet transformation (WT) scheme can be embedded into a known image coder and used in the image objects coding.

The spherical wavelet coefficients yield excellent compression capabilities with minimal set of features because the spherical wavelet kernels have more localized support and therefore can be adapted more quickly to the fine details. The spherical domain is explained into a square using a simple cut by elegant boundary symmetries. These boundary symmetries permit the construction of a smooth polynomial surface; the spherical wavelets generally offer better visual reconstruction as it is most evident on the skull model.

3.2.4 3D mesh deformation using compression algorithm

We implemented compression methods for our 3D mesh deformation based on spherical geometry image, and wavelet transform. Both approaches were applied directly on the geometry images with no explicit mesh data structures. They use the boundary extension rules, and show high-pass detail in local tangential frames estimated from the low-pass surface. The main problem with this approach is the large distortion induced by the planar mapping although multi-chart and spherical geometry images were introduced to overcome this difficulty [9, 28].

The following scheme 5 represents the different steps of our compression algorithm (Fig. 5):

Fig. 5
figure 5

Overview of the compression pipeline

Full size image

Multi-layer Compression-deformed mesh consists in compressing each mesh in the sequences of deformed geometric data. Therefore, efficient compression techniques were applied to the 3D deformed sequence before distributing it over the network. Our deformation method works even better on meshes since in meshes vertex adjacency information is provided a priori. We develop a compression method applied to our 3D deformed objects with constant topology and geometry variable in order to facilitate the transformation of a deformed object to another object. Consequently, we can eliminate a passing object until the target object is obtained. This compression method is based on the transformed wavelet and remeshing method using spherical geometry images compression. The 3D geometry is resampled on a regular grid. It is compactly encoded as an RGB image. It is mostly used to represent large scale features of the mesh (overall shape and deep creases). The 3D wavelet transform is based on lifting scheme in the 3D encoder.

With less number of wavelet coefficients, our algorithm gave a good reconstructed object compared to the works of hoppe [9] and recently that of Rabab.M [27] , which have some limitations related to their proposed spherical parametrization approaches. For shapes containing many extremities, the parametrization onto the sphere suffers from distortions. The latter give rise to rippling effects under lossy reconstruction. In such cases, the compression is much less effective than semi-regular remeshing. Also in comparison with the method of Tang [27] when using 3D triangle mesh compression based on vector quantization with k-ring vector prediction our result demonstrates the capabilities of the proposed compression algorithm mainly for high-resolution objects to preserve geometric features and to have better rate-distortion performance.

4 Implementation and results

We have implemented compression method for our 3D deformed objects , based on trust region spherical geometry image and wavelet transform. Both approaches work directly on the geometry images, with no explicit mesh data structures. Both make use of the boundary extension rules, and express high-pass detail in local tangential frames estimated from the low-pass surface.

First, the 3D mesh was mapped to the spherical parameterization domain to have bijective parameterizations with lowly area and region distortion. Then, the geometry image was obtained as a color image and a surface image. Finally, the trust region spherical based wavelet coefficients were computed for efficient representation of the 3D mesh. This compression will be used to facilitate transmission of the vertex of a deformed object to another in order to make easier the passage of a deformed object to another one. Thus, we can eliminate a passing object until the target object is obtained, have an efficient rendering operations and consequently minimize the Mean Square Error (MSE) value. This error presents the deviation of the reconstructed positions from the original one.

$$ MSE= \sum\limits_{i = 1}^{N}{\left\| {v_{i} - v_{i}^{\prime}} \right\|}^{2} $$
(2)

To evaluate the effectiveness of the proposed approach,, we used Face, Bunny and Rabbit meshes to test the PSNR performance at the fixed bit rate. Here, PSNR was computed between the quantized mesh M ′ and the original mesh M as follows:

$$ {PSNR}={10.log_{10}\frac{N}{{\sum}_{i=1}^{N}\Vert{v_{i}-v_{i}^{\prime}}\Vert^{2}}} $$
(3)

Where N is the number of vertices of M, v i and \({v_{i}^{\prime }}\) represent the positions of the i-th vertex of M and M ′, respectively.

4.1 Comparison in term of compression

Robust feature representation is very important to the whole system as it ensures the alignment of the feature points. It is expected that these features are invariant to rotation, scale, and illumination.

Scheme 6 presents the different steps of our algorithm for Face object (Fig. 6):

Fig. 6
figure 6

Steps of 3D Face compression

Full size image

The variation of MSE and PSNR at the same bit rate is shown in Table 1:

Table 1 The variation of MSE and PSNR of Bunny, Rabbit and Face objects
Full size table

In comparison with the method of Tang [31] when using 3D triangle mesh compression based on vector quantization with k-ring vector prediction(KRPVQ), at the same bit rate with different meshes our result demonstrates the capabilities of the proposed compression algorithm mainly for high-resolution objects to preserve geometric features and to have better rate-distortion performance.

From the above-illustrated experimental results, we can clearly see that the proposed technique can obtain much better rate-distortion performance. The spherical wavelet coefficients show excellent compression abilities with minimal set of features.

In other hand compared to the work proposed in [27], entitled 3D Face Compression and Recognition using Spherical Wavelet Parametrization, we notice that the error rate in our work is very low. For example, the error of the Face object using our algorithm is equal to 5.0642e-007 compared to 0.14 in [27].

Figure 7 presents a 3D face compression algorithm proposed in [27] using different percentages of wavelet coefficients.

Fig. 7
figure 7

Wavelet approximation of face image. a using 2 % of wavelet coefficients b using 5 % of wavelet coefficients c using 10 % of wavelet coefficients d using 20 % of wavelet coefficients e Using all coefficients [27]

Full size image

Figure 8 shows the reconstructed versions of our 3D Face compression algorithm using different percentages of wavelet coefficients.

Fig. 8
figure 8

Wavelet approximation of face image. a using 2 % of wavelet coefficients b using 5 % of wavelet coefficients c using 10 % of wavelet coefficients d using 20 % of wavelet coefficients e Using all coefficients

Full size image

Visually, we see that our objects are well reconstituted and very similar to the original object compared to the objects in [27].

Using less number of wavelet coefficients, our compression algorithm provides a good reconstructed object compared to the works of hoppe [9] and recently that of Rabab.M [27] , which have some limitations related to their proposed spherical parametrization approaches for shapes containing many extremities, their parametrization onto the sphere suffers from distortions. The latter give rise to rippling effects under lossy reconstruction.

Scheme 9 presents the different phases of our algorithm for Bunny object (Fig. 9):

Fig. 9
figure 9

Steps of 3D Bunny compression

Full size image

Figure 10 shows the reconstructed versions of the Bunny object using different percentages of wavelet coefficients used in our compression algorithm.

Fig. 10
figure 10

Compression based spherical geometry image: a using 2 % of wavelet coefficients b using 4 % of wavelet coefficients c using 6 % of wavelet coefficients d using 10 % of wavelet coefficients

Full size image

4.2 Multi-layer compression algorithm for 3d deformed mesh

3D deformed objects require even larger memory and transmission bandwidth since a sequence consists of a large number of frames. For this reason, we used the result of our compression algorithm.

The compressed object must be deformed using our deformation algorithm based on the Laplacian coordinated and multi library wavelet neural networks architecture as an approximation tools to align the vertex and minimize the distortion of the fixed vertex while minimizing the rate of this deformation vertex. The absolute vertex positions were reconstructed from their relative coordinates by solving a sparse linear system. Based on the elementary operation of moving a single vertex, more advanced editing operations can be easily built. Constraining curves and handle regions can be done by appropriately grouping handle vertices. Then, the correspondence between the two objects was established and a 3D alignment of vertex, based on that matching, was performed. For each feature region in the original object, a feature region in target object should be found using the similarity measure and a correspondence between the source and target meshes should be carried out. Such matching cannot be directly defined because of the complexity of the involved topological and geometric information. Instead, the correspondence was achieved in an indirect manner with the help of parameterization techniques, which consists in establishing a bijective mapping between the source mesh surface and the target meshes. We used our compressed object in order to facilitate the transformation of a deformed object to another object. As a result, we can eliminate a passing object until the target object is obtained.

To evaluate the performance of the wavelet networks structure, in terms of a 3D deformed object capacity, we used a wavelet network in which the library is made up of six mother wavelets (MexicanHat, Slog1, Polywog 1, Beta1, Beta 2 and Beta 3). To estimate the basis of the wavelet number in the hidden layer, we applied this approach using a wavelet network with 15 wavelets. The 3D deformed object complexity was directly related to the selected wavelet number and to the training iteration number to construct the network. The number of wavelets in the hidden layer used for Bunny object is presented in Table 2.

Table 2 The number of wavelets used for Bunny deformation
Full size table

The figure below 11 show a comparison of our deformation processes without compression (a) and our algorithm with compression (b) when the alignment is easier for Bunny Object. The first deformation sequence of the object Bunny in Fig. 11(a) presents our deformation method based on MLWNN. The second sequence of deformation(b) shows our method using the compression algorithm. When working with a compressed object the number of vertices was reduced. Hence, the alignment of the vertex of an object to deformed object became easier because the search space was reduced. Consequently, we can eliminate one passing object until reaching the target object. Our scheme needs low computation complexity. It is also compatible with the existing connectivity compression schemes.

Fig. 11
figure 11

3d Bunny deformation scheme without compression algorithm (a) and used compression method in (b)

Full size image

5 Conclusion

We proposed a multi-layer compression algorithm for 3D mesh deformation based on wavelet neural network architecture. Our framework compressed models in each layer of deformation sequence using geometry image obtained by trust region spherical parameterization .We applied an effective compression technique for vertex geometry data to facilitates the alignment of vertex from an object to another in deformation processes. Our compression was performed by using both the spherical geometrical image obtained by our trust region spherical parameterization and the spherical-based wavelet coefficients for efficient representation of the 3D object. The spherical wavelet transformation was applied to decompose the geometry image into multi-resolution sub-images characterizing the underlying functions in a local fashion in both spatial and frequency domains. Experimental results show that the progressive compression algorithm has an efficient compression abilities with minimal set of features used to design good deformation scheme.