3D High Resolution Mesh Deformation Based on Multi Library Wavelet Neural Network Architecture

Abstract

This paper deals with the features of a novel technique for large Laplacian boundary deformations using estimated rotations. The proposed method is based on a Multi Library Wavelet Neural Network structure founded on several mother wavelet families (MLWNN). The objective is to align features of mesh and minimize distortion with a fixed feature that minimizes the sum of the distances between all corresponding vertices. New mesh deformation method worked in the domain of Region of Interest (ROI). Our approach computes deformed ROI, updates and optimizes it to align features of mesh based on MLWNN and spherical parameterization configuration. This structure has the advantage of constructing the network by several mother wavelets to solve high dimensions problem using the best wavelet mother that models the signal better. The simulation test achieved the robustness and speed considerations when developing deformation methodologies. The Mean-Square Error and the ratio of deformation are low compared to other works from the state of the art. Our approach minimizes distortions with fixed features to have a well reconstructed object.

1 Introduction

The Deformation of geometric meshes plays a central role in computer graphics, especially in the areas of computer animation and computer-aided design. Mesh deformation is an important element in the analysis of moving bodies and shape optimization. The ability to automatically update an existing mesh to conform to a modified geometry is an obligatory capability to enable the rapid prototyping of several other geometric designs. Deformation transfer applies the deformation showed by a source triangle mesh onto a different target triangle mesh and computes the set of transformations induced by the deformation of the source mesh, maps the transformations through the correspondence from the source to the target, and solves an optimization problem to consistently apply the transformations to the target shape. In order to re-use a deformation created for one object to deform another, the particular parameters that control the deformation must be adapted to the new object. In numerous cases, adapting these parameters is just as time consuming as starting from scratch. Several successful techniques have been developed in particular, multi-resolution techniques [14]. Recently introduced differential domain approaches are very effective in preserving surface details, which is important for generating high-quality results. Conversely, large deformations such as those found with characters performing nonrigid and highly exaggerated movements remain challenging today, and existing techniques often produce implausible results with unnatural volume changes. The deformations are computed with the help of a minimisation method. We developed a new mesh deformation method worked in the domain for Region of Interest (ROI) based on a Multi library Wavelet Neural Network (MLWNN) structure founded on several mother wavelet families to align the features of mesh and to minimize distortion with a fixed feature that minimizes the sum of the distances between all corresponding vertices. Our approach computes deformed ROI and updates ROI vertices. We used linear differential coordinates as means of preserving the high frequency details of the surface. The differential coordinates denote the details and are defined by a linear transformation of the mesh vertices. This representation leads to a conceptually simple, yet, powerful method for interactive, feature-preserving and shape modeling method. Thanks to are local rotations of the relative coordinates, the orientation of the details is preserved [17]. In our approach we first calculated the spherical parameterization of two meshes in order to have bijective parameterizations with low area and region distortion. Then, we computed the corresponding feature region sets, and used Laplacian boundary technique for large deformations 3D meshes based on a MLWNN structure founded on several mother wavelet families (MLWNN) to optimize and align the features of mesh.

2 Related Work

The deformation process is a generalization of the concept introduced by expression cloning, which transfers facial expressions from one face mesh to another [22]. The first detail-preserving mesh deformation methods were based on multi-resolution techniques [9, 15, 36], to allow for more global and complex deformation. Many authors proposed to cast mesh deformation as an energy minimazing problem [16, 30, 33–35].

Typically, the energy functional used in these methods have terms to preserve details (often through Laplacian coordinates), as well as position-constraint terms to allow direct manipulation. Presenting other terms in the optimization (volume or skeleton constraints) was even advocated in [11], as an expedient way to design a more complex deformation with ease, without the traditional shearing artifacts appearing in large scale deformation. Though these current techniques do not currently scale, the optimizations involved are frequently nonlinear and require slow-converging Gauss–Newton iterations [10].

This limitation can be overcome through a coarser mesh embedding (using, e.g., mean value coordinates [12]) at the expense of significantly less design control. Sumner and Der propose an approach to handle deformation via a mesh-based Inverse Kinematics, and to learn the space of natural deformations from a series of example meshes [6, 31], enhancing the efficiency of deformation design by restricting the results to acceptable ones. Shi introduced a fast Multigrid Algorithm for Mesh Deformation to support the aforementioned scenario [29], a novel prolongation and restriction operators used in the multigrid cycles. Combined with a simple, but effective graph coarsening strategy, this algorithm can outperform other multigrid solvers and the factorization stage of direct solvers in both time and memory costs for large meshes. Skeleton Subspace Deformation [18], and several variants have been used in the graphics industry for quite some time as a natural and efficient representation for character animation in games and films.

Mesh deformation is closely related to shape interpolation and morphing. Morphing can be extended from surfaces to solids by minimizing distortions in a local volume [2]. A tetrahedral mesh must be constructed for the input triangular mesh, which we avoid by using a simpler volumetric graph. Sheffer and Kraevoy [28] propose a morphing and deformation method based on pyramid coordinates that rely on mesh refinement to establish a mapping between the models. Reconstruction from pyramid coordinates to vertex coordinates requires solving a nonlinear system. Kent et al. [15], propose an algorithm for the morphing of two objects topologically equivalent to the sphere. The presented mapping is accomplished by a mere projection to the sphere and thus is applicable solely to star shaped objects. Schreiner et al. [12] present a method that directly creates and optimizes a continuous map between the meshes instead of using a simpler intermediate domain to compose parameterizations.

The free form deformation (FFD) approach was introduced firstly by Sederberg and Parry [27]. The user can translate the lattice points and the object is deformed according to the deformation of the lattice (Fig. 1).

Fig. 1

FFD on the bunny model with a regular lattice [27]

3 Mesh Deformation

The mathematical formulation of the deformation process is founded on [26]. Though, extending everything from $\mathfrak {R}^2$ to $\mathfrak {R}^3$ covers different methods for solving the minimization problem in question. The user controls the deformation using a set of N control points. Let ${P_{i}}$ be the original position of the point handle i ($1 \, \le \, i\le \, N$) and ${q_{i}}$ its deformed position. Given any point x in space, a function ${d(x,P_{i})}$ that measures the distance between x and ${P_{i}}$ is defined. The simple Euclidean distance function can be used although a better alternative exists for the purpose of deforming a 3D mesh.

To define the deformation at point x, we solve for the best rigid or similarity transformation ${T_{x}}$ that minimizes

$$\begin{aligned} {E}=\sum _{i}\omega _{i}(x)\left| T_{x}(p_{i})- q_{i}\right| ^2 \end{aligned}$$

(1)

where the weights $\omega _{i}(x)$ are of the form

$$\begin{aligned} \omega _{i}(x)=d(P_{i},x)^{-2\alpha } \end{aligned}$$

(2)

With $\alpha$, being a fall-off parameter controlling how strongly the deformation at x is influenced by far away (as measured by d) point handles. The deformation at x is simply defined to map x to $T_{x}(X)$.

Note that if ${x={p_{i}}}$ for some i then $\omega _{i}(x)=1$, $T_{x}(p_{i})=q_{i}$.

The following figure shows an example of deformation of the dragon object.

Fig. 2

Deformations of the dragon model. Left original model. Center and right dragon mouth deformed in different ways. Handle curves shown on top [5]

Surface mesh deformation system resides in:

• A triangulated surface mesh (surface mesh in the following).

• A set of vertices defining the region to deform (referred to as the region-of interest and abbreviated ROI).

• A subset of vertices from the ROI that the user wants to move (referred to as the control vertices).

• A target position for each control vertex (defining the deformation constraints).

4 The Laplacian representation

Laplacian techniques [21, 30] cast mesh deformation as minimizing an energy function which covers rapports for both detail preservation and position constraints. The simplest form of differential coordinates is the Laplacian coordinate. The Laplacian coordinate defines the mesh geometry detail which is expressed as the difference between a vertex and its one-ring neighbor vertices. Then, the Laplacian coordinate is encoded in a global coordinate system. It faces the transformation problem: the Laplacian coordinates need to be appropriately transformed to the appropriate orientation of details in the deformed mesh. Kin-Chung [13], gives dual Laplacian deformation algorithm to run the whole model which can avoid transformation problem to a certain extent. The history of Laplacian mesh editing starts with the work of Marc Alexa about the use of differential coordinates for mesh morphing and deformation [1]. The differential coordinates of a mesh can be interpreted as the difference of the original mesh and a smoothed version of this mesh (target mesh).

Generally speaking, deformation is regularly carried out in some parts of a model, while the other parts (a majority of the whole model) are unchanged. Taking the whole model into consideration, the editing operation may be a complex process, especially for large mesh models. Therefore, it is essential to develop effective editing methods for the deformation of ROI. The Laplacian representation of the mesh is enhanced to be invariant to locally linearized rigid transformations and scaling this representation leads to efficient, interactive and intuitive shape modeling including local control and detail preservation. The differential coordinates represent the geometric details. They are defined with respect to a common global coordinate system. Laplacian mesh editing allows deforming 3D objects, while their surface details are preserved because they allow the simulation of realistic deformations. This representation allows a direct detail-preserving reconstruction of the modified mesh by solving a linear least squares system. The differential coordinates are not rotation-invariant, since they are defined in a global coordinate frame. As we show below, this can cause distortion of the orientation of the details on the reconstructed surface. The differential coordinates of a mesh can be interpreted as the difference between the original mesh and a smoothed version of this mesh based on this Laplacian representation. Our method is based on the Laplacian representation designed for large rotations. We develop useful editing operations: interactive free-form deformation in a ROI based on a MLWNN structure.

5 Mesh Deformation in ROI

The deformation process computes the set of transformations induced by the deformation of the source mesh, maps the transformations through the correspondence between the source and the target mesh, and solves an optimization problem to consistently use for the transformations to the target mesh.

3D objects representations deal with the advantage of being able to characterize a large variety of complex geometries. Because of such specificities an initial stage, which consists of establishing a correspondence between the source and target meshes, is essential. Such a correspondence cannot be directly defined, because of the complexity of the topological and geometric information involved. The correspondence is achieved in an indirect manner with the help of parameterization techniques, which consist of establishing a bijective mapping between the source mesh surface and the target meshes. Most 3D surface-based mesh deformation techniques involve two steps. The first is to find the mapping from the source to the target meshes and establish the feature correspondence between them. The parameterization process requires that the mapping of the meshes must be bijective, i.e. generating a one-to-one correspondence between the source and the parameterized meshes. The second step is to choose a continuous path for each vertex and produce a smooth sequence of intermediate geometries by interpolating the corresponding vertices. A linear procedure is achieved for this interpolation in most cases. For this reason we used our trust region spherical parametrization to ensure that we have a bijective parametrization and a low area and region distortion [20].

Fig. 3

Editing the Mannequin model with different locality effects. a and c show the original model with the same handle vertex (at the tip of the nose) but different regions of interest (ROI). The dots mark the locations of anchor points that surround the ROI. b and d show the result of dragging the handle vertex a long the same distance with the two different radii of ROI. Since the radius of interest in (c) is larger, the effect of the editing operation is more global [17]

6 Correspondence

The correspondence between the source and the target triangular mesh describes how the deformation of the source mesh should be moved to the target. The correspondence system solves a minimization problem analogous to the one we use for deformation process. But the objective function is intended to deform one mesh into the other, The user controls the deformation by supplying a set of marker points specified as pairs of source and target vertex indices.

6.1 Feature Correspondence

In order to guarantee that the main characteristics of the object are preserved during the deformation process, it is necessary to replace the user specified corresponding feature points so that they share the same position in the parameter domain. Such a replacement requires a global deformation of the whole parametric domain, so that the corresponding meshes should be smoothly deformed without foldovers. The process is referred to as mesh warping. In order to complete this mission we make use of the Laplacian coordinate that allows to displace all mesh vertices based only on the known displacement of some control points (feature vertices).

Fig. 4

The correspondence of the vertices of the source mesh with the places of the surface of the target mesh (green arrows) and the correspondence of the vertex of the target mesh with the places on the surface of the source mesh (red arrow). (Colour figure online)

The construction of the base domain correspondence map consists of the following steps:

• Globally aligning the source and destination base domains and projecting the source base domain to the target base domain.

• Applying an iterative relaxation procedure to improve the mapping.

• Using the adjustment of the coarse correspondence to produce the final mapping.

6.2 Features Alignment

For each input mesh, an abstract representation is produced .The feature points on the spherical map for each model are grouped and an initial alignment for them is performed based on MLWNN that minimizes the sum of the distances between all corresponding vertices. Then, the feature points and areas are scaled and relocated to match each other. Finally, all overlapping generated from this process is eliminated so that the spherical maps for each mesh remain bijective with respect to the original input geometries.

The initial feature alignment process reduces the distances between features without modifying the local vertex positions on the spherical maps used our MLWNN. This eliminates most of the positional differences. As discussed in the previous section, the constraint matrix is over determined; such a global rotation will not accommodate all the relative differences between corresponding features or align corresponding feature points without changing the relative locations of feature points within the same spherical map.

We propose a new mesh editing framework with an intuitive interface and efficient reconstruction algorithm.

7 Mesh Deformation Based on Multi library Wavelet Neural Network Architecture

7.1 Classical Wavelet Neural Network Architecture

Wavelets have proven to be powerful bases for use in numerical analysis and signal processing. Their power lies in the fact that they only require a small number of coefficients to represent general functions and large data sets accurately.

Wavelets occur in family of functions and each is defined by dilation $a_{i}$ which controls the scaling parameter and translation $t_{i}$ this latter controls the position of a single function named the mother wavelet $\psi (x)$.

Mapping functions to a time-frequency phase space,WNN can reflect the time-frequency properties of functions. Given an n-element training set, the overall response of a WNN is shown in the following equation:

$$\begin{aligned} \hat{y}(x)=\sum _{i\, = \,1}^{N_{p}}\omega _{i}\Psi _{i} \end{aligned}$$

(3)

where $N_{p}$ is the number of wavelet nodes in the hidden layer and $\omega _{i}$ is the synaptic weight of WNN. This can also be considered as the decomposition of a function in a weighted sum of wavelets, where each weight $\omega _{j}$ is proportional to the wavelet coefficient scaled and shifted by $a_{i}$ and $t_{i}$. This establishes the idea for wavelet networks [7, 25].

7.2 Multi Library Wavelet Neural Network (MLWNN) [3]

A MLWNN can be regarded as a function approximator which estimates an unknown functional mapping:

$$\begin{aligned} y = f(x) +\epsilon \end{aligned}$$

(4)

where f is the regression function and the error term $\epsilon$ is a zero-mean random variable of disturbance. Constructing a MLWNN involves two stages:

First, we should construct a wavelet library $\omega =\left\{ \omega 1,\omega 2, \ldots ,\omega _{n}\right\}$ of discretely dilated and translated versions of some mother wavelet functions $\psi _{1},\psi _{2}, \ldots ,\psi _{n}$ [23, 24, 4].

$$\begin{array}{l} W_{j}= \begin{pmatrix} \Psi _{i}^j:\Psi _{i}^j(x)=\alpha _{i}\Psi ^j(a_{i}(x-t_{i}))\\ \alpha _{i}=( \sum _{k=1}^{N}[\Psi ^{j}(a_{i}(x_{k}-t_{i}))]^2)^{1/2}\\ i=1, \ldots ,L , and ,j=1, \ldots ,n\\ \end{pmatrix} \end{array}$$

(5)

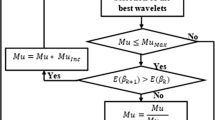
where $x_{k}$ is the sampled input and L is the number of wavelets in each sub library $W_{j}$. Then we select the best M wavelets based on the training data from multi wavelet library W, in order to build the regression.

$$\begin{aligned} \hat{y}(x)=\sum _{i\,\in\, I}W_{i}\Psi _{i}^1(x)+\sum _{i \,\in \,I}W_{i}\Psi _{i}^2(x)+ \cdots +\sum _{i\,\in\, I}W_{i}\Psi _{i}^n(x) \end{aligned}$$

(6)

This network is composed of three layers: a layer with $N_{i}$ inputs, a hidden layer with $N_{p}$ wavelets and an output linear neuron receiving the weighted outputs of wavelets. Both input and output layers are fully connected to the hidden layer.

Fig. 5

MWNN architecture

Once the two input models are parameterized in a common domain to establish a one-to-one correspondence between the models, the main features of the objects are aligned properly, based on wavelet network with respect to their corresponding features of interest. Finally, the deformation sequence is obtained using a linear interpolation scheme. The objective of the mesh interpolation step is to determine appropriate trajectories for each vertex connecting the initial position, defined on the source surface, to the final position, defined on the target shape. An interpolation in the wavelet domain makes it possible to control interpolation starting time and speed at various resolutions.

7.3 Our Proposed Mesh Deformation Based on Multi Library Wavelet Neural Network

7.3.1 Multi Library Wavelet Neural Network for 3D Mesh Feature Alignment

In order to define a geometric mesh object, we concentrate on the use of feature points. We assume that the shape of the object is defined by the locations of the predefined feature points on the surface of the mesh. Further, the deformation of the mesh can be completely defined by the movements of these feature points (alternatively referred to as control points) from their neutral positions either in absolute or in normalized units. The objective of our algorithm is to achieve a feature alignment process that reduces the distances between features without modifying the local vertex positions on the spherical maps. If there is k input mesh and each mesh has n features defined, the transformation can be expressed as the following optimization problem (Eq. 7):

$$\begin{array} {ll} \begin{pmatrix} min\sum _{j=1}^n dist\lbrace {{P_{i}(j)-P_{1}(j)}}\rbrace, \quad i=1,2,3, \ldots ,k \\ dist\lbrace {P_{i}^{'}(j)-P_{i}^{'}(l)}\rbrace =dist\lbrace {P_{i}(j)-P_{i}(l)}\rbrace , \quad \forall j,l =1,2,3, \ldots ,n \end{pmatrix} \end{array}$$

(7)

where $P_{i}$ represents the matrix containing coordinates for all feature points on mesh i and $P_{i}^{\prime }$ represents the coordinates after transformation.

$$\begin{aligned} P_{i}=\begin{pmatrix} x_{i1}&{}y_{i1}&{}z_{i1}\\ x_{i2}&{}y_{i2}&{}z_{i2}\\ x_{i3}&{}y_{i3}&{}z_{i3}\\ . &{}.&{}.\\ .&{}.&{}.\\ .&{}.&{}.\\ x_{in}&{}y_{in}&{}z_{in} \end{pmatrix} \end{aligned}$$

(8)

The general process of our proposed mesh deformation based on MLWNN architecture is presented in Fig. 6.

Fig. 6

Overview of the feature-based MLWNN algorithm

7.3.2 Our 3D Mesh Deformation Techniques

First, the trust region optimized spherical parameterizations are computed for both models (this step can be carried out as preprocessing and the mapping can be stored along with the mesh representation). Then, feature regions are detected on both models using ROI and matched between the two models. Next, feature point pairs are extracted and an optimized spherical parameterization is computed for the second model with respect to the feature point pairs. Finally we used a wavelet network approximation to optimize the alignment feature of mesh, minimize distortion with fixed features and to minimize the sum of the distances between all corresponding vertices. This method works even better on meshes, since in meshes vertex adjacency information is provided a priori.

We can summarize our deformation process by:

• Step 1 Two triangular meshes MA and MB. For each mesh, we calculate the spherical parameterization and optimize the spherical parameterization of MA and MB in order to have bijective parameterizations.

• Step 2 For MA and MB we compute the corresponding feature region sets FA and FB.

• Step 3 Fix the number of wavelets in the hidden layer in order to fix the deformation ratio.

• Step 4 Repeat steps 5 to 8.

• Step 5 Present the block row by row s (t) to the network.

• Step 6 Train the network to achieve optimum approximation of the original signal s(t)(MA and MB).

• Step 7 Save the network parameters (wi, ti and di).

• Step 8 Collect all the parameters in a dynamic matrix IC.

• Step 9 If the stop condition (all the blocks are presented to the network) is not verified go to step 3.

• Step 10 Establish a correspondence of the two nodes with the highest degree in the two graphs and perform a 3D alignment of F1 and F2 up to rotation based on that correspondence; for each feature region in FB find a feature region in FA using the similarity measure and match the correspondence between the source and the target mesh.

• Step 11 Object reconstruction from the differential coordinates based deformation technique used MLWNN.

Our approach computes deformed ROI, updates and optimizes ROI vertices to align features of mesh using MLWNN. Our method is focused on creating the series of deformation objects using spherical parameterization as a common domain of the source and target objects. This parameterization domain is the natural domain to use, given that our object is a sphere, and as such-makes the mapping step easier. We used an effective spherical mapping algorithm using trust region optimization scheme minimizing angle and area distortions which guarantee a bijective spherical parameterization. Thus, creating a good spherical geometry image [20]. Then, the corresponding feature regions are detected on both models using region growing and the two models are matched. Subsequently, feature point pairs are extracted and an optimized spherical parameterization is computed for the second model with respect to the common feature points. We used MLWNN architecture to align features of mesh and to minimize distortion with a fixed feature that minimizes the sum of the distances between all corresponding vertices. The interpolation in the wavelet domain makes it possible to control interpolation starting time and speed at various resolutions. Our proposed algorithm is presented in Fig. 7:

Fig. 7

Deformation techniques based MLWNN

8 Implementation and Results

In our implementation of deformations technique we used estimated rotations of 3D meshes based on MLWNN structure founded on several mother wavelet families. We solved an optimization problem to consistently apply to transformations to the target object.

Our trust region spherical parameterization algorithm [20] is integrated as a common domain of the source and target objects. Our approach reduce the computation distortion required for the procedure of the parameterization of the mesh in a sphere, since all calculations are performed in the space of the sphere to reduce the distortion angle and region: ratio of inverted triangle (IT) at mapping each of the triangles. The idea is to use the trust region method for nonlinear minimization ratio of ITs when mapping each triangle of surface during the parameterization of the object on the sphere to have a good system by minimizing angle and area distortion. The following figure shows the original and target objects that we used.

Fig. 8

Original and target objects

The size of each 3D object is presented in Table 1:

Table 1 The size of each 3D object

To evaluate the quality of the reconstructed object we use the Mean-Square Error (MSE). Generally the performance of mesh deformation is based on the two following criteria: the deformation rate and the quality of the reconstructed object. In our approach, the performance of mesh deformation depends on several other criteria: the type of wavelets used in the hidden layer.

$$\begin{aligned} MSE=\frac{1}{N_{i}}\sum _{k=1}^{N_{i}}(M_{N}(x_{NK},y_{NK},z_{NK})-M(x_{K},y_{K},z_{K}))^2 \end{aligned}$$

(9)

M is the mesh to be deformed; K is the number of observations.

8.1 Direct Distances Between all Corresponding Vertices

The user defines a ROI which contains a handle, a neighbour and fixed vertices. During one deformation step, all handle vertices are translated in the same direction for the same displacement. The fixed vertices of the original and the target object do not move. In other words: the handle vertices are translated by the factor 1 and the fixed vertices by the factor 0. It is clear that the neighbour vertices will move in the same direction, but with a smaller magnitude. Each neighbour vertex located between them has to be assigned to a factor. This factor depends on the distance of the corresponding vertex to the handle vertices.

The ratio $r(\mathop {x}\limits ^{\rightarrow })$ is defined as the distance of the neighbour vertex $\mathop {x}\limits ^{\rightarrow }$ to the next handle vertex $\mathop {x}\limits ^{\rightarrow }_{h}$ divided by the minimal distance of a fixed vertex to a handle one.

$$\begin{aligned} r(\mathbf {x})=\frac{\vert \mathbf {x}-\mathbf {x_{h}}\vert }{min(\vert \mathbf {x_{f}}-\mathbf {x_{h}}\vert )} \end{aligned}$$

(10)

For this ratio, it is valid that where N is the set of neighbour vertices, if the neighbourhood is defined by a radius around the handle vertices. Using this ratio directly would lead to a linear behaviour which is not smooth in an ordinary sense. Thus, the ratio is mapped to a Gaussian. The searched factorisation function g: ${\mathfrak {R}}^{+}[0,1]$ is defined by the Eq. (11)

$$\begin{aligned} g(\mathbf {x})=0.5\times\exp ^{(-(\mathbf {r(x)}/0.25))} \end{aligned}$$

(11)

Using the Gaussian (11) as a transition function led to good results, and therefore, it was used in the implementation. Thus, the neighbour vertices were determined by a user controlled frame selection. Some problems can occur because the ratio can exceed 1. This problem could be overcome by using the Gaussian function because it asymptotically approaches the axis. But this way of interpolating the vicinity of the handle vertices has its limitations, if the transformation is more than just a translation. This induces the implementation of a Laplacian mesh editing tool based on wavelet network architecture to minimize the sum of the distances between all corresponding vertices.

For this reason we fixed the number of wavelets in the hidden layer in order to fix the deformation ratio. With Laplacian mesh editing it is possible to deform 3D objects while their surface details are preserved. We used a Wavelet network approximation to optimize the alignment feature for mesh and minimize the sum of the distances between all corresponding vertices. Thus, we minimize distortion with fixed features.

We can see from Table 2, that we used 15 wavelets in the hidden layer, which minimized the sum of the distance of a fixed vertex. Our algorithm achieved a minimal distance between all corresponding vertices to have a good object reconstruction.

We set 15 wavelets used in the hidden layer to construct the WaveNet. This choice of number is sufficient to have acceptable results. When we increased the number of wavelet, the search space of the best wavelet increased, hence the time of calculation and simulation increased too. If the stop condition (all the blocks are presented to the network) is not verified, go to step 3 in our approach and fix a new number of wavelet in the hidden layer.

Table 2 The variation of distance of fixed vertex

We used the minimal distance of fixed vertices to compute the measured rate deformations:

$$\begin{aligned} D= \frac{\vert \mathbf {x}-\mathbf {x_{h}}\vert }{min(\vert \mathbf {x_{f}}-\mathbf {x_{h}}\vert )}\times100\, \% \end{aligned}$$

(12)

The frame rates in the table were calculated when the handles were already selected and the user was manipulating certain handles. If the user adds new handles or removes old handles, then we need to re-compute the inverse for some matrices and the frame rate will decrease. The Variation of MSE and deformation rate in terms of wavelet library using MLWNN architecture are presented in Table 3.

Table 3 The variation of MSE and deformation rate

From the results in Table 3 we see that the MSE depends on the wavelet library and the number of wavelets in the hidden layer from Table 2. We can see that the MSE and the ratio of deformation are low. Compared to other works, our approach minimizes the sum of the distances between all corresponding vertices, and minimizes distortion with fixed features to have a good reconstructed object in the deformation process. This could help users to create more intermediate deformed mesh results with preserved topological features.

A 3D object deformation based on MLWNN is presented. This structure has the advantage of constructing the network by several mother wavelets and the advantage to solve the problem of high dimensions using the best wavelet mother that models the signal better.

We demonstrate that representing the geometric information of a triangle mesh in differential form enables detail-preserving interactive mesh modeling.

The absolute vertex positions are reconstructed from their relative coordinates by solving a sparse linear system. Based on the elementary operation of moving a single vertex, more advanced editing operations can be easily built. Constraining curves and handle regions can be done by appropriately grouping handle vertices, then, establishing the correspondence of the two objects and performing a 3D alignment of vertex based on that correspondence; for each feature region in FB find a feature region in FA using the similarity measure and match the correspondance between the source and target meshes.

In [8] the author uses a skin-detached surface based on the simplified mesh to align vertex until reaching the deformed object (figure a). We found that there are some exceptional cases in which this method cannot achieve correct deformation. On the other hand our algorithm used a direct approximation algorithm in the area of interest. The alignment is efficient based on wavelet network to minimize the distortion of the fixed vertex without including a simplification algorithm (figure b). Therefore, the execution time in our algorithm is reduced in comparison with the calculation algorithm in [8] and [14]. Figure 9 presents a visual comparison for 3d bunny deformation.

Fig. 9

Comparison results for the deformation of 3D bunny object

Figure 10 presents an exemple of the feature region sets F of original objects.

Fig. 10

Feature region of object

Such a correspondence cannot be directly defined because of the complexity of the topological and geometric information involved. Instead, the correspondence is achieved in an indirect manner with the help of parameterization techniques, which consists of establishing a bijective mapping between the source mesh surface and the target meshes.

According to the parameterization process, the mapping of the meshes must be bijective, i.e. generating a one-to-one correspondence between the source and the parameterized meshes.

Figure 11 presents an example of 3D objects parameterization of the sphere using our trust region spherical parameterization approach [20].

Fig. 11

The spherical parameterization of original and target object (Horse, Bunny, Cat and Face)

The rapport of the original and deformed objects as function of the axis x, y and z is seen in the curves in Fig. 12.

Fig. 12

The rapports by X, Y and Z of the original object and the deformed object

The number of wavelets in the hidden layer used for such object is presented in Tables 4, 5, 6, and 7.

To evaluate the performance of the wavelet networks structure, in terms of a 3D deformed object capacity, we used a wavelet network in which the library is made up of six mother wavelets (MexicanHat, Slog1, Polywog 1, Beta1, Beta 2 and Beta 3). To estimates on the basis of the wavelet number in the hidden layer, we applied this approach using a wavelet network with 15 wavelets (for example in Table 4 we have: 4 MexicanHat, 5 Slog1, 2 Polywog1, 1 Beta1, 2 Beta2 and 1 Beta3). The 3D deformed object complexity is directly related to the selected wavelet number and to the training iteration number to construct the network.

Our deformation technique for such object is shown in Figs. 13, 14, 15, and 16.

Table 4 The number of wavelets used for Horse deformation

Fig. 13

Deformation technique based on MLWNN on the Horse model

Table 5 The number of wavelets used for Cat deformation

Fig. 14

Deformation technique based on MLWNN on the Cat model

Table 6 The number of wavelets used for Face deformation

Fig. 15

Deformation technique based on MLWNN on the Face model

Table 7 The number of wavelets used for Bunny deformation

Fig. 16

Deformation technique based on MLWNN on the Bunny model

9 Conclusion

Robustness and speed are primary considerations when developing deformation methods for animatable mesh objects. The goal of this paper is to present a robust and fast geometric mesh deformation algorithm. It deals with the features of a novel technique for large laplacian boundary deformations using estimated rotations of 3D meshes based on a MLWNN structure founded on several mother wavelet families and using spherical parameterization as a common domain of the source and target objects.

New mesh deformation methods worked in the dual domain for ROI. Our approach computes deformed ROI, updates and optimizes ROI to align features of mesh using MLWNN. This structure has the advantage of constructing the network by several mother wavelets and the advantage to solve the problem of high dimensions using the best wavelet mother that model the signal better.

3D object are complex, more detailed, and have a longer format. It is getting increasingly difficult to efficiently store and transmit these models. The focus of futur work is to design an efficient and powerful algorithm for compressing and transmitting deformed geometric data. we developed a new technique for the compression of 3D deformed objects by using our wavelet network to reduce the size and to facilitate the transmission, storage and manipulation of 3D objects, while retaining useful information.