1 Introduction

Image interpolation is a process that is often used to perform an image zoom or simply to increase the resolution of an original image from its down-sampled version [10]. Interpolation has been widely used in many image processing applications such as facial reconstruction, multiple description coding (MDC), super resolution and digital high-definition television (HDTV) [3, 9, 18]. The rapid advancements in hardware and display devices have made it possible to process high-resolution digital color images as shown in Fig. 1. In order to efficiently utilize the display power of these state of-the-art viewing devices, input signals from a lower-resolution source must be upscaled to higher resolutions through interpolation. However, the multichannel nature of color images demands efficient signal processing algorithms that take into account the existing inter-channel correlations when performing image size expansion. In this work, we propose a new technique that generates sharper super-resolved images. Various techniques have been proposed in order to scale the image from low resolution to high resolution and its reverse. Fundamentally, they can be classified into three categories: isotropic interpolation-based, edge-directed, and transform-based methods. The isotropic interpolation method [3, 9, 10, 18] considers the source image as a sub-sampled discrete version of the original “continuous” image. Nearest-neighbor, bilinear, and bi-cubic interpolation are some of the examples of this method. In the nearest-neighbor method, the source image is scaled by sampling the nearest pixels in the source image. This is also known as zero-order interpolation. It is a computationally efficient algorithm; however, the up-scaled image quality is degraded owing to the aliasing effect. In the bilinear and the bi-cubic interpolation methods, image quality is improved compared to the nearest neighbor method; however, the high-frequency content of the image still suffers from a blurring effect. Edge directed interpolation (EDI) [4, 11, 12, 19] uses statistical sampling to ensure quality while scaling the image instead of averaging the pixels, as in a bilinear interpolation average of the covariance of pixels. Hence, the sharpness and the continuity of the edges are preserved. Li [12] proposed an EDI using the statistical and geometrical properties of the pixel to interpolate the unknown pixel. A covariance of the pixel in a local block is required for the computation of the prediction coefficient. This algorithm works well for preserving the sharpness and continuity of edges. However, only four pixels are taken from the source image; hence, the prediction error is obvious in this algorithm. A modified training window structure has been proposed [16, 17] in order to overcome this shortcoming.

The training window in the second step of NEDI is modified to the form of sixth order linear interpolation with a 5 × 9 training window. M. Li [11] suggested the Markov random field (MRF)-based model. The image is modeled with MRF, and edge estimation is extended in other directions by increasing the neighboring pixels in the kernel. Similarly, an improved edge-directed image interpolation algorithm with low time complexity which is the combination of Newton’s method and edge-directed method is proposed by Wang Xing-Yuan and Chen Zhi-Feng [20].

Fig. 1
figure 1

High resolution display video wall

Full size image

This algorithm is able to preserve the sharpness of edges in the interpolated image. Transforms like DCT and wavelet transform are efficient for compressing the energy into a few transformed coefficients. As a result of multiplying these transformed coefficients, a scaled image can be obtained. The algorithm in [17] is based on the use of orthogonal wavelets as preconditioning transforms. Lama et al. in [8] suggested the adaptive directional to interpolate the image. In this method, directional lifting based wavelet is applied. The theory of projection onto convex sets (POCS) is the basis for the iterative technique proposed by K. Ratakonda in [14]. In this algorithm, scaling is accomplished in two steps. First the initial image is obtained by the conventional bilinear technique, then the iterative algorithm is applied on the initial image to obtain the final magnified image. Additionally, Chun-Ho Kim [5] proposed the winscale algorithm which is based on an area pixel model and domain filtering, and it uses a maximum of four pixels from the original image to calculate the pixel of a scaled image. The winscale algorithm uses the same hardware as the bilinear method; however, it is more complex in terms of the number of operations per pixel. Limitations of winscale in described in detail by E. Aho et al. [1].

Finally, we present a new algorithm that interpolates the image with consideration of preserving the original image edge and computational cost. The proposed technique uses (DT-CWT) to decompose the low-resolution image into different sub-band coefficients. We assume that a given image is the LL band of the wavelet coefficients of a high-resolution image as shown in Fig. 2. In order to predict the coefficients on the finest scale, we model the statistical relationship between the coefficients at coarser scales using a hidden markov tree (HMT). Finally, the magnified image is obtained combining the predicted high-frequency sub-band images and input image by using inverse discrete complex wavelet transform (ID-CWT).

Fig. 2
figure 2

Interpolation using DT-CWT and HMM

Full size image

2 Dual tree complex wavelet transform

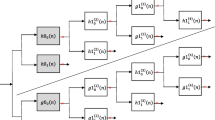
The DT-CWT is an enhancement to the traditional critically sampled DWT to overcome the shortcomings with important additional properties: it is nearly shift invariant and offers higher directional selectivity [7]. There are six directional subbands capturing features along the lines at angles of ±15°, ±45°, and ±75°. The DT-CWT allows the characterization of images by providing explicit information about singularities in a broad range of orientations. The DT-CWT of a signal X(n) is implemented by using 2 critically sampled DWTs in parallel on the same data, as shown in Fig. 3. Since for N point signals, they generate 2 N DWT coefficients, the transform is doubly expansive. The filters are designed in a specific way such that the sub-band signals of the upper DWT can be interpreted as the real part of a complex wavelet transform, and the sub-band signals of the lower DWT can be interpreted as the imaginary part. When designed in this way, the DT-CWT is nearly shift invariant, in contrast to the classic DWT.

Fig. 3
figure 3

Dual-tree complex wavelet transform a Analysis b Synthesis

Full size image

2.1 Statistical modeling of complex wavelet transform

The main idea of the wavelet domain interpolation is to exploit the properties of wavelet coefficients for estimating the extreme points in the higher frequency bands [13]. First, the intra-scale characteristic of coefficients is studied. Within the same scale, coefficients representing the smooth region in an image have small magnitudes while large magnitudes represent singular regions. Each wavelet coefficient is modeled by a gaussian mixture model (GMM) that has multiple means and variances. The overall marginal probability distribution function (PDF) is given by a two-state model with hidden states (S i   = 1/2), where one Gaussian is used to model the coefficients around zero for small region, while another is used for the higher-magnitude coefficients which constitute the singularities. These two states are illustrated in Fig. 4. Similarly, the PDF plot of wavelet coefficients of Lena image is shown in Fig. 5. Each coefficient is assumed to fall into one of these distributions, and HMT model is trained by the expectation maximization (EM). Then, the overall density function is given by:

$$ f\left({w}_i\right)=p\left({S}_i=m\right)f\left({w}_i/{S}_i=m\right), $$
(1)

where, p(S i   = m) is obtained using the EM. Given the state S i , the conditional probability f(w i | S i   = m) of the coefficient value w i corresponding to the Gaussian distribution is obtained as:

Fig. 4
figure 4

Two state Gaussian model

Full size image
Fig. 5
figure 5

PDF plot of wavelet coefficient in Lena image

Full size image
$$ f\left({w}_i/{S}_i=m\right)=\frac{1}{\sqrt{2\pi {\sigma}_{{}^{i,m}}^2}} \exp \left(-\frac{{w_i}^2}{2{\sigma}_{i,m}^2}\right) $$
(2)

Second, the unknown high-frequency coefficients are estimated by using the inter-scale relationship, which is defined by the Markov stochastic model [2]. This model uses both the persistency and non-Gaussianity properties of the wavelet coefficients. For any image, each parent wavelet coefficient in the HMT hierarchy has four children. Owing to persistence, the relative size of the coefficients propagates across the scale. To describe these dependencies, the two-state HMT model uses the state transition probabilities f(S i   = m| S p(i)   = n) between the hidden states S i of the children, given that of the parent S p(i) :

$$ \begin{array}{l}f\left({S}_i=m/{S}_{p(i)}=n\right)=\\ {}\left(\begin{array}{c}\hfill f\left(\left.{S}_i=1\right|{S}_{p(i)}=1\right)f\left(\left.{S}_i=1\right|{S}_{p(i)}=2\right)\hfill \\ {}\hfill f\left(\left.{S}_i=2\right|{S}_{p(i)}=1\right)f\left(\left.{S}_i=2\right|{S}_{p(i)}=2\right)\kern0.5em \hfill \end{array}\right)\end{array} $$
(3)

where according to the persistence assumption, f(S i  = 1|S p(i) = 1) ≫ f(S i  = 2|S p(i) = 1) and

$$ f\left(\left.{S}_i=2\right|{S}_{p(i)}=2\right)\gg f\left(\left.{S}_i=2\right|{S}_{p(i)}=1\right) $$
(4)

Therefore, the associated probabilities P are

$$ \begin{array}{c}\hfill P\left(\left.{S}_i=2\right|{S}_{p(i)}=1\right)=0\hfill \\ {}\hfill P\left(\left.{S}_i=1\right|{S}_{p(i)}=1\right)=1\kern0.5em \hfill \end{array} $$
(5)

The probability that the large coefficient changes into the small coefficient converges to 0.5 across scales.

$$ \begin{array}{c}\hfill P\left(\left.{S}_i=1\right|{S}_{p(i)}=2\right)=1/2\hfill \\ {}\hfill P\left(\left.{S}_i=2\right|{S}_{p(i)}=2\right)=1/2\hfill \end{array}. $$
(6)

Therefore, state transition probabilities ε can be approximated by following the model of universal HMT [15].

$$ \left[\begin{array}{cc}\hfill {\varepsilon}_{i,p(i)}^{11}\hfill & \hfill {\varepsilon}_{i,p(i)}^{12}\hfill \\ {}\hfill {\varepsilon}_{i,p(i)}^{21}\hfill & \hfill {\varepsilon}_{i,p(i)}^{22}\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0.5\hfill \\ {}\hfill 0\hfill & \hfill 0.5\hfill \end{array}\right]. $$
(7)

Once the state of the child coefficient is confirmed, we generate corresponding coefficient values based on different infterpolation methods [6]. The state value of coefficients clearly indicates the pixel characteristics around the location i,e, the state value S i   = 1, indicates the coefficient blongs to low frequency region while the high S i   = 2 corresponds to high frequency regions. In the proposed method unknown coefficients values belonging to the high frequency region are generated using a linear interpolation instead of random values based on the variance. Coefficients along the direction yielding the lowest high frequency energy among all the directions are selected for interpolation. While, in case of low frequency region, pixel intensity of neighboring pixels are almost identical. Thus we generate the child coefficients based from the variance same as its parents.

In this paper, the DWT wavelet coefficients are modeled using three independent HMT models. In this way, we tie together all trees belonging to each of the three detail subbands to decrease the computational complexity and prevent overfitting to the data.

For the DT-CWT coefficients, the complex wavelet coefficient comprise real and complex components w = (w r , w c ). Thus, the conditional probability for the complex coefficient f(w i | S i   = m) is expressed as:

$$ f\left({w}_i/{S}_i=m\right)=\frac{1}{\sqrt{2\pi {\sigma}_{{}^{i,m}}^2}} \exp \left(-\frac{w{r_i}^2}{2{\sigma}_{i,m}^2}\right) \exp \left(-\frac{w{c_i}^2}{2{\sigma}_{i,m}^2}\right) $$
(8)

Scale-to-scale Markov transitions of the complex wavelet HMT and real DWT HMT have almost identical structures. The differences will be the use of six subband trees instead of three.

3 Experimental results

In this section, we present experimental results of evaluating the performance of the proposed algorithm using different test images, one of which is shown in Fig. 5. The performance is compared with several standard methods, such as bilinear interpolation, edge directed interpolation and in [12] and adaptive directional lifting based interpolation. We consider two types of performance metrics, which are visual quality and peak signal to nosie ratio (PSNR). The visual comparison is performed using two images. We have selected gray scale Lena image of size 512 × 512 and high resolution color image of size 1920 × 1080. Figure 6 shows the interpolation of Lena image using different interpolation method. Figure 6a shows the original image. Figure 6b shows an interpolated image using new edge directed interpolation (NEDI) [12]. Figure 6c shows a magnified image using the bilinear method. Figure 6d shows a magnified image using the adaptive directional lifting (ADL) based method. Finally, Fig. 6e shows the image upscaled using the proposed method. Visually, experiments from the three different filters yield very similar results and conclusions, but the PSNR tells quite a different story. In order to obtain PSNR measurement, we take the 2 N × 2 N and downsample it to obtain N × N image. PSNR values of reconstructed images are shown in Table 1. The reconstructed images generally attain most of their quality in few iterations and practically do not change after 5–6 iterations of EM, both in visual quality and in PSNR measurements. The log likelihood of high frequency coefficients estimated during expectation maximization remains constant after 5–6 iterations as shown in Fig. 7. Since we obtain the variances and mean of coefficients using only few iterations, the use of EM does not make the overall system more complex. Although the PSNR is not a good indication of image quality, it is nevertheless frequently used, and the results are tabulated in Table 1 for the bilinear interpolation, NEDI methods and ADL method. The highest PSNR values among the different methods are highlighted in bold. From this table values, the proposed method outperforms the conventional algorithms in terms of PSNR. Similarly, In Fig. 8, we demonstrate the interpolation of high resolution color image using different methods and their comparison with the proposed method. One can see that the proposed algorithm resizes the high-frequency component better without the ringing artifacts present in bilinear and other methods. We used a half-size downsampled image using nearest neighbor method to interpolate to the original size and compute the PSNR.

Fig. 6
figure 6

Experimental results: a Original image Lena, b Interpolated image using the NEDI method, c Bilinear method, d ADL-based method, and e proposed method

Full size image
Table 1 Competitive results
Full size table
Fig. 7
figure 7

Log-likelihood vs number of iterations a Real HH coefficients b Imaginary HH coefficients

Full size image
Fig. 8
figure 8

Experimental results: a Original image, b Interpolated image using the NEDI method, c Bilinear method, d ADL-based method, and e proposed method

Full size image

4 Conclusions

In this paper, we proposed an efficient up-sampling algorithm based on the DT-CWT and HMM method. The proposed up-sampling method yields much better visual quality in high resolution color images and better PSNR for both the color and gray scale images compared to current state of the art in the literature of high-resolution display systems. The better performance comes at the expense of increase in complexity. However it is not a significantly high. We believe, many modifications can be done on the proposed method that can further improve its performance and reduce computational complexity. Finally, owing to the combined DT-CWT and HMM concept of the proposed method, it can be efficiently used for the interpolation of HD images.