1 Introduction

The term audio scrambling has a long history. A century ago, audio scrambling was the only way to hide analog audio information transmitted, and the scrambling relied mainly on altering the audio signal in the time domain, the frequency domain, or both. Later, scrambling of other media types was used. For example, scrambling techniques were used in copyright protection of cable TV broadcast; secure image transfer from satellites to ground stations, and military communications [22].

With the rapid development of information technology, the applications of audio scrambling varied significantly; although it is still used in the field of security, it is considered as a pre-process or post-process of watermarking, information hiding, fingerprinting, and encryption.

The techniques that use scrambling have many applications; for example, Fingerprinting is one of the effective means of copyright protection of multimedia transmitted to massive users using the multicast method [8], the development of robust data hiding system helps more technologies find new and promising applications [15], and watermarking is one of the methods used in Intellectual Property (IP) protection which is an important element in multimedia transmission and delivery systems [4].

In this paper we propose a new Audio Scrambling algorithm based on Cellular Automata (ASCA). Cellular automata (CA) is a discrete model of computation that could be used to solve any computable task. This work seeks to find out how to best benefit from CA characteristics in audio scrambling, where different CA types were tested to see which one will lead to a higher scrambling degree. Also, the experiments were applied to 30 audio files in WAV format which contains music and speech files of different sizes and the robustness of cellular automata techniques was tested against data loss attack where 1/3 of the data is lost.

The remaining of this paper is organized as follows: in Section 2 we review related work briefly; Section 3 covers essential cellular automata background information; Section 4 describes the scrambling algorithm proposed and the scrambling degree measurement; Section 5 gives the analysis and discussion of the experimental results; Section 6 compares the work done with previous schemes, and finally, in Section 7, we conclude the work done and discuss possible directions for future work.

2 Related works

A lot of research has been done in the field of scrambling. For digital images, many scrambling methods are available, such as those based on Arnold transformation [18], Advanced Encryption Standard (AES) and error-correcting code [9], cat chaotic mapping [24], and dynamic twice interval-division [21], among others.

Cellular automata have also been used for digital image scrambling: Ye and Li [23] described the use of CA with chaotic behavior, while Abu Dalhoum et al. [1] proved that CA with complex behavior scrambles better than those with chaotic behavior. In this paper we extend work done in digital image scrambling and apply it to digital audio.

Many researchers have worked on audio scrambling: the work done in [12] and used in [13, 14], for example, uses variable dimension operation to address problems in one dimensional linear mapping. The algorithm changes the dimension of coordinates and uses a transformation matrix to scramble the audio.

In [5], two scrambling algorithms are given, namely, the cyclic displacement scrambling transformation (CDST) and the complete binary tree’s inorder traversal scrambling transformation (ITST), then the two algorithms are combined. The combined algorithm takes two positive integers as keys; the first is used in CDST, while the other determines the order of execution of the two algorithms.

Work done in [6] focuses on the compressed domain, where a progressive audio scrambling and descrambling scheme is applied to MP3 audio, the algorithm is progressive in the sense that it does multiple rounds of scrambling based on keys to produce a set of audio outputs of differing qualities. In order to reconstruct the original, all the keys must be available; if some of the keys are missing then the reconstructed audio has lower quality than the original.

In this paper we propose a new audio scrambling technique that depends on CA in generating the scrambling key, and we study different types of CA in terms of audio scrambling. The proposed algorithm is applied to audio in WAV format, and does not require any additional padding; moreover, experimental results show that the algorithm is applicable to speech and music audio files with different sizes, and can break the correlations between audio samples effectively, in addition to being robust to data loss attacks. Section 6 discusses scrambling algorithms applied to WAV audio files further.

3 Cellular automata

Cellular automata (CA) are simple and highly parallel models of computation which can exhibit complex behavior [17]. They are used in many applications covering different fields, for example, CA is used to model complex biochemical systems [10], and to build vehicular traffic models [3].

This paper uses two dimensional cellular automata. The model implies a grid of identical cells, each cell can be in one of two states, zero or one (also called on or off, dead or alive). From a given initial state, the state of the grid cells changes from one iteration (generation) to the next, or stays the same, based on a transition function (or rule) which depends on the state of the specified cell and the states of its neighbors in the previous generation. The transition function is applied simultaneously to every cell in the grid.

3.1 Cellular automata neighborhood and boundary condition

The actual neighborhood chosen is usually crucial for the global behavior of a CA [16]. In this paper we consider two common 2D neighborhoods, von Neumann and Moore. In von Neumann’s neighborhood every cell has four neighbors: the cells at its North, South, East, and West, whereas in Moore’s neighborhood the cells at the four diagonals are also considered.

In an infinite grid, every cell has a full neighborhood, but in a finite grid there must be a way to handle cells on the edges. We will consider both null and periodic boundary conditions in our experiments. A CA is said to have a null boundary if the left (right) neighbor of every leftmost (rightmost) cell is set to a zero state cell, and a periodic boundary if the extreme cells at opposite sides are adjacent to one another [19].

3.2 Cellular automata lambda parameter (λ)

Not all types of cellular automata result in a complex behavior and there are many attempts to group cellular automata with the same behavior. According to Wolfram, it seems that the patterns which arise from different types of cellular automata can almost always be assigned to one of just four basic classes [20]. In class 1, patterns evolve into a stable, homogeneous state; in class2 patterns evolve to periodic state; in class3 a chaotic behavior appears; and in class4, configurations contain structures which interact in complex ways.

A way to describe the relation between the transition rules and the behavior of the CA is the λ parameter, defined by Langton [11]. A small value of λ indicates that the CA evolves to a stable state, which corresponds to Wolfram class 1; a higher value describes a periodic behavior, as in class 2; for values close to 1, the CA behavior tends to be chaotic, as in class 3; for some critical values of λ, the CA exhibits complex behavior, as in class 4. Ideally, all transition functions with the same λ exhibit similar behavior [2].

3.3 Calculating the transition rule number

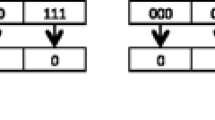
In [23] the rule number (C) is calculated as follows:

$$ \label{eq0} C=\displaystyle\sum\limits_{s=0}^{1}\displaystyle\sum\limits_{n=0}^{8}f(s,n)\times2^{2n+s} $$
(1)

where f is the transition function, s is the current state at time t and n is the number of neighboring cells with s = 1. The transition function f produces the state s at time t + 1, if the combination between the current state at time t and the neighboring cells with s = 1 results in s t + 1 = 1, then the amount 22n + s is added to the rule number. The Moore neighborhood is assumed in this equation.

3.4 Conway’s Game of Life (GOL)

The rules of Conway’s game of life are simple [7], and can be described as follows:

  • Survival. If a cell is alive at time t, it will remain alive at time t + 1 if and only if it has either two or three neighbors alive at time t.

  • Birth. If a cell is dead at time t, it becomes alive at time t + 1 if exactly three of its neighbors are alive at time t.

  • Death. If a cell is alive at time t, it will die at time t + 1 if less than two (isolation) or more than three (overpopulation) neighbors are alive at time t.

4 Audio scrambling based on cellular automata

The technique we are proposing can be divided into two processes: first the audio is scrambled and used as the base for further processing, or perhaps sent directly; then the audio is descrambled to generate the final version for distribution (in case of watermarking) or to retrieve the ciphered information (in case of encryption). Both the scrambling and descrambling processes depend on the key generation process to produce the indices used for scrambling.

4.1 Scrambling algorithm

The scrambling algorithm takes the audio file as input and produces a scrambled audio plus a key as the output. The key specifies the indices used for scrambling. The procedure starts by determining the length of the audio file which will be used to increase the dimension of the audio, then a list of the new indices is generated using rules of the game of life, a Moore neighborhood and a periodic boundary. This list is used to fill the two dimensional matrix with the original audio samples, then the dimension is decreased and the scrambled audio file is written with the same sample rate and number of bits per sample as its original. The algorithm can be described as follows:

  1. (1)

    Read audio file X and determine its length: length(X).

  2. (2)

    Select M such that (M − 1)2 < length(X) < M 2. Build an M ×M empty matrix A.

  3. (3)

    Calculate the last index (in row first order) occupied by the wave samples if they were inserted into a matrix of size M ×M. All positions before this point are within range.

  4. (4)

    Get the new list of indices Q, using the key generation process described in Section 4.2.

  5. (5)

    Initialize a pointer to point to the first cell in the audio array: ptr = 1.

  6. (6)

    For each index in Q, if it is within range, then \(A\left [ index \right ] = X\left [ ptr \right ]\). Increment ptr.

  7. (7)

    While ptr is less than length(X), insert the remaining values in A, in row first order using the same procedure.

  8. (8)

    Decrease the dimension of A from 2D to 1D.

  9. (9)

    Repeat steps 5 to 8, N times if needed.

After the scrambling process, the scrambled audio file R is written in the same format, with the same sample rate and number of bits per sample. Figure 1a shows an audio wave file, Fig. 1b shows a list of indices retrieved from the key generation process described in Section 4.2, Fig. 1c shows the audio file scrambled before decreasing the dimension. The length of the key is less than the length of the audio, so the remaining values are inserted in row first order. The black cell is out of range and will be discarded when the dimension is decreased.

Fig. 1
figure 1

Audio scrambling process, (a) original audio, (b) list of new indices, (c) scrambled audio

Full size image

4.2 Key generation process

The key generation process is used by the scrambling and descrambling processes. It takes the value of M calculated in Section 4.1, and produces a list of indices Q. The key generation process is based on 2D cellular automata and can be described as follows:

  1. (1)

    Create a CA with an M ×M grid and a random initial state configuration.

  2. (2)

    Initialize a status matrix B of size M × M to zero.

  3. (3)

    Run the Game of life rules (using Moore neighborhood and periodic boundary) for (NOG) generations starting from the initial state configuration. Subsequent state configurations are K 1, K 2, ⋯ , K NOG .

  4. (4)

    For k = 1, 2, ⋯ , NOG, if \(K_k \left [i,j \right ]=1\) and \(B \left [i,j \right ]=0\), add (i,j) to the list of new indices Q, and set \(B \left [i,j \right ]\) to 1.

  5. (4)

    Return Q.

The number of generations (NOG) must not exceed the number needed to scramble the whole audio file, in most applications a small number of generations is enough to get a high scrambling degree (as shown in the experiments in Section 5.1), because the difference in the scrambling degree decreases when the number of generations increases, so there is little benefit from running the algorithm for too many generations.

4.3 Descrambling algorithm

The descrambling algorithm is the inverse of the scrambling algorithm; it simply takes the scrambled audio file generated by the scrambling algorithm and the initial configuration of CA to return the original file. If the algorithm is repeated or the number of generations is changed, then the algorithm requires NOG and N. Note that the descrambling algorithm can use the initial configuration to reproduce the key, and K 1, K 2, ⋯ , K NOG are not required. If no attacks or audio processing operations were made to the scrambled file, the algorithm returns a file identical to the original.

4.4 Measuring the scrambling degree

The average scrambling degree measurement is used to evaluate image scrambling schemes as in [1, 23]; we have used the same measurement to analyze the effect of different cellular automata types on audio scrambling, but before applying it to audio files, two important things must be considered: first, the audio file amplitude contains negative values and needs to be normalized; second, audio and image files are different, so the difference should be computed in a different way, as shown in the equations below. Let P(i) denote the original audio data, and L is the length of the audio file, then the difference D for cell (i), is calculated as follows:

$$ \label{eq1} D(i)=\frac{1}{4}\displaystyle\sum\limits_{\acute{i}}\left [ P(i)-P(\acute{i}) \right ]^2 $$
(2)

where \((\acute{i}) = \left \{ (i-1),(i-2),(i+1),(i+2) \right \}\). After computing the cell difference, the mean difference M for the audio is calculated as:

$$ \label{eq2} M=\frac{\textstyle\sum_{i=3}^{L-2}D(i)}{L-4} $$
(3)

Finally the scrambling degree SD is defined as:

$$ \label{eq3} SD=\frac{\grave{M}-M}{\grave{M}+M} $$
(4)

Where \(\grave{M}\) is the mean difference of the scrambled file and M is the mean difference of the original audio file; the value of the scrambling degree in (4) ranges from − 1 to 1, where higher values indicate better scrambling.

5 Experimental results and analysis

In this section, we study different types of CAs in terms of audio scrambling, and we evaluate the robustness of the proposed algorithm against data loss attack, focusing on the relation between the algorithms robustness and the scrambling degree.

The data set used to study the behavior of CAs contains 30 audio files with different waves. The resolution of all the audio files used is 16 bit and the audios are in WAV format. Those numbered from 1 to 15 are speech audio files; while those numbered from 16 to 30 are music audio files. All speech audio files have one channel, with a sampling rate of 16000 Hertz and a Bit rate of 256 kbps. The speech audio files duration ranges from 0.810562 to 23.1853 s. Table 1 shows the details of the music audio files.

Table 1 Details of audio files used to study CA behavior
Full size table

Although some of the audio files have multiple channels, only one channel is used in the experiments.

5.1 Correlation analysis of the Number of Generations (NOG)

The scrambling key in the proposed algorithm depends on cellular automata, so the number of generations parameter is vital to produce keys. Table 2 shows the experiments made using the data set described. The experiments were made with no repetition (N = 0). From Table 2 it can be seen that the greater the NOG, the higher the scrambling degree obtained.

Table 2 Different NOGs effect on scrambling degree
Full size table

Based on the proposed algorithm, the scrambling degree increases as the number of generations increase, because if no more indices are specified by GOL rules the algorithm will insert the remaining values in a row first order (step 7 of the scrambling algorithm in Section 4.1), which will make the correlation between the samples higher and the scrambling degree lower, especially when there are gaps between the indices specified by the key.

Scrambling 1.wav for one generation produces an audio file scrambled with the degree 0.83620. By increasing the number of generations to five, the scrambling degree goes up significantly to 0.92165. Increasing the number of generations to twenty, the scrambling degree increases to 0.92875. The difference between using one generation and five is 0.08545 whereas the difference between five generations and twenty is 0.0071. The experimental results suggest that the influence of changing the number of generations decreases gradually when the number of generations increases, because when the key becomes longer, less values are inserted in order. The increase also stops when the length of the key is equal to the length of the audio file or when the whole audio file is scrambled.

In all our experiments we will use fifteen generations. Figure 2 shows the test audio files scrambled for 15 generations with N = 0. Although the scrambled waves shown in the figure have very different shape and form from their original, the level of scrambling is enhanced significantly when N is greater than zero as given in Section 5.5.

Fig. 2
figure 2

Scrambled wave plots of different audio files with NOG = 15

Full size image

5.2 Correlation analysis of neighborhood type

Although many different possible neighborhood types exist, we have only tested von Neumann and Moore neighborhood types.

Table 3 shows the scrambling degree obtained when the audio files are scrambled using Moore and von Neumann neighborhood types. The scrambling experiments use the same key for both neighborhood types, and the scrambling is not repeated (N = 0).

Table 3 Scrambling degree when different neighborhood types are used with NOG = 15
Full size table

The Moore neighborhood provides significantly better scrambling results than von Neumann neighborhood, this is because the neighborhood effect applies to all cells in the grid and many of the CA properties are strongly dependent on the neighborhood [16]. Figure 3 shows the result of scrambling 15.wav and 28.wav using different neighborhood types.

Fig. 3
figure 3

Audio files scrambled using different neighborhood types

Full size image

5.3 Correlation analysis of boundary condition

Table 4 shows the scrambling degree obtained when the audio files are scrambled using periodic and null boundaries with no repetition (N = 0) and NOG = 15. The periodic boundary gives better randomness quality [1], but based on the results shown in Table 4, the difference between the two boundary types is not as significant as the difference between the tested neighborhood types. Also it can be seen from this table that on average the periodic boundary gives a slightly higher scrambling degree than the null boundary.

Table 4 Scrambling degree when different CA types are used
Full size table

5.4 Correlation analysis of lambda values

Table 5 shows different transition rules which we have chosen to test their effect on audio scrambling. The table also shows their rule numbers.

Table 5 The lambda value and rule number of different transition functions
Full size table

Table 6 shows the scrambling degrees obtained for different lambda values, in the experiments. No repetition was used (N = 0). The results show that the complex behavior of the Game of Life rule (GOL) which occurs around λ = 0.2734 gives the highest scrambling effect. This result could have been foreseen from Wolfram analysis of CAs, but it is nice to see it confirmed.

Table 6 Scrambling degree when using different transition rules and NOG = 15
Full size table

5.5 Correlation between confusion and repetition

In all the previous experiments, the audio files were scrambled with no repetition (N = 0), in Table 7, it can be seen that the repetition for only one time increases the scrambling degree and hence the confusion. Figure 4 shows the wave of 13.wav and 20.wav with and without repetition. Although in both the scrambled waves do not show any of the original audio structure, scrambling with repetition is better and have a higher scrambling degree.

Table 7 Relation between repetition (N) and scrambling degree
Full size table
Fig. 4
figure 4

Audio files scrambled before and after repetition where NOG = 15

Full size image

5.6 Robustness experiments

In an effort to measure the algorithm robustness, we applied the data loss attack where we eliminated 1/3 of the data samples of the data set audio files. Each audio file was scrambled twice, the first time with no repetitions (N = 0) and the second time the scrambling was repeated four times (N = 4), in order to show the relation between the scrambling degree and the robustness of the algorithm. Figure 5 shows the recovered waves of 1.wav and 19.wav after data loss. The scrambling degree for 1.wav is 0.92747 when N = 0 and 0.93951 when N = 4. The scrambling degree for 19.wav is 0.95558 when N = 0 and 0.96559 when N = 4.

Fig. 5
figure 5

Recovered audio file after data loss attack with NOG = 15

Full size image

From Fig. 5 it can be seen that the structure of the recovered wave is so similar to the original, especially when N = 4 (because with better scrambling the samples are distributed in a way that breaks the correlation between samples), so even if the data is lost the audio recovers most of its original structure.

When listening to the recovered audio we can absolutely understand it, although with the lower scrambling degree it can be noticed that there are isolated clicks in the audio, and with the higher scrambling degree some noise is introduced.

6 Comparison with previous schemes

Audio scrambling algorithms can be evaluated by many aspects, including high security and difficulty to descramble, complexity and applicability to real time applications, robustness, key size, in addition to the scrambled audio length and the need for padding, restrictions on the audio length, audio type, dimension, etc. the choice of which algorithm to use is usually dependent on the application and resources available. In this section we will discuss those different aspects and compare between some of the audio scrambling algorithms proposed.

Some of the scrambling algorithms map the original audio samples X 1, X 2, ..., X length(x) to the scrambled audio samples X′1, X′2, ..., X′ length(x) where the length of X is preserved as in our proposed algorithm (ASCA), other algorithms require padding so the original audio samples are mapped to X′1, X′2, ..., X′ length(x) + y where y is the length of padded audio samples. Also in some algorithms suitable padding maybe occasionally required [22].

Cyclic displacement scrambling transformation (CDST) and the complete binary tree’s in order traversal scrambling transformation (ITST), and their combined algorithm proposed in [5] does not require any additional padding, while the audio scrambling algorithm based on variable dimension space (ASVDS) proposed in [12] requires padding.

ASVDS was proposed to address the problems of one-dimensional linear mapping, it increases the audio dimension to a variable dimension space, although changing the dimension gives better scrambling, it is notable that increasing the audio dimension higher than 2D does not necessarily increases the algorithm efficiency. CDST, ITST, and the combination between them scramble the audio in one dimension, while our proposed algorithm (ASCA) increases the dimension to 2D only.

Because audio scrambling applications are mostly in the security domain, the key strength and length are important, and the requirement of both aspects is dependent on the application, for example, some of the scrambling algorithms does not need any key and does not achieve efficient scrambling as the others as in the case of ITST, but it might be very beneficial in case it is used as part of a process where at some step a key is added.

CDST requires only one integer to descramble, which is possible to decrypt if available to the public [5]. The combination algorithm uses two integer numbers to descramble, and finally ASVDS uses a transformation matrix of size n ×n where n is the dimension. In ASVDS if the algorithm increases the audio to two dimensions, the key will be a 2 ×2 matrix and the determinant of that matrix is a relative prime of the square root of the scrambled audio length. Table 8 summarizes the comparison between the audio scrambling algorithms.

Table 8 Comparing ASCA with previous schemes
Full size table

Other than the aspects we discussed above, there are benefits from relying on CA, for example, it is not a specific approach to scrambling but a general purpose discrete model of computation that could be used to solve any computable task which can be of a special benefit in systems that rely on this model. Moreover, CA is known for being a parallel model, which increases the performance of applications relying on it.

7 Conclusions and future work

A new scrambling technique for digital audio has been introduced. The proposed scheme takes advantage of 2D cellular automata with complex behavior to achieve a high scrambling degree. The paper studies the effect of using von Neumann neighborhood versus Moore neighborhood and the periodic boundary versus the null boundary. Five transition rules with different Lambda values were tested. The process is suitable for speech and music clips of different sizes and no extra padding is needed. The descrambling process is straightforward when the right key is available.

Experimental results suggest that the proposed technique breaks the correlation of adjacent data samples effectively. The relation between the scrambling degree achieved and the robustness of the algorithm is also studied, the results show that the algorithm is robust to data loss attack and the robustness becomes better when the scrambling degree is higher.

Some of the most popular CA types were studied in terms of digital audio scrambling, but many more exists; future plans include the extensive study of other CA types and other possible combinations, and extending this scheme to scramble video files.

Studying the best approach to extend the algorithm to include multi-channel audio is also left for future work. This extension can be done by treating each channel separately, or by considering inter-channel dependencies.

Other future plans will include the use of this algorithm as a part of watermarking, information hiding, fingerprinting, and encryption applications.