1. Introduction

The use of structures made from functionally graded materials has been increasing significantly in recent years in various engineering applications, such as aerospace, biomedical and civil engineering ones. The main characteristic of these materials is the continuous variation of their properties in one or more directions. This makes it possible to create structures with very interesting characteristics, such as a high resistance to temperature shocks, low transverse shear stresses, and high strength-toweight ratios. With the wide application of FG structures, understanding the behavior of FG beams becomes an important task.

Researchers have investigated the behavior of FG beams using the classical beam theory (CBT), called the Euler–Bernoulli theory, the first order or Timoshenko theory (FSBT), and higher-order beam theories (HSBTs).

Aydogdu and Taskin [1] studied the free vibration of simply supported FG beams employing the Euler–Bernoulli and shear-deformation beam theories. Using the Rayleigh–Ritz method, Pradhan and Chakraverty [2] investigated the free vibration of Euler–Bernoulli and Timoshenko FG beams with different boundary conditions. By means of the finite-element method and the Euler–Bernoulli beam theory, Alshorbagy et al. [3] studied the free vibration of FG beams. They used the principle of virtual work to derive the equations of motion. In the same way, Shahba et al. [4] obtained a solution for the free vibration and stability of an axially FG tapered beam.

It should be noted that the CBT is applicable only to slender beams. For moderately deep ones, this theory underestimates deflections and overestimates the buckling load and natural frequencies, because it neglects the effect of shear deformation [5]. Based on the FSBT, Nguyen et al. [6] proposed an improved first-order shear-deformation beam theory for the static and free vibration analyses of axially FG beams loaded. The dynamic instability of a functionally graded Timoshenko beam on a Winkler foundation was investigated by Mohanty et al. [7] using the finite-element method. Yaghoobi and Yaghoobi [8] examined the buckling behavior of sandwich plates having FG face sheets and resting on an elastic foundation.

In order to take into account the transverse shear deformation, studies on FG beams were performed invoking a higher-order shear-deformation beam theory [9]. Based on this theory, Tounsi and his coworkers developed several models for examining the static and dynamic behavior of FG material structures [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].

Bennai et al. [26] presented a hyperbolic shear -and normal- deformation beam theory to study the vibration and buckling responses of FG sandwich beams under various boundary conditions.

Yaghoobi and Fereidoon [27] presented a simple refined nth-order shear-deformation theory to investigate the mechanical and thermal buckling behavior of FG plates supported by an elastic foundation. Using a refined trigonometric higher-order beam theory based on the concept of position of the neutral surface, Bourada et al. [28] studied the bending and vibration behavior of FG beams. Thai and Vo [29] examined the effect of the volume fraction of constituents and shear deformation on the bending and vibration behavior of FG beams employing different higher-order shear-deformation beam theories. Invoking various higher-order shear-deformation beam theories and the Rayleigh–Ritz method, Pradhan and Chakraverty [30] studied the vibration responses of FG beams with various boundary conditions.

In fabrication of FG materials, microvoids or pores can occur in them during the sintering process owing to large differences in solidification temperatures between material constituents [31]. Consequently, it is imperative to take into account the effects of these porosities or imperfections on the global behavior of FG beams.

Studies on the stability and bending behavior of porous FG structures, especially for beams, are still limited in number [32]. Wattanasakulpong and Ungbhakorn [33] examined the linear and nonlinear vibrations of FG porous Euler–Bernoulli beams with elastically restrained ends by using the differential transformation method. Ait Atmane et al. [34] studied the free vibration of such beams by means of a shear-deformation theory. Mouaici et al. [35] presented an analytical solution for free vibrations of FG porous plates using a shear-deformation plate theory based on the position of neutral surface.

As far as we know, studies on FG porous structures have been performed mainly in the cases of porosity varying across their thickness. Only Chen et al. [32] has studied the static bending and buckling of FG porous beams, using the Timoshenko beam theory, with two different porosity distributions and without an elastic foundation.

In this paper, a new refined quasi-3D shear-deformation theory for bending, buckling, and free vibration analyses of a functionally graded porous beam resting on a Pasternak elastic foundation is presented. The present theory has only three unknowns and three governing equations, but it satisfies stress-free boundary conditions on the top and bottom surfaces of the beam without a need for any shear correction factor. The displacement field of the theory takes into account the stretching effect due to its 3D nature. Two different porosity distributions are considered in this analysis, and the mechanical properties of the FG porous beams are assumed as functions of these distributions. The model is applied to a simply supported beam made of a porous material. The general solution is obtained, and the results found are compared with those available in the literature.

Numerical examples are given to show the effects of porosity on the buckling, bending, and free vibration of porous beams resting on an elastic foundation.

2. Effective Material Properties of Porous FG beams

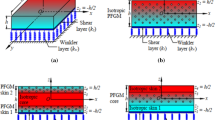
Consider a FG porous beam of thickness h and length L , as shown in the Fig. 1. The beam is assumed to rest on a Winkler–Pasternak elastic foundation. The mechanical characteristic of the beam varies according to the distribution of porosity. In the following, two different porosity distributions across the beam thickness are considered [32]:

Fig. 1.
figure 1

Porosity distributions 1 (a) and 2 (b) [32].

Full size image

Porosity distribution 1, with

$$ {\displaystyle \begin{array}{c}E(z)={E}_1\left[1-{e}_0\cos \left(\uppi \zeta \right)\right],\kern1em G(z)={G}_1\left[1-{e}_0\cos \left(\uppi \zeta \right)\right],\\ {}\rho (z)={\rho}_1\left[1-{e}_m\cos \left(\uppi \zeta \right)\right],\end{array}} $$
(1)

and Porosity distribution 2, with

$$ {\displaystyle \begin{array}{c}E(z)={E}_1\left[1-{e}_0\cos \left(\frac{\uppi}{2}\upzeta +\frac{\uppi}{4}\right)\right],\kern1em G(z)={G}_1\left[1-{e}_0\cos \left(\frac{\uppi}{2}\upzeta +\frac{\uppi}{4}\right)\right],\\ {}\rho (z)={\rho}_1\left[1-{e}_m\cos \left(\frac{\uppi}{2}\upzeta +\frac{\uppi}{4}\right)\right],\end{array}} $$
(2)

where ζ = z / h , e0 = 1− E0 / E1 = 1−G0 / G1 (0 <e0 < 1) is the porosity coefficient, and the minimum and maximum Young’s moduli, E0 and E1 , are related to the minimum and maximum shear moduli, G0 and G1 , as

$$ {G}_i={E}_i/\left[2\left(1+v\right)\right]\kern1em \left(i=0,1\right) $$

The porosity coefficient for the mass density is defined as

$$ {e}_m=1-{\rho}_0/{\rho}_1\kern1em \left(0<{e}_m<1\right), $$

where ρ0 and ρ1 are the minimum and maximum mass densities, respectively.

The relationship between density and Young’s modulus for an open-cell metal foam is [36, 37]

$$ \frac{E_0}{E_1}={\left(\frac{\rho_0}{\rho_1}\right)}^2. $$

This equation was used to obtain the relationship

$$ {e}_m=1-\sqrt{1-{e}_0}, $$

where the subscripts “0” and “1” denote the properties of FG material constituents (metal and ceramic).

3. Refined Quasi-3D Theory for Functionally Graded Porous Beams

3.1. Kinematics

The displacement field satisfying the conditions of zero transverse shear stresses (and hence zero strains) at ( x , y , ± h 2 ) on the outer (top) and inner (bottom) surfaces of the beam is given as

$$ {\displaystyle \begin{array}{c}u\left(x,y,z,t\right)={u}_0-z\frac{\partial {w}_b}{\partial x}+f(z)\frac{\partial {w}_s}{\partial x},\\ {}w\left(x,y,z,t\right)={w}_b+g(z){w}_s,\end{array}} $$

with

$$ f(z)=z\left(1-\frac{4{z}^2}{3{h}^2}\right),\kern1em g(z)= rf^{\prime }(z), $$

where u0 , v0 , wb , and ws are four unknown displacement functions of beam midsurface and r = 1 .

The kinematic relations are

$$ {\varepsilon}_x={\varepsilon}_x^0+z{k}_x+f(z){\eta}_x,\kern1em {\varepsilon}_z=g^{\prime }(z){\varepsilon}_z^0,\kern1em {\gamma}_{xz}=f^{\prime }(z){\gamma}_{xz}^0+g(z){\gamma}_{xz}^0, $$
(3)

where

$$ {\varepsilon}_x^0={u}_{0,x},\kern1em {\varepsilon}_z^0={w}_s,\kern1em {k}_x=-{w}_{b, xx},\kern1em {\eta}_x={w}_{s, xx},\kern1em {\gamma}_{xz}^0={w}_{s,x}. $$

3.2. Constitutive relations

The linear constitutive relations are

$$ {\sigma}_x={Q}_{11}{\varepsilon}_x+{Q}_{13}{\varepsilon}_z,\kern1em {\sigma}_y={Q}_{13}{\varepsilon}_x+{Q}_{33}{\varepsilon}_z,\kern1em {\tau}_{xz}={Q}_{55}{\gamma}_{xz}, $$
(4)

where (σ x ,σ z ,τ xz ) and (ε x ,ε z , γ xz ) are stress and strain components, respectively. Using the material properties defined by Eqs. (1) and (2), the stiffness coefficients Qij can be expressed as

$$ {Q}_{11}={Q}_{33}=\frac{E(z)\left(1-v\right)}{\left(1-2v\right)\left(1+v\right)},\kern1em {Q}_{13}=\frac{vE(z)}{\left(1-2v\right)\left(1+v\right)},\kern1em {Q}_{55}=\frac{E(z)}{2\left(1+v\right)}. $$

3.3. Equations of motion

The Hamilton principle was used to derive the equations of motion. This principle can be presented in the analytical form

$$ \underset{t_1}{\overset{t_2}{\int }}\left(\delta U+\delta {U}_F-\delta K+\delta W\right) dt=0, $$
(5)

where δU is the variation of strain energy, δUF is the variation of potential energy of elastic foundation, δ K is the variation of kinetic energy, and δW is the variation of the work performed.

The variation of strain energy of the beam is expressed as

$$ \delta U=\underset{0}{\overset{L}{\int }}\underset{-h/2}{\overset{+h/2}{\int }}\left({\sigma}_x\delta {\varepsilon}_x+{\sigma}_z\delta {\varepsilon}_z+{\tau}_{xz}\delta {\gamma}_{xz}\right) dxdz. $$
(6)

Inserting Eqs. (3) and (4) into Eq. (6) and integrating it across the plate thickness, we have

$$ \delta U=\underset{0}{\overset{L}{\int }}\left\{{N}_1\delta {\varepsilon}_x^0+{M}_1\delta {k}_x+{P}_1\delta {\eta}_x+{R}_3\delta {\varepsilon}_z^0+{Q}_5\delta {\gamma}_{xz}^0+{K}_5\delta {\gamma}_{xz}^0\right\} dx. $$
(7)

The stress resultants N, M, P, Q, and R are defined as

$$ {\displaystyle \begin{array}{c}\left({N}_i,{M}_i,{P}_i\right)=\underset{-h/2}{\overset{h/2}{\int }}{\sigma}_i\left(1,z,f(z)\right) dz\kern1em \left(i=1\right),\\ {}\left({K}_i,{Q}_i\right)=\underset{-h/2}{\overset{h/2}{\int }}{\sigma}_i\left(f^{\prime }(z),g(z)\right) dz\kern1em \left(i=5\right),\\ {}{R}_i=\underset{-h/2}{\overset{h/2}{\int }}{\sigma}_ig^{\prime }(z) dz,\kern1em \left(i=3\right).\end{array}} $$
(8)

Using Eq. (4) in Eq. (8), the stress resultants of FG beams can be related to the total strains as

$$ {\displaystyle \begin{array}{c}{N}_i={A}_{ij}{\varepsilon}_j^0+{B}_{ij}{k}_j+{C}_{ij}{\eta}_j+{F}_{ij}{\varepsilon}_z^0,\kern1em \left(i=1\right),\\ {}{M}_i={B}_{ij}{\varepsilon}_j^0+{G}_{ij}{k}_j+{H}_{ij}{\eta}_j+{K}_{ij}^{\prime }{\varepsilon}_z^0,\kern1em \left(i=1\right),\\ {}{P}_i={C}_{ij}{\varepsilon}_j^0+{H}_{ij}{k}_j+{L}_{ij}{\eta}_j+{O}_{ij}{\varepsilon}_z^0,\kern1em \left(i=1\right),\\ {}{Q}_i={Q}_{ij}^{\prime }{\gamma}_j^0+{P}_{ij}^{\prime }{\gamma}_j^0,\kern1em \left(i=5\right),\kern1em {K}_i={Q}_{ij}^{\prime }{\gamma}_j^0+{S}_{ij}{\gamma}_j^0,\kern1em \left(i=5\right),\\ {}{R}_i={F}_{ij}{\varepsilon}_j^0+{K}_{ij}^{\prime }{k}_j+{O}_{ij}{\eta}_j+{U}_{ij}{\varepsilon}_z^0,\kern1em \left(i=3\right),\end{array}} $$

where Aij , Bij , Cij , etc., are beam stiffnesses, defined as

$$ {\displaystyle \begin{array}{c}\left({A}_{ij},{B}_{ij},{C}_{ij},{F}_{ij}\right)=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{ij}\left(1,z,f(z),g^{\prime }(z)\right) dz,\\ {}\left({G}_{ij},{H}_{ij},{K}_{ij}^{\prime },{L}_{ij}\right)=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{ij}\left({z}^2, zf(z), zg^{\prime }(z),{f}^2(z)\right) dz,\\ {}\left({O}_{ij},{P}_{ij}^{\prime },{Q}_{ij}^{\prime },{S}_{ij}\right)=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{ij}\left(f(z)g^{\prime }(z),{g}^2(z),g(z)f^{\prime }(z),f{\prime}^2(z)\right) dz,\\ {}{U}_{ij}=\underset{-h/2}{\overset{h/2}{\int }}{Q}_{ij}\left(g{\prime}^2(z)\right) dz.\end{array}} $$

The variation of kinetic energy is expressed as

$$ {\displaystyle \begin{array}{c}\delta K={\int}_0^L{\int}_{-h/2}^{+h/2}\left[\rho \left(\dot{u}\delta u+\dot{w}\delta w\right)\right] dxdz\\ {}\delta K={\int}_0^L\Big({I}_1{\ddot{u}}_0\delta {u}_0+{I}_1{\ddot{w}}_b\delta {w}_b+{I}_2\left({\ddot{u}}_{0,x}\delta {w}_b-{\ddot{w}}_{b,x}\delta {u}_0\right)-{I}_4\left({\ddot{u}}_{0,x}\delta {w}_s-{\ddot{w}}_{s, xx}\delta {u}_0\right)-{I}_3\left({\ddot{w}}_{b, xx}+{\ddot{w}}_{b, xx}\right)\delta w\\ {}+{I}_5\left({\ddot{w}}_{b, xx}\delta {w}_s+{\ddot{w}}_{s, xx}\delta {w}_b\right)-{I}_6{\ddot{w}}_{s, xx}\delta {w}_s+{I}_7\left({\ddot{w}}_b\delta {w}_s+{\ddot{w}}_s\delta {w}_b\right)+{I}_g{\ddot{w}}_s\delta {w}_s\left)\kern0.24em \right\} dx\end{array}} $$
(9)

where the inertia terms are defined by the equations

$$ \delta W=-{\int}_0^L q\delta wdx+{\int}_0^L{N}_0{\left(\frac{\partial \delta w}{\partial x}\right)}^2 dx, $$
(10)

where q is the transverse load and N0 is the axial force.

The variation of potential energy of the elastic foundation can be expressed as

$$ \delta {U}_F={\int}_0^L\left({k}_ww-{k}_p{\nabla}^2w\right)\delta w\; dx, $$
(11)

where kw and kp are the stiffness of Winkler foundation and the shear stiffness of the elastic foundation, respectively.

Inserting expressions for δU , δUF , δW , and δ K from Eqs. (7), (9), (10), and (11) into Eq. (5), integrating it by parts, and collecting the coefficients of u0, v0, wb, and ws, the following equations of motion of the beam were obtained:

$$ {\displaystyle \begin{array}{c}\delta {u}_0:\kern1em {N}_{1,x}={I}_1{\ddot{u}}_0-{I}_2{\ddot{w}}_{b,x}+{I}_4{\ddot{w}}_{s,x},\\ {}\delta {w}_b:\kern1em {M}_{1, xx}+q+{N}_0\delta {w}_{, xx}-{k}_w\left({w}_b-y\ast {w}_s\right)+{k}_p\left({w}_{b, xx}-y\ast {w}_{s, xx}\right)={I}_1{\ddot{w}}_b+{I}_2{\ddot{u}}_{0,x}-{I}_3{\ddot{w}}_{b, xx}+{I}_5{\ddot{w}}_{s, xx}+{I}_7{\ddot{w}}_s,\\ {}\delta {w}_s:\kern1em {P}_{1, xx}+{Q}_{5.x}+{K}_{5,x}-{R}_3-y\ast q+{N}_0\delta {w}_{, xx}+y\ast {k}_w\left({w}_b-y\ast {w}_s\right)\\ {}-y\ast {k}_p\left({w}_{b, xx}-y\ast {w}_{s, xx}\right)=-{I}_4{\ddot{u}}_{0,x}+{I}_5{\ddot{w}}_{b, xx}-{I}_6{\ddot{w}}_{s, xx}+{I}_7{\ddot{w}}_b+{I}_g{\ddot{w}}_s.\end{array}} $$
(12)

4. Solution Procedure

To solve Eqs. (12) analytically, the Navier method was used under specified boundary conditions. The displacement functions satisfying the equations of simply supported FG beams were assumed in the form of Fourier series:

$$ \left\{\begin{array}{c}{u}_0\\ {}{w}_b\\ {}{w}_s\end{array}\right\}=\sum \limits_{m=1}^{\infty}\left\{\begin{array}{c}{U}_m\cos (ax){e}^{i\omega t}\\ {}{W}_{bm}\sin (ax){e}^{i\omega t}\\ {}{W}_{sm}\sin (ax){e}^{i\omega t}\end{array}\right\}, $$
(13)

where Um, Wbm, and Wsm are arbitrary parameters to be determined, ω is the eigenfrequency associated with an mth eigenmode, and α = mπ/l. The transverse load q was also expanded in a Fourier series as

$$ q=\sum \limits_{m=1}^{\infty }{q}_m\sin (ax), $$
(14)

where qm = 4q0/(mπ) (m = 1, 3, 5, …) for a uniformly distributed load of density q0.

Inserting Eqs. (13) and (14) into Eq. (12), the following problem was obtained:

$$ \left(\left[\begin{array}{ccc}{k}_{11}& {k}_{12}& {k}_{13}\\ {}{k}_{12}& {k}_{22}& {k}_{23}\\ {}{k}_{13}& {k}_{23}& {k}_{33}\end{array}\right]-{\omega}^2\left[\begin{array}{ccc}{m}_{11}& {m}_{12}& {m}_{13}\\ {}{m}_{12}& {m}_{22}& {m}_{23}\\ {}{m}_{13}& {m}_{23}& {m}_{33}\end{array}\right]\right)\left\{\begin{array}{c}{U}_m\\ {}{W}_{bm}\\ {}{W}_{sm}\end{array}\right\}=\left\{\begin{array}{c}0\\ {}{q}_m\\ {}-y\ast {q}_m\end{array}\right\}, $$
(15)

where y* = −g(h/2) and

$$ {\displaystyle \begin{array}{c}{k}_{11}=-{A}_{11}{\alpha}^2,\kern1em {k}_{12}={B}_{11}{\alpha}^3,\kern1em {k}_{13}=-{C}_{11}{\alpha}^3+{F}_{13}\alpha, \kern1em {k}_{22}=-{G}_{11}{\alpha}^4-{k}_w-{k}_p{\alpha}^2+{N}_0{\alpha}^2,\\ {}{k}_{23}={H}_{11}{\alpha}^4-{K}_{13}^{\prime }{\alpha}^2+y\ast {k}_w+y\ast {k}_p{\alpha}^2+{g}_0{N}_0{\alpha}^2,\\ {}{k}_{33}=-{L}_{11}{\alpha}^4+2{O}_{13}{\alpha}^2-\left({Q}_{55}^{\prime }+{P}_{55}^{\prime}\right){\alpha}^2-{U}_{33}-y{\ast}^2\left({k}_w+{k}_p{\alpha}^2\right)+{g_0}^2{N}_0{\alpha}^2,\\ {}{m}_{11}=-{I}_1,\kern1em {m}_{12}={I}_2\alpha, \kern1em {m}_{13}=-{I}_4\alpha, \kern1em {m}_{22}=-{I}_1-{I}_3{\alpha}^2,\kern1em {m}_{23}={I}_5{\alpha}^2-{I}_7,\kern1em {m}_{33}=-{I}_6{\alpha}^2-{I}_8.\end{array}} $$

The solution of problem (15) allows one to calculate the bending responses, the critical buckling load Ncr, and the natural frequencies of FG porous beams.

5. Results and Discussion

In this section, various numerical examples are presented and discussed to verify the accuracy of the present quasi-3D theory in predicting the bending, buckling, and free vibration responses of simply supported nonporous and FG porous beams of length l and thickness h.

The material properties adopted here are as follows.

Metal (aluminum, Al): E0 = Em = 70 GPa, v = 0.3, and ρ0 = ρm = 2702 Kg/m3.

Ceramic (alumina, Al2O3): El = Ec = 380 GPa. v = 0.3, and ρl = ρc = 3960 Kg/m3.

For convenience, the following nondimensional parameters are introduced:

$$ \overline{\omega}=\sqrt[4]{\frac{\rho_cA{l}^4{\omega}^2}{EI}},\kern1em \overset{\wedge }{\omega }=\frac{\omega {l}^2}{h}\sqrt{\frac{\rho_c}{E_c},}\kern1em \overline{w}\left(\frac{l}{2}\right)=w\left(\frac{l}{2}\right)100\frac{E_cI}{q{l}^4},\kern1em {N}_{cr}=\frac{E_0{l}^2}{EI},\kern1em {K}_w=\frac{k_w{l}^4}{EI},\kern1em {K}_p=\frac{k_p{l}^2}{EI}. $$

To validate our results, they were compared with literature data. For this purpose, the fundamental natural frequencies, the midspan deflection, and the parameter of buckling loads of isotropic homogeneous beams on an elastic foundation predicted by the present quasi-3D model are compared in Tables 1-3 with those found by Ying et al., Ait Atmane et al., Chen et al., and Venkateswara and Kanaka [38,39,40,41].

Table 1. Comparison of the Parameter \( \overline{\omega} \) of Fundamental Frequency of Isotropic Homogeneous Beams Resting on an Elastic Foundation
Full size table
Table 2. Comparisons of the Midspan Deflection \( \overline{w} \) of Isotropic Homogeneous Beams Resting on an Elastic Foundations under a Uniform Load
Full size table
Table 3. The parameter Ncr of Buckling Load of an Isotropic Homogeneous Beam with l/h = 20 Resting on an Elastic Foundation
Full size table

In Table 1, the fundamental frequencies of isotropic homogeneous beams obtained by the present method are compared with those determined by Ying et al., [38] and Ait Atmane et al. [39], and a good agreement is seen to exist between them.

Table 2 compares the midspan deflections of isotropic homogeneous beams obtained by the present model with those found by Ying et al. [38] and Chen et al. [39]. As is evident, there is no significant distinctions between the solutions, except for deflections of the beams with l/h = 5, where slight differences are seen. This is due to the fact that the theories used in [38, 39] does not take into account the normal deformation (εz = 0), which has a very great influence on short beams.

Table 3 compares the parameter Ncr of buckling load of an isotropic homogeneous beam resting on an elastic foundation (l/h = 20) given by the present theory with the results found by Venkateswara and Kanaka [41] and Ait Atmane et al. [39], and a close agreement is seen to exist between them.

In Fig. 2, the nondimensional fundamental frequency as a function of the ratio l/h is presented for two porosity distributions and for an isotropic homogeneous beam without an elastic foundation. Two conclusions can be drawn from this figure. First, a growth in l/h increased the fundamental dimensionless frequency in all the three cases studied. Second, the homogeneous beam (without a porosity) had a higher frequency than the porous ones.

Fig. 2.
figure 2

The nondimensional fundamental frequency \( \overset{\wedge }{\omega } \) versus l/h of an isotropic ceramic beam (without a porosity) (1) and FG beams with porosity distributions 1 (2) and 2 (3) resting on an elastic foundation.

Full size image

Figure 3 plots the nondimensional fundamental frequency \( \overset{\wedge }{\omega } \) versus l/h of FG porous beams on an elastic foundation for different values of the Pasternak parameter Kp and porosity distributions 1 and 2.

Fig. 3.
figure 3

The nondimensional fundamental frequency \( \overset{\wedge }{\omega } \) versus l/h of FG beams with porosity distributions 1 (a) and 2 (b) resting on Pasternak foundations with Kp = 0 (1), 2 (2), 4 (3), 6 (4), 8 (5), and 10 (6).

Full size image

Figure 4 illustrates the effect of Winkler and Pasternak parameters on the midspan deflection \( \overline{\omega} \) of isotropic (without a porosity) and porous beams As is seen, the midspan deflection tends to decrease as these parameters grow.

Fig. 4.
figure 4

Midspan deflection \( \overline{w} \) of an isotropic beam (ceramic) (1) and FG beams with porosity distributions 1 (2) and 2 (3) versus Kp (a) and Kw (b).

Full size image

The effect of elastic foundation parameters on the buckling loads Ncr is presented in Fig. 5. It can be seen that Ncr is a linear function of both parameters. We should also note that, in the case of Pasternak foundation, the buckling load is very little influenced by the state of the beam (porous or not), contrary to the case of Winkler foundation, where clear differences between buckling loads are seen in the three cases considered (ceramic beam and porous beams with porosity distributions 1 and 2).

Fig. 5.
figure 5

Buckling loads Ncr versus the foundation parameters Kp (a) and Kw (b) for an isotropic (ceramic) beam (1) and FG beams with porosity distributions 1 (2) and 2 (3).

Full size image

6. Conclusion

A new refined quasi-3D theory has been proposed for bending, buckling, and free vibration analyses of perfect and imperfect FG beams. Two different porosity distributions were considered for calculating the mechanical properties of the beams. The stretching effect was naturally taken into account in the mathematical formulation of the theory. The Navier solution was used for the simply supported beams. Numerical examples showed that the theory proposed gave solutions well agreeing with literature data. The effects of porosity distribution and slenderness ratio on the midspan deflection, the fundamental frequency, and the critical buckling load were also discussed.