Investigation of Strain Rate Effects on the Dynamic Response of a Glass/Epoxy Composite Plate Under Blast Loading by Using the Finite-Difference Method

Nonlinear equations of motion for a laminated composite plate under blast loading, based on the first-order shear deformation theory, are derived. The governing equations are solved by the finite-difference method in conjunction with the Newmark time integration scheme. The rules of material property degradation are modified to allow for strain rate effects. A progressive damage model is developed based on the modified rules of material property degradation and Hashin-type failure criteria to predict different failure modes. The validity of the method is demonstrated by quantitative and qualitative comparisons of present results with those available in the literature. Results for clamped glass/epoxy laminated composite plates with constant and strain-rate-dependent mechanical properties under a blast load are presented and compared for various ply stacking sequences, and pertinent conclusions are outlined.

1. Introduction

Due to their appropriate high energy absorption capacity, composite materials have extensive applications in structures subjected to high-intensity dynamic loads and rapid deformations. Under dynamic loads, such as blasts, the structures experience medium and high strain rates. Since mechanical properties can vary with strain rate, the dynamic response of the structures depends on the strain rate. In addition to strain rate effects, the geometrical nonlinearity due to large deformations and transverse shear strains is also an important factor in a structural analysis in such conditions.

Composite structures under blast loads have been studied experimentally, analytically, and numerically by various researchers. Reddy [1] examined the transient response of laminated composite panels by using the finite-element method, which allows for geometrical nonlinearities. Librescu and Nosier [2] investigated the response of laminated composite flat panels to sonic boom and explosive blast loads by employing the technique of integral transforms. The transverse shear deformations, the transverse normal stresses, and higher-order effects are taken into consideration in their analysis. Turkmen and Mecitoglu [3] studied the dynamic response of a stiffened laminated composite plate subjected to blast loads experimentally and numerically. Turkmen [4] presented theoretical and experimental investigations into the dynamic response of cylindrically curved laminated composite shells subjected to blast loading by using the Galerkin and Runge–Kutta–Verner methods. Utilizing the Galerkin and finite-difference methods, Kazanci and Mecitoglu [5] studied the nonlinear dynamic response of a laminated composite plate subjected to blast loads. Chenetal [6] presented a semi-analytical finite-strip method for an analysis of the geometrically nonlinear response of rectangular composite laminated plates to dynamic loading.

But none of the above-mentioned studies consider the effects of strain rate. Batra and Hassan [7] developed a mathematical model for analyzing the transient response of a composite plate subjected to underwater blast loads. They considered strain rate effects on the transverse and shear stiffnesses. Zhu et al. [8] presented a micromechanics model taking into account the transverse shear stress, the strain rate, and inelasticity to analyze the transient response of a laminated composite plate.

In the present work, the response of a laminated composite plate under blast loading is investigated. In the macromechanical approach, the finite-difference method and a progressive damage modeling algorithm considering the geometric nonlinearity are used. The effects of transverse shear strain and strain rate are studied. Coupled nonlinear equations of motion for a laminated plate based on the first-order shear deformation theory (FSDT) are derived and reduced to nonlinear ordinary differential equations in the time domain by using finite-difference approximations for displacements. The Newmark time integration scheme in association with the Newton–Raphson iteration method is employed to solve the system of nonlinear equations. The mechanical properties are updated based on the values of calculated strain rate at each material point. Furthermore, the degradation of mechanical properties due to failure is considered using the rules of sudden degradation of material properties and Hashin-type failure criteria for composite materials. The damage evolution and the strain-rate-dependence of longitudinal, transverse and shear mechanical properties can be considered by the model. Moreover, the present macromechanical model is less complex than micromechanics models.

2. Governing Equations

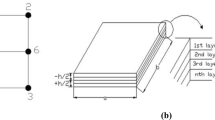
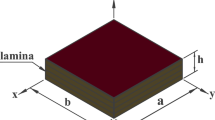
Figure 1 shows a rectangular laminated composite plate subjected to a blast load. The displacement field, according to the first-order shear deformation theory, can be expressed as [9]

Fig. 1

Laminated composite plate under a blast load.

$$ \begin{array}{c}\hfill u\left( x, y, z, t\right)={u}_0\left( x, y, t\right)+ z{\varphi}_x\left( x, y, z\right),\hfill \\ {}\hfill v\left( x, y, z, t\right)={v}_0\left( x, y, t\right)+ z{\varphi}_y\left( x, y, z\right),\hfill \\ {}\hfill w\left( x, y, z, t\right)={w}_0\left( x, y, t\right),\hfill \end{array} $$

where u, v, and w are displacements in the x, y, and z directions, respectively; u ₀ , v ₀ , and w ₀ denote displacements on the plane z = 0;φ _x and φ _y are rotations of the transverse normal about the x and y axes, respectively.

$$ \left\{\begin{array}{c}\hfill {\varepsilon}_{x x}\hfill \\ {}\hfill \begin{array}{c}\hfill {\varepsilon}_{y y}\hfill \\ {}\hfill {\gamma}_{x y}\hfill \end{array}\hfill \\ {}\hfill {\gamma}_{x z}\hfill \\ {}\hfill {\gamma}_{y z}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill {\varepsilon}_{x x}^0\hfill \\ {}\hfill \begin{array}{c}\hfill {\varepsilon}_{y y}^0\hfill \\ {}\hfill {\gamma}_{x y}^0\hfill \end{array}\hfill \\ {}\hfill {\gamma}_{x z}^0\hfill \\ {}\hfill {\gamma}_{y z}^0\hfill \end{array}\right\}+ z\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill {\kappa}_{x x}\hfill \\ {}\hfill {\kappa}_{y y}\hfill \end{array}\hfill \\ {}\hfill {\kappa}_{x y}\hfill \\ {}\hfill {\kappa}_{x z}\hfill \\ {}\hfill {\kappa}_{y z}\hfill \end{array}\right\}=\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill {u}_{0, x}+\frac{1}{2}{w_{0, x}}^2\hfill \\ {}\hfill {v}_{0, y}+\frac{1}{2}{w_{0, y}}^2\hfill \end{array}\hfill \\ {}\hfill {u}_{0, y}+{v}_{0, x}+{w}_{0, x}{w}_{0, y}\hfill \\ {}\hfill {w}_{0, x}+{\varphi}_x\hfill \\ {}\hfill {w}_{0, y}+{\varphi}_y\hfill \end{array}\right\}+ z\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {\varphi}_{x, x}\hfill \\ {}\hfill {\varphi}_{y, y}\hfill \end{array}\hfill \\ {}\hfill {\varphi}_{x, y}+{\varphi}_{y, x}\hfill \end{array}\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill \hfill \end{array}\right\}, $$

(1)

where, ε ⁰ _xx , ε ⁰ _yy , γ ⁰ _xy , γ ⁰ _xz , and γ ⁰ _zy are the membrane strains; κ _xx ,κ _yy ,κ _xy ,κ _zx , and κ _zy are the flexural strains or curvatures, but ε _zz is obviously equal to zero; z is the distance of an arbitrary point from the reference surface. The stress–strain relations for a kth layer are

$$ {\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill {\sigma}_{xx}\hfill \\ {}\hfill {\sigma}_{yy}\hfill \end{array}\hfill \\ {}\hfill {\sigma}_{yz}\hfill \\ {}\hfill {\sigma}_{zx}\hfill \\ {}\hfill {\sigma}_{xy}\hfill \end{array}\right\}}^{(k)}={\left[\begin{array}{c}\hfill \begin{array}{c}\hfill {\overline{Q}}_{11}\hfill \\ {}\hfill {\overline{Q}}_{12}\hfill \end{array}\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill {\overline{Q}}_{16}\hfill \end{array}\ \begin{array}{c}\hfill \begin{array}{c}\hfill {\overline{Q}}_{12}\hfill \\ {}\hfill {\overline{Q}}_{22}\hfill \end{array}\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill {\overline{Q}}_{26}\hfill \end{array}\ \begin{array}{c}\hfill \begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\hfill \\ {}\hfill 2{\overline{Q}}_{44}\hfill \\ {}\hfill 2{\overline{Q}}_{45}\hfill \\ {}\hfill 0\hfill \end{array}\ \begin{array}{c}\hfill \begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\hfill \\ {}\hfill 2{\overline{Q}}_{45}\hfill \\ {}\hfill 2{\overline{Q}}_{55}\hfill \\ {}\hfill 0\hfill \end{array}\ \begin{array}{c}\hfill \begin{array}{c}\hfill {\overline{Q}}_{16}\hfill \\ {}\hfill {\overline{Q}}_{26}\hfill \end{array}\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill 2{\overline{Q}}_{66}\hfill \end{array}\right]}^{(k)}{\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill {\varepsilon}_{xx}\hfill \\ {}\hfill {\varepsilon}_{yy}\hfill \end{array}\hfill \\ {}\hfill {\varepsilon}_{yz}\hfill \\ {}\hfill {\varepsilon}_{zx}\hfill \\ {}\hfill {\varepsilon}_{xy}\hfill \end{array}\right\}}^{(k)}, $$

(2)

where ${{\overline{Q}}_{ij}}^{(k)}$ at i, j = 1, 2, 6 are the inplane reduced stiffness coefficients and i, j = 4, 5 denote the through-the-thickness shear stiffness coefficients; ε _yz ,ε _zx , andε _xy represent the tensorial shear strains, which are half of the engineering shear strains γ _yz , γ _zx , and γ _xy , respectively. ${{\overline{Q}}_{ij}}^{(k)}$ can be obtained from the relationships

$$ {\left[\overline{Q}\right]}^{(k)}={\left[{T}^{-1}\right]}^{(k)}{\left[ Q\right]}^{(k)}{\left[ T\right]}^{(k)}, $$

$$ {\left[ T\right]}^{(k)}\left[\begin{array}{cccc}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {m}^2\hfill \\ {}\hfill {n}^2\hfill \end{array}\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill - mn\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {n}^2\hfill \\ {}\hfill {m}^2\hfill \end{array}\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill m n\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\hfill \\ {}\hfill m\hfill \\ {}\hfill n\hfill \\ {}\hfill 0\hfill \end{array}\hfill & \hfill \begin{array}{cc}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill 0\hfill \\ {}\hfill 0\hfill \end{array}\hfill \\ {}\hfill - n\hfill \\ {}\hfill m\hfill \\ {}\hfill 0\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill 2 mn\hfill \\ {}\hfill -2 mn\hfill \end{array}\hfill \\ {}\hfill 0\hfill \\ {}\hfill 0\hfill \\ {}\hfill {m}^2-{n}^2\hfill \end{array}\hfill \end{array}\hfill \end{array}\right], $$

where [T] ^{(k )} is the transformation matrix, m = cosθ _k , n = sinθ _k , and θ _k denotes the orientation angle of fibers in laminate

axes for a kth layer. Q ^(k) _ij can be expressed in terms of engineering constants:

$$ \begin{array}{ccc}\hfill \begin{array}{c}\hfill {Q}_{11}^{(k)}=\frac{E_{11}^{(k)}}{1-{\upsilon}_{12}^{(k)}{\upsilon}_{21}^{(k)}},\hfill \\ {}\hfill {Q}_{66}^{(k)}={G}_{12}^{(k)},\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill {Q}_{12}^{(k)}=\frac{\upsilon_{12}^{(k)}{E}_{12}^{(k)}}{1-{\upsilon}_{12}^{(k)}{\upsilon}_{21}^{(k)}},\hfill \\ {}\hfill {Q}_{44}^{(k)}={G}_{23}^{(k)},\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill {Q}_{22}^{(k)}=\frac{E_{22}^k}{1-{\upsilon}_{12}^{(k)}{\upsilon}_{21}^{(k)}}\hfill \\ {}\hfill {Q}_{55}^{(k)}={G}_{13}^{(k)}.\hfill \end{array}\hfill \end{array}, $$

Other components of the stiffness matrix [Q]^{(k )} are zero. E ^(k)₁₁ , E ^k₂₂ , G ^(k)₁₂ , G ^(k)₂₃ and G ^(k)₁₃ are the longitudinal, transverse, in-plane shear, and out-of-plane stiffnesses of a kth layer; υ ^(k)₁₂ and υ ^(k)₂₁ represent the major and minor Poisson’s ratios.

The constitutive equations for the laminate can be derived by through-the-thickness integration:

$$ \left\{\begin{array}{c}\hfill \begin{array}{c}\hfill {N}_{xx}\hfill \\ {}\hfill {N}_{yy}\hfill \\ {}\hfill {N}_{xy}\hfill \end{array}\hfill \\ {}\hfill {M}_{xx}\hfill \\ {}\hfill {M}_{yy}\hfill \\ {}\hfill {M}_{xy}\hfill \end{array}\right\}=\left[\begin{array}{cccc}\hfill \begin{array}{ccc}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {A}_{11}\hfill \\ {}\hfill {A}_{12}\hfill \end{array}\hfill \\ {}\hfill {A}_{16}\hfill \end{array}\hfill \\ {}\hfill {B}_{11}\hfill \\ {}\hfill {B}_{12}\hfill \\ {}\hfill {B}_{16}\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {A}_{12}\hfill \\ {}\hfill {A}_{22}\hfill \\ {}\hfill {A}_{26}\hfill \end{array}\hfill \\ {}\hfill {B}_{12}\hfill \\ {}\hfill {B}_{22}\hfill \\ {}\hfill {B}_{26}\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {A}_{16}\hfill \\ {}\hfill {A}_{26}\hfill \\ {}\hfill {A}_{66}\hfill \end{array}\hfill \\ {}\hfill {B}_{16}\hfill \\ {}\hfill {B}_{26}\hfill \\ {}\hfill {B}_{66}\hfill \end{array}\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {B}_{11}\hfill \\ {}\hfill {B}_{12}\hfill \\ {}\hfill {B}_{16}\hfill \end{array}\hfill \\ {}\hfill {D}_{11}\hfill \\ {}\hfill {D}_{12}\hfill \\ {}\hfill {D}_{16}\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {B}_{12}\hfill \\ {}\hfill {B}_{22}\hfill \\ {}\hfill {B}_{26}\hfill \end{array}\hfill \\ {}\hfill {D}_{12}\hfill \\ {}\hfill {D}_{22}\hfill \\ {}\hfill {D}_{26}\hfill \end{array}\hfill & \hfill \begin{array}{c}\hfill \begin{array}{c}\hfill {B}_{16}\hfill \\ {}\hfill {B}_{26}\hfill \\ {}\hfill {B}_{66}\hfill \end{array}\hfill \\ {}\hfill {D}_{16}\hfill \\ {}\hfill {D}_{26}\hfill \\ {}\hfill {D}_{66}\hfill \end{array}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill {\varepsilon}_{xx}^0\hfill \\ {}\hfill {\varepsilon}_{yy}^0\hfill \\ {}\hfill {\varepsilon}_{xy}^0\hfill \end{array}\hfill \\ {}\hfill {\kappa}_{xx}\hfill \\ {}\hfill {\kappa}_{yy}\hfill \\ {}\hfill {\kappa}_{xy}\hfill \end{array}\right\}, $$

(3a)

$$ \left\{\begin{array}{c}\hfill {Q}_y\hfill \\ {}\hfill {Q}_x\hfill \end{array}\right\}={K}_s\left[\begin{array}{cc}\hfill {A}_{44}\hfill & \hfill {A}_{45}\hfill \\ {}\hfill {A}_{45}\hfill & \hfill {A}_{55}\hfill \end{array}\right]\left\{\begin{array}{c}\hfill {\gamma}_{y z}^0\hfill \\ {}\hfill {\gamma}_{x z}^0\hfill \end{array}\right\}, $$

(3b)

where N _xx , N _yy , and N _xy are the membrane normal and shear forces per unit length; M _xx ,M _yy , and M _xy are the bending and twisting moments per unit length; Q _x and Q _y are the through-the-thickness shearing forces per unit length. A _ij , B _ij , and D _ij are expressed as

The parameter K _s in (3b) is a shear correction coefficient. The recommended value of the coefficient for a rectangular section is 5/6 [10].

$$ \begin{array}{c}\hfill \left({A}_{ij},{B}_{ij},{D}_{ij}\right)={\displaystyle \sum_{k=1}^n{\displaystyle \underset{z_k}{\overset{z_{k+1}}{\int }}{{\overline{Q}}_{ij}}^{(k)}\left(1, z,{z}^2\right) dz,}\ i, j=2,6}\hfill \\ {}\hfill {A}_{ij}={\displaystyle \sum_{k=1}^n{\displaystyle \underset{z_k}{\overset{z_{k+1}}{\int }}{{\overline{Q}}_{ij}}^{(k)} dz, i, j=4,5.}}\hfill \end{array} $$

Using the dynamic version of the principle of virtual displacements in association with constitutive equations and strain–displacement relations, the following nonlinear equations of the first-order theory can be obtained [9]:

$$ -\left({N}_{x x, x}+{N}_{x y, x}\right)+{I}_0{u}_{0, tt}+{I}_1{\varphi}_{x, tt}=0, $$

(4a)

$$ -\left({N}_{xy, x}+{N}_{y y, y}\right)+{I}_0{v}_{0, y y}+{I}_1{\varphi}_{y, tt}=0, $$

(4b)

$$ -\left({Q}_{x, x}+{W}_{y, y}\right)-{\left({N}_{x x}{w}_{0, x}+{N}_{x y}{w}_{0, y}\right)}_{, x}-{\left({N}_{x y}{w}_{0, x}+{N}_{y y}{w}_{0, y}\right)}_{, y}- q+{I}_0{w}_{0, tt}=0, $$

(4c)

$$ -\left({M}_{x x, x}+{M}_{x y, y}\right)+{Q}_x+{I}_1{u}_{0, tt}+{I}_2{\varphi}_{x, tt}=0, $$

(4d)

$$ -\left({M}_{xy, x}+{M}_{y y, y}\right)+{Q}_y+{I}_1{v}_{0, tt}+{I}_2{\varphi}_{y, tt}=0. $$

(4e)

The mass moments of inertia I _i in Eqs. (4a-4e) are defined as

$$ \left({I}_0,{I}_1,{I}_2\right)={\displaystyle \underset{- h/2}{\overset{h/2}{\int }}\left(1, z,{z}^2\right)}{\rho}_0 dz, $$

where h , ρ ₀ , and q are the laminate thickness and density, and the transverse distributed load, respectively.

3. Blast Loading

In a blast loading, the pressure increases to a peak overpressure ( p _max ) and then decays to the ambient pressure p ₀ in time t ₀ (the positive phase); it continues to decay below the ambient pressure and then returns to the pressure once more (the negative phase).When the blast source is far enough from the target, the Friedlander equation [5] can be used to describe the air blast pressure:

$$ p(t)={p}_{\max}\left(1- t/{t}_0\right){e}^{-\alpha t/{t}_0}, $$

where a is the waveform parameter. The underwater blast pressure is expresses as [7]

$$ p(t)={p}_{\max }{e}^{- t/\lambda}. $$

(5)

In an underwater blast wave, no negative phase exists, and λ is a constant. The quantities p _max , t ₀ ,a , and λ depend on the explosive type and weight and on the distance between the explosive and target. In addition to the peak overpressure, the impulse should also be taken into the consideration in a blast event, which is defined as the area underneath the pressure–time curve and is the measure of the energy transferred to the target. The impulse controls the level of deflection of the target, and the slope of the impulse–time curve controls the strain rate experienced by the target [11].

4. Progressive Damage Model

The progressive damage model introduced by Shokrieh [12] is developed using two-dimensional Hashin-type failure criteria, the rules of sudden degradation of material properties, and empirical relations for the mechanical properties in terms of strain rate.

4.1. Sudden degradation of material properties

The failure modes and the rules of sudden degradation of material properties for a strain-rate-dependent composite can be expressed as follows:

for the tension failure of fiber,

$$ \begin{array}{c}\hfill \mathrm{if}\kern0.5em {\sigma}_{11}>0,{\left(\frac{\sigma_{11}}{ X t}\right)}^2+{\left(\frac{\sigma_{12}}{S}\right)}^2=\left\{\begin{array}{c}\hfill \ge 1,\kern0.5em \mathrm{failed}\to eft=0,\hfill \\ {}\hfill \le 1,\ \mathrm{elastic}\to eft=1,\hfill \end{array}\right.\hfill \\ {}\hfill \left[{E}_{11}\left({\dot{\varepsilon}}_{11}^k\right),{E}_{22}\left({\dot{\varepsilon}}_{22}^k\right),{G}_{12}\left({\dot{\varepsilon}}_{12}^k\right),{\upsilon}_{12},{\upsilon}_{21}\right]\to \left[0,0,0,0,0\right],\hfill \\ {}\hfill \left[{X}_t\left({\dot{\varepsilon}}_{11}^k\right),{X}_c\left({\dot{\varepsilon}}_{11}^k\right),{Y}_t\left({\dot{\varepsilon}}_{22}^k\right),{Y}_c\left({\dot{\varepsilon}}_{22}^k\right), S\left({\dot{\varepsilon}}_{12}^k\right)\right]\to \left[0,0,0,0,0\right];\hfill \end{array} $$

(6a)

for the compression failure fiber,

$$ \begin{array}{c}\hfill \mathrm{if}\kern0.5em {\sigma}_{11}<0,{\left(\frac{\sigma_{11}}{X_c}\right)}^2=\left\{\begin{array}{c}\hfill \ge 1\kern0.5em \mathrm{failed}\to \kern0.5em efc=0,\hfill \\ {}\hfill <1\kern0.5em \mathrm{elastic}\kern0.5em \to efc=1,\hfill \end{array}\right.\hfill \\ {}\hfill \left[{E}_{11}\left({\dot{\varepsilon}}_{11}^{(k)}\right),{E}_{22}\left({\dot{\varepsilon}}_{22}^{(k)}\right),{G}_{12}\left({\dot{\varepsilon}}_{12}^{(k)}\right),{\upsilon}_{12},{\upsilon}_{21}\right]\to \left[0,0,0,0,0\right],\hfill \\ {}\hfill \left[{X}_t\left({\dot{\varepsilon}}_{11}^{(k)}\right),{X}_c\left({\dot{\varepsilon}}_{11}^{(k)}\right),{Y}_t\left({\dot{\varepsilon}}_{22}^{(k)}\right),{Y}_c\left({\dot{\varepsilon}}_{22}^{(k)}\right), S\left({\dot{\varepsilon}}_{12}^{(k)}\right)\right]\to \left[0,0,0,0,0\right];\hfill \end{array} $$

(6b)

for the fiber-matrix shearing failure,

$$ \begin{array}{c}\hfill \mathrm{if}\kern0.5em {\sigma}_{11}<0,{\left(\frac{\sigma_{11}}{X_c}\right)}^2+{\left(\frac{\sigma_{12}}{S}\right)}^2=\left\{\begin{array}{c}\hfill \ge 1\kern0.5em \mathrm{failed}\to efms=0,\hfill \\ {}\hfill <1\ \mathrm{elastic}\to efms=1,\hfill \end{array}\right.\hfill \\ {}\hfill \left[{E}_{11}\left({\dot{\varepsilon}}_{11}^{(k)}\right),{E}_{22}\left({\dot{\varepsilon}}_{22}^{(k)}\right),{G}_{12}\left({\dot{\varepsilon}}_{12}^{(k)}\right),{\upsilon}_{12},{\upsilon}_{21}\right]\to \hfill \\ {}\hfill \to \left[{E}_{11}\left({\dot{\varepsilon}}_{22}^{\left( k+1\right)}\right),{E}_{22}\left({\dot{\varepsilon}}_{22}^{(k)}\right),0,0,0\right],\hfill \\ {}\hfill \begin{array}{c}\hfill \left[{X}_t\left({\dot{\varepsilon}}_{11}^{(k)}\right),{X}_c\left({\dot{\varepsilon}}_{11}^{(k)}\right),{Y}_t\left({\dot{\varepsilon}}_{22}^{(k)}\right),{Y}_c\left({\dot{\varepsilon}}_{22}^{(k)}\right), S\left({\dot{\varepsilon}}_{12}^{(k)}\right)\right]\to \hfill \\ {}\hfill \to \left[{X}_t\left({\dot{\varepsilon}}_{11}^{\left( k+1\right)}\right),{X}_c\left({\dot{\varepsilon}}_{11}^{\left( k+1\right)}\right),{Y}_t\left({\dot{\varepsilon}}_{22}^{\left( k+1\right)}\right),{Y}_c\left({\dot{\varepsilon}}_{22}^{\left( k+1\right)}\right),0\right];\hfill \end{array}\hfill \end{array} $$

(6c)

for the matrix compression failure:

$$ \begin{array}{c}\hfill \mathrm{if}\kern0.5em {\sigma}_{22}<0,{\left(\frac{\sigma_{22}}{Y_c}\right)}^2+{\left(\frac{\sigma_{12}}{S}\right)}^2=\left\{\begin{array}{c}\hfill \ge 1,\kern0.5em \mathrm{failed}\to emc=0,\hfill \\ {}\hfill <1,\kern0.5em \mathrm{elastic}\to emc=1,\hfill \end{array}\right.\hfill \\ {}\hfill \left[{E}_{11}\left({\dot{\varepsilon}}_{11}^{(k)}\right),{E}_{22}\left({\dot{\varepsilon}}_{22}^{(k)}\right),{G}_{12}\left({\dot{\varepsilon}}_{12}^{(k)}\right),{\upsilon}_{12},0\right],\hfill \\ {}\hfill \mapsto \left[{E}_{11}\left({\dot{\varepsilon}}_{11}^{(k)}\right),0,{G}_{12}\left({\dot{\varepsilon}}_{12}^{(k)}\right),{\upsilon}_{12},0\right],\hfill \\ {}\hfill \begin{array}{c}\hfill \left[{X}_t\left({\dot{\varepsilon}}_{11}^{(k)}\right)\right],{X}_c\left({\dot{\varepsilon}}_{11}^{(k)}\right),{Y}_t\left({\dot{\varepsilon}}_{22}^{(k)}\right),{Y}_c{\left({\dot{\varepsilon}}_{22}^{(k)}\right)}_c, S\left({\dot{\varepsilon}}_{12}^{(k)}\right)\to \hfill \\ {}\hfill \to \left[{X}_t\left({\dot{\varepsilon}}_{11}^{\left( k+1\right)}\right),{X}_c\left({\dot{\varepsilon}}_{11}^{\left( k+1\right)}\right),{Y}_t\left({\dot{\varepsilon}}_{22}^{\left( k+1\right)}\right),0, S\left({\dot{\varepsilon}}_{12}^{\left( k+1\right)}\right)\right],\hfill \end{array}\hfill \end{array} $$

(6e)

where σ₁₁ is the stress in the fiber direction,σ₂₂ is the stress in the direction transverse to the fiber, and σ₁₂ is the in-plane shear stress. X _t , X _c , Y _t , Y _c , and S are the longitudinal tensile strength, the longitudinal compressive strength, the transverse tensile strength, the transverse compressive strength, and the in-plane shear strength, respectively; eft , efc , efms , emt , and emc denote the damage variables in fiber tension, fiber compression, fiber-matrix shearing, matrix tension, and matrix compression failure modes, respectively. In addition, ${\dot{\varepsilon}}_{11}^{(k)},{\dot{\varepsilon}}_{11}^{(k)},\mathrm{and}\ {\dot{\varepsilon}}_{12}^{(k)},$ are the rates of longitudinal, transverse, and shear strains at a kth time step, respectively; σ₁₁ ,σ ₂₂ , and σ₁₂ for an nth layer are calculated from the relationship

$$ {\left\{\begin{array}{c}\hfill {\sigma}_{11}\hfill \\ {}\hfill {\sigma}_{22}\hfill \\ {}\hfill {\sigma}_{12}\hfill \end{array}\right\}}^{(n)}={\left[\begin{array}{c}\hfill \begin{array}{ccc}\hfill {m}^2\hfill & \hfill {n}^2\hfill & \hfill -2 mn\hfill \end{array}\hfill \\ {}\hfill \begin{array}{ccc}\hfill {n}^2\hfill & \hfill {m}^2\hfill & \hfill \hfill \end{array}\hfill \\ {}\hfill \begin{array}{ccc}\hfill - mn\hfill & \hfill mn\hfill & \hfill {m}^2-{n}^2\hfill \end{array}\hfill \end{array}\right]}^{(n)}{\left\{\begin{array}{c}\hfill {\sigma}_{xx}\hfill \\ {}\hfill {\sigma}_{yy}\hfill \\ {}\hfill {\sigma}_{xy}\hfill \end{array}\right\}}^{(n)}. $$

4.2. Mechanical property–strain rate relations

The mechanical properties of a composite are functions of strain rate. When a composite plate is exposed to a dynamic loading, different points of the plate are subjected to different time-dependent strain rates, and therefore they have different mechanical properties. Shokrieh and Omidi [13-15] investigated the effect of strain rate on the mechanical properties of unidirectional glass/epoxy composites by using a servohydraulic apparatus at varying strain rates, ranging from 0.001 to 100 1/s. In their study, the mechanical properties are plotted versus the logarithms of strain rate, and the data are fitted by using the regression function

$$ M\left(\dot{\varepsilon}\right)=\alpha +\beta {\dot{\varepsilon}}^{\gamma}, $$

(7)

where M and $\dot{\varepsilon}$ are the mechanical property and strain rate, respectively; α , β , and γ are material constants. Table 1 shows the values of α , β , and γ for various mechanical properties of glass/epoxy composites.

TABLE 1 Material Constants in the Regression Function of the Mechanical Properties of Glass/Epoxy Composites [13-15]

5. Finite-Difference Model

Inserting Eqs. (3a) and (3b) into Eqs. (4a)-(4e) and using Eq. (1), the equations of motion can be expressed in terms of the displacements u ₀ , v ₀ , w ₀ ,φ _x , and φ _y . The nonlinear coupled partial differential equations can be reduced to a set of ordinary differential equations in the time domain by using the finite-difference approximation for the displacement field. Employing the central finite-difference approximations, the differential equations, initial conditions, and boundary conditions can be converted into finite-difference expressions at a mesh point (i, j) . The central finite-difference equations for the firstand second-order derivatives of an arbitrary variable f can be written as

$$ \begin{array}{c}\hfill \begin{array}{c}\hfill {f_{,}}_x=\frac{1}{2 h}\left(-{f}_{-1+ i, j}+{f}_{1+ i, j}\right),\hfill \\ {}\hfill {f}_{, y}=\frac{1}{2 h}\left(-{f}_{i,-1+ j}+{f}_{1,1+ j}\right),\hfill \end{array}\hfill \\ {}\hfill {f}_{, xx}=\frac{1}{h^2}\left({f}_{-1+ i, j}-2{f}_{i, j}+{f}_{1+ i, j}\right),\hfill \\ {}\hfill {f}_{, xy}=\frac{1}{4{h}^2}\left({f}_{-1+ i,-1+ j}-{f}_{-1+ i,1+ j}-{f}_{1+ i,-1+ j}+{f}_{1+ i,1+ j}\right),\hfill \\ {}\hfill f, y y=\frac{1}{h^2}\left({f}_{i,-1+ j}-2{f}_{i, j}+{f}_{i,1+ j}\right),\hfill \end{array} $$

(8)

where f _{i, j} and h denote the value of f at the mesh point (i, j) and the spatial length scale, respectively. The finite-difference form of Eq. (4a) is given in Appendix A. Equations (4b)-(4e) can be similarly converted into finite-difference expressions by using Eqs. (7).

Figure 2 shows an example of the finite-difference mesh. For each mesh point, five ordinary differential equations in the time domain are obtained. After assembling these equations for all mesh points, the matrix form of the equations can be written as

Fig. 2

Finite-difference mesh.

$$ \mathrm{M}\ddot{\mathrm{U}}={\mathrm{F}}_{\mathrm{ext}}(t)-{\mathrm{F}}_{\mathrm{int}}\left(\mathrm{U}\right), $$

(9)

where M , F _ext , and F _int are the mass matrix and the external and internal force vectors, respectively. U and Ü are the displacement and acceleration vectors, respectively. The displacement vector can be written as

$$ \mathrm{U}={\left\{{\mathrm{u}}_{i, j},{\mathrm{v}}_{i, j},{\mathrm{w}}_{i, j},{\varphi}_x^{i, j},{\varphi}_y^{i, j}\right\}}^T, i=1,2,\dots, n-1, j=1,2,\dots, m-1. $$

As shown in Fig. 2, n and m represent the numbers of division in the x and y directions, respectively. In order to reduce the set of ordinary differential equations (9) to algebraic ones, the time derivatives are approximated using the Newmark implicit time integration scheme [9]. At the time t + Δt , equation (9) can be rewritten as

$$ \mathrm{M}{\ddot{\mathrm{U}}}^{\left( t+\varDelta t\right)}+{K}^{(t)}\Delta \mathrm{U}={\mathrm{F}}_{ext}^{\left( t+\varDelta t\right)}\left(\mathrm{t}\right)-{\mathrm{F}}_{\mathrm{int}}^{(t)}\left(\mathrm{U}\right), $$

where K is the tangential stiffness matrix, which is defined as

$$ K=\frac{\partial {\mathrm{F}}_{\mathrm{int}}}{\partial \mathrm{U}}. $$

(10)

The solution procedure is as follows

Step 1: calculate a ₁ = αΔt, a₂ = (1 − α)Δt, a₃ = 1/(βΔt ²), a₄ = a₃ Δt, a5 = 1/(2β) − 1;

Step 2: initialize ${\mathrm{U}}^{(0)},{\mathrm{U}}^{(0)},\ \mathrm{and}\ {\ddot{\mathrm{U}}}^{(0)}$

Step 3: calculate ${}^{(0)}\widehat{\mathrm{K}}={\mathrm{K}}^{(t)}+{a}_0\mathrm{M}\;\mathrm{and}\ \widehat{\mathrm{F}}{=}^{(0)}{\mathrm{F}}_{ext}^{\left( t+\varDelta t\right)}+\mathrm{M}\left({a}_1{\dot{\mathrm{U}}}^{(t)}+{a}_2{\ddot{\mathrm{U}}}^{(t)}\right)-{\mathrm{F}}_{\mathrm{int}}^{(t)};$

Step 4: solve ${}^{(0)}\widehat{\mathrm{K}}^{(1)}\varDelta U={}^{(0)}\widehat{\mathrm{F}}\ \mathrm{and}\ \mathrm{calculate}\ {}^{(1)}\mathrm{F}_{\operatorname{int}}^{\left( t+\varDelta t\right)};$

Step 5: set iteration i = 2

Step 6: update ^{(i − 1)}K^{(t + Δt)} using (10)

Step 7: calculate ${}^{\left( i-1\right)}{\ddot{\mathrm{U}}}^{\left( t+\varDelta t\right)}={a_0}^{\left( i-1\right)}\varDelta \mathrm{U}-{a}_1{\dot{\mathrm{U}}}^{(t)}-{a}_2{\ddot{\mathrm{U}}}^{(t)}{,}^{\left( i-1\right)}\widehat{\mathrm{K}}{=}^{\left( i-1\right)}{\mathrm{K}}^{\left( t+\varDelta t\right)}+{a}_0\mathrm{M},\ {\mathrm{and}}^{\left( i-1\right)}\mathrm{R}={\mathrm{F}}_{\mathrm{ext}}^{\left( t+\varDelta t\right)}-{\mathrm{M}}^{\left( i-1\right)}{\mathrm{U}}^{\left( t+\varDelta t\right)}{-}^{\left( i-1\right)}{\mathrm{F}}_{\mathrm{int}}^{\left( t+\varDelta t\right)};$ Step 8: solve ${}^{\left( i-1\right)}{\widehat{\mathrm{K}}}^{(i)} d\mathrm{U}{=}^{\left( i-1\right)}\mathrm{R}\ \mathrm{and}\ {\mathrm{update}}^{(i)}\varDelta \mathrm{U}{+}^{(i)} d\mathrm{U};$

Step 9: update ⁽ⁱ⁾F ^{(t + Δt)}_int ;

Step 10: check convergence:

if yes, go to step 11, if no, set i = i +1 and go to step 6; Step 11: calculate acceleration, velocity and displacement vectors:

$$ {\ddot{U}}^{\left( t+\varDelta t\right)}={a}_0\varDelta \mathrm{U}-{a}_1{\dot{\mathrm{U}}}^{(t)}-{a}_2{\ddot{U}}^{(t)},{\dot{\mathrm{U}}}^{\left( t+\varDelta t\right)}={\dot{\mathrm{U}}}^{(t)}+{a}_3{\ddot{\mathrm{U}}}^{(t)}+{a}_4{\ddot{\mathrm{U}}}^{\left( t+\varDelta t\right)},\ \mathrm{and}\ {\mathrm{U}}^{\left( t+\varDelta t\right)}={\mathrm{U}}^{(t)}+\varDelta \mathrm{U}; $$

Step 12: calculate the strain and stress tensors using Eqs. (1) and (2), respectively;

Step 13: calculate the strain rate ${\dot{\upvarepsilon}}^{\left( t+\varDelta t\right)}=\frac{1}{\varDelta t}\left({\upvarepsilon}^{\left( t+\varDelta t\right)}-{\upvarepsilon}^{(t)}\right);$

Step 14: check for the failure in layers using Eqs. (6):

if failed, use the rules of sudden material property degradation and go to 14, if not, go to step 15

Step 15: update material properties using Eq. (7);

Step 16: go to the next time step.

Here, Δt is the time step, i denotes the iteration, and α and β determine the stability and accuracy of the scheme. In the present work, the constant-average acceleration method with α = β = 0.5 is used.

6. Verification Study

In order to validate the present model, a comparison with the results obtained by Batra and Hassan [7] was carried out. In [7], the response of a composite panel exposed to an underwater explosive load is obtained using the three-dimensional finite-element method. A 10-mm-thick, 220 × 220-mm square AS4/PEEK composite panel with a fiber volume content of 0.6 was used. The mechanical properties were:

$$ E{}_1=130.86\ \mathrm{GPa},\kern0.5em {E}_2=14.7\kern0.5em \mathrm{GPa},\kern0.5em {\mathrm{G}}_{12}={G}_{23}5.44\kern0.5em \mathrm{GPa},\ X=1375\kern0.5em \mathrm{MPa},\ {X}_c=1080\kern0.5em \mathrm{MPa},\ {Y}_t=78\kern0.5em \mathrm{MPa},\kern0.5em {Y}_c=150\kern0.5em \mathrm{MPa},\kern0.5em \mathrm{S}=70\kern0.5em \mathrm{MPa},\ \rho =1640\mathrm{kg}/{\mathrm{m}}^3,\mathrm{and}{\upsilon}_{12}=0.3. $$

The plate was made of four plies with fiber orientation S = 0°, clamped along all four edges, and subjected to a nonuniform blast pressure from 64 kg of TNT with a standoff distance of 10 m. The pressure distribution over the plate was:

$$ p\left( r, t\right)=\left(-0.0005{r}^4+0.01{r}^3-0.0586{r}^2-0.001 r+\right) p(t), $$

where r is the distance from the center of the plate in cm, and p t ( ) denotes the pressure at the center of the plate, which can be expressed by Eq. (5) with p _max = 17.68 MPa and λ = 0.424 . The strain rate effects on the transverse and shear stiffnesses are considered in [7], but due to the lack of information in [7], all material properties were assumed to be constant in the verification study. Figure 3 depicts a comparison between the deflection δ at the center of the plate reported in [7] and that obtained from the present model. The failure modes given by the present model and in [7] are also shown in Fig. 4. A good agreement can be observed between the results.

Fig. 3

Comparison of deflections δ at the center of the plate: (––––) — present; (––○––) — data from [7].

Fig. 4

Comparison of predicted failure modes: (a) [7] and (b) present model.

7. Numerical Results and Discussion

A 16-mm-thick, 200 × 200-mm glass/epoxy composite plate with a [0] _s ply stacking was considered. The fiber volume fraction of the composite was 50%. The plate was clamped at all edges and subjected to a uniform underwater blast load. The parameters of the load (Eq. (5)) from 51 kg of TNT with a standoff distance of 15 m are p _max = 10 MPa and λ = 0 4.

In order to investigate the strain rate effects two material models were considered.

Static model. The mechanical properties were obtained from static tests and were constant (see Table 1):

$$ {E}_{11}=37.243\kern0.5em \mathrm{GPa},\kern0.5em {E}_{22}=10.037\ \mathrm{GPa},\kern0.5em {G}_{12}={G}_{23}=4.919\kern0.5em \mathrm{GPa},\ X\mathrm{t}=788.122\kern0.5em \mathrm{MPa},\ {X}_{\mathrm{c}}=243.497\kern0.5em \mathrm{MPa},\kern0.5em {Y}_t=43.451\kern0.5em \mathrm{MPa},\ {Y}_c=109.97\kern0.5em \mathrm{MPa},\kern0.5em \mathrm{and}\kern0.5em S=31.316\kern0.5em \mathrm{MPa},. $$

Dynamic model. The mechanical properties were strain-rate-dependent and were calculated from Eq. (7). The density and Poisson’s ratio did not vary with strain rate:

$$ \rho =2100\mathrm{kg}/{\mathrm{m}}^3,\kern0.5em \mathrm{and}\kern0.5em {\upsilon}_{12}=0.237. $$

From convergence studies, it was found that 400 mesh points and a time increment of 0.012 ms were adequate for the numerical simulation.

7.1. Effect of strain rate

Figure 5 depicts the time histories of deflection at the center of a plate with a [0]s ply stacking sequence. Results of the static and dynamic models are shown by dashed and solid curves, respectively. As seen, the maximum deflection at the center (absolute value) obtained from the static model is larger than that given by the dynamic one. This is due to the fact that, the stiffness in the dynamic model increases with strain rate, and therefore the static model, which has constant mechanical properties, is softer than the dynamic one. This result is consistent with that obtained by Zhu et al. [8].

Fig. 5

Deflection at the center of the plate for the static (1) and dynamic (2) models.

Figure 6 shows the maximum stresses for the static and dynamic models during the loading. It can be observed that the stresses obtained from the static model are higher than those given by the dynamic one (except for σ₁₃ ). This can be explained by the fact that the maximum deflection at the center for the static model is greater than for the dynamic one, which leads to greater strains and stresses for the static model. As shown in Fig. 6, the maximum out-of-plane shear stress calculated from the dynamic model is slightly higher than that found from the static one. However, the mean value of σ₁₃ during the loading is 20 MPa for the static model and only 15.6 MPa for the dynamic one.

Fig. 6

Maximum stresses for the static (□) and dynamic (■) models.

7.2. Effect of stacking sequence

To investigate the effect of stacking sequence on the dynamic response of a composite plate under a blast load, 200 × 200 × 16-mm glass/epoxy composite clamped plates with [0] _s , [0 / 90] _s , [+45 / −45] _s , and [0 / 90 / +45 / −45]s layups were analyzed. The maximum deflections w _max at the center of the plates are given in Fig. 7. As seen, the trends for the static and dynamic models are the same. It can be observed that, for both the models, the maximum deflection at the center of the [+45 / −45] _s plate is larger than that of the other ones. This is due to the higher flexibility of the [+45 / −45] _s stacking sequence in comparison with those of the other stacking sequences.

Fig. 7

Maximum deflection at the center for various stacking sequences: for static (□) and dynamic (■) models.

7.3. Effect of strain rate on failure modes

Figure 8 exhibits fringe plots of various damage variables at the top surface of a 200 × 200 × 16-mm clamped glass/epoxy composite plate with the [0]s stacking sequence under a uniform underwater blast load with λ = 0.4 and p _max = 10 MPa. It can be concluded from these plots that, for all failure modes, at a specific time, the failed region obtained using the static model is larger than that given by the dynamic model. This is due to the fact that the strength of the dynamic model increases with strain rate and is higher than that of the static one. It can also be observed that, for a specific failure mode, the location of damage initiation for the static and dynamic models are similar.

Fig. 8

Comparison of failure modes for the static (a) and dynamic (b) models.

The propagation of cracks in interfaces, which is known as the delamination failure mode, depends on the transverse normal (σ33 ) and transverse shear stresses (σ13 , and σ 23 ). According to the 3-D Hashin-type criteria, the delamination failure mode can be predicted using the relations [12]

$$ \begin{array}{c}\hfill \mathrm{if}\kern0.5em {\sigma}_{33}\ge 0,\Rightarrow {\left(\frac{\sigma_{33}}{Z_t}\right)}^2+{\left(\frac{\sigma_{13}}{S_{13}}\right)}^2+{\left(\frac{\sigma_{23}}{S_{23}}\right)}^2=\left\{\frac{\ge 1,\kern0.5em \mathrm{failed}}{<1,\ \mathrm{elastic}}\right.\hfill \\ {}\hfill \mathrm{if}\kern0.5em {\sigma}_{33}<0,\Rightarrow {\left(\frac{\sigma_{33}}{Z_c}\right)}^2+{\left(\frac{\sigma_{13}}{S_{13}}\right)}^2+{\left(\frac{\sigma_{23}}{S_{23}}\right)}^2=\left\{\frac{\ge 1,\kern0.5em \mathrm{failed},}{<1,\ \mathrm{elastic},}\right.\hfill \end{array} $$

(11)

where Z _t and Z _c denote the normal tensile and compressive strengths, respectively. S ₁₃ and S ₂₃ represent the out-of-plane shear strengths. As mentioned before, based on the first-order theory, the transverse normal stress is zero. Therefore, Eq. (11) is reduced to

$$ {\left(\frac{\sigma_{13}}{S_{13}}\right)}^2+{\left(\frac{\sigma_{23}}{S_{23}}\right)}^2=\left\{\begin{array}{c}\hfill \ge 1,\ \mathrm{failed}\to edel=0,\hfill \\ {}\hfill <1,\kern0.5em \mathrm{elastic}\to edel=1,\hfill \end{array}\right. $$

where, edel is the damage variable for the delamination failure mode. In Fig. 9, at S ₁₃ = S ₂₃ = S = 31.316 MPa, the delamination failure mode at the bottom surface according to the static and dynamic material models is shown. As seen, in both the cases, the delamination occurs at the edges perpendicular to the fiber direction. Similar fringe plots were also obtained for the top surface. Since variations in the out-of-plane strength and stiffness with strain rate were unknown, these characteristics were assumed to be constant.

Fig. 9

Delamination failure mode for the static (a) and dynamic (b) models.

Although a 2-D model was used for modeling of the delamination, this failure mode is a three-dimensional phenomenon. A proper modeling of delamination can be carried out using 3-D theories and approaches for composite plates.

Conclusions

In the present study, nonlinear equations of motion for a laminated composite plate under blast loading based on the first-order shear deformation theory (FSDT) are derived. The rules of material property degradation in association with Hashin-type failure criteria are used to model various failure modes. The equations derived are solved numerically using the finite-difference method. The validity of the model is examined by quantitative and qualitative comparisons of calculation results with those presented in the literature. The rate effects are taken into account by using rate-dependent material properties. The following conclusions can be drawn from the present work.

• The maximum deflection at the center of the plate considered and the maximum stresses obtained using the static model (with constant material properties) are higher than those obtained using the dynamic model (with strain-rate dependent material properties).

• The influence of stacking sequence on the maximum deflection at the center of the plate obtained using the static and dynamic models is similar; the largest maximum deflection is obtained for composite plate with the [+45 / −45] _s stacking sequence.

• At a certain time, for all failure modes, the failed regions found using the static model are larger than those obtained using the dynamic model. However, in a specific failure mode, the location of damage initiation is the same for both the models.

Appendix A

In order to convert Eq. (4a) into a finite difference form, N _xx and N _xy are written in terms of displacements and rotations by using Eqs. (3a), (3b) and (1) for a mesh point (i, j) :

$$ \begin{array}{c}\hfill {N}_{x x}^{i, j}={A}_{11}^{i, j}\left[{u}_{, x}^{i, j}+\frac{1}{2}{\left({w}_{, x}^{i, j}\right)}^2\right]+{A}_{12}^{i, j}\left[{v}_{, y}^{i, j}+\frac{1}{2}{\left({w}_{, y}^{i. j}\right)}^2\right]\hfill \\ {}\hfill +{A}_{13}^{i, j}\left({u}_{, y}^{i, j}+{v}_{, x}^{i, j}+{w}_{, x}^{i, j}{w}_{, y}^{i, j}\right)+{B}_{11}^{i, j}{\varphi}_{x, x}^{i, j}+{B}_{12}^{i, j}{\varphi}_{y, y}^{i, j}+{B}_{13}^{i, j}\left({\varphi}_{x, y}^{i, j}+{\varphi}_{y, x}^{i, j}\right),\hfill \\ {}\hfill {N}_{x y}^{i, j}={A}_{13}^{i, j}\left[{u}_{, x}^{i, j}+\frac{1}{2}{\left({w}_{, x}^{i, j}\right)}^2\right]+{A}_{23}^{i, j}\left[{v}_{, y}^{i, j}+\frac{1}{2}{\left({w}_{, y}^{i, j}\right)}^2\right]\hfill \\ {}\hfill +{A}_{33}^{i, j}\left({u}_{, y}^{i, j}+{v}_{, x}^{i, j}+{w}_{, x}^{i, j}{w}_{, y}^{i, j}\right)+{B}_{13}^{i, j}{\varphi}_{x, x}^{i, j}+{B}_{23}^{i, j}{\varphi}_{y, y}^{i, j}+{B}_{33}^{i, j}\left({\varphi}_{x, y}^{i, j}+{\varphi}_{y, x}^{i, j}\right).\hfill \end{array} $$

The derivatives of N _xx and N _xy with respect to x can be obtained as

$$ \begin{array}{c}\hfill {N}_{x x, x}^{i, j}={A}_{11}^{i, j}\left({u}_{,\mathrm{x} x}^{i, j}+{w}_{, x}^{i, j}{w}_{, x x}^{i, j}\right)+{A}_{12}^{i, j}\left({v}_{, y x}^{i, j}+{w}_{, y}^{i, j}{w}_{, y x}^{i, j}\right)\hfill \\ {}\hfill +{A}_{13}^{i, j}\left({u}_{, y x}^{i, j}+{v}_{, x x}^{i, j}+{w}_{, x\mathrm{x}}^{i, j}{w}_{, y}^{i, j}+{w}_{, x}^{i, j}{w}_{, y x}^{i, j}\right)+{B}_{11}^{i, j}{\varphi}_{x, x x}^{i, j}+{B}_{12}^{i, j}{\varphi}_{y, y x}^{i, j}+{B}_{13}^{i, j}\left({\varphi}_{x, y x}^{i, j}+{\varphi}_{y, x x}^{i, j}\right),\hfill \end{array} $$

(A.1)

$$ \begin{array}{c}\hfill {N}_{x y, y}^{i, j}={A}_{13}^{i, j}\left({u}_{, x y}^{i, j}+{w}_{, x}^{i, j}{w}_{, x y}^{i, j}\right)+{A}_{23}^{i, j}\left({v}_{, y y}^{i, j}+{w}_{, y}^{i, j}{w}_{, y y}^{i, j}\right)\hfill \\ {}\hfill +{A}_{33}^{i, j}\left({u}_{, y y}^{i, j}+{v}_{, x y}^{i, j}+{w}_{, x\mathrm{y}}^{i, j}{w}_{, y}^{i, j}+{w}_{, x}^{i, j}{w}_{, y y}^{i, j}\right)+{B}_{13}^{i, j}{\varphi}_{x, x y}^{i, j}+{B}_{23}^{i, j}{\varphi}_{y, y y}^{i, j}+{B}_{33}^{i, j}\left({\varphi}_{x, y y}^{i, j}+{\varphi}_{y, x y}^{i, j}\right).\hfill \end{array} $$

(A.2)

Finding the finite-difference form of derivatives of displacements and rotations by using Eqs. (8) and inserting the finite-difference expressions in (A.1) and (A.2), one can obtain the finite-difference form of Eq. (4a):

$$ \begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill -\frac{1}{8{h}^3}\left\{4{A}_{23}^{i, j}\left[2 h\left({v}_{i-1+ j}-2{v}_{i, j}+{v}_{i,1+ j}\right)+\left(-{w}_{i,-1+ j}+{w}_{i,1+ j}\right)\left({w}_{i,1+ j}-2{w}_{i, j}+{w}_{i,1+ j}\right)\right]\right.\hfill \\ {}\hfill +4{A}_{11}^{i, j}\left[2 h\left({u}_{-1+ i, j}-2{u}_{i, j}+{u}_{1+ i, j}\right)+\left(-{w}_{-1+ i, j}+{w}_{1+ i, j}\right)\Big({w}_{-1+ i, j}-2{w}_{i, j}+{w}_{1+ i, j}\right]\hfill \\ {}\hfill +{A}_{12}^{i, j}\Big[2 h\left({v}_{-1+ i,-1+ j}-{v}_{-1+ i,1+ j}-{v}_{1+ i,-1+ j}+{v}_{1+ i,1+ j}\right)\hfill \\ {}\hfill \left.+\left(-{w}_{i,-1+ j}+{w}_{i,1+ j}\right)\left({w}_{-1+ i,-1+ j}-{w}_{-1+ i,1+ j}-{w}_{1+ i,-1+ j}+{w}_{1+ i,1+ j}\right)\right]\hfill \end{array}\hfill \\ {}\hfill +{A}_{33}^{i, j}\left[8 h\left({u}_{i,-1+ j}-2{u}_{i, j}+{u}_{i,1+ j}\right)+2 h\left({v}_{-1+ i,-1+ j}-{v}_{-1+ i,1+ j}-{v}_{1+ i,-1+ j}+{v}_{1+ i,1+ j}\right)\right.\hfill \\ {}\hfill +4\left({w}_{i,-1+ j}-2{w}_{i, j}+{w}_{i,1+ j}\right)\left(-{w}_{-1+ i, j}+{w}_{1+ i, j}\right)\hfill \\ {}\hfill \begin{array}{l}\left.+\left(-{w}_{i,-1+ j}+{w}_{i,1+ j}\right)\left({w}_{-1+ i,-1+ j}-{w}_{-1+ i,1+ j}-{w}_{1+ i,-1+ j}+{w}_{1+ i,1+ j}\right)\right]\\ {}+{A}_{13}^{i, j}\left[2 h\left({u}_{-1+ i,-1+ j}-{u}_{-1+ i,1+ j}-{u}_{1+ i,-1+ j}+{u}_{1+ i,1+ j}\right)\right.\\ {}\left.+\left(-{w}_{-1+ i, j}+{w}_{1+ i, j}\right)\left({w}_{-1+ i, j}-{w}_{-1+ i,1+ j}-{w}_{1+ i,-1+ j}+{w}_{1+ i,1+ j}\right)\right]\end{array}\hfill \end{array}\hfill \\ {}\hfill +{A}_{13}^{i, j}\left[2 h\left({u}_{-1+ i.-1+ j}-{u}_{-1+ i,1+ j}-{u}_{1+ i,-1+ j}+{u}_{1+ i,1+ j}\right)+8 h\left({v}_{-1+ i, j}-2{v}_{i, j}+{v}_{1+ i, j}\right)\right.\hfill \\ {}\hfill +4\left(-{w}_{i,-1+ j}+{w}_{i,1+ j}\right)\left({w}_{-1+ i, j}-2{w}_{i, j}+{w}_{1+ i, j}\right)\hfill \\ {}\hfill +\left(-{w}_{-1+ i, j}+{w}_{1+ i, j}\right)\left({w}_{-1+ i, j}-{w}_{-1+ i,1+ j}+{w}_{i,1+ j}\right)\left({w}_{-1+ i, j}-2{w}_{i, j}+{w}_{1+ i, j}\right)\hfill \end{array}\hfill \\ {}\hfill \left.+\left(-{w}_{-1+ i, j}{+}_{1+ i, j}\right)\left({w}_{-1+ i,-1+ j}-{w}_{-1+ i,1+ j}-{w}_{1+ i,-1+ j}+{w}_{1+ i,1+ j}\right)\right]\hfill \\ {}\hfill +8 h{B}_{11}^{i, j}\left({\varphi}_x^{-1+ i, j}-2{\varphi}_x^{i, j}+{\varphi}_x^{1+ i, j}\right)+2 h{B}_{13}^{i, j}\left({\varphi}_x^{-1+ i,-1+ j}-{\varphi}_x^{-1+ i,1+ j}-{\varphi}_x^{1+ i,-1+ j}+{\varphi}_x^{1+ i,1+ j}\right)\hfill \\ {}\hfill +8 h{B}_{23}^{i, j}\left({\varphi}_y^{i,-1+ j}-2{\varphi}_y^{i, j}+{\varphi}_y^{i,1+ j}\right)\hfill \end{array}\hfill \\ {}\hfill +2 h{B}_{13}^{i, j}\left({\varphi}_x^{-1+ i,-1+ j}-{\varphi}_x^{-1+ i,1+ j}-{\varphi}_x^{1+ i.1+ j}+4{\varphi}_y^{-1+ i, j}-8{\varphi}_y^{i, j}+4{\varphi}_y^{1+ i, j}\right)\hfill \\ {}\hfill +2 h{B}_{12}^{i, j}\left({\varphi}_y^{-1+ i,-1+ j}-{\varphi}_y^{-1+ i,1+ j}-{\varphi}_y^{1+ i,1+ j}+{\varphi}_y^{1+ i,1+ j}\right)+2 h{B}_{33}^{i, j}\left(4{\varphi}_x^{i,-1+ j}-8{\varphi}_x^{i, j}\right.\hfill \\ {}\hfill \left.\left.+4{\varphi}_x^{i,1+ j}+{\varphi}_y^{-1+ i,-1+ j}-{\varphi}_x^{-1+ i,1+ j}-{\varphi}_x^{1+ i,1+ j}+{\varphi}_x^{1+ i,1+ j}\right)\right\}+{I}_0{\ddot{u}}_{i, j}+{I}_1{\ddot{\varphi}}_x^{i, j}=0\hfill \end{array}\hfill \\ {}\hfill \hfill \\ {}\hfill \hfill \\ {}\hfill \hfill \end{array} $$