Finite-Layer Method: a Unified Approach to a Numerical Analysis of Interlaminar Stresses, Large Deflections, and Delamination Stability of Composites Part 1. Linear Behavior

A new method for a stress–strain analysis of layered composites, named the finite-layer method, is proposed, which is based on the consideration of each particular layer as a constituent of the entire laminate. This method serves as a unified approach to the development of new algorithms for computing stresses in composite layers, interlaminar contact stresses, large deflections, and critical buckling loads of thin-walled laminated structures with delaminations. The calculation of a laminated structure is reduced to solving a boundary-value problem for a system of first-order ordinary differential equations. The number of equations depends on the number of layers in the composite. The resolving system of differential equations is a stiff system. The stable numerical method of discrete orthogonalization is used for solving the boundary value problem. Part 1 is dedicated to the application of the proposed method to a linear analysis of free-edge stresses in composite laminates, to a study of the deformation of composite plates with delaminations and bending of composite beams with patches, and to calculations of adhesive joints.

Introduction. Description of the Method

Many structural composite elements or their large-sized parts can be regarded as multilayer strip-beams or wide plates subjected to cylindrical bending. In this case, their stress–strain state (SSS) depends only on two — longitudinal and transverse — coordinates. In the direction of the third coordinate, lying in a plane parallel to layers, the SSS does not vary. The multilayer package as a whole consists of separate layers which deform jointly.

The essence of the finite-layer method (FLM) suggested consists in the fact that a multilayer package subjected to a given set of force loads and a temperature field is divided into separate layers, and the interlaminar normal and tangential contact stresses are introduced into consideration.

The first step is construction of such a deformation model of a layer that most accurately takes into account the distribution of stresses on faces of the layer. In fact, this is a refined model of bending of a beam-layer with account of transverse normal and shear strains. In the present study, the model is a system of six ordinary differential equations in resolving functions — the average displacements, the average rotation angle of cross section, and the integral characteristics of stress field in the transverse cross section: the longitudinal and shear forces and the bending moment. The system is supplemented with corresponding boundary conditions and expressions for displacements and stresses at any point of transverse section of the layer in terms of resolving functions, normal and tangential contact stresses, and their derivatives. Within the framework of the FLM, the layer deformation model developed can be regarded as an analogue of the shape function of the standard FEM. In the general case, the model is different for different layers, and it can be refined further to increase the approximation accuracy in reducing the three-dimensional problem of deformation of a thin layer to a one-dimensional problem along one of these directions and to take into account the singularities at angular points of the layer, where the type of boundary conditions changes.

At the following step, from the conditions of equality of transverse and longitudinal displacements for each contact surface of layers, two differential equations are additionally derived in new resolving functions — the tangential stress and its first derivative with respect to the longitudinal coordinate. The boundary conditions for these equations are found. As a result, the calculation of SSS of the layers and the interlaminar stresses in an n-layer package is reduced to a boundary-value problem for a coupled system consisting of 6n + 2(n −1) ordinary differential equations of the first order.

The final stage is the numerical solution of the boundary-value problem obtained for the resolving system of ordinary differential equations and the calculation of all components of the SSS, including the interlaminar stresses. Owing to introduction of two rapidly varying resolving functions into the system — the interlaminar tangential stress and its first derivative, whose distribution over the contact surface has a pronounced form of a boundary layer, — the resulting system of ordinary differential equations becomes “stiff” [1]. The integration of such systems by standard shooting methods or by reducing them to Cauchy problems is impossible because of the exponential fading of the required solution on a section which is much smaller than the integration region.

The most suitable method for solving the boundary-value problems described by “stiff” systems of equations is the method of discrete orthogonalization suggested by S. K. Godunov [2]. The development and application of the method to solving wide classes of linear and nonlinear problems of mechanics was realized by Ya. M. Grigorenko and his school [3–7]. In fact, the Godunov–Grigorenko method is an exact numerical method that allows one to obtain a solution accurate “to equations”. This method is efficiently employed to solve boundary-value problems for systems containing a great number of equations with an implicit expression of their right-hand sides in terms of resolving functions, which are calculated by using complex computing algorithms [4,7].

It is an advantage of the method that the calculations are carried out with functions having a clear physical meaning. This makes it possible to solve the problems for integration regions consisting of separate sections in the presence of discontinuities of the resolving functions and jump-like variations in the coefficients and free members of the right-hand sides of the system upon transition from one section to another [8]. This method served as the basis in creating effective computing complexes for calculating the strength, stability, and vibrations of thin-walled structures whose surfaces have an intricate branched and multiply connected shape [9].

In the present study, the Godunov–Grigorenko method of discrete orthogonalization is applied to solving boundary-value problems in the case where the type of the right-hand sides of the system of equations and the number of required resolving functions differ on some sections inside the integration interval. Such problems arise in calculating layered structures with layers of different length and multilayer packages with delaminations.

1. Construction of a Deformation Model for a Thin Layer

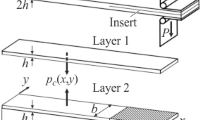
Let us consider a plane orthotropic layer of thickness h, width b, and length L. The layer is referred to a Cartesian system of coordinates x, y, and z (Fig. 1). The coordinate plane xy is the midplane of the layer and divides the thickness h into halves. The layer is subjected to the normal and tangential stresses p _i (x) and q _i (x) , the boundary forces and moments N _i ,Q _i , and Mi (i = 1, 2), a uniform transverse strain ε ₀, and temperature T. Axes 1, 2, and 3 — the orthotropy axes of the layer material — coincide with the coordinate axes x, y, and z.

Fig. 1

Plane orthotropic layer.

The layer is in the conditions of cylindrical bending. We assume that

(1) the constituents of displacement of points of the layer along the x and z axes do not vary in the direction of y coordinate,

$$ u=u\left( {x,z} \right),\quad w=w\left( {x,z} \right),\quad \frac{{\partial u}}{{\partial y}}=0,\quad \frac{{\partial w}}{{\partial y}}=0; $$

(2) the displacement along the y axis does not depend on the x and z coordinates,

$$ v=v(y),\quad \frac{{\partial v}}{{\partial x}}=0,\quad \frac{{\partial v}}{{\partial z}}=0; $$

(3) the strain in the direction of y axis is constant, independent of the coordinates x, y, and z,

$$ {\varepsilon_y}={\varepsilon_0}=\mathrm{const}. $$

In view of these assumptions, the full system of equations of the linear theory of thermoelasticity, describing the deformation of an orthotropic layer under the action of a given load, has the following form:

— equilibrium equations

$$ \frac{{\partial {\sigma_x}}}{{\partial x}}+\frac{{\partial {\tau_{xz }}}}{{\partial z}}=0,\quad \frac{{\partial {\tau_{xz }}}}{{\partial x}}+\frac{{\partial {\sigma_z}}}{{\partial z}}=0; $$

(1)

— geometrical relations

$$ {\varepsilon_x}=\frac{{\partial u}}{{\partial x}},\;{\varepsilon_0}=\frac{dv }{dy },\;{\varepsilon_z}=\frac{{\partial w}}{{\partial z}},\;{\varepsilon_{xz }}=\frac{{\partial u}}{{\partial z}}+\frac{{\partial w}}{{\partial x}},\;{\varepsilon_{xy }}=0,\;{\varepsilon_{yz }}=0; $$

— elasticity relations

$$ \begin{array}{*{20}{c}} {{\varepsilon_x}=\frac{{{\sigma_x}}}{{{{\bar{E}}_1}}}-\frac{{{\sigma_z}}}{\bar{E}}+\left( {{\alpha_1}+{\nu_{12 }}{\alpha_2}} \right)T-{\nu_{12 }}{\varepsilon_0},\quad {\tau_{xz }}={G_{13 }}{\varepsilon_{xz }},} \\ {{\varepsilon_z}=\frac{{{\sigma_z}}}{{{{\bar{E}}_3}}}-\frac{{{\sigma_x}}}{\bar{E}}+\left( {{\alpha_3}+{\nu_{32 }}{\alpha_2}} \right)T-{\nu_{32 }}{\varepsilon_0},\quad {\tau_{yz }}=0,} \\ {{\sigma_y}={E_2}\left( {{\varepsilon_0}-{\alpha_2}T+\frac{{{v_{21 }}}}{{{E_1}}}{\sigma_x}+\frac{{{\nu_{23 }}}}{{{E_3}}}{\sigma_z}} \right),\quad {\tau_{xy }}=0.} \\ \end{array} $$

Here, ${{\bar{E}}_1}=\frac{{{E_1}}}{{1-{\nu_{12 }}{\nu_{21 }}}}$, ${{\bar{E}}_3}=\frac{{{E_3}}}{{1-{\nu_{23 }}{\nu_{32 }}}}$, and $\bar{E}=\frac{{{E_1}}}{{{\nu_{31 }}+{\nu_{12 }}{\nu_{32 }}}}=\frac{{{E_3}}}{{{\nu_{13 }}+{\nu_{12 }}{\nu_{23 }}}}$; E _i and ν _ij (i, j = 1, 2, 3) are the elastic moduli of the material and the Poisson ratios; E ₃ ν ₃₂ = E ₂ ν ₂₃ , E ₂ ν ₂₁ = E ₁ ν ₁₂ , and E ₁ ν ₁₃ = E ₃ ν ₃₁; G ₁₃ is the shear modulus in the xz plane; α _i are the coefficients of linear thermal expansion.

On faces of the layer, the conditions in stresses

$$ \begin{array}{*{20}{c}} {{\tau_{xz }}\left( {x,\frac{h}{2}} \right)={q_1}(x),\quad {\tau_{xz }}\left( {x,-\frac{h}{2}} \right)={q_2}(x),} \hfill \\ {{\sigma_z}\left( {x,\frac{h}{2}} \right)={p_1}(x),\quad {\sigma_z}\left( {x,-\frac{h}{2}} \right)={p_2}(x).} \hfill \\ \end{array} $$

(2)

must be fulfilled.

Let us construct statically allowable distributions of stresses in the layer satisfying equilibrium equations (1) and conditions (2). For this purpose, we present the stresses in the form of expansions along the z coordinate with coefficients a _i , b _j , and c _k $\left( {i=0,1,j=\overline{0,2};k=\overline{0,3}} \right)$ in terms of the longitudinal coordinate x:

$$ {\sigma_x}={a_0}+{a_1}z,\quad {\tau_{xz }}={b_0}+{b_1}z+{b_2}{z^2},\quad {\sigma_z}={c_0}+{c_1}z+{c_2}{z^2}+{c_3}{z^3}. $$

(3)

Let us introduce integral characteristics of the stress field in the transverse section of the layer, namely the longitudinal force N , the shear force Q , and the bending moment M :

$$ N=b\int\limits_{{-\frac{h}{2}}}^{{\frac{h}{2}}} {{\sigma_x}dz,} \quad Q=b\int\limits_{{-\frac{h}{2}}}^{{\frac{h}{2}}} {{\tau_{xz }}dz,} \quad M=b\int\limits_{{-\frac{h}{2}}}^{{\frac{h}{2}}} {{\sigma_x}zdz.} $$

(4)

Inserting expansion (3) into Eqs. (1), in view of conditions (2) and expressions (4), after some transformations, we find that the equilibrium equations of the layer and the static boundary conditions on its surfaces are fulfilled exactly if the stresses are given by the expressions

$$ \begin{array}{*{20}{c}} {{\sigma_x}\left( {x,z} \right)=\frac{N}{bh }+\frac{12M }{{b{h^3}}}z,} \\ {{\sigma_z}\left( {x,z} \right)=\frac{{{p_1}+{p_2}}}{2}+\frac{3z }{2h}\left[ {1-\frac{1}{3}{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {{p_1}-{p_2}} \right)+\frac{h}{8}\left[ {1-{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left[ {\left( {1+\frac{2z }{h}} \right){{{q^{\prime}}}_1}-\left( {1-\frac{2z }{h}} \right){{{q^{\prime}}}_2}} \right],} \\ {{\tau_{xz }}\left( {x,z} \right)=\frac{3}{2}\frac{Q}{bh}\left[ {1-{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]-\frac{{{q_1}+{q_2}}}{4}\left[ {1-3{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]+\frac{{{q_1}-{q_2}}}{h}z,} \\ \end{array} $$

(5)

and the three differential equations

$$ \frac{dN }{dx }=-b\left( {{q_1}-{q_2}} \right),\quad \frac{dQ }{dx }=-b\left( {{p_1}-{p_2}} \right),\quad \frac{dM }{dx }=Q-bh\frac{{{q_1}+{q_2}}}{2}. $$

(6)

are satisfied.

We should note that the expression for the stress σ _z (x, z) , normal to the midsurface of the layer, contains the first derivatives of the external tangential loads ${{q^{\prime}}_1}(x)$ and ${{q^{\prime}}_2}(x)$. Next, we assume that, within the limits of the part of the layer considered, the external surface loads are continuous functions and have continuous derivatives up to the third one inclusive.

$$ \frac{{\partial w}}{{\partial z}}=\frac{{{\sigma_z}}}{{{{\bar{E}}_3}}}-\frac{{{\sigma_x}}}{\bar{E}}+\left( {{\alpha_3}+{\nu_{32 }}{\alpha_2}} \right)T-{\nu_{32 }}{\varepsilon_0}, $$

(7)

$$ \frac{{{\tau_{xz }}}}{{{G_{13 }}}}=\frac{{\partial u}}{{\partial z}}+\frac{{\partial w}}{{\partial x}}, $$

(8)

$$ {\sigma_x}={{\bar{E}}_1}\frac{{\partial u}}{{\partial x}}+\frac{{{{\bar{E}}_1}}}{\bar{E}}{\sigma_z}-{{\bar{E}}_1}\left[ {\left( {{\alpha_1}+{\nu_{12 }}{\alpha_2}} \right)T-{\nu_{12 }}{\varepsilon_0}} \right]. $$

(9)

From relation (7), after insertion of dependences (5) in it and integration with respect to z , we come to the expression for the transverse displacements of points of the layer

$$ \begin{array}{*{20}{c}} {w\left( {x,z} \right)={w_0}-\frac{N}{{\bar{E}bh}}z-\frac{6M }{{\bar{E}b{h^3}}}{z^2}+\left\{ {\frac{{{p_1}+{p_2}}}{2}z+\frac{hz }{8}\left[ {1-\frac{1}{3}{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {{{{q^{\prime}}}_1}-{{{q^{\prime}}}_2}} \right)+\frac{{3{z^2}}}{4h}\left[ {1-\frac{1}{6}{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]{p_1}+{p_2}} \right.} \\ {\left. {+\frac{{{z^2}}}{8}\left[ {1-\frac{1}{2}{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {{{{q^{\prime}}}_1}-{{{q^{\prime}}}_2}} \right)} \right\}+\left[ {\left( {{\alpha_3}+{\nu_{32 }}{\alpha_2}} \right)T-{\nu_{32 }}{\varepsilon_0}} \right]z,} \\ \end{array} $$

where w ₀ is the transverse displacement (deflection) of the midline at z = 0.

Let us present the longitudinal displacements of points of the layer as a third-degree polynomial in z with coefficients u ₀ , α, β, and γ depending on x :

$$ u\left( {x,z} \right)={u_0}+\alpha z+\beta {z^2}+\gamma {z^3},\;\frac{{\partial u}}{{\partial z}}=\alpha +2\beta z+3\gamma {z^2}. $$

Here, u ₀ is the longitudinal displacement of points of the midline; α is the slope of the tangent to the deformed contour of cross section at z = 0 ; the functions β and γ are determined from the first pair of conditions (2) for tangential stresses. As a result, relation (8) takes the form

$$ \begin{array}{*{20}{c}} {\frac{{{\tau_{xz }}}}{{{G_{13 }}}}=\left( {\alpha +\frac{{d{w_0}}}{dx }} \right)\left[ {1-{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]+\frac{z}{{{G_{13 }}h}}\left[ {\left( {1+\frac{2z }{h}} \right){q_1}-\left( {1-\frac{2z }{h}} \right){q_2}} \right]} \\ {+\frac{hz }{{24{{\bar{E}}_3}}}\left[ {1-{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {{{{q^{\prime\prime}}}_1}-{{{q^{\prime\prime}}}_2}} \right)+\frac{{{z^2}}}{{8{{\bar{E}}_3}}}\left[ {1-{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {\frac{{{{{p^{\prime}}}_1}-{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}-{{{q^{\prime\prime}}}_2}}}{2}} \right).} \\ \end{array} $$

According to expression (5), the left-hand side of this equality is a quadratic function of z , and the right-hand one is a fourth-degree polynomial. At the same time, both the sides satisfy the conditions for the tangential stress on layer faces. Integrating the previous equality with respect to the thickness, in view of expressions (4), we have

$$ \frac{{d{w_0}}}{dx }=\frac{3}{2}\frac{Q}{{{G_{13 }}bh}}-\alpha -\frac{{{q_1}+{q_2}}}{{4{G_{13 }}}}-\frac{{{h^2}}}{{160{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime}}}_1}-{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}-{{{q^{\prime\prime}}}_2}}}{2}} \right). $$

(10)

Likewise, by considering expression (9), after two integrations across the layer thickness, with account of Eqs. (4), we find that

$$ \frac{{d{u_0}}}{dx }=\frac{{N+{N_T}-{N_{\varepsilon }}}}{{{{\bar{E}}_1}bh}}-\frac{h}{{2\bar{E}}}\left( {\frac{{{p_1}+{p_2}}}{h}+\frac{{{{{q^{\prime}}}_1}-{{{q^{\prime}}}_2}}}{6}} \right)-\frac{h}{24}\left[ {\frac{{{{{q^{\prime}}}_1}-{{{q^{\prime}}}_2}}}{K}-\frac{{{h^2}}}{{2{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime\prime}}}_1}-{{{p^{\prime\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}-{{{q^{\prime\prime}}}_2}}}{6}} \right)} \right], $$

(11)

$$ \frac{{d\alpha }}{dx }=\frac{12M }{{{{\bar{E}}_1}b{h^3}}}-\frac{6}{{5\bar{E}}}\left( {\frac{{{p_1}-{p_2}}}{h}+\frac{{{{{q^{\prime}}}_1}+{{{q^{\prime}}}_2}}}{12 }} \right)-\frac{3}{10}\left[ {\frac{1}{K}\left( {\frac{{{p_1}-{p_2}}}{h}+\frac{{{{{q^{\prime}}}_1}+{{{q^{\prime}}}_2}}}{2}} \right)-\frac{{{h^2}}}{{10{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime\prime}}}_1}-{{{p^{\prime\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime\prime}}}_1}-{{{q^{\prime\prime\prime}}}_2}}}{12 }} \right)} \right]. $$

(12)

Here, $\frac{1}{K}=\frac{1}{{{G_{13 }}}}-\frac{1}{\bar{E}};\;{N_T}={{\bar{E}}_1}bh\left( {{\alpha_1}+{\nu_{12 }}{\alpha_2}} \right)T$ and ${N_{\varepsilon }}={{\bar{E}}_1}bh{\nu_{12 }}{\varepsilon_0}$ are the longitudinal forces in the cross section of the layer caused by the temperature field T and the strain ε ₀, respectively.

Thus, from relations (7)-(9), we derived three differential equations (10)-(12) in the displacements of points of the axial line, u ₀ and w ₀ , and the rotation angle α.

Let us introduce the displacements u _av and w _av averaged across the thickness and the rotation angle θ _av :

$$ \begin{array}{*{20}{c}} {{u_{av }}(x)=\frac{1}{h}\int\limits_{{-\frac{h}{2}}}^{{\frac{h}{2}}} {u\left( {x,z} \right)dz={u_0}+\beta \frac{{{h^2}}}{12 },} } \\ {{w_{av }}(x)=\frac{1}{h}\int\limits_{{-\frac{h}{2}}}^{{\frac{h}{2}}} {w\left( {x,z} \right)dz={w_0}-\frac{M}{{2\bar{E}bh}}+\frac{{9{h^2}}}{{160{{\bar{E}}_3}}}\left( {\frac{{{p_1}-{p_2}}}{h}+7\frac{{{{{q^{\prime}}}_1}+{{{q^{\prime}}}_2}}}{54 }} \right),} } \\ {{\theta_{av }}(x)=\frac{1}{h}\int\limits_{{-\frac{h}{2}}}^{{\frac{h}{2}}} {\omega \left( {x,z} \right)dz=}\;\alpha -\left( {\frac{1}{{{G_{13 }}}}+\frac{1}{K}} \right)\frac{Q}{2bh }+\frac{{{q_1}-{q_2}}}{4K }-\frac{{{h^2}}}{{20{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime}}}_1}-{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}+{{{q^{\prime\prime}}}_2}}}{12 }} \right),} \\ \end{array} $$

where ${\theta_{av }}(x)=\frac{1}{h}\int\limits_{{-\frac{h}{2}}}^{{\frac{h}{2}}} {\omega \left( {x,z} \right)dz}$ is the average rotation angle at the point [10]. As a further simplification of the system, we exclude the second and third derivatives of external loads ${{p^{\prime\prime}}_1}$, ${{p^{\prime\prime}}_2}$, ${{q^{\prime\prime\prime}}_1}$, and ${{q^{\prime\prime\prime}}_2}$ from the equations. For this purpose, we pass to an angle θ that differs from the average angle θ _av by a small value:

$$ \theta (x)={\theta_{av }}(x)+\frac{{{h^2}}}{{50{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime}}}_1}-{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}+{{{q^{\prime\prime}}}_2}}}{12 }} \right). $$

(13)

The final form of the stress–strain state of the layer is described by

— the system of six ordinary linear differential equations of the first order with variable coefficients

$$ \begin{array}{*{20}{c}} {\frac{dN }{dx }=-b\left( {{q_1}-{q_2}} \right),} \\ {\frac{dQ }{dx }=-b\left( {{p_1}-{p_2}} \right)} \\ {\frac{dM }{dx }=Q-bh\frac{{{q_1}+{q_2}}}{2},} \\ {\frac{{d{u_{av }}}}{dx }=\frac{{N+{N_T}-{N_{\varepsilon }}}}{{{{\bar{E}}_1}bh}}-\frac{h}{{2\bar{E}}}\left( {\frac{{{p_1}+{p_2}}}{h}+\frac{{{{{q^{\prime}}}_1}-{{{q^{\prime}}}_2}}}{6}} \right),} \\ {\frac{{d{w_{av }}}}{dx }=\frac{Q}{{2{G_{13 }}bh}}-\theta +\frac{{{h^2}}}{{50{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime}}}_1}-{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}+{{{q^{\prime\prime}}}_2}}}{12 }} \right),} \\ {\frac{{d\theta }}{dx }=\frac{12M }{{{{\bar{E}}_1}b{h^3}}}+\frac{7}{10K}\left( {\frac{{{p_1}-{p_2}}}{h}+\frac{{{{{q^{\prime}}}_1}+{{{q^{\prime}}}_2}}}{7}} \right);} \\ \end{array} $$

(14)

— the expressions for displacements of points of the cross section

$$ \begin{array}{*{20}{c}} {w\left( {x,z} \right)={w_{av }}-\frac{{9{h^2}}}{{160{{\bar{E}}_3}}}\left( {\frac{{{p_1}-{p_2}}}{h}+7\frac{{{{{q^{\prime}}}_1}+{{{q^{\prime}}}_2}}}{54 }} \right)-\frac{N}{{\bar{E}bh}}z+\frac{M}{{2\bar{E}bh}}\left[ {1-3{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]} \\ {+\frac{1}{\bar{E}}\left\{ {\frac{{{p_1}+{p_2}}}{2}z+\frac{hz }{8}\left[ {1-\frac{1}{3}{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {{{{q^{\prime}}}_1}-{{{q^{\prime}}}_2}} \right)+\frac{{3{z^2}}}{4h}\left[ {1-\frac{1}{6}{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {{p_1}-{p_2}} \right)} \right.} \\ {\left. {+\frac{{{z^2}}}{8}\left[ {1-\frac{1}{2}{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]\left( {{{{q^{\prime}}}_1}-{{{q^{\prime}}}_2}} \right)} \right\}+\left[ {\left( {{\alpha_3}+{\nu_{32 }}{\alpha_2}} \right)T-{\nu_{32 }}{\varepsilon_0}} \right]z,} \\ \end{array} $$

(15)

$$ \begin{array}{*{20}{c}} {u\left( {x,z} \right)={u_{av }}+az-\beta \frac{{{h^2}}}{12}\left[ {1-3{{{\left( {\frac{2z }{h}} \right)}}^2}} \right]+y{z^3},} \\ {\alpha =\theta +\left( {\frac{1}{{{G_{13 }}}}+\frac{1}{K}} \right)\frac{Q}{2bh }-\frac{{{q_1}+{q_2}}}{4K }+\frac{{3{h^2}}}{{100{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime}}}_1}-{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}+{{{q^{\prime\prime}}}_2}}}{12 }} \right),} \\ {\beta =\frac{1}{2h}\left[ {\frac{{{q_1}-{q_2}}}{K}-\frac{{{h^2}}}{{2{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime}}}_1}+{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}+{{{q^{\prime\prime}}}_2}}}{6}} \right)} \right],} \\ {\gamma =-\frac{2}{{{h^2}}}\left[ {\frac{1}{K}\left( {\frac{Q}{bh }-\frac{{{q_1}+{q_2}}}{2}} \right)+\frac{{{h^2}}}{{10{{\bar{E}}_3}}}\left( {\frac{{{{{p^{\prime}}}_1}-{{{p^{\prime}}}_2}}}{h}+\frac{{{{{q^{\prime\prime}}}_1}+{{{q^{\prime\prime}}}_2}}}{12 }} \right)} \right];} \\ \end{array} $$

(16)

— expressions (5) for stresses in the layer.

The boundary conditions for the resulting system of differential equations at the edges x = 0 and x = L are given by three quantities — by one from each of the pairs (N, u _av ), (Q,w _av ), and (M,θ _av ). The resolving equations, the boundary conditions, and the expressions for displacements and stresses include the derivatives of external surface loads up to the second one inclusive.

In fact, the last three equations of system (14) are the compatibility conditions. They were deduced not by using the Castigliano variational principle but by averaging the displacements and rotation angles across the thickness of the layer, which leads to the same results [11].

The model obtained describes the cylindrical bending of a layer under a generalized plane deformation determined

by the value ε _y = ε ₀ . For the case of a plane stress state, at σ _y = 0 , all dependences can be derived from the presented expressions assuming that E ₂ = v ₁₂ = v ₂₁ = v ₂₃ = v ₃₂ = 0 .

2. Resolving System of Differential Equations for a Multilayer Package

The derivation of the resolving system of equations can briefly be shown with the example of a two-layer package. In the equations, the index av will not be used. The subscript at the resolving functions and the superscript in parentheses at physicomechanical characteristics of the material correspond to the number of a layer. The temperature of all layers is taken the same. We divide the package into separate layers of thickness h ₁, h ₂ and introduce the stresses p _c (x) and q _c(x) on the contact surface (Fig. 2). It is assumed that the external loads on package surfaces — the stresses p ₁, p ₂ and q ₁, q ₂ — do not depend on x .

Fig. 2

Two-layer package.

The system of differential equations (14) for each layer is written as follows:

layer 1

$$ \begin{array}{*{20}{c}} {\frac{{d{N_1}}}{dx }=-b\left( {{q_1}-{q_c}} \right),} \\ {\frac{{d{Q_1}}}{dx }=-b\left( {{p_1}-{p_c}} \right),} \\ {\frac{{d{M_1}}}{dx }={Q_1}-b{h_1}\frac{{{q_1}+{q_c}}}{2},} \\ {\frac{{d{u_1}}}{dx }=\frac{{{N_1}+{N_{T1 }}-{N_{{\varepsilon 1}}}}}{{\bar{E}_1^{(1) }b{h_1}}}-\frac{{{h_1}}}{{2{{\bar{E}}^{(1) }}}}\left( {\frac{{{p_1}+{p_c}}}{{{h_1}}}-\frac{{{{{q^{\prime}}}_c}}}{6}} \right),} \\ {\frac{{d{w_1}}}{dx }=\frac{{{Q_1}}}{{2G_{13}^{(1) }b{h_1}}}-{\theta_1}+\frac{{h_1^2}}{{50\bar{E}_3^{(1) }}}\left( {\frac{{{{{p^{\prime}}}_c}}}{{{h_1}}}-\frac{{{{{q^{\prime\prime}}}_c}}}{12 }} \right),} \\ {\frac{{d{\theta_1}}}{dx }=\frac{{12{M_1}}}{{\bar{E}_1^{(1) }bh_1^3}}+\frac{7}{{10{K^{(1) }}}}\left( {\frac{{{p_1}-{p_2}}}{{{h_1}}}+\frac{{{{{q^{\prime}}}_c}}}{7}} \right),} \\ \end{array} $$

(17)

layer 2

$$ \begin{array}{*{20}{c}} {\frac{{d{N_2}}}{dx }=-b\left( {{q_c}-{q_2}} \right),} \\ {\frac{{d{Q_2}}}{dx }=-b\left( {{p_c}-{p_2}} \right),} \\ {\frac{{d{M_2}}}{dx }={Q_2}-b{h_2}\frac{{{q_c}+{q_2}}}{2},} \\ {\frac{{d{u_2}}}{dx }=\frac{{{N_2}+{N_{T2 }}-{N_{{\varepsilon 2}}}}}{{\bar{E}_1^{(2) }b{h_2}}}-\frac{{{h_2}}}{{2{{\bar{E}}^{(2) }}}}\left( {\frac{{{p_c}+{p_2}}}{{{h_2}}}-\frac{{{{{q^{\prime}}}_c}}}{6}} \right),} \\ {\frac{{d{w_2}}}{dx }=\frac{{{Q_2}}}{{2G_{13}^{(2) }b{h_2}}}-{\theta_2}+\frac{{h_2^2}}{{50\bar{E}_3^{(2) }}}\left( {\frac{{{{{p^{\prime}}}_c}}}{{{h_2}}}+\frac{{{{{q^{\prime\prime}}}_c}}}{12 }} \right),} \\ {\frac{{d{\theta_2}}}{dx }=\frac{{12{M_2}}}{{\bar{E}_1^{(2) }bh_2^3}}+\frac{7}{{10{K^{(2) }}}}\left( {\frac{{{p_c}-{p_2}}}{{{h_2}}}+\frac{{{{{q^{\prime}}}_c}}}{7}} \right).} \\ \end{array} $$

The right-hand sides of Eqs. (17) contain the unknown functions p _c , ${{p^{\prime}}_c}$, and q _c , ${{q^{\prime}}_c}$, ${{q^{\prime\prime}}_c}$. Using the conditions of equality of transverse displacements of the layers on the contact surface, ${w_1}\left( {x,-\frac{{{h_1}}}{2}} \right)={w_2}\left( {x,\frac{{{h_2}}}{2}} \right)$, and expression (15), we have

$$ {p_c}={c_1}{N_1}+{c_2}{N_2}+{c_3}{M_1}+{c_4}{M_2}+{c_5}{w_2}+{c_7}{{q^{\prime}}_c}+{d_1}{p_1}+{d_2}{p_2}+{d_0}. $$

(18)

Differentiating expression (18) and inserting the derivatives of resolving functions from Eqs. (17), we obtain

$$ {{p^{\prime}}_c}={e_1}{Q_1}+{e_2}{Q_2}+{e_3}{\theta_1}+{e_4}{\theta_2}+{e_5}{{q^{\prime\prime}}_c}+{f_1}{q_1}+{f_2}{q_2}. $$

(19)

The condition of equality of longitudinal displacements on the contact surface, ${u_1}\left( {x,-\frac{{{h_1}}}{2}} \right)={u_2}\left( {x,\frac{{{h_2}}}{2}} \right)$, in combination with Eqs. (16), gives

$$ {{q^{\prime\prime}}_c}={a_1}{Q_1}+{a_2}{Q_2}+{a_3}{u_1}+{a_4}{u_2}+{a_5}{\theta_1}+{a_6}{\theta_2}+{a_7}{q_c}+{b_1}{q_1}+{b_2}{q_2}. $$

(20)

Using expressions (18)-(20), the functions p _c , ${{p^{\prime}}_c}$, and ${{q^{\prime\prime}}_c}$ are determined in terms of the resolving functions N _i , Q _i , M _i , u _i , w _i , and θ _i (i = 1,2) and functions q _c and ${{q^{\prime}}_c}$. The coefficients a _j , c _j , e _j $\left( {j=\overline{1,7}} \right)$ and b _k , d _k , f _k (k = 1, 2) entering into these formulas are expressed in terms of characteristics of the layers; the quantity d ₀ depends on temperature T and the strain ε ₀.

Let us join the functions q _c and ${{q^{\prime}}_c}$ to the resolving functions. Then, the calculation of the two-layer laminate is reduced to the solution of the boundary-value problem for a coupled system of 14 ordinary linear differential equations of the first order, including 12 equations (17) and two additional equations

$$ \frac{{d{q_c}}}{dx }={{q^{\prime}}_c},\;\;\frac{{d{{{q^{\prime}}}_c}}}{dx }={{q^{\prime\prime}}_c}. $$

(21)

At each edge x = 0 and x = L , it is necessary to assign seven boundary conditions: six conditions for the basic resolving functions — one from each of the pairs (N ₁,u ₁ ), (Q ₁,w ₁), (M ₁,θ _1av ) , (N ₂ , u ₂ ), (Q ₂ ,w ₂ ), and (M ₂ , θ _2av ), and one additional condition for the tangential stress q _c . Here,θ_1av and θ_2av are the average rotation angles determined by Eq. (13).

In many practical problems, at the edge of a layer, the contact surface appears either on the free butt end or on the adjacent section with a free face. For these cases, the boundary condition for the tangential stress is q _c = 0 .

The described algorithm for deriving the coupled system of resolving differential equations is naturally extended to a multilayer package with an arbitrary number of layers.

3. Calculation Results

Let us show the possibilities of the method suggested by the example of solution of some statics problems for elements of multilayer structures.

Two-layer plate with a defect. We will consider a plate consisting of two orthotropic layers with dissimilar physicomechanical characteristics. In the midplane of the plate, there is a symmetric delamination of length a . The upper layer is divided by a crack across the entire width of the plate (Fig. 3). Both layers are extended in the crack direction by an identical strain ε ₀.

Fig. 3

Two-layer plate with a delamination and a crack.

The initial data for calculation are L = 200 mm, a = 100 mm, b = 200 mm, and ε ₀ = 0.01;

• layer 1: h ₁ = 2.5 mm, $E_1^{(1) }=E_2^{(1) }=60\;\mathrm{GPa}$, $E_3^{(1) }=10.5\;\mathrm{GPa}$, $G_{13}^{(1) }=6\;\mathrm{GPa}$, $\nu_{13}^{(1) }=\nu_{21}^{(1) }=\nu_{12}^{(1) }=\nu_{23}^{(1) }=0.07$, and $\nu_{31}^{(1) }=\nu_{32}^{(1) }=0.4;$

• layer 2: h ₂ = 2.5 mm, $E_1^{(2) }=30\;\mathrm{GPa}$, $E_2^{(2) }=20\;\mathrm{GPa}$, $E_3^{(2) }=7\;\mathrm{GPa}$, $G_{13}^{(2) }=3\;\mathrm{GPa}$, $\nu_{31}^{(2) }=\nu_{32}^{(2) }=0.07$, $\nu_{21}^{(2) }=0.24\nu_{12}^{(2) }=0.16$, $\nu_{31}^{(2) }=0.3$, and $\nu_{32}^{(2) }=0.2$.

Due to symmetry, we consider only half of the plate. The boundary conditions are:

• x = 0 : layer 1 — N ₁ = Q ₁ = M ₁ = 0; layer 2 — N ₂ = Q ₂ = M ₂ = 0; q _c = 0 ;

• x = 0 and L/2 : layer 1 — N ₁ = Q ₁ = M ₁ = 0; layer 2 — u ₂ = w ₂ =θ ₂ = 0; q _c = 0 .

The resolving system of differential equations on the fastened section 0 ≤ x ≤ (L − a)/2 coincides with the system (17), (21). For the delamination zone at (L − a)/2 ≤ x ≤ L/2 , we must put that p _c = ${{p^{\prime}}_c}$ = q _c = ${{q^{\prime}}_c}$ = ${{q^{\prime\prime}}_c}$ = 0 in the resolving system.

The calculated distributions of interlaminar tangential q _c and normal p _c stresses along the length of the plate are shown in Fig. 4. The results of an analysis of the deflections of contact surfaces of the layers disclosed that, under the action of tensile strain, a gap arises between the layers along the entire length of the delamination zone. Accordingly, upon application of a compression strain ε ₀ = −0.01 , a contact of the layers with slippage will occur in the delamination zone. For this case, it must be assumed that q _c = ${{q^{\prime}}_c}$ = ${{q^{\prime\prime}}_c}$ = 0 in the resolving system of differential equations on the section with delamination, and the values of p _c and ${{q^{\prime}}_c}$ have to be determined only from the conditions of equality of transverse displacements of contact surfaces of the layers. The calculation results for the case of compression are shown in Fig. 5. It is seen that the peak of the tangential stress increased in magnitude from 5.16 to 5.22 MPa. The magnitude of the normal stress at the top of delamination decreased from 2.59 to 1.56 MPa. On the delaminated section, a contact compression stress appeared near the top of delamination, which, with distance, became equal to zero without changing its sign.

Fig. 4

Distribution of tangential (a) and normal (b) stresses along the length of the plate. ε ₀ = 0.01.

Fig. 5

Distribution of tangential (a) and normal (b) stresses in the case of compression (ε ₀ = −0.01 ).

Beam with a doubler. An orthotropic beam has a symmetric doubler of length a on its middle part (Fig. 6). The beam is rigidly fixed at its butt ends and loaded with a uniform pressure p ₁ (plane stress state, σ _y = 0) . In this example, the doubler (layer 1) has a smaller length than the beam (layer 2). In calculations, this is taken into account as follows. On the section with the doubler, 0 ≤ x ≤ a/2 , the resolving system of equations is assumed in form (17), (21). Outside the doubler, at a/2 ≤ x ≤ L/2 , the right-hand sides of the equations of layer 1 in the resolving system (17) are taken to be zero; in the right-hand sides of Eqs. (17) for layer 2 and Eqs. (21), we put that p _c = ${{p^{\prime}}_c}$ = q _c = ${{q^{\prime}}_c}$ = ${{q^{\prime\prime}}_c}$ = 0.

Fig. 6

A beam with a doubler.

The boundary conditions are:

• x = 0 — layer 1: u ₁ = Q ₁ =θ ₁ = 0; layer 2: u ₂ = Q ₂ =θ ₂ = 0; q _c = 0 ;

• x = L/2 — layer 1: N ₁ = Q ₁ = M ₁ = 0; layer 2: u ₂ = w ₂ =θ ₂ = 0; q _c = 0 .

• The initial data: L = 200 mm, a = 100 mm, b = 100 mm, h ₁ = h ₂ = 5 mm, and p ₁ = −0 1 . MPa.

• The material of the layers is the same: E ₁ = 30 GPa, E ₂ = 20 GPa, E ₃ = 7 GPa, G ₁₃ = 3 GPa, ν ₁₃ = 0.07, and ν ₃₁ = 0.3.

Figure 7 illustrates the distributions of interlaminar tangential and normal stresses along the length of the beam.

Fig. 7

Distribution of tangential (a) and normal (b) stresses along the length of the beam.

The distributions of longitudinal and shear forces and bending moments in the layers of the beam are shown in Fig. 8. The dashed lines designate the total forces and the bending moment in the beam, which are determined by the expressions

$$ {N_{\varSigma }}={N_1}+{N_2},\;\;{Q_{\varSigma }}={Q_1}+{Q_2},\;\;{M_{\varSigma }}={M_1}+{M_2}+{N_1}\frac{{{h_1}}}{2}-{N_2}\frac{{{h_2}}}{2}. $$

Fig. 8

Distribution of longitudinal (a) and shear (b) forces and bending moments (c) in layers of the beam. Explanations in the text.

Adhesive joint. Let us compare the calculation results of an single lap joint obtained with the FLM and the Goland–Reissner solution taken from [12].

A three-layer adhesive joint is stretched by a force N ₀ (Fig. 9). The loaded butt ends of layers 1 and 3 are not displaced in the vertical direction and do not rotate. The initial data: a = c = 12.7 mm, b = 25.4 mm, h ₁ = h ₂ = 1.62 mm, h ₂ = 0.25 mm, and N ₀ = 1 kN. The material of the layers is isotropic: layers 1 and 3 — E = 70 GPa and ν = 0.3; the adhesive layer 2 — E = 4.82 GPa and ν = 0.4.

Fig. 9

Single lap joint.

The calculation results for tangential stresses on the adhesive surface of layers 1–2 are presented in Fig. 10a; the dashed line shows the results obtained in [12].

Fig. 10

Distribution of tangential (a) and normal (b) stresses over adhesive surfaces and their strain state (c).

The distributions obtained by the FLM are asymmetric to the center of the adhesive joint. The peak of tangential stresses on the surface appearing on the free edge of the adherend layer is lower than on the opposite edge.

Figure 10b shows the normal stresses on surfaces of the adhesive joint. It is seen that, at the right edge of contact surface between layers 1–2, due to the presence of the free butt end of layer 1, the peak value of the normal stress decreases, and it even becomes compressive. The data of Fig. 10c illustrate the strain state of the adhesive joint under the action of a tensile force.

Conclusions

The results presented, as well as solutions of other test problems not included in the given publication, allow us to conclude that the finite-layer method suggested is efficient in analyzing the SSS of the class of layered structures considered.

In the following publications, a geometrically nonlinear deformation model of a layer and the corresponding resolving system of differential equations, describing the elastic deformation of a multilayer package in the quadratic approximation, will be presented. The results of calculations, of the SSS of adhesive joints, large deflections, and the stability of layered beams and plates with delaminations will be reported.