Finite-Layer Method: Evaluation of Stresses and the Modal Components of Energy Release Rate on the Midplane of Edge-Cracked Composite Specimens

On the basis of the finite-layer method, a technique for calculating the two-dimensional stress-strain state and interlaminar stresses in edge-cracked specimens in tests on determination of the Mode I, II, and III fracture toughnesses of composites is proposed. Taking into account the symmetry and antisymmetry of specimens, the calculation is reduced to a boundary-value problem for a system of partial differential equations describing the deformation of one of the layers. Using the method of straight lines, the two-dimensional problem is reduced to a one-dimensional boundary-value problem, which is solved by the stable Godunov–Grigorenko numerical method. Calculations for specimens subjected to three types of the tests are performed, and the distributions of normal and tangential stresses on the specimen midplane and the distributions of modal components of the fracture toughnesses G_I, G_II, and G_III along the delamination front line are presented. Comparisons with results of the one-dimensional solution and with known results obtained by the virtual crack closure technique are presented.

Introduction

The approach offered in [1–3] to an analysis of the stress-strain state (SSS) of structural elements made of layered composites, named the finite-layer method (FLM), was extended in [4] to the two-dimensional problems on bending and twisting of plates with delaminations. In [5], the FLM was employed to calculate the SSS of specimens used for determination of the fracture toughness of composite materials in double-cantilever beam (mode I) and three-point bending (a mode II) tests. New analytical expressions for determining the parameters of SSS and formulas for calculating their compliance and the energy release rate (ERR) were obtained on the assumption that all required functions depend only on one coordinate reckoned along the longitudinal axis of specimen. This convential assumption is based on the fastening and loading conditions of beam specimens. However, for plate specimens with edge delaminations, under the action of local loads in twisting (mode III), the parameters of SSS essentially depend on two coordinates in the plate plane.

This work is a further development of the approach expounded in [4,5], with reference to the analysis of SSS in a two-dimensional statement and to calculation of the modal components G _I, G _II, and G _III of ERR in tests on the three types composite specimens with delaminations mentioned. The specimens were considered as two-layer orthotropic plates, with layers of equal thickness with a local across-the width delamination. Two opposite longitudinal edges of the plates are free. The FLM allows one to carry out joint calculations of both layers of a plate with account of their contact interaction. Here, a slightly simplified calculation model based on the sufficiently accurate assumption that the loads applied and support reactions are evenly distributed between layers is used. After partition of the plate into two layers and introduction of interlaminar stresses into consideration, this assumption allows one to perform calculations for only one of the layer on the basis of symmetry and antisymmetry conditions.

The two-dimensional boundary-value problem for a plate-layer, with the use of the method of straight lines, is reduced a one-dimensional boundary-value problem. For this purpose, a number of straight lines equally spaced apart are introduced parallel to the longitudinal coordinate of the plate. After replacement of derivatives with respect to the transverse coordinate with difference expressions, the system of partial differential equations is reduced to a coupled system of ordinary differential equations of the first order in the values of resolving functions on the lines. The resolving functions on the extreme lines obey the boundary conditions on the longitudinal edges of the plate.

Solution of the boundary-value problem for the “stiff” system of linear ordinary differential equations by the stable numerical Godunovs--Grigirenko method [6–8] gives a full set of all functions describing the SSS of the plate. An essential advantage of the given approach is that, in calculations, both the normal and shear strains and the corresponding displacements on the fastening plane of layers, which is the specimen midplane, are found. This allows one to use the method for determination of the values G _I, G _II, and G _III proposed in [5], which is based on direct calculations of the Irvin integral without invoking the virtual crack closure technique.

For each kind of the tests mentioned, the calculated two-dimensional distributions of normal and shear stresses on the specimen midplane are given, including their peak values at the tip of delamination. For the double-cantilever beam and three-point bending tests, a comparison with calculation results obtained in [5] in a one-dimensional statement is given. It is shown that, in the three-point bending, besides the longitudinal shear stresses (mode II), low transverse shear stresses (mode III) also operate on the midplane along the delamination front. In twisting an edge-cracked specimen, the distributions on the modal components G _II and G _III along the delamination front are compared with the results of finite-element calculations given in [9].

1. Governing Equations

The system of equations describing the SSS of specimens is obtained as a special case of the system given in [4] for a two-layer orthotropic plate whose layers have identical physicomechanical characteristics and thickness.

The equations for layer 1 (the superscrip in parentheses specifies the layer number) are

$$ \begin{array}{l}\frac{\partial {N}_x^{(1)}}{\partial x}+\frac{\partial {N}_{xy}^{(1)}}{\partial y}={q}_c,\frac{\partial {N}_{xy}^{(1)}}{\partial x}+\frac{\partial {N}_y^{(1)}}{\partial y}={t}_c,\frac{\partial {Q}_x^{(1)}}{\partial x}+\frac{\partial {Q}_y^{(1)}}{\partial y}={p}_c,\hfill \\ {}\frac{\partial {M}_x^{(1)}}{\partial x}+\frac{\partial {M}_{xy}^{(1)}}{\partial y}={Q}_x^{(1)}-\frac{h}{2}{q}_c,\kern1em \frac{\partial {M}_{xy}^{(1)}}{\partial x}+\frac{\partial {M}_y^{(1)}}{\partial y}={Q}_y^{(1)}-\frac{h}{2}{t}_c,\hfill \\ {}\frac{\partial {u}_{av}^{(1)}}{\partial x}=\frac{N_x^{(1)}-{v}_{21}{N}_y^{(1)}}{E_1h}-\frac{v_{13}}{2{E}_3}\left[{p}_c-\frac{h}{6}\left(\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y}\right)\right],\hfill \\ {}\frac{\partial {v}_{av}^{(1)}}{\partial y}=\frac{N_y^{(1)}-{v}_{12}{N}_x^{(1)}}{E_2h}-\frac{v_{23}}{2{E}_3}\left[{p}_c-\frac{h}{6}\left(\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y}\right)\right],\frac{\partial {u}_{av}^{(1)}}{\partial y}+\frac{\partial {v}_{av}^{(1)}}{\partial x}=\frac{N_{xy}^{(1)}}{G_{12}h},\hfill \\ {}\frac{\partial {w}_{av}^{(1)}}{\partial x}=-{\tilde{\uptheta}}_x^{(1)}+\frac{6}{5{G}_{13}h}\left({Q}_x^{(1)}-\frac{h}{12}{q}_c\right)\hfill \\ {}-\frac{1}{5{E}_3h}\left\{{v}_{13}\frac{\partial {M}_x^{(1)}}{\partial x}+{v}_{23}\frac{\partial {M}_y^{(1)}}{\partial x}-\frac{h^2}{10}\left[-\frac{\partial {p}_c}{\partial x}+\frac{h}{12}\left(\frac{\partial^2{q}_c}{\partial {x}^2}+\frac{\partial^2{t}_c}{\partial x\partial y}\right)\right]\right\},\hfill \\ {}\frac{\partial {w}_{av}^{(1)}}{\partial y}=-{\tilde{\uptheta}}_x^{(1)}+\frac{6}{5{G}_{23}h}\left({Q}_y^{(1)}-\frac{h}{12}{t}_c\right)\hfill \\ {}-\frac{1}{5{E}_3h}\left\{{v}_{13}\frac{\partial {M}_x^{(1)}}{\partial y}+{v}_{23}\frac{\partial {M}_y^{(1)}}{\partial y}-\frac{h^2}{10}\left[-\frac{\partial {p}_c}{\partial_y}+\frac{h}{12}\left(\frac{\partial^2{q}_c}{\partial x\partial y}+\frac{\partial^2{t}_c}{\partial {y}^2}\right)\right]\right\},\hfill \\ {}\frac{\partial {\tilde{\uptheta}}_x^{(1)}}{\partial x}=\frac{12\left({M}_x^{(1)}-{v}_{21}{M}_y^{(1)}\right)}{E_1{h}^3}-\frac{6}{5}\frac{v_{13}}{E_3h}\left[-{p}_c+\frac{h}{12}\left(\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y}\right)\right],\hfill \\ {}\frac{\partial {\tilde{\uptheta}}_y^{(1)}}{\partial y}=\frac{12\left({M}_y^{(1)}-{v}_{12}{M}_x^{(1)}\right)}{E_2{h}^3}-\frac{6}{5}\frac{v_{23}}{E_3h}\left[-{p}_c+\frac{h}{12}\left(\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y}\right)\right]\hfill \\ {}\frac{\partial {\tilde{\uptheta}}_x^{(1)}}{\partial y}+\frac{\partial {\tilde{\uptheta}}_y^{(1)}}{\partial x}=\frac{12{M}_{xy}^{(1)}}{G_{12}{h}^3};\hfill \end{array} $$

(1)

the equations for layer 2 are

$$ \begin{array}{l}\frac{\partial {N}_x^{(2)}}{\partial x}+\frac{\partial {N}_{xy}^{(2)}}{\partial y}=-{q}_c,\kern1em \frac{\partial {N}_{xy}^{(2)}}{\partial x}+\frac{\partial {N}_y^{(2)}}{\partial_y}=-{t}_c,\kern1em \frac{\partial {Q}_x^{(2)}}{\partial_x}+\frac{\partial {Q}_y^{(2)}}{\partial_y}=-{p}_c,\hfill \\ {}\frac{\partial {M}_x^{(2)}}{\partial x}+\frac{\partial {M}_{xy}^{(2)}}{\partial y}={Q}_x^{(2)}-\frac{h}{2}{q}_c,\kern1em \frac{\partial {M}_{xy}^{(2)}}{\partial x}+\frac{\partial {M}_y^{(2)}}{\partial_y}={Q}_y^{(2)}-\frac{h}{2}{t}_c,\hfill \\ {}\frac{\partial {u}_{av}^{(2)}}{\partial x}=\frac{N_x^{(2)}-{v}_{21}{N}_y^{(2)}}{E_1h}-\frac{v_{13}}{2{E}_3}\left[{p}_c+\frac{h}{6}\left(\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y}\right)\right],\hfill \end{array} $$

(2)

$$ \begin{array}{c}\hfill \frac{\partial {v}_{av}^{(2)}}{\partial y}=\frac{N_y^{(2)}-{v}_{12}{N}_x^{(2)}}{E_2h}-\frac{v_{23}}{2{E}_3}\left[{p}_c+\frac{h}{6}\left(\frac{\partial {q}_c}{\partial_x}+\frac{\partial {t}_c}{\partial y}\right)\right],\hfill \\ {}\hfill \frac{\partial {u}_{av}^{(2)}}{\partial y}+\frac{\partial {v}_{av}^{(2)}}{\partial x}=\frac{N_{xy}^{(2)}}{G_{12}h},\hfill \\ {}\hfill \frac{\partial {w}_{av}^{(2)}}{\partial x}=-{\tilde{\uptheta}}_x^{(2)}+\frac{6}{5{G}_{23}h}\left({Q}_y^2-\frac{h}{12}{t}_c\right)\hfill \\ {}\hfill -\frac{1}{5{E}_3h}\left\{{v}_{13}\frac{\partial {M}_x^{(2)}}{\partial x}+{v}_{23}\frac{\partial {M}_y^{(2)}}{\partial x}-\frac{h^2}{10}\left[\frac{\partial {p}_c}{\partial x}+\frac{h}{12}\left(\frac{\partial^2{q}_c}{\partial {x}^2}+\frac{\partial^2{t}_c}{\partial x\partial y}\right)\right]\right\},\hfill \\ {}\hfill \frac{\partial {w}_{av}^{(1)}}{\partial y}=-{\tilde{\uptheta}}_y^{(1)}+\frac{6}{5{G}_{23}h}\left({Q}_y^{(1)}-\frac{h}{12}{t}_c\right)\hfill \\ {}\hfill -\frac{1}{5{E}_3h}\left\{{v}_{13}\frac{\partial {M}_x^{(1)}}{\partial y}+{\partial}_{23}\frac{\partial {M}_y^{(1)}}{\partial y}-\frac{h^2}{10}\left[-\frac{\partial {p}_c}{\partial y}+\frac{h}{12}\left(\frac{\partial^2{q}_c}{\partial x\partial y}+\frac{\partial^2{t}_c}{\partial {y}^2}\right)\right]\right\},\hfill \\ {}\hfill \frac{\partial {\tilde{\uptheta}}_x^{(2)}}{\partial x}=\frac{12\left({M}_x^{(2)}-{v}_{21}{M}_y^{(2)}\right)}{E_1{h}^3}-\frac{6}{5}\frac{v_{13}}{E_3h}\left[{p}_c+\frac{h}{12}\left(\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y}\right)\right],\hfill \\ {}\hfill \frac{\partial {\tilde{\uptheta}}_y^{(2)}}{\partial y}=\frac{12\left({M}_y^{(2)}-{v}_{12}{M}_x^{(2)}\right)}{E_2{h}^3}-\frac{6}{5}\frac{v_{23}}{E_3h}\left[{p}_c+\frac{h}{12}\left(\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y}\right)\right],\hfill \\ {}\hfill \frac{\partial {\tilde{\uptheta}}_x^{(2)}}{\partial y}+\frac{\partial {\tilde{\uptheta}}_y^{(2)}}{\partial x}=\frac{12{M}_{xy}^{(2)}}{G_{12}{h}^3}.\hfill \end{array} $$

(2)

Here, N ^(k) _x , N ^(k) _xy , N ^(k) _y , Q ^(k) _x , Q ^(k) _y , M ^(k) _x , M ^(k) _xy , andM ^(k) _y are the running forces and moments [4]; u ^(k) _av , v ^(k) _av , w ^(k) _av , v ^(k) _av , θ ^(k) _x,av and θ ^(k) _y,av are the thickness-average displacements and rotation angles; k = 1, 2, is the layer number;

$$ \begin{array}{c}\hfill {\tilde{\uptheta}}_x^{(k)}={\theta}_{x,av}^{(k)}+\frac{Q_x^{(k)}}{2{G}_{13}h}-\frac{h^2}{10}{\gamma}_1^{(k)},\kern1em {\tilde{\uptheta}}_y^{(k)}={\theta}_{y,av}^{(k)}+\frac{Q_y^{(k)}}{2{G}_{23}h}-\frac{h^2}{10}{\gamma}_2^{(k)},\hfill \\ {}\hfill {\gamma}_1^{(k)}=-\frac{2}{G_{23}{h}^3}\left({Q}_x^{(k)}-\frac{h}{2}{q}_c\right)+\frac{2}{E_3{h}^3}\left({v}_{13}\frac{\partial {M}_x^{(k)}}{\partial x}+{v}_{23}\frac{\partial {M}_y^{(k)}}{\partial x}\right)\hfill \\ {}\hfill -\frac{1}{5{E}_3h}\left[{\left(-1\right)}^k\frac{\partial {p}_c}{\partial x}+\frac{h}{12}\left(\frac{\partial^2{q}_c}{\partial {x}^2}+\frac{\partial^2{t}_c}{\partial x\partial y}\right)\right],\hfill \\ {}\hfill {\gamma}_2^{(k)}=-\frac{2}{G_{23}{h}^3}\left({Q}_y^{(k)}-\frac{h}{2}{t}_c\right)+\frac{2}{E_2{h}^3}\left({v}_{13}\frac{\partial {M}_x^{(k)}}{\partial y}+{v}_{23}\frac{\partial {M}_y^{(k)}}{\partial y}\right)\hfill \\ {}\hfill -\frac{1}{5{E}_3h}\left[{\left(-1\right)}^k\frac{\partial {p}_c}{\partial y}+\frac{h}{12}\left(\frac{\partial^2{q}_c}{\partial x\partial y}+\frac{\partial^2{t}_c}{\partial {y}^2}\right)\right];\hfill \end{array} $$

E _i ,G _ij , and v _ij (i, j = 1,2,3) are the elastic moduli and Poisson ratio of the orthotropic layer material; E _i v _ij = E _j v _ji ; h is layer thickness; p _c is the normal stress on the contact plane of layers; q _c and t _c are shear stresses along the x and y axes, respectively. In the delamination zone, it is necessary to take that p _c = q _c = t _c = 0.

The conditions of equality of displacements in the fastening zone of layers give three equations (two differential and one algebraic) relating forces, moments, displacements, and rotations to the stresses operating on the contact plane:

$$ \begin{array}{c}\hfill \frac{4h}{15{G}_{13}}{q}_c-\frac{7{h}^3}{450{E}_3}\left(\frac{\partial^2{q}_c}{\partial {x}^2}+\frac{\partial^2tlc}{\partial x\partial y}\right)-{u}_{av}^{(1)}+{u}_{av}^{(2)}+\frac{h}{2}{\tilde{\uptheta}}_x^{(1)}+\frac{h}{2}{\tilde{\uptheta}}_x^{(2)}\hfill \\ {}\hfill -\frac{h}{12{E}_3}\left({v}_{13}\frac{\partial {N}_x^{(1)}}{\partial x}+{v}_{23}\frac{\partial {N}_y^{(1)}}{\partial x}\right)+\frac{h}{12{E}_3^{(2)}}\left({v}_{13}\frac{\partial {N}_y^{(2)}}{\partial x}\right)-\frac{Q_x^{(1)}+{Q}_x^{(2)}}{10{G}_{13}}\hfill \\ {}\hfill +\frac{1}{10{E}_3}\left({v}_{13}\frac{\partial {M}_x^{(1)}}{\partial x}+\frac{\partial {M}_y^{(1)}}{\partial x}\right)+\frac{1}{10{E}_3}\left({v}_{13}\frac{\partial {M}_x^{(2)}}{\partial x}+\frac{\partial {M}_y^{(12)}}{\partial x}\right)=0,\hfill \\ {}\hfill \frac{4h}{15{G}_{23}}{t}_c-\frac{7{h}^3}{450{E}_3}\left(\frac{\partial^2{q}_c}{\partial x\partial y}+\frac{\partial^2{t}_c}{\partial {y}^2}\right)-{v}_{av}^{(1)}+{v}_{av}^{(2)}+\frac{h}{2}{\tilde{\uptheta}}_y^{(1)}+\frac{h}{2}{\tilde{\uptheta}}_y^{(2)}\hfill \\ {}\hfill -\frac{h}{12{E}_3}\left({v}_{13}\frac{\partial {N}_x^{(1)}}{\partial y}+{v}_{23}\frac{\partial {N}_y^{(1)}}{\partial y}\right)+\frac{h}{12{E}_3}\left({v}_{13}\frac{\partial {N}_x^{(2)}}{\partial y}+{v}_{23}\frac{\partial {N}_y^{(2)}}{\partial y}\right)-\frac{Q_y^{(1)}+{Q}_y^{(2)}}{10{G}_{23}}\hfill \\ {}\hfill +\frac{1}{10{E}_3}\left({v}_{13}\frac{\partial {M}_x^{(1)}}{\partial y}+{v}_{23}\frac{\partial {M}_y^{(1)}}{\partial y}\right)+\frac{1}{10{E}_3}\left({v}_{13}\frac{\partial {M}_x^{(2)}}{\partial y}+{v}_{23}\frac{\partial {M}_y^{(2)}}{\partial y}\right)=0,\hfill \\ {}\hfill \frac{7h}{10{E}_3}{p}_c-{w}_{av}^{(1)}+{w}_{av}^{(2)}-\frac{1}{2{E}_3}\left({v}_{13}{N}_x^{(1)}+{v}_{23}{N}_y^{(1)}\right)-\frac{1}{2{E}_3}\left({v}_{13}{N}_x^{(2)}+{v}_{23}{N}_y^{(2)}\right)\hfill \\ {}\hfill +\frac{1}{E_3h}\left({v}_{13}{M}_x^{(1)}+{v}_{23}{M}_y^{(1)}\right)-\frac{1}{E_3h}\left({v}_{13}{M}_x^{(2)}+{v}_{23}{M}_y^{(2)}\right)=0.\hfill \end{array} $$

The system of 29 Eqs.(1)-(3) contains 26 basic resolving functions ${N}_x^{(k)},{N}_{xy}^{(k)},{N}_y^{(k)},{Q}_x^{(k)},{Q}_y^{(k)},{M}_x^{(k)},{M}_{xy}^{(k)},{M}_y^{(k)},{u}_{av}^{(k)},{v}_{av}^{(k)},{w}_{av}^{(k)},{\tilde{\uptheta}}_x^{(k)},\kern0.5em \mathrm{and}\kern0.5em {\tilde{\uptheta}}_y^{(k)}$ and three additional functions of interlaminar stresses p _c , q _c , and t _c .

1.1. Double-cantilever beam (mode I). On Fig. 1, the specimen [10] used in tests for determination of the fracture toughness G _IC (mode I) of composite materials is shown, and its dimensions and loading conditions are indicated. Let us divide the specimen into two layers along its midplane. By virtue of symmetry, in the fastening zone of layers, there are only the normal stresses p _c (x, y), but shear stresses are equal to zero, and the following equalities are obeyed by the running forces, moments, displacements, and rotations in layers:

Fig. 1

Test specimen (mode I).

$$ {f}^{(2)}={f}^{(1)},{g}^{(2)}=-{g}^{(1)}, $$

(4)

where f = {N _x , N _xy , N _y ,u _av ,v _av } and g = {Q _x ,Q _y ,M _x ,M _xy ,M _y ,w _av ,${\tilde{\uptheta}}_x$,${\tilde{\uptheta}}_y$}. The first two equations of (3) turn into identities, but the third one gives an expression for the normal stress in the fastening zone in terms of running forces, moments, and the average deflection:

$$ {p}_c=\frac{20}{7h}{E}_3{w}_{av}-\frac{20}{7{h}^2}\left[{v}_{13}\left({M}_x-\frac{h}{2}{N}_x\right)+{v}_{23}\left({M}_y-\frac{h}{2}{N}_y\right)\right]. $$

Thus, calculation of the SSS of a specimen is reduced to calculation of one of the layers, but the result for the other layer is given by Eqs. (4). Further, we will consider only the top layer, with its number 1 omitted.

In view of the above-said, the system of Eqs. (1) is reduced to the resolving system of partial differential equations

$$ \frac{\partial {N}_x}{\partial x}=-\frac{\partial {N}_{xy}}{\partial y},\frac{\partial {N}_{xy}}{\partial x}=-\frac{\partial {N}_y}{\partial y},\frac{\partial {Q}_x}{\partial x}={p}_c-\frac{\partial {Q}_y}{\partial_y}, $$

$$ \begin{array}{c}\hfill \frac{\partial {M}_x}{\partial x}={Q}_x-\frac{\partial {M}_{xy}}{\partial y},\kern1em \frac{\partial {M}_{xy}}{\partial x}={Q}_y-\frac{\partial {M}_y}{\partial y},\hfill \\ {}\hfill \frac{\partial {u}_{av}}{\partial x}=\frac{N_x-{v}_{21}{N}_y}{E_1h}-\frac{v_{13}}{2{E}_3}{p}_c,\kern1em \frac{\partial {v}_{av}}{\partial x}=\frac{N_{xy}}{G_{12}h}-\frac{\partial {u}_{av}}{\partial y},\hfill \\ {}\hfill \frac{\partial {w}_{av}}{\partial x}=\frac{35}{27}{\tilde{\uptheta}}_x+\frac{42\upomega}{37}\frac{Q_x}{G_{13}h}-\frac{5v}{37{G}_{12}h}\left(\frac{\partial {M}_{xy}}{\partial y}+\frac{h}{5}\frac{\partial {N}_{xy}}{\partial y}\right)+\frac{v_{32}h}{37}\left(\frac{\partial^2{u}_{av}}{\partial {y}^2}+\frac{5h}{12}\frac{\partial^2{\tilde{\uptheta}}_x}{\partial {y}^2}\right),\hfill \\ {}\hfill \frac{\partial {\tilde{\uptheta}}_x}{\partial x}=\frac{12\left({M}_x-{v}_{21}{M}_y\right)}{E_1{h}^3}+\frac{6}{5}\frac{v_{13}}{E_3h}{p}_c,\kern1em \frac{12{M}_{xy}}{G_{12}{h}^3}-\frac{\partial {\tilde{\uptheta}}_x}{\partial y}.\hfill \end{array} $$

(5)

Here

$$ \begin{array}{c}\hfill {N}_y={v}_{12}{N}_x+{E}_2h\frac{\partial {v}_{av}}{\partial y}+\frac{v_{32}h}{2}{p}_c,\kern1em {M}_y={v}_{12}{M}_x+\frac{E_2{h}^3}{12}\frac{\partial {\tilde{\uptheta}}_y}{\partial y}-\frac{v_{32}{h}^2}{10}{p}_c,\hfill \\ {}\hfill {Q}_y=\frac{5}{6}{G}_{23}h\left(\frac{\partial {w}_{av}}{\partial y}+{\tilde{\uptheta}}_y\right)+\frac{G_{23}}{6{E}_3}\left({v}_{13}\frac{\partial {M}_x}{\partial y}+{v}_{23}\frac{\partial {M}_y}{\partial y}+\frac{h^2}{10}\frac{\partial {p}_c}{\partial y}\right),\hfill \\ {}\hfill {p}_c=\frac{20{E}_3}{7h\delta }{w}_{av}-\frac{20\mu }{7{h}^2\delta}\left({M}_x-\frac{h}{2}{N}_x\right)+\frac{10{E}_2{v}_{23}}{7\delta}\left(\frac{\partial {v}_{av}}{\partial_y}-\frac{h}{6}{\tilde{\uptheta}}_y\right),\hfill \\ {}\hfill \delta =1-{v}_{23}{v}_{32},\kern1em \mu ={v}_{13}+{v}_{12}{v}_{23},\kern1em v={v}_{32}-\mu \frac{G_{12}}{E_3},\kern1em \omega =1-\frac{5\mu }{42}\frac{G_{13}}{E_3}.\hfill \end{array} $$

1.2. Hinge-supported delaminated beam and plate with edge delaminations (modes II and III). The specimen [10] for determination of the fracture toughness G _IIC (mode II) of a composite material and its dimensions are shown on Fig. 2. In testing a beam hinge-supported on its edges, the specimen in the middle of span L is loaded with a force P uniformly distributed across its width.

Fig. 2

Test specimen (mode II).

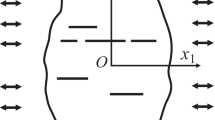
On Fig. 3, the specimen for determination of the fracture toughness G _IIIC (mode III) and its dimensions are shown. We should note that the directions of coordinate axes and designations of dimensions differ from the conventional ones [9,10] and correspond to the unified approach used here to solving the given class of problems. In tests, three angular points of the b ₀ × L ₀ loading quadrangle are fixed and have zero vertical displacements. For the fourth point, a vertical displacement w ₀ is given.

Fig. 3

Test specimen (mode III).

In both the tests considered, the SSS is antisymmetric about the specimen midplane. On the midplane, there are only the shear stresses q _c (x, y), and t _c (x, y), but the normal ones are equal to zero. In this case, Eqs. (4) is valid and

$$ f=\left\{{Q}_x,{Q}_y,{M}_x,{M}_{xy},{M}_y,{w}_{av},{\tilde{\uptheta}}_x,{\tilde{\uptheta}}_y\right\},\kern1em g=\left\{{N}_x,{N}_{xy},{N}_y,{u}_{av},{v}_{av}\right\}. $$

Let us introduce two functions r (x, y) and s (x, y) according to the expressions

$$ r=\frac{\partial {q}_c}{\partial x}+\frac{\partial {t}_c}{\partial y},\frac{\partial r}{\partial y}=\frac{\partial^2{q}_c}{\partial x\partial y}+\frac{\partial^2{t}_c}{\partial {y}^2},\frac{\partial r}{\partial x}=\frac{\partial^2{q}_c}{\partial {x}^2}+\frac{\partial^{2{t}_c}}{\partial x\partial y}=s. $$

In Eqs. (3), the third equality is identity, but the first two ones give expressions for the shear stress tc (x, y) and function s(x, y) in terms of the basic resolving functions, the shear stress q _c (x, y), and the function r(x, y) :

$$ \begin{array}{c}\hfill {t}_c=\frac{60{G}_{23}}{17h}\left[\frac{57{h}^3}{3600{E}_3}\frac{\partial r}{\partial y}+2{v}_{av}-h{\tilde{\uptheta}}_y-\frac{h}{6}\left(\frac{\partial {w}_{av}}{\partial y}+{\tilde{\uptheta}}_y\right)\right.\hfill \\ {}\hfill \left.-\frac{7}{30{E}_3}\left({v}_{13}\frac{\partial {M}_x}{\partial y}+{v}_{23}\frac{\partial {M}_y}{\partial y}\right)+\frac{h}{6{E}_3}\left({v}_{13}\frac{\partial {N}_x}{\partial y}+{v}_{23}\frac{\partial {N}_y}{\partial y}\right)\right],\hfill \\ {}\hfill s=\frac{450{E}_3}{7{h}^3\delta}\left[\frac{4h}{15{G}_{13}}\left(1-\mu \frac{G_{13}}{E_3}\right){q}_c-2{u}_{av}+h{\tilde{\uptheta}}_x\right.+\frac{Q_x}{5{G}_{13}}\left(1+\mu \frac{G_{13}}{E_3}\right)\hfill \\ {}\hfill \left.+\frac{v}{5{G}_{12}}\left(\frac{\partial {M}_{xy}}{\partial y}-\frac{5h}{6}\frac{\partial {N}_{xy}}{\partial y}\right)+\frac{v_{32}{h}^2}{6}\left(\frac{\partial^2{u}_{av}}{\partial {y}^2}-\frac{h}{10}\frac{\partial^2{\tilde{\uptheta}}_x}{\partial {y}^2}\right)\right].\hfill \end{array} $$

As a result, the system of Eqs. (2) is reduced to a resolving system of partial differential equations containing, besides the basic resolving functions, two additional functions, q _c (x, y) and r(x, y).For layer 1, the system has the form

$$ \begin{array}{c}\hfill \frac{\partial {N}_x}{\partial x}={q}_c-\frac{\partial {N}_{xy}}{\partial y},\frac{\partial {N}_{xy}}{\partial x}={t}_c-\frac{\partial {N}_y}{\partial y},\frac{\partial {Q}_x}{\partial x}=-\frac{\partial {Q}_y}{\partial y},\hfill \\ {}\hfill \frac{\partial {M}_x}{\partial x}={Q}_x-\frac{\partial {M}_{xy}}{\partial y}-\frac{h}{2}{q}_c,\kern1em \frac{\partial {M}_{xy}}{\partial x}={Q}_y-\frac{\partial {M}_y}{\partial y}-\frac{h}{2}{t}_c,\hfill \\ {}\hfill \frac{\partial {u}_{av}}{\partial x}=\frac{N_x-{v}_{21}{N}_y}{E_1}+\frac{v_{13}h}{12{E}_3}r,\kern1em \frac{\partial {v}_{av}}{\partial x}=\frac{N_{xy}}{G_{12}h}-\frac{\partial {u}_{av}}{\partial y},\hfill \\ {}\hfill \frac{\partial {w}_{av}}{\partial x}=-{\tilde{\uptheta}}_x+\frac{6}{5}\frac{Q_x}{G_{13}h}\left(1-\frac{\mu }{6}\frac{G_{13}}{E_3}\right)-\frac{q_c}{10{G}_{13}}\left(1-\mu \frac{G_{13}}{E_3}\right)\hfill \\ {}\hfill -\frac{v}{5{G}_{12}h}\frac{\partial {M}_{xy}}{\partial y}+\frac{v_{32}{h}^2}{60}\frac{\partial^2{\tilde{\uptheta}}_x}{\partial {y}^2}+\frac{h^2\delta }{600{E}_3}s,\hfill \\ {}\hfill \frac{\partial {\tilde{\uptheta}}_x}{\partial x}=\frac{12\left({M}_x-{v}_{21} My\right)}{E_1{h}^3}-\frac{v_{13}}{10{E}_3}r,\kern1em \frac{\partial {\tilde{\uptheta}}_y}{\partial x}=\frac{12{M}_{xy}}{G_{12}{h}^3}-\frac{\partial {\tilde{\uptheta}}_x}{\partial y};\frac{\partial {q}_c}{\partial x}=r\frac{\partial {t}_c}{\partial y},\frac{\partial r}{\partial x}=s.\hfill \end{array} $$

Here,

$$ \begin{array}{c}\hfill {N}_y={v}_{12}{N}_x+{E}_2h\frac{\partial {v}_{av}}{\partial y}-\frac{v_{32}{h}^2}{12}r,{M}_y={v}_{12}{M}_x+\frac{E_2{h}^3}{12}\frac{\partial {\tilde{\uptheta}}_y}{\partial y}+\frac{v_{32}{h}^3}{120}r,\hfill \\ {}\hfill {Q}_y=\frac{5}{6}{G}_{23}h\left(\frac{\partial {w}_{av}}{\partial y}+{\tilde{\uptheta}}_y\right)+\frac{h}{12}{t}_c+\frac{G_{23}}{6{E}_3}\left({v}_{13}\frac{\partial {M}_x}{\partial y}+{v}_{13}\frac{\partial {M}_y}{\partial y}-\frac{h^3}{120}\frac{\partial r}{\partial y}\right).\hfill \end{array} $$

2. The Method of Strength Lines for Solving the Problems on Bending and Twisting of a Plate with Free Longitudinal Edges

Let us draw straight lines, parallel to the x axis, with coordinates $yi=i\varDelta, i=\overline{-1,N+1},\varDelta =b/N$. The lines y ₀ and y _N are boundary ones and coincide with contour lines of the plate; the lines y ₋₁, and y _N+1 are out of the contour. The partial derivatives of the required function φ(x, y) with respect to the y coordinate in Eqs. (5) and (6) are replaced with difference expressions with the help of the following patterns:

• on internal lines, $i=\overline{1,N-1},$

$$ \frac{\partial {\varphi}_i}{\partial y}=\frac{\varphi_{i+1}-{\varphi}_{i-1}}{2\varDelta },\frac{\partial^2{\varphi}_i}{\partial {y}^2}=\frac{\varphi_{i-1}-2{\varphi}_i+{\varphi}_{i+1}}{\varDelta^2},\frac{\partial 3{\varphi}_i}{\partial {y}^3}=\frac{-{\varphi}_{i-2}+2{\varphi}_{i-1}-2{\varphi}_{i+1}+{\varphi}_{i+2}}{2{\varDelta}^3}; $$

• on boundary lines, i = 0, N,

$$ \begin{array}{c}\hfill \frac{\partial {\varphi}_0}{\partial y}=\frac{-3{\varphi}_0+4{\varphi}_1-{\varphi}_2}{2\varDelta },\frac{\partial^2{\varphi}_0}{\partial {y}^2}=\frac{\varphi_0-2{\varphi}_1+{\varphi}_2}{\varDelta^2},\frac{\partial^3{\varphi}_0}{\partial {y}^3}=\frac{-{\varphi}_0+3{\varphi}_1-3{\varphi}_2+{\varphi}_3}{\varDelta^3},\hfill \\ {}\hfill \frac{\partial {\varphi}_N}{\partial y}=\frac{\varphi_{N-2}-4{\varphi}_{N-1}+3{\varphi}_N}{2\varDelta },\frac{\partial^2{\varphi}_N}{\partial {y}^2}=\frac{\varphi_{N-2}-{\varphi}_{N-2}-2{\varphi}_{N-1}+{\varphi}_N,}{\varDelta^2}\hfill \\ {}\hfill \frac{\partial^3{\varphi}_N}{\partial {y}^3}=\frac{-{\varphi}_{N-3}-3{\varphi}_{N-2}-3{\varphi}_{N-1}+{\varphi}_N}{\varDelta^3}.\hfill \end{array} $$

The derivatives of functions w _aw,0 and w _av,N are calculated using the values w _av,−1 and w _av,N+1 on the out-of-contour lines:

$$ \begin{array}{c}\hfill \frac{\partial {w}_{av,0}}{\partial y}=\frac{w_{av,1}-{w}_{av,-1}}{2\varDelta },\kern1em \frac{\partial {w}_{av,N}}{\partial y}=\frac{w_{av,N+1}-{w}_{av,N-1}}{2\varDelta },\hfill \\ {}\hfill \frac{\partial^2{w}_{av,0}}{\partial {y}^2}=\frac{w_{av,1}-2{w}_{av,0}+{w}_{av,1}}{\varDelta^2},\kern1em \frac{\partial^2{w}_{av,N}}{\partial {y}^2}=\frac{w_{av,N-1}-2{w}_{av,N}+{w}_{av,N+1}}{\varDelta^2}.\hfill \end{array} $$

2.1. Resolving system for the symmetric case (mode I). The system of partial differential equations (5) is replaced with a coupled system of ordinary differential equations in required functions on the straight lines. For internal lines, $i=\overline{1,N-1},$ the system has the form

$$ \begin{array}{c}\hfill \frac{d{N}_{x,i}}{dx}=-\frac{N_{xy,i+1}-{N}_{xy,i-1}}{2\varDelta },\frac{d{N}_{xy,i}}{dx}=-\frac{N_{y,i+1}-{N}_{xy,i-1}}{2\varDelta },\frac{d{Q}_{x,i}}{dx}={p}_{c,i}-\frac{Q_{y,i+1}-{Q}_{y,i+1}}{2\varDelta },\hfill \\ {}\hfill \frac{d{M}_{x,i}}{dx}={Q}_{x,i}-\frac{M_{xy,i+1}-{M}_{xy,i-1}}{2\varDelta },\kern1em \frac{d{M}_{xy,i}}{dx}={Q}_{y,i}-\frac{M_{y,i+1}-{M}_{y,i-1}}{2\varDelta },\hfill \\ {}\hfill \frac{d{u}_{av,i}}{dx}=\frac{N_{x,i}-{v}_{21}{N}_{y,i}}{E_1h}-\frac{v_{13}}{2{E}_3}{p}_{c,i},\frac{d{v}_{av,i}}{dx}=\frac{N_{xy,i}}{G_{12}h}-\frac{u_{av,i+1}-{u}_{av,i-1}}{2\varDelta },\hfill \\ {}\hfill \frac{d{w}_{av,i}}{dx}=-\frac{35}{37}{\tilde{\theta}}_{x,1}+\frac{42\omega }{37}\frac{Q_{x,i}}{G_{13}h}-\frac{5v}{37{G}_{12h}}-\frac{5v}{37{G}_{12}h}\left(\frac{M_{xy,i+1}-{M}_{xy,i-1}}{2\varDelta }+\frac{h}{5}\frac{N_{xy,i+1}-{N}_{xy,i-1}}{2\varDelta}\right)\hfill \\ {}\hfill +\frac{v_{32}h}{37}\left(\frac{u_{av,i-1}-2{u}_{av,i}+{u}_{av,i+1}}{\varDelta^2}+\frac{5h}{12}\frac{{\tilde{\theta}}_{x,i-1}-2{\tilde{\theta}}_{x,1}+{\tilde{\theta}}_{x,i-1}}{\varDelta^2}\right),\hfill \\ {}\hfill \frac{d{\tilde{\theta}}_{x,i}}{dx}=\frac{12\left({M}_{x,i}-{v}_{21}{M}_{y,i}\right)}{E_1{h}^3}+\frac{6{v}_{13}}{5{E}_3h}{p}_{c,i},\frac{d{\tilde{\theta}}_{y,i}}{dx}=\frac{12{M}_{xy,i}}{G_{12}{h}^3}-\frac{{\tilde{\theta}}_{x,i+1}-{\tilde{\theta}}_{x,i-1}}{2\varDelta}\hfill \end{array} $$

Here,

$$ \begin{array}{c}\hfill {N}_{y,i}={v}_{12}{N}_{x,i}+{E}_2h\frac{v_{av,i+1}-{v}_{av,i-1}}{2\varDelta }+\frac{v_{32}h}{2}{p}_{c,i},\hfill \\ {}\hfill {M}_{y,i}={v}_{12}{M}_{x,i}=\frac{E_2{h}^3}{12}\frac{{\tilde{\theta}}_{y,i+1}-{\tilde{\theta}}_{y,i-1}}{2\varDelta }-\frac{v_{32}{h}^2}{10}{p}_{c,i},\hfill \\ {}\hfill {Q}_{y,i}=\frac{5}{6}{G}_{23}h\left(\frac{w_{av,i+1}-{w}_{av,i-1}}{2\varDelta }+{\tilde{\theta}}_{y,i}\right)\hfill \\ {}\hfill +\frac{G_{23}}{6{E}_3}\left({v}_{13}\frac{M_{x,i+1}-{M}_{x,i+1}}{2\varDelta }+{v}_{23}\frac{M_{y,i+1}-{M}_{y,i+1}}{2\varDelta }+\frac{h^2}{10}\frac{p_{c,i+1}-{p}_{c,i-1}}{2\varDelta}\right).\hfill \\ {}\hfill {p}_{c,i}=\frac{20{E}_3}{7h\delta }{w}_{av,i}-\frac{20\mu }{7{h}^2\delta}\left({M}_{x,i}-\frac{h}{2}{x}_{,i}\right)+\frac{10{E}_2{v}_{23}}{7\delta}\left(\frac{v_{av,i+1}-{v}_{av,i-1}}{2\varDelta }-\frac{h}{6}\frac{{\tilde{\theta}}_{y,i+1}-{\tilde{\theta}}_{y,i-1}}{2\varDelta}\right).\hfill \end{array} $$

Let us subject the sought-for solution to boundary conditions on the longitudinal contour lines free from loads. On the line i = 0, two required functions, N _xy,0 = 0 and M _xy,0 = 0, are known; the conditions N _y,0 = 0, M _y,0 = 0, and Q _y,0 = 0 give

$$ \begin{array}{c}\hfill {v}_{av,0}=\frac{2\varDelta }{3}\left(\frac{4av,1-{v_{av}}_{,2}}{2\varDelta }+\frac{v_{12}}{E_2h}{N}_{x,0}+\frac{v_{32}}{2{E}_2}{p}_{c,0}\right),\hfill \\ {}\hfill {\tilde{\theta}}_{y,0}=\frac{2\varDelta }{3}\left(\frac{4{\tilde{\theta}}_{y,1}-\tilde{\theta}y,2}{2\varDelta }+\frac{12{v}_{12}}{E_2{h}^3}{M}_{x,0}-\frac{6{v}_{32}}{5{E}_2h}{p}_{c,0}\right),\hfill \\ {}\hfill {w}_{av,-1}={w}_{v,1}+2\varDelta \left[{\tilde{\theta}}_{y,0}+\frac{1}{5{E}_3h}\left({v}_{13}\frac{-3{M}_{x,0}+4{M}_{x,1}-{M}_{x,2}}{2\varDelta}\right.\right.\hfill \\ {}\hfill \left.\left.={v}_{23}\frac{4{M}_{y,1}-{M}_{y,2}}{2\varDelta }+\frac{h^2}{10}\frac{-{3}_{pc,0}+4{p}_{c,1}-{p}_{c,2}}{2\varDelta}\right)\right].\hfill \end{array} $$

Now, the following six equations remain on the line i = 0 :

$$ \begin{array}{c}\hfill \frac{d{N}_{x,0}}{dx}=-\frac{4{N}_{xy,1}-{N}_{xy,2}}{2\varDelta },\kern1em \frac{d{Q}_{x,0}}{dx}={p}_{c,0}-\frac{4{Q}_{y,1}-{Q}_{y,2}}{2\varDelta },\hfill \\ {}\hfill \frac{d{M}_{x,0}}{dx}={Q}_{x,0}-\frac{4{M}_{xy,1}-{M}_{xy,2}}{2\varDelta },\frac{d{u}_{av,0}}{dx}=\frac{N_{x,0}}{E_1h}-\frac{v_{13}}{2{E}_3}{p}_{c,0},\hfill \\ {}\hfill \frac{d{w}_{av,0}}{dx}=-\frac{35}{37}{\tilde{\theta}}_{x,0}+\frac{42\omega }{37}\frac{Q_{x,0}}{G_{13}h}-\frac{5v}{37{G}_{12}h}\left(\frac{4{M}_{xy,1}-{M}_{xy,2}}{2\varDelta }+\frac{h}{5}\frac{4{N}_{xy,1}-{N}_{xy,2}}{2\varDelta}\right)\hfill \\ {}\hfill +\frac{v_{32}h}{37}\left(\frac{u_{av,0}-2{u}_{av,1}+{u}_{av,2}}{\varDelta^2}+\frac{5h}{12}\frac{{\tilde{\theta}}_{x,0}-2{\tilde{\theta}}_{x,1}+{\tilde{\theta}}_{x,2}}{\varDelta^2}\right),\hfill \\ {}\hfill \frac{d{\tilde{\theta}}_{x,0}}{dx}=\frac{12{M}_{x,0}}{E_1{h}^3}+\frac{6{v}_{13}}{5{E}_3h}{p}_{c,0}.\hfill \end{array} $$

In a similar way, boundary conditions are imposed on the contour line i = N.

As a result, the resolving system of ordinary differential equations can be written in the vector form

$$ \begin{array}{c}\hfill \frac{d\overline{Y}(x)}{dx}=A\overline{Y}(x),\kern1em \overline{Y}(x)=\left(\begin{array}{c}\hfill {\overline{Y}}_0(x)\hfill \\ {}\hfill {\overline{Y}}_i(x)\hfill \\ {}\hfill {\overline{Y}}_N(x)\hfill \end{array}\right)\kern2em \left(i=\overline{1,N-1}\right),\hfill \\ {}\hfill {\overline{Y}}_0(x)={\left({N}_{x,0}\;{Q}_{x,0}\;{M}_{x,0}\;{u}_{av,0}\;{w}_{av,0}\;{\tilde{\theta}}_{x,0}\right)}^T,\hfill \\ {}\hfill {\overline{Y}}_i(x)={\left({N}_{x,i}\;{N}_{xy,i\;}{Q}_{xy,i\;}{M}_{x,i}\;{M}_{xy,i}\;{u}_{av,i}\;{v}_{av,i}\;{w}_{av,0}\;{\tilde{\theta}}_{x,i}\;{\tilde{\theta}}_{y,i}\right)}^T,\hfill \\ {}\hfill {\overline{Y}}_N(x)={\left({N}_{x,N}\;{Q}_{x,N}\;{M}_{x,N}\;{u}_{av,N}\;{w}_{av,N}\;{\tilde{\theta}}_{x,N}\right)}^T.\hfill \end{array} $$

The system is homogeneous, its order is n = 10N + 2 ; elements of the matrix A depend on the physicomechanical characteristics of material, plate thickness, and the step between the straight lines.

The boundary conditions are

$$ \begin{array}{c}\hfill {N}_{x,0} = {Q}_{x,0} = {M}_{x,0} = 0,\kern0.75em {N}_{x,i} = {N}_{xy,i} = {Q}_{x,i} = {M}_{x,i} = {M}_{xy,i} = 0,\hfill \\ {}\hfill {N}_{x,N}+{Q}_{x,N}={M}_{x,N}=0;\hfill \end{array} $$

on the edge x = 0 and

$$ \begin{array}{c}\hfill {N}_{x,0}={M}_{x,0}=0,\ {N}_{x,i} = {N}_{xy,i} = {M}_{x,i} = {M}_{xy,i} = 0,\hfill \\ {}\hfill {N}_{x,N}={M}_{x,N}=0,\kern1em {Q}_{x,0}={Q}_{x,i}={Q}_{x,N}=\frac{P}{b}.\hfill \end{array} $$

on the edge x = L.

On the joint between the fastened and unfastened areas, along the delamination front, the continuity of all required functions is retained, excep of ${\tilde{\theta}}_x$ and ${\tilde{\theta}}_y$, which are discontinuous owing the jump of the normal stress p _c .The value of the discontinuities is found from the conditions of continuity of the average rotation angles θ _x,av and θ _y,av [4,5].

2.2. Resolving system for the antisymmetric case (modes II and III). The system of partial differential equations (6) is replaced with a coupled system of the ordinary differential equations. For internal lines $\left(i=\overline{1,N-1}\right),$

$$ \begin{array}{c}\hfill \frac{d{N}_{x,i}}{dx}={q}_{c,i}-\frac{N_{xy,i+1}-{N}_{xy,i-1}}{2\varDelta },\hfill \\ {}\hfill \frac{d{N}_{xy,i}}{dx}={t}_{c,i}-{v}_{12}\frac{N_{x,i+1}-{N}_{x,i+1}}{2\varDelta }-{E}_2h\frac{v_{av,i-1}-2{v}_{av,i}+{v}_{av,i+1}}{\varDelta^2}+\frac{v_{32}{h}^2}{12}\frac{r_{r+1}-{r}_{r-1}}{2\varDelta },\hfill \\ {}\hfill \frac{d{Q}_{x,i}}{dx}=\frac{-5}{6}{G}_{23}h\left(\frac{w_{av,i-1}-2{w}_{zv,i}+{w}_{av,i+1}}{\varDelta^2}+\frac{{\tilde{\theta}}_{y,i+1}-{\tilde{\theta}}_{y,i-1}}{2\varDelta}\right)-\frac{h}{12}\frac{t_{c,i+1}-{t}_{c,i-1}}{2\varDelta}\hfill \\ {}\hfill -\frac{G_{23}}{6{E}_3}\left(\mu \frac{M_{x,i-1}-2{M}_{x,i}+{M}_{x,i+1}}{\varDelta^2}+{v}_{32}\frac{E_2{h}^3}{12}\frac{-{\tilde{\theta}}_{y,i-2}+2-{\tilde{\theta}}_{y,i-1}-2-{\tilde{\theta}}_{y,i+1}+-{\tilde{\theta}}_{y,i+2}}{2{\varDelta}^3}\right.\hfill \\ {}\hfill \left.-\frac{h^3\delta }{120}\frac{r_{i-1}-2{r}_i+{r}_{i+1}}{\varDelta^2}\right),\hfill \\ {}\hfill \frac{d{M}_{x,i}}{dx}={Q}_{x,i}-\frac{M_{xy,i+1}-{M}_{xy,i-1}}{2\varDelta }-\frac{h}{2}{q}_{c,i},\hfill \\ {}\hfill \frac{d{M}_{xy,i}}{dx}={Q}_{y,i}-{v}_{12}\frac{M_{x,i+1}-{M}_{x,i-1}}{2\varDelta }-\frac{E_2{h}^3}{12}\frac{{\tilde{\theta}}_{y,i-1}-2{\tilde{\theta}}_{y,i}+{\tilde{\theta}}_{y,i+1}}{\varDelta^2}\hfill \\ {}\hfill -\frac{v_{32}{h}^3}{12}\frac{r_{i+1}-{r}_{i-1}}{2\varDelta }-\frac{h}{2}{t}_{c,i},\hfill \\ {}\hfill \frac{d{u}_{av,i}}{dx}=\frac{N_{x,i}-{v}_{21}{N}_{y,i}}{E_1h}+\frac{v_{13}h}{12{E}_3}{r}_i=\frac{d{v}_{av,i}}{dx}=\frac{N_{xy,i}}{G_{12}h}-\frac{u_{av,i+1}-{u}_{av,i-1}}{2\varDelta },\hfill \\ {}\hfill \frac{d{w}_{av,i}}{dx}={\tilde{\theta}}_{x,i}+\frac{6}{5}\frac{Q_{x,i}}{G_{13h}}\left(1-\frac{u}{6}\frac{G_{13}}{E_3}\right)-\frac{q_{c,i}}{10{G}_3}\left(1-\mu \frac{G_{13}}{E_3}\right)\hfill \\ {}\hfill -\frac{v}{5{G}_{12}h}\frac{{M_{xy,i}}_{+1}-{M_{xy,i}}_{-1}}{2\varDelta }+\frac{{\tilde{\theta}}_{x,i-1}-2{\tilde{\theta}}_{x,i-1}}{\varDelta^2}+\frac{h^2\delta }{600{E}_3}{s}_i,\hfill \\ {}\hfill \frac{d{\tilde{\theta}}_{x,i}}{dx}=\frac{12\left({M}_{x,i}-{v}_{21}{M}_{y.i}\right)}{E_1{h}^3}-\frac{v_{13}}{10{E}_3}{r}_i,\frac{d{\tilde{\theta}}_{y,i}}{dx}=\frac{12{M}_{xy,i}}{G_1{h}^3}-\frac{{\tilde{\theta}}_{x,i+1}-2{\tilde{\theta}}_{x,i-1}}{2\varDelta },\hfill \\ {}\hfill \frac{d{q}_{c,i}}{dx}={r}_i-\frac{t_{c,i+1}-{t}_{c,i-1}}{2\varDelta },\frac{d{r}_i}{dx}={s}_i.\hfill \end{array} $$

Here,

$$ \begin{array}{c}\hfill \begin{array}{l}{N}_{y,i}={v}_{12}{N}_{x,i}+{E}_{2h}\frac{{v_{av,i}}_{+1}-{v}_{av,i-1}}{2\varDelta }-\frac{v_{32}{h}^2}{12}{r}_i,\\ {}{M}_{y,i}={v}_{12}{M}_{x,i}+\frac{E_2{h}^3}{12}\frac{{\tilde{\theta}}_{y,i+1}-{\tilde{\theta}}_{y,i-1}}{2\varDelta }+\frac{v_{32}{h}^3}{120}{r}_i,\\ {}{Q}_{y,i}=\frac{5}{6}{G}_{23}h\left(\frac{w_{av,i+1}-{w}_{av,i-1}}{2\varDelta}\right)+\frac{h}{12}{t}_{c,i}\end{array}\hfill \\ {}\hfill \begin{array}{l}+\frac{G_{23}}{6{E}_3}\left({v}_{13}\frac{M_{x,i+1}-{M}_{x,i-1}}{2\varDelta }+{v}_{23}\frac{M_{y,i+1}-{M}_{y,i-1}}{2\varDelta }-\frac{h^3}{120}\frac{r_{i+1}-{r}_{i-1}}{2\varDelta}\right),\\ {}{t}_{c,i}=\frac{60{G}_{23}}{17h}\left[\begin{array}{c}\hfill \frac{57{h}^3}{3600{E}_3}\frac{r_{i+1}-{r}_{i-1}}{2\varDelta }+2{v}_{av,i}-h{\tilde{\theta}}_{y.i}-\frac{h}{6}\left(\frac{w_{av,i+1}-{w}_{av,i-1}}{2\varDelta }+{\tilde{\theta}}_{y,i}\right)-\hfill \\ {}\hfill -\frac{7}{30{E}_3}\left({v}_{13}\frac{M_{x,i+1}-{M}_{x,i-1}}{2\varDelta }+{v}_{23}\frac{M_{y,i+1}-{M}_{y,i-1}}{2\varDelta}\right)+\hfill \\ {}\hfill +\frac{h}{6{E}_3}\left({v}_{13}\frac{N_{x,i+1}-{M}_{x,i-1}}{2\varDelta }+{v}_{23}\frac{N_{y,i+1}-{N}_{y,i-1}}{2\varDelta}\right)\hfill \end{array}\right],\\ {}{s}_i=\frac{450{E}_3}{7{h}^3\delta}\left[\begin{array}{c}\hfill \frac{4h}{15{G}_{13}}\left(1-\mu \frac{G_{13}}{E_3}\right){q}_{,i}-2{u}_{av,i}+h{\tilde{\theta}}_{x,i}+\frac{Q_{x,i}}{5{G}_{13}}\left(1+\mu \frac{G_{13}}{E_3}\right)+\hfill \\ {}\hfill +\frac{v}{5{G}_{12}}\left(\frac{M_{xy,i+1}-{M}_{xy,i-1}}{2\varDelta }-\frac{5h}{6}\frac{N_{xy,i+1}-{N}_{xy,i-1}}{2\varDelta}\right)+\hfill \\ {}\hfill +\frac{v_{32}{h}^2}{6}\left(\frac{u_{av,i-1}-2{u}_{av,i}+{u}_{av,i+1}}{\varDelta^2}-\frac{h}{10}\frac{{\tilde{\theta}}_{x,i-1}-2{\tilde{\theta}}_{x,i}+{\tilde{\theta}}_{x,i+1}}{\varDelta^2}\right)\hfill \end{array}\right].\end{array}\hfill \end{array} $$

On the line i = 0, N _xy,0 = 0 and M _xy,0 = 0 ; in view of the boundary condition t _c,0 = 0, the conditions N _y,0 = 0, M _y,0 = 0, and Q _y,0 = 0 give

$$ \begin{array}{c}\hfill {v}_{av,0}=\frac{2\varDelta }{3}\left(\frac{4{v}_{av,1}-{v}_{av,2}}{2\varDelta }+\frac{v_{12}}{E_2h}{N}_{x,0}-\frac{v_{32}h}{12{E}_2{r}_0}\right),\hfill \\ {}\hfill {\tilde{\theta}}_{y,0}=\frac{2\varDelta }{3}\left(\frac{4{\tilde{\theta}}_{y,1}-{\tilde{\theta}}_{y,2}}{2\varDelta }+\frac{12{v}_{12}}{E_2{h}^3}{M}_{x,0}+\frac{v_{32}}{10{E}_2}{r}_0\right),\hfill \\ {}\hfill {w}_{av-1}={w}_{v,1}+2\varDelta \left[{\tilde{\theta}}_{y,0}+\frac{1}{5{E}_3h}\left({\tilde{\theta}}_{y,0}+\frac{1}{5{E}_3h}+{v}_{23}\frac{4{M}_{y.1}-{M}_{y.2}}{2\varDelta }-\frac{h^3}{120}\frac{-3{r}_0+4{r}_1-{r}_2}{2\varDelta}\right)\right].\hfill \end{array} $$

On the line i = 0, there remain eight equations:

$$ \begin{array}{c}\hfill \frac{d{N}_{x,0}}{dx}={q}_{c,0}-\frac{4{N}_{xy,1}-{N}_{xy,2}}{2\varDelta },\hfill \\ {}\hfill \frac{d{Q}_{x,0}}{d_x}=-\frac{5}{6}{G}_{23}h\left(\frac{w_{av,-1}-2{w}_{av,0}+{w}_{av,1}}{\varDelta^2}+\frac{-3{\tilde{\theta}}_{y,0}+4{\tilde{\theta}}_{y,1}-{\tilde{\theta}}_{y,2}}{2\varDelta}\right)-\frac{h}{12}\frac{4{t}_{c,1}-{t}_{c,2}}{2\varDelta}\hfill \\ {}\hfill -\frac{G_{23}}{6{E}_3}\left(\upmu \frac{M_{x,0}-2{M}_{x,1}+{M}_{x,2}}{\varDelta^2}+{v}_{32}\frac{E_2{h}^3}{12}\frac{-{\tilde{\theta}}_{y,0}+3{\tilde{\theta}}_{y,1}-3{\tilde{\theta}}_{y,2}+{\tilde{\theta}}_{y,3}}{2{\varDelta}^3}-\frac{h^3\delta }{120}\frac{r_0-2{r}_1+{r}_2}{\varDelta^2}\right),\hfill \\ {}\hfill \frac{d{M}_{x,0}}{dx}={Q}_{x,0}-\frac{4{M}_{xy,1}-{M}_{xy,2}}{2\varDelta }-\frac{h}{2}{q}_{c,0},\frac{d{u}_{av,0}}{dx}=\frac{N_{x,0}}{E_1h}+\frac{v_{13}h}{12{E}_3}{r}_0,\hfill \\ {}\hfill \frac{d{w}_{av,0}}{dx}=-{\tilde{\theta}}_{x,i}+\frac{6}{5}\frac{Q_{x,0}}{G_{13}h}\left(1-\frac{v_{13}}{6}\frac{G_{13}}{E_3}\right)-\frac{q_{c,0}}{10{G}_3}\left(1-{v}_{13}\frac{G_{13}}{E_3}\right)\hfill \\ {}\hfill -\frac{v_{13}}{5{E}_3h}\frac{4{M}_{xy,1}-{M}_{xy,2}}{2\varDelta }+\frac{h^2}{600{E}_3}{s}_0,\hfill \\ {}\hfill \frac{d{\tilde{\theta}}_{x,0}}{dx}=\frac{12{M}_{x,0}}{E_1{h}^3}-\frac{v_{13}}{10{E}_3}{r}_0,\frac{d{q}_{c,0}}{dx}={r}_0-\frac{4{t}_{c,1}-{t}_{c,2}}{2\varDelta },\frac{d{r}_0}{dx}={s}_0.\hfill \end{array} $$

The transformation of equations on the boundary line i = N is carried out in a similar way.

The resolving system contains n = 12N + 4 ordinary differential equations, whose vector form is

$$ \begin{array}{c}\hfill \frac{d\overline{Y}(x)}{dx}=B\overline{Y}(x),\kern1em \overline{Y}(x)=\left(\begin{array}{c}\hfill \overline{Y_0}(x)\hfill \\ {}\hfill \overline{Y_i}(x)\hfill \\ {}\hfill \overline{Y_N}(x)\hfill \\ {}\hfill \overline{Z_j}(x)\hfill \\ {}\hfill \overline{R_j}(x)\hfill \end{array}\right)\kern1em \left(i=\overline{1,N-1},\kern1em j=\overline{0,N}\right),\hfill \\ {}\hfill \begin{array}{l}\overline{Y_0}(x)={\left({N}_{x,0}{Q}_{x,0}{M}_{x,0}{u}_{av,0}{w}_{av,0}{\tilde{\theta}}_{x,0}\right)}^T,\\ {}\overline{Y_i}(x)={\left({N}_{x,i}{N}_{xy,i}{Q}_{x,i}{M}_{xy,i}{u}_{av,i}{v}_{av,i}{w}_{av,i}{\tilde{\theta}}_{x,i}{\tilde{\theta}}_{y,i}\right)}^T,\\ {}{\overline{Y}}_N(x)={\left({N}_{x,N}{Q}_{x,N}{M}_{x,N}{u}_{av,N}{w}_{av,N}{\tilde{\theta}}_{x,N}\right)}^T,\\ {}{\overline{Z}}_j(x)={\left({q}_{c,j}\right)}^T,{\overline{R}}_j(x)={\left({r}_j\right)}^T.\end{array}\hfill \end{array} $$

Elements of the matrix B are determined by coefficients of the right-hand sides of the equations.

For the specimen shown on Fig. 2, the boundary conditions for the basic resolving functions on the edges x = 0, L

are

$$ \begin{array}{c}\hfill {N}_{x,0}={w}_{av,0}={M}_{x,0}=0,\kern1em {N}_{x,i}={N}_{x,y,i}={w}_{av,i}={M}_{x,i}={M}_{xy,i}=0,\hfill \\ {}\hfill {N}_{x,N}={w}_{av,N}={M}_{x,N}=0;\hfill \end{array} $$

For the shear stresses on the edge x = 0, q _{c, j} = 3P/(8bh) ; on the edge x = L, q _c,j = 0.

Along a line with the load P, the transverse forces vary stepwise, and the function ${\tilde{\theta}}_x$ is discontinuous. Along the delamination, the functions ${\tilde{\theta}}_x$ and ${\tilde{\theta}}_y$ are discontinuous and ensure the continuity of the average rotation angles θ _x,av and θ _y,av [4,5].

For the specimen shown on Fig. 3, its fastening and loading are described in Sect. 3.3.

3. Calculation Results

Let us present the results of calculation performed in the two-dimensional statement for all three types of specimens by using the approach suggested. The distributions of running forces, moments, and thickness-average displacements and rotations in layers and of the normal and shear stresses on the specimen midplane were determined. From these data, the displacements on layer interfaces, necessary for calculating the values of modal components of ERR, were calculated.

The initial data on the geometry and physicomechanical characteristics of the specimens (see Figs. 1, 2), tested according the schemes of a double-cantilever beam (mode I) and three-point bending (mode II), are given in [5].

3.1. Mode I: bending of a double-cantilever beam. On Fig. 4, as an example, distributions of the longitudinal running force and moment in layer 1 of the specimen are shown. On Fig. 5, the distribution of the normal stress on the contact plane of layers at N = 40 is given.

Fig. 4

Distribution of the running force N _x and running moment M _x .

Fig. 5

The normal stress p _c on the specimen midplane (a) and on the line y = b/2 (b).

At identical physicomechanical characteristics and layer thicknesses, the normal displacement of points of the bottom contact plane of layer 1 is determined by the expression [4]

$$ {w}_c={w}_{ac}-\frac{1}{E_3h}\left[{v}_{13}\left({M}_x-\frac{h}{2}{N}_x\right)+{v}_{23}\left({M}_y-\frac{h}{2}{N}_y\right)\right]-\frac{7h}{20{E}_3}{P}_c. $$

On the fastened region, at 0 ≤ x < l (l = L − a), w _c = 0 . Along the delamination front, on the line x = l, the function w _c is discontinuous owing to the jump of the stress p _c .

Calculation of the only, in this case, modal component G _I (y) of ERR can be performed in the way suggested in [5]:

$$ {G}_I(y)={p}_c\left(1,y\right){\left|{}^{-}{w}_c\left(l,y\right)\right|}^{+}, $$

where p _c (l, y)|⁻ − is the normal stress on the delamination front line at the left (the maximum stress), and w _c (l, y)|⁺ is the normal displacement of points of the layer contact plane on the front line at the right (the value of discontinuity of displacement).

On Fig. 6, the distribution of the modal component G _I (y) across the specimen width is shown, and, for comparison, the value found in [5] in a one-dimensional statement is given.

Fig. 6

The modal component G_I (y).

3.2. Mode II: three-point bending of a hinge-supported delaminated beam. On Fig 7, distributions of the shear stresses q _c and t _c operating along the x and y axes on the specimen midplane are shown (Fig. 8).

Fig. 7

The shear stress q_c on the specimen midplane (a) and on the line y = b/2 (b).

Fig. 8

The shear stress t_c on the specimen midplane (a) and on the line of its maximum value (b).

In this specimen, on the delamination front line, prevailing in magnitude are the longitudinal shear stresses q _c . The presence of the low transverse stress t _c is caused by changes in the cross section of layers in the unfastened zone. In separate bending, the rectangular cross sections of each layer become trapezoidal. On the front line, these trapezoids are connected together. In the double-cantilever beam (mode I), the trapezoids are connected along identical (the smaller) bases, but in the three-point-bent beam (mode II), the trapezoids are connected along bases of different length. In the second case, transverse shear stresses ensuring the compatibility of displacements of points of the contact surface of layers arise.

Using the functions describing the SSS of the specimen, which are found from the solution of the boundary-value problem, we calculate the longitudinal u _c and transverse v _c displacement of points of the contact plane of layer, and then, following [5], we determine the modal components of ERR:

$$ \begin{array}{c}\hfill {G}_{II}(y)=\frac{q_c^2\left({x}_{\max },y\right)}{q_c^{\prime}\left({x}_{\max \prime },y\right)}{\left.{u}_c^{\prime}\left(l,y\right)\right|}^{+},\hfill \\ {}\hfill {G}_{III}^{\prime }(y)={t}_c\left(l,y\right){\left|{}^{-}{v}_c\left(l,y\right)\right|}^{+}.\hfill \end{array} $$

(7)

Here, qc (xmax, y) and q ^′ _c (x _max′, y) are the maximum values of the longitudinal shear stress and its derivative with respect to x (designated by a prime) near to the delamination front at the left; x _max and x _max′ are the corresponding coordinates of maxima of these functions; u ^′ _c (l, y)|⁺ is the value of derivative of the longitudinal displacement of points of the contact plane of layer on the front line at the right; t _c (l, y)|⁻ is the transverse shear stress on a the delamination front line at the left; v _c (l, y)|⁺ is the transverse displacement of points of the contact plane of layer on the front line at the right.

On Fig. 9, the distributions of modal components along the delamination front line are shown. For the specimen considered, the values of G _III (y) are negligible in comparison with those of G _II (y).In the middle of the specimen, the value G _II (b/2) = 34 J/m² coincides with the result found in [5] in a one-dimensional statement.

Fig. 9

The modal components GI(y).

3.3. Mode III: Twisting of an edge-cracked plate. Let us compare the solution found by the method suggested with finite-element calculations performed by using the virtual crack closure technique [9], which will be considered here as standard ones, although they contain certain calculation errors.

Dimensions of the [0/(±45)₃/(∓45)3/0]s specimen considered (see Fig. 3) were as follows: L = 1.5d, a = L/2, b = 3.5d, L ₀ = 1.25d, b ₀ = 3d, d = 25.4 mm, and h = 2.4 mm; the elastic characteristics of the unidirectional G400-800/R6376 composite assumed in calculations were as follows: E ₁ = 151 GPa, E ₂ = E ₃ = 8.97 GPa, G ₁₂ = G ₁₃ = G ₂₃ = 5.15 GPa, and v ₂₁ = v ₃₁ = v ₃₂ = 0.325.

The b ₀ × L ₀ loading quadrangle, whose three angular points are fixed and a vertical displacement w ₀ = 4,63 mm is given for its fourth one, is located asymmetrically about the middle of width b of the specimen, closer to the x axis [9]. In solving the problem by the method of straight lines, the number of lines N = 56 and grid pitch were chosen so that the sides of this quadrangle parallel to an x axis coincided with grid lines. It was assumed that L ₀ = L, i.e., the angular points of the loading quadrangle are located on the edges x = 0 and x = L of the sample.

On Fig. 10, distributions of the shear stresses qc and tc on the midplane are shown. On Fig. 11, the distributions of the modal components G _II (y) and G _III (y) calculated by formulas (7) illustrated. Here, the results found in [9] are presented.

Fig. 10

The shear stresses q_c (a) and t_c (b).

Fig. 11

The modal components G_II (y) and G_III (y).(♦) — results of [9].

From the data in Fig. 11, it is visible that, in the “plateau” area, the value of GIII obtained is 6% lower than the result of finite-element calculation. A repeated calculation was performed on the condition that the dimensions of the specimen and loading quadrangle along the x axis are equal to (L + L ₀)/2 . In this case, the value of G _III exceeded the result given in [9] by 11%. Thus, the first result is a conservative estimate of G _III.

We should note that the given problem revealed an increased sensitivity of results not only to the account of the overhangs outside the loading quadrangle, but also to the elastic characteristics of material. The results found in [9] at the changed values of G ₂₃ = 2.51 GPa and v ₃₂ = 0.54 showed that G _III in the middle part of specimen increased by 10% on the average. This result agrees with calculations by the method used here.

Conclusion

A comparison of results of the present work and the analysis performed in [5] points to the efficiency of the approach based on the FLM. With reference to the class of problems considered, a further development of the method have to be carried out in the direction of layer-by-layer calculation of composite packages with differently oriented layers in order to find the modal components of ERR, which is necessary for obtaining refined estimates of origination and development of interlaminar delaminations [11], and also in the direction of development of methods for solving boundary-value problems for systems of differential equations at given displacements of points located inside an area considered.