Introduction. Spectral analysis of speech signals is related to to the most dynamically developing directions of study in the field of acoustic measurements. With reference to digital spectral analysis, the problem is, as a rule, reduced to determining the envelope of a power spectrum in the interval of quasi-stationarity of a speech signal of duration one frame [1, 2]. The spectral envelope is responsible for the timbre and voice recognition of the speaker [3,4,5]. Here the small samples problem arises [6,7,8]. The theory recommends parametric methods of spectral analysis to overcome this, such as the Berg method, autocorrective, covariational, and so forth. [9, 10] These may be studied as variants to classical methods [11] based on the discrete Fourier transform. The autoregressive model [4] used in the parametric methods corresponds well with the "acoustic pipe" model of the vocal pathway of the speaker [2]. However, application of the autoregression model does not fully solve the small sample problem, which is merely transformed into another acute problem of the parametric methods of spectral analysis: the optimization of order p < ∞ of the autoregressive model [3, 12]. This optimization is usually associated with the Akaike informational measure and analogs [13,14,15]. However, when processing speech signals in the observational sliding window mode of small duration τ = 5–30 ms, the effectiveness of these criteria sharply decreases [16, 17].

The objective of this article is to study the capabilities and effectiveness of a hybrid technique under conditions of small samples of observations. The subject of the study is a hybrid method of the spectral analysis of speech signals which unites the advantages of non-linear parametric and classical linear methods. The problem is formulated as optimization in the terms of the multivariant verification of R hypotheses p = pr, r = \(\stackrel{-}{1, R}\) on the order p ≥ 1 of the autoregressive model. The criterion will be the principle of the maximum level of correspondence of the autoregressive model of the Schuster periodogram as the most informative characteristic relative to the fine structure of a speech signal [3].

This article is written for development of the results of previous work of the author [4, 10], performed in coauthorship with the staffof the Laboratory of Algorithms and Techniques for the Analysis of Network Structures of NIU "Higher School of Economics".

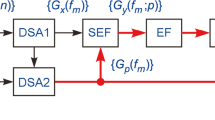
Problem definition. We consider a speech signal {x(n)} in the discrete time n = 0, 1, …, N – 1 in the observation interval of finite duration τ < ∞, where N = τF is the sample size; and F is the frequency of time sampling. We define the spectral density of power (SDP) of a signal through an autoregressive model of the general form [1]:

$${G}_{p}\left(f\right)={\upsigma }_{p}^{2}T{\left|1-\sum_{i=1}^{p}{a}_{p}\left(i\right)\mathrm{exp}\left(-\mathrm{j}2\uppi ifT\right)\right|}^{-2},$$
(1)

where ap(i) is the ith element of the p-vector ap of the coefficients of the linear autoregression of the pth order; is the scale factor; and T = F–1.

The parameters ap and \({\upsigma }_{p}^{2}\) are defined in (1) from the sample {x(n)} by means of one of the known methods of parametric spectral analysis, such as the Berg method, autocorrective, covariational, and so forth [1]. However, in any variant the order p must be set a priori. The problem consists in the fact that depending on the value of p established in (1), the form of the autoregressive model of a speech signal varies, and especially strongly in the conditions of small samples [3]. Taking this into account, the problem is reduced to determining the measure of optimization of the order of a spectral estimate (1) in the sliding window mode for observations of finite duration τ.

Criterion of optimization. Since an autoregressive model (1) is inseparably linked with the envelope of the SDP of a speech signal [17], we will define the pectrum of signal power through the discrete Fourier transform [2]:

$$\begin{array}{cc}{G}_{x}\left({f}_{m}\right)=\frac{{\left|\sum_{n=0}^{M-1}x\left(n\right)\mathrm{exp}\left(-\mathrm{j}2\uppi nm{M}^{-1}\right)\right|}^{2}}{FM},& m=\mathrm{0,1},\dots ,M-1,\end{array}$$
(2)

where fm = m Δf is the discrete frequency with a shift of Δf = FM –1 = const in relation to the frequency fm–1; and M is the size of the set of readings of a speech signal in the frequency domain (M < ∞).

In this theory, expression (2) is known as a Schuster periodogram [1]. This periodogram of dimensionality M = 2k ≥ N, where k is some integral number, is calculated using algorithms for the fast Fourier transform [18]. Here only the first N from M (N ≪ M) readings of the speech signal in expression (2) are distinct from zero. For example, for a duration of the observation window τ = 5–30 ms and sampling frequency F = 8 kHzFootnote 1 for the case k = 10, we will have M = 1024 with the equality N = 40–240 (this is the typical relation of the number of readings of a speech signal in the frequency and time fields, respectively) [10].

Due to the linear nature of the discrete Fourier transform, expression (2) contains the maximal useful information about the SDP, and therefore it can be used as a spectral reference sampler in the problem of optimizing the autoregressive model. For this purpose, we rewrite (1) in the form of an inverse conversion

$${G}_{p}\left({f}_{m}\right)={\upsigma }_{p}^{2}T{\left|{A}_{p}\left(\mathrm{j}{f}_{m}\right)\right|}^{-2}$$

of the square of the modulus of the complex coefficient of transmission

$$\begin{array}{cc}{A}_{p}\left(\mathrm{j}{f}_{m}\right)=1-\sum_{i=1}^{p}{a}_{p}\left(i\right)\mathrm{exp}\left(-\mathrm{j}2\uppi im{M}^{-1}\right),& m=\stackrel{-}{0;M-1},\end{array}$$
(3)

of the transversal filter of the pth order on the extracted sample of discrete frequency {fm}. The signal {y(n)} at the exit of such a filter in the frequency domain is described by expression [4]:

$$\begin{array}{cc}{G}_{y}\left({f}_{m};p\right)={\left|{A}_{p}\left(\mathrm{j}{f}_{m}\right)\right|}^{2}{G}_{x}\left({f}_{m}\right)={\upsigma }_{p}^{2}T\frac{{G}_{x}\left({f}_{m}\right)}{{G}_{p}\left({f}_{m}\right)},& m=\stackrel{-}{0;M-1}.\end{array}$$
(4)

Expression (4) defines the operation of smoothing or whitewashing the envelope \({\overline{G} }_{x}\) ( fm ) of the power spectrum at input (2). Here, in the ideal for the spectral envelope of \({\overline{G} }_{y}\) ( fm; p) at exit of the equalizer network (3), the system of equations ∀m < M: \(\overline{G }\) y ( fm; p) = G0 = const is valid. In terms of the inverse problem [3] "from a speech signal to its voice radiant," this defines the hypothetical white noise as the generating process for the autoregressive model (1).

However, in practice the form of the envelope of the SDP (4) may differ substantially from rectangular, due first of all to the non-ideal nature of the autoregressive model used. (1). The basic value in this sense has order p. We optimize its value within the finite set (R-set) of the variants p1 < p2 < ... < pR by the principle of the maximum likelihood of the form of the envelope of the SDP (4) to rectangular.

Taking into account the above-specified, we use the modified standard of the COSH distance (COSH is the hyperbolic cosine) function [19] as the function of the purpose of the optimization problem being solved:

$$\begin{array}{c}\uprho \left(p\right)=\sqrt{\left[{M}^{-1}\sum_{m=0}^{M-1}{G}_{0}{\overline{G} }_{y}^{-1}\left({f}_{m};p\right)\right]\left[{M}^{-1}\sum_{m=0}^{M-1}{\overline{G} }_{y}\left({f}_{m};p\right){\overline{G} }_{y}^{-1}\right]}\\ ={M}^{-1}\sqrt{\left[\sum_{m=0}^{M-1}{\overline{G} }_{y}^{-1}\left({f}_{m};p\right)\right]\left[\sum_{m=0}^{M-1}{\overline{G} }_{y}\left({f}_{m};p\right)\right]}-1\ge 0,\end{array}$$
(5)

with the property of scale invariance to the SDP of a speech signal at input. With equality of the envelope \(\overline{G }\) y ( fm; p) to an arbitrary constant G0 , measure (5) will be identically equal to zero. According to the results of [3], the limit accuracy of the autoregressive model (1) will be reached in this case. As measure (5) increases, the accuracy of the autoregressive model decreases, and therefore measure (5) may be examined as an objective index of the error of the generated autoregressive model. From this follows the criterion for adopting solutions in the problem of spectral analysis of a speech signal: on the set R of examined variants {pr, r ≤ R}, the optimal estimate of the SDP {G*(fm)} corresponds to expression (1) in the selection of the order of an autoregressive model according to the rule

$${p}^{*}=\mathrm{Arg}\underset{\forall r\le R}{\mathrm{min}}\uprho \left(p\right){|}_{p={p}_{r}}.$$
(6)

Practical implementation of the proposed criterion reduces mainly to an estimate of the envelope of the SDP at exit of the leveling network (3) and to calculation of the modified COSH distance (5) within the set of variants \(\overline{G }\) y ( fm; pr ) , r = \(\stackrel{-}{1, R}\) , in the interval of observations of finite duration τ. Here, is necessary to use fast computational methods.

Example of practical implementation. Turning away from the Berg method [20], which possesses at the same time fast response and high resolution capability by frequency, we use the Levinson recursion [21] to adapt the vector of coefficients of the SDP (1) for the sample { x(n) } of finite size N :

$$\begin{array}{c}\forall q=\stackrel{-}{1,p}:{a}_{q}\left(i\right)={a}_{q-1}\left(i\right)+{c}_{q}{a}_{q-1}\left(q-i\right),i=\stackrel{-}{1,p};\\ {c}_{q}=\frac{2\sum_{n=q}^{N-1}{\upeta }_{q-1}\left(n\right){\nu }_{q-1}\left(n-1\right)}{\sum_{n=q}^{N-1}\left[{\upeta }_{q-1}^{2}\left(n\right){\nu }_{q-1}^{2}\left(n-1\right)\right]};\\ {\upeta }_{q}\left(n\right)={\upeta }_{q-1}\left(n\right)+{c}_{q}{\nu }_{q-1}\left(n-1\right);\\ {\nu }_{q}\left(n\right)={\nu }_{q-1}\left(n-1\right)+{c}_{q}{\upeta }_{q-1}\left(n\right);\\ {\nu }_{0}\left(n\right)={\upeta }_{0}\left(n-1\right)=x\left(n\right),n=\mathrm{0,1},\dots ,N-1.\end{array}$$
(7)

Here, in accordance with [1], the stability of the formulated autoregressive model, in the sense of digital filtering [22] independently of the sampling composition, is guaranteed. The scale factor \({\upsigma }_{p}^{2}\) does not play a large role in expression (1). As a rule [4], this is established from the condition of normalizing the estimate of the SDP on variance to the level set by the user.

For selection of the spectral envelope (4) by analogy with [3], the standard recirculator is used. Its dynamic in the frequency domain is described by the difference equation [18]:

$${\overline{G} }_{y}\left({f}_{m;p}\right)=b{\overline{G} }_{y}\left({f}_{m}-\Delta f;p\right)+{G}_{y}\left({f}_{m};p\right),m=\stackrel{-}{1,M},$$
(8)

where b = const.

The operation of the recirculator reduces to accumulating the spectral components of the speech signal in sliding window mode in the frequency domain. The size of a window defines the inertance of the reciirculator which is governed in (8) by the parametric value of b. Depending on the type of analyzed speech frame (vocalizedFootnote 2 or not), the quantitative index of inertance θ = –Δf/ln b = –FM –1/ln b must be in agreement either with the frequency of the fundamental component of the speech signal [2], or with the resolution capability of the spectral analyser at frequency θ = τ–1 = FN –1. The first variant was described in sufficient detail in [3]. For this reason, we will later examine the spectral analysis of non-vocal frames containing voiceless consonants of the speech of a conventional speaker. For this variant [4]:

$$b=\mathrm{exp}\left(-\uptau F{M}^{-1}\right)=\mathrm{exp}\left(-N{M}^{-1}\right).$$
(9)

For example, for τ = 5–30 ms, F = 8 kHz, and M = 1024, we obtain b = 0.80– 0.96.

Expressions (1)–(9) in the aggregate define the hybrid technique of the spectral analysis of a speech signal (x (n)} using at the same time the Schuster periodogram and the Berg method as a methodological basis. The proposed hybrid technique was for the first time implemented in practice, based on author software,Footnote 3 using which the experiment described later was set up and conducted.

Program and results of experiment. The object of the experimental study was a synthesized 10th-order autoregressive process, imitating the consonant "sh"of the Russian alphabet in the speech of the speaker being studied (the author of this article) and specified by the vector of autoregression coefficients \({\mathbf{a}}_{10}^{\boldsymbol{*}}\) = (1.708427645; 2.186231624; 2.390214916; 2.155074921; 1.246001575; 0.49162809; –0.068969197; –0.416448837; –0.334798662, –0.08981284). The generating process for the autoregression process was white Gaussian noise with variance \({\upsigma }_{10}^{2}\). The synthesized signal of sufficient duration T0 = 3 s was linearly divided in the Phoneme Training program into frames {x(n)} of duration τ, equal to 5, 10, and 30 ms. As a result, for each of the three durations τ of the observation window, a representative database up to L = T0/τ = 300 independent frames was formulated. For a signal sampling frequency F = 8 kHz, the sample size N for each such frame was 40, 80, and 240 readings, respectively. Further, for each frame, the Schuster periodogram (2) of dimensionality M = 1024 and frequency step Δf = 8000/1024 = 7.8125 Hz was calculated using the fast Fourier transform. At the same time with the Schuster periodogram, the Berg method obtained a spectral estimate (1) at R = 16 alternate variants of its order p = 5–20. The total computational complexity of the computational procedure (7) was on the order of 3NpR = 3∙240∙20 = 14.4∙103 elementary operations in the interval of duration τ. This, with a margin, is responsible for the efficiency of modern information systems and real-time technologies [18, 19]. Further, according to expressions (8) and (9), estimates are obtained for the spectral envelope \(\overline{G }\) y ( fm; pr ) of the signal {y(n)} at output of the leveling filter (3), for all variants pr, r ≤ R. The corresponding value of the characteristics of ρ(p) is determined from these estimates in accordance with (6). The obtained values were averaged further from the results of L independent tests of observations for each duration τ. As a result the relative error of the experimental data [4, 5] was no greater than ε = 165∙(300)–1/2 = 9.5% with a confidence probability 0.9 and above.

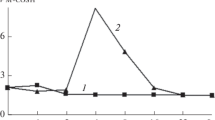
Figure 1 shows a typical family of Berg spectral estimates obtained in the same observation window of duration τ = 10 ms. The corresponding Schuster periodogram (2) is shown by a dashed line for comparison One may observe the advantages of the variant of a spectral estimate of order p = 10. They are confirmed by the graph of the corresponding SDP (4) in Fig. 2, where the dashed line reflects the form of the spectral envelope: for p = 10, the form is maximally close to rectangular. The histogram in Fig. 3 — the operating characteristics (5) of the hybrid techniques for τ = 10 ms — serves as rigorous substantiation of order p = 10. In accordance with the histogram, a strong argument for the use of criterion (6) is the global minimum ρ (10) ≈ 0.085 of the operating characteristicss ρ(p). Under the examined conditions, the minimum point also defines the best value p* = 10 of the order of the autoregressive model (1).

Fig. 1.
figure 1

A family of Berg spectral estimates of order p = 5, 10, and 20 (curves 1–3) against the background of the Schuster periodogram (curve 4) at duration τ = 10 ms.

Full size image
Fig. 2.
figure 2

Spectral power density of the signal at the output of the leveling filter (4) (curve 1) of order p =10 at duration τ = 10 ms and its spectral envelope (curve 2).

Full size image
Fig. 3.
figure 3

Working characteristics of the criterion ρ(p) (6) and {BIC} ϕ(p) at duration τ = 10 ms.

Full size image

The conclusions drawn are not trivial, if one comparea the behavior of the two operating characteristics: the proposed criterion ρ(p) and the Akaike information criterion in its modified variant of BIC (the Bayesian information criterion) [14]:

$$\upphi \left(p\right)\triangleq N\mathrm{ln}{\upsigma }_{p}^{2}+p.\mathrm{ln}N.$$

For τ = 10 ms, the dependence ϕ(ρ) is also provided as a scatter plot in Fig. 3, and the minimum of the dependence is reached at the point p = 7. This is a substantially different result in comparison with the order established above, p* = 10. As a result, in the case being studied, one may speak of the gain in precision of the hybrid technique in comparison with the Berg method when applying the Akaike criterion, defined as [3]:

$$B\left(p\right)=\frac{\uprho \left(p\right)-\uprho \left({p}^{*}\right)}{\uprho \left(p\right)}\cdot 100=\frac{\uprho \left(7\right)-\uprho \left(10\right)}{\uprho \left(7\right)}\cdot 100=\frac{0.12-0.085}{0.12}\cdot 100\simeq 29.2\%.$$

When the duration of a speech frame is reduced to τ = 5 ms, the gain increases to B(p) = 36.6%. In order to illustrate the obtained results, Fig. 4a shows the family of operating characteristics (histograms) ρ(p) of the hybrid technique for three observational durations. These characteristics are similar in nature, and a tendency is observed towards smoothing the base in neighborhoods of the minimum point p* = 10 s, as the duration τ of a frame increases. This fact is explained by the known universality of higher-order autoregressive models [1].

Fig. 4.
figure 4

A family of histograms of the operating characteristics (6) (a) and the dependencies (10) (b) at τ = 30, 10, and 5 ms (rows 1–3, respectively).

Full size image

Discussion of obtained results. The results of the second and final stage of the experimental studies can serve as additional reasons for the proposed hybrid technique of spectral analysis and its criterion (6). At this stage, the autoregressive model (1) was adapted to sample the observations by the Berg method in the same condition as in the first stage. In variant (3), the autoregressive model was also used in order to smooth the envelop of the Schuster periodogram (2). However the envelope of the SDP Gy(fm; p) was compared, according to its form in (6), not with the rectangular envelope G0 = const, but with the envelope \(\overline{G }\) y ( fm; p*) of the SDP at exit of the ideal smoothing filter (3) for which the vectorial equality ap = \({\mathbf{a}}_{10}^{\boldsymbol{*}}\) is fulfilled. Figure 5 presents a graph of the true SDP (1) against the same Schuster periodogram that is portrayed in Fig. 1. By analogy with (5), we write as the characteristics in this variant

Fig. 5.
figure 5

The true power spectral density of the signal at the smoothing filter at input (3) (curve 1) against the background of the Schuster periodogram (curve 2) at τ = 10 ms.

Full size image
$$\uprho \left(p\right)={M}^{-1}\sqrt{\left[\sum_{m=0}^{M-1}{\overline{G} }_{y}^{*}\left({f}_{m};p\right){\overline{G} }_{y}^{-1}\left({f}_{m};p\right)\right]}\sqrt{\left[\sum_{m=0}^{M-1}{\overline{G} }_{y}\left({f}_{m};p\right){\overline{G} }_{y}^{*-1}\left({f}_{m};p\right)\right]}$$
(10)

This is only a hypothetical variant, unrealizable in practice due to the definition of the spectral analysis problem under conditions of a priori uncertainty. There is interest in the comparison of dependence (10) with the characteristics (5) within the criterion used (6).

Figure 4b shows the family of histograms of the dependence of ρ(p) for the three durations of observations that were studied, from which follows the practically perfect analogy with the data of Fig. 4a, Hence, one may derive a conclusion on successful resolution of the small samples problem by using the proposed hybrid technique.

Conclusion. In the proposed hybrid technique of the spectral analysis of speech signals in the sliding window of observations mode, the Berg spectral estimate interacts with the Schuster periodogram estimate, although in practice they usually compete with each other. As a result, it was possible, in the hybrid technique, to consolidate the known advantages of the Berg method (speed of convergence and resolution capability by frequency) and Schuster (precision of representations of the thin structure of a speech signal in the frequency domain). The results of the experiment that was performed serve as proof.

The results obtained may be used in development of systems of digital spectral analysis of speech signals, as well as of signals of a speech-like structure for the fields of technical, economic, and biomedical diagnostic [6,7,8,9, 12].

Conflict of interest. The author declare no conflict of interest.