Introduction. The autoregression model of the speech signal is widely used in systems of automatic processing and transmission of speech over digital communication channels to encode speech information with radical data compression [1, 2]. In conditions of a priori uncertainty of the thin structure of the speech signal, the autoregression model is adapted to it in the mode of a sliding observation window [3, 4]. At the same time, the length τ of the window is strictly limited from above by the length of the intervals of stationarity of the speech signal [5]. As a result, in practice, the problem of small samples often arises [6, 7]. It manifests itself in the insufficient accuracy of the autoregressive model used, associated with an unreasonable choice of order [8]. The severity of this problem becomes especially obvious, given that in the theory there is no strict criterion of the accuracy of the autoregressive model, and the existing criteria, for example, Akaike, Schwartz, etc. [9], are not very suitable for application to the speech signal, since they are designed for homogeneous ergodic processes. Therefore, the task of measuring the accuracy index of the autoregression model on a sample of finite volume N = τF, where F is the sampling rate of observations.

The purpose of the study is to develop methodological foundations for optimizing autoregression models of the speech signal, taking into account its variability and features of the speaker's vocal tract [10, 11]. The article is written in the development of the results of previous works [2, 3].

Problem statement. Since the autoregressive model is directly related to the linear power spectrum envelope of the speech signal [12, 13], we will define this spectrum within the speech frame x(n), where n = 0, 1, …, N - 1. When choosing the method of spectral analysis, we will follow the logic of the work [7, 14] and give preference to the discrete Fourier transform as a kind of linear signal processing that is not related to the known effects of parametric estimates of the power spectrum: displacements and splitting of spectral lines in conditions of small sample observations. Based on the discrete Fourier transform, Schuster's periodogram [15]:

$${G}_{x}\left({f}_{m}\right)={\left(FM\right)}^{-1}{\left|\sum_{n=0}^{M-1}x\left(n\right)\mathrm{ exp} \left(- \mathrm{j }2\uppi nm{M}^{-1}\right)\right|}^{2}, m=\mathrm{0,1},\dots ,\mathrm{M}-1$$
(1)

defines an instantaneous power spectrum estimate (PSE) signal on a selected set of discrete frequencies fm = m∆f = mM-1F. If M = 2k > N , where k is some integer, the periodogram is designed for the use of fast Fourier transform algorithms [16]. In this case, only the first N of M samples of the time series {x(n)} on the right side of (1) are nonzero. For example, with the duration of the speech frame τ = 20–30 ms and the sampling rate F = 8 kHz (coordinated with the bandwidth of a standard telephone communication channel) where k = 10, the dimension will be M = 1024 ≫ N = 160–240.

According to the methodology of parametric spectral analysis, we define the autoregressive model in the frequency domain by the general expression [17]:

$${G}_{p}\left({f}_{m}\right)={\upsigma }_{p}^{2}T{\left|1-\sum_{n=0}^{M-1}{a}_{p}\left(i\right)\mathrm{ exp} \left(- \mathrm{j }2\uppi nm{M}^{-1}\right)\right|}^{2},$$
(2)

where T = F-1 ; \({\upsigma }_{p}^{2}\) is a scale factor; ap (i) is the ith element of the vector coefficient of the pth order linear autoregression. The parameters \({\upsigma }_{p}^{2}\) and ap (i) are determined from the sample {x(n)} according to the spectral analysis method used. For example, in the Berg method, for these purposes, a recursive computational procedure of the form [15]:

$$\begin{array}{c}{\forall }_{q}=\stackrel{-}{1,p};{ a}_{q}\left(i\right)={a}_{q-1}\left(i\right)+{{c}_{q}a}_{q-1}\left(r-i\right), i=\stackrel{-}{1,q}; {c}_{q}=\frac{2\sum_{n=q}^{N-1}{\upeta }_{q-1}\left(n\right){v}_{q-1}\left(n-1\right)}{\sum_{n=q}^{N-1}\left[{n}_{q-1}^{2}\left(n\right){v}_{q-1}^{2}\left(n-1\right)\right]};\\ {\upeta }_{q}\left(n\right)={\upeta }_{q-1}\left(n\right)+{{c}_{q}v}_{q-1}\left(n-1\right); {v}_{q}\left(n\right)={v}_{q-1}\left(n-1\right)+{{c}_{q}\upeta }_{q-1}\left(n\right), n=\mathrm{0,1},\dots ,N-1\end{array}$$
(3)

is used when it is initialized by the system of equations

$${\forall }_{n}<N; {v}_{0}\left(n\right)={\upeta }_{0}\left(n-1\right)=x\left(n\right).$$

The final values of the recursion (3) together with (2) determine the autoregression model of the spectral envelope \({\overline{G} }_{x}\left({f}_{m}\right)\) of the speech signal. The accuracy of this model depends on its order. Here, the scale multiplier \({\upsigma }_{p}^{2}\) does not play any role because it has nothing to do with the shape of the spectral envelope. Therefore, the task is to determine the accuracy index of the autoregressive model (2) depending on the order p and its subsequent measurement regime using a sliding window of observations {x(n)}.

Accuracy index. We rewrite expression (2) in the form of an inverse transformation

$${G}_{p}\left({f}_{m}\right)={\upsigma }_{p}^{2}T{\left|{A}_{p}\left(\mathrm{j}{f}_{m}\right)\right|}^{-2}$$

of the square of the modulus of the complex transmission coefficient Ap(j fm) of the pth order transverse filter

$${A}_{p}\left({\mathrm{j}f}_{m}\right)=-1\sum_{i=1}^{p}{a}_{p}\left(i\right)\mathrm{ exp} \left({-j2\uppi imM}^{-1}\right), m=\stackrel{-}{0;M-1}.$$
(4)

This filter is used to equalize in the frequency domain the envelope \({\overline{G} }_{x}\left({f}_{m}\right)\) of the Schuster periodogram (1), which in this case acts as a reference spectral sample [3]. The signal at the output of the leveling filter

$${G}_{y}\left({f}_{m};p\right)={\left|{A}_{p}\left(\mathrm{j}{f}_{m}\right)\right|}^{2} {G}_{x}\left({f}_{m}\right)={\upsigma }_{p}^{2}T\frac{{G}_{x}\left({f}_{m}\right)}{{G}_{p}\left({f}_{m}\right)}, m=\stackrel{-}{0;M-1}$$
(5)

determines the PSE of the sequence {y(n)} of impulses that excite the vocal tract of a test speaker within the framework of the inverse task of speech formation [18]: from the speech signal to its voice source.

Ideally, PSE (5) is a rectangular sequence K = 0.5FF0-1 of harmonic components with a shift between themselves by the frequency of the fundamental pitch F0 [19]. However, in practice, the shape of the spectral envelope \({\overline{G} }_{y}\left({f}_{m};p\right)\) can differ significantly from the rectangular one, primarily due to the imperfection of the autoregression model used (2). From this point of view, the order of the model is of fundamental importance. We optimize the value of p within the finite set (R-set) of alternatives p1 < p2 < … < pR.

The optimization is based on the obvious understanding: the higher the accuracy of the autoregressive model, the more pronounced in PSE (5) are the harmonic components and the closer the shape of their envelope \(\left\{{\overline{G} }_{y}\left({f}_{m};p\right)\right\}\) to the rectangular G0 = const will be for all m < M. When taking this into account, we will use as a criterion function a modified measure of COSH distance (COSH, hyperbolic cosine) ρ(p) with the property of scale invariance in the frequency domain [20]:

$$\begin{array}{c}\uprho \left(p\right)=\sqrt{\left[{M}^{-1}\sum_{m=0}^{M-1}{G}_{0}{\overline{G} }_{y}^{-1}\left({f}_{m};p\right)\right] \left[{M}^{-1}\sum_{m=0}^{M-1}{\overline{G} }_{y}\left({f}_{m};p\right){G}_{0}^{-1}\right]}-1\\ ={M}^{-1}\sqrt{\left[\sum_{m=0}^{M-1}{\overline{G} }_{y}^{-1}\left({f}_{m};p\right)\right] \left[\sum_{m=0}^{M-1}{\overline{G} }_{y}\left({f}_{m};p\right)\right]}-1\ge 0.\end{array}$$
(6)

Measure (6) is identically zero if the spectral envelope is equal to an arbitrary constant: \({\overline{G} }_{y}\left({f}_{m};p\right)={G}_{0}\forall m<M.\) As follows from the results of the work [3], it is in this version of the PSE (5) that the accuracy of the autoregression model (2) will be maximum. With an increase in ρ(p), the accuracy decreases. Measure (6) can then be considered an objective indicator of the accuracy of the generated autoregressive model. Hence follows this decision-making criterion in the problem of optimizing the model order on the set R of the alternatives under consideration:

$${p}^{*}=Arg \underset{\forall r\le R}{\mathrm{min}}\uprho {\left.\left(p\right)\right|}_{p={p}_{r}}.$$
(7)

The optimal model satisfies expression (2) when you select its order p ≤ pR according to rule (7). Practical implementation is reduced to the measurement of indicator (6) in the mode of the sliding window of observations.

Method for measuring the accuracy index. The structural diagram of the device for measuring the accuracy index (6) and optimizing the order of the autoregressive model (2) is presented in Fig. 1. The device contains series-connected elements: analog-to-digital ADC transformer; FB frame builder; the first unit of digital spectral analysis DSA1; blocks for aligning SEF and detecting ED the spectral envelope; blocks for calculating the trajectory of partial results BCPI and selecting the minimum MSS of the partial accuracy indicators; determination and reading of the results RR; two clock pulse generators CPG1, CPG2; the second block of DSA2. Red lines indicate many dimensional (dimension M) functional connections. Adjustable parameters of the device are the sampling period T of the speech signal and the length τ of the observation window.

Fig. 1.
figure 1

Block diagram of the device for measuring the accuracy indicator and the optimal order of the autoregressive model of a speech signal: ADC, analog-to-digital converter; FB, frame builder; DSA1, DSA2, the digital spectral analysis blocks; SEF, spectral envelope flattening block; ED, envelope detector; BCPI, block for calculating partial indicators; MSS, minimum selection scheme; RR, result reading block; CPG1, CPG2, the clock pulses generators.

Full size image

The operation of the device begins with the launch of generators that are necessary to synchronize the operation of individual elements of the computational process (3)–(6). With the help of the generators periodically (with a period of τ) the frames of the voice signal {x(n)} are formed and updated at the inputs of the blocks DSA1, DSA2. Accordingly, PSE (1), (2) will be periodically updated at their outputs. Moreover, according to (2), the model is updated simultaneously in R different variants {Gp(fm)} depending on the order p = pr for all r ≤ R. i.e. in accordance with the expression (5) there will be R variants of the spectral envelope \({\overline{G} }_{y}\left({f}_{m};p\right).\) To isolate them in the device one uses a spectral envelope detector. Its practical implementation works according to a recirculator scheme [16]:

$${\overline{G} }_{y}\left({f}_{m};p\right)=b{\overline{G} }_{y}\left({f}_{m}-\Delta f; p\right)+{G}_{y}\left({f}_{m};p\right), m=\stackrel{-}{1,M},$$
(8)

based on the procedure of accumulating or smoothing the speech signal in the frequency domain. The constant b on the right side of (8) affects the inertia of such accumulation. The quantitative index of inertia θ = ∆f/ln b must be consistent with the frequency F0 of the fundamental pitch of the speech signal. Hence in the first approximation we will write

$$b=\mathrm{exp}\left(-\Delta f/{F}_{0}\right)=\mathrm{exp}\left(-F/\left({MF}_{0}\right)\right)$$

and, for example, in the operating range of values F0 = 100–200 Hz [3], for F = 8 kHz, M = 1024 we obtain b = 0.93–0.97.

The main result of the operation of the device is that the indicator of the potentially achievable accuracy of the autoregression model (2) is superimposed in the R-channel scheme of the minimum selection block MSS (cf. Fig. 1) according to criterion (7) for selecting the optimal order. In accordance with the order p* the optimal autoregression model is read using the RR block {G*(fm)}.

The program and the results of the experiment. In the experiment, the pilot version of the device was used (cf. Fig. 1), implemented on the basis of the author's software module Phoneme Training.Footnote 1 The program is publicly available, its interface is described in detail in the work [11].

The objects of the experimental study were the signals of the six vowel sounds of Russian speech of the test speaker — the author of this article. Sufficiently long (2–3 s) duration of each signal was initially acquired for automatic sequential segmentation into a set of frames of duration τ = 30 ms with a time shift duration of 10 ms. At the sampling rate F = 8 kHz, the dimension of frame N was 240 samples. The shape of the observation window is rectangular. As a result, a representative database of L = 200–300 eponymous samples was formed for each vowel sound of speech. Next, for each sample the Schuster periodogram (1) with dimension M = 1024 and frequency increment Δf = 8000:1024 = 7.8125 Hz is calculated. Also the autoregressive model of the speech signal determines the spectral Berg estimates (2) for R = 40 alternative versions of order p = 10–50. In accordance with Levinson's recursion (3), the total complexity of the computational procedure is of the order of 3NpR = 3·240·50 = 36,000 elementary multiplication-addition operations on the interval of one speech frame. This volume with a margin corresponds to the performance of modern speech systems and technologies [21].

In the course of the experiment, for each of the 40 alternatives for b = 0.96, according to (8), estimates of the spectral envelope \({\overline{G} }_{y}\left({f}_{m};p\right)\) were obtained according to which, in accordance with criterion (7), we established the optimal value of the order p*, the corresponding autoregression model (2) and the indicator (6) of its accuracy. Then the results were averaged according to the results of L tests for each vowel phoneme of the test speaker. As a result, the relative error of experimental estimates [3] was ε = 1.65L–1/2 = 1.65(200–300)–1/2 with a confidence probability of 0.9 no more than 10–12%.

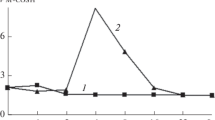
Figure 2 shows a graph of the operating characteristic ρ(p) of the proposed method (1)–(7) in relation to the vowel sound of speech "a". Vertical segments in the control points of this graph determine the boundaries of the confidence interval of the values of the indicator according to the results of multiple measurements. The curve ρ(p) has a single minimum p* = 32 that indicates the effectiveness of criterion (7) and, in general, of the acoustic measurement method. The achieved effect can be characterized by the value of the gain B in terms of the accuracy of the autoregressive model (2) due to the optimization of its order p* with respect to its standard value p = 10 [2]:

Fig. 2.
figure 2

Performance characteristic (with confidence limits according to the results of multiple measurements of the accuracy index) of the proposed method for measuring the accuracy of the autoregression model on the example of the vowel sound "a" of the speech of test speaker.

Full size image
$$B=\frac{\uprho \left(10\right)-{\uprho }^{*}}{\uprho \left(10\right)}100.$$
(9)

According to the data of Fig. 2 the value calculated by formula (9) was B = 79.48%.

To illustrate the obtained result, Fig. 3 presents the family of Berg spectral estimates for autoregressive models of order p = 10 (curves 1–3) versus Schuster's periodogram (curve 4) on the example of the same (typical) frame {x(n)} of the vowel sound "a". All curves are normalized by the average power to unity. The model of order p = 32 is optimal in terms of accuracy. Figure 4 shows the graph corresponding to order \({\overline{G} }_{y}\left({f}_{m};p\right)\) of the PSE (5) at the output of the leveling filter (4), as well as the envelope p = 32 (shown by the dashed line). Its shape is close to rectangular. The indicator (6) in this case ischaracterized by the minimum ρ* = ρ (32) ≈ 0.04 (cf. Fig. 2).

Fig. 3.
figure 3

Berg spectral estimates for the speech sound frame "a" of orders 32; 50 (curves 1–3) against the background of the Schuster periodogram (curve 4).

Full size image
Fig. 4.
figure 4

Graphs of the normalized power spectrum estimation (5) of the speech sound signal "a" at the output of the flattening filter (4) with order of the autoregression model.

Full size image

The conclusions drawn remain true for the rest of the vowel sounds of the test speaker's speech. At the same time, according to criterion (7), their optimal model order values can vary greatly from each other, for example, for the "o" sound we have p* = 22. At the same time, one can recognize in each case the winning values obtained from the score (9). A histogram of their distribution for vowel phonemes is shown in Fig. 5. Optimization made it possible to increase the accuracy of the autoregression model of the speech signal by more than 60%, depending on the speech sound of the test speaker and the specifics of his vocal tract. The maximum gain was achieved for the (Russian) upper vowel sounds "и", "y", "ы", which can be attributed to the features of a particular speaker.

Fig. 5.
figure 5

Histogram of distribution of the score B (9) by vowel phoneme signals.

Full size image

Discussion of the results obtained. Unlike Berg's method, Schuster's periodogram currently finds almost no independent application in the problems of spectral analysis of time series due to its inappropriate statistical characteristics [15]. Instead of Schuster's periodograms, for these purposes one uses the methods of Bartlett, Welch, and others, based on the effect of averaging periodogram PSE on samples of observations of large volume N ≫ M. However, according to the conditions of the task considered in this article, the exact opposite relation holds, which excludes statistical averaging and thereby limits the possibility of Shuster's periodogram as a PSE of the speech signal. Therefore, a natural question arises regarding the validity of expression (1) as a reference spectral sample. The answer to this is given in the results of the second, final, stage of experimental studies, within the framework of which the comparative efficiency of the method proposed above was studied in two options for specifying a spectral sample: in a practically implemented version of the periodogram (1), and also in a speculative (hypothetical) version of Welch

$${G}_{x}\left({f}_{m}\right)={I}^{-1}\sum_{i=1}^{I}{G}_{x}^{\left(i\right)}\left({f}_{m}\right), \forall m\le M-1,$$
(10)

with I-fold averaging of Schuster's partial periodograms on the observation interval with a total duration of τI. Here the symbol \({G}_{x}^{\left(i\right)}\left({f}_{m}\right)\) denotes the partial periodogram (1) within the boundaries of the ith speech frame {x(n)} of finite volume N.

The results obtained are presented in Fig. 6 as graphs of two spectral estimates of the phoneme "a" signal of the test speaker: Welch (10) with I = 240 (blue line) and Berg (red line) with the optimal order p* = 32 of the model (2). Berg's estimate was not averaged, i.e., one of the frames {x(n)} was used, however, it agrees well with the envelope average periodogram estimate.

Fig. 6.
figure 6

The average Schuster periodogram (blue line) compared with the Berg estimate of the order p = 32 (red line) at the input of the flattening filter (4).

Full size image

The PSE envelope at the output of the leveling filter in this case is no longer more uniform in comparison with the similar graph in Fig. 4. Moreover, its accuracy indicator (6) ρ(32) = 0.051 did not go beyond the corresponding confidence interval [0.02; 0.06] at the optimum point of the working characteristic (cf. Fig. 2). Hence we can conclude that the averaging of the Schuster periodogram according to the Welch method (10) gives almost nothing in terms of improving the accuracy of the formed autoregression model (2). Schuster's periodogram in this case plays the role of a non-final PSE, and a source of useful information regarding the fine structure of the speech signal. In this capacity, it is flawless due to the linearity of the processing of the speech signal during the discrete Fourier transform [7].

Conclusion. As a result of the study, an indicator of the accuracy of the autoregression model of the speech signal and a method for measuring it in the sliding window of observations mode of finite duration τ are proposed. Within the framework undertaken to optimize the autoregression model, the Berg spectral estimate and the Schuster periodogram mutually complement each other, although in practice they usually compete with each other [15, 17]. In this case, the optimization criterion was for the first time rigorously formulated in terms of the inverse problem of speech production. In contrast to criteria such as AIC, BIC, and the like [8, 9], the proposed criterion does not require synchronization of the observation window with the pitch period of the speech signal, which greatly weakens the precision of the problem due to a priori uncertainty [3].

The results obtained are intended for use in automatic processing and digital speech transmission systems with radical data compression based on linear prediction coefficients [1, 2].