1 Introduction

The dynamic behavior of rotors is of specific importance due to their dynamical complexity and very high speeds. Furthermore, considering the manufacturing defects and dynamics of the supports or deriving systems, relying on experimental analysis alone in design methods will be time-consuming and expensive. Therefore, many industrial companies and researchers have considered the application of analytical and numerical mathematical models with appropriate accuracy and comprehensiveness for a correct prediction of the rotor dynamic behavior.

Lu et al. [1] focused on the nonlinear behaviors of a dual-rotor system supported by a rolling element bearing. Yang et al. [2] established dynamic equations of defective ball bearing–rotor system based on the two local defect models. Khair Al-Solihat et al. [3] investigated the nonlinear dynamic and force transmissibility characteristics of a flexible shaft–disk rotor system supported by suspension system with nonlinear stiffness and damping. Bai et al. [4] presented a 6DOF rotordynamic model which includes the non-linearity of ball bearings and the bending vibration of rotor and offered an experimental rig for the research of the subharmonic resonance of the ball bearing–rotor system. Das et al. [5] used the Method of Multiple Scales (MMS) to carry out an analysis of a simplified system to get an idea about the dominant frequencies of excitation. Ji [6] employed a Jeffcott rotor with an additional magnetic bearing locating at the disc to investigate the effect of time delays on the non-linear dynamical behavior of the system. Ji et al. [7] also examined the effect of non-linear magnetic forces on the non-linear response of the shaft for the case of superharmonic resonance in this paper. Fu et al. [8] investigates the effects of interval uncertain parameters on the dynamic behaviors of a rotor system with a transverse breathing crack in the shaft.

In some special operating conditions, the proper assumption choice leading to correct results is not clear. Many investigations have been done on vibration analysis of rotors with constant angular velocity, while it is necessary to model the changes in rotor angular velocity in order to verify the results in the transient region. The best existing models consider the variations in angular velocity as a function of time, so this function is mainly assumed as linear or exponential [9, 10]. However, this method of modeling is only appropriate for rotors with operating speeds less than the first critical speed. In high-speed rotors, where the optimum operating speed is higher than the first critical speed, this modeling approach will lead to errors. In some cases, while passing through the rotor natural frequencies, the produced energy by the source will result in increased amplitudes of lateral vibration of the system and energy waste, rather than increasing the rotor speed [11, 12]. This fact describes the reason for considering an extra degree of freedom (torsion degree of freedom) for a correct prediction of the rotor vibrations and behavior through the critical speed.

A review of the literature shows that the previous studies have mainly focused on decoupled vibrations of the rotating systems (lateral or torsional vibrations). While fewer investigations have been performed on vibrations of coupled rotating systems (coupled lateral and torsional vibrations), where crack occurrence [13] on the rotor, gears [14], wear between the rotor and stator [15, 16], mass unbalances, or a combination of the factors [17] have been introduced as the root cause of such couplings. In this regard, Al-Bedoor performed nonlinear modeling and analysis of coupled lateral-torsional vibrations due to the mass unbalance of a 4° of freedom rotor, assuming a mass unbalance for the rotor [18]. Bernasconi studied torsional vibrations due to the coupling between lateral and torsional vibrations. He considered the rotational vibrations caused by the lateral ones. The coupling in his work was due to the two factors of mass unbalance and nonlinear gyroscopic effect. He indicated that the resulting coupling from the nonlinear gyroscopic effect is capable of producing torsional vibrations with a frequency twice the rotation frequency of the rotor [19]. Considering the gyroscopic effect on a 6-degree of freedom model, Shen not only achieved the same results as Bernasconi’s [19] but also extended his study to the ideal energy source case [20].

Many studies have been performed for estimation of the effective system parameters, such as stiffness and damping of the bearings, unbalance level and acceleration rate of passing through the system critical speeds [21,22,23]. According to such investigations, rotor nonlinear effects in combination with unbalance can lead to very different dynamic responses in the rotor, where various methods have been reported for passing through the bending mode. Of such examples, can be named the work by Zapomel. They studied the zero increase in rotor speed in bending mode and considered passing through the mode with altering the stiffness of the support [24]. In this approach, by reducing the stiffness before the critical speed and increasing it again after passing through this limit, stress and strains of the rotor are decreased, making it possible to use a lower power rate in the deriving system.

In another research, an increase in angular speed was performed by Gasch et al. for passing through bending mode and the amount of this increase was obtained from a relation depending on the mass unbalance. They also found out that since the speed of passing through the critical speeds increases with increased angular acceleration, the deformation due to passing through the mode decreases, and thus the rotor deforms less. Even a 4-time decrease or more have been reported for the maximum response amplitude through the bending mode. In addition, the beating phenomenon, implying a difference between the operating speed and critical speed, has been observed during passing through the critical speed. Moreover, increased angular acceleration in the rotor with minimum damping has been reported to be more effective [25,26,27,28].

Millsaps et al. proposed the variable angular acceleration approach as another method for reducing the amplitudes of rotor vibrations through the bending mode [29]. Sudden changes in angular acceleration were also forbidden in order to avoid the stimulation of torsional vibrations in the rotor. Unlike internal damping, application of external damping leads to reduced amplitudes of rotor vibrations through the bending mode [30], so that even the operating speed in rotors with greater external damping compared to internal damping, has been reported to be 80 percent greater than the critical speed.

Existing researches show various combinations of modeling with different assumptions. If the assumption combinations are proper and cohesive, the modeling results can be trusted. However, these models are limited to very specific operating conditions or simple rotor configurations, and due to assumptions not compatible with the real model and rotor structure, incorrect analysis can become huge. One of the most important and influential parameters in predicting the behavior of the rotor when passing the critical frequencies of the system is to consider nonlinear structural terms, which in all the works mentioned, has been neglected.

To place the present work in context of these recent publications, the authors have sought to construct a wide-ranging parameter study of the basic configuration of a high-order nonlinear rotating shaft. For this means, the system governing equations with nonlinear structural terms are derived by Lagrange method and solved numerically. In addition, effects of parameters such as the value and location of unbalanced mass and acceleration of passing through the mode are studied.

Furthermore, on the most previous studies, equations of motion in lateral directions are uncoupled from axial direction, which cause to solving these equations for 4 degree of freedom (2 displacement and 2 rotation in lateral directions). But here, all equations in 6 degree of freedom are coupled and solved together.

The significant contributions of this work are as follows:

  1. 1.

    Derivation and solution of the coupled higher-order nonlinear equations of motion for a flexible rotor system with acceleration.

  2. 2.

    Computational results for the several important parameters to determine their effect on vibration and LCO to provide the capability to assess the sensitivity of the results to such parameters in possible future experiments and flexible balancing procedures.

  3. 3.

    Demonstration that in the analysis of rotor-bearing systems, up-to 4th order of nonlinearity should be considered in kinetic and strain energy equations to obtain correct results, especially when the rotor passes through critical speeds.

2 Theoretical/computational model

2.1 Formulation

In this Section, dynamic modeling of a nonlinear rotor due to inertia with linear supports has been studied. For this means, first, kinetic and potential energies of the system are derived and thereafter, equations of motion of a nonlinear elastic rotor are obtained by Lagrange equations and solved with FEM. Note that the contents of this section (Theoretical/computational Model) have already been published in an article previously written by the authors [31]. But for a better understanding and easier access for the readers of this article, it is repeated here again.

2.1.1 Kinetic energy derivation

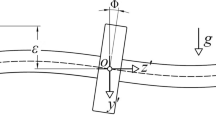
Since the inertia matrix is defined more easily in the main inertia axes, the angular velocity for obtaining the rotational kinetic energy is also calculated in this coordinate system. In fact, the inertia matrix includes moments of inertia and inertia products, which changes as the coordinate position with respect to the body differs. It can be shown that there is a unique position of the axes for which, the inertia products are zero and moments of inertia remain constant, where the inertia matrix, in this case, is diagonal. The axes of the coordinates system in which the inertia products are zero are called the main axes. In order to calculate the kinetic energy, the center of gravity of the model should be specified. As shown in Fig. 1, rotor system consists of flexible shaft on flexible bearings with springs and dampers. In order to find the main inertia axes, the coordinates system should be translated and rotated according to Table 1 and as indicated in Fig. 2.

Fig. 1
figure 1

Rotor system figure

Full size image
Table 1 Derivation method for main axes coordinates system
Full size table
Fig. 2
figure 2

Rotation and translation of the axes

Full size image

In order to calculate the rotational kinetic energy, the angular velocity vector in inertia coordinates is defined as below:

$$\omega = R_{\psi } \left[ {R_{\theta } \dot{r}_{\varphi } + \dot{r}_{\theta } } \right] + \dot{r}_{\psi }$$
(1)

In the above relation, \(r_{\varphi } ,r_{\theta } ,r_{\psi }\) are defined as:

$$\begin{aligned} r_{\varphi } = & \left[ {\begin{array}{*{20}c} \varphi & 0 & 0 \\ \end{array} } \right]^{T} ,r_{\theta } = \left[ {\begin{array}{*{20}c} 0 & \theta & 0 \\ \end{array} } \right]^{T} ,r_{\psi } \\ = & \left[ {\begin{array}{*{20}c} 0 & 0 & \psi \\ \end{array} } \right]^{T} \\ \end{aligned}$$
(2)

and:

$$R_{\psi } = \left[ {\begin{array}{*{20}c} {\cos (\psi )} & {\sin (\psi )} & 0 \\ { - \sin (\psi )} & {\cos (\psi )} & 0 \\ 0 & 0 & 1 \\ \end{array} } \right],R_{\theta } = \left[ {\begin{array}{*{20}c} {\cos (\theta )} & 0 & { - \sin (\theta )} \\ 0 & 1 & 0 \\ {\sin (\theta )} & 0 & {\cos (\theta )} \\ \end{array} } \right],R_{\varphi } = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 \\ 0 & {\cos (\varphi )} & {\sin (\varphi )} \\ 0 & { - \sin (\varphi )} & {\cos (\varphi )} \\ \end{array} } \right]$$
(3)

With substituting Eqs. (3) and (2) in (1), the angular velocity vector in inertia coordinates is defined as below:

$$\omega = \left\{ {\begin{array}{*{20}c} {\omega_{1} } \\ {\omega_{2} } \\ {\omega_{3} } \\ \end{array} } \right\}$$
(4)

in which:

$$\omega_{1} = \left( {1 - \frac{{\theta^{2} }}{2}{\mkern 1mu} } \right)\dot{\varphi }\cos (\psi ) + \dot{\theta }\sin (\psi )$$
(5)
$$\omega_{2} = \dot{\theta }\cos (\psi ) - \dot{\varphi }\left( {1 - \frac{{\theta^{2} }}{2}{\mkern 1mu} } \right)\sin (\psi )$$
(6)
$$\omega_{3} = \theta \dot{\varphi } + \dot{\psi }$$
(7)

In order to calculate the translational kinetic energy, the velocity of the center of gravity should be obtained. The position of center of gravity and unbalanced mass is defined in form of:

$$r_{{\text{c}}} = \left[ {\begin{array}{*{20}c} u & v & w \\ \end{array} } \right]^{{\text{T}}}$$
(8)
$$r_{u} = r_{{\text{c}}} {\mathbf{ + }}R_{\varphi }^{T} R_{\theta }^{T} R_{\psi }^{T} e_{\varepsilon }$$
(9)

where

$${\mathbf{e}}_{\varepsilon } = \left[ {\begin{array}{*{20}c} {\varepsilon \cos (\alpha )} & {\varepsilon \sin (\alpha )} & 0 \\ \end{array} } \right]^{{\text{T}}}$$
(10)

in which \(\varepsilon\) and \(\alpha\) are the mass unbalance radius and angle. The kinetic energy of the system is resulted from the following relation.

$$T = T_{t} + T_{r}$$
(11)

where \(T_{t} ,T_{r}\) refer to the rotational and translational kinetic energies, respectively, computed from Eqs. (12) and (13).

$$T_{r} = \int {\frac{1}{2}\omega^{T} J\omega } {\text{d}}z$$
(12)
$$T_{t} = \int {\frac{1}{2}m(\dot{r}_{c} )^{2} } {\text{d}}z + \frac{1}{2}m_{u} (\dot{r}_{u} )^{2}$$
(13)

With \(m\) being the mass per length, \(m_{u}\) the unbalanced mass and J the rotational moment of inertia matrix per length about the main axes defined as:

$${\mathbf{J}} = \left[ {\begin{array}{*{20}c} {Jt} & 0 & 0 \\ 0 & {Jt} & 0 \\ 0 & 0 & {Jp} \\ \end{array} } \right]$$
(14)

So, the rotational and translational kinetic energies may be written as follows:

$$\begin{gathered} T_{r} = \frac{1}{2}\int {\left[ {J_{p} } \right.} (\dot{\psi } + \theta \dot{\phi })^{2} + J_{t} (\cos (\psi )\dot{\phi } + \sin (\psi )\dot{\theta })^{2} + J_{t} (\cos (\psi )\dot{\theta } - \sin (\psi )\dot{\phi })^{2} \hfill \\ \left. { + J_{t} \sin (\psi )(\cos (\psi )\dot{\theta } - \sin (\psi )\dot{\phi })\theta ^{2} \dot{\phi }} \right] - J_{t} \cos (\psi )(\cos (\psi )\dot{\phi } + \sin (\psi )\dot{\theta })\theta ^{2} \left. {\dot{\phi }} \right]{\text{d}}z \hfill \\ \end{gathered}$$
(15)
$$T_{t} = \int {\left[ {\frac{{m\,\dot{u}^{2} }}{2} + \frac{{m\,\dot{v}^{2} }}{2} + \frac{{m\,\dot{w}^{2} }}{2}} \right]} {\text{d}}z + \frac{1}{2}m_{u} \left[ {\dot{u}_{u}^{2} + \dot{v}_{u}^{2} + \dot{w}_{u}^{2} } \right]$$
(16)

In the above equations, the dot over the variables denotes the derivative with respect to time. Also, Jp and Jt are moments of inertia per rotor length. As shown in Eqs. (15) and (16), the nonlinear terms of kinetic energy are considered up to 4th order, which makes the results of this research more accurate. More details and reasons about considering these higher order terms are provided in Sect. 3.6.

2.1.2 Potential energy derivation

In order to extract potential energy of the rotor, displacement field are as below, assuming axial and torsional rigidity of rotor:

$${\mathbf{u}} = \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u(z,t)} \\ {v(z,t)} \\ { - x\theta (z,t) + y\varphi (z,t)} \\ \end{array} } \right\}$$
(17)

Based on the Von-Karman large deflection relations governing the strain in Euler–Bernoulli beam, the strains created in beam can be expressed as follows:

$$\varepsilon_{zz} = \frac{{\partial {\mkern 1mu} w}}{\partial Z} + \frac{1}{2}\left[ {\left( {\frac{{\partial {\mkern 1mu} u}}{\partial Z}} \right)^{2} + \left( {\frac{{\partial {\mkern 1mu} v}}{\partial Z}} \right)^{2} } \right]$$
(18)

By placing Eq. (17) in Eq. (18) with considering Euler–Bernoulli assumption (φ = –∂v/∂z and θ = ∂u/∂z):

$$\varepsilon_{zz} = - y\varphi^{\prime} + x\theta^{\prime} + \frac{1}{2}\left[ {\varphi^{2} + \theta^{2} } \right]$$
(19)

Potential energy due to elasticity of rotor can be obtained as follow:

$$\begin{gathered} U = \frac{E}{2}\int_{0}^{l} {\int_{A}^{{}} {\varepsilon_{zz}^{2} {\text{d}}A{\text{d}}z = } } \hfill \\ \frac{E}{2}\int_{0}^{l} {\int_{A}^{{}} {\left( { - y\varphi^{\prime} + x\theta^{\prime} + \frac{1}{2}\left[ {\varphi^{2} + \theta^{2} } \right]} \right)^{2} {\text{d}}A{\text{d}}z} } \hfill \\ \end{gathered}$$
(20)

At the end potential energy obtained as follow:

$$U = \frac{EI}{2}\int_{0}^{l} {\left[ {\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}z}}} \right)^{2} + \left( {\frac{{{\text{d}}\varphi }}{{{\text{d}}z}}} \right)^{2} } \right]} {\text{d}}z + \frac{EA}{2}\int_{0}^{l} {\left[ {\frac{{\theta^{4} }}{4} + \frac{{\varphi^{4} }}{4} + \frac{{\varphi^{2} \theta^{2} }}{2}} \right]} {\text{d}}z$$
(21)

As seen in Eq. (21), the nonlinear terms of strain energy are considered up to 4th order too (like kinetic energy). Always, no more than second order of nonlinearity terms are considered in researches of Rotordynamics. The reason for considering these higher order terms is explained in Sect. 3.6.

Also, the work done by deriving system torque can be obtained as follow:

$$W = T_{a} \psi$$
(22)

where \(T_{a}\) is applied torque by deriving system.

2.2 Finite element solution

In order to solve the problem by finite element method, a standard element with two nodes is considered, so that each node contains six degrees of freedom. According to this issue, the rotor is divided to 10 elements (Fig. 3) and the displacement vector on each element can be expressed according to the following equation.

$$q^{e} (t) = \left[ {u^{r} ,v^{r} ,w^{r} ,\varphi^{r} ,\theta^{r} ,\psi^{r} ,u^{s} ,v^{s} ,w^{s} ,\varphi^{s} ,\theta^{s} ,\psi^{s} } \right]^{T}$$
(23)
Fig. 3
figure 3

Rotor FEM model

Full size image

The terms related to the displacement field can be expressed in terms of the displacement of the nodes and the shape functions according to the following equations.

$$u(z,t) = {\mathbf{N}}_{u} (z)\left[ {u^{r} ,\theta^{r} ,u^{s} ,\theta^{s} } \right]^{T}$$
(24)
$$v(z,t) = {\mathbf{N}}_{v} (z)\left[ {v^{r} ,\varphi^{r} ,v^{s} ,\varphi^{s} } \right]^{T}$$
(25)
$$w(z,t) = {\mathbf{N}}_{w} (z)\left[ {w^{r} ,w^{s} } \right]^{T}$$
(26)
$$\psi (z,t) = {\mathbf{N}}_{\psi } (z)\left[ {\psi^{r} ,\psi^{s} } \right]^{T}$$
(27)

So that the shape functions can be expressed as follows:

$${\mathbf{N}}_{u} (z) = \left[ {1 - 3\xi^{2} + 2\xi^{3} ,(\xi - 2\xi^{2} + \xi^{3} )l_{e} ,3\xi^{2} - 2\xi^{3} ,(\xi^{3} - \xi^{2} )l_{e} } \right]$$
(28)
$${\mathbf{N}}_{v} (z) = \left[ {1 - 3\xi^{2} + 2\xi^{3} ,( - \xi + 2\xi^{2} - \xi^{3} )l_{e} ,3\xi^{2} - 2\xi^{3} ,(\xi^{2} - \xi^{3} )l_{e} } \right]$$
(29)
$${\mathbf{N}}_{w} (z),{\mathbf{N}}_{\psi } (z) = \left[ {1 - \xi ,\xi } \right]$$
(30)

2.3 Derivation of equations of motion

Equations of motion of a vibrating system can be defined in different coordinate systems. In order to describe the motion of an n-degree of freedom system, n-independent coordinates are required, to a set of which is referred as the generalized coordinate, indicated by qi, where i = 1, 2,…,n. Using Lagrange equation, equations of motion of a vibrating system can be derived in terms of energy parameters. Lagrange equations for an n-degree of freedom system are as below:

$$\frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{\partial T}{{\partial \dot{q}_{i} }}} \right) - \frac{\partial T}{{\partial q_{i} }} + \frac{\partial U}{{\partial q_{i} }} - \frac{\partial W}{{\partial q_{i} }} = 0$$
(31)

and equations of motion of the concerned system may be written in matrix form:

$${\mathbf{M}}^{e} {\ddot{\mathbf{q}}}^{e} {\mathbf{ + C}}^{e} {\dot{\mathbf{q}}}^{e} {\mathbf{ + K}}^{e} {\mathbf{q}}^{e} {\mathbf{ = F}}_{n}^{e}$$
(32)

where \({\mathbf{q}}^{e}\) represents the developed vector of unknowns, \({\mathbf{M}}^{e}\) is the mass matrix for an element, \({\mathbf{K}}^{e}\) is stiffness element matrix, \({\mathbf{C}}^{e}\) is damping matrix and \({\mathbf{F}}_{n}^{e}\) is nonlinear force vector. Stiffness and damping of the bearing will be added to corresponding rows and columns of stiffness and damping matrices. All nonlinear expressions that are ultimately derived from the Lagrange equation are presented in the force vector. Due to its very long components, it cannot be written in the text of the article.

2.4 Validation of computational model

To validate the formulation of the present work, the results of rotor vibrations are compared with the results from a well-known rotordynamic software, Dyrobes, which offers complete rotordynamic analysis, vibration analysis, bearing performance, and balancing calculations based on Finite Element Analysis [32].

For this reason, a constant rotation speed (ω0 = 1000 rpm) is applied without any torque, and vibration time responses are compared for a rotor system with the specification of Table 2 in the next section. The lateral vibration of the first rotor node in x and y-directions are compared in Figs. 4 and 5 for the first 0.5 s. The figures show excellent agreements between results.

Table 2 Rotor specifications
Full size table
Fig. 4
figure 4

Vibration time history of the rotor first node displacement in x-direction

Full size image
Fig. 5
figure 5

Vibration time history of the rotor first node displacement in y-direction

Full size image

3 Results

3.1 Rotor time responses

Results of the vibration for a rotating cylindrical flexible shaft with the specification of Table 2 are plotted in this section. The material of the shaft is aluminum and the stiffness and damping coefficient of the both bearings in both x and y directions assumed 100,000 N/m and 20 Ns/m. Support stiffness is considered low, because with this degree of stiffness, better figures are plotted and critical speeds are better compared together.

The mass unbalance denoted by mu = 3 gr is also situated at a radius of (ε) from the shaft centerline, on the position (zu) of the second node (see Fig. 3). Note that the applied torque on the shaft is 50*Jp (Jp is the moment of inertia of rotor section), which causes to rotor angular acceleration of α = 50 rad/s2.

The first 3 critical speeds of the shaft are calculated and shown in Table 3 in rad/s. The first and second critical speeds are related to the first (cylindrical) and second (conical) rigid critical speeds and the third one is the first flexible critical speed (bending). The shape of the deformed centerline of the rotor about these critical speeds is shown in Figs. 6, 7 and 8.

Table 3 Rotor calculated critical speeds
Full size table
Fig. 6
figure 6

Rotor centerline about 1st critical speed

Full size image
Fig. 7
figure 7

Rotor centerline about 2nd critical speed

Full size image
Fig. 8
figure 8

Rotor centerline about 3rd critical speed

Full size image

It should be noted that when the rotor is working near the first critical speed, the centerline of the shaft will make a cylinder in the space, which is because of the first mode shape. Near the second critical speed, the centerline will make two cones in the space, which is because of the second mode shape. these 2 first modes are called rigid modes of rotor because the bending of the shaft is negligible in these rotational speeds.

But when the rotor is working near the third critical speed, the shaft is no more rigid and the shaft centerline will have the sinusoidal deformation. this mode shape is called the first bending mode shape of the rotor.

Vibrations and time response history graphs of several typical nodes of the shaft are plotted from Figs. 9, 10, 11, 12, 13, 15, 16, to show the effects of passing through the first 3 critical speeds. In Fig. 9 the first 30 s time response of the first node is plotted in x-direction. Increasing the amplitude of vibration due to passing the 3 calculated critical speeds can be seen clearly in this figure, in which the maximum vibration amplitude of the first node (at first bearing) is increased from the 1st to the 3rd critical speed, up to more than 1 mm. Note that vibration of the rotor is in the form of Limit Cycle Oscillation (LCO) which is the property of nonlinear problems (whether for beams, plates or other mechanical elements [33,34,35]) compared to linear problems, in which the amplitude of vibration is increased continuously in resonance situation.

Fig. 9
figure 9

Vibration time history of the rotor first node displacement in x-direction

Full size image
Fig. 10
figure 10

Vibration time history of the rotor end node displacement in x-direction

Full size image
Fig. 11
figure 11

Vibration time history of the rotor central node displacement in x-direction

Full size image
Fig. 12
figure 12

Vibration time history of the rotor first node rotation angle in x-direction

Full size image
Fig. 13
figure 13

Vibration time history of the rotor central node rotation angle in x-direction

Full size image

In Fig. 10 the first 30 s time response of the last node is plotted in the x-direction. Increasing the amplitude of vibration due to passing the 3 calculated critical speeds can be seen clearly in this figure too. The little difference between Figs. 9 and 10, is because of the different distances of unbalanced mass from the first and last nodes. The difference between these two figures is about t = 17 s. The amplitude of the first node vibration is zero, but the last node is not. It's due to changing of the shape modes when rotational speed increases from second critical speed to third critical speed.

In the second mode shape (Fig. 7), at a certain moment, one end of the rotor is above the bearing’s axis and another end of the rotor is under this axis. But in the third mode shape (Fig. 8), both ends of the rotor are on one side of the bearing’s axis. It means when the rotor speeds up from second to third critical speed, one end of the rotor should pass from the bearings axis and goes to another side. It means one side of the rotor will experience zero amplitude of vibration during this displacement.

It can be concluded the end of the rotor, which is closer to unbalanced mass (closer to unbalance forces) will have zero vibration amplitude. For example, in this case, the unbalanced mass is located on the second node, so the first node amplitude of vibration is zero in t = 17 s.

this phenomenon also can occur from the first to the second mode, but usually, these modes are close to each other and this phenomenon is not visible.

In Fig. 11 the first 30 s time response of the 6th node (central node) is plotted in the x-direction. The interesting difference in Fig. 11 from the previous figures is that the effects of 1st and 3rd critical speeds are clear in this figure, but 2nd critical speed (about t = 6 s) has no effect on the vibration of this node. The reason is that the amplitude of the central node in the 2nd mode shape (conical shape) is zero and this node does not sense passing through this critical speed due to the symmetry of this rotor system. In the flexible balancing procedure, it should be noted that the proximity sensors at the central point cannot be used for balancing the second critical speed of symmetric rotors.

In Figs. 12 and 13, vibration of the shaft rotation angle in x-direction (φ) is plotted for the first and central node. Time response history of this angle for first node is like the displacement time response history in x-direction (Fig. 9) and effects of all 3 critical speeds are visible. But this angular vibration figure for central node (Fig. 13) is completely different from time response of displacement for this node (Fig. 11). In Fig. 11, passing through 2nd critical speed has no Effects on displacement vibration, but In Fig. 13, passing through 1st and 3rd critical speeds is ineffective.

This difference can be interpreted in this way that for symmetric rotor systems, the shape of first and third modes do not rotate the central node in x (or y) direction and just make some displacements, but the shape of second mode just make some rotations in the central node without any displacements in both directions.

Vibrations in the y-direction are as like as in x-direction, just with the phase difference of π/2, because of the same properties of the rotor system in both x and y-direction. So, the figures on y-direction are not repeated again here for the purpose of summarizing this section.

Rotor time responses in the z-direction (w) are plotted below. With the assumption of the rotor rigidity in axial and rotational directions, Fig. 14 shows the displacement of all nodes in the z-direction. The rotor has no displacement and vibration in this direction due to the absence of any axial load. In this model, due to the absence of opposite torques on the shaft, and the absence of axial forces, it can be assumed that the rotor is rigid in axial and rotational directions. In another separate future article by authors, due to the presence of these forces and torques, flexibility in torsional and axial directions has been considered.

Fig. 14
figure 14

Time history of the rotor displacement in z-direction

Full size image

In Fig. 15, the time response of the rotational angle (ψ) is plotted for all nodes. This figure is in the form of a parabolic chart due to applied torque, which causes angular acceleration.

Fig. 15
figure 15

Time history of rotational angle in z-direction

Full size image

Figure 16 shows the time response history of rotational speed (ω), which is increased in a straight line with a slope of angular acceleration (α = 50). After 30 s, rotation speed is increased from 0 to about 1500 rad/s and rotor passed through first 3 critical speeds. Note that a little distortion is observed when rotor passed the 3rd critical speed.

Fig. 16
figure 16

Time history of the rotational speed in z-direction

Full size image

3.2 Effects of unbalanced mass value (mu)

In this section, the effects of unbalanced mass value on the rotor vibration and amplitudes of limit cycle oscillation are studied for the same rotor with the specification of Table 2, just with variable mu = 1, 3, 6 and 20 gr. In these figures just the maximum points of vibration are plotted for a better observation. Note that in this research, more emphasis has been placed on presenting a new model with high accuracy for analyzing the behavior of the rotor in passing through critical speeds. Therefore, in behavioral analysis researches, some results may not have practical applications.

In Fig. 17 the vibration of the rotor first node is plotted for different unbalanced mass values. By increasing mu from 1 to 3 gr, the amplitude of vibration is increased in passing through critical speeds (blue and green lines). When mu is increased to 6 gr (yellow line), the amplitude of vibration is increased again and the rotor cannot pass through the 3rd critical speed. Applied torque is not enough to pass 3rd critical speed and rotor can just to pass through 1st and 2nd critical speeds. So, rotor after the 3rd critical speed will have a limit cycle oscillation with constant amplitude and rotation speed. Since this study tries to show the importance of considering higher order nonlinear terms in calculations related to rotor dynamics, for an aluminum shaft 1.2 m long, the deformation of about 3 mm cannot be very critical for the resistance of the shaft.

Fig. 17
figure 17

Vibration time history of the rotor first node displacement in x-direction

Full size image

This phenomenon occurs because of increasing the energy dissipation of the rotor system. Under certain conditions, the structural vibration of the system, may act like an energy sink, i.e. instead of the drive energy being spent to increase the drive speed, a major part of that energy is diverted to vibrate the structure. This is formally known as the Sommerfeld effect. In such cases, the energy supplied by the source to the flexible spinning shaft is spent to excite the bending modes rather than to increase the drive speed.

By increasing the mu again up to 20 gr (red line), the amplitude of oscillations is increased again but the rotor can just pass the first critical speed, which means the energy dissipation of the system is very high.

In Fig. 18, the vibration of the rotating angle in the x-direction (φ) for the first node is shown. The effects of increasing the mu are like Fig. 17, in which the more unbalanced mass value causes a higher amplitude for angular vibration in the x-direction. The only difference is that the maximum amplitude for rotor with mu = 6 gr (which cannot pass the 3rd critical speed) is higher than the maximum amplitude for rotor with mu = 20 gr (which cannot pass the 2nd critical speed), which maybe is due to a bigger effect of 2nd mode shape (comparing to 3rd mode shape) on the angle of the first node in the x-direction (φ1).

Fig. 18
figure 18

Vibration time history of the rotor first node rotation angle in x-direction

Full size image

Rotor rotation angle and rotation speed in the z-direction are plotted in Figs. 19 and 20. In Fig. 19 it is shown that when the rotor cannot pass critical speeds, the parabolic form of rotation angle time history changes to a straight line in 3rd critical speed (yellow line) and 2nd critical speed (red line). It means the rotation of the rotor in z-direction will change from constant rotation acceleration to constant rotation speed. This figure indicates the amount of rotor rotation in Radians and if divided by 2π, cycles of rotor rotation can be calculated. It should be noted that in some rotodynamic systems, the number of rotor rotation cycles can be important.

Fig. 19
figure 19

Time history of the rotation angle in z-direction

Full size image
Fig. 20
figure 20

Time history of the rotation speed in z-direction

Full size image

Figure 20 clearly demonstrated that when the rotor with mu = 20 gr cannot pass 2nd critical speed (red line), the rotation speed will be held constant and rotor will have limit cycle oscillation (LCO). This also happened for rotor with mu = 6 gr at 3rd critical speed (yellow line). Note that a little distortion is observed again when rotor with mu = 3 gr passed the 3rd critical speed (green line).

3.3 Effects of radius of unbalances mass (ε)

In this section, the effects of unbalanced mass radius on the rotor vibration and amplitudes of limit cycle oscillation are studied for the same rotor with the specification of Table 2, just with variable ε = 3, 5, 10 and 25 mm and mu = 20 gr. In these figures just the maximum points of vibration are plotted for a better observation.

In Fig. 21 the vibration of the rotor first node is plotted for different unbalanced mass radiuses. By increasing ε from 3 to 5 mm, the amplitude of vibration is increased in passing through critical speeds (blue and green lines). When ε is increased to 10 mm (yellow line), the amplitude of vibration is increased again and the rotor cannot pass through the 3rd critical speed. This phenomenon occurs because of increasing the energy dissipation of the rotor system. Applied torque is not enough to pass 3rd critical speed and rotor can just to pass through 1st and 2nd critical speeds. So, rotor after the 3rd critical speed will have a limit cycle oscillation with constant amplitude and rotation speed. By increasing the ε again up to 25 mm (red line), the amplitudes of oscillations are increased again but the rotor can just pass the first critical speed, which means the energy dissipation of the system is very high.

Fig. 21
figure 21

Vibration time history of the rotor first node displacement in x-direction

Full size image

In Fig. 22, the vibration of the rotating angle in the x-direction (φ) for the first node is shown. The effects of increasing the mu are like Fig. 18, in which the more unbalanced mass radius causes a higher amplitude for angular vibration in the x-direction. The only difference is that the maximum amplitude for rotor with ε = 10 mm (which cannot pass the 3rd critical speed) is higher than the maximum amplitude for rotor with ε = 25 mm (which cannot pass the 2nd critical speed), which maybe is due to a bigger effect of 2nd mode shape (comparing to 3rd mode shape) on the angle of the first node in the x-direction (φ1).

Fig. 22
figure 22

Vibration time history of the rotor first node rotation angle in x-direction

Full size image

Rotor rotation angle and rotation speed in the z-direction are plotted in Figs. 23 and 24. In Fig. 23 it is shown that when the rotor cannot pass critical speeds, the parabolic form of rotation angle time history changes to a straight line in 3rd critical speed (yellow line) and 2nd critical speed (red line). It means the rotation of the rotor in z-direction will change from constant rotation acceleration to constant rotation speed.

Fig. 23
figure 23

Time history of the rotation angle in z-direction

Full size image
Fig. 24
figure 24

Time history of the rotation speed in z-direction

Full size image

Figure 24 clearly demonstrated that when the rotor with ε = 25 mm cannot pass 2nd critical speed (red line), the rotation speed will be held constant and rotor will have limit cycle oscillation (LCO). This also happened for rotor with ε = 10 mm at 3rd critical speed (yellow line). Note that a little distortion is observed again when rotor with ε = 5 mm passed the 3rd critical speed (green line).

3.4 Effects of applied torque

In this section, the effects of applied torque on the rotor vibration and amplitudes of limit cycle oscillation are studied for the same rotor with the specification of Table 2, with variable α = 30, 50, 100 and 150 rad/s2 (it is assumed that applied torque equals to α*Jp), mu = 6 gr and ε = 25 mm. In these figures just the maximum points of vibration are plotted too for a better observation. In this paper, for simplicity, the motor is assumed to be an ideal source that applies a constant torque to the system. In a separate future article by authors, the issue of non-ideal source will be considered and its effects on rotor performance will be investigated.

In Fig. 25 the vibration of the rotor first node is plotted for different applied torques. By increasing α from 30 to 50 rad/s2, the amplitudes of vibrations decrease slightly in passing through 1st and 2nd critical speeds (blue and green lines) and rotor negotiated critical speeds earlier due to increasing the angular acceleration. In both cases, rotor cannot pass through 3rd critical speed and just two peaks are observed. When α is increased to 100 rad/s2 (yellow line), the amplitude of vibration a little is decreased again and the rotor cannot pass through the 3rd critical speed yet.

Fig. 25
figure 25

Vibration time history of the rotor first node displacement in x-direction

Full size image

By increasing the α up to 150 rad/s2 (red line), the amplitudes of oscillations are decreased again, the rotor can pass the 3rd critical speed (3 peaks are observed) and then rotor cannot pass through the 4th critical speed.

In Fig. 26, the vibration of the rotating angle in the x-direction (φ) for the first node is shown. The effects of increasing the α are like Fig. 25, in which the more applied torque causes a lower amplitude for angular vibration in the x-direction.

Fig. 26
figure 26

Vibration time history of the rotor first node rotation angle in x-direction

Full size image

Rotor rotation angle and rotation speed in the z-direction are plotted in Figs. 27 and 28. In Fig. 27 it is shown that when the rotor cannot pass critical speeds, the parabolic form of rotation angle time history changes to a straight line in 3rd critical speed (yellow, green and blue lines) and 4th critical speed (red line). It means the rotation of the rotor in z-direction will change from constant rotation acceleration to constant rotation speed.

Fig. 27
figure 27

Time history of the rotation angle in z-direction

Full size image
Fig. 28
figure 28

Time history of the rotation speed in z-direction

Full size image

Figure  28 clearly demonstrated that when the rotor with α = 150 rad/s2 cannot pass 4th critical speed (red line), the rotation speed will be held constant and rotor will have limit cycle oscillation (LCO). This also happened for rotor with α = 30, 50 and 100 rad/s2 at 3rd critical speed (yellow, green and blue lines). Note that a little distortion is observed when rotor with α = 150 rad/s2 passed the 3rd critical speed (red line).

To investigate the behavior of the rotor while decelerating, other physical factors must be added to the problem that cause negative angular acceleration. But due to the length of the article, the authors prefer to study this phenomenon in the future papers.

3.5 Effects of unbalanced mass position (zu)

In this section, the effects of changing the position of unbalanced mass on z axis on the rotor vibration and amplitudes of limit cycle oscillation are studied for the same rotor with the specification of Table 2, with different positions of unbalanced mass (zu). In these figures, just the maximum points of vibration are plotted too for a better observation.

In Fig. 29 the vibration of the rotor first node is plotted for different zu. By changing this position from 1st to 6th (central) node (see Fig. 2), the amplitudes of vibrations are decreased first and then increased passing through critical speeds. The best case with the minimum amplitude is when this mass position is on the 3rd node. Just when the unbalanced mass is on the first node, the rotor cannot pass through the 3rd critical speed.

Fig. 29
figure 29

Vibration time history of the rotor first node displacement in x-direction

Full size image

Note that when the unbalanced mass is on the central node, passing through 2nd critical speed has no effect on the amplitude of oscillations (black line). Because the unbalanced forces on the central node of rotor do not excite the 2nd mode shape.

In Fig. 30, the vibration of the rotating angle in the x-direction (φ) for the first node is shown. The effects of changing the position of unbalanced mass on z axis are like Fig. 29, in which by changing this position from 1st to 6th (central) node (see Fig. 3), the amplitudes of vibrations are decreased first and then increased passing through critical speeds. The rest of the features of the previous figure are repeated in this figure too.

Fig. 30
figure 30

Vibration time history of the rotor first node rotation angle in x-direction

Full size image

Rotor rotation angle and rotation speed in the z-direction are plotted in Figs. 31 and 32. In Fig. 31 it is shown that when the rotor cannot pass critical speed, the parabolic form of rotation angle time history changes to a straight line in 3rd critical speed (blue line). It means the rotation of the rotor in z-direction will change from constant rotation acceleration to constant rotation speed. All other cases passed through all critical speeds and probably have the same parabolic forms.

Fig. 31
figure 31

Time history of the rotation angle in z-direction

Full size image
Fig. 32
figure 32

Time history of the rotation speed in z-direction

Full size image

Figure 32 clearly demonstrated that when the rotor cannot pass 3rd critical speed (blue line), the rotation speed will be held constant. Note that little distortions are observed when rotor in other cases passed the 3rd critical speed.

3.6 Effects of nonlinearities

Almost, in all previous researches in the field of Rotordynamics, the 2nd order nonlinear terms are the highest order of nonlinearity in equations. But, in order to get the more accurate results, up-to 4th order of nonlinearity is considered in this work, as explained in the formulation section. The reason is illustrated in the next 2 figures.

The nonlinear terms up-to 4th order, are considered in deriving the kinetic and strain energy. The results of research demonstrated that in the analysis of rotor-bearing systems, up-to 4th order of nonlinearity should be considered in kinetic and strain energy equations to obtain correct results, especially when the rotor passes through critical speeds. Also, a convergence study has been derived by considering up to the 6th order of nonlinearity. The results of the rotor vibrations were not differing from those considered up to the 4th order of nonlinearity.

In Fig. 33, the time response history of the rotor vibrations in x-direction are plotted for a rotor with the specification of Table 2, just with different mu = 4.2 gr. If up-to 2nd order nonlinear terms are considered in formulations, the rotor will pass through the 3rd critical speed (red line), but by considering up-to 4th nonlinear terms, the results change completely and the rotor cannot pass through the 3rd critical speed (blue line).

Fig. 33
figure 33

Time history of the rotor vibration in x-direction

Full size image

In Fig. 34, the rotational speed results of the rotor are plotted for these 2 rotors with different nonlinear formulations too. This figure demonstrated again that the rotor with higher order nonlinear terms cannot pass through the 3rd critical speed (blue line), but the other rotor passes this critical speed (red line).

Fig. 34
figure 34

Time history of the rotational speed in z-direction

Full size image

3.7 Stability analysis

Waterfall and stability boundary diagrams for the dynamic behavior of the rotor-bearing system are plotted in this section. Waterfall diagrams for rotor with the different unbalanced masses, mu = 1,6 and 30 gr are plotted respectively in Figs. 35, 36 and 37.

Fig. 35
figure 35

Waterfall diagram of rotor with mu = 1 gr

Full size image
Fig. 36
figure 36

Waterfall diagram of rotor with mu = 6 gr

Full size image
Fig. 37
figure 37

Waterfall diagram of rotor with mu = 30 gr

Full size image

These diagrams are in good agreement with the results of Sect. 3.2. As shown in Fig. 35, in which the unbalanced mass is mu = 1 gr, vibration amplitude increases about first and second critical speeds (red zone) and also about 3rd critical speed (orange zone). As the bearings are linear, just the synchronous vibrations are observed in this figure.

Figure 36 shows that by increasing the unbalanced mass from 1 to 6 gr, the vibration amplitude increases (as shown before in Sect. 3.2), and the highest amplitudes are again about critical speeds (red and orange zones). Also, some turbulences are observed at about 3rd critical speeds (orange zone), which means the instability and Sommerfeld effects begin in these rotational speeds.

By increasing mu again up to 30 gr (Fig. 37), this turbulence zone gets bigger (orange zone) and also some turbulences are observed about 2nd critical speed (red zone), which means the rotor instability will be occurred in earlier critical speeds by increasing the unbalanced mass. Also, it is noted that as the bearings are linear, just the synchronous forces from the unbalanced mass are applied to the rotor-bearing system, so just the synchronous vibrations are observed in the waterfall diagrams.

The boundary between stability and instability behavior of the rotor-bearing system is plotted in Figs. 38 and 39. In these figures, the relation between the unbalanced mass and angular acceleration is plotted when the rotor gets non-stable. With consideration of applied torque as T = α*Jp, it can be said that the relation between torque and unbalanced mass is plotted as the boundary between stable and non-stable zones.

Fig. 38
figure 38

The boundary between stability and instability of the rotor passing 3rd critical speed

Full size image
Fig. 39
figure 39

The boundary between stability and instability of the rotor passing 2nd critical speed

Full size image

At a speed of about 1000 rpm, it can be noted the presence of sub-synchronous components. It would be appropriate to plot the 1000 rpm curve separately to show its frequency content. But, due to the length of the article, the authors prefer to study this phenomenon in the future papers.

In Fig. 38, this diagram is plotted for the rotor, when passes through the 3rd critical speed and stable and non-stable zones are determined. Also, a fitted line (red line) with a linear equation (which seems to be the best choice) is plotted to specify clearly the bound of instability.

In Fig. 39, this diagram is plotted for the rotor, when passes through the 2nd critical speed and stable and non-stable zones are determined again. Also, a fitted line (red line) with a cubic equation (which seems to be the best choice for this figure) is plotted to specify clearly the bound of instability.

4 Conclusions

A new computational model based upon well-established fundamental principles and new results are shown for the nonlinear vibrations of a rotating shaft with applied torque and acceleration passing through critical speeds. Because of the wide range of significant parameters, general conclusions are difficult to reach. However, specific conclusions for each parameter studied are included in each of the sub-sections of Sect. 3. As overarching conclusions, increasing unbalanced mass value and radius will cause to increasing the amplitude of lateral vibrations and makes it difficult to pass through critical speeds.

The effects of applied torque are distinctly different, and increasing the applied torque will decrease the vibration amplitude and the rotor can easier pass to higher critical speeds. Also changing the location of mass unbalanced in z-direction has different effects on rotor responses that positioning on the first (or last) and the central node will cause to increasing the amplitude of lateral vibrations. Videos of the rotor rotations (2D and 3D responses) for selected parameters are available upon request.

This work also demonstrated that in the analysis of rotor-bearing systems, up-to 4th order of nonlinearity should be considered in kinetic and strain energy equations to obtain more accurate results, especially when the rotor passes through critical speeds. Determination of boundary between stability and instability behavior of rotor passing through critical speed is also another significant result of this research.