1 Introduction

Since the advent of porous shape memory alloys (PSMA) in 90th decade, they have found several industrial and biological applications due to excellent mechanical and biological properties. These advanced materials have the benefits of both shape memory alloys (SMA) and porous materials. SMAs have the ability to recover large applied deformations upon heating to a specific temperature called austenite finish temperature. This property is called shape memory effect (SME). If the temperature at which the deformation is applied is higher than the austenite finish one, the deformation will be recovered after unloading. This behavior is known as superelasticity. Among shape memory materials, Nitinol (NiTi) is one of the most promising candidates for industrial and biomedical applications because of high value of maximum recoverable strain, good biocompatibility, corrosion resistance, and similar mechanical properties to body tissues specially bone tissue.

Nowadays, commercial porous NiTi samples are fabricated to be used as bone scaffolds in tissue engineering. Similar to bone, NiTi scaffolds recover up to 8% of the applied strains during a hysteresis cycle in the superelastic regime [1] (the value is more than 1% for bone). In addition, porous structure of PSMAs allows the designer to adjust the mechanical properties of the scaffold, specially its elastic modulus, to be compatible with those of bone [2]. If the elastic modulus of a scaffold is considerably higher than that of surrounding bones (lower than 20 GPa), the stress waves are absorbed by the scaffold and the stress shielding phenomenon will occur leading to osteoporosis [2]. Also, the bone cells may grow into the porous surface of the scaffold providing a good fixation between these two. In addition to the above mentioned mechanical advantages, interconnected pores of the microstructure of a bone scaffold allows the body fluids to be transported between tissues [3]. All these advantages of porous NiTi may enhance osseointegration and bone ingrowth [4] leading to fast healing of patients.

As mentioned above, the mechanical properties of a scaffold must be tailored to be similar to that of bone for the sake of proper function. Since the fabrication and characterization of PSMAs are time consuming, expensive and sometimes uncontrollable, it is desirable to develop powerful numerical approaches for predicting the mechanical response of PSMAs before fabrication. Accordingly, several attempts have been made by researchers worldwide to develop numerical models for the simulation of the mechanical response of PSMAs. In this regard, micromechanical averaging technique [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19] and finite element method [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] are the most popular ones.

In micromechanical averaging approach, a PSMA is supposed as a composite material in which the pores are considered as inclusions and the matrix is assumed to be as dense SMA. Then, a suitable homogenization approach such as Eshelby dilute inclusion technique, Mori–Tanaka scheme, or self-consistent method is used to obtain the macroscopic response of PSMA. Although this method is extensively used for the simulation of the mechanical response of PSMAs, it is just applicable for low porosity samples due to the highly inhomogeneous stress field in highly porous SMAs [14, 20].

In the finite element approach, a suitable geometrical model is constructed for the porous structure and a proper constitutive equation is attributed to the bulk material. To construct the geometrical model of the porous microstructure, two main approaches, i.e. unit cell method (UCM) [20, 27, 31,32,33,34,35,36] and multi cell method (MCM) [23, 28, 34, 37, 38] might be utilized.

In the UCM technique, it is assumed that the porous microstructure is produced by a periodic distribution of pores along different directions. Calling the repeating unit as unit cell, it is just necessary to model one unit cell with suitable periodic boundary conditions. Although, this method is computationally efficient, the assumption of a regular distribution of pores will cause the overestimation (higher stress value at the same value of strain) of the material response due to the constraints of periodicity.

In the MCM approach, a representative volume element (RVE) is constructed as the geometrical model of porous sample. This RVE might be a representative model of the real microstructure of the porous sample containing a random distribution of pores through the material. Karamooz Ravari et al. [34] showed that using a MCM can lead to more accurate results in comparison with UCM. In addition, the RVE can be treated as a periodic unit at which the periodic boundary conditions are imposed. Since the RVE is not small enough to be called a unit cell and big enough to be called a representative of the real microstructure, it is called mesoscale model [21, 24]. Panico and Brinson [24] demonstrated that using suitable boundary conditions, a mesoscale model would predict the macroscopic response of PSMAs with good accuracy and the lowest computational efforts.

Beside the above mentioned methods, some theoretical [39], scaling [37, 38], and phenomenological methods [40] are proposed. The main goal of these studies were to introduce computationally efficient and fast methods to predict the macroscopic mechanical response of PSMAs.

In this paper, a mesoscale finite element model based on Voronoi tessellation of three-dimensional (3-D) space is developed for the simulation of the mechanical response of PSMAs. To do so, two main steps are followed. In the first step a 3-D constitutive model of dense SMA, based on microplane theory, is introduced and formulated to be attributed as the bulk material of PSMA. Then, a geometrical model of PSMA is developed using Voronoi tessellation of 3-D space and suitable boundary conditions are applied on. In this paper, two kinds of periodic boundary conditions, i.e. mechanically periodic boundary conditions and geometrically periodic boundary conditions, are applied to the model. The results are obtained in the form of stress–strain response and compared to the experimental findings reported in the literature. In addition, the effects of number of cells, level of randomness, and the applied boundary conditions on the stress strain response are assessed.

Since in this proposed approach a representative model of the real geometry is utilized, the stress concentration can be taken into account so that, unlike the micromechanical averaging techniques, it is not limited to small values of porosity. In addition, the model is big enough to be a good representative of the real geometry and the cells are considered to be as low as possible for the sake of computational efficiency. Accordingly, unlike UC models, the obtained results would be more similar to experimental ones. In addition, UC models cannot predict some microstructural phenomena, such as localization, while this model can. Comparing with MUC models, such as those based on micro-CT images, the proposed model is computationally more efficient.

2 Materials and method

In order to simulate the thermomechanical response of PSMAs, two main steps must be followed. First, a suitable constitutive model for the simulation of the thermomechanical response of dense SMAs must be developed. Then, a geometrical model which represents the real microstructure of the PSMA must be constructed. By attributing the constitutive response of dense SMA to the geometrical model and performing the simulation through finite element method, the thermomechanical response of PSMA could be obtained. In this section, first, a constitutive model of dense SMA based on microplane theory is explained. Then, a geometrical model based on Voronoi tessellation method is developed. Finally, the necessary periodic boundary conditions are introduced.

2.1 Microplane constitutive model for dense SMAs

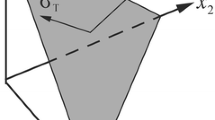
As mentioned above, in this paper, the constitutive model based on microplane theory is chosen for simulation purposes. Using this approach, all the material parameters, that are necessary for 3-D simulations, can be obtained using one-dimensional (1-D) response of the base material. The main idea of this theory is to generalize 1-D constitutive models to 3-D ones using a homogenization process [41,42,43,44,45,46,47,48,49]. To do so, it is supposed that the stress components on each generic plane passing through material points, called microplane, are the projection of the macroscopic stress tensor. After projecting the stress tensor on each microplane as normal and shear components, a suitable 1-D constitutive model is defined between the corresponding stresses and strains. Finally, a homogenization process, e.g. complementary virtual work, is utilized to generalize the 1-D constitutive equations to 3-D ones [41,42,43]. Referring to Fig. 1, the macroscopic traction vector at a material point, \( \varvec{t} \), might be projected on a microplane as normal, \( \sigma_{N} \), and shear, \( \sigma_{T} \), components. The traction vector and these two projected components can be formulated using the following equations [41, 42]:

$$ t_{i} = \sigma_{ij} n_{j} $$
(1)
$$ \sigma_{N} = \sigma_{ij} n_{i} n_{j} = \sigma_{ij} N_{ij} $$
(2)
$$ \sigma_{T} = \sigma_{ik} n_{k} n_{j} + \sigma_{jk} n_{k} n_{i} - 2\sigma_{N} n_{i} n_{j} /2 \sqrt {\sigma_{pr} \sigma_{ps} n_{r} n_{s} - \sigma_{N}^{2} } = T_{ij} \sigma_{ij} $$
(3)

where \( \sigma_{ij} \) is the macroscopic stress tensor, and \( n_{i} \) are the components of the unit normal vector to a microplane. It is previously proved that by splitting the normal component, \( \sigma_{N} \), to the volumetric and deviatoric parts (Eq. 4), the microplane elastic moduli are equal to the macroscopic ones [41, 42]:

$$ \sigma_{N} = \sigma_{V} + \sigma_{D} . $$
(4)
Fig. 1
figure 1

Projection of the macroscopic stress tensor on a microplane as normal and shear components

Full size image

In microplane theory, it is assumed that the martensite transformation is just associated with the shear component of microplane stresses [41, 42]. Accordingly, the following constitutive relations between the 1-D stresses and strains are obtained:

$$ \varepsilon_{V} = \left( {1 - 2\nu } \right)\sigma_{V} /E $$
(5)
$$ \varepsilon_{D} = \left( {1 + \nu } \right)\sigma_{D} /E $$
(6)
$$ \varepsilon_{T} = \left( {1 + \nu } \right)\sigma_{T} /E + \varepsilon^{ *} \xi_{s} $$
(7)

in the above relations, \( \varepsilon_{V} \) is the volumetric strain, \( \varepsilon_{D} \) the deviatoric strain, \( \varepsilon_{T} \) the shear strain, \( \nu \) the Poisson ratio, \( \varepsilon^{*} \) a material parameter called maximum recoverable strain, \( \xi_{s} \) the value of stress-induced martensite volume fraction, and \( E \) the elastic modulus of SMA which can be calculated using the Ruess model as follow [41, 42]:

$$ \frac{1}{E} = {{\left( {1 - \left( {\xi_{s} + \xi_{T} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {1 - \left( {\xi_{s} + \xi_{T} } \right)} \right)} {E_{A} + \left( {\xi_{s} + \xi_{T} } \right) /E_{M} }}} \right. \kern-0pt} {E_{A} + \left( {\xi_{s} + \xi_{T} } \right) /E_{M} }} $$
(8)

where \( E_{A} \) and \( E_{M} \) are respectively the elastic modulus of pure austenite and pure martensite, and \( \xi_{T} \) the value of temperature-induced martensite volume fraction. The value of stress- and temperature-induced martensite volume fraction at a given point, i, on an arbitrary loading path, \( \varGamma \), in the region, \( R_{k} \), might be obtained using the phenomenological relation of Eq. (9) and the phase diagram shown in Fig. 2 [50]:

$$ \xi_{i, q} = \left\{ {\begin{array}{*{20}l} {f_{i,q} \left( {\xi_{i,s0} ,\xi_{i,T0} , \tau_{i} , \bar{\sigma }_{i} , T_{i} } \right)} \hfill & {if\; i \in R_{k} \;and \;\tau_{i} \cdot n_{k} > 0} \hfill \\ {\xi_{i0, q} } \hfill & {otherwise} \hfill \\ \end{array} } \right.. $$
(9)
Fig. 2
figure 2

The phase diagram used for the calculation of martensite volume fractions

Full size image

Considering T as the temperature, \( \tau \) as the tangent vector to the loading path, \( \bar{\sigma } \) as the equivalent von-Misses stress, and \( \xi_{s0} \) and \( \xi_{T0} \) respectively as the initial values of stress- and temperature-induced martensite volume fractions, the evolution function, \( f_{i,q} \) can be expressed using the following relations [50]:

$$ f_{i,s} = \left\{ {\begin{array}{*{20}l} {\frac{{\xi_{s0} }}{2}\left( {Y_{A} + 1} \right)} \hfill & {if\;R_{k} = A} \hfill \\ {\xi_{s0} } \hfill & {if\;R_{k} = M_{T} } \hfill \\ {\frac{1}{2}\left\{ {\left( {\xi_{s0} - 1} \right)Y_{{M_{D1} }} + \left( {\xi_{s0} + 1} \right)} \right\}} \hfill & {if\;R_{k} = M_{D1} } \hfill \\ {\frac{1}{2}\left\{ {\left( {\xi_{s0} - 1} \right)Y_{{M_{D1} }} + \left( {\xi_{s0} + 1} \right)} \right\}} \hfill & {if\;R_{k} = M_{D2} , M_{D3} } \hfill \\ \end{array} } \right. $$
(10)
$$ f_{i,T} = \left\{ {\begin{array}{*{20}l} {\frac{{\xi_{T0} }}{2}\left( {Y_{A} + 1} \right)} \hfill & {if \;R_{k} = A} \hfill \\ {\frac{{1 - \xi_{s0} - \xi_{T0} }}{2}\left( {1 - Y_{{M_{T} }} } \right) + \xi_{T0} } \hfill & {if\;R_{k} = M_{T} } \hfill \\ {\frac{{\xi_{T0} }}{2}\left( {1 + Y_{{M_{D1} }} } \right)} \hfill & {if\;R_{k} = M_{D1} } \hfill \\ {\frac{{1 - \xi_{s0} - \xi_{T0} }}{4}\left( {1 + Y_{{M_{D2} }} } \right)\left( {1 - Y_{{M_{T} }} } \right)} \hfill & {if\;R_{k} = M_{D2} } \hfill \\ {\frac{{\xi_{T0} }}{2}\left( {1 + Y_{{M_{D1} }} } \right)} \hfill & {if\;R_{k} = M_{D3} } \hfill \\ \end{array} } \right. $$
(11)

where \( Y_{A} = \cos \left( {\pi \left[ {C_{As} \left( {T - A_{s} } \right) - \bar{\sigma }} \right] /\left[ {C_{As} \left( {T - A_{s} } \right) - C_{Af} \left( {T - A_{f} } \right)} \right]} \right) \), \( Y_{{M_{D1} }} = \cos \left( {\pi \left[ {\bar{\sigma } - \sigma_{s}^{cr} - C_{M} \left( {T - M_{s} } \right)} \right]/\left[ {\sigma_{f}^{cr} - \sigma_{s}^{cr} } \right]} \right) \), \( Y_{{M_{D2,3} }} = \cos \left( {\pi \left[ {\bar{\sigma } - \sigma_{s}^{cr} } \right]/\left[ {\sigma_{f}^{cr} - \sigma_{s}^{cr} } \right]} \right) \), \( Y_{{M_{T} }} = \cos \left( {\pi \left[ {T - M_{s} } \right]/\left[ {M_{f} - M_{s} } \right]} \right) \), and \( M_{f} \), \( M_{s} \), \( A_{s} \), and \( A_{f} \) are martensite finish, martensite start, austenite start, and austenite finish temperatures respectively. \( C_{M} \), \( C_{As} \), and \( C_{Af} \) are the slopes of the transformation bands in the phase diagram as shown in Fig. 2. The subscript, i, denotes the given point, and the subscript q stand for s and T.

By applying the principle of complementary virtual work, the 1-D constitutive relations of Eqs. (5) to (7) can be generalize to a 3-D one. Considering a unit hemisphere whose surface and volume are respectively \( \varOmega \) and V, the following relation will stand between the 1-D and 3-D stresses and strains [43]:

$$ \mathop \smallint \limits_{V}^{{}} \varepsilon_{ij} \delta \sigma_{ij} dV = \mathop \smallint \limits_{\varOmega }^{{}} \left( {\varepsilon_{V} \delta \sigma_{V} + \varepsilon_{D} \delta \sigma_{D} + \varepsilon_{T} \delta \sigma_{T} } \right)d\varOmega . $$
(12)

Substituting Eqs. (2)–(7) into Eq. (12) and some simplifications, the following constitutive relation between stress and strain tensors would be obtained [35, 41, 42]:

$$ \varepsilon_{ij} = - \frac{\nu }{E}\sigma_{rr} \delta_{ij} + \frac{1 + \nu }{E}\sigma_{ij} + \frac{3}{2\pi }\varepsilon^{ *} \xi_{s} \mathop \smallint \limits_{\varOmega }^{{}} {\text{T}}_{\text{ij}} d\varOmega . $$
(13)

The numerical implementation of the above mentioned constitutive model is performed and completely described by the authors [51] and is not presented here for the sake of brevity. This constitutive model is also enhanced by the authors to take the effects of tension–compression asymmetry [43, 52] as well as cyclic loading [53] into account.

2.2 Voronoi geometrical model

As mentioned earlier, it is necessary to construct a geometrical model which is a good representative of the real microstructure of the porous sample. Since it is not possible to reproduce the real microstructure of a porous sample in general, some simplified models might be used. The most well-known models utilized for the construction of microstructure of porous materials are based on the tessellation of 2-D or 3-D space according to Voronoi formulation. Considering a set of initial points which are distributed through the space, and some cells corresponding to each point of the set, the Voronoi tessellation of the space is defined in such a way that all the points in each cell have the minimum distance with their corresponding initial point rather than other initial points. After constructing the Voronoi diagram of the 3-D space, some cells are chosen randomly to be considered as pores. To do so, considering \( N \) cells in the domain, a set of indexes, i.e. \( \left[ {\begin{array}{*{20}c} 1 & 2 & { \ldots } & N \\ \end{array} } \right] \), is constructed. Each index of the set is associated with a cell in the domain. Then a random integer number between 1 and \( N \) is generated and its associated cell is considered as a pore in the material. When a cell is chosen as a pore, it is removed from the part. After selecting each cell, the index of that cell is stored in another set called “pores’ set”. If the index of a cell already exists in the “pores’ set”, that cell is ignored and another cell is chosen. The selection of pore cells is continued until the desired value of porosity is achieved. Since the pores are chosen randomly, it is possible that the pore are arranged in such a way that the part is divided into two (or more) portions. To prevent this from happening, after selecting each cell, it is examined that the main domain is still continues by checking the number of total parts in the model. If the number of parts is greater than 1, the selected cell, which cause the part to be torn in two or more, is ignored and another cell is chosen, again randomly. Note that, to prevent this cell to be chosen again, it is added to the pores’ set too. Figure 3 demonstrates the flowchart for the procedure presented above.

Fig. 3
figure 3

The procedure for generating a porous RVE using Voronoi tessellation method. In this flowchart, \( V_{f} \) is the volume of the \( f - th \) cell, \( V_{pore} \) the total volume of all the selected pores, \( V_{T} \) the total volume of the RVE

Full size image

In this paper, ABAQUS finite element package is utilized for the sake of numerical implementation. To construct the Voronoi diagram of 3-D space, first a set of regularly distributed points, shown in Fig. 4, are generated using a python script. Then, all these points are moved to a random position in a spherical domain utilizing the following equation:

$$ x_{i} = x_{0i} + \left( {2 \times \phi - 1} \right) \times \lambda \times \frac{a}{2} $$
(14)

in this relation, \( \phi \) is a random number between 0 and 1, \( \lambda \) the level of randomness, \( a = L/N \) the distance between two adjacent regular points, N the number of points in each direction, and L the length of the initial cubic domain (Fig. 4b). \( i \) stands for 1, 2, 3, and the subscript \( 0 \) donates the value of \( x_{i} \) coordinate in the regular grid. It is worth-mentioning that by increasing the value of \( \lambda \) from 0 to 1, the level of randomness increases too. For the value of \( \lambda = 0 \), the initial points would remain regularly distributed in the domain.

Fig. 4
figure 4

Regularly distributed initial points for generating Voronoi tessellation a 3-D view, b 2-D view

Full size image

After producing the initial points in the domain, the Voronoi tessellation of the space must be performed. To do so, in this paper, the available pyvoro python program which is written and maintained by Rycroft [54] is utilized. The output of the program is prepared as a set of cells corresponding to each initial point. Each cell of the set includes a set of faces which create that cell. Each face is comprised of a set of vertexes and their connections to create that face. These data are then used to create a Voronoi tessellated cubic domain in ABAQUS finite element package. To do so, first, three independent vertexes of each face are used to construct a local coordinate system. Then, all the points of a face and their connections are used to create that face of the cell as a shell. After creating all the faces of a cell, the closed volume surrounded by these faces is transformed to a volume. This process is repeated until all the cells are produced. Finally, all the cells are assembled to create the tessellated domain. Figure 5a, b show the Voronoi tessellated domains using N = 5 and N = 8 respectively. For these two figures the value of \( \lambda \) is chosen to be 0.5.

Fig. 5
figure 5

Voronoi tessellation of a 3-D domain using a 5 initial points b 8 initial points

Full size image

2.3 Interconnected pores

Since the most promising application of PSMAs, especially porous NiTi, is to be used as bone scaffolds, having interconnected pores is of great importance. Interconnected pores provide a pathway for blood and other body fluids between neighboring tissues and enhance their nutrition. In order to construct a geometrical model with interconnected pores, first, an index is assigned to each cell of the Voronoi tessellated domain. Once the first cell is chosen randomly, to be a pore, a set of indexes of its neighboring cells are created. Then, the next cell is chosen from those existed in this set. After selecting the second cell, its index is removed from the set, and the indexes of its neighboring cells are added to this set. This process is continued until the desired value of porosity is achieved. Notice that after selecting each cell, the continuity of the domain is checked and the indexes which cause in-continuity would be removed from the set.

2.4 Boundary conditions

To be able to obtain reasonable results with good accuracy, it is necessary to apply suitable boundary conditions on the model. The formulation of periodic boundary conditions has been comprehensively investigated in the literature [17,18,19, 55, 56]. In this section, first, the general periodic boundary condition with periodic directions along the axes of Cartesian coordinate system is briefly formulated. Then, the periodic boundary conditions utilized in this paper are introduced. Because of the translational symmetry of unit cells, the displacements identically transform from one cell to another. Accordingly, the relative displacements at an arbitrary point, \( P \), in a unit cell to those at its counterpart in another cell might be related to the macroscopic strains, \( \varepsilon_{x}^{0} , \varepsilon_{y}^{0} , \varepsilon_{y}^{0} , \gamma_{xy}^{0} , \gamma_{xz}^{0} , and \gamma_{yz}^{0} \), using the following relation [56]:

$$ \left\{ {\begin{array}{*{20}l} {u^{\prime} - u = \left( {x^{\prime} - x} \right)\varepsilon_{x}^{0} + \left( {y^{\prime} - y} \right)\gamma_{xy}^{0} + \left( {z^{\prime} - z} \right)\gamma_{xz}^{0} } \hfill \\ {v^{\prime} - v = \left( {y^{\prime} - y} \right)\varepsilon_{y}^{0} + \left( {z^{\prime} - z} \right)\gamma_{yz}^{0} } \hfill \\ {w^{\prime} - w = \left( {z^{\prime} - z} \right)\varepsilon_{z}^{0} } \hfill \\ \end{array} } \right. $$
(15)

in which \( \left( {x,y,z} \right) \) and \( \left( {x^{\prime}, y^{\prime}, z^{\prime}} \right) \) are respectively the coordinates of \( P \) and \( P^{\prime} \). Note that in the derivation of the above-mentioned displacement field, the rigid body rotation is constrained considering the following conditions:

$$ \frac{\partial w}{\partial x} = \frac{\partial v}{\partial x} = \frac{\partial w}{\partial y} = 0\,@\,x = y = z = 0. $$
(16)

Supposing a unit cell with the dimension of \( 2b \times 2b \times 2b \), the coordinates of point \( P^{\prime} \) can be related to those of point \( P \) as follow [56]:

$$ \left( {x^{\prime}, y^{\prime}, z^{\prime}} \right) = \left( {x + 2ib, y + 2jb, z + 2kb} \right) $$
(17)

where i, j and k determine the position of the cell at which, point \( P^{\prime} \) is located. Substituting Eqs. (17) into (15) leads to the following displacement constraints [55, 56]:

$$ \left\{ {\begin{array}{*{20}l} {u\left( {@x = b} \right) - u\left( {@x = - b} \right) = 2b\varepsilon_{x}^{0} } \hfill \\ {v\left( {@x = b} \right) - v\left( {@x = - b} \right) = 0 } \hfill \\ {w\left( {@x = b} \right) - w\left( {@x = - b} \right) = 0 } \hfill \\ \end{array} } \right. $$
(18)
$$ \left\{ {\begin{array}{*{20}l} {u\left( {@y = b} \right) - u\left( {@y = - b} \right) = 2b\gamma_{xy}^{0} } \hfill \\ {v\left( {@y = b} \right) - v\left( {@y = - b} \right) = 2b\varepsilon_{y}^{0} } \hfill \\ {w\left( {@y = b} \right) - w\left( {@y = - b} \right) = 0 } \hfill \\ \end{array} } \right. $$
(19)
$$ \left\{ {\begin{array}{*{20}l} {u\left( {@z = b} \right) - u\left( {@z = - b} \right) = 2b\gamma_{xz}^{0} } \hfill \\ {v\left( {@z = b} \right) - v\left( {@z = - b} \right) = 2b\gamma_{yz}^{0} } \hfill \\ {w\left( {@z = b} \right) - w\left( {@z = - b} \right) = 2b\varepsilon_{z}^{0} } \hfill \\ \end{array} } \right.. $$
(20)

In this paper, two kinds of boundary conditions are applied to the model. In the first model, it is supposed that the cells’ faces on the boundaries of the porous sample are not periodic (which is the case until now) so that the geometrically periodic boundary conditions, which are formulated above, cannot be applied. Accordingly, a mechanically periodic boundary condition proposed by Shen and Brinson [57] is used for the sake of numerical implementation. This kind of boundary condition and its associated model is called BM1 model throughout this manuscript. As shown in Fig. 6, in BM1 model it is assumed for side faces that the opposite faces has the same value of displacement along their normal directions. For upper and lower faces it is supposed that the lower face is fixed along its normal direction and the upper one is compressed by the value of \( \delta \) along that direction [36].

Fig. 6
figure 6

Mechanical periodic boundary condition applied in BM1 model

Full size image

In the second model, called BM2 model, the periodic boundary condition, formulated at the beginning of this section, is going to be applied. To do so, it is first necessary to tessellate the domain in such a way that the cells of the Voronoi diagram would be periodic too. In another word, there must be the same faces, edges, and vertexes on two opposite faces on which the periodic boundary condition is going to be applied. To generate such a geometric model, it is just necessary to distribute the initial points in a periodic manner. Referring to Fig. 7, for the boundary points near the boundary \( R_{i} \), the coordinate of the counterpart points, \( x_{i}^{'} \), near boundary \( R_{i}^{'} \) might be calculated using the following equation:

$$ \left\{ {\begin{array}{*{20}l} {x_{i}^{ '} = L - x_{i} } \hfill \\ {x_{j}^{ '} = x_{j} \quad j = 1, \ldots ,3\; and \;j \ne i} \hfill \\ \end{array} } \right.. $$
(21)
Fig. 7
figure 7

2-D illustration of BM2 boundary condition

Full size image

Notice that in Fig. 7 only the boundary points are shown for the sake of better clearness. Figure 8 shows a 3-D domain tessellated by a periodic Voronoi diagram using N = 4, and \( \lambda = 0.5 \).

Fig. 8
figure 8

Periodic Voronoi tessellation of 3-D cubic domain a 3-D view b 2-D view

Full size image

3 Results and discussion

To construct the geometrical model of the PSMA, a python script is developed through python 2.7-amd64 to be used as the input of ABAQUS 6.13-4 finite element package. Since both initial point distribution and pore choosing are done randomly, for each set of the parameters, \( N \) and \( \lambda \), 25 models are produced and their average output response is reported throughout the paper. The model is meshed using 10-node modified quadratic tetrahedron elements with four integration points denoted by C3D10 M in ABAQUS. For each simulation, a mesh sensitivity study is conducted by repeatedly reducing the mesh size and rerunning the analysis until changes in the results are negligible. All the simulations are performed on an Intel® Core™ i7-4710HQ CPU @ 2.50 GHz with 12.0 GB ram. This section of the paper is organized as follow. First the effect of number of cells, N, on the stress–strain response of PSMA is investigated for the sake of convergence of the results. In this regard both BM1 and BM2 models are assessed. Then, the effects of the value of randomness, \( \lambda \), is studied and the results are compared with the experimental findings for 42 and 13% porous NiTi reported in [5] and [8] respectively.

3.1 The effects of the number of cells

To see how the number of cells affects the predicted stress–strain response of PSMAs, finite element models of porous samples with 20, 42, and 70 percent porosity under uniaxial loading are constructed using both BM1 and BM2 models. For all the simulations the material is considered to be NiTi with the material parameters reported in Table 1, which are associated with the experimental measurements of a 42% porous sample as reported by Karamooz Ravari et al. [36]. Referring to the experimental measurements, the test temperature is \( T = A_{f} \), so that the material is initially in austenite phase and \( \xi_{s0} = \xi_{T0} = 0 \).

Table 1 Material parameters utilized for numerical simulations of the 42% porous NiTi
Full size table

Figure 9a, b show respectively the uniaxial stress–strain response of 42% porous NiTi obtained using BM1 and BM2 models with \( \lambda = 0 \). As it can be seen, the stress level decreases by increasing the number of cells in the Voronoi tessellated domain. In addition, the stress–strain response converges to a unique curve by increasing the number of cells. In order to assess the effects of the number of cells, the value of the maximum deviation of the stress–strain response from the converged curve is depicted in Fig. 10a, b for both BM1 and BM2 models. Referring to this figure, by increasing the number of cells, the maximum deviation from the converged stress–strain curve decreases and decays to zero for all values of porosity. The maximum deviation from the converged results increases by increasing the value of porosity. However, the rate at which the results converge also increases as the porosity increases. Referring to Fig. 10, the value of the number of cells at which the convergence of the response is obtained are respectively 9 and 6 for BM1 and BM2 models. It can also be concluded from this figure that the rate of convergence of the second model, BM2, is higher than that of the first one, BM1. In another word, BM2 model is more efficient than BM1 model from computational point of view.

Fig. 9
figure 9

The effect of the number of cells on the uniaxial stress–strain response of 42% NiTi sample obtained using a BM1 model b BM2 model

Full size image
Fig. 10
figure 10

Maximum deviation of the converged stress–strain curve for different values of number of cells obtained using a BM1 model, b BM2 model

Full size image

The minimum number of cells at which the convergence of the stress–strain response is occurred (the deviation is smaller than 10%) is illustrated in Fig. 11 for different values of the level of randomness and the porosity of 42% (the same results are obtained for different values of porosity but not presented here for the sake of brevity). As shown in Fig. 11, the level of randomness has a slight effect on the number of cells. The trend is almost similar for BM1 and BM2 models. The number of cells decreases by increasing the level of randomness up to the value of 0.4 and gets fixed for greater values. Notice that the number of cells is always smaller for BM2 model than for BM1 model.

Fig. 11
figure 11

The effect of the level of randomness on the number of cells at which convergence is obtained

Full size image

To see how the proposed model behave under different loading histories, a biaxial loading strategy, similar to that used by Sepe et al. [19], is considered here. For this simulation, the same material parameters with those of uniaxial case are used, and a compressive strain of about 0.036 is applied on both perpendicular sides of the RVE. Figure 12 shows the stress in one direction versus the strain of that direction for different number of cells using BM2 model. As can be seen, the stress–strain response converges to a specific curve by increasing the number of cells. The changes in the response is not significant when the number of cells increases more than 6 which means that the response almost converges. The maximum difference between the stress–strain response using 6 and 7 cells is about 5.34 MPa which is negligible in comparison to the level of applied stress. Similar observation is made using BM1 model with at least 9 cells in each direction. The above-mentioned results show that the required number of cells for obtaining the desired convergence is independent of the loading history. It is worth-mentioning that the same simulations are performed for porosities of 20 and 70 percent and the maximum different between that obtained stress–strain respond using 6 and 7 cells in each direction is found to be about 4.83 and 7.07, respectively.

Fig. 12
figure 12

The effect of the number of cells on the biaxial stress–strain response of 42% NiTi sample obtained using BM2 model

Full size image

According to the obtained results of this subsection BM2 model with at least 6 cells in each direction is used for all the rest of simulations throughout the paper for the sake of computational efficiency.

3.2 The effects of the level of randomness and comparison with experiment

The effects of the value of randomness on the stress–strain response of 42% porous NiTi is depicted in Fig. 13 and the results are compared with the experimental curve reported by Entchev and Lagoudas [5]. As is seen, increasing the value of randomness causes the reduction of the stress level in the stress–strain response of PSMA. In addition, by increasing the value of randomness, the stress–strain response would decay to a specific curve. Based on the results reported in Fig. 13, the difference between the stress–strain response gets smaller by increasing the level of randomness so that for greater values than \( \lambda = 0.6 \) the response changes scarcely. Comparing the obtained results with experiment, the predictions of the model for \( N \ge 6 \) and \( \lambda \ge 0.6 \) is in good agreement with the experimental response showing the ability of the proposed model for the simulation of the mechanical response of PSMAs.

Fig. 13
figure 13

Effects of the level of randomness on the stress–strain response of the 42% porous NiTi and comparison with experiment

Full size image

In order to assess the effects of the value of porosity on the predictions of the proposed model, a finite element model of a 13% porous NiTi is generated based on BM2 model. The material parameters utilized in this case are obtained using the data provided in [8, 35]. This sample is loaded at a constant temperature of 58 °C which is higher than the austenite finish temperature so that the material is initially in the austenite phase. Since the experimental stress–strain response of the material was reported at a constant temperature [8], only the transformation stresses associated with that temperature are available. Although it is not possible to obtain the phase diagram using just this stress–strain response, one can adjust the parameters corresponding to the phase diagram so that the same transformation stresses are achieved. Considering the subscript “s” as “start” and “f” as “finish” and the superscript “M” as “martensite” and “A” as “austenite” the following equations might be used for the calculation of the material parameters:

$$ \sigma_{s}^{M} = \sigma_{s}^{cr} + C_{M} \left( {T - M_{s} } \right) $$
(22)
$$ \sigma_{f}^{M} = \sigma_{f}^{cr} + C_{M} \left( {T - M_{s} } \right) $$
(23)
$$ \sigma_{s}^{A} = C_{As} \left( {T - A_{s} } \right) $$
(24)
$$ \sigma_{f}^{A} = C_{Af} \left( {T - A_{f} } \right). $$
(25)

Using the above-mentioned equations, the material parameters associated with the 13% porous NiTi are calculated and reported in Table 2.

Table 2 Material parameters utilized for numerical simulations of the 13% porous NiTi
Full size table

The effects of the level of randomness on the stress–strain response of the 13% porous NiTi are depicted and compared with the experimental curve in Fig. 14. As it is obvious, the trend is similar to that observed in the case of 42% porous NiTi. However, it seems that the rate of convergence of the results is faster for the 13% porous sample. To investigate this observation, the value of the maximum error with the curve of \( \lambda = 1 \) is plotted as a function of the level of randomness for different values of porosity in Fig. 15. Referring to this figure, the impact of the level of randomness on the maximum error is more pronounced for higher values of porosity. At the porosity of 20%, the value of error is about 26.4% for \( \lambda = 0.0 \) which rapidly decreases by increasing the value of \( \lambda \) such that at \( \lambda = 0.3 \), the value of error is about 4.5%. However, for higher values of porosity, higher value of \( \lambda \) is needed in order to achieve convergence. As it can be seen, \( \lambda \ge 0.6 \) would provide reasonable results for all values of porosity.

Fig. 14
figure 14

Effects of the level of randomness on the stress–strain response of the 13% porous NiTi and comparison with experiment

Full size image
Fig. 15
figure 15

The value of the maximum error with the curve of λ = 1 as a function of the level of randomness for different values of porosity

Full size image

4 Conclusion

In this paper, a new model for the simulation of the thermomechanical response of PSMAs is presented. In this model, the Voronoi tessellation of a 3-D cubic domain is used to construct the geometry of the PSMA and the microplane theory is utilized as the constitutive model of the matrix. Two types of boundary conditions, called BM1 and BM2, are applied to the models and the stress–strain responses are obtained through finite element analysis. The effects of number of cells, level of randomness, and type of boundary conditions on the obtained response are investigated. The results show that by increasing the number of cells in both BM1 and BM2 models, the stress level decreases and saturates to a specific curve. However, the number of cells at which this convergence happens is greater for the first model in comparison with the second one. In addition, increasing the value of randomness up to 0.6 decreases the level of stress in stress–strain response. By further increasing of this parameter, no considerable changes are observed. In another word, increasing the value of randomness to the values greater than 0.6 won’t change the stress–strain response significantly in comparison with the models with \( \lambda = 0.6 \). The obtained results are also compared with the experimental findings reported in the literature demonstrating good agreement. It shows that the proposed model can be used for the simulation of the mechanical response of PSMAs used in biomedical applications.