Introduction

In recent years, porous shape memory alloys (PSMAs) have attracted a lot of attention due to their superior mechanical properties with combined advantages of both shape memory alloys and porous materials. These materials can recover the applied deformations due to either shape memory effect, upon a temperature rise, or superelasticity at high temperatures. In addition, the mechanical properties of PSMAs can be adjusted by controlling the amount of porosity. These properties, beside high damping capacity, interconnected pores, low stiffness, high strength, and low weight, make them promising candidates for being used as bone implants (Ref 1), energy absorbers (Ref 2), and light weight intelligent systems (Ref 3).

After exploration of shape memory alloys, several attempts were made for modeling their mechanical behaviors (Ref 4-7). As each material point may go through a complex multiaxial loading path, it is essential to develop three-dimensional constitutive equations for modeling the mechanical behavior of SMAs. Among these, Liang and Rogers (Ref 8) presented a multi-dimensional thermomechanical constitutive model for SMAs based upon a combined micromechanics-macromechanics approach. Graesser and Cozzarelli (Ref 9) extended a one-dimensional evolutionary model of SMAs’ behavior to three dimensions using just one internal variable. They then reduced their model to uniaxial, shear, and non-proportional biaxial loadings. Lagoudas and Pavlin (Ref 10) developed a three-dimensional rate-independent thermomechanical constitutive model for fully dense SMAs which accounts for plastic strains during stress-induced martensite phase transformation and implemented it using return mapping. Panico and Brinson (Ref 11) proposed a macroscopic phenomenological model based on the classical framework of thermodynamics of irreversible processes. Their model accounts for the effects of multiaxial stress states, non-proportional loading histories, and the evolution of both twinned and detwinned martensites. Popov and Lagoudas (Ref 12) presented a 3D constitutive model for polycrystalline SMAs based on a modified phase transformation diagram which takes both the direct conversion of austenite to detwinned martensite and the detwinning of self-accommodated martensite into account. Arghavani et al. (Ref 13) developed a phenomenological constitutive model for SMAs within the framework of irreversible thermodynamics with the use of a scalar and a tensorial internal variable. In 2002, Brocca et al. (Ref 14) proposed microplane theory as a tool for modeling the behavior of SMAs. This idea was further developed by Kadkhodaei et al. (Ref 15, 16) and Mehrabi et al. (Ref 17) to model the shape memory effect as well as superelasticity. In microplane modeling, the macroscopic stress tensor at a material point is projected on each microplane passing though that point, and 1D constitutive laws are defined in micro-level. Then, a homogenization process is used to generalize 1D relations to 3D ones. This constitutive modeling approach is shown to be thermodynamically consistent (Ref 18) and is capable of modeling non-proportional (Ref 15-17, 19) loading paths, anisotropic behavior (Ref 20), and tension-compression asymmetry (Ref 21, 22) in shape memory alloys.

The early attempts to fabricate PSMAs were made in the 90 decade in Russia (Ref 23-26) and China (Ref 27, 28). As the mechanical properties of a PSMA are affected by several microstructural and material parameters, prediction of the mechanical properties of PSMA is quite challenging. Several studies have been performed to simulate the mechanical properties of PSMAs especially within the superelastic regime. In some studies, the micromechanical averaging approaches were used to simulate the macroscopic stress-strain behavior of PSMAs. Pavlin and Lagoudas (Ref 29) used micromechanical averaging technique to establish the effective elastic and inelastic behaviors based on information about the mechanical response of the individual phases as well as shape and volume fraction of the inhomogeneities. They also studied the effects of pore shape and compared their results with experimental stress-strain behavior of a 42% porous NiTi sample. Zhao et al. (Ref 30) processed porous NiTi with several different porosities using spark plasma sintering. They then presented a model for the macroscopic compression behavior of PSMAs using the Eshelby’s inhomogeneous inclusion method. They compared the analytically obtained results for a 13% porous sample with the experiment. Lagoudas and Pavlin (Ref 10) developed a three-dimensional rate-independent thermomechanical constitutive model for fully dense SMAs which accounts for transformation and plastic strains during stress-induced martensitic phase transformation. They further used this constitutive equation in an incremental formulation of the Mori-Tanaka averaging scheme to predict the mechanical response of two different porous NiTi samples with large and small pore sizes (Ref 31). Nemat-Nasser et al. (Ref 32) fabricated porous NiTi specimens with 12% porosity using spark plasma sintering method. They characterized the products experimentally using quasi-static and dynamic tests at various initial temperatures. They further modeled the PSMA as a three-phase composite containing the parent phase (austenite) as the matrix, the product phase (martensite), and the voids as the embedded inclusions. Zhao and Taya (Ref 33) presented two models, open cell and close cell, for predicting the stress-strain response of porous NiTi under compressive loading. In each modeling approach, two different shapes of pores, i.e., spherical and ellipsoidal, were considered. They employed the Eshelby’s equivalent inclusion method and Mori-Tanaka mean-field theory in both models. They compared the results of their models with the experimental findings reported in (Ref 30) and showed that the predictions of the open cell model with ellipsoidal pore shape are closer to experimental results. Toi and Choi (Ref 34) extended a one-dimensional constitutive model for shape memory alloys to take into account the effects of porosity and strain rate using internal state variables representing the porosity and the martensite volume fraction. Then, they applied the proposed method for the simulation of the quasi-static and dynamic behaviors of SMAs and PSMAs. Liu et al. (Ref 35) utilized the Eshelby’s inclusion method and Mori-Tanaka scheme to compare different constitutive models with different yield functions for PSMAs. They also proposed a new formula for the yield function and showed that their new yield function predicts stress-strain response more accurately. Zhu and Dui (Ref 36) proposed a constitutive model for the macroscopic mechanical behavior of porous NiTi in which hydrostatic stress for porous NiTi and tensile-compressive asymmetry of dense NiTi were taken into account. Olsen and Zhang (Ref 37) presented a new constitutive model for PSMAs based on Gurson-Tvergaard-Needleman formulation accounting for forward and reverse stress-induced phase transformation as well as plastic deformation. Using this model, they investigated the effect of existence of micro-voids on the superelastic-plastic behavior of SMAs. Considering both the effects of hydrostatic stress and the tensile-compressive asymmetry, Liu et al. (Ref 38) developed a constitutive model of the macroscopic behavior of PSMAs.

Finite element analysis has also been employed by a number of researchers for prediction of the mechanical behavior of PSMAs. Qidwai et al. (Ref 39) employed unit cell method to obtain the mechanical behavior of PSMAs in compression. They considered cylindrical and spherical shapes as the approximation of open and close pores, respectively. DeGiorgi and Qidwai (Ref 40) used the mesoscale analysis based on a two-dimensional finite element method to evaluate a representative volume element in order to determine the effective response of PSMAs. The pores were defined by setting the stiffness of corresponding elements to zero. Panico and Brinson (Ref 41) simulated the mesoscopic mechanical behavior of PSMAs under cyclic loading. They also evaluated the complex interaction between porosity, local phase transformation, and macroscale response. Sepe et al. (Ref 42) utilized a repetitive unit cell model made of a circular hole in a dense SMA matrix to examine the constitutive behavior and the dissipation energy capability of porous NiTi for several porosity levels.

There are some phenomenological, theoretical, and scaling approaches for modeling the mechanical response of PSMAs in the literature. Sayed et al. (Ref 43) presented a phenomenological two-phase constitutive model for pseudoelastoplastic behavior of PSMAs. They used a unit cell finite element model with spherical pore shapes to calibrate their constitutive model. Maîtrejean et al. (Ref 44, 45) proposed porous/bulk density ratio scaling relations for simulating the superelastic behavior of PSMAs in the same way as proposed by Gibson and Ashby (Ref 46). They used two-dimensional (Ref 45) and three-dimensional (Ref 44) finite element models to obtain the constants of the scaling relations. Liu et al. (Ref 47) adopted a unit cell model to establish a constitutive relation for PSMAs. They then determined the stress distribution, phase distribution, and martensite volume fraction for the model under both pure hydrostatic stress and compression. Ashrafi et al. (Ref 48, 49) developed 3-D phenomenological constitutive models for the pseudo-elastic behavior and shape memory effect of PSMAs within the framework of irreversible thermodynamics.

In this paper, a new unit cell model is proposed to predict the mechanical stress-strain response of PSMAs. To this end, one-eighth of a sphere is cut parallel to xy, xz, and yz faces to satisfy the desired porosity. The position of the cutting planes is calculated for a range of possible porosities between 0 and 47.6%, which is the maximum value of porosity when the planes are tangent to the sphere. To assess the effects of random microstructure of PSMAs, a random model is produced by generating several spheres in random positions and adjusting their radius to meet the desired porosity. The three-dimensional constitutive relations based on microplane modeling approach (Ref 15-22) are attributed to the bulk material through a material user subroutine UMAT. Then, finite element simulations are performed to obtain the stress-strain response of porous shape memory alloys under uniaxial compression. The results show that, for small values of pore volume fraction (PVF), the effects of random microstructure are negligible. However, for large values of PVF, by increasing the level of randomness, the stress-strain response of PSMA tends to a limit curve which correlates with experiment.

Microplane Method for Three-Dimensional Constitutive Response of SMA

In this section, a brief description of microplane theory is presented for constitutive modeling of shape memory alloys. The main idea of this theory is to develop 1D constitutive relations to 3D ones. Therefore, only the material parameters of simple tension (compression) are needed for the 3D modeling. There are two main formulations for deriving macroscopic governing equations named “static constraint” and “kinematic constraint”. In static constraint formulation, the stress vector on each microplane is supposed to be the projection of macroscopic stress tensor while in kinematic constraint one, this projection rule is assumed for strain vector and macroscopic strain tensor. In addition, there is another formulation where both constraints are co-exist called “double constraint formulation”. Carol and Bazant (Ref 50) showed that if the kinematic constraint is used, the obtained constitutive relations could be just used for a limited range of Poisson’s ratio. Accordingly, in this paper the static constraint formulation is utilized for the evolution of SMA constitutive relations. In static constraint formulation, three main steps, (1) projection of the macroscopic stress tensor on each microplane, (2) definition of 1D constitutive laws on the micro-level, and (3) homogenization process on the material point to generalize the 1D relations to 3D ones should be followed (Ref 19). As depicted in Fig. 1, the normal and shear stresses on any microplane can be described using Eq 1 and 2 (Ref 15-17, 22):

Fig. 1
figure 1

Stress components on a microplane

Full size image
$$\sigma_{\text{N}} = N_{\text{ij}} \sigma_{\text{ij}}$$
(1)
$$\sigma_{\text{T}} = T_{\text{ij}} \sigma_{\text{ij}} ,$$
(2)

where σ ij is macroscopic stress tensor, σ N normal stress, σ T shear stress, \(N_{\text{ij}} = n_{\text{i}} n_{\text{j}}\) and \(T_{\text{ij}} = \frac{1}{2}\left( {t_{\text{i}} n_{\text{j}} + t_{\text{j}} n_{\text{i}} } \right)\) where \(t_{\text{i}} = {{(\sigma_{\text{ik}} n_{\text{k}} - \sigma_{\text{N}} n_{\text{i}} )} \mathord{\left/ {\vphantom {{(\sigma_{\text{ik}} n_{\text{k}} - \sigma_{\text{N}} n_{\text{i}} )} {\sqrt {\sigma_{\text{jr}} \sigma_{\text{js}} n_{\text{r}} n_{\text{s}} - \sigma_{\text{N}}^{2} } }}} \right. \kern-0pt} {\sqrt {\sigma_{\text{jr}} \sigma_{\text{js}} n_{\text{r}} n_{\text{s}} - \sigma_{\text{N}}^{2} } }}\) is the unit vector parallel to resultant shear stress on the plane and n i are the components of the unit normal vector n to a microplane. It is shown that using the volumetric-deviatoric split of the normal stress, the micro-level elastic moduli are equal to the macroscopic ones (Ref 15, 16). The volumetric, σV, and deviatoric, σD, parts can be formulated as follows

$$\sigma_{\text{V}} = \frac{1}{3}\delta_{\text{ij}} \sigma_{{i{\text{j}}}}$$
(3)
$$\sigma_{\text{D}} = \left( {N_{\text{ij}} - \frac{1}{3}\delta_{\text{ij}} } \right)\sigma_{\text{ij}} ,$$
(4)

where δ ij is the Kronecker’s delta. It is assumed that the martensitic transformation is only associated with shear deformation and that the normal stress component causes only elastic strains. Consequently, the volumetric and deviatoric parts of the normal strain and the elastic shear strain can be described as follows (Ref 17)

$$\varepsilon_{\text{V}} = \frac{(1 - 2\nu )}{{E(\xi_{\text{s}} )}}\sigma_{\text{V}}$$
(5)
$$\varepsilon_{\text{D}} = \frac{(1 + \nu )}{{E(\xi_{\text{s}} )}}\sigma_{\text{D}}$$
(6)
$$\varepsilon_{T} = \frac{(1 + \nu )}{{E(\xi_{\text{s}} )}}\sigma_{\text{T}} + \xi_{\text{s}} \varepsilon^{*} ,$$
(7)

where ν is SMA’s Poisson ratio, ε V the volumetric part of the normal strain, and ε D deviatoric part of the normal strain, ɛ T the shear strain, ξ s the stress-induced martensite volume fraction, ɛ* the maximum recoverable strain, and E(ξ s) the elastic modulus of the material which is calculated using the Reuss model (Ref 51) as follows:

$$\frac{1}{{E(\xi_{\text{s}} )}} = \frac{{1 - \xi_{\text{s}} }}{{E_{\text{A}} }} + \frac{{\xi_{\text{s}} }}{{E_{\text{M}} }},$$
(8)

where E A and E M are the elastic modulus of pure austenite and pure martensite phases, respectively. By applying the principle of complementary virtual work, Eq 9 is obtained for the components of the macroscopic strain tensor (Ref 15-17):

$$\varepsilon_{\text{ij}} = \varepsilon_{\text{V}} \delta_{\text{ij}} + \frac{3}{2\pi }\int\limits_{\Omega } {\left( {\varepsilon_{\text{D}} N_{\text{ij}} + \varepsilon_{\text{T}} T_{\text{ij}} } \right)} d\Omega ,$$
(9)

where Ω is the surface of a unit hemisphere, and ε ij macroscopic strain tensor. By substituting Eq 5, 6, and 7 into Eq 9, and after some straightforward algebra, the following equation is obtained:

$$\varepsilon_{\text{ij}} = - \frac{\nu }{{E(\xi_{\text{s}} )}}\sigma_{\text{mm}} \delta_{\text{ij}} + \frac{1 + \nu }{{E(\xi_{\text{s}} )}}\sigma_{\text{mn}} \cdot \frac{3}{2\pi }\int_{\Omega } {\left( {N_{\text{mn}} N_{\text{ij}} + T_{\text{mn}} T_{\text{ij}} } \right)d\Omega } + \varepsilon^{*} \cdot \xi_{\text{s}} \cdot \frac{3}{2\pi }\int_{\Omega } {T_{\text{ij}} d\Omega }$$
(10)

To complete the definition of constitutive relation, an appropriate evolution for stress-induced martensite volume fraction should be used. Referring to Fig. 2, the evolution relations for martensite volume fraction can be described using the following relations which are obtained based on what proposed by Brinson (Ref 5):

Fig. 2
figure 2

Stress-strain curve of dense SMA

Full size image

If \(\dot{\overline{\sigma} } \ge 0\) and \(\sigma_{\text{M}}^{\text{s}} < \bar{\sigma } < \sigma_{\text{M}}^{\text{f}}\) then

$$\xi_{\text{s}} = \frac{{1 - \xi_{\text{s0}} }}{2}\cos \left( {\frac{\pi }{{\sigma_{\text{M}}^{\text{s}} - \sigma_{\text{M}}^{\text{f}} }}\left( {\bar{\sigma } - \sigma_{\text{M}}^{\text{f}} } \right)} \right) + \frac{{1 + \xi_{\text{s0}} }}{2}$$

and if \(\dot{\overline{\sigma} } < 0\) and \(\sigma_{\text{A}}^{\text{f}} < \bar{\sigma } < \sigma_{\text{A}}^{\text{s}}\) then

$$\xi_{\text{s}} = \frac{{\xi_{\text{s0}} }}{2}\left[ {\cos \left( {\frac{\pi }{{\sigma_{\text{A}}^{\text{s}} - \sigma_{\text{A}}^{\text{f}} }}\left( {\sigma_{\text{A}}^{\text{s}} - \bar{\sigma }} \right)} \right) + 1} \right],$$

where ξ s0 is the initial stress-induced martensite fraction, \(\bar{\sigma }\) is the von Mises equivalent stress, σ s and σ f are the start and finish transformation stresses, respectively, and the subscripts M and A denote the martensite and austenite phases.

Unit Cell Model

Figure 3 shows the microstructure of a 13% porous NiTi specimen fabricated by spark plasma sintering (Ref 30). Referring to this figure, the microstructure of porous NiTi can be supposed as a combination of some spheres penetrated into each other. These spheres are the particles of the raw NiTi powder used for fabrication. As shown in Fig. 4, a unit cell is proposed to model the microstructure of porous NiTi using 8 overlapping spheres situated at the corners of a cube and penetrated into each other with a value of 2δR, where R is the radius of the spheres and δ is the value of penetration. Referring to Fig. 4 it can be concluded that the proposed unit cell has three symmetry planes including xy, xz, and yz. Accordingly, the model can be reduced to just one-eighth of a sphere with appropriate boundary conditions that will be presented in section 5. The geometry of the new reduced unit cell is shown in Fig. 5(a). To generate this model, one-eighth of a sphere is first generated and then is cut using three planes parallel to xy, xz, and yz faces located in a distance of (1−δ)R from the corresponding faces as shown in Fig. 5(b).

Fig. 3
figure 3

Microstructure of a 13% porous NiTi sample (Ref 30)

Full size image
Fig. 4
figure 4

The proposed unit cell for porous SMA

Full size image
Fig. 5
figure 5

(a) The unit cell proposed for modeling porous SMAs. (b) The method of generating the unit cell model

Full size image

Figure 6 shows the value of the pore volume fraction (PVF) in the model against the penetration value δ. The figure shows that the amount of PVF decreases by increasing δ. By changing the position of the planes, the minimum and maximum possible values for PVF are 0 and 47.6%, respectively.

Fig. 6
figure 6

Pore volume fraction vs. penetration value

Full size image

Random Model

As the real microstructures of porous materials are rarely regular, it would be of interest to assess the effects of random microstructure of such materials. Karamooz et al. (Ref 52, 53) demonstrate that the microstructural imperfections can severely affect the mechanical response of cellular materials. To this end, based on the unit cell model described in previous section, a random model is generated where N unit cells are repeated along x, y, and z axes, and the centers of the spheres are moved to a random position determined using the following equation:

$$x_{i} = x_{0i} + \beta \left( {2\alpha - 1} \right)R,$$
(11)

where x i are coordinates of the new position of the spheres’ centers, x 0i are the initial coordinates of the centers, β is the level of randomness, and α is a random value between 0 and 1.

After generating the random microstructure, the PVF may be different from the desired one. Therefore, the PVF of the new model is calculated and is compared with the desired value. Ift does not fall within the desired range, the spheres’ radii are changed such that the presumed PVF is obtained. Considering N unit cells along each axis, the length of the model L = 2 × N × R × (1−δ). Figure 7 shows a random model with N = 1 and β = 0.1.

Fig. 7
figure 7

A random model for microstructure of PSMAs

Full size image

Boundary Conditions

Since the unit cell model is used for simulation of PSMAs, appropriate boundary conditions must be imposed to obtain reliable results. Li (Ref 54) conducted an elaborative study on the ways of boundary condition enforcement to unit cell models under different situations. As the proposed unit cell in this paper have three symmetry planes, a combination of symmetry boundary conditions and periodic ones can be considered. To do so, the normal translational degree of freedom normal to the x = 0, y = 0, and z = 0 is set to zero while the x = L, y = L, and z = L faces are constrained to remain planar. A normal displacement of the value Δ is applied to the nodes of the y = L face to resemble the compression of the PSMA. As shown in Fig. 8, the value of Δ varies with time to define the loading-unloading in y direction. In this study, Δmax = 0.046 × L is the maximum value of the compressive displacement.

Fig. 8
figure 8

Variations of the compressive displacement amplitude with time

Full size image

In addition, for the case of random model, the displacement normal to the x = 0, y = 0, and z = 0 planes set to zero while the x = L, and z = L are constrained to be planar and left free. It is because, the nodes of the opposite faces are not mirrored, and therefore it is not possible to apply the microstructural periodic boundary conditions. It is shown that this boundary condition yields smaller size for the representative volume element (Ref 41).

Results and Discussion

Unit Cell Model

In this paper, the material parameters presented by Toi and Choi (Ref 34) are used for modeling purposes. Table 1 shows these material parameters. To assign the constitutive relations presented in section 2 to the bulk material of PSMA, a user material subroutine (UMAT) is developed for ABAQUS commercial finite element package.

Table 1 Material parameters used for modeling (Ref 34)
Full size table

The model is meshed using 10-node modified quadratic tetrahedron elements with four integration points denoted by C3D10M in ABAQUS. A mesh sensitivity study is conducted by repeatedly reducing the mesh size and rerunning the analysis until changes in the results are negligible. Accordingly, the appropriate mesh size is found to be about 0.2R. To assess the effects of the size of the unit cell, some models with different number of unit cells are generated and their stress-strain responses are compared with each other. Figure 9 shows the resulted meshed RVEs for a 13% porous sample and Fig. 10 compares their stress-strain responses. As it is obvious, the difference between these stress-strain curves is slight, so it can be concluded that only one unit cell is sufficient for the modeling purposes. Notice that all the RVEs have three symmetry planes and can be reduced to one-eighth with the boundary conditions of section 5 for computational efficiency.

Fig. 9
figure 9

The meshed model of the RVEs with (a) N = 1, (b) N = 2, (c) N = 3

Full size image
Fig. 10
figure 10

The effects of the number of unit cells on the stress-strain response of PSMAs

Full size image

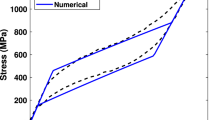
Figure 11 compares the predicted stress-strain curve for 13% porous NiTi using this model with the experimental response reported by Zhao et al. (Ref 30). A good correlation is observed between the modeling and experimental results indicating the validity of the proposed approach. Unlike dense SMAs, due to the inhomogeneity of stress in PSMAs, the phase transformation does not happen suddenly. Therefore, a smooth transition from elastic region to transformation region is observed. A similar trend was also reported by Panico and Brinson (Ref 41).

Fig. 11
figure 11

Stress-strain curve of a 13% porous NiTi

Full size image

Effect of Pore Volume Fraction on the Stress-Strain Curve

In this subsection, the effects of pore volume fraction on the stress-strain curve of PSMAs are assessed using the unit cell model. First, the value of δ should be calculated to obtain the desired PVF using Fig. 6. The values of δ for different PVFs considered in this study are presented in Table 2.

Table 2 The values of δ for different PVFs
Full size table

Figure 12 shows the stress-strain curve of PSMAs with different values of PVF. As shown in this figure, the transformation stresses reduce as the PVF increases because the applied macroscopic stress can cause higher local stresses in some regions where the transformation initiates. It causes a smaller hysteresis cycle in the stress-strain curve too. It is also observed that the hardening rate during phase transformation is smaller for larger PVFs. This observation is opposed to what was reported by Panico and Brinson (Ref 41). They predicted that the hardening rate in phase transformation region of PSMA’s response is much higher than that of dense SMA. However, Zhao and Taya (Ref 33) and Sepe et al. (Ref 42) obtained similar trend to what is reported in the present paper. This phenomenon could be due to the reduction in the amount of stresses for the start and finish of martensitic transformation as well as the elastic modulus of PSMA. When the PVF increases, the stress concentration around the pores increases and causes strain localization. Accordingly, smaller macroscopic stress is needed to achieve a specific value of strain meaning a smaller hardening rate. As another reason by increasing the value of PVF, the values of austenite and martensite elastic modulus decrease leading to reduction in the total stiffness of the material. To prove this claim, as shown in Fig. 2, the slopes of loading and unloading portions of the stress-strain curve are used to calculate the elastic moduli of austenite and martensite, respectively. Figure 13 shows the variation of austenite as well as martensite elastic modulus of PSMA as a function of PVF. Referring to this figure, it is obvious that these elastic moduli are both decreased almost linearly by increasing the value of PVF. Since the slop of the stress-strain response in the transformation region is a direct function of these elastic moduli, the hardening rate decreases by increasing the value of PVF.

Fig. 12
figure 12

Stress-strain responses of PSMAs for different PVFs

Full size image
Fig. 13
figure 13

Variation of austenite as well as martensite elastic modulus of the porous samples as a function of PVF

Full size image

Effect of Randomness Value on the Stress-Strain Response

Since the microstructures of porous materials are almost random, it is worthwhile to assess the effects of random microstructure on the stress-strain curve of PSMAs with different PVFs. To achieve this goal, a random model is generated according to the procedure described in section 4. Due to the random inherence of the model, the results can be different from case to case. To reduce the effect of randomness, for each level of randomness (β), five simulations are run and the average stress-strain curve is reported.

To reduce the effects of size dependency, the number of unit cells in each edge of the cube is repeatedly increased until variations in the results become negligible. Using this method, the difference between the results for N = 2 and N = 3 are negligible. Therefore, all the simulations are performed using N = 2. Figure 14 shows a meshed illustration of a random model with N = 2 and β = 0.1. In this figure, the black bold lines show the edges of the cell walls. It should be noted that the random model is meshed using the same element type as that used for unit cell model and that mesh study is also carried out for each value of β.

Fig. 14
figure 14

The meshed illustration of a random model with N = 2 and β = 0.1

Full size image

Figure 15(a)-(c) shows the average stress-strain response of PSMAs with the PVF values of 5, 15, and 35% when the values of 0.0, 0.1, and 0.2 are selected for the parameter β. It can be seen that the value of β does not considerably affect the stress-strain curve of PSMA with small values of PVF. However, the effect of β is more pronounced for larger values of PVF.

Fig. 15
figure 15

The average stress-strain curve of PSMAs for different amounts of β when PVF is (a) 5%, (b) 15%, and (c) 35%

Full size image

The stress-strain response of a 42% porous NiTi specimen fabricated by Entchev and Lagoudas (Ref 29) is compared with the numerical stress-strain responses for several values of β in Fig. 16(a). These simulations are performed using the material parameters reported in Table 3. These material parameters are obtained using those reported in (Ref 29).

Fig. 16
figure 16

(a) Stress-strain response of 42% porous Niti for several values of β (b) the average value of maximum von-Misses stresses in the pores of the PSMA vs. the level of randomness

Full size image
Table 3 Material parameters utilized for the simulation of 42% porous NiTi
Full size table

As shown in Fig. 16(a), by increasing the value of β, the stress-strain response saturates to a limit curve which correlates with the experimental one. In addition, it can be concluded from this figure that the transformation stresses, tangent modulus, and the rate of hardening in transformation region increase by an increase in the level of randomness. These observations may be attributed to the more uniform stress distribution in the random microstructures rather than regular ones. To support this claim, as shown in Fig. 14, the maximum von-Misses stress in each cell of the finite element model is obtained, and the average value of this maximum stresses, \(\sigma_{ \hbox{max} }^{av}\), is depicted in Fig. 16(b) as a function of β. Referring to this figure, the average value of maximum stresses in the pores decreases by increase in the value of β (meaning more uniform stress distribution in the pores). Notice that the finite element model is constructed by eight cells.

Conclusion

This paper deals with the numerical simulation of the mechanical stress-strain response of porous shape memory alloys under uniaxial compression. A three-dimensional SMA constitutive model based on microplane theory is attributed to the bulk material. A unit cell model is generated by cutting one-eighth of a sphere with three planes parallel to xy, xz, and yz placed at a predefined position to obtain a desirable pore volume fraction. The bulk material is attributed to the model using a user material subroutine (UMAT) in ABAQUS, and the model is solved using finite element analysis. The results are shown to be in good agreement with available experimental findings. The effect of pore volume fraction on the stress-strain response is also assessed. The results show that the transformation stresses and the rate of hardening during transformation decrease by an increase in the value of pore volume fraction. To investigate the effects of random microstructure, a random model is also proposed by repeating N unit cells along x, y, and z axes followed by moving the centers of the spheres to a random position. The results illustrate that randomness in the microstructure does not have significant effects on the stress-strain response of PSMAs for low pore volume fractions. However, as the pore volume fraction increases, the effects of randomness are more pronounced.