Asymptotic homogenization of fibre-reinforced composites: a virtual element method approach

Abstract

A virtual element method approach is presented for solving the unit cell problem, in application of the asymptotic homogenization method, and computing the antiplane shear homogenized material moduli of a composite material reinforced by cylindrical inclusions of arbitrary cross section. Validation of the proposed numerical method is proved by comparison with analytical and numerical reference solutions, for a number of micro-structural arrays and for different grading properties of the material constituents. A point on numerical efficiency is also made with respect to the possibility of local refinement granted by the innovative numerical procedure which relies on a mesh conformity concept ampler than the one of classical finite element method. The flexibility of the method allows for a large variety of microstructure shapes.

1 Introduction

Composite materials are extensively used in engineering applications due to their interesting material properties as for instance high strength to weight ratios which can be optimized for withstanding operational loads. Application of composite materials requires accurate yet practical methods of analysis of their mechanical response. It is commonly accepted that even for large structural components, the behavior of these frameworks depends on the composite microstructure. Analysis methods are therefore devised seeking to approximate composite structural mechanics by analyzing a representative (smaller) part of the composite microstructure, commonly called a representative volume element (RVE). The term RVE seems to have been coined by Hill [28] and has also been detailed extensively by Hashin [26]. RVE based methods decouple analysis of a composite material into analyses at the local and global levels. The local level analysis models the microstructural details to determine effective elastic properties. The composite structure is then replaced by an equivalent homogeneous material having the calculated effective properties. Such a process of calculating effective properties is called material homogenization [43].

Homogenization theory as a means of determining effective material properties for composite materials containing inclusions with a microstructure received a significant thrust in research effort dating from the early 70s [15, 32, 39] with more insights into mathematical aspects and engineering applications of homogenization theory to diverse fields [15]. Many of these extensive contributions began in France in the late 1970s and continued through the 1980s [15, 22, 33, 35, 36, 40, 43]. If on the one hand most scientists and scientific works were involved into more mathematical aspects of the theory as convergence estimates for elliptic operators specific of these kinds of media or the influence of different boundary conditions on convergence estimates of solutions of the microscopic balance equation [43], a parallel research line was focused on computational aspects of homogenization theory as applied to composite material analysis [29, 31, 37, 38, 41, 45] also gaining advantage from the progressively growing large scale computing facilities.

With no claim of giving here a complete review of the immeasurable literature inherent to the latter research course, we wish to focus on some of the key aspects of this type of approaches which, to some extent, all share common tasks, one being the need of solving a boundary value problem at the microscale level on the so called representative unit cell or representative unit volume element. It is well known that such a problem possibly faces some entangled typical features as strong gradients or even localized discontinuity of the solution, when highly different material phases are present in the unit cell or when the geometric disposition of inclusions into a matrix implies resolving complex irregular regions. In this regard, a significant issue is represented by random media, for which an asymptotic homogenization approach still applies requiring to solve a high number of representative unit cell problems randomly generated [31] and then to determine average material properties in a statistical sense. For these reasons, an efficient, versatile, possibly low cost computational tool is of great importance in circumventing the aforementioned difficulties for the practical application of the homogenization method [31]. Classically, the most utilized method in the above application is the finite element method which is capable of giving highly satisfactory results, yet possibly suffering from the mentioned difficulties inherent of these applications.

The virtual element method (VEM) is a new technology for the approximation of partial differential equation problems, introduced as an evolution of modern mimetic finite difference schemes [10, 12], which shares the same variational background of the finite element method [9, 30, 46]. The initial motivation of VEM is the need to construct an accurate Galerkin scheme with the flexibility to deal with highly general polygonal/polyhedral meshes, including hanging vertices and non-convex shapes, retaining the conformity of the method, i.e. the property to build an approximated solution which shares the same regularity features as the analytical solution of the problem under consideration. By making use also of non-polynomial shape functions, but avoiding the explicit construction of the local basis functions, the VEM can easily handle general polygons/polyhedrons without complex integrations on the element and easily implement highly regular discrete spaces [18].

Polygonal meshes can be very useful for the application at hand where, for instance, meshing the domain of the unit cell with complex inclusion shapes may constitute a problem of its own when using standard techniques. In this regard, the VEM permits to very easily use features as hanging nodes, adaptively moving and refined meshes. Indeed, the interest in numerical methods that are capable of dealing with general polytopal meshes is significantly increasing in the mathematical and engineering community. Several works in the area of polygonal finite element method [42] as well as in applications concerning advanced problems in structural mechanics, [1, 16, 21, 34, 44] have been presented. Recently, applications of the Virtual Element method to problems of computational solids and structural mechanics have been introduced in [11] for (possibly incompressible) two dimensional linear elasticity, in [25] for three dimensional linear elasticity, in [13] for general two dimensional elastic and inelastic problems, in [20, 25] for large deformation elasticity in two and three dimensions and in [2, 3, 8] for higher order interpolations and highly nonlinear inelastic material behavior. Other recent applications involve contact mechanics problems [16], topology optimization [24], and 2D elasticity in mixed form [6, 7].

The aim of the present contribution is therefore to devise a procedure based on VEM method for solving the unit cell problem when asymptotic homogenization of a composite material reinforced with cylindrical parallel fibre is applied. The treatment in the present context refers to the shear antiplane problem [4, 5, 31] a classical problem of computational homogenization for which many contributions both in the framework of approximate and closed form solutions have been presented in the recent past.

Attention will focus on the specific features granted by the newly developed methodology in overcoming efficiently the numerical difficulties that may arise due to geometric features of the domain, material properties of matrix and fibre inclusion and steep variation of the solution across the material interfaces. A hint on a possible strategy for local mesh refinement guided by a somehow heuristic rule is also provided only to indicate a possible future research direction, namely the development of a robust a posteriori error estimator for the local refinement.

The paper outline is as follows. In Sect. 2, the mathematical statement of the problem under consideration is introduced and the homogenized equation is presented; Sect. 3 focuses on the development of a virtual element method for the cell problem and the relative solution strategy; in Sect. 4 a numerical campaign is carried out to validate the proposed formulation, to assess its accuracy and to show practical applicability of the method to parametric analysis of the influence of the unit cell geometrical/material features on the effective properties. A short insight on a heuristic local mesh refinement strategy closes the section. Finally, some concluding remarks and future directions are drawn in Sect. 5.

2 Asymptotic homogenization of fibre reinforced composite materials

Homogenization theory developed from studies of partial differential equations with rapidly varying coefficients. Two explicit assumptions are made in homogenization theory. First, it is assumed that fields vary on multiple spatial scales due to the existence of a microstructure. Second, it is assumed that the microstructure is spatially periodic. The aim is to represent a complex, rapidly-varying medium by a slowly-varying medium in which the fine-scale structure is averaged out in an appropriate way.

For the developments of the present work, we will refer to a composite material made of two constituents, namely long cylindrical fibre-like inclusions, embedded into a material surrounding matrix. Fibres are arranged according to a regular grid or lattice determined by two families of planes, respectively parallel to and forming an angle $\varphi$ with $x_1$ axis, as can be seen in Fig. 1a. The heterogeneous microstructure in the plane orthogonal to the inclusion axis consists of a two dimensional array of unit cells, developing periodically along the $x_1$ and $\varphi$ directions. The unit cell, i.e. the micro structure of the composite, can be appreciated in Fig. 1b. The cell sides measure $L_1$ and $L_2$ respectively, while the cell angle is denoted by $\varphi$.

Fig. 1

Composite material with long cylindrical inclusions. a Microstructure lattice with cell doubly periodic arrangement. b Unit cell fibre/matrix geometric features

In order to compute the effective material shear moduli of the composite via asymptotic homogenization a family of problems is introduced, indexed by a parameter $\varvec{\varepsilon }$: the ratio of the microstructure size to the total size of the analysis region (Fig. 1a). The homogenization limit is obtained by letting $\varvec{\varepsilon }$ go to zero.

In the framework of antiplane shear deformation, the problem of determining the longitudinal displacement field $w_{\varvec{\varepsilon }}$ in the composite domain is stated as follows:

$$ \text {div}({\varvec{G}} \nabla w_{\varvec{\varepsilon }})=0,\quad \text {in } \quad \varOmega ^{\text {f}}_{\varvec{\varepsilon }}\cup \varOmega ^{\text {m}}_{\varvec{\varepsilon }}; $$

(1)

$$ \llbracket \varvec{G}\nabla w_{\varvec{\varepsilon }} \cdot \varvec{\nu }\rrbracket =0, \quad \text {on } \quad \varGamma _{\varvec{\varepsilon }}; $$

(2)

$$ \varvec{G}\nabla w_{\varvec{\varepsilon }} \cdot \varvec{\nu }= \frac{1}{\varvec{\varepsilon }}D\llbracket w_{\varvec{\varepsilon }} \rrbracket , \quad \text {on } \quad \varGamma _{\varvec{\varepsilon }}. $$

(3)

Here $\varOmega ^{\text {f}}_{\varvec{\varepsilon }}$ and $\varOmega ^{\text {m}}_{\varvec{\varepsilon }}$ denote fibre and matrix domains respectively, $\varGamma _{\varvec{\varepsilon }}$ is the union of fibre/matrix interfaces, $\varvec{\nu }$ is the normal unit vector to $\varGamma _{\varvec{\varepsilon }}$ pointing into $\varOmega ^{\text {m}}_{\varvec{\varepsilon }}$, and square brackets $\llbracket \cdot \rrbracket$ denote the jump of the enclosed quantity across the interface, defined as extra-fibre value minus intra-fibre value.

Equation (1) is the field equilibrium equation; Eq. (2) represents the continuity of the normal-to-interface component of the shear stress hence equilibrium at fibre/matrix interface; (3) describes the interface constitutive law, being D a material parameter characterizing fibre/matrix strength. These equations must be complemented by suitable boundary conditions on the boundary of the domain $\varOmega =\varOmega ^{\text {f}}_{\varvec{\varepsilon }}\cup \varGamma _{\varvec{\varepsilon }}\cup \varOmega ^{\text {m}}_{\varvec{\varepsilon }}$.

Fibres and matrix are assumed to be linear elastic, and their shear moduli are collected in the constitutive tensor $\varvec{G}$, which specializes in

$$ \varvec{G}=\varvec{G}^{\text {f}}\quad \text {in}\,\, \varOmega ^{\text {f}}_{\varvec{\varepsilon }}, \quad \varvec{G}=\varvec{G}^{\text {m}}\quad \text {in}\,\, \varOmega ^{\text {m}}_{\varvec{\varepsilon }}. $$

(4)

The matrix material is homogeneous and isotropic, so that $\varvec{G}^{\text {m}}= G^{\text {m}}{\mathbf{I}}$, with ${\mathbf{I}}$ the second order identity tensor and $G^{\text {m}}$ the matrix shear modulus. In general fibres are taken of a linear elastic, cylindrically-orthotropic material; in the case of circular cross section their material moduli may be functionally-graded along the fibre radius. In the latter case, introducing a polar coordinate system $(O,r,\theta )$ as depicted in Fig. 1b, the fibre elasticity tensor is:

$$ \varvec{G}^{\text {f}}= ( G^{\text {r}}\varvec{e}^{\text {r}}\otimes \varvec{e}^{\text {r}}+ G^{\theta }\varvec{e}^{\theta }\otimes \varvec{e}^{\theta })g(\rho ), $$

(5)

where

$$ \rho =\frac{r}{R} $$

(6)

is the radial dimensionless coordinate, $\varvec{e}^{\text {r}}$ and $\varvec{e}^{\theta }$ are the radial and tangential unit vectors, respectively, $\otimes$ denotes the tensor product, and the dimensionless function $g(\rho )$ expresses the material grading law along the radial direction. Accordingly, $G^{\text {r}}g(0)$ and $G^{\theta }g(0)$ [respectively, $G^{\text {r}}g(1)$ and $G^{\theta }g(1)$] are the radial and tangential shear moduli at the fibre axis [respectively, boundary].

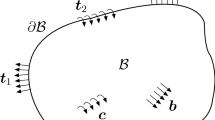
Fibre/matrix interfaces are assumed to have zero-thickness and to be imperfect. The linear spring-layer model, linearly relating the displacement discontinuity $\llbracket w_{\varvec{\varepsilon }} \rrbracket$ to the interface traction $\varvec{G}\nabla w_{\varvec{\varepsilon }} \cdot \varvec{\nu }$, in terms of the spring constant parameter D is adopted [17, 27, 33]. According to this model, interfaces have a physical thickness t which, though much smaller than the microstructural length scales $L_1$ and $L_2$, rescales as the latter ones in the homogenization process [see Fig. 1a and cfr. Eq. (3)] to justify the present zero-thickness model.

Well posedness of the above problem is guaranteed by the following hypotheses:

$$ G^{\text {m}}>0, \quad G^{\text {r}}>0, \quad G^{\theta }>0, \quad D>0,\quad g(\rho )>0\quad \text {in}\ (0,1]. $$

(7)

2.1 Homogenized equilibrium equation

The asymptotic homogenization method employed to derive the homogenized or effective constitutive tensor of the composite material is sketched here for the sake of compactness. Accounts on details and theoretical background may be found for example in [15, 40]. In what follows, notation and presentation as of [4, 5] will be adopted.

As shown in Fig. 1a, two different length scales characterize the problem under consideration. Hence, two different space variables are introduced: the macroscopic one, x, and the microscopic one, $y=x/\varvec{\varepsilon }$, $y \in Q$, being Q the unit cell (see Fig. 1b), whose intra-fibre space, extra-fibre space and fibre-matrix interface are denoted by $Q^{\text {f}}$, $Q^{\text {m}}$ and $\varGamma$, respectively. Accordingly, the divergence and gradient operators are given by the following relations:

$$ \text {div}= \text {div}_{x} + \frac{1}{\varvec{\varepsilon }}\, \text {div}_{y}, \quad \nabla = \nabla _{x} + \frac{1}{\varvec{\varepsilon }} \nabla _{y}. $$

(8)

An asymptotic expansion of the unknown displacement field is considered in the form:

$$ w_{\varvec{\varepsilon }}(x,y)=w_{0}(x,y) + \varvec{\varepsilon }w_{1}(x,y) + \varvec{\varepsilon }^2 w_{2}(x,y)+ \cdots , $$

(9)

where $w_{0}$ is the macroscopic or average value of the field variable, $w_{1}$, $w_{2}$ are Q-periodic functions in y representing perturbations in the field variable due to the microstructure, with zero integral average over Q.

Equation (9) implies that quantities on the local level like stress vary $\varvec{\varepsilon }$ times more rapidly than corresponding global level quantities. Substituting (9) into Problem (1)–(3) and equating the power-like terms of $\varvec{\varepsilon }$, three differential problems for $w_{0}$, $w_{1}$ and $w_{2}$ are obtained, respectively. The problem for $w_{0}$ is:

$$ \text {div}_{y}(\varvec{G}\nabla _{y} w_{0})=0, \quad \text {in } \quad Q ^{\text {f}}\cup Q ^{\text {m}}; $$

(10)

$$ \llbracket \varvec{G}\nabla _{y} w_{0} \cdot \varvec{\nu }\rrbracket = 0, \quad \text {on } \quad \varGamma; $$

(11)

$$ \varvec{G}\nabla _{y} w_{0} \cdot \varvec{\nu }=D\llbracket w_{0} \rrbracket , \quad \text {on }\quad \varGamma. $$

(12)

Problem (10)–(12), taking into account (7), implies that $w_{0}=w_{0}(x)$ [33]. The problem for $w_{1}$ is:

$$ \text {div}_{y}[\varvec{G}(\nabla _{y} w_{1} + \nabla _{x} w_{0})]=0, \quad \text {in } \quad Q ^{\text {f}}\cup Q ^{\text {m}}; $$

(13)

$$ \llbracket \varvec{G}(\nabla _{y} w_{1} + \nabla _{x} w_{0})\cdot \varvec{\nu }\rrbracket = 0, \quad \text {on } \quad \varGamma; $$

(14)

$$ \varvec{G}(\nabla _{y} w_{1} + \nabla _{x} w_{0})\cdot \varvec{\nu }= D\llbracket w_{1} \rrbracket , \quad \text {on }\quad \varGamma.$$

(15)

Introducing the cell function $\varvec{\chi }(y)$, the function $w_{1}$ is represented in the following form [15, 40]:

$$ w_{1}(x,y)=-\varvec{\chi }(y) \cdot \nabla _{x} w_{0}(x), $$

(16)

where the components $\chi _h, h=1,2$, are the unique, null average, Q-periodic solutions of the cell problem:

$$ \text {div}_{y}[\varvec{G}(\nabla _y \chi _{h}- \varvec{e}_h)]=0, \quad \text {in } \quad Q ^{\text {f}}\cup Q ^{\text {m}}; $$

(17)

$$ \llbracket \varvec{G}(\nabla _y \chi _{h}- \varvec{e}_h) \cdot \varvec{\nu }\rrbracket = 0, \quad \text {on } \quad \varGamma; $$

(18)

$$ \varvec{G}(\nabla _y \chi _{h}- \varvec{e}_h) \cdot \varvec{\nu }=D\llbracket \chi _{h} \rrbracket, \quad \text {on }\quad \varGamma , $$

(19)

with $\varvec{e}_{h}$ the unit vector parallel to the $y_{h}$ axis.

The problem for $w_{2}$ hence results:

$$ \text {div}_{y}[\varvec{G}(\nabla _{y} w_{2} + \nabla _{x} w_{1})] = -\,\text {div}_{x}[\varvec{G}(\nabla _{y} w_{1} + \nabla _{x} w_{0} )], \quad \text {in } \quad Q ^{\text {f}}\cup Q ^{\text {m}}; $$

(20)

$$ \llbracket \varvec{G}(\nabla _{y} w_{2} + \nabla _{x} w_{1})\cdot \varvec{\nu }\rrbracket = 0 , \quad \text {on }\quad \varGamma; $$

(21)

$$ \varvec{G}(\nabla _{y} w_{2} + \nabla _{x} w_{1})\cdot \varvec{\nu }= D\llbracket w_{2} \rrbracket, \quad \text {on }\quad \varGamma.$$

(22)

Integrating (20) both in $Q^{\text {f}}$ and in $Q^{\text {m}}$, using the Gauss-Green Lemma, adding the two contributions and exploiting (21), the following equation is obtained:

$$ \frac{1}{|Q|}\int _{Q ^{\text{f}}{\cup}Q ^{\text{m}}} {\text{div}}_{x}[{\varvec{G}}(\nabla _{y}w_{1} +\nabla _{x} w_{0}) ] {\text{d}}a=0,$$

(23)

where ${\text {d}}a$ is the area element of $Q ^{\text {f}}\cup Q ^{\text {m}}$ and $|\cdot |$ is the Lebesgue measure. Substituting (16) into (23), the homogenized equation for the macroscopic displacement $w_{0}$ is finally derived:

$$ \text {div}_x(\varvec{G}^{\#}\nabla _{x} w_{0})=0. $$

(24)

Here $\nabla _{x} w_{0}$ is the macroscopic shear strain, and

$$ \varvec{G}^{\#}= \frac{1}{|Q|}\int _{Q ^{\text {f}}\cup Q ^{\text {m}}} \varvec{G}({\mathbf{I}}-\nabla _y^\text {t}\varvec{\chi }) \, {\text {d}}a $$

(25)

are the effective shear moduli, where the superscript $^\text {t}$ denotes the transpose.

Equation (25) yields the effective shear moduli of the composite material in terms of the solution $\varvec{\chi }$ of the cell problem. The cell function is involved with the particular form assumed for $\varvec{G}^{\text {f}}$. In the following section, a virtual element methodology is presented to solve the above problem for various setups of the unit cell and of the fibre/matrix constitutive laws.

3 A $C^0$ virtual element method

Letting the auxiliary cell function be:

$$ \tilde{\varvec{\chi }} = \varvec{\chi }- (y_1\varvec{e}_1+y_2\varvec{e}_2), $$

(26)

a weak formulation for the cell problem (17)–(19) is provided by the virtual work principle:

$$\left\{\begin{array}{ll} {\text{Find}}\,{\tilde{\chi}}_s \in {\tilde{\mathbf{V}}}& {\text {such\,that}} \\ a(\tilde{\chi }_s,\delta \chi _s) = 0 & \forall \, \delta \chi _s \in \mathbf{V},\; s=1,2 \end{array}\right.$$

(27)

where $\tilde{\mathbf{V}}:=H^1_{sp}(\varOmega )$ is the space of the admissible auxiliary cell functions which are shift $Q$-periodic, i.e. such that the corresponding $\varvec{\chi }(y_1,y_2)$ function, restricted to matrix subdomain, satisfies:

$$ \varvec{\chi }^{\text {m}}(y_1+L_1,y_2)=\varvec{\chi }^{\text {m}}(y_1,y_2)=\varvec{\chi }^{\text {m}}(y_1+L_2\cos \varphi ,y_2+L_2\sin \varphi ).$$

(28)

and where ${\mathbf{V}}:=H^1_p(\varOmega )$ is the space of their admissible $Q$-periodic variations. The bilinear form characterizing the variational formulation is:

$$a(\tilde{\chi }_s,\delta \chi _s) = \int _{\varOmega } {\text {div}}_{y}[\varvec{G}(\nabla _y {\tilde{\chi }}_s)] \,\delta \chi _s\,{\mathrm{d}} {\mathbf{x}}$$

(29)

which, exploiting Gauss-Green lemma, considering constitutive equation (19) and that unit normal vectors to $\partial \varOmega ^m$ on opposite sides of the unit cell are opposite, becomes:

$$ a(\tilde{\chi }_s,\delta \chi _s)= \int _{\varOmega } \nabla \delta \chi _s\, \cdot \, \varvec{G}(\nabla _y \tilde{\chi _s}) \mathrm{d}{\mathbf{x}}+ \int _{\partial \varOmega ^f} \llbracket \delta \chi _s \rrbracket \, D \, \llbracket \tilde{\chi }_s \rrbracket \,\mathrm{d}l $$

(30)

The form $a(\cdot ,\cdot )$ is symmetric, continuous and coercive on $\tilde{\mathbf{V}}$, so that problem (27) is well posed.

3.1 The virtual element space

Proceeding with presenting the virtual element method for the problem under consideration, we state right from the onset that the definition of the VEM discrete space of approximation shares consistent similarities with the finite element method for elliptic problems in primal form. The discrete (virtual) space of admissible cell functions is the same one introduced in [10,11,12, 25]. We here follow the guidelines and notation of [2].

Let ${\mathcal {T}}_h$ be a simple polygonal mesh on $\varOmega$, i.e. any decomposition of $\varOmega$ in a finite set of simple polygons $E$, without holes and with boundary given by a finite number of non-flipping straight line segments. Furthermore, such mesh is intended to be conforming with respect to $\varGamma$ interface, whose discretized counterpart is the union of edges of polygons lying adjacent of it. Here $\mathcal{E}_h$ denotes the set of the edges of ${\mathcal {T}}_h$. An edge of a polygon E is indicated by e, (i.e. $e \in \partial E$), and m represents the number of edges of E. A sample element is drawn in Fig. 2. Like the finite element space, the space $\tilde{\mathbf{V}}_h$ is defined introducing spaces $\tilde{\mathbf{V}}_{h|E}$ local to elements by means of the associated local degrees of freedom.

Fig. 2

Sample polygonal element with $m=5$ straight edges. Vertices, edge ordering and numbering are indicated. Local degrees of freedom for $k=2$ order interpolation are indicated as: black circles—vertex degrees of freedom, red diamonds—edge degrees of freedom, blue square—internal degree of freedom. (Color figure online)

Given a positive integer k, representing the “degree of accuracy” of the method, for any polygon $E\in {\mathcal {T}}_h$, the local virtual element space, is defined as:

$$\begin{aligned} {\tilde{\mathbf{V}}}_{h|E}=\big \{&\tilde{\chi }_{sh} \in H^1(E) \cap C^0(E) : {\text {div}}_{y}[\varvec{G}(\nabla _y \tilde{\chi }_{sh})] \in {\mathsf {P}}_{k-2}(E) ,\\&{\tilde{\chi }}_{sh}|_e \in {\mathsf {P}}_k(e) \quad \forall e \in \partial E\big \} , \end{aligned}$$

(31)

where $\mathsf {P}_k(E)$ denotes the space of polynomials of degree (up to) k defined on E, setting $\mathsf {P}_{-1}(E) = \{ 0 \}$, and where $s=1,2$, respectively. To ease notation, in the following, the subscript s will be omitted, assuming implicitly that any derivation is valid for $\tilde{\chi }_{1h}$ and $\tilde{\chi }_{2h}$, respectively, therefore indicating either unknown with $\tilde{\chi }_h$.

A sample polygon with $m=5$ edges is represented in Fig. 2 with relative vertices and edges ordering. For any $E\in {\mathcal {T}}_h$, the degrees of freedom for the unknown field $\tilde{\chi }_h \in \tilde{\mathbf{V}}_{h|E}$ over E are:

• (for $k>0$): m interpolatory values for $\tilde{\chi }_h$, chosen as the values $\tilde{\chi }_h(\nu _i)$ at vertices $\nu _i$ of E, $i=1,2, \ldots ,m$;

• (for $k>0$): $m(k-1)$ interpolatory values for $\tilde{\chi }_h$, chosen as the values $\tilde{\chi }_h(\varvec{x}^{e}_j)$ at edge internal (i.e. not comprising extrema of edge e) nodes $\{\varvec{x}^{e}_j \}$ , $j=1, \ldots ,k-1$;

• (for $k>1$): $k(k-1) / 2$ non-interpolatory (also termed internal degrees of freedom) values for $\tilde{\chi }_h$, chosen as area-averaged scaled integral moments of $\tilde{\chi }_h$ with respect to the monomials of the canonical basis of $\mathsf {P}_{k-2}(E)$.

Remark 1

Upon choosing local-to-element scaled space coordinates $(\xi \; \eta )$, given by:

$$ \xi = \frac{x - x_c}{h_E} \ , \quad \eta = \frac{ y - y_c}{h_E}, $$

(32)

where $( x_c \; y_c)$ denotes the coordinates of the centroid of E, and $h_E$ its diameter, the definition of the $k(k-1)/2$ internal degrees of freedom, arising for $k>1$, is set by considering the following basis for the space $\mathsf {P}_{k}(E)$

$$ \varTheta ^{k} = \left\{ \xi ^{\alpha } \eta ^{\beta } \ \text { with } \ \alpha ,\beta \in {\mathbb {N}}, \, \alpha + \beta \le k \right\} .$$

(33)

The $r:=k(k+1)/2$ monomials of basis (33) are named accordingly $q_1,q_2, \ldots ,q_r$ and ordered as of Pascal’s triangle.

The dimension of the space ${\tilde{\mathbf{V}}}_{h|E}$ results

$$ n = {\text {dim}}({\tilde{\mathbf{V}}}_{h|E}) = mk + k (k+1) / 2, $$

(34)

A local “Lagrange-type” approximation for $\tilde{\chi }_h \in \tilde{\mathbf{V}}_{h|E}$ is still retained:

$$ \tilde{\chi }_h = \mathbf{N} ^V \hat{\tilde{\chi }}_h, $$

(35)

where ${\mathbf {N}} ^V$ is a $(1 \times n)$ matrix collecting the basis functions of $\tilde{\mathbf{V}}_{h|E}$, and $\hat{\tilde{\chi }}_h$ is the vector of the corresponding local degrees of freedom previously listed. Normality rule still applies as in standard finite element analysis, i.e. any $i-th$ basis function has unit value on the $i-th$ degree of freedom ($i=1, \ldots ,n$) and vanishes for the remaining ones, with the specification that, for any internal degree of freedom, evaluation of a basis function in correspondence to such a degree of freedom is to be intended as the averaged scaled moment with respect to the corresponding monomial of basis $\varTheta ^{k-2}$ [cf. Eq. (33)], i.e.

$$ \frac{1}{|E|}\int _E N^V_i q_j \mathrm{d}{\mathbf{x}}\quad i = 1, \ldots ,n ; \quad j = 1, \ldots ,r. $$

(36)

The ordering of the degrees of freedom in vector $\hat{\tilde{\chi }}_h$ and of the associated basis functions for the local space is the one stated previously and reported for the simple case $k=2$, $m=5$ with a pictorial view in Fig. 2. Concisely: first all the vertex DOFs according to vertex numbering, then edge-wise edge DOFs following edge sequencing, finally internal DOFs, according to the ordering of the first r monomials in Pascal’s triangle.

As in standard FE methods, the global space $\tilde{\mathbf{V}}_h \subseteq \tilde{\mathbf{V}}$ is built by assembling the local spaces $\tilde{\mathbf{V}}_{h|E}$ as usual:

$$ \tilde{\mathbf{V}}_h = \{ \tilde{\chi }_h \in \tilde{\mathbf{V}} \ : \ \tilde{\chi }_h |_{E} \in \tilde{\mathbf{V}}_{h|E} \; \forall E\in {\mathcal {T}}_h\}.$$

(37)

with the functions $\tilde{\chi }_h$ satisfying the properties [10, 11]:

• $\tilde{\chi }_h$ is a polynomial of degree $\le k$ on each edge e of $E$;

• $\text {div}_{y}[\varvec{G}(\nabla _y \tilde{\chi }_h)]$ is a polynomial of degree $\le k-2$ in $E$.

• $\tilde{\chi }_h$ is globally continuous on $\partial E$;

It is to be noted that the functions $\tilde{\chi }_h\in \tilde{\mathbf{V}}_{h|E}$ are explicitly known on $\partial E$; whereas they are fully implicit inside the element $E$. It also results: $\mathsf {P}_k(E) \subseteq \tilde{\mathbf{V}}_{h|E}$.

A virtual element method (VEM) for the above problem is constructed following a procedure that closely resembles the finite element approach, i.e. by restricting the original variational formulation (27) to the discrete space $\tilde{\mathbf{V}}_h$ and approximating the ensuing terms:

$$\left\{ {\begin{array}{ll} \text{find}\, \tilde{\chi }_h\,\in {\tilde{\mathbf{V}}}_h & \text{such that}\\a_h(\tilde{\chi }_h,\delta \chi _h) = 0& \forall \,\delta \chi _h \in {\mathbf{V}}_h, \end{array} } \right..$$

(38)

where $\tilde{\mathbf{V}}_h \subset {\mathbf{V}}$ is the virtual element space introduced previously, and $a_h(\cdot ,\cdot ) \, : \, \tilde{\mathbf{V}}_h \times {\mathbf{V}}_h \rightarrow {\mathbb R}$ is a discrete bilinear form approximating $a(\cdot ,\cdot )$.

The discrete bilinear form is built element by element, assuming:

$$ a_h(\tilde{\chi }_h,\delta \chi _h)=\sum _{{E\in {\mathcal {T}}_h}} a_h^{E}(\tilde{\chi }_h,\delta \chi _h)\quad \forall \, \tilde{\chi }_h \in \tilde{\mathbf{V}}_h,\,\delta \chi _h\,\in {\mathbf{V}}_h.$$

(39)

3.2 Projector for the gradient

Either the functions of the space $\tilde{\mathbf{V}}_h$ or their gradient are not known explicitly; hence, the bilinear forms $a_h^E(\cdot ,\cdot )$ cannot be evaluated at element level by standard Gauss integration. Therefore, following [2] (see also [10, 12]) a projection operator $\varPi$ is here introduced, representing the approximated gradient associated with the virtual auxiliary cell function $\tilde{\chi }_h$. This key ingredient of the virtual element method is defined as the following $L^2$ projection:

$$\begin{aligned} \varPi : &\tilde{\mathbf{V}}_{h|E} \longrightarrow [\mathsf {P}_{k-1}(E)]^{2} \nonumber \\&\quad \tilde{\chi }_h \; \mapsto \quad \varPi (\tilde{\chi }_h) , \end{aligned}$$

(40)

Given $\tilde{\chi }_h \in \tilde{\mathbf{V}}_{h|E}$, such an operator $\varPi$ is defined as the unique vector-valued function $\varPi (\tilde{\chi }_h) \in [\mathsf {P}_{k-1}(E)^{2}]$ that satisfies the condition:

$$ \int _{E} \varPi (\tilde{\chi }_h)^T \varvec{g}^{P} = \int _{E} (\nabla \tilde{\chi }_h)^T \varvec{g}^{P} ,\quad \forall \varvec{g}^{P} \in [\mathsf {P}_{k-1}(E)]^{2},$$

(41)

where, for ease of computation, Voigt notation is introduced for gradient vectors and relevant scalar product. The $\varPi$ operator represents the best approximation of the gradient field (in the square integral norm) in the space of piecewise polynomial vectors of degree $(k-1)$. Although the functions in $\tilde{\mathbf{V}}_{h|E}$ are virtual i.e. not explicitly known in the element interior, the right hand side in (41) (and thus the operator $\varPi$) can be readily computed as it is made clear in the sequel, and provide a suitable approximation of the gradient term required by the weak form which becomes:

$$ a^E_h(\tilde{\chi }_h , \delta \chi _h) = \int _{E} \left[ \varPi (\delta \chi _h)\right] ^T \varvec{G}\varPi (\tilde{\chi }_h) + \int _{\partial \varOmega ^f} \llbracket \delta \chi _h \rrbracket \, D \, \llbracket \tilde{\chi }_h \rrbracket \,\mathrm{d}l + S^E \left( \tilde{\chi }_h , \delta \chi _h \right) $$

(42)

where $S^E(\cdot ,\cdot )$ is a suitable stabilizing term, needed to preserve the coercivity of the system, and described in the sequel.

Remark 2

Since the functions of $\tilde{\mathbf{V}}_h$ have piecewise polynomial restrictions on the element boundaries, the imposition of general boundary conditions as the ones typically found in computational homogenization problems, i.e. Dirichlet periodic boundary conditions on unit cell sides and jump at fibre/matrix interface follow the same procedure as in standard finite element approaches [38, 43] and can be implemented with no difficulty. Likewise, Neumann boundary conditions may be implemented by adding the usual boundary integral to the formulation.

The dimension of the virtual element space and of the polynomial space of approximated gradients [cf. Eqs. (34), (40)] are, respectively:

$$\begin{aligned} n &:= {\text {dim}}({\tilde{\mathbf{V}}}_{h|E}) = km + r \\ \ell &:= {\text {dim}}( [{\mathsf {P}}_{k-1}(E) ]^2) = k(k+1) \; . \end{aligned}$$

(43)

The vector valued basis functions for $[\mathsf {P}_{k-1}(E)]^2$ are taken as in (33) and ordered coherently in the following matrix:

$$\begin{aligned} {\mathbf {N}} ^P=\left[ \begin{array}{cccccccccccc} 1 &\quad 0 &\quad \xi &\quad 0 &\quad \eta &\quad 0 &\quad 0 &\quad \cdots &\quad \eta ^{k-1} &\quad 0 &\quad \\ 0 &\quad 1 &\quad 0 &\quad \xi &\quad 0 &\quad \eta &\quad 0 &\quad \cdots &\quad 0 &\quad \eta ^{k-1} \end{array} \right] . \end{aligned}$$

(44)

in such a way that, for any $\varvec{g}^{P} \in [\mathsf {P}_{k-1}(E)]^2$, $\varvec{g}^{P} = {\mathbf {N}} ^P \hat{\varvec{g}}$, with $\hat{\varvec{g}} \in \mathbb {R}^\ell$. Substituting the above definitions into Eq. (41), gives:

$$ \int _{E} \left( {\mathbf {N}} ^P \varPi ^{\text {m}} \hat{\tilde{\chi }}_h \right) ^{\text {T}} {\mathbf {N}} ^P \hat{\varvec{g}} = \int _{\partial E} \left( {\mathbf {N}} ^V \hat{\tilde{\chi }}_h \right) ^{\text {T}} \left( {\mathbf {N}} _E {\mathbf {N}} ^P \hat{\varvec{g}} \right)$$

(45)

which, integrating by parts the right hand side term yields

$$ \hat{\varvec{g}}^{\text {T}} \varPi ^{\text {m}} \mathcal {G} \hat{\tilde{\chi }}_h = \hat{\varvec{g}}^{\text {T}} \mathcal {B} \hat{\tilde{\chi }}_h, $$

(46)

with the matrices

$$ \mathcal {G} = \int _{E} \left( {\mathbf {N}} ^P\right) ^{\text {T}} {\mathbf {N}} ^P \in \mathbb {R}^{\ell \times \ell } $$

(47)

$$ \mathcal {B} = \int _{\partial E} \left( {\mathbf {N}} _E {\mathbf {N}} ^P\right) ^{\text {T}} {\mathbf {N}} ^V - \int _{E} \left( \varvec{\partial }{\mathbf {N}} ^P\right) ^{\text {T}} {\mathbf {N}} ^V \in \mathbb {R}^{\ell \times n}. $$

(48)

In the above expressions, $\varvec{\partial }= [\partial _{x} \, \partial _y]$ represents the divergence vector operator and ${\mathbf {N}} _E$ the unit normal vector to the polygon boundary.

Details on the computation of matrices (47) and (48) may be found in [2].

3.3 Stiffness matrix

Eq. (46) provides the required operator $\varPi ^{\text {m}}$ as the solution of a linear system [2]:

$$\varPi ^{\text {m}} = \mathcal {G}^{-1} \mathcal {B},$$

(49)

where $\mathcal {G}$ is clearly symmetric and positive definite.

Combining Eqs. (45) and (49), from (42), one obtains:

$$\int _{E} \left( \varPi (\delta \tilde{\chi }_h)\right) ^{\text {T}} \varvec{G}\varPi (\tilde{\chi }_h) = \int _{E} \left( {\mathbf {N}} ^P \mathcal {G}^{-1} \mathcal {B} \delta \hat{\tilde{\chi }}_h \right) ^{\text {T}} \varvec{G}\left( {\mathbf {N}} ^P \mathcal {G}^{-1} \mathcal {B} \hat{\tilde{\chi }}_h \right) = \delta \hat{\tilde{\chi }}^{\text {T}}_h {\mathbf {K}} _{\text {c}} \hat{\tilde{\chi }}_h $$

(50)

which defines explicitly the first part of the local element stiffness:

$$ {\mathbf {K}} _{\text {c}} = \mathcal {B}^{\text {T}} \mathcal {G}^{\text {-T}} \left[ \int _{E} \left( {\mathbf {N}} ^P \right) ^{\text {T}} \varvec{G}{\mathbf {N}} ^P \right] \mathcal {G}^{-1} \mathcal {B}. $$

(51)

3.3.1 Element matrix stabilization term

The discrete bilinear form cannot be composed of the consistent term alone, otherwise the coercivity of the system may be lost and physically unsound modes could arise. The presence of a stability term is therefore standard for the Virtual Element Method, as illustrated for instance in [1, 8, 10,11,12,13, 18]. In this sense, the presentation herein will be limited to stating the form of the stabilizing operator. Recalling that $\mathsf {P}_k(E) \subseteq \tilde{\mathbf{V}}_{h|E}$, let ${\mathbf{D}}$ denote the matrix associated to the change of basis from the space $\mathsf {P}_{k}(E)$ to $\tilde{\mathbf{V}}_{h|E}$. A stabilization strategy is obtained by considering the form $S^E(\tilde{\chi }_h,\delta {\chi }_h) = \delta \hat{\tilde{\chi }}_h^T {\mathbf {K}} _{S} \hat{\tilde{\chi }}_h$, taking:

$$ {\mathbf {K}} _{S} = \tau \, \text {tr}\,\left( {\mathbf {K}} _c\right) \left[ {\mathbf{I}}- {\mathbf{D}}\left( {\mathbf{D}}^{\text {T}} {\mathbf{D}}\right) ^{-1} {\mathbf{D}}^{\text {T}} \right] , $$

(52)

with $\tau$ a positive real number to be chosen appropriately [2, 8]. The total stiffness operator results

$$ a^E_h(\tilde{\chi }_h,\delta {\chi }_h) := \delta \hat{\tilde{\chi }}_h^T {\mathbf {K}} \hat{\tilde{\chi }}_h \quad \text {with} \quad {\mathbf {K}} = {\mathbf {K}} _c + {\mathbf {K}} _{S}. $$

(53)

The role of the stabilization matrix ${\mathbf {K}} _{S}$ is to keep the positivity of the discrete (local) energy form (up to the infinitesimal rigid body motions. We refer to the initial paper [10] for more details on the motivations of the stabilization term, while a comparison with the standard “single Gauss point” quadrilateral FEM element and the related hourglass mode control can be found in [19].

3.3.2 Boundary conditions

The line integral appearing in Eq. (30) is computed at global level as a sum of edge integrals of the jump of the auxiliary cell function $\tilde{\chi }_h$ along the discretization of the interior fibre/matrix interface. As such, it plays the role of an interior boundary condition and gives a corresponding contributions to the consistent stiffness in the rows corresponding to interpolatory degrees of freedom of the nodes lying on the edges of the elements facing the fibre/matrix interface. Likewise, periodicity boundary conditions on the cell function is enforced through the nodal values of the auxiliary cell function on the opposite edges of the matrix boundary. The latter requirement is carried out ensuring the appropriate vertices localization along the two couples of opposite sides of the matrix boundary which will have to be copied photographically. This aspect will be touched upon in the next section together with ensuing implications.

4 Numerical results

The numerical tests are divided in three subsections: (i) validation and accuracy assessment for a large number of material unit cell setups, (ii) application of the VEM computational homogenization tool to the parametric analysis of the overall properties of a selection of composite materials with different material properties and inclusion shapes, (iii) exploration of a heuristic local mesh refinement strategy and relevant implications on the computational cost for a given accuracy level.

4.1 Validation and accuracy assessment: circular fibres

The material setup of a unit cell is assigned through the dimensionless geometric parameters $\varphi$, $\kappa =L_2/L_1$, $v_f = |Q^{\text {f}}|/|Q|$, and the following material ones:

• orthotropy ratio $\sigma ^2=G^{\theta }/G^{\text {r}}$

• fibre/matrix stiffness ratio (contrast factor) $\xi =G^{\text {r}}g(1) /G^{\text {m}}$;

• grading intensity factor $\omega =g(0)/g(1)$;

• dimensionless interface parameter $\delta =D/(G^{\text {m}}L_1)$.

The simulations carried out in the present section for validation purposes refer to isotropic exponentially-graded circular fibres: in particular, $\sigma =1$ and $g(\rho ) = \exp (-\lambda \rho )$ (i.e. exponential grading along radial axis). Consequently, it turns out that $g(0)=1$, and $G^{\text {r}}=G^{\theta }$ represent the shear modulus at the fibre axis.

The simulations refer to two types of unit cell geometries, i.e. square array (i.e. $\varphi = \pi /2$, $\kappa = 1$) and parallelogram-like array (i.e. $\varphi = \pi /3$, $\kappa = 1$), for different values of the volume fraction. Each case is meshed adopting three type of element discretizations, respectively: triangles (Tri-mesh), polygons (Poly-mesh), and quadrilaterals (Quad-mesh). A pictorial representation of the presented geometrical schemes is given in Fig. 3. Such complex geometry have been meshed resorting to a free meshing tool [23] particularly suitable for devising a mesh which requires a certain amount of stored information in order to detect the interior fibre/matrix interface and to photographically match the boundary nodes on opposite sides of the unit cell, a requirement mandatory for correct implementation of interior and periodic boundary conditions.

Fig. 3

Square and parallelogram $\kappa =1$ unit cell with circular inclusion ($v_f = 0.5$.) Representative mesh types. a–d Tri-mesh. b–e Poly-mesh. c–f Quad-mesh

Solutions in terms of average shear moduli are computed, respectively with $k=1$ and $k=2$ order of interpolations, assuming as a reference solution the highly accurate analytical method presented in [5] based on the Weierstrass basis functions for the solution of the cell problem and referring to a high number of terms introduced in the local series expansions for the representation of the cell function ($N = 100$ see [5]). The Euclidean relative error norm $\varepsilon _{\varvec{G}^{\#}}$ curves for the homogenized moduli versus mesh size $h_E$ for the examined cases are reported in Fig. 4 which shows optimal agreement with the reference solution and a slight outperformance of polygonal discretizations, especially for higher values of the volume fraction i.e. when the unit cell progressively approaches the packaging limit and the region between fibre and matrix shrinks, consequently narrowing and distorting the local elements.

Fig. 4

Validation of the VEM methodology in terms of relative error norm of the homogenized moduli versus element size $h_E$. Square unit cell ($\varphi = \pi /2$, $\kappa =1$) (a, b). Parallelogram unit cell (c–d) ($\varphi = \pi /2$, $\kappa =1$) unit cell with circular inclusion. Volume fractions: $v_f = 0.5$ (a), $v_f = 0.75$ (b), $v_f = 0.35$ (c), $v_f = 0.6$ (d). Representative mesh types: red triangle Tri-mesh. Green-pentagon: Poly-mesh. Black squares: Quad-mesh. Dashed line: $k = 1$. Continuous line: $k=2$. (Color figure online)

A set of parametric analyses, commonly carried out in typical design process of engineered composite materials are presented in the sequel, aiming at showing the practical applicability of the newly developed method to technical problems. In Fig. 5, results pertaining to the parametric influence of the interface strength parameter D, for various volume fractions are reported for a family of composite arrays and exponential grading. In Fig. 6, results pertaining the parametric influence of the grading intensity factor $\omega$, for various volume fractions are reported and in conjunction with exponentially graded circular fibres. Last, Fig. 7, the parametric analysis results of the cylindrical orthotropy factor $\sigma ^2$ is presented. All the derived results confirm the feasibility of the method to cope with parametric analysis and design in an efficient reliable way.

Fig. 5

Dimensionless effective modulus $G^{\#}$ versus fibre volume fraction $v_f$. Square unit cell with circular inclusion. Stiffness contrast factor: $\xi = 50$. Isotropic fibre: $\sigma =1$. Grading type: exponential. Influence of interface stiffness D: $\delta = 0.1$—blue diamonds, $\delta = 1$—grey circles, $\delta = 10$—black upper triangles, $\delta = 100$—magenta lower triangles, $\delta = 1000$—red squares, $\delta = +\infty$—green stars. Grading intensity $\omega = 4$. (Color figure online)

Fig. 6

Dimensionless effective modulus $G^{\#}$ versus fibre volume fraction $v_f$. Square unit cell with circular inclusion. Stiffness contrast factor: $\xi = 50$. Isotropic fibre: $\sigma =1$. Grading type: exponential. Influence of grading intensity: $\omega = 1$—green stars, $\omega = 2$—red squares, $\omega = 4$—black triangles, $\omega = 8$—blue diamonds. Perfect interface ($\delta = +\infty$). (Color figure online)

Fig. 7

Dimensionless effective modulus $G^{\#}$ versus fibre volume fraction $v_f$. Square unit cell with circular inclusion. Stiffness contrast factor: $\xi = 50$. Grading type: exponential. Grading intensity $\omega = 4$. Orthotropic fibre. Influence of orthotropy parameter: $\sigma ^2 = 1/100$—blue diamonds, $\sigma ^2 = 1/10$—grey circles, $\sigma ^2 = 1$—black upper triangles, $\sigma ^2 = 10$—magenta lower triangles, $\sigma ^2 = 100$—red squares. Perfect interface ($\delta = +\infty$). (Color figure online)

4.2 Elliptical fibres

A single composite arrangement with non circular inclusion is taken into examination, cf. Fig. 8, where elliptical inclusions in a square matrix are considered with the maximum/minimum axis ratio of 2 [31]. Both fibre and matrix are made of homogeneous isotropic elastic material with shear stiffness contrast factor $G^f/G^m = 18$; perfect interfaces are assumed throughout. The solution for the shear moduli are computed for the Tri-mesh and Poly-mesh discretizations, as can be appreciated from Fig. 9, and compared to a reference solutions obtained with quadratic triangular displacement-based finite elements on a very fine mesh. The homogenized principal shear moduli are reported in Fig. 10 confirming the accuracy of the method even in case of complex fibre cross section shapes, keeping in mind that the case is quite simple, but still retaining an indication on how the proposed methodology is worth to be applied even in more complex situations, i.e. when cross fibre sections may present sharp edges or highly involved geometries: a situation which is more and more common, especially in applications of advanced composite materials, for instance, in mechanical and aerospace engineering where inclusion aspect ratio and geometry, other than circular or elliptical, is object of design itself [31].

Fig. 8

Unit cell with elliptical fibre inclusion

Fig. 9

Square unit cell with elliptical inclusion. Representative mesh types. a Tri-mesh. b Poly-mesh

Fig. 10

Unit cell with elliptical fibre inclusion. Homogenized principal shear moduli for isotropic homogeneous constituents. Red triangle: Tri-mesh; green-pentagon: Poly-mesh; black squares: Quad-mesh for Q4 reference solution. Aspect ration $\kappa = 2$, shear constrast $\xi = 20$.). (Color figure online)

4.3 A simple strategy for local mesh refinement

It has been previously stated that a critical aspect of the problem at hand is mesh distortion sensitivity, for those cases in which either the value of volume fraction, the shape, or the geometric disposition of the inclusion within the matrix may render the numerical solution stiff and potentially inaccurate. It is to be emphasized that, arrangements quite close to the packaging limit are technically interesting in some cases, as they may provide higher durability with respect to debonding phenomena at fibre/matrix interface. On account of the previous considerations, a sample simulation is re-run with geometric and material setup presented in Sect. 4.1, for a square unit cell with volume fraction $v_f = 0.5$, $\sigma = 1$, $\xi = 50$, $\omega = 4$, perfect interface. Simulation refer to Tri-mesh and Poly-mesh, respectively. A heuristic local refinement algorithm is proposed by means of a reasonably sound recognition of the cell domain locations in which the auxiliary cell function present the steepest gradient, i.e. across fibre/matrix interface, and in the vicinity of the exterior boundary of the cell, hence where the discretization needs to be more accurate.

The VEM permits to refine an m side convex polygon without holes in an efficient simple way, that is by subdividing it into m squares, by tracing the rays from the centroid to all edges midpoints, as proposed in [14]. The newborn midside nodes are the so called hanging nodes, prohibited in finite element technology, whilst in the present context they are consented since they give rise to a number of new quadrilaterals within the refined element, and they transform each of the subdivided edge into a couple of aligned contiguous straight edges for each of the adjacent polygons which simply increase their edge count by a unit. As it is straightforwardly noted, the procedure relies heavily on a relaxed concept of mesh topology conformity which is proper to VEM and whose versatility may play a crucial role in the problem under consideration.

From the practical standpoint, the proposed iterative refinement of the mesh proceeds starting from a relatively coarse mesh and processing first all the elements sharing at least one node with either of the aforementioned boundary lines. Subsequently, the refinement processes every element refined at the previous iterations plus all the original elements adjacent to any of the refined ones. This simple and fast algorithm produces a refined mesh which is somehow coarse at far from boundaries, and becomes progressively finer across such locations where a steep gradient of the unknown field is expected. A pictorial view of the result at the second refinement iteration is portrayed in Fig. 11 showing the obtained non uniformity of the mesh size over the domain. Despite its roughness and lack of mathematical structure, the proposed heuristic way of refining the mesh produces the same level of accuracy on $\varepsilon _{\varvec{G}^{\#}}$, chosen here as $10^{-3}$, with approximately $17 \%$ less degrees of freedom than the corresponding solution obtained with uniform refinement of the Poly-mesh (cfr. Sect. 4.1). The result is interesting in terms of computational cost saving and encouraging in the sense of deriving a mathematically sound adaptive mesh algorithm based on a robust and reliable a posteriori error estimator.

Fig. 11

Square unit cell ($v_f = 0.5$) local mesh refinement after 2 iterations. a Tri-mesh. b Poly-mesh. Shaded areas correspond to elements stemming from a single refinement iteration

5 Conclusion

The paper presented a virtual element method of higher order for the computational asymptotic homogenization of unidirectionally long fibre reinforced composite materials characterized by a microstructure with a doubly periodic lattice of unit cells, each containing a single fibre of circular or elliptical shape embedded into a surrounding matrix. In the framework of antiplane shear deformation, the derivation of average or effective shear moduli requires the solution of the so called cell problem on the unit cell domain. The problem under consideration, being characterized by strong gradient at both fibre/matrix interface and matrix boundary, is formulated and solved by a virtual element method granting $C^0$ regularity. The methodology is capable of handling interior boundary interface conditions modeling imperfect bonding as well as periodicity of the cell function at exterior boundaries.

Comparison with established reference solutions on a large family of numerical tests validated the method for various constitutive setups, and different unit cell geometries for both circular and elliptical fibre cross sections and with material grading of the constitutive properties. A key aspect of the proposed methodology, namely the versatility of meshing operations with respect to element shapes and local mesh refinement is exploited in heuristic fashion; the idea of local refinement in the vicinity of areas where a steep gradient of the unknown field is expected is explored with favorable results in terms of computational cost. Ongoing research development include: devising a rigorous a posteriori error estimator for a robust local refinement strategy, as well as applying the proposed methodology for the large scale simulation of random composites, as well as taking into account more complex phenomena as inelastic nonlinear behavior of the constituents and a fibre/matrix complex constitutive law simulating debonding.