VEM Approach for Homogenization of Fibre-Reinforced Composites with Curvilinear Inclusions

Abstract

We propose a curvilinear virtual element method (VEM) for the asymptotic homogenization of fibre-reinforced composites with straight long fibres having general curvilinear cross sections. This technique is able to exactly represent the microstructural curvilinear geometry still granting all the standard features of VEM methods for elliptical boundary value problems. The method is here applied to doubly periodic fibre arrangements. Accuracy and computational efficiency of the proposed homogenization procedure is confirmed by numerical examples by comparison with semi-analytical solutions.

I first met Prof. Wriggers through his books, when I was a Ph.D. student. Subsequently, I had multiple opportunities to attend his courses and seminars at prestigious international research institutions such as University of California at Berkeley where we first met personally in 2010. I was more recently involved in collaborative research with Prof. Wriggers and his co-workers during a research stay in Hannover at Leibniz University for the development of VEM methods in 2D contact mechanics. I personally find Peter a brilliant scientist and a great computational mechanicist, and a very charming and friendly person to go along with. My sincere wishes on his 70th birthday.

1 Introduction

Composite materials are extensively used materials in many engineering applications due to their interesting properties, as, for instance, high strength-to-weight ratio and tunable features of the constituents.

The present communication focuses on fibre reinforced composite materials analysed via asymptotic homogenization method. In particular, the analysis is here developed for composites with long fibre-like inclusions having random size and shape of the cross section, and doubly periodic space distribution within the hosting medium. In this latter case, the computation of homogenized quantities will require solving a boundary value problem at the microscale on the unit cell domain [1,2,3].

In this framework, a major issue of micro scale computational modeling is represented by meshing curved fibre/matrix subdomains and relevant interfaces thus requiring efficient discretization for any realization and any given loading condition for a composite.

Recently, the Virtual Element Method (VEM) has been introduced and proved an efficient alternative to standard finite element method [4, 5]. It represents a generalization of the FE method with the capability of dealing with very general polygonal/polyhedral meshes. The VEM has already been successfully adopted to solve linear elasticity problems [6,7,8], as well as with complex material nonlinearity such as plasticity, viscoelasticity, damage and shape memory problems, see, e.g. [9,10,11,12,13] for a short representative list of related works. In the framework of computational homogenization, VEM based procedures with straight edges have been proposed in [14, 15], for evaluating homogenized material moduli of a doubly periodic composite material reinforced by cylindrical circular inclusions, either with linear elastic or inelastic material behavior, while the same problem with random inclusion has been tackled with a VEM procedure in [16].

In this communication we present a curvilinear VEM method (i.e. with the possibility of using curvilinear polygonal elements [17,18,19,20]) for the antiplane shear homogenization problem of doubly periodic composites with fibres having general cross section. In particular, VEM elements characterized by linear and higher order polynomial approximation are proposed. Homogeneous and functionally graded constitutive laws are considered for the fibre constituents of the composite. Numerical applications are developed to assess the effectiveness of the proposed VEM elements by comparisons with more established techniques showing efficiency of the proposed methodology.

2 Asymptotic Homogenization of Doubly Periodic Fibre Reinforced Composite Materials

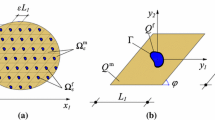
We here consider a composite material with two material components, a surrounding matrix with long cylindrical fibre-like inclusions, embedded into it according to a doubly periodic grid characterized by an angle $\phi$, as can be seen in Fig. 1a. The bimaterial microstructure in the plane orthogonal to the ffibres consists of a two dimensional array of unit cells, developing periodically along the $x_1$ and $\phi$ directions, see Fig. 1b. The cell sides measure $L_1$ and $L_2$ respectively, being $\phi$ the cell angle.

Fig. 1

Composite material with long cylindrical inclusions. a Microstructure lattice with cell doubly periodic arrangement. b Unit cell fibre/matrix geometric features

In order to compute the effective material shear moduli of the composite via asymptotic homogenization a family of problems is introduced, indexed by a parameter ${{\boldsymbol{\varepsilon }}}$: the ratio of the microstructure size to the total size of the analysis region (Fig. 1a). The homogenization limit is obtained by letting ${{{\boldsymbol{\varepsilon }}}}$ go to zero.

In the framework of antiplane shear deformation, the problem of determining the longitudinal displacement field $w_{{{\boldsymbol{\varepsilon }}}}$ in the composite domain is stated as follows:

$$\begin{aligned} \mathrm{div}({{\boldsymbol{G}}} \nabla w_{{{\boldsymbol{\varepsilon }}}})&=0\,,&\qquad&\text {in}\, \Omega ^\mathrm{f}_{{{\boldsymbol{\varepsilon }}}}\cup \Omega ^\mathrm{m}_{{{\boldsymbol{\varepsilon }}}} \,; \end{aligned}$$

(1)

$$\begin{aligned} {[[}{{\boldsymbol{G}}} \nabla w_{{{\boldsymbol{\varepsilon }}}} \cdot {{\boldsymbol{\nu }}} {]]}&=0\,,&\qquad&\text {on}\, \Gamma _{{{\boldsymbol{\varepsilon }}}} \,; \end{aligned}$$

(2)

$$\begin{aligned} {{\boldsymbol{G}}} \nabla w_{{{\boldsymbol{\varepsilon }}}} \cdot {{\boldsymbol{\nu }}}&= \frac{1}{{{\boldsymbol{\varepsilon }}}}D{[[}w_{{{\boldsymbol{\varepsilon }}}} {]]}\,,&\qquad&\text {on}\, \Gamma _{{{\boldsymbol{\varepsilon }}}} \,. \end{aligned}$$

(3)

Here $\Omega ^\mathrm{f}_{{{\boldsymbol{\varepsilon }}}}$ and $\Omega ^\mathrm{m}_{{{\boldsymbol{\varepsilon }}}}$ denote fibre and matrix domains respectively, $\Gamma _{{{\boldsymbol{\varepsilon }}}}$ is the union of fibre/matrix interfaces, ${{\boldsymbol{\nu }}}$ is the normal unit vector to $\Gamma _{{{\boldsymbol{\varepsilon }}}}$ pointing into $\Omega ^\mathrm{m}_{{{\boldsymbol{\varepsilon }}}}$, and square brackets ${[[}\cdot {]]}$ denote the jump of the enclosed quantity across the interface, defined as extra-fibre value minus intra-fibre value.

Equation (1) is the field equilibrium equation; Eq. (2) represents the continuity of the normal-to-interface component of the shear stress hence equilibrium at fibre/matrix interface; (3) describes the interface constitutive law, being D a material parameter characterizing fibre/matrix strength. These equations must be complemented by suitable boundary conditions on the boundary of the domain $\Omega =\Omega ^\mathrm{f}_{{{\boldsymbol{\varepsilon }}}}\cup \Gamma _{{{\boldsymbol{\varepsilon }}}}\cup \Omega ^\mathrm{m}_{{{\boldsymbol{\varepsilon }}}}$.

Fibres and matrix are assumed to be linear elastic, and their shear moduli are collected in the constitutive tensor ${{\boldsymbol{G}}}$, which specializes in

$$\begin{aligned} {{\boldsymbol{G}}}={{\boldsymbol{G}}}^\mathrm{f} \quad \text {in}\,\, \Omega ^\mathrm{f}_{{{\boldsymbol{\varepsilon }}}}\,, \qquad {{\boldsymbol{G}}}={{\boldsymbol{G}}}^\mathrm{m} \quad \text {in}\,\, \Omega ^\mathrm{m}_{{{\boldsymbol{\varepsilon }}}}\,. \end{aligned}$$

(4)

Fibre/matrix interfaces are assumed to have zero-thickness and can encompass a spring-layer model, with linear relation for the displacement discontinuity ${[[}w_{{{\boldsymbol{\varepsilon }}}} {]]}$ and interface traction ${{\boldsymbol{G}}} \nabla w_{{{\boldsymbol{\varepsilon }}}} \cdot {{\boldsymbol{\nu }}}$, with D a given spring constant parameter [21,22,23]. According to this model, interfaces have a physical thickness t which, though much smaller than the microstructural length scales $L_1$ and $L_2$, rescales as the latter ones in the homogenization process.

2.1 Homogenized Equilibrium Equation and Effective Material Moduli

The asymptotic homogenization method employed to derive the homogenized or effective constitutive tensor of the composite material is briefly recapped in this section. More details and theoretical background may be found for example in [1, 3] and in [24, 25] for the specific problem of antiplane shear deformation.

As shown in Fig. 1a, two different length scales characterize the problem under consideration. Hence, two different space variables are introduced: the macroscopic one, x, and the microscopic one, $y=x/{{\boldsymbol{\varepsilon }}}$, $y \in Q$, being Q the unit cell (see Fig. 1b), whose intra-fibre space, extra-fibre space and fibre-matrix interface are denoted by $Q^\mathrm{f}$, $Q^\mathrm{m}$ and $\Gamma$, respectively. Accordingly, the divergence and gradient operators are given by the following relations:

$$\begin{aligned} \mathrm{div} = \mathrm{div}_{x} + \frac{1}{{{\boldsymbol{\varepsilon }}}}\, \mathrm{div}_{y} \,, \qquad \nabla = \nabla _{x} + \frac{1}{{{\boldsymbol{\varepsilon }}}} \nabla _{y}\,. \end{aligned}$$

(5)

An asymptotic expansion of the unknown displacement field is considered in the form:

$$\begin{aligned} w_{{{\boldsymbol{\varepsilon }}}}(x,y)=w_{0}(x,y) + {{\boldsymbol{\varepsilon }}} w_{1}(x,y) + {{\boldsymbol{\varepsilon }}}^2 w_{2}(x,y)+ \cdots \,, \end{aligned}$$

(6)

where $w_{0}$ is the macroscopic or average value of the field variable, $w_{1}$, $w_{2}$ are Q-periodic functions in y representing perturbations in the field variable due to the microstructure, with zero integral average over Q.

Introducing the cell function ${{\boldsymbol{\chi }}}(y)$, the function $w_{1}$ is represented in the following form [1, 3]:

$$\begin{aligned} w_{1}(x,y)=-{{\boldsymbol{\chi }}}(y) \cdot \nabla _{x} w_{0}(x) \,, \end{aligned}$$

(7)

where the components $\chi _h, h=1,2$, are the unique, null average, Q-periodic solutions of the ensuing cell problem [24, 25].

The problem for $w_{2}$ hence results:

$$\begin{aligned} \mathrm{div}_{y}[{{\boldsymbol{G}}} (\nabla _{y} w_{2} + \nabla _{x} w_{1})]&= -\mathrm{div}_{x}[{{\boldsymbol{G}}} (\nabla _{y} w_{1} + \nabla _{x} w_{0} )]\,,&\quad&\text {in}\, \text {d}^\mathrm{f}\cup \text {d}^\mathrm{m} \, ; \end{aligned}$$

(8)

$$\begin{aligned} {[[}{{\boldsymbol{G}}} (\nabla _{y} w_{2} + \nabla _{x} w_{1})\cdot {{\boldsymbol{\nu }}} {]]}&= 0 \,,&\quad&\text {on}\, \Gamma ; \end{aligned}$$

(9)

$$\begin{aligned} {{\boldsymbol{G}}} (\nabla _{y} w_{2} + \nabla _{x} w_{1})\cdot {{\boldsymbol{\nu }}}&= D{[[}w_{2} {]]}\,,&\quad&\text {on}\, \Gamma \,. \end{aligned}$$

(10)

Integrating (8) both in $Q^\mathrm{f}$ and in $Q^\mathrm{m}$, using the Gauss-Green Lemma, adding the two contributions and exploiting (9), the following equation is obtained:

$$\begin{aligned} \frac{1}{|Q|}\int _{\text {d}^\mathrm{f}\cup \text {d}^\mathrm{m}} \mathrm{div}_{x} [ {{\boldsymbol{G}}}(\nabla _{y} w_{1} +\nabla _{x} w_{0}) ] \mathrm{d}a =0 \,, \end{aligned}$$

(11)

where $\mathrm{d} a$ is the area element of $\text {d}^\mathrm{f}\cup \text {d}^\mathrm{m}$ and $|\cdot |$ is the Lebesgue measure. Substituting (7) into (11), the homogenized equation for the macroscopic displacement $w_{0}$ is finally derived:

$$\begin{aligned} \mathrm{div}_x({{\boldsymbol{G}}}^{\#} \nabla _{x} w_{0})=0\,. \end{aligned}$$

(12)

Here $\nabla _{x} w_{0}$ is the macroscopic shear strain, and

$$\begin{aligned} {{\boldsymbol{G}}}^{\#}= \frac{1}{|Q|}\int _{\text {d}^\mathrm{f}\cup \text {d}^\mathrm{m}} {{\boldsymbol{G}}}(\mathbf{I}-{\nabla _y^{\boldsymbol{\intercal }}}{{\boldsymbol{\chi }}}) \, \mathrm{d} a \end{aligned}$$

(13)

are the effective shear moduli, where the superscript $^{\boldsymbol{\intercal }}$ denotes the transpose.

Equation (13) yields the effective shear moduli of the composite material in terms of the cell function ${{\boldsymbol{\chi }}}$, solution of the cell problem. In the following section, a curvilinear virtual element methodology to solve the above problem for various is presented.

3 $C^0$ Curved Virtual Element Method

A weak formulation for the cell problem is provided by the virtual work principle [15, 16]. In this regard, the space of the admissible auxiliary cell functions $\tilde{{{\boldsymbol{\chi }}}}$ which are shift $\text {d}$-periodic is introduced, i.e. for $s \in \{1,2\}$:

$$ \begin{aligned} \tilde{\mathbf{V}} = \Big \{ \tilde{\chi }\in L^2(\text {d}) \text { such that }&\tilde{\chi }|_{\text {d}^\mathrm{f}} \in H^1(\text {d}^\mathrm{f}) \text { for }, \\&\tilde{\chi }|_{\text {d}^\mathrm{m}} \in H^1(\text {d}^\mathrm{m}), \ { \tilde{\chi }(y_1,y_2) \mathbf {+} y_s \text { is d-periodic}} \Big \}. \end{aligned} $$

We denote by ${\mathbf{V}}$ the space of the admissible $\text {d}$-periodic variations of $\tilde{\mathbf{V}}$. The bilinear form characterizing the variational formulation is:

$$\begin{aligned} \begin{aligned} a(\tilde{\chi }_s,\delta \chi _s)&= - \int _{\text {d}} \mathrm{div}_{y}[{{\boldsymbol{G}}} (\nabla _y \tilde{\chi }_s)] \,\delta \chi _s\,\mathrm{d}{} \mathbf{x} \end{aligned} \end{aligned}$$

(14)

which, applying Gauss-Green lemma, considering the constitutive equation and that unit normal vectors to $\partial \text {d}^\mathrm{m}$ on opposite sides of the unit cell are opposite, becomes:

$$\begin{aligned} a({\tilde{\chi }_s},{\delta {\chi _s}}) = {\int _{\text {d}}} {\nabla _y} {\delta {\chi _s}}\, \cdot \, {{{\boldsymbol{G}}}} ({\nabla _y} {\tilde{\chi _s}}) \mathrm{d}{} \mathbf{x} + {\sum _{j=1}^{F}} \int _{\Gamma } {[[}{\delta {\chi _{s}}} {]]}\, D \, {[[}{\tilde{\chi }_s} {]]}\,\mathrm{d} . \end{aligned}$$

(15)

The form $a(\cdot ,\cdot )$ is symmetric, continuous and coercive on $\tilde{\mathbf{V}}$, hence the variational problem is well posed.

3.1 The Virtual Element Space

In order to devise a discretization of the boundary value problem under consideration adopting virtual elements with curved edges, we exploit the construction outlined in [14, 16, 17]. Let ${\mathcal T}_h$ be a simple polygonal mesh on $\text {d}$, i.e. any decomposition of $\text {d}$ in a finite set of simple polygons $e$, without holes and with boundary given by a finite number of edges. Whenever an element has an edge lying on an interface $\Gamma$, such edge is then allowed to be curved in order to describe exactly the geometry of the problem. We assume that each interface $\Gamma$ is parametrized by an invertible $C^1$ mapping $\gamma$ from an interval in the real line into $\Gamma$. It is not restrictive to assume that each curved edge is a subset of only one $\Gamma$ and therefore regular. In order to simplify the notation in the following we sometimes drop the index j, simply use $\Gamma$ and

$$ {\boldsymbol{\gamma }}\ : \ [0,L] \longrightarrow \Gamma $$

to indicate a generic curved part of the fibre/matrix interface and its associated parametrization.

The virtual element space is built elementwise. Indicating with $E \in {\mathcal T}_h$ a generic polygonal element of. Note that E may have some curved edge, laying on some curved interface $\Gamma$ ($j \in \{1,2,..,F\}$). For any of such curved edges e, let ${\boldsymbol{\gamma }}_e : [a,b] \rightarrow e$ denote the restriction of the parametrization describing $\Gamma$ to the edge e. Then we indicate the space of mapped polynomials (living on e) as

$$ \widetilde{{\mathcal P}}_k(e) = \Big \{ p \circ {\boldsymbol{\gamma }}_e^{-1} \, : \, p \in {\mathcal P}_k[a,b] \Big \} . $$

The local virtual element space on E is then defined as

$$\begin{aligned} \begin{aligned} \mathbf{V}_h(E) = \Big \{ v \in H^1(E) \cap C^0(E) \, : \,v|_e \in {\mathcal P}_k(e) \text { if } e \text { is straight} , \\ v|_e \in \widetilde{{\mathcal P}}_k(e) \text { if } e \text { is curved} , - \Delta v \in {\mathcal P}_{k-2}(E) \Big \} . \end{aligned} \end{aligned}$$

(16)

The associated degrees of freedom are (see [17] for the simple proof)

• pointwise evaluation at every vertex of polygon E;

• pointwise evaluation at $k-1$ distinct points lying on every edge of E;

• area-averaged moments $\int _E v p_{k-2}$ for all $p_{k-2} \in {\mathcal P}_{k-2}(E)$.

The global space is obtained by a standard procedure preserving interelement $C^0-$-continuity:

$$ \tilde{\mathbf{V}}_h = \Big \{ v \in \tilde{\mathbf{V}} \, : \, v|_E \in \mathbf{V}_h(E) \ \forall E \in {\mathcal T}_h \Big \} , $$

Global degrees of freeedom are the obvious extension of the local ones. The discretization of the problem is a combination of the scheme proposed in [14] for the case with standard straight edges and the curved-edge technology introduced in [17] for a model linear diffusion problem. Implementation details can thus be found in the aforementioned references.

3.2 Numerical Test

A composite arrangement with elliptical inclusions in square matrices is considered, cf. Fig. 2 with maximum/minimum axis ratio of 2 [26]. Fibre/matrix shear stiffness contrast factor is here $G^f/G^m = 18$, with perfect interfaces. The solution for the shear moduli are computed for the Tri-mesh and Poly-mesh discretizations, as can be appreciated from Fig. 2, and compared to a reference solutions obtained with quadratic triangular displacement-based finite elements on a very fine mesh. The homogenized principal shear moduli are reported in Fig. 3 confirming the accuracy of the method even in case of complex curvilinear fibre cross section geometry. The accuary of the present computation opens the door for the proposed methodology to even more involved geometries of the composite constituents, i.e. when cross fibre sections may present sharply curved edges which may be selected as to taylor material specific features [26].

Fig. 2

Square unit cell with elliptical inclusion. Curvilinear meshes. a Triangles. b Voronoi-like polygons

Fig. 3

Unit cell with elliptical fibre inclusion. Homogenized principal shear moduli for isotropic homogeneous constituents. Red triangle: Tri-mesh; green-pentagon: Poly-mesh; black squares: Quad-mesh for Q4 reference solution. Aspect ration $\kappa = 2$, shear constrast $\xi = 20$

4 Conclusion

In this contribution we have presented a curvilinear VEM for homogenization of unidirectional fiber-reinforced composite materials with inclusion curvilinear cross section. The procedure proves efficient and accurate as confirmed by several numerical results.