1 Introduction

Large space structures usually carry one or several antenna subsystems for different space missions. During the deployment and the on-orbit service of space structures, the attitude of the antenna subsystem need to be adjusted according to different space missions. The application of manipulator to the attitude adjustment and the vibration suppression of the antenna is an important issue. In this study, the antenna system is simplified as a rigid-flexible system including a rigid arm and a flexible beam with a torsional spring at the joint and only the in-plane vibration of the antenna system is taken into consideration. Such a rigid-flexible system is usually named as the L-shaped beam in many previous researches.

Recent years have witnessed numerous studies on the dynamic characteristics of the rigid-flexible multibody systems [1,2,3,4]. Researchers [5,6,7,8] have paid attention to the study on the nonlinear dynamic behavior or the vibration suppression of a flexible beam carrying an attached mass. A lot of researches have focused on more complex beam structures as well. For example, Ashworth and Barr [9] analyzed the nonlinear resonant behaviors of both L-shaped and T-shaped beam structures due to parametric excitation theoretically. Balachandran and Nayfeh [10] obtained the analytic solutions of the principal parametric resonance and the 2:1 internal resonance for the in-plane vibration of an L-shaped beam structures. Nayfeh et al. [11] studied the three-mode interaction resonant response of a system of three degrees of freedom with quadratic nonlinearities. Apiwattanalunggarn et al. [12] proposed a nonlinear component mode synthesis method and studied the dynamic characteristics of the composite structures. Erturk et al. [13] established a distributed parameter model to analyze the coupled electromechanical behavior of the piezoelectric energy harvester on a basis of the L-shaped beam-mass structure. Furthermore, Vyas and Bajaj [14] introduced a T-beam micro-resonator design due to the 2:1 internal resonance and illustrated the nonlinear frequency-amplitude response of the system. Wang and Bajaj [15] studied the forced nonlinear response of a three-beam structure with attached mass undergoing three-mode interactions. They revealed that the amplitude response may undergo a pitchfork bifurcation or a saddle-node bifurcation, or a Hopf bifurcation. Onozato et al. [16] investigated the chaotic vibrations of a post-buckled L-shaped beam with an axial constraint. Very recently, Harne et al. [17] analyzed the nonlinear internal resonance and saturation phenomena of an L-shaped vibration energy harvester.

In the available literature, the theoretical researches of the nonlinear dynamics of serial systems have received much attention. As experimental investigation is another essential tool to understand the nonlinear dynamics responses of the beam structures, many researchers have made efforts to study the nonlinear dynamics of the flexible beam systems experimentally as well. For instance, Haddow et al. [18] studied the nonlinear resonances of a flexible L-shaped beam-mass structure analytically and experimentally, and demonstrated the jumping and saturation phenomena of the structure. Then Nayfeh and Balachandran [19] investigated the nonlinear responses of the similar structure subjected to primary resonance excitations experimentally. They reported that there existed the periodic and chaotic solutions, Hopf and saddle-node bifurcations and saturation phenomena. Nayfeh et al. [20] analyzed the linear and nonlinear responses of two light-weight beams in a T-shape configuration under a harmonic excitation experimentally and obtained some phenomena predicted by theoretical method. Warminski et al. [21] analytically and experimentally studied the modal interaction of an L-shaped auto-parametric beam with different flexibilities in two orthogonal directions. Cao et al. [22] focused on the theoretical and experimental investigation of planar nonlinear vibrations and chaotic dynamics of an L-shaped beam structure subjected to harmonic excitation. Recently, Wang et al. [23] dealt with the experimental and numerical investigations of the characteristics of particle damper attached to the top free end of an L-shaped cantilever beam.

Furthermore, in order to obtain the periodic solutions of a nonlinear differential equation of high dimensions, Rosenberg [24] proposed the concept of nonlinear normal modes first. Then, Shaw and Pierre [25] presented the invariant manifold method to derive nonlinear normal modes. Afterwards, Nayfeh [26, 27] developed the method of multiple scales to construct the nonlinear normal modes of continuous systems with internal resonance. Many researchers [28,29,30,31,32,33] used the method of multiple scales to study the nonlinear normal modes of various systems. Very recently, Renson et al. [34] reviewed the recent advances in computational methods both for undamped and damped nonlinear normal modes.

The free vibration of a space antenna system is an important issue since there is no persistent external excitation during on-orbit service of the antenna. This study deals with the analytical and experimental studies on the nonlinear resonance of a space antenna system of two degrees of freedom with the consideration of the coupling between the motion of the rigid arm and the deformation of the flexible beam. The traditional method of multiple scales [35] is not suitable for the rigid-flexible system since the mass matrix here is not a constant matrix. In this study, a multiple scales method in matrix form is developed for the rigid-flexible system, in which the interaction of two modes is considered, based on the research in [36]. The remainder of the paper is organized as follows. In Sect. 2, the nonlinear dynamic equations of in-plane vibration of the antenna system are derived by using the Lagrange equation. In Sect. 3, the nonlinear resonance is analyzed by using the method of multiple scales. Afterwards, the approximate solutions are determined and their stabilities are discussed. In Sect. 4, the numerical results are presented to validate the approximate solutions of nonlinear resonance analysis. In Sect. 5, the experimental setup and experimental scheme are illustrated, and the results of the nonlinear vibration experiments are shown. Finally, some conclusions are drawn in Sect. 6.

2 Model of a rigid-flexible antenna system

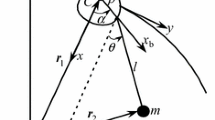
As shown in Fig. 1, the study focuses on the in-plane vibration of an antenna system, which consists of a rigid arm and a flexible beam. The arm is hinged to the main body of the satellite via a torsional spring and the beam is fixed at the free tip of the arm. The main body of the satellite is usually much heavier than the antenna system. Thus, the motion of the antenna system is assumed to have a little influence on the main body of the satellite. That is, the main body of the satellite can be considered as fixed in an inertial frame of reference in the study. In addition, it is assumed that the slender beam has a uniform cross-section and is made of an isotropic material such that it can be modeled as an Euler–Bernoulli beam when the deformation of the beam is small, and the rotation speed of the antenna system is slow.

Fig. 1
figure 1

The simplified model of a rigid-flexible L-shape antenna system

Full size image

An inertial frame OXY of reference and a body frame oxy of reference are established as shown in Fig. 1, where the motions of the rigid arm is described by rotation angle θ, and the deformation of the beam is represented by \(w(x,t)\) in the body frame. Thus, the kinetic energy and the potential energy of the antenna system are given as

$$T = \frac{1}{2}m\dot{\varvec{r}}_{1}^{T} \dot{\varvec{r}}_{1} + \frac{1}{2}J\dot{\theta }^{2} + \frac{1}{2}\int_{0}^{L} {\rho A\dot{\varvec{r}}_{p}^{T} \dot{\varvec{r}}_{p} } {\text{d}}x$$
(1)
$$V = \frac{1}{2}k_{1} \theta^{2} + \frac{1}{2}\int_{0}^{L} {EI\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }}} \right)}^{2} {\text{d}}x$$
(2)

where m, l, J and r 1 are the mass, the length, the inertia moment and the position vector of the mass center of the arm, respectively. ρ, A, L and EI are the density of beam material, the cross section area of beam, the length of beam, and the bending stiffness of beam, respectively. \({\varvec{r}}_{p}\) is the position vector of an arbitrary point on the beam. \(k_{1}\) is the stiffness of the torsional spring.

Base on the assumed modes method, the dynamic deformation of the flexible beam can be described by the modal shape function and the modal coordinate of a cantilever beam [37,38,39]. In this study, only the first-order frequency vibration is taken into consideration. Hence, the dynamic deformation \(w(x,t)\) of beam can be approximately given as \(w(x,t) = \varphi (x)q(t)\). Here, \(\varphi (x)\) is the first normalized modal shape function of a cantilever beam.

Now, the following dimensionless parameters are introduced

$$\tau = \omega_{r} t,\overline{q} = \frac{q}{L},\;b = \frac{l}{L},\;d = \frac{m}{\rho AL},\;k = \frac{{k_{1} }}{{\rho AL^{3} \omega_{r}^{2} }},\;\kappa_{2} = \frac{EI}{{\rho AL\omega_{r}^{2} }}\int_{0}^{L} {\left( {\frac{{{\text{d}}^{2} \varphi (x)}}{{{\text{d}}x^{2} }}} \right)^{2} } {\text{d}}x$$
(3)

where \(\omega_{r} = \lambda_{r}^{2} \sqrt {EI / (\rho A)}\) and \(\lambda_{r} = 1.8751 /L\). The generalized coordinate vector is chosen as \({\varvec{\upeta}} = \left[ {\begin{array}{*{20}c} {\eta_{1} } \, {\eta_{2} } \\ \end{array} } \right]^{\text{T}} = \left[ {\begin{array}{*{20}c} \theta {{\overline{q}} } \\ \end{array} } \right]^{\text{T}}\). By substituting the kinetic energy and the potential energy into the Lagrange equation of the second kind, hence, the dynamic equation of the antenna system can be derived as

$$\varvec{M}(\varvec{\eta})\varvec{\ddot{\eta }} + \varvec{K\eta } - \varvec{P}(\varvec{\eta},\dot{\varvec{\eta }}) = 0$$
(4)

where

$$\left\{ {\begin{array}{*{20}l} {\varvec{M}(\varvec{\eta}) = \left[ {\begin{array}{*{20}c} {\frac{1}{3}(db^{2} + 1) + b^{2} + \frac{1}{L}\bar{q}\left( {\bar{q}\int_{0}^{L} {\varphi^{2} (x)} {\text{d}}x - 2b\int_{0}^{L} {\varphi (x)} {\text{d}}x} \right)} & {\frac{1}{{L^{2} }}\int_{0}^{L} {x\varphi (x)} {\text{d}}x} \\ {\frac{1}{{L^{2} }}\int_{0}^{L} {x\varphi (x)} {\text{d}}x} & {\frac{1}{L}\int_{0}^{L} {\varphi^{2} (x)} {\text{d}}x} \\ \end{array} } \right]} \hfill \\ {\varvec{K} = \left[ {\begin{array}{*{20}c} k & {} \\ {} & {\kappa_{2} } \\ \end{array} } \right],\varvec{P}(\varvec{\eta},\dot{\varvec{\eta }}) = \left[ {\begin{array}{*{20}c} { - \frac{2}{L}\dot{\bar{q}}\dot{\theta }\left( {\bar{q}\int_{0}^{L} {\varphi^{2} (x){\text{d}}x} - b\int_{0}^{L} {\varphi (x)} {\text{d}}x} \right)} \\ {\frac{1}{L}\dot{\theta }^{2} \left( {\bar{q}\int_{0}^{L} {\varphi^{2} (x)} {\text{d}}x - b\int_{0}^{L} {\varphi (x)} {\text{d}}x} \right)} \\ \end{array} } \right]} \hfill \\ \end{array} } \right.$$
(5)

The dot in Eq. (4) is defined as the derivative with respect to the dimensionless time τ.

3 Nonlinear resonance analysis

In this section, the method of multiple scales is used to analyze the nonlinear resonance of the coupled system of two degrees of freedom governed by Eq. (4). Thus, a third-order uniform approximate solution is assumed for Eq. (4) as follows

$$\varvec{\eta}=\varvec{\eta}_{0} + \varepsilon\varvec{\eta}_{1} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{2}\varvec{\eta}_{2} (T_{0} ,T_{1} ,T_{2} ) + \varepsilon^{3}\varvec{\eta}_{3} (T_{0} ,T_{1} ,T_{2} ) + \cdots$$
(6)

where \(T_{r} = \varepsilon^{r} t,\;\;r = 0,1,2 \cdots\), and ε is a small bookkeeping parameter. By substituting Eq. (6) into Eq. (4) and expanding all matrices and vectors, equating the same power of ε, one has

$$\varvec{K}_{0}\varvec{\eta}_{0} - \varvec{P}_{0} = 0$$
(7)
$$\varvec{M}_{0} D_{0}^{2}\varvec{\eta}_{1} + \varvec{R}_{0}\varvec{\eta}_{1} = 0$$
(8)
$$\begin{aligned} \varvec{M}_{0} D_{0}^{2}\varvec{\eta}_{2} + \varvec{R}_{0}\varvec{\eta}_{2} & = - 2\varvec{M}_{0} D_{0} D_{1}\varvec{\eta}_{1} - \varvec{M}_{1} (\varvec{\eta}_{1} )D_{0}^{2}\varvec{\eta}_{1} - \varvec{K}_{2} (\varvec{\eta}_{1} ,\varvec{\eta}_{1} )\varvec{\eta}_{0} \\ & \quad - \varvec{K}_{1} (\varvec{\eta}_{1} )\varvec{\eta}_{1} + \varvec{P}_{12} D_{1}\varvec{\eta}_{1} + \varvec{P}_{2} (\varvec{\eta}_{1} ,D_{0}\varvec{\eta}_{1} ) \\ \end{aligned}$$
(9)
$$\begin{aligned} \varvec{M}_{0} D_{0}^{2}\varvec{\eta}_{3} + \varvec{R}_{0}\varvec{\eta}_{3} & = - 2\varvec{M}_{0} D_{0} D_{2}\varvec{\eta}_{1} - 2\varvec{M}_{0} D_{0} D_{1}\varvec{\eta}_{2} - \varvec{M}_{0} D_{1}^{2}\varvec{\eta}_{1} \\ & \quad - 2\varvec{M}_{1} (\varvec{\eta}_{1} )D_{0} D_{1}\varvec{\eta}_{1} - \varvec{M}_{1} (\varvec{\eta}_{1} )D_{0}^{2}\varvec{\eta}_{2} - \varvec{M}_{1} (\varvec{\eta}_{2} )D_{0}^{2}\varvec{\eta}_{1} \\ & \quad - \varvec{M}_{2} (\varvec{\eta}_{1} ,\varvec{\eta}_{1} )D_{0}^{2}\varvec{\eta}_{1} - \varvec{K}_{1} (\varvec{\eta}_{1} )\varvec{\eta}_{2} - \varvec{K}_{1} (\varvec{\eta}_{2} )\varvec{\eta}_{1} - \varvec{K}_{2} (\varvec{\eta}_{1} ,\varvec{\eta}_{1} )\varvec{\eta}_{1} \\ & \quad - 2\varvec{K}_{2} (\varvec{\eta}_{1} ,\varvec{\eta}_{2} )\varvec{\eta}_{0} - \varvec{K}_{3} (\varvec{\eta}_{1} ,\varvec{\eta}_{1} ,\varvec{\eta}_{1} )\varvec{\eta}_{0} + \varvec{P}_{12} (D_{1}\varvec{\eta}_{2} + D_{2}\varvec{\eta}_{1} ) \\ & \quad + 2\varvec{P}_{21} (\varvec{\eta}_{1} ,D_{0}\varvec{\eta}_{2} + D_{1}\varvec{\eta}_{1} ) + 2\varvec{P}_{21} (\varvec{\eta}_{2} ,D_{0}\varvec{\eta}_{1} ) + \varvec{P}_{3} (\varvec{\eta}_{1} ,D_{0}\varvec{\eta}_{1} ) \\ & \quad + \varvec{P}_{211} (\varvec{\eta}_{1} ,\varvec{\eta}_{2} ) + \varvec{P}_{22} (D_{0}\varvec{\eta}_{1} ,D_{1}\varvec{\eta}_{1} + D_{0}\varvec{\eta}_{2} ) \\ \end{aligned}$$
(10)

where \(D_{r} = \partial /\partial T_{r}\) represents the differential operators, and other matrices and vectors in Eqs. (7)–(10) read

$$\varvec{M}_{0} = \varvec{M}(\varvec{\eta}_{0} ),\varvec{K}_{0} = \varvec{K}(\varvec{\eta}_{0} ),\varvec{P}_{0} = \varvec{P}(\varvec{\eta}_{0} ,D_{0}\varvec{\eta}_{0} )$$
(11)
$$\varvec{M}_{1} (\varvec{x}) = \left[ {\frac{{\partial \varvec{M}}}{{\partial \eta_{i} }}\varvec{x}_{i} } \right],\varvec{K}_{1} (\varvec{x}) = \left[ {\frac{{\partial \varvec{K}}}{{\partial \eta_{i} }}\varvec{x}_{i} } \right],\varvec{P}_{11} = [P_{11ij} ] = \left[ {\frac{{\partial \varvec{P}_{i} }}{{\partial \eta_{j} }}} \right],\varvec{P}_{12} = [P_{12ij} ] = \left[ {\frac{{\partial \varvec{P}_{i} }}{{\partial \dot{\eta }_{j} }}} \right]$$
(12)
$$\varvec{M}_{2} (\varvec{x},\varvec{y}) = \left[ {\frac{1}{2}\frac{{\partial^{2} \varvec{M}}}{{\partial \eta_{i} \partial \eta_{j} }}\varvec{x}_{i} \varvec{y}_{j} } \right],\varvec{K}_{2} (\varvec{x},\varvec{y}) = \left[ {\frac{1}{2}\frac{{\partial^{2} \varvec{K}}}{{\partial \eta_{i} \partial \eta_{j} }}\varvec{x}_{i} \varvec{y}_{j} } \right]$$
(13)
$$\left\{ {\begin{array}{*{20}l} {\varvec{P}_{2} (\varvec{x},\varvec{y}) = \left\{ {P_{2k} (\varvec{x},\varvec{y})} \right\} = \left\{ {\frac{1}{2}\left( {\frac{{\partial \varvec{P}_{k} }}{{\partial \eta_{i} }}\varvec{x}_{i} + \frac{{\partial \varvec{P}_{k} }}{{\partial \dot{\eta }_{j} }}\varvec{y}_{j} } \right)^{2} } \right\}} \hfill \\ {\varvec{P}_{21} (\varvec{x},\varvec{y}) = \left\{ {P_{21k} (\varvec{x},\varvec{y})} \right\} = \left\{ {\frac{1}{2}\frac{{\partial^{2} \varvec{P}_{k} }}{{\partial \eta_{i} \partial \dot{\eta }_{j} }}\varvec{x}_{i} \varvec{y}_{j} } \right\}} \hfill \\ {\varvec{P}_{211} (\varvec{x},\varvec{y}) = \left\{ {P_{211k} (\varvec{x},\varvec{y})} \right\} = \left\{ {\frac{1}{2}\frac{{\partial^{2} \varvec{P}_{k} }}{{\partial \eta_{i} \partial \eta_{j} }}\varvec{x}_{i} \varvec{y}_{j} } \right\}} \hfill \\ {\varvec{P}_{22} (\varvec{x},\varvec{y}) = \left\{ {P_{22k} (\varvec{x},\varvec{y})} \right\} = \left\{ {\frac{1}{2}\frac{{\partial^{2} \varvec{P}_{k} }}{{\partial \dot{\eta }_{i} \partial \dot{\eta }_{j} }}\varvec{x}_{i} \varvec{y}_{j} } \right\}} \hfill \\ \end{array} } \right.$$
(14)
$$\left\{ {\begin{array}{*{20}l} {\varvec{K}_{3} (\varvec{x},\varvec{y},\varvec{z}) = \left[ {\frac{1}{6}\frac{{\partial^{3} \varvec{K}}}{{\partial \eta_{i} \partial \eta_{j} \partial \eta_{k} }}\varvec{x}_{i} \varvec{y}_{j} \varvec{z}_{k} } \right]} \hfill \\ {\varvec{P}_{3} (\varvec{x},\varvec{y}) = \left\{ {P_{3k} (\varvec{x},\varvec{y})} \right\} = \left\{ {\frac{1}{6}\left( {\frac{{\partial \varvec{P}_{k} }}{{\partial \eta_{i} }}\varvec{x}_{i} + \frac{{\partial \varvec{P}_{k} }}{{\partial \dot{\eta }_{j} }}\varvec{y}_{j} } \right)^{3} } \right\}} \hfill \\ \end{array} } \right.$$
(15)
$$\varvec{R}_{0} = \varvec{K}_{0} - \varvec{P}_{11} - \varvec{P}_{12} D_{0} + \varvec{Q}_{0} ,\varvec{Q}_{0} = \left. {\left[ {\left\{ {\frac{{\partial \varvec{K}}}{{\partial \eta_{1} }}\varvec{\eta}_{0} } \right\}\left\{ {\frac{{\partial \varvec{K}}}{{\partial \eta_{2} }}\varvec{\eta}_{0} } \right\}} \right]} \right|_{{\varvec{\eta}_{0} }}$$
(16)

In Eqs. (12),…,(16), () i and () ij are the entries of a vector or a matrix, respectively, and all derivatives are evaluated at η = η 0. In Eqs. (12),…,(15), x, y and z represent η 1, η 2, \(D_{0}\varvec{\eta}_{1}\), \(D_{1}\varvec{\eta}_{1}\), \(D_{2}\varvec{\eta}_{1}\), \(D_{0}\varvec{\eta}_{2}\) and \(D_{1}\varvec{\eta}_{2}\) in Eqs. (9)–(10). Furthermore, in Eqs. (14) and (15)

$$\left( {\frac{{\partial \varvec{P}_{k} }}{{\partial\eta_{i} }}\varvec{x}_{i} + \frac{{\partial \varvec{P}_{k} }}{{\partial \dot{\eta }_{j} }}\varvec{y}_{j} } \right)^{{m_{1} }} = \sum\limits_{n = 0}^{{m_{1} }} {C_{{m_{1} }}^{n} } \frac{{\partial^{{m_{1} }} \varvec{P}_{k} }}{{\partial\eta_{i}^{n} \partial \dot{\eta }_{j}^{{m_{1} - n}} }}\varvec{x}_{i}^{n} \varvec{y}_{j}^{{m_{1} - n}} ,m_{1} = 2,3$$
(17)

At first, η 0 can be determined by solving Eq. (7). Then, if M 0 is nonsingular, Eq. (8) can be rewritten as

$$D_{0}^{2}\varvec{\eta}_{1} + \varvec{S}_{0}\varvec{\eta}_{1} = 0$$
(18)

where \(\varvec{S}_{0} = \varvec{M}_{0}^{ - 1} \varvec{R}_{0}\) is a matrix function with respect to η 0. By solving Eq. (18), the first-order approximation solution can be obtained as

$$\varvec{\eta}_{1} = A_{1} \exp ({\text{i}}\omega_{1} T_{0} )\varvec{p}_{1} + \overline{A}_{1} \exp ( - {\text{i}}\omega_{1} T_{0} )\varvec{p}_{1} + A_{2} \exp ({\text{i}}\omega_{2} T_{0} )\varvec{p}_{2} + \overline{A}_{2} \exp ( - {\text{i}}\omega_{2} T_{0} )\varvec{p}_{2}$$
(19)

where eigenvalues \(\omega_{1}\), \(\omega_{2}\) and corresponding eigenvectors p 1, p 2 represent the natural frequencies and the mode shapes of Eq. (4) around η 0, respectively, which are acquired by solving the following eigenvalue problem.

$$\omega^{2} \varvec{p} = \varvec{S}_{0} \varvec{p}$$
(20)

It is obvious that the system may undergo 2:1 or 3:1 internal resonances according to the square and cubic nonlinear terms in the system equation. To identify the conditions of internal resonances, the parameter combination of k, d and b are taken into account when \(\kappa_{2} = 1\). By solving Eq. (20), the conditions of internal resonances can be obtained as follows

  1. 1.

    \({\text{if}}\; \left( {k + \frac{1}{3}(db^{2} + 1) + b^{2} } \right)^{2} = \frac{100}{16}k\left( {\frac{1}{3}(db^{2} + 1) + b^{2} - 0.569^{2} } \right),\omega_{2} = 2\omega_{1} \quad {\text{holds}};\)

  2. 2.

    \({\text{if}}\; \left( {k + \frac{1}{3}(db^{2} + 1) + b^{2} } \right)^{2} = \frac{400}{36}k\left( {\frac{1}{3}(db^{2} + 1) + b^{2} - 0.569^{2} } \right),\omega_{2} = 3\omega_{1} \quad {\text{holds}};\)

  3. 3.

    \({\text{if}}\; \left( {k + \frac{1}{3}(db^{2} + 1) + b^{2} } \right)^{2} = \frac{289}{16}k\left( {\frac{1}{3}(db^{2} + 1) + b^{2} - 0.569^{2} } \right),\omega_{2} = 4\omega_{1} \quad {\text{holds}}.\)

Figure 2 shows the parameter plane in the parameter space of (d, b, k), where different kinds of internal resonances occur. In Fig. 2, there exist several kinds of internal resonances, such as 3:1 and 2:1 internal resonances.

Fig. 2
figure 2

The parameters for complete resonance condition. a \(\omega_{2} = 2\omega_{1}\), b \(\omega_{2} = 3\omega_{1}\), c \(\omega_{2} = 4\omega_{1}\)

Full size image

In the following two subsections, 2:1 and 3:1 internal resonances are investigated in detail, respectively.

3.1 2:1 Internal resonances

To describe the closeness of \(\omega_{2}\) to \(2\omega_{1}\), a detuning parameter \(\sigma\) is defined as \(\omega_{2} = 2\omega_{1} + \varepsilon \sigma\). By substituting the expressions of η 0 and η 1 into Eq. (9), a unique solution η 2 is obtained only if the secular terms are orthogonal to every solution \(\varvec{u}_{j}\), which is given by

$$\omega_{j}^{2} \varvec{M}_{0}^{T} \varvec{u}_{j} = \varvec{R}_{0}^{T} \varvec{u}_{j} (j = 1,2)$$
(21)

Then, eliminating the secular terms gives rise to the following differential equations

$$(\varvec{u}_{1}^{T} \varvec{v}_{1} )D_{1} A_{1} + {\text{i}}(\varvec{u}_{1}^{T}\varvec{\alpha}_{1} )\overline{A}_{1} A_{2} \exp ({\text{i}}\sigma T_{1} ) = 0$$
(22)
$$(\varvec{u}_{2}^{T} \varvec{v}_{2} )D_{1} A_{2} + {\text{i}}(\varvec{u}_{2}^{T}\varvec{\alpha}_{2} )A_{1}^{2} \exp ( - {\text{i}}\sigma T_{1} ) = 0$$
(23)

where

$$\left\{ {\begin{array}{*{20}l} {\varvec{v}_{1} = 2\omega_{1} \varvec{M}_{0} \varvec{p}_{1} + {\text{i}}\varvec{P}_{12} \varvec{p}_{1} } \hfill \\ {\varvec{\alpha}_{1} = \omega_{1}^{2} \varvec{M}_{1} (\varvec{p}_{2} )\varvec{p}_{1} + \omega_{2}^{2} \varvec{M}_{1} (\varvec{p}_{1} )\varvec{p}_{2} - 2\varvec{K}_{2} (\varvec{p}_{1} ,\varvec{p}_{2} )\varvec{\eta}_{0} - \varvec{K}_{1} (\varvec{p}_{2} )\varvec{p}_{1} - \varvec{K}_{1} (\varvec{p}_{1} )\varvec{p}_{2} } \hfill \\ \quad \;\; +\, \varvec{P}_{21} (\varvec{p}_{1} ,\varvec{p}_{2} ) + \varvec{P}_{21} (\varvec{p}_{2} ,\varvec{p}_{1} ) + \omega_{1} \omega_{2} (\varvec{P}_{22} (\varvec{p}_{1} ,\varvec{p}_{2} ) + \varvec{P}_{22} (\varvec{p}_{2} ,\varvec{p}_{1} )) \hfill \\ {\varvec{v}_{2} = 2\omega_{2} \varvec{M}_{0} \varvec{p}_{2} + {\text{i}}\varvec{P}_{12} \varvec{p}_{2} } \hfill \\ {\varvec{\alpha}_{2} = \omega_{1}^{2} \varvec{M}_{1} (\varvec{p}_{1} )\varvec{p}_{1} - \varvec{K}_{2} (\varvec{p}_{1} ,\varvec{p}_{1} )\varvec{\eta}_{0} - \varvec{K}_{1} (\varvec{p}_{1} )\varvec{p}_{1} + \varvec{P}_{21} (\varvec{p}_{1} ,\varvec{p}_{1} ) - \omega_{1}^{2} \varvec{P}_{22} (\varvec{p}_{1} ,\varvec{p}_{1} )} \hfill \\ \end{array} } \right.$$

As \(\varvec{u}_{j}\) is the eigenvector, it can be normalized such that \(\varvec{u}_{j}^{T} \varvec{v}_{j} = 1\). Afterwards, by letting \(A_{j} = a_{j} \exp ({\text{i}}\beta_{j} )/2\), \(j = 1,2\) in Eqs. (22) and (23) and separating the real and imaginary parts, one arrives at the modulation equations as follows

$$D_{1} a_{1} = \frac{1}{2}a_{1} a_{2} \left( {\varvec{u}_{1}^{T}\varvec{\alpha}_{1} } \right)\sin \gamma$$
(24)
$$a_{1} D_{1} \beta_{1} = - \frac{1}{2}a_{1} a_{2} \left( {\varvec{u}_{1}^{T}\varvec{\alpha}_{1} } \right)\cos \gamma$$
(25)
$$D_{1} a_{2} = - \frac{1}{2}a_{1}^{2} \left( {\varvec{u}_{2}^{T}\varvec{\alpha}_{2} } \right)\sin \gamma$$
(26)
$$a_{2} D_{1} \beta_{2} = - \frac{1}{2}a_{1}^{2} \left( {\varvec{u}_{2}^{T}\varvec{\alpha}_{2} } \right)\cos \gamma$$
(27)

where

$$\gamma = \beta_{2} - 2\beta_{1} + \sigma T_{1}$$
(28)

From Eqs. (24) and (26), one has [35]

$$\frac{1}{2}a_{1}^{2} + \frac{1}{2}c_{0} a_{2}^{2} = E_{0}$$
(29)

where \(c_{0} = {{\left( {\varvec{u}_{1}^{T}\varvec{\alpha}_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {\varvec{u}_{1}^{T}\varvec{\alpha}_{1} } \right)} {\left( {\varvec{u}_{2}^{T}\varvec{\alpha}_{2} } \right)}}} \right. \kern-0pt} {\left( {\varvec{u}_{2}^{T}\varvec{\alpha}_{2} } \right)}} = c_{1} /c_{2}\) and \(E_{0}\) is an energy constant determined by initial mode amplitudes. When \(c_{0} > 0\), Eq. (29) is called the equation of elliptic-type, whereas Eq. (29) is called the equation of hyperbolic-type when \(c_{0} < 0\). In addition, Eqs. (25) and (27) can be combined to

$$a_{2} D_{1} \gamma = \sigma a_{2} + \left( { - \frac{1}{2}c_{2} a_{1}^{2} + c_{1} a_{2}^{2} } \right)\cos \gamma$$
(30)

With help of Eqs. (26) and (29), Eq. (30) can be rewritten in the complete differential form as

$$a_{1}^{2} a_{2} \cos \gamma - \frac{\sigma }{{c_{2} }}a_{2}^{2} = L_{0}$$
(31)

where L 0 is an integral constant.

When \(c_{0} > 0\), let \(a_{1}^{2} = 2E_{0} \xi (T_{1} )\). Then, \(a_{2}^{2} = 2E_{0} {{(1 - \xi (T_{1} ))} \mathord{\left/ {\vphantom {{(1 - \xi (T_{1} ))} {c_{0} }}} \right. \kern-0pt} {c_{0} }}\) holds according to Eq. (29). Combining Eqs. (24) and (31) gives

$$\frac{{c_{0} }}{{2c_{1}^{2} E_{0} }}\left( {\frac{{{\text{d}}\xi }}{{{\text{d}}T_{1} }}} \right)^{2} = f_{1} (\xi )^{2} - f_{2} (\xi )^{2}$$
(32)

where

$$f_{1} (\xi )^{2} = \xi^{2} (1 - \xi ),f_{2} (\xi )^{2} = \frac{{c_{0} }}{{8E_{0}^{3} }}\left[ {L_{0} + \frac{{2\sigma E_{0} }}{{c_{2} c_{0} }}(1 - \xi )} \right]^{2}$$
(33)

The analytical solution of Eq. (32) exists if and only if \(f_{1} (\xi )^{2} \ge f_{2} (\xi )^{2}\) holds. There are three intersections \(\xi_{1}\), \(\xi_{2}\) and \(\xi_{3}\) determined by the curves f 1 and f 2 as shown in Fig. 3. According to the assumption of \(a_{1}^{2} = 2E_{0} \xi (T_{1} )\), \(\xi\) is a positive number. Hence, the bounded aperiodic oscillation of the original system occurs when \(\xi \in (\xi_{2} ,\xi_{3} )\) holds, as indicated by the heavy line in Fig. 3.

Fig. 3
figure 3

The conditions of periodic and aperiodic oscillations for \(c_{0} > 0\)

Full size image

In the case of \(c_{0} < 0\), let \(a_{1}^{2} = 2(E_{0} - |E_{0} |c_{0} \xi (T_{1} ))\). Then, one obtains \(a_{2}^{2} = 2 |E_{0} |\xi (T_{1} )\) and

$$\frac{1}{{2\left| {E_{0} } \right|c_{2}^{2} }}\left( {\frac{{{\text{d}}\xi }}{{{\text{d}}T_{1} }}} \right)^{2} = f_{1} (\xi )^{2} - f_{2} (\xi )^{2}$$
(34)

where

$$f_{1} (\xi )^{2} = \xi \left( {\frac{{E_{0} }}{{\left| {E_{0} } \right|}} - c_{0} \xi } \right)^{2} ,f_{2} (\xi )^{2} = \frac{1}{{8\left| {E_{0} } \right|^{3} }}\left( {L_{0} + \frac{2\sigma }{{c_{2} }}\left| {E_{0} } \right|\xi } \right)^{2}$$
(35)

As illustrated in Fig. 4a, there are three intersections \(\xi_{1}\), \(\xi_{2}\) and \(\xi_{3}\) determined by the curves f 1 and f 2 as well. When \(\xi \in (\xi_{1} ,\xi_{2} )\) or \(\xi \in (\xi_{2} ,\xi_{3} )\), as indicated by the heavy line in Fig. 4a, the bounded aperiodic oscillation of original system occurs. There is only one intersection \(\xi_{1}\) as shown in Fig. 4b which indicates that the unbounded aperiodic oscillation of original system may occur when \(\xi > \xi_{1}\).

Fig. 4
figure 4

The conditions of periodic and aperiodic oscillations for \(c_{0} < 0\). a \(c_{0} < 0,E_{0} < 0\), b \(c_{0} < 0,E_{0} > 0\)

Full size image

Furthermore, for the case of \(c_{0} > 0\), Eq. (32) can be written as

$$\frac{{c_{0} }}{{2c_{1}^{2} E_{0} }}\left( {\frac{{{\text{d}}\xi }}{{{\text{d}}T_{1} }}} \right)^{2} = (\xi_{3} - \xi )(\xi - \xi_{2} )(\xi - \xi_{1} )$$
(36)

when \(\xi \in (\xi_{2} ,\xi_{3} )\). By introducing the transformation of \((\xi_{3} - \xi ) = (\xi_{3} - \xi_{2} )\sin^{2} y\), one has

$$\left\{ {\begin{array}{*{20}l} {a_{1} = \pm \sqrt {2E_{0} \left[ {\xi_{3} - (\xi_{3} - \xi_{2} ){\text{sn}}^{2} (\rho_{1} t,\eta )} \right]} } \hfill \\ {a_{2} = \pm \sqrt {\frac{{2E_{0} }}{{c_{0} }}\left[ {1 - \xi_{3} + (\xi_{3} - \xi_{2} ){\text{sn}}^{2} (\rho_{1} t,\eta )} \right]} } \hfill \\ \end{array} } \right.$$
(37)

where

$$\rho_{1} = c_{1} \varepsilon \sqrt {\frac{{E_{0} (\xi_{3} - \xi_{1} )}}{{2c_{0} }}} ,\quad\eta = \sqrt {\frac{{\xi_{3} - \xi_{2} }}{{\xi_{3} - \xi_{1} }}}$$
(38)

For the case of \(c_{0} < 0\), one obtains the following expressions as

$$\left\{ {\begin{array}{*{20}l} {a_{1} = \pm \sqrt 2 \sqrt {E_{0} - \left| {E_{0} } \right|c_{0} \left( {\xi_{3} - (\xi_{3} - \xi_{2} ){\text{sn}}^{2} (\rho_{1} t,\eta )} \right)} } \hfill \\ {a_{2} = \pm \sqrt {2\left| {E_{0} } \right|} \sqrt {\xi_{3} - (\xi_{3} - \xi_{2} ){\text{sn}}^{2} (\rho_{1} t,\eta )} } \hfill \\ \end{array} } \right.$$
(39)

where

$$\rho_{1} = c_{2} \varepsilon \sqrt {\frac{{\left| {E_{0} } \right|(\xi_{3} - \xi_{1} )}}{2}} ,\quad\eta = \sqrt {\frac{{\xi_{3} - \xi_{2} }}{{\xi_{3} - \xi_{1} }}}$$
(40)

Then, the approximate solution of 2:1 resonance can be analytically obtained as

$$\varvec{\eta}=\varvec{\eta}_{0} + \varepsilon \left[ {a_{1} \cos (\omega_{1} t + \beta_{1} )\varvec{p}_{1} + a_{2} \cos (2\omega_{1} t + 2\beta_{1} + \gamma )\varvec{p}_{2} } \right]$$
(41)

It should be noted that the solutions of the nonlinear normal modes of the original system correspond to the steady state solutions of Eqs. (24), (26) and (30). Then, these mode solutions are asymptotically stable if the eigenvalues of the Jacobian matrix of Eqs. (24), (26) and (30) at the corresponding steady-state point are in the left-half of complex plane. Hence, the non-trivial constant solutions are corresponding to \(\sin \gamma = 0\). Then, the case of \(\cos \gamma = 1\) [40] is considered. By linearizing Eqs. (24), (26) and (30) near the non-trivial constant solutions, the characteristic equation is given as follows

$$\det \left[ {\begin{array}{*{20}c} \lambda & 0 & { - \frac{1}{2}\overline{a}_{1} \overline{a}_{2} c_{1} } \\ 0 & \lambda & {\frac{1}{2}\overline{a}_{1}^{2} c_{2} } \\ {\frac{{\overline{a}_{1} }}{{\overline{a}_{2} }}c_{2} } & { - c_{1} - \frac{1}{2}\frac{{\overline{a}_{1}^{2} }}{{\overline{a}_{2}^{2} }}c_{2} } & \lambda \\ \end{array} } \right] = 0$$
(42)

where λ is the eigenvalue of the characteristic equation. The solutions of Eq. (42) are

$$\lambda_{1} = 0,\quad\lambda_{2,3}^{2} = - \overline{a}_{1}^{2} \left( {c_{1} c_{2} + \frac{1}{4}\overline{h}^{2} c_{2}^{2} } \right)$$
(43)

where \(\overline{h} = \overline{a}_{1} /\overline{a}_{2}\). The coupled mode is stable if \(c_{1} c_{2} + \overline{h}^{2} c_{2}^{2} /4 > 0\). Otherwise, it is unstable.

According to the steady state solution of Eq. (30), the following equation can be obtained

$$h^{2} c_{2} - 2c_{1} - 2\frac{\sigma }{{a_{2} }} = 0$$
(44)

where \(h = a_{1} /a_{2}\) is the steady-state amplitude ratio. Figure 5 illustrates the variation of h with \(\sigma /a_{2}\) when \(\omega_{2} :\omega_{1} \approx 2:1\) holds for fixed parameters \(d = 3\), \(b = 0.6\), \(k = 0.6\), \(\kappa_{2} = 1\) and \(L = 10\), respectively. As shown in Fig. 5, the system has two stable coupled-mode solutions when \(\sigma /a_{2} > - 0.1853\) and no mode solution when \(\sigma /a_{2} < - 0.1853\).

Fig. 5
figure 5

Variation of \(h\) with \(\sigma /a_{2}\) for 2:1 internal resonance

Full size image

3.2 3:1 Internal resonances

To describe the closeness of \(\omega_{2}\) to \(3\omega_{1}\), a detuning parameter σ is defined as \(\omega_{2} = 3\omega_{1} + \varepsilon \sigma\). By substituting the expressions of η 0 and η 1 into Eq. (9) and eliminating the secular terms, one has

$$D_{1} A_{j} (T_{1} ,T_{2} ) = 0$$
(45)

Hence, the second-order approximation of Eq. (4) reads

$$\varvec{\eta}_{2} =\varvec{\varDelta}(\omega )\left[ { - \varvec{M}_{1} (\varvec{\eta}_{1} )D_{0}^{2}\varvec{\eta}_{1} - \varvec{K}_{2} (\varvec{\eta}_{1} ,\varvec{\eta}_{1} )\varvec{\eta}_{0} - \varvec{K}_{1} (\varvec{\eta}_{1} )\varvec{\eta}_{1} + \varvec{P}_{2} (\varvec{\eta}_{1} ,D_{0}\varvec{\eta}_{1} )} \right]$$
(46)

where \(\varvec{\varDelta}(\omega ) = \varLambda^{ - 1} (\omega ) = (\varvec{R}_{0} - \varvec{M}_{0} \omega^{2} )^{ - 1}\) is a matrix that matched each frequency of those harmonic terms in the right-hand side of Eq. (46). Then, by substituting the expressions of η 0, η 1 and η 2 into Eq. (10), one can get a unique solution η 3 only if the secular terms are orthogonal to every solution \(\varvec{u}_{j}\) given by

$$\omega_{j}^{2} \varvec{M}_{0}^{T} \varvec{u}_{j} = \varvec{R}_{0}^{T} \varvec{u}_{j} (j = 1,2)$$
(47)

Hence, the solvability conditions are obtained as follows

$$(\varvec{u}_{1}^{T}\varvec{\alpha}_{1} )A_{1}^{\prime } + (\varvec{u}_{1}^{T}\varvec{\alpha}_{10} )A_{1}^{2} \overline{A}_{1} + (\varvec{u}_{1}^{T}\varvec{\alpha}_{12} )A_{1} A_{2} \overline{A}_{2} + (\varvec{u}_{1}^{T}\varvec{\alpha}_{13} )A_{2} \overline{A}_{1}^{2} \exp ({\text{i}}\sigma T_{2} ) = 0$$
(48)
$$(\varvec{u}_{2}^{T}\varvec{\alpha}_{2} )A_{2}^{\prime } + (\varvec{u}_{2}^{T}\varvec{\alpha}_{20} )A_{2}^{2} \overline{A}_{2} + (\varvec{u}_{2}^{T}\varvec{\alpha}_{21} )A_{2} A_{1} \overline{A}_{1} + (\varvec{u}_{2}^{T}\varvec{\alpha}_{23} )A_{1}^{3} \exp ( - {\text{i}}\sigma T_{2} ) = 0$$
(49)

where \(()^{\prime }\) denotes derivative with respect to \(T_{2}\) and the details of \(\varvec{\alpha}_{j}\), \(\varvec{\alpha}_{j0}\) and \({\varvec{\upalpha}}_{sr}\), \(j,r,s = 1,2,3\) are listed in “Appendix”. By letting \(A_{j} (T_{2} ) = a_{j} (T_{2} )\exp (\text{i}\beta_{j} (T_{2} )) /2\), \(j = 1,2\) in Eqs. (48) and (49) and separating the real and imaginary parts, one obtains the following modulation equations

$$4\dot{a}_{1} + a_{1}^{3} v_{101} + a_{1} a_{2}^{2} v_{121} + a_{1}^{2} a_{2} \left( {v_{131} \cos \gamma - v_{132} \sin \gamma } \right) = 0$$
(50)
$$4a_{1} \dot{\beta }_{1} + a_{1}^{3} v_{102} + a_{1} a_{2}^{2} v_{122} + a_{1}^{2} a_{2} \left( {v_{131} \sin \gamma + v_{132} \cos \gamma } \right) = 0$$
(51)
$$4\dot{a}_{2} + a_{2}^{3} v_{201} + a_{2} a_{1}^{2} v_{211} + a_{1}^{3} \left( {v_{231} \cos \gamma + v_{232} \sin \gamma } \right) = 0$$
(52)
$$4a_{2} \dot{\beta }_{2} + a_{2}^{3} v_{202} + a_{2} a_{1}^{2} v_{212} + a_{1}^{3} \left( { - v_{231} \sin \gamma + v_{232} \cos \gamma } \right) = 0$$
(53)

where \(v_{jr} = \varvec{u}_{j}^{T}\varvec{\alpha}_{jr}\) and \(v_{jr1}\) and \(v_{jr2}\) are the real and imaginary parts of \(v_{jr}\), respectively, \(\gamma (T_{2} ) = \beta_{2} (T_{2} ) - 3\beta_{1} (T_{2} ) + \sigma T_{2}\). Hence, the second-order approximation of system is obtained as follows

$$\begin{aligned}\varvec{\eta}& =\varvec{\eta}_{0} + \varepsilon [a_{1} (t)\cos (\omega_{1} t + \beta_{1} (t))\varvec{p}_{1} + a_{2} (t)\cos (\omega_{2} t + \beta_{2} (t))\varvec{p}_{2} ] \\ & \quad + \frac{1}{2}\varepsilon^{2} \left\{ {\sum\limits_{j = 1}^{2} {\sum\limits_{r = 1}^{2} {\varvec{\varDelta}(\omega_{j} + \omega_{r} )a_{j} a_{r} \cos ((\omega_{j} + \omega_{r} )t + \beta_{j} (t) + \beta_{r} (t))} } \varvec{z}_{1jr} } \right. \\ & \left. {\quad + \sum\limits_{j = 1}^{2} {\sum\limits_{r = 1}^{2} {\varvec{\varDelta}(\omega_{j} - \omega_{r} )a_{j} a_{r} \cos ((\omega_{j} - \omega_{r} )t + \beta_{j} (t) - \beta_{r} (t))\varvec{z}_{2jr} } } } \right\} \\ \end{aligned}$$
(54)

where

$$\begin{aligned} \varvec{z}_{1jr} = \omega_{r}^{2} \varvec{M}_{1} (\varvec{p}_{j} )\varvec{p}_{r} - \omega_{j} \omega_{r} \varvec{P}_{22} (\varvec{p}_{j} ,\varvec{p}_{r} ) - \varvec{K}_{2} (\varvec{p}_{j} ,\varvec{p}_{r} )\varvec{\eta}_{0} - \varvec{K}_{1} (\varvec{p}_{j} )\varvec{p}_{r} \hfill \\ \varvec{z}_{2jr} = \omega_{r}^{2} \varvec{M}_{1} (\varvec{p}_{j} )\varvec{p}_{r} + \omega_{j} \omega_{r} \varvec{P}_{22} (\varvec{p}_{j} ,\varvec{p}_{r} ) - \varvec{K}_{2} (\varvec{p}_{j} ,\varvec{p}_{r} )\varvec{\eta}_{0} - \varvec{K}_{1} (\varvec{p}_{j} )\varvec{p}_{r} \hfill \\ \end{aligned}$$
(55)

By combining Eqs. (51) and (53), one obtains the following equation

$$\begin{aligned} 4a_{1} a_{2} \dot{\gamma } & = a_{1} a_{2}^{3} (3v_{122} - v_{202} ) + 3a_{1}^{2} a_{2}^{2} (v_{131} \sin \gamma + v_{132} \cos \gamma ) \\ & \quad + a_{2} a_{1}^{3} (3v_{102} - v_{212} ) - a_{1}^{4} ( - v_{231} \sin \gamma + v_{232} \cos \gamma ) + 4a_{1} a_{2} \sigma \\ \end{aligned}$$
(56)

The solutions of the nonlinear normal modes of the original system are corresponding to the steady-state solutions of Eqs. (50), (52), and (56). The stability of these modes coincides with that of the corresponding constant solutions of the modulation equations. The solutions of the corresponding characteristic equation are

$$\lambda_{1} = 0,\lambda_{2,3}^{2} = - \overline{a}_{1}^{2} \overline{a}_{2}^{2} B$$
(57)

where \(B = v_{232}^{2} \overline{h}^{4} + 6v_{132} v_{232} \overline{h}^{2} - \left( {2v_{232} v_{202} - 6v_{122} v_{232} + 6v_{102} v_{132} - 2v_{212} v_{132} } \right)\overline{h} - 3v_{132}^{2}\), and \(\overline{h} = \overline{a}_{1} /\overline{a}_{2}\). The coupled mode is stable if \(B > 0\). Otherwise, it is unstable.

According to the steady state solution of Eq. (56), one obtains

$$- v_{232} h^{4} + (3v_{102} - v_{212} )h^{3} + 3v_{132} h^{2} + \left[ {(3v_{122} - v_{202} ) + \frac{4\sigma }{{a_{2}^{2} }}} \right]h = 0$$
(58)

where \(h = a_{1} /a_{2}\). The variation of h with \(\sigma /a_{2}^{2}\) for 3:1 internal resonance is shown in Fig. 6. In Fig. 6, the parameters are set as \(d = 3\), \(b = 0.3\), \(k = 0.38\), \(\kappa_{2} = 1\) and \(L = 0.3\) to meet the requirement of \(\omega_{2} \approx 3\omega_{1}\) when 3:1 internal resonance occurs. In Fig. 6, there exist one stable and one unstable coupled-mode solutions when \(\sigma /a_{2}^{2} < 24.48\) or \(\sigma /a_{2}^{2} > 52.11\) holds, one stable and three unstable coupled-mode solutions when \(24.48 < \sigma /a_{2}^{2} < 30.12\), two stable and two unstable coupled-mode solutions when \(30.12 < \sigma /a_{2}^{2} < 50.98\), two stable coupled-mode solutions when \(50.98 < \sigma /a_{2}^{2} < 51.71\), and three stable coupled-mode solutions when \(51.71 < \sigma /a_{2}^{2} < 52.11\).

Fig. 6
figure 6

Variation of \(h\) with \(\sigma /a_{2}^{2}\) for 3:1 internal resonance

Full size image

4 Numerical results

In this section, to validate the analytic results, the approximate solutions given by Eqs. (41) and (54) are compared with the numerical results of the dynamic equations of the rigid-flexible system Eq. (4) solved via the Runge–Kutta method, respectively.

In the case of 2:1 internal resonance, to meet the requirement of \(\omega_{2} :\omega_{1} \approx 2:1\), the physical parameters were set as \(d = 3\), \(b = 0.6\), \(k = 0.6\), \(\kappa_{2} = 1\) and \(L = 10\), respectively. Then in the case of 3:1 internal resonance, the physical parameters were set as \(d = 3\), \(b = 0.3\), \(k = 0.38\), \(\kappa_{2} = 1\) and \(L = 10\), respectively, to meet the requirement of \(\omega_{2} :\omega_{1} \approx 3:1\). There is a good agreement between the numerical solutions and the approximate solutions for both 2:1 internal resonance and 3:1internal resonance as shown in Fig. 7a, b, respectively, with the initial state \((a_{10} ,a_{20} ,\beta_{10} ,\beta_{20} ) = (0.05,0.05,0,0)\). In addition, Fig. 8 shows numerical integrations of Eqs. (24), (26) and (30) with the initial state \((a_{10} ,a_{20} ,\gamma ) = (0.1,0.2,\uppi /12)\). The energy in the system continues to be exchanged between the two modes as shown in Fig. 8.

Fig. 7
figure 7

Comparison between the approximate solutions and the numerical solutions. a The case of 2:1 internal resonance, b The case of 3:1 internal resonance

Full size image
Fig. 8
figure 8

Modal amplitudes for 2:1 internal resonance

Full size image

5 Experimental investigation of nonlinear resonance

From the results of the analytic analysis, the nonlinear bifurcation phenomena have been found in the rigid-flexible structure of concern. Furthermore, in this section, an experimental study is performed to verify the analytic analysis in Sect. 3.

As shown in Fig. 9, the experiment equipment is composed of an L-shape rigid-flexible structure, a laser displacement sensor and data acquisition software. Similar with the figure shown in Fig. 1, the L-shape rigid-flexible structure is composed of a rigid metal arm and a flexible metal beam-2 made of aluminium in the experimental setup shown in Fig. 9. Such a rigid-flexible structure is fixed at the free tip of a cantilever beam-1 which can be equivalent to a torsional spring. Hence, the rotation angle of the arm is the same as that of the free tip of the beam-1, and the deformation of the beam w shown in Fig. 1 is corresponding to the deformation of the flexible beam-2 which is measured by the laser displacement sensor directly. As well known, the rotation of the free tip of a cantilever beam under the external moment applied to the same position can be expressed as \(\theta_{B} = - M_{e} l^{*} /(EI^{*} )\). Then the equivalent stiffness of the torsional spring can be derived as \(k_{1} = EI^{*} /l^{*}\), where \(EI^{*}\) and \(l^{*}\) are the bending stiffness of the flexible beam-1 and the distance between the free tip of the flexible beam-1 and the clamping position of the flexible beam-1, respectively. By adjusting the clamping position, the equivalent stiffness of the torsional spring can be regulated to meet the requirement of the internal resonance. Moreover, the translation of the free tip of the flexible beam-1 has little influence on the dynamic behavior of the beam-2 since it is parallel to the axis of the beam-2 and the axial vibration of the beam-2 is neglected. All the experimental data are collected during the quasi-steady-state vibration to assure the authenticity of the vibration signals.

Fig. 9
figure 9

Schematics and photographs of the experimental setup. a Schematic of the experimental setup, b photograph of the main experimental apparatus for 3:1 internal resonance

Full size image

The length and the mass of the arm were 0.11 m and 0.0749 kg, whereas the length and the mass of the beam-2 as 0.297 m and 0.0185 kg. The bending stiffnesses of beam-1 and beam-2 were 0.0906 Nm2 and 0.079 Nm2. By adjusting the clamping position, the length of beam-1 was set as 0.129 m, then the equivalent stiffness of the torsional spring was 0.7023 Nm to meet the requirement of \(\omega_{2} \approx 3\omega_{1}\) when the 3:1 internal resonance occurred. The vibration responses of the beam-2 were measured by a laser displacement sensor.

Figure 10 illustrates the time history of the displacement of the free tip of beam-2 for the experiment case of 3:1 internal resonance and the corresponding frequency spectrum for the case is illustrated in Fig. 11. As shown in Fig. 11, the frequencies of the experimental system meet the requirement of \(\omega_{2} \approx 3\omega_{1}\). Hence, the mode amplitude ratio for the 3:1 internal resonance can be obtained as shown in Fig. 12 by a red circle A. Then, the vibration responses of the beam-2 and their mode amplitudes a 1 and a 2 are excited by adjusting the initial deformation of the free tip of the beam-2. For the same detuning parameter σ, \(\sigma /a_{2}^{2}\) and h will vary with the change of a 1 and a 2. So dozens of experimental data can be obtained. Figure 12 presents the variation of the ratio of steady-state amplitudes h with respect to \(\sigma /a_{2}^{2}\). As shown in Fig. 12, the experimental data are coincident well with the stable solutions correspond to the analytical predictions and the unstable solutions predicted by the analysis are not occurred in the experiment. The results indicate that the approximate amplitude ratios derived from the analytic method agree well with the experimental data.

Fig. 10
figure 10

Time history of the free tip response of beam-2 for 3:1 internal resonance

Full size image
Fig. 11
figure 11

Frequency spectrum for 3:1 internal resonance

Full size image
Fig. 12
figure 12

Experimental and analytical results of amplitude ratio for 3:1 internal resonance

Full size image

Similarly, the experiment for 2:1 internal resonance was carried out, wherein the length and the mass of the arm were set as 0.205 m and 0.11 kg, whereas the length and the mass of the beam-2 as 0.295 m and 0.0159 kg. In this case, the bending stiffnesses of beam-1 and beam-2 were 0.1184 Nm2and 0.1026 Nm2. In order to meet the requirement of \(\omega_{2} \approx 2\omega_{1}\), the length of the beam-1 was set as 0.041 m by adjusting the clamping position, and then the equivalent stiffness of the torsional spring was 2.8878 Nm. The distance between the measured point B and the free tip of the beam-2 is 0.173 m. Figure 13 presents the time history of the displacement of the point B for 2:1 internal resonance, and the corresponding frequency spectrum for the case is depictured in Fig. 14. As shown in Fig. 14, the two frequencies meet the requirement of \(\omega_{2} \approx 2\omega_{1}\). Hence, by changing the initial deformation of the free tip of the beam-2, dozens of experimental data of the mode amplitude ratio for the 2:1 internal resonance can be obtained. As shown in Fig. 15, the experimental data coincide well with the stable solutions obtained by the analytical predictions.

Fig. 13
figure 13

Time history of the point B of beam-2 for 2:1 internal resonance

Full size image
Fig. 14
figure 14

Frequency spectrum for 2:1 internal resonance

Full size image
Fig. 15
figure 15

Analytical and experimental results of amplitude ratio for 2:1 resonance

Full size image

As shown in Figs. 10 and 13, the vibrations of beams in the experimental research damped very slowly since the damping is very small, which is also true for a real flexible space structure. So the responses of the experimental cases during a small period can be treated as a quasi-steady-state motion approximately.

Moreover, the natural frequencies of 3:1 and 2:1 internal resonances are listed in Table 1. As shown in Table 1, the natural frequencies of the experimental cases are very close to the analytical ones. The results indicate that the dynamic equation derived based on the assumed modes method in this research is feasible.

Table 1 Comparison of natural frequencies of analytical and experimental results for 3:1 and 2:1 internal resonances
Full size table

From the experiment results, the nonlinear bifurcation phenomena is observed. There is a agreement between the experiment and the analytic results in a wide range of \(\sigma /a_{2}^{2}\), however, there is no experimental data in the right of Fig. 12 corresponding to positive value of \(\sigma /a_{2}^{2}\). The main reason is that the detuning parameter \(\sigma\) is always negative with respect to the physical parameters in the experimental study due to the restriction of the rigid-flexible structure. The curves shown in Figs. 6 and 12 are reversed in each other. The reason is that the corresponding coefficients are in different unfolding parameters regions, hence, their topologies are different.

6 Conclusions

This study investigates the nonlinear internal resonances of an L-shape rigid-flexible antenna system theoretically and experimentally. The study shows that the antenna system has various internal resonances, such as those of 3:1 and 2:1, under different combinations of structural parameters. Using the method of multiple scales, one can derive the approximate solutions of those internal resonances. Then the frequency-amplitude responses of internal resonances are determined and the stabilities of the internal resonances are analyzed. The approximate solutions of those internal resonances are consistent with numerical solutions.

An important contribution of the study is to analyze the nonlinear internal resonances of the L-shape rigid-flexible structure via experimental tests. There is a good agreement between the analytical and experimental results both of which indicate that there exists bifurcation phenomena of the frequency-amplitude response of an internal resonance.