Nonlinear normal modes of a tethered satellite system of two degrees of freedom under internal resonances

Abstract

The aim of this study was to investigate the nonlinear normal modes (NNMs) of an in-plane tethered satellite system (TSS) during state-keeping phase. The equations of the in-plane motion are derived for the TSS, and the analytic solutions under the three-to-one and one-to-one internal resonances are obtained by applying the method of multiple scales expressed in matrix forms. It is indicated by studying the stability properties of the NNMs that the number of NNMs is more than one over a wide range of the detuning parameter under both internal resonances. Finally, several numerical simulations are made to verify the analytical results.

1 Introduction

The technology of TSS has received considerable attention during the last two decades since it has lots of advantages in space missions [1, 2]. Most studies on the dynamics and control of TSS are based on the particle model [3, 4]. However, the attitude dynamics of satellite may play an important role in space missions like the satellite’s formation flight [5–7].

The TSS exhibits abundant nonlinear dynamical behaviors such as the quasi-periodic motions, period doubling bifurcation and chaos. Peláez et al. investigated the periodic librations and their control for an electrodynamic tether system in inclined orbit [8–11]. Luongo and Vestroni [12] analyzed the periodic oscillations of TSS under internal resonances and presented an effective control law of longitudinal force to reduce the primary and secondary instability regions [13]. Based on the Leray-Schauder degree theory, Rossi et al. [14] established the conditions for the existence of the periodic motions of TSS subjected to the atmospheric drag and the non-spherical Earth. Williams [15] obtained the periodic solutions of electrodynamic tethers using Legendre pseudospectral method and designed a feedback control strategy to track the periodic oscillations. Recently, Nakanishi et al. [16] investigated the in-plane periodic solutions of a dumbbell satellite system in elliptic orbits. Kojima and Sugimoto [17] studied the stability properties of periodic motions of an electrodynamic tether system in an inclined elliptic orbit. Burov et al. addressed the periodic motions of an orbital cable system equipped with an elevator. They employed the Poincaré theory to determine the existence of families of the periodic motions [18]. Steiner et al. [19] analyzed the out-of-plane oscillations of TSS by means of center manifold theory.

In the above researches, the satellite is treated as an ideal particle instead of rigid body. To get an insight into the dynamics of TSS, the satellite’s body must be taken into account. Burov and Troger studied the dynamics of the system with a massive body and a gyrostat that is connected by an inextensible weightless tether. They employed Mohr circles to interpret their equilibria geometrically [20]. Takeichi et al. modeled the satellite as a rigid body and studied the periodic solutions of the libration via Lindstedt perturbation method. The results showed the periodic solution of TSS is the minimum energy one [21]. Aslanov [22] obtained the approximate and exact solutions of the oscillations of a tethered system with the rigid-body attitude in terms of the elementary functions and the elliptic Jacobi functions. He also revealed the effect of the tether elasticity on the oscillations of the system [23]. Jin et al. [24, 25] investigated the coexistent quasi-periodic oscillations of a subsatellite during station-keeping phase in the case of the three-to-one internal resonance.

For the purpose of searching for periodic solutions of nonlinear differential equations, the idea of construction of the NNMs was first proposed by Rosenberg for finite-degree-of-freedom systems [26]. If there is an internal resonance in a system, it is difficult to determine the NNMs [27]. Nayfeh et al. used a complex-variable invariant-manifold approach to construct the normal modes of weakly nonlinear discrete systems with internal resonance. They showed the number of NNMs may be more than that of linear normal modes in contrast to the case of non-internal resonance [28]. Wu et al. [29] introduced the undivided even-dimensional invariant manifold to define and construct the NNMs. Li et al. [30] applied the method of multiple scales to compute the approximate solutions of NNMs of a two-degree-of-freedom system under internal resonance and investigated the bifurcations of the NNMs.

This paper studies the NNMs and their stabilities for a TSS, in which the mother satellite is treated as a rigid body. The study begins with the modeling of the in-plane motion of the TSS during station-keeping phase in Sect. 2. The method of multiple scales in matrix form is employed to compute the approximate solutions for the NNMs, and their stabilities are analyzed in Sect. 3. The case studies are given in Sect. 4.

2 Modeling of a tethered satellite system

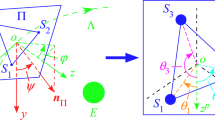
Consider an in-plane tethered satellite system moved in an unperturbed Kepler circular orbit, as shown in Fig. 1. The mother satellite is treated as a rigid body of mass M, and the subsatellite is envisioned to be a point of mass m that is attached to the mother satellite through an inelastic massless tether of length l at a joint point of distance, $\rho$, to the mass center of the mother satellite. It is assumed that the mass of the mother satellite is much greater than that of the subsatellite, and the center of mass of the system coincides with that of the mother satellite, where the mother satellite moves in an unperturbed Kepler circle orbit of radius R and true anomaly $\nu$. The Earth-centered inertial frame is denoted by O-XYZ, the origin of which is located at the center of the Earth. The origin of orbital frame $C\hbox {-}xyz$ is put at the mass center of the system, with the x-axis pointing toward the center of the Earth, the y-axis following the tangent of orbit and the z-axis completing the right-handed coordinate system. The body frame $C\hbox {-}x_{b} y_{b} z_{b}$ is established along with the principal axes of the spacecraft.

Fig. 1

Tethered satellite system of two degree of freedom

According to Fig. 1, it is easy to write out the position vector of the mother satellite and the subsatellite in inertial frame as

$$\begin{aligned} {{\varvec{r}}}_{1} =\left[ {{\begin{array}{l} {R\cos v} \\ {R\sin v} \\ \end{array} }} \right] , \end{aligned}$$

(1)

and

$$\begin{aligned} {{\varvec{r}}}_{2} =\left[ {{\begin{array}{l} {(R-l\cos \theta -\rho \cos \alpha )\cos v+(\rho \sin \alpha +l\sin \theta )\sin v} \\ {(R-l\cos \theta -\rho \cos \alpha )\sin v-(\rho \sin \alpha +l\sin \theta )\cos v} \\ \end{array} }} \right] . \end{aligned}$$

(2)

The potential energy of the system is expressed in the following form [31]

$$\begin{aligned} V= & {} -\frac{\mu _{e} M}{\left| {{{\varvec{r}}}_{1}} \right| }-\frac{\mu _{e} m}{\left| {{{\varvec{r}}}_{2} } \right| }-\frac{1}{2}\frac{\mu _{e}}{\left| {{{\varvec{r}}}_{1}} \right| ^{3}}(I_{x} +I_{y} +I_{z})\nonumber \\&+\,\frac{3}{2}\frac{\mu _{e}}{\left| {{{\varvec{r}}}_{1}} \right| ^{3}}\left( I_{x} \cos ^{2}\alpha +I_{y} \sin ^{2}\alpha +I_{z}\right) , \end{aligned}$$

(3)

where $\mu _{e} =3.986\times 10^{14}\,\hbox {m}^{3}\hbox {/s}^{2}$ is the gravitational parameter of Earth, $I_{x}, I_{y}$ and $I_{z}$ are the principal moments of inertia of the mother satellite expressed in the body frame.

The kinetic energy of the system is

$$\begin{aligned} T=\frac{1}{2}I_{z} \left( {\frac{\hbox {d}\alpha }{\hbox {d}t}+\frac{\hbox {d}\nu }{\hbox {d}t}} \right) ^{2}+\frac{1}{2}m\left| {\frac{\hbox {d}{{\varvec{r}}}_{2}}{\hbox {d}t}} \right| ^{2}+\frac{1}{2}M\left| {\frac{\hbox {d}{{\varvec{r}}}_{1}}{\hbox {d}t}} \right| ^{2}. \end{aligned}$$

(4)

The generalized coordinates are chosen as $q_{1}=\theta$ and $q_{2} =\alpha$ in using the following Lagrange’s equations

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}\left( {\frac{\partial L}{\partial \dot{q}_{i}}}\right) -\frac{\partial L}{\partial q_{i}}=0,\quad i=1,2. \end{aligned}$$

(5)

In this paper, the mother satellite is considered as a symmetric rigid body, i.e., $I_x =I_y$. So the nonlinear equations of motion near local equilibrium position $(\theta =0,\alpha =0)$ are

$$\begin{aligned} \left\{ {\begin{array}{l} \ddot{\theta }+a_1 \ddot{\alpha }+3a_{3} \theta +a_{1} (\dot{\alpha }^{2}+2\dot{\alpha })(\theta -\alpha )=0, \\ \ddot{\theta }+a_2 \ddot{\alpha }+3a_{3} \alpha -(\dot{\theta }^{2}+2\dot{\theta })(\theta -\alpha )=0, \\ \end{array}} \right. \end{aligned}$$

(6)

where $a_{1} =\rho \hbox {/}l, a_{2} =a_{1} +I_{z} \hbox {/(}m\rho l)$, $a_{3} =1+a_{1}$. The overdot denotes the derivative with respect to the dimensionless time $\tau =(\hbox {d}\nu \hbox {/d}t)\cdot t$. Equation (6) can be written in matrix form

$$\begin{aligned} {{\varvec{M}}}\ddot{{{\varvec{X}}}}+{{\varvec{KX}}}+{{\varvec{C}}}(2\dot{{{\varvec{X}}}} +\dot{{{\varvec{X}}}}^{2}){{\varvec{IX}}}=\mathbf{0 }, \end{aligned}$$

(7)

where

$$\begin{aligned}&{{\varvec{M}}}=\left[ {{\begin{array}{cc} 1&{} {a_{1}} \\ 1&{} {a_{2}} \\ \end{array} }} \right] ,\quad {{\varvec{K}}}=\left[ {{\begin{array}{cc} {3a_{3}}&{} 0 \\ 0&{} {3a_{3}} \\ \end{array} }} \right] ,\quad {{\varvec{C}}}=\left[ {{\begin{array}{cc} 0&{} {-a_1 } \\ 1&{} 0 \\ \end{array} }} \right] ,\quad \nonumber \\&{{\varvec{X}}}=\left( {{\begin{array}{cc} \theta \\ \alpha \\ \end{array} }} \right) ,\quad \dot{{{\varvec{X}}}}^{2}=\left( {{\begin{array}{cc} {\dot{\theta }^{2}} \\ {\dot{\alpha }^{2}} \\ \end{array} }} \right) ,\quad {{\varvec{I}}}=\left( {{\begin{array}{c} {-1} \\ 1 \\ \end{array} }} \right) ^{\mathrm{T}}. \end{aligned}$$

(8)

This is a two-degree-of-freedom system with quadratic and cubic nonlinearity, in which the nonlinear resonant phenomenon may occur.

3 Nonlinear resonance analysis

The method of multiple scales [25] will be employed to determine a second-order uniform expansion of the matrix solution of Eq. (7). One defines time scales ${T}_r =\varepsilon ^{r}\tau ,\;\;r=0,1,2\ldots$, where $\varepsilon$ is a small bookkeeping parameter. Let the solution of Eq. (7) be

$$\begin{aligned} {{\varvec{X}}}=\varepsilon {{\varvec{X}}}_1 (T_0, T_2 )\,+\,\varepsilon ^{2}{{\varvec{X}}}_{2} (T_{0}, T_{2} )\,+\,\varepsilon ^{3}{{\varvec{X}}}_{3} (T_{0}, T_{2} )+\cdots . \end{aligned}$$

(9)

By substituting Eq. (9) into Eq. (7) and equating the same power of $\varepsilon$, one has

$$\begin{aligned}&{{\varvec{M}}}D_{0}^{2} {{\varvec{X}}}_{1} +{{\varvec{KX}}}_{1} =0, \end{aligned}$$

(10a)

$$\begin{aligned}&{{\varvec{M}}}D_{0}^{2} {{\varvec{X}}}_{2} +{{\varvec{KX}}}_{2} =-2[{{\varvec{M}}}D_{1} D_{0} {{\varvec{X}}}_{1} +{{\varvec{C}}}(D_{0} {{\varvec{X}}}_{1}){{\varvec{IX}}}_{1}], \nonumber \\ \end{aligned}$$

(10b)

$$\begin{aligned}&{{\varvec{M}}}D_{0}^{2} {{\varvec{X}}}_{3} +{{\varvec{KX}}}_{3} =-2[{{\varvec{M}}}(D_{2} D_{0} {{\varvec{X}}}_{1}\nonumber \\&\quad +\,D_{1} D_{0} {{\varvec{X}}}_{2} )+{{\varvec{C}}}(D_{0} {{\varvec{X}}}_{1} ) {{\varvec{IX}}}_{2} ]\nonumber \\&\quad -\,{{\varvec{C}}}[2(D_{1} {{\varvec{X}}}_{1} +D_{0} {{\varvec{X}}}_{2} ) +(D_{0} {{\varvec{X}}}_{1} )^{2}]{{\varvec{IX}}}_{1} -{{\varvec{M}}}D_{1}^{2} {{\varvec{X}}}_{1},\nonumber \\ \end{aligned}$$

(10c)

where $D_r =\partial \hbox {/}\partial T_r$ represents the differential operators. The solution of Eq. (10a) yields

$$\begin{aligned} {{\varvec{X}}}_{1} ={\varvec{\varGamma }} [{{\varvec{A}}}(T_{2}){{\varvec{E}}}(\omega , T_{0}) +\bar{{{\varvec{A}}}}(T_{2})\bar{{{\varvec{E}}}}(\omega , T_{0})], \end{aligned}$$

(11)

with

$$\begin{aligned}&{\varvec{\varGamma }} =\left[ {{\begin{array}{ll} 1&{} 1 \\ {\varGamma _1 }&{} {\varGamma _2 } \\ \end{array} }} \right] ,\quad {{\varvec{A}}}(T_2 )\nonumber \\&\quad =\left[ {{\begin{array}{ll} A_1 (T_2 )&{}\quad 0 \\ 0&{}\quad A_2 (T_2 ) \\ \end{array}}} \right] ,\quad {{\varvec{E}}}(\omega , T_{0} ) =\left( {\begin{array}{ll} \hbox {e}^{i\omega _{1} T_{0} } \\ \hbox {e}^{i\omega _{2} T_{0} } \\ \end{array}} \right) ,\nonumber \\ \end{aligned}$$

(12)

where $\varGamma _r =\omega _r^2 \hbox {/}(3a_3 -a_2 \omega _r^2 )$, $\omega _r$ is a natural frequency of the linearized Eq. (7) with the restriction of $0<\omega _1 <\omega _2$.

Fig. 2

Natural frequencies of varying system parameters

Substituting Eq. (11) into the right-hand side of Eq. (10b) yields

$$\begin{aligned}&{{\varvec{M}}}D_0^2 {{\varvec{X}}}_2 +{{\varvec{KX}}}_2 =-2\{{{\varvec{M}}}{\varvec{\varGamma }} [D_1 {{\varvec{A}}}(T_2 )D_0 {{\varvec{E}}} (\omega , T_0 )\nonumber \\&\quad +\,D_1 \bar{{{\varvec{A}}}}(T_2 )D_0 \bar{{{\varvec{E}}}}(\omega , T_0 )] \nonumber \\&\quad +\,{{\varvec{C}}}{\varvec{\varGamma }} [{{\varvec{A}}}(T_2 )D_0 {{\varvec{E}}} (\omega , T_0 )+\bar{{{\varvec{A}}}}(T_2 )D_0 \bar{{{\varvec{E}}}}(\omega , T_0 )]{{\varvec{I}}}{\varvec{\varGamma }} \nonumber \\&\quad \cdot \,[{{\varvec{A}}}(T_2 ){{\varvec{E}}}(\omega , T_0 )\;+\bar{{{\varvec{A}}}}(T_2 )\bar{{{\varvec{E}}}}(\omega , T_0)]\}. \end{aligned}$$

(13)

The second-order approximation of the solution of Eq. (7) can be expressed as

$$\begin{aligned}&{{\varvec{X}}}_2 =-2\varvec{\varDelta } (\omega ){{\varvec{C}}}{\varvec{\varGamma }} [{{\varvec{A}}} (T_2 )D_0 {{\varvec{E}}}(\omega , T_0 )\nonumber \\&\quad +\,\,\bar{{{\varvec{A}}}}(T_2 )D_0 \bar{{{\varvec{E}}}} (\omega , T_0 )]{{\varvec{I}}}{\varvec{\varGamma }} \nonumber \\&\quad \cdot \, \hbox {[}{{\varvec{A}}}(T_2 ){{\varvec{E}}}(\omega , T_0 )\;+\bar{{{\varvec{A}}}} (T_2 )\bar{{{\varvec{E}}}}(\omega , T_0)\hbox {],} \end{aligned}$$

(14)

where ${\varvec{\varDelta }}(\omega )=({{\varvec{K}}}-{{\varvec{M}}}\omega ^{2})^{-1}$ is a matrix. Note that the variable $\omega$ matches each frequency of those harmonic terms in the right-hand side of Eq. (14), so that Eq. (10c) becomes

$$\begin{aligned}&{{\varvec{M}}}D_{0}^{2} {{\varvec{X}}}_{3} +{{\varvec{KX}}}_{3} =-2[{{\varvec{M}}}D_{2} D_{0} {{\varvec{X}}}_{1} +{{\varvec{C}}}(D_{0} {{\varvec{X}}}_{1} ){{\varvec{IX}}}_{2} ]\nonumber \\&\quad -\,{{\varvec{C}}}[2D_{0} {{\varvec{X}}}_{2} +(D_{0} {{\varvec{X}}}_{1} )^{2}]{{\varvec{IX}}}_{1}. \end{aligned}$$

(15)

In order to check the conditions of internal resonances, the natural frequencies which vary with the system parameters $a_{1}$ and $a_{2}$ are shown in Fig. 2. One can see from this figure that there exists the three-to-one internal resonance under different combinations of the parameters, whereas the one-to-one internal resonance occurs only when the value of parameter $a_{2}$ is near 1 and $a_{1}$ is very small.

3.1 Three-to-one internal resonances

To describe the nearness of $\omega _{2}$ to $3\omega _{1}$, a detuning parameter $\sigma$ is defined as $\omega _{2} =3\omega _{1} +\varepsilon ^{2}\sigma$. By substituting Eqs. (11) and (14) into Eq. (15) and eliminating the secular terms, one obtains

$$\begin{aligned}&i\lambda _{r} D_{2} A_{r} \hbox {/}2=-P_{r} A_{r} \left| {A_{3-r}} \right| ^{2}+R_{r} A_{r} \left| {A_{r}}\right| ^{2}\nonumber \\&\quad +\,U_{r} A_{3-r} [(r-1)A_{1}^{2} +(2-r)\bar{{A}}_{1}^{2} ]e^{(-1)^{r-1}i\sigma T_{2}},\nonumber \\ \end{aligned}$$

(16)

where $\lambda _{r} =\omega _{r} (1+2a_{1} \varGamma _{r} +a_{1} a_{2} \varGamma _{r}^{2} )$, $P_{r} =P_{1r}+a_{1} \varGamma _{r} P_{2r}$, $R_{r} =R_{1r}+a_{1} \varGamma _{r} R_{2r}$, $U_{r} =U_{1r} +a_{1} \varGamma _{r} U_{2r}$. The coefficients, $P_{rs}$, $R_{rs}$ and $U_{rs}$, ($r, s=1, 2$) can be found in Ref. [25]. Letting $A_{r} (T_{2})=\rho _{r} (T_{2}) \hbox {e}^{i\beta _{r} (T_{2})}\hbox {/}2$ in Eq. (16) and separating the real parts and the imaginary parts, one arrives at a set of modulation equations as follows

$$\begin{aligned}&2\lambda _{1} D_{2} \rho _{1} =U_{1} \rho _{1}^{2} \rho _{2} \sin \gamma , \end{aligned}$$

(17a)

$$\begin{aligned}&2\lambda _{2} D_{2} \rho _{2} =-U_{2} \rho _{1}^{3} \sin \gamma , \end{aligned}$$

(17b)

$$\begin{aligned}&2\lambda _{1} \rho _{1} D_{2} \beta _{1} =P_{1} \rho _{1} \rho _{2}^{2} -R_{1} \rho _{1}^3 -U_{1} \rho _{1}^{2} \rho _{2} \hbox {cos}\gamma , \end{aligned}$$

(17c)

$$\begin{aligned}&2\lambda _{2} \rho _{2} D_{2} \beta _{2} =P_{2} \rho _{1}^{2} \rho _{2} -R_{2} \rho _2^3 -U_2 \rho _1^3 \hbox {cos}\gamma , \end{aligned}$$

(17d)

where

$$\begin{aligned} \gamma =\beta _{2} -3\beta _{1} +\sigma T_{2}. \end{aligned}$$

(18)

There are two possibilities: the uncoupled NNM with $\rho _{1} =0,\;\;\rho _{2}\ne 0$ and the coupled NNM with $\rho _1 \ne 0,\;\;\rho _{2}\ne 0$. In the first case, the uncoupled NNM is

$$\begin{aligned} \theta =\varepsilon \rho _{2} \cos (\omega _{2} t+\beta _{2} ),\quad \alpha =\varepsilon \varGamma _{2} \rho _{2} \cos (\omega _{2} t+\beta _{2}). \end{aligned}$$

(19)

In what follows, a mixed polar-Cartesian representation for the complex-valued amplitudes of modes will be employed to analyze the stability of NNMs [32]. By substituting $A_{1} =(1\hbox {/}2)(p-iq)e^{is(T_{2})}$ and $A_{2} =(1\hbox {/}2)\rho _{2} e^{i\beta _{2} (T_{2})}$ into the first equation of Eq. (16), one arrives at

$$\begin{aligned}&(2\lambda _{1} {s}'p-2i\lambda _{1} {s}'q-2i\lambda _{1} {p}'-2\lambda _{1} {q}'\nonumber \\&\quad +\,R_{1} p^{3}-iR_{1} p^{2}q+R_{1} pq^{2}-iR_{1} q^{3}\nonumber \\&\quad -\,\rho _{2}^{2} P_{1} p+i\rho _{2}^{2} P_{1} q)\nonumber \\&\quad -\,U_{1} \rho _{2} (p^{2}+2ipq-q^{2})e^{i(3s(T_{2}) -\sigma T_{2}-\beta _{2} (T_{2}))}=0,\nonumber \\ \end{aligned}$$

(20)

where “$^{\prime }$” denotes the derivative with respect to $T_{2}$. According to Eq. (20), when $s(T_{2})=(\beta _{2} (T_{2})+\sigma T_{2} )/3$, we have $e^{-i(3s(T_{2})-\sigma T_{2}-\beta _{2} (T_{2}))}=1$ and ${s}'={\beta }'_{2} \hbox {/}3+\sigma \hbox {/}3$. At the same time, Eq. (17d) goes to ${\beta }'_{2} =-R_{2} \rho _{2}^{2} \hbox {/}(2\lambda _{2})$ in the uncoupled mode, thus ${s}'=\sigma \hbox {/}3-R_{2} \rho _{2}^{2} \hbox {/}(6\lambda _{2})$. As a result, Eq. (20) becomes autonomous one. Having separated the real part and the imaginary part of the autonomous equation with the substitution of ${\beta }'_{2} =-R_{2} \rho _{2}^{2} \hbox {/}(2\lambda _{2})$, the two first-order ordinary differential equations in variables p and q are obtained. The linearized version of the differential equation near their equilibrium position ($p=0, q=0$) takes the following form

$$\begin{aligned}&{p}'-\left[ {\left( {\frac{R_{2}}{6\lambda _{2}} +\frac{P_{1}}{2\lambda _{1}}} \right) \rho _{2}^{2} -\frac{\sigma }{3}}\right] q=0, \end{aligned}$$

(21)

$$\begin{aligned}&{q}'+\left[ {\left( {\frac{R_{2}}{6\lambda _{2}}+\frac{P_{1} }{2\lambda _{1}}}\right) \rho _{2}^{2}-\frac{\sigma }{3}}\right] p=0. \end{aligned}$$

(22)

Given the coefficients in Eqs. (21) and (22) are identical, this leads to a pair of pure imaginary eigenvalues. Consequently, the uncoupled mode is neutrally stable. In addition, if

$$\begin{aligned} \frac{2\sigma }{\rho _{2}^{2}}=\frac{\lambda _{1} R_{2} +3\lambda _{2} P_{1} }{\lambda _{1} \lambda _{2}}, \end{aligned}$$

(23)

the two eigenvalues coalesce into zero, and there is a degeneracy. In this case, the degenerate uncoupled mode merges with the unstable coupled mode.

As for the coupled NNMs, their approximate solutions are

$$\begin{aligned} \left\{ {\begin{array}{l} \theta =\varepsilon [\rho _{1} \cos (\omega _1 t+\beta _{1})\\ \qquad +\,\rho _{2} \cos (3\omega _{1} t+3\beta _{1} \hbox {+}\gamma )], \\ \alpha =\varepsilon [\varGamma _{1} \rho _{1} \cos (\omega _{1} t+\beta _{1})\\ \qquad +\,\varGamma _{2} \rho _{2} \cos (\hbox {3}\omega _{1} t+\hbox {3}\beta _{1} +\gamma )]. \\ \end{array}} \right. \end{aligned}$$

(24)

Differentiating Eq. (18) once with respect to $T_{2}$ and using Eqs. (17c) and (17d), one obtains

$$\begin{aligned}&4\lambda _{1} \lambda _{2} \rho _{1} \rho _{2} {\gamma }'=2\lambda _{1} \rho _{1} (P_{2} \rho _{1}^{2} \rho _{2} -R_{2} \rho _{2}^{3} -U_{2} \rho _{1}^{3} \cos \gamma ) \nonumber \\&\qquad -\,6\lambda _{2} \rho _{2} (P_{1} \rho _{1} \rho _{2}^{2} -R_{1} \rho _{1}^{3} -U_{1} \rho _{1}^{2} \rho _{2} \cos \gamma )\nonumber \\&\qquad +\,4\lambda _{1} \lambda _{2} \rho _{1} \rho _{2} \sigma . \end{aligned}$$

(25)

Note that the solutions of the NNMs of the original system correspond to the steady state of Eqs. (17a), (17b) and (25). Thus, the nontrivial constant solutions can be obtained by setting $\sin \bar{{\gamma }}=0$. The stability of these modes coincides with that of the corresponding fixed points of the modulation equations. Linearizing Eqs. (17a), (17b) and (25) near the nontrivial constant solutions gives the following characteristic equation

$$\begin{aligned} \det \left[ {{\begin{array}{lll} {-\Lambda }&{}\quad 0&{}\quad {\frac{U_1 }{2\lambda _1 }\bar{{\rho }}_1^2 \bar{{\rho }}_2 } \\ 0&{}\quad {-\Lambda }&{}\quad {-\frac{U_2 }{2\lambda _2 }\bar{{\rho }}_1^3 } \\ {\left( \frac{P_2 }{\lambda _2 }+\frac{3R_1 }{\lambda _1 }\right) \bar{{\rho }}_1 +\frac{3}{2}\left( \frac{U_1 }{\lambda _1 }\bar{{\rho }}_2 -\frac{U_2 }{\lambda _2 }\frac{\bar{{\rho }}_1^2 }{\bar{{\rho }}_2 }\right) }&{}\quad {-\left( \frac{R_2 }{\lambda _2 }+\frac{3P_1 }{\lambda _1 }\right) \bar{{\rho }}_2 +\frac{U_1 }{\lambda _1 }\bar{{\rho }}_1 +\frac{U_2 }{2\lambda _2 }\frac{\bar{{\rho }}_1^3 }{\bar{{\rho }}_2^2 }}&{}\quad {-\Lambda } \\ \end{array} }} \right] =0, \end{aligned}$$

(26)

where $\Lambda$ is the eigenvalue of the characteristic equation. The solutions of Eq. (26) are

$$\begin{aligned} \Lambda _{1} =0, \quad \Lambda _{2,3}^{2} =-\left( {\frac{\bar{{\rho }}_1 \bar{{\rho }}_2}{2\lambda _1 \lambda _{2}}} \right) ^{2}B, \end{aligned}$$

(27)

where $B=U_{2}^{2} \lambda _{1}^{2} \bar{{c}}^{4}+6\lambda _{1} \lambda _{2} U_{1} U_{2} \bar{{c}}^{2}-2(3U_{1} R_{1} \lambda _{2}^{2}+\lambda _{1}^{2} R_{2} U_{2} +3\lambda _{1} \lambda _{2} P_{1} U_{2} +\lambda _{1} \lambda _{2} P_{2} U_{1} )\bar{{c}}-3U_{1}^{2} \lambda _{2}^{2}$, $\bar{{c}}=\bar{{\rho }}_{1} \hbox {/}\bar{{\rho }}_{2}$. The coupled mode is stable if $B>0$; otherwise, it is unstable.

The steady-state solution of Eq. (25) meets

$$\begin{aligned}&(2\lambda _{1} U_{2} \cos \bar{{\gamma }})c^{3}-(2\lambda _{1} P_{2} +6\lambda _{2} R_{1})c^{2}\nonumber \\&\quad -\,(6\lambda _{2} U_{1} \cos \bar{{\gamma }})c \nonumber \\&\quad +\,\left( 2\lambda _{1} R_{2} +6\lambda _{2} P_{1} -4\lambda _{1} \lambda _{2} \frac{\sigma }{\rho _{2}^{2}}\right) =0, \end{aligned}$$

(28)

where $c=\rho _{1} \hbox {/}\rho _{2}$ is called a steady-state amplitude ratio. Since $\cos \bar{{\gamma }}=1$ and $\cos \bar{{\gamma }}=-1$ provide the same solution, thus taking $\cos \bar{{\gamma }}=1$ as an example, Eq. (28) becomes

$$\begin{aligned}&c^{3}-\left( \frac{P_{2}}{U_{2}}+\frac{3\lambda _{2} R_{1}}{\lambda _1 U_2 }\right) c^{2}-\left( \frac{3\lambda _2 U_1}{\lambda _1 U_2 }\right) c\nonumber \\&\quad +\,\left( \frac{R_2 }{U_2 }+\frac{3\lambda _2 P_1}{\lambda _1 U_2 }-\frac{2\lambda _2 }{U_2 }\frac{\sigma }{\rho _2^2 }\right) =0. \end{aligned}$$

(29)

The variation of c with $\sigma \hbox {/}\rho _2^2$ is depictured in Fig. 3 for the case of the three-to-one internal resonance. Figure 3 shows that, besides the neutrally stable uncoupled mode, there exists one stable coupled-mode solution when $\sigma \hbox {/}\rho _2^2 <-63.837$ or $\sigma \hbox {/}\rho _2^2 >-6.936$ and three stable coupled-mode solutions when $-63.837<\sigma \hbox {/}\rho <-52.4$, as well as two stable coupled-mode solutions and one unstable coupled-mode solution if $-52.4<\sigma \hbox {/}\rho _2^2 <-6.936$. The two complex conjugate eigenvalues of the intermediate solution coalesce to zero as $\sigma \hbox {/}\rho _2^2$ approaches -52.4 from the left. For $\sigma \hbox {/}\rho _2^2 >-52.4$, one of these eigenvalues becomes real and positive so that the solution loses its stability via a center-saddle bifurcation.

Fig. 3

Steady-state c-vs-$\sigma \hbox {/}\rho _2^2$ response for the three-to-one resonance

3.2 One-to-one internal resonances

In the case of $\omega _1 \approx \omega _2$, the detuning parameter $\sigma$ is defined as $\omega _2 =\omega _1 +\varepsilon ^{2}\sigma$. By substituting Eqs. (11) and (14) into Eq. (15) and eliminating the secular terms in Eq. (16), one has

$$\begin{aligned} S_{1r} +a_1 \varGamma _r S_{2r} =0,\;\;r=1,2, \end{aligned}$$

(30)

where

$$\begin{aligned} \left\{ {\begin{array}{lll} S_{r1} &{}=&{}-2i\omega _1 (1+a_r \varGamma _1 )D_2 A_1 + \left[ -2i\omega _2 (1+a_r \varGamma _2 )D_2 A_2 +M_{3r} A_2 \left| {A_2 } \right| ^{2}+M_{4r} A_2 \left| {A_1 } \right| ^{2}\right] e^{i\sigma T_2 }\\ &{}&{}+\,M_{1r} A_1 \left| {A_2 } \right| ^{2}+M_{2r} A_1 \left| {A_1 } \right| ^{2}+M_{5r} A_1^2 \bar{{A}}_2 e^{-i\sigma T_2 }+M_{6r} \bar{{A}}_1 A_2^2 e^{2i\sigma T_2 }, \\ S_{r2} &{}=&{}-2i\omega _2 (1+a_r \varGamma _2 )D_2 A_2 +[-2i\omega _1 (1+a_r \varGamma _1 )D_2 A_1 +N_{3r} A_1 \left| {A_2 } \right| ^{2}+N_{4r} A_1 \left| {A_1 } \right| ^{2}]e^{-i\sigma T_2 } \\ &{}&{}+\,N_{1r} A_2 \left| {A_2 } \right| ^{2}+N_{2r} A_2 \left| {A_1 } \right| ^{2}+N_{5r} A_2^2 \bar{{A}}_1 e^{i\sigma T_2 }+N_{6r} \bar{{A}}_2 A_1^2 e^{-2i\sigma T_2 }. \\ \end{array}} \right. \end{aligned}$$

(31)

The coefficients $M_{sr}$ and $N_{sr}$, $s=1,2,\ldots , 6$ are listed in “Appendix 1”.  After the substitution of Eq. (31) into Eq. (30), it follows that

$$\begin{aligned} \left\{ {\begin{array}{ccc} iK_{1} D_{2} A_{1} &{}=&{}M_{1} A_{1} \left| {A_{2}} \right| ^{2} +M_{2} A_{1} \left| {A_{1} }\right| ^{2}+\left[ -ik_{1} D_{2} A_{2} +M_{3} A_{2} \left| {A_{2}} \right| ^{2} \right. \\ &{}&{}\left. +\,M_4 A_2 \left| {A_{1}} \right| ^{2}\right] e^{i\sigma T_2 }+M_5 A_1^2 \bar{{A}}_{2} e^{-i\sigma T_{2}}+M_6 \bar{{A}}_1 A_2^2 e^{2i\sigma T_{2} }, \\ iK_2 D_2 A_2 &{}=&{}N_1 A_2 \left| {A_2 } \right| ^{2}+N_2 A_2 \left| {A_1 } \right| ^{2}+[-ik_2 D_2 A_1 +N_3 A_1 \left| {A_2 } \right| ^{2} \\ &{}&{}+\,N_4 A_1 \left| {A_1 } \right| ^{2}]e^{-i\sigma T_2 }+N_5 A_2^2 \bar{{A}}_1 e^{i\sigma T_2 }+N_6 \bar{{A}}_2 A_1^2 e^{-2i\sigma T_2 }, \\ \end{array}} \right. \end{aligned}$$

(32)

where $K_r =2\omega _r (1+2a_1 \varGamma _r +a_1 a_2 \varGamma _r^2 )$, $M_s =M_{s1} +a_1 \varGamma _1 M_{s2}$, $N_s =N_{s1} +a_1 \varGamma _2 N_{s2}$, $k_r =2\omega _r (1+a_1 \hbox {(}\varGamma _1 +\varGamma _2 )+a_1 a_2 \varGamma _1 \varGamma _2 )$. Letting $A_r (T_2 )=\rho _r (T_2 )\hbox {e}^{i\beta _r (T_{2} )}\hbox {/}2$ in Eq. (32) and separating the real parts and the imaginary parts, a set of modulation equations can be obtained as follows

$$\begin{aligned}&\eta D_2 \rho _1 =\rho _2 \left[ b_1 \rho _1 \rho _2 \sin 2\gamma +(b_2 +b_3 )\rho _1^2 \sin \gamma \right. \nonumber \\&\qquad \qquad \quad \left. +\,b_4 \rho _2^2 \sin \gamma \right] , \end{aligned}$$

(33a)

$$\begin{aligned}&\eta D_2 \rho _2 =-\rho _1 \left[ b_5 \rho _1 \rho _2 \sin 2\gamma \right. \nonumber \\&\quad \qquad \qquad \left. +\,(b_6 +b_7 )\rho _2^2 \sin \gamma +b_8 \rho _1^2 \sin \gamma \right] , \end{aligned}$$

(33b)

$$\begin{aligned}&\eta \rho _1 D_2 \beta _1 =c_1 \rho _1^3 +c_2 \rho _1 \rho _2^2 -b_1 \rho _1 \rho _2^2 \cos 2\gamma \nonumber \\&\qquad \qquad \qquad +\,(b_2 -b_3 )\rho _1^2 \rho _2 \hbox {cos}\gamma -b_4 \rho _2^3 \cos \gamma , \end{aligned}$$

(33c)

$$\begin{aligned}&\eta \rho _2 D_2 \beta _2 =c_3 \rho _2^3 +c_4 \rho _1^2 \rho _2 -b_5 \rho _1^2 \rho _2 \cos 2\gamma \nonumber \\&\qquad \qquad \qquad +\,(b_6 -b_7 )\rho _1 \rho _2^2 \hbox {cos}\gamma -b_8 \rho _1^3 \cos \gamma ,\nonumber \\ \end{aligned}$$

(33d)

where

$$\begin{aligned} \gamma =\beta _2 -\beta _1 +\sigma T_2, \end{aligned}$$

(34)

and coefficients $\eta$, $b_r$ and $c_r,\;\;r=1,2\ldots$, are listed in “Appendix 2”.

In the case of the one-to-one internal resonance, there is only one possibility, that is, $\rho _1 \ne 0,\;\;\rho _2 \ne 0$. And the coupled nonlinear normal mode is obtained in the following form

$$\begin{aligned} \left\{ {\begin{array}{l} \theta =\varepsilon [\rho _1 \cos (\omega _1 t+\beta _1 )+\rho _2 \cos (\omega _1 t+\beta _1 \hbox {+}\gamma )],\hbox { } \\ \alpha =\varepsilon [\varGamma _1 \rho _1 \cos (\omega _1 t+\beta _1 )+\varGamma _2 \rho _2 \cos (\omega _{1} t+\beta _{1} \hbox {+}\gamma )]. \\ \end{array}} \right. \end{aligned}$$

(35)

Differentiating Eq. (34) with respect to $T_2$ and using Eqs. (33c) and (33d), one has

$$\begin{aligned}&\eta \rho _1 \rho _2 {\gamma }'=(c_4 -c_1 )\rho _1^3 \rho _2 +(c_3 -c_2 )\rho _1 \rho _2^3\nonumber \\&\quad -(b_5 \rho _1^2 -b_1 \rho _2^2 )\rho _1 \rho _2 \cos 2\gamma \nonumber \\&\quad +(b_6 -b_7 -b_2 +b_3 )\rho _1^2 \rho _2^2 \cos \gamma -(b_8 \rho _1^4\nonumber \\&\quad -b_4 \rho _2^4 )\cos \gamma +\eta \rho _1 \rho _2 \sigma . \end{aligned}$$

(36)

Similarly, both $\cos \bar{{\gamma }}=1$ and $\cos \bar{{\gamma }}=-1$ correspond to the same nontrivial constant solution; thus taking $\cos \bar{{\gamma }}=1$ as an example, then Eq. (36) becomes

$$\begin{aligned}&b_8 c^{4}+(b_5 +c_1 -c_4 )c^{3}-(b_6 -b_7 -b_2 +b_3 )c^{2}\nonumber \\&\quad +\left( b_1 +c_2 -c_3 -\eta \frac{\sigma }{\rho _2^2 }\right) c-b_4 =0, \end{aligned}$$

(37)

where $c=\rho _1 \hbox {/}\rho _2$ is the same meaning. Figure 4 shows the variation of c with $\sigma \hbox {/}\rho _2^2$ for the case of the one-to-one internal resonance. Due to the natural frequency, $\omega _2$ is larger than $\omega _1$, and the detuning parameter $\sigma$ is always positive. Therefore, only a positive branch of $\sigma \hbox {/}\rho _2^2$ is drawn in Fig. 4. The stability of these modes is determined by the eigenvalues of the Jacobian matrix of Eqs. (33a), (33b) and (34), evaluated at the corresponding nontrivial solution. It can be seen from Fig. 4, for the case of the one-to-one internal resonance, there exist two stable coupled-mode solutions when $\sigma \hbox {/}\rho _2^2 >23.87$, one stable coupled-mode and one unstable coupled-mode solutions when $22.78<\sigma \hbox {/}\rho _2^2 <23.87$ and no mode solution if $0<\sigma \hbox {/}\rho _2^2 <22.78$.

Fig. 4

Steady-state c-vs-$\sigma \hbox {/}\rho _2^2$ response for the one-to-one resonance

4 Numerical studies

The uncoupled case of the three-to-one resonance was considered first. One can seen from Eq. (19) that the amplitudes of angle $\theta$ and $\alpha$ of the uncoupled NNMs are $\hbox {|}\varepsilon \rho _2 \hbox {|}$ and $\hbox {|}\varepsilon \varGamma _2 \rho _2 \hbox {|}$ with the ratio of $\hbox {|}\rho _2 \hbox {|/|}\varGamma _2 \rho _2 \hbox {|}$. The parameters $a_2$ and $\rho _{20}$ were set as 1.2 and 0.1, respectively. The initial states were taken as $(\theta _0,\dot{\theta }_0,\alpha _0,\dot{\alpha }_0 \hbox {)}=(\rho _{20},0,\varGamma _2 \rho _{20},0)$. The variations of the two amplitude ratios with the detuning parameter are plotted in Fig. 5. As shown in Fig. 5, the two curves are close to each other. In the coupled case, according to Eq. (24), the amplitude of angle $\theta$ is $\hbox {|}\varepsilon (\rho _1 +\rho _2 )\hbox {|}$ if $\rho _1 \rho _2 >0$, and it is $\hbox {|}\sqrt{(3\rho _2 -\rho _1 )^{3}\hbox {/}(27\rho _2 )}\hbox {|}$ if $\rho _1 \rho _2 <0$. The amplitude of angle $\alpha$ is $\hbox {|}\varepsilon (\varGamma _1 \rho _1 +\varGamma _2 \rho _2 )\hbox {|}$ if $\varGamma _1 \rho _1 \varGamma _2 \rho _2 >0$ and it is $\hbox {|}\sqrt{(3\varGamma _2 \rho _2 -\varGamma _1 \rho _1 )^{3}\hbox {/}(27\varGamma _2 \rho _2 )}\hbox {|}$ if $\varGamma _1 \rho _1 \varGamma _2 \rho _2 <0$. In the numerical simulations, the initial conditions were set at $(\rho _{10} +\rho _{20},0,\varGamma _1 \rho _{10} +\varGamma _2 \rho _{20},0)$ and $a_1 =0.764$. The curves of the two amplitude ratios are shown in Fig. 6. One can see from Fig. 6 that two curves are in accordance with each other.

Fig. 5

Amplitude–frequency curve for the three-to-one resonance

Fig. 6

Amplitude ratio versus parameter $\sigma \hbox {/}\rho _2^2$ for the three-to-one resonance

In the case of the one-to-one resonance, the amplitudes of angle $\theta$ and $\alpha$ determined by Eq. (35) were $\hbox {|}\varepsilon (\rho _1 +\rho _2 )\hbox {|}$ and $\hbox {|}\varepsilon (\varGamma _1 \rho _1 +\varGamma _2 \rho _2 )\hbox {|}$, respectively. The parameters $a_1$ and $a_2$ were set as 0.0001 and 1. As shown in Fig. 7, the approximate solution and the numerical solution are very close to each other.

Fig. 7

Amplitude ratio versus $\sigma \hbox {/}\rho _2^2$ for the one-to-one resonance

Fig. 8

Time histories of $c=15$ for the three-to-one resonance

Fig. 9

Time histories of $c=-1$ for the three-to-one resonance

Fig. 10

Time histories of $c=3$ for the one-to-one resonance

In order to check the validity of the stability analysis, several numerical cases were simulated by integrating Eq. (7). As shown in Fig. 3, the coupled NNM is stable at $c=15$. And the corresponding initial states were $(\theta _0,\dot{\theta }_0,\alpha _0,\dot{\alpha }_0 \hbox {)=(0.2686,0,0.3056,0)}$. The time histories of $\theta$ and $\alpha$ are plotted in Fig. 8. It shows that the system behaves as a stable NNM motion. According to Fig. 3, the coupled NNM is unstable at $c=-1$, and the corresponding initial states were $(0,0,-0.0506,0)$. Similarly, the time histories of $\theta$ and $\alpha$ are shown in Fig. 9. It suggests that the NNM motion of the system is unstable.

Fig. 11

Time histories of $c=0.7$ for the one-to-one resonance

In the case of the one-to-one internal resonance, according to the analytical results, the NNM motion would be stable at $c=3$. The stable motions are displayed in Fig. 10. The system would fall into an unstable NNM motion at $c=0.7$ as shown in Fig. 11.

5 Conclusions

The nonlinear normal modes of a tethered satellite system with the three-to-one and one-to-one resonances are studied. The approximate solutions of different nonlinear normal modes and their stabilities are obtained. In the case of the three-to-one resonance, there exist the uncoupled and coupled modes in the system, including either two stable modes or four stable modes, or one unstable and three stable modes. In the case of the one-to-one resonance, the system possesses either two stable modes, or one stable and one unstable nonlinear normal modes. Meanwhile, numerical simulations are made to demonstrate the validity of the analytical solutions obtained by the multiple scale method and the results of stability analysis.

Appendices

Appendix 1

$$\begin{aligned} M_{11}= & {} -2a_{1} \left[ 4\omega _1^2 (\varGamma _2 -1)^{2}(a_1 \delta _{211} \varGamma _1 -\delta _{221} )\right. \\&\,+\,\,\omega _2^2 (\varGamma _1 -1)\left( 4\delta _{221} -\varGamma _2^{2}-4\delta _{121} \varGamma _2\right. \\&\left. \left. +\,\,4a_1 \delta _{111} \varGamma _2^{2}-4a_1 \delta _{211} \varGamma _2 \right) \right] \\ M_{21}= & {} -a_1 \left( {\varGamma _1 -1} \right) \omega _1^2 \left( 4\varGamma _1^{2}a_1 \delta _{111} +4\varGamma _1^{2}a_1 \delta _{211}\right. \\&\left. -\,\varGamma _1^{2}-4\varGamma _1 \delta _{121} -4\delta _{221} \varGamma _1 -8a_1 \delta _{211} \varGamma _1 +8\delta _{221} \right) \\ M_{31}= & {} -a_1 \left( {\varGamma _2 -1} \right) \omega _2^2 \left( 4a_1 \delta _{111} \varGamma _2^{2}+4\varGamma _2^{2}a_1 \delta _{211}\right. \\&\left. -\,\varGamma _2^{2}-4\delta _{121} \varGamma _2 -4\delta _{221} \varGamma _2 -8a_1 \delta _{211} \varGamma _2 +8\delta _{221} \right) \\ M_{41}= & {} -2a_1 \left[ \omega _1^2 (\varGamma _2 -1)\left( 4\delta _{221} -4a_1 \delta _{211} \varGamma _1 +4\varGamma _1^{2}a_1 \delta _{111}\right. \right. \\&\left. \left. -\,\varGamma _1^{2}-4\varGamma _1 \delta _{121} \right) +4\omega _2^2 (\varGamma _1 -1)^{2}(a_1 \delta _{211} \varGamma _2 -\delta _{221} )\right] \\ M_{51}= & {} a_1 \left[ \omega _1^2 (\varGamma _2 -1)\left( -16\varGamma _1^{2}a_1 \delta _{211} +4\varGamma _1^{2}a_1 \delta _{111} -12\delta _{221}\right. \right. \\&\left. -\,4\varGamma _1 \delta _{121} +12a_1 \delta _{211} \varGamma _1 +16\delta _{221} \varGamma _1 -\varGamma _1^{2}\right) \\&-\,4\omega _2^2 (\varGamma _1 -1)^{2}(-\delta _{221} +a_1 \delta _{211} \varGamma _2 )\\&-\,2\omega _1 \omega _2 (\varGamma _1 -1)\left( 4a_1 \delta _{111} \varGamma _2 \varGamma _1\right. \\&+\,2a_1 \delta _{211} \varGamma _1 -8a_1 \delta _{211} \varGamma _2 \varGamma _1\\&-\,2\varGamma _1 \delta _{121} +4\delta _{221} \varGamma _1 -\varGamma _1 \varGamma _2 +2a_1 \delta _{211} \varGamma _2\\&\left. \left. -\,2\delta _{121} \varGamma _2 +4\delta _{221} \varGamma _2 -4\delta _{221} \right) \right] \\ M_{61}= & {} -a_1 [4\omega _1^2 (\varGamma _2 -1)^{2}(-\delta _{221} +a_1 \delta _{211} \varGamma _1 )\\&+\,2\omega _1 \omega _2 (\varGamma _2 -1)(4a_1 \delta _{111} \varGamma _2 \varGamma _1\\&+\,2a_1 \delta _{211} \varGamma _1 -8a_1 \delta _{211} \varGamma _2 \varGamma _1 \\&-\,2\varGamma _1 \delta _{121} +4\delta _{221} \varGamma _1 -\varGamma _1 \varGamma _2 +2a_1 \delta _{211} \varGamma _2\\&-\,2\delta _{121} \varGamma _2 +4\delta _{221} \varGamma _2 -4\delta _{221} ) \\&-\,\omega _2^2 (\varGamma _1 -1)\left( 16\delta _{221} \varGamma _2 -16\varGamma _2^{2}a_1 \delta _{211}\right. \\&\left. -\,4\delta _{121} \varGamma _2 +4a_1 \delta _{111} \varGamma _2^{2}+12a_1 \delta _{211} \varGamma _2 {-}12\delta _{221} {-}\varGamma _2^{2}\right) \\ N_{11}= & {} -a_1 (\varGamma _2 -1)\omega _2^2 (4a_1 \delta _{111} \varGamma _2^{2}+4\varGamma _2^{2}a_1 \delta _{211}\\&-\,\varGamma _2^{2}-4\delta _{121} \varGamma _2 -4\delta _{221} \varGamma _2 -8a_1 \delta _{211} \varGamma _2 +8\delta _{221} ) \\ \end{aligned}$$

$$\begin{aligned} N_{21}= & {} -2a_1 [\omega _1^2 (\varGamma _2 -1)\left( 4\delta _{221} -4a_1 \delta _{211} \varGamma _1 +4\varGamma _1^{2}a_1 \delta _{111}\right. \\&\left. -\,\varGamma _1^{2}-4\varGamma _1 \delta _{121} \right) +4\omega _2^2 (\varGamma _1 -1)^{2}(a_1 \delta _{211} \varGamma _2 -\delta _{221} )] \\ N_{31}= & {} -2a_1 \left[ 4\omega _1^2 (\varGamma _2 -1)^{2}(a_1 \delta _{211} \varGamma _1 -\delta _{221} )\right. \\&+\,\omega _2^2 (\varGamma _1 -1)\left( 4a_1 \delta _{111} \varGamma _2^{2}-\varGamma _2^{2}+4\delta _{221}\right. \\&\left. \left. -\,4\delta _{121} \varGamma _2 -4a_1 \delta _{211} \varGamma _2 \right) \right] \\ N_{41}= & {} -a_1 \omega _1^2 (\varGamma _1 -1)(4\varGamma _1^{2}a_1 \delta _{111} +4\varGamma _1^{2}a_1 \delta _{211}\\&-\,\varGamma _1^{2}-4\varGamma _1 \delta _{121} -4\delta _{221} \varGamma _1 -8a_1 \delta _{211} \varGamma _1 +8\delta _{221} )\\ N_{51}= & {} -a_1 \left[ 4\omega _1^2 (\varGamma _2 -1)^{2}(-\delta _{221} +a_1 \delta _{211} \varGamma _1 )\right. \\&+\,2\omega _1 \omega _2 (\varGamma _2 -1)\left( 4a_1 \delta _{111} \varGamma _2 \varGamma _1 +2a_1 \delta _{211} \varGamma _1 \right. \\&-\,8a_1 \delta _{211} \varGamma _2 \varGamma _1 -2\varGamma _1 \delta _{121} +4\delta _{221} \varGamma _1\\&\left. -\,\varGamma _1 \varGamma _2 +2a_1 \delta _{211} \varGamma _2 -2\delta _{121} \varGamma _2 +4\delta _{221} \varGamma _2 -4\delta _{221} \right) \\&-\,\omega _2^2 (\varGamma _1 -1)\left( 16\delta _{221} \varGamma _2 -16\varGamma _2^{2}a_1 \delta _{211}\right. \\&\left. \left. -\,4\delta _{121} \varGamma _2 +4a_1 \delta _{111} \varGamma _2^{2}+12a_1 \delta _{211} \varGamma _2\right. \right. \\&\left. \left. -12\delta _{221} -\varGamma _2^{2}\right) \right] \\ N_{61}= & {} a_1 \left[ \omega _1^2 (\varGamma _2 -1)(-16\varGamma _1^{2}a_1 \delta _{211} +4\varGamma _1^{2}a_1 \delta _{111} -12\delta _{221}\right. \\&-\,4\varGamma _1 \delta _{121} +12a_1 \delta _{211} \varGamma _1 +16\delta _{221} \varGamma _1 -\varGamma _1^{2}) \\&-\,2\omega _1 \omega _2 (\varGamma _1 -1)(4a_1 \delta _{111} \varGamma _2 \varGamma _1 +2a_1 \delta _{211} \varGamma _1\\&-\,8a_1 \delta _{211} \varGamma _2 \varGamma _1 -2\varGamma _1 \delta _{121} +4\delta _{221} \varGamma _1 -\varGamma _1 \varGamma _2 \\&+\,2a_1 \delta _{211} \varGamma _2-\,2\delta _{121} \varGamma _2 +4\delta _{221} \varGamma _2 -4\delta _{221} )\\&\left. -\,4\omega _2^2 (\varGamma _1 -1)^{2}(-\delta _{221} +a_1 \delta _{211} \varGamma _2 )\right] \\ M_{12}= & {} 8(\varGamma _2 -1)^{2}(-\delta _{121} +\varGamma _1 a_1 \delta _{111})\\&+\,2(\varGamma _1 -1)\left( 4a_1 \delta _{111} \varGamma _2^{2}-4a_1 \delta _{211} \varGamma _2 \right. \\&\left. -\,4\delta _{121} \varGamma _2 +4\delta _{221} -1\right) \\ M_{22}= & {} \omega _1^2 (\varGamma _1 -1)(8\varGamma _1^{2}a_1 \delta _{111}-\,4\varGamma _1 a_1 \delta _{111}\\&-\,8\varGamma _1 \delta _{121} -4a_1 \delta _{211} \varGamma _1 -1+4\delta _{121} +4\delta _{221} ) \\ M_{32}= & {} \omega _2^2 (\varGamma _2 -1)(8a_1 \delta _{111} \varGamma _2^{2}-4a_1 \delta _{111} \varGamma _2 -8\delta _{121} \varGamma _2\\&-\,4a_1 \delta _{211} \varGamma _2 -1+4\delta _{121} +4\delta _{221} ) \\ M_{42}= & {} 2\omega _1^2 (\varGamma _2 -1)(-4a_1 \delta _{211} \varGamma _1 -4\varGamma _1 \delta _{121} -1+4\delta _{221} \\&+\,4\varGamma _1^{2}a_1 \delta _{111} )+8\omega _2^2 (\varGamma _1 -1)^{2}(-\delta _{121} +a_1 \delta _{111} \varGamma _2 ) \\ M_{52}= & {} \omega _1^2 (\varGamma _2 -1)\left( 16\delta _{121} +4a_1 \delta _{211} \varGamma _1 +12\varGamma _1^{2}a_1 \delta _{111}\right. \\&\left. +\,1-4\delta _{221} -12\varGamma _1 \delta _{121} -16\varGamma _1 a_1 \delta _{111} \right) \\&-\,2\omega _1 \omega _2 (\varGamma _1 -1)(4a_1 \delta _{111} \varGamma _2 \varGamma _1 -2\varGamma _1 \delta _{121}\\&-\,4\varGamma _1 a_1 \delta _{111} +2a_1 \delta _{211} \varGamma _1 +1+8\delta _{121} \\&+\,2a_1 \delta _{211} \varGamma _2 -4\delta _{221} -4a_1 \delta _{111} \varGamma _2 -2\delta _{121} \varGamma _2 )\\&+\,4\omega _2^2 (\varGamma _1 -1)^{2}(-\delta _{121} +a_1 \delta _{111} \varGamma _2 ) \end{aligned}$$

$$\begin{aligned} M_{62}= & {} 4\omega _1^2 (\varGamma _2 -1)^{2}(-\delta _{121} +\varGamma _1 a_1 \delta _{111} )\\&-\,2\omega _1 \omega _2 (\varGamma _2 -1)(4a_1 \delta _{111} \varGamma _2 \varGamma _1 -2\varGamma _1 \delta _{121}\\&-\,4\varGamma _1 a_1 \delta _{111} +2a_1 \delta _{211} \varGamma _1 +1+8\delta _{121} +2a_1 \delta _{211} \varGamma _2\\&-\,4\delta _{221} -4a_1 \delta _{111} \varGamma _2 -2\delta _{121} \varGamma _2 ) \\&+\,\omega _2^2 (\varGamma _1 -1)(-16a_1 \delta _{111} \varGamma _2 +4a_1 \delta _{211} \varGamma _2\\&-\,12\delta _{121} \varGamma _2 +1+12a_1 \delta _{111} \varGamma _2^{2}-4\delta _{221} +16\delta _{121} ) \\ N_{12}= & {} \omega _2^2 (\varGamma _2 -1)(8a_1 \delta _{111} \varGamma _2^{2}-4a_1 \delta _{111} \varGamma _2\\&-\,8\delta _{121} \varGamma _2 -4a_1 \delta _{211} \varGamma _2 -1+4\delta _{121} +4\delta _{221} ) \\ N_{22}= & {} 2\omega _1^2 (\varGamma _2 -1)(-4a_1 \delta _{211} \varGamma _1 -4\varGamma _1 \delta _{121}\\&-\,1+4\delta _{221} +4\varGamma _1^{2}a_1 \delta _{111} )\\&+\,8\omega _2^2 (\varGamma _1 -1)^{2}(-\delta _{121} +a_1 \delta _{111} \varGamma _2 ) \\ N_{32}= & {} 8\omega _1^2 (\varGamma _2 -1)^{2}(-\delta _{121} +\varGamma _1 a_1 \delta _{111} )\\&+\,2\omega _2^2 (\varGamma _1 -1)(-4a_1 \delta _{211} \varGamma _2 -4\delta _{121} \varGamma _2 +4\delta _{221}\\&-\,1+4a_1 \delta _{111} \varGamma _2^{2}) \\ N_{42}= & {} \omega _1^2 (\varGamma _1 -1)(8\varGamma _1^{2}a_1 \delta _{111} -4\varGamma _1 a_1 \delta _{111}\\&-\,8\varGamma _1 \delta _{121} -4a_1 \delta _{211} \varGamma _1 -1+4\delta _{121} +4\delta _{221} ) \\ N_{52}= & {} 4\omega _1^2 (\varGamma _2 -1)^{2}(-\delta _{121} +\varGamma _1 a_1 \delta _{111} )\\&-\,2\omega _1 \omega _2 (\varGamma _2 -1)(4a_1 \delta _{111} \varGamma _2 \varGamma _1 -2\varGamma _1 \delta _{121} -4\varGamma _1 a_1 \delta _{111} \\&+\,2a_1 \delta _{211} \varGamma _1 +1+8\delta _{121} +2a_1 \delta _{211} \varGamma _2 -4\delta _{221}\\&-\,4a_1 \delta _{111} \varGamma _2 -2\delta _{121} \varGamma _2 ) \\&+\,\omega _2^2 (\varGamma _1 -1)(-16a_1 \delta _{111} \varGamma _2 +4a_1 \delta _{211} \varGamma _2 -12\delta _{121} \varGamma _2\\&+\,1+12a_1 \delta _{111} \varGamma _2^{2}-4\delta _{221} +16\delta _{121} ) \\ N_{62}= & {} \omega _1^2 (\varGamma _2 -1)(16\delta _{121} +4a_1 \delta _{211} \varGamma _1 +12\varGamma _1^{2}a_1 \delta _{111}\\&+\,1-4\delta _{221} -12\varGamma _1 \delta _{121} -16\varGamma _1 a_1 \delta _{111} ) \\&-\,2\omega _1 \omega _2 (\varGamma _1 -1)(4a_1 \delta _{111} \varGamma _2 \varGamma _1 -2\varGamma _1 \delta _{121} -4\varGamma _1 a_1 \delta _{111}\\&+\,2a_1 \delta _{211} \varGamma _1 +1+8\delta _{121} +2a_1 \delta _{211} \varGamma _2\\&-\,4\delta _{221} -4a_1 \delta _{111} \varGamma _2 -2\delta _{121} \varGamma _2 )\\&+\,4\omega _2^2 (\varGamma _1 -1)^{2}(-\delta _{121} +a_1 \delta _{111} \varGamma _2 ) \end{aligned}$$

where $\delta _{ijr} =\Delta _{ij} (2\omega _r ),\;\delta _{ij3} =\Delta _{ij} (\omega _1 +\omega _2 ),\;\delta _{ij4} =\Delta _{ij} (\omega _1 -\omega _2 ),\;i,j,r=1,2$.

Appendix 2

$$\begin{aligned}&\eta =4(K_1 K_2 -k_1 k_2 ), \quad b_1 =K_2 M_6 -k_1 N_5, \quad \\&b_2 =k_1 N_6 -K_2 M_5, \quad b_3 =K_2 M_4 -k_1 N_2, \quad \\&b_4 =K_2 M_3 -k_1 N_1, \quad b_5 =K_1 N_6 -k_2 M_5, \quad \\&b_6 =k_2 M_6 -K_1 N_5, \quad b_7 =K_1 N_3 -k_2 M_1, \quad \\&b_8 =K_1 N_4 -k_2 M_2, \quad c_1 =k_1 N_4 -K_2 M_2, \quad \\&c_2 =k_1 N_3 -K_2 M_1, \quad c_3 =k_2 M_3 -K_1 N_1, \quad \\&c_4 =k_2 M_4 -K_1 N_2. \end{aligned}$$