1 Introduction

Viscoelastic behavior is well represented by relaxation function and/or creep function that are related each other in Laplace domain. This means that, knowing only one function, the other one is recovered through an inverse Laplace transform. From a physical point of view the aforementioned statement assesses that a unique mechanical model is necessary to simulate both functions. However, in practical applications the number of model parameters discriminates the choice of the model in two parallel paths. Specifically, if the minimum number of model parameters is mandatory, then two different models are considered: the Maxwell model for capturing relaxation function and the Kelvin–Voigt model for creep function [1–4]. Further, if only one model is required, then this unique model is characterized by a large number of parameters being composed of several Maxwell models in series and/or in parallel with Kelvin–Voigt models.

From above considerations it is apparent that, on one hand if one prefers few parameters, to be identified, then two different models are necessary to characterize the same material, obscuring a physical meaning and violating a theoretical aspect, provided by the relation in Laplace domain. On the other hand, choosing a unique model the computational effort increases significantly.

In this decade, researchers dealing with constitutive law pertinent viscoelastic materials put forward the successful idea to introduce viscoelastic laws embedded with fractional calculus [5–12].

Fractional calculus can be regarded as an extension of the classical differential calculus. Until now a limited use of such tool can be observed in mechanics [13–25], probably due to the presence of many definitions of fractional operators as well as the lack of an easy geometrical meaning. However, the common point to all definitions of fractional operators is that they are simply convolution integrals with power law kernel. The beauty of such operators is that they exactly behave as ordinary derivatives and integrals, that is, all the rules of classical operators with integer order hold true, including Leibniz rule and integration by parts [26, 27].

At this point the following question arises: what is the main difference between a classical viscoelastic law and the fractional viscoelastic one?

In classical viscoelastic law the stress function is related to an integer order time derivative of the strain function [1], this leads to have an exponential function as a kernel in the correspondent integral form (Boltzman Integral), while if the stress function is related to a real order time derivative of the strain function, the kernel will be a power law function in the correspondent integral form. Moreover, since the kernel of the integral form of viscoelastic constitutive law is related to the relaxation or creep function, it means that when a fractional constitutive law is considered the relaxation and creep function will be a power law function. After all, the latter is not a novel concept, in fact at the beginning of the twentieth century, Nutting and Gemant [28, 29] observed that, for viscoelastic materials such as rubber, bitumen, polymers, concrete etc., the experimental data were properly fitted by a power law function. In this regard, the power law decay representation for relaxation data was firstly considered by the polymer scientists, while the mechanics community chose the classical models as the Maxwell model, the Kelvin–Voight model and complex combinations of these elementary models to capture viscoelastic phenomena [1–4].

In literature there are many papers in which the best fitting of the peculiar viscoelastic functions of materials that exhibit a linear viscoelastic behavior (rubber, bitumen, polymers, giant reeds) using a fractional model [30–38] is performed. However there are not present studies where constitutive laws embedded with fractional calculus have been used for predicting the response of materials that exhibit a non-linear viscoelastic behavior, as polymer melts.

This paper is building on Acierno et al.’s findings reported in [39, 40] where, in agreement with previous literature [41–43], among several non-Newtonian models, they proposed a set of non-linear equations, to predict the non-Newtonian behavior of a type of L.D. polyethylene known as IUPAC sample.

In particular in this paper the authors propose the fractional model to capture the non-linear viscoelastic behavior of polymer melts. Starting from the equilibrium values of the parameters of the fractional model, describing the mechanical behavior of the fluid in the limit of liner viscoelasticity and obtained from the best fitting of the relaxation function, the trend of the shear viscosity of polymer melts, as function of shear rate, is performed. The good match of the proposed results with both experimental data [44, 45] and results obtained using the classical constitutive laws [39, 40], assesses that this proposed model is an alternative approach with respect to classical one, especially for range of shear rate pertinent with viscoelastic behavior, while for higher values of shear rate, since the behavior turns to liquid one, then the classical model is more appropriate.

2 Linear viscoelasticity: fractional and classical Maxwell model

At the beginning of the twentieth century, Nutting and Gemant [28, 29] observed that, for viscoelastic materials that exhibit a linear viscoelastic behavior such as rubber, bitumen, polymers, concrete etc., the experimental data, coming from the relaxation test, were well fitted by a power law decay, that is

$$\varPhi \left( t \right) \propto \left( t \right)^{ - \alpha } \quad 0 < \alpha < 1$$
(1)

If we select the coefficient of proportionality in Eq. (1) in the form \({{C_{\alpha 0} } \mathord{\left/ {\vphantom {{C_{\alpha 0} } {\varGamma \left( {1 - \alpha } \right)}}} \right. \kern-0pt} {\varGamma \left( {1 - \alpha } \right)}}\), where \(\varGamma \left( \cdot \right)\) is the Gamma function, while \(C_{\alpha 0}\) and \(\alpha\) are coefficients obtained by a best fitting procedure from the relaxation test, then Eq. (1) becomes

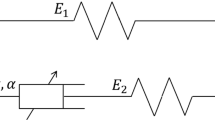
$$\varPhi \left( t \right) = \frac{{C_{\alpha 0} }}{{\varGamma \left( {1 - \alpha } \right)}}t^{ - \alpha }$$
(2)

This viscoelastic model characterized by such relaxation function is termed in literature [26] as spring-pot element and it is depicted in Fig. 1.

Fig. 1
figure 1

Spring-pot model

Full size image

The Laplace transform of \(\varPhi \left( t \right)\) given in Eq. (2) is

$$\varPhi \left( s \right) = C_{\alpha 0} \, s^{\alpha - 1}$$
(3)

and then invoking the fundamental relation in Laplace domain between the relaxation function and the creep function

$$\varPhi \left( s \right)D\left( s \right) = 1/s^{2}$$
(4)

where \(\varPhi \left( s \right)\) and \(D\left( s \right)\) are the Laplace transforms of relaxation function \(\varPhi \left( t \right)\) and creep function \(D\left( t \right)\) respectively, the inverse Laplace transform of \(D\left( s \right) = {1 \mathord{\left/ {\vphantom {1 {\left( {C_{\alpha 0} \, s^{1 + \alpha } } \right)}}} \right. \kern-0pt} {\left( {C_{\alpha 0} \, s^{1 + \alpha } } \right)}}\) returns the creep function in the form

$$D\left( t \right) = \frac{1}{{C_{\alpha 0} \,\varGamma \left( {1 + \alpha } \right)}}t^{\alpha }$$
(5)

Recent findings reported in [30–35] underscore the strength of choosing a spring-pot to capture the linear viscoelastic behavior using only one model for evaluating, with the same two parameters, both creep and relaxation functions. Specifically, for fitting relaxation test it is required the identification of the two parameters \(C_{\alpha 0}\) and \(\alpha\) as apparent from Eq. (2). Once the relaxation function is determined it follows the creep function from Eq. (5) and vice versa. In such a model, the stress \(\tau \left( t \right)\) is related to a fractional derivative of the strain \(\gamma \left( t \right)\) in the form

$$\tau \left( t \right) = C_{\alpha 0} \left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right)\left( t \right)$$
(6)

and the strain to a fractional integral of the stress

$$\gamma \left( t \right) = \frac{1}{{C_{\alpha 0} }}\left( {D_{{0^{ + } }}^{ - \alpha } \tau } \right)\left( t \right)$$
(7)

being the symbol \(\left( {{}_{C}D_{{0^{ + } }}^{\alpha } \cdot } \right)\left( t \right)\) the Caputo’s fractional derivative defined as

$$\left( {{}_{C}D_{{0^{ + } }}^{\alpha } f} \right)\left( t \right) = \frac{1}{{\varGamma \left( {1 - \alpha } \right)}}\int\limits_{0}^{t} {\dot{f}\left( {\bar{t}} \right)/\left( {t - \bar{t}} \right)^{\alpha } d\bar{t}}$$
(8)

where a dot over a function denotes first order time derivative, while \(\left( {D_{{0^{ + } }}^{ - \alpha } \cdot } \right)\left( t \right)\) is the Riemann–Liouville fractional integral defined as

$$\left( {D_{{0^{ + } }}^{ - \alpha } f} \right)\left( t \right) = \frac{1}{\varGamma \left( \alpha \right)}\int\limits_{0}^{t} {f\left( {\bar{t}} \right)/\left( {t - \bar{t}} \right)^{1 - \alpha } } d\bar{t}$$
(9)

Note that the constitutive laws in Eqs. (6) and (7) interpolate the purely elastic behavior (\(\alpha = 0\)) and the purely viscous one (\(\alpha = 1\)).

Another consistent fractional model, to capture the viscoelastic behavior, is the fractional Maxwell model derived adding a spring in series to the spring-pot, as depicted in Fig. 2.

Fig. 2
figure 2

Fractional Maxwell model

Full size image

The constitutive law concerning this model is expressed in the form

$$\lambda_{\alpha 0} \left( {{}_{C}D_{{0^{ + } }}^{\alpha } \tau } \right)\left( t \right) + \tau \left( t \right) = C_{\alpha 0} \left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right)\left( t \right)$$
(10)

being \(\lambda_{\alpha 0}\) the ratio between \(C_{\alpha 0}\) and the modulus \(G_{0}\) of the spring (\(\lambda_{\alpha 0} = C_{\alpha 0} /G_{0}\)). It is worth stressing that the classical Maxwell model is recovered from the fractional one replacing the spring-pot with a regular dashpot characterized by a constant \(\mu_{0}\) that means setting \(\alpha = 1\) in the relationship \(\lambda_{\alpha 0} = \left( {\lambda_{0} } \right)^{\alpha } = \left( {\mu_{0} /G_{0} } \right)^{\alpha }\).

To obtain the relaxation function \(\varPhi \left( t \right)\) of the fractional Maxwell model, write the Laplace transform of Eq. (10)

$$\lambda_{\alpha 0} \, s^{\alpha } \tau \left( s \right) + \tau \left( s \right) = C_{\alpha 0} \, s^{\alpha } \gamma \left( s \right)$$
(11)

and, considering \(\gamma \left( s \right) = 1/s\), being the strain imposed a unit step function, the stress response coincides with the Laplace transform of the relaxation function

$$\varPhi \left( s \right) = C_{\alpha 0} \left( {\frac{{s^{\alpha - 1} }}{{1 + \lambda_{\alpha 0} \, s^{\alpha } }}} \right)$$
(12)

Then performing the inverse Laplace transform, the relaxation function \(\varPhi \left( t \right)\) is given by

$$\varPhi \left( t \right) = G_{0} \, E_{\alpha } \left[ { - \left( {\frac{{t^{\alpha } }}{{\lambda_{\alpha 0} }}} \right)} \right]$$
(13)

where \(E_{\alpha } \left[ \cdot \right]\) is the one-parameter Mittag–Leffler function [27] defined in the form

$$E_{\alpha } \left[ z \right] = \sum\limits_{k = 0}^{\infty } {\frac{{z^{k} }}{{\varGamma \left( {\alpha k + 1} \right)}}}$$
(14)

On the other hand the creep function may be obtained by the inverse Laplace Transform of \(\varPhi \left( s \right)^{ - 1} s^{ - 2}\) in according to Eq. (4)

$$D\left( t \right) = \frac{{\lambda_{\alpha 0} + \frac{{t^{\alpha } }}{{\varGamma \left( {1 + \alpha } \right)}}}}{{C_{\alpha 0} }}$$
(15)

that is a power law function in accordance with the Nutting and Gemant observation.

Once again, setting \(\alpha = 1\) and \(\lambda_{\alpha 0} = \left( {\lambda_{0} } \right)^{\alpha } = \left( {\mu_{0} /G_{0} } \right)^{\alpha }\), both relaxation and creep functions pertinent the classical Maxwell model are respectively derived in the form

$$\begin{aligned} \varPhi \left( t \right) & = G_{0} \exp \left( { - \frac{t}{{\lambda_{0} }}} \right) \\ D\left( t \right) & = \frac{t}{{\mu_{0} }} + \frac{1}{{G_{0} }} \\ \end{aligned}$$
(16a, b)

It has to be stressed that this formulation is valid for small values of stress and/or deformation since Boltzman integral requires the validity of the superposition principle.

3 Non-linear viscoelasticity: classical and fractional formulation

Experimental tests on polymer melts have shown that such materials exhibit a non-linear behavior. To capture this non-linear behavior in Acierno et al. [39, 40] a model of non-linear viscoelasticity with relaxation times depending on material has been introduced and validated through experimental results [44, 45]. For readers’ convenience it will be reported the equation of the aforementioned model as

$$\begin{aligned}\varvec{\uptau}_{i} + \lambda_{i} \frac{{\delta \varvec{\uptau}_{i} }}{\delta t} = 2G_{i} \,\lambda_{i} \,{\mathbf{D}} \hfill \\ G_{i} = G_{0i} \,x_{i} \;\;\;\;\lambda_{i} = \lambda_{0i} \,x_{i}^{1.4} \hfill \\ \frac{{dx_{i} }}{dt} = \frac{{\left( {1 - x_{i} } \right)}}{{\lambda_{i} }} - \frac{{a\,x_{i} }}{{\lambda_{i} }}\sqrt {\frac{{E_{i} }}{{G_{i} }}} \hfill \\ \end{aligned}$$
(17a\hbox{-}c)

where \({\varvec{\uptau}}_{i}\) is the stress tensor, \(E_{i} = 1/2 \, tr \, {\varvec{\uptau}}_{i}\) (the symbol \({\text{t}}r\) indicates the operation of trace), \(G_{0i}\) and \(\lambda_{0i}\) are the equilibrium values of \(G{\kern 1pt}_{i}\) and \(\lambda {\kern 1pt}_{i} \;\) describing the mechanical behavior of the fluid in the limit of linear viscoelasticity and evaluable from the best fitting of the relaxation function, as detailed later. Moreover, \(a\) is a model parameter, \({\mathbf{D}} = \frac{1}{2}\left( {\nabla {\mathbf{v}} + \nabla {\mathbf{v}}^{T} } \right)\) is the symmetric part of the velocity gradient \(\nabla {\mathbf{v}}\) and \(\delta /\delta t\) is the so called contravariant convected derivative [41] defined as

$$\frac{{\delta {\varvec{\uptau}}_{i} }}{\delta t} = \frac{{d{\varvec{\uptau}}_{i} }}{dt} - \nabla {\mathbf{v}} \cdot {\varvec{\uptau}}_{i} \left( t \right) - {\varvec{\uptau}}_{i} \left( t \right) \cdot \nabla {\mathbf{v}}^{T}$$
(18)

The scalar dimensionless quantities \(x_{i} \le 1\) can be regarded as internal variables describing how the existing element is far from equilibrium, representing the connectivity of the macromolecular network with respect to that of equilibrium [42]. The first equation of (17b) expresses the fact that the elastic modulus is proportionally to the concentration of junctions. Conversely, the second equation of (17b) is essentially empirical. Equation (17c) gives the rate of change of the variable \(x_{i}\) including a term (the second one on the right-hand side) which is the rate of destruction of junction due to the existing stress and a term (the first one on the right-hand side) which gives the net rate of reformation due to the thermal motion.

Finally the shear viscosity \(\mu\) and the stress tensor \({\varvec{\uptau}}\) are determined as

$$\begin{aligned} \mu & = \sum\limits_{i = 1}^{n} {\mu_{i} } = \sum\limits_{i = 1}^{n} {\lambda_{i} } G_{i} \\ {\varvec{\uptau}} & = \sum\limits_{i = 1}^{n} {{\varvec{\uptau}}_{i} } \\ \end{aligned}$$
(19)

the latter represents a spectral decomposition of the stress tensor. Further, for steady shear flow, assuming \({\mathbf{v}} = \left[ {\begin{array}{*{20}c} {x_{2} \;\dot{\gamma }} & 0 & 0 \\ \end{array} } \right]^{T}\), (being \(\dot{\gamma }\) the rate of shear) with \(\left( {x_{1} ,x_{2} ,x_{3} } \right)\) reference axes, only the tangential stress \(\tau^{12}\) and the normal stress \(\tau^{11}\) are the non-null components of the stress tensor. Then the governing Eq. (17) revert to

$$\begin{aligned} \tau^{12} & = \sum\limits_{i = 1}^{n} {\tau_{i}^{12} = } \, \sum\limits_{i = 1}^{n} {G_{i} \,\lambda_{i} \,\dot{\gamma }} \, \;\;\;\;\;\tau^{11} = \sum\limits_{i = 1}^{n} {\tau_{i}^{11} = \sum\limits_{i = 1}^{n} {2\,G_{i} \,\lambda_{i}^{2} \,\dot{\gamma }^{2} } } \\ G_{i} & = G_{0i} \,x_{i} \;\;\;\;\;\lambda_{i} = \lambda_{0i} \,x_{i}^{1.4} \\ \frac{{\left( {1 - x_{i} } \right)}}{{x_{i} }} & = \lambda_{i} \,a\,\dot{\gamma } \\ \end{aligned}$$
(20a\hbox{-}c)

having taken into account that the symmetric part of the velocity gradient is particularized as

$${\mathbf{D}} = \frac{1}{2}\left( {\nabla {\mathbf{v}} + \nabla {\mathbf{v}}^{T} } \right) = \left[ {\begin{array}{*{20}c} 0 & {\frac{1}{2}\dot{\gamma }} & 0 \\ {\frac{1}{2}\dot{\gamma }} & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]$$
(21)

Introducing a fractional constitutive law, for steady shear flow modelled through fractional Maxwell elements, the velocity is in the form \({\mathbf{v}} = \left[ {\begin{array}{*{20}c} {x_{2} \left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right)} & 0 & 0 \\ \end{array} } \right]^{T}\), while the symmetric part of the velocity gradient turns into

$${\mathbf{D}} = \frac{1}{2}\left( {\nabla {\mathbf{v}} + \nabla {\mathbf{v}}^{T} } \right) = \left[ {\begin{array}{*{20}c} 0 & {\frac{1}{2}\left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right)} & 0 \\ {\frac{1}{2}\left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right)} & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]$$
(22)

hence the model is described by the following set of equations

$$\begin{aligned} \tau^{12} & = \sum\limits_{i = 1}^{n} {\tau_{i}^{12} = } \, \sum\limits_{i = 1}^{n} {G_{i} \;\lambda_{\alpha i} \;\left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right)} \, \;\;\;\;\;\tau^{11} = \sum\limits_{i = 1}^{n} {\tau_{i}^{11} = \sum\limits_{i = 1}^{n} {2\;G_{i} \;\lambda_{\alpha i}^{2} \left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right)^{2} } } \\ G_{i} & = G_{0i} \;x_{i} \;\;\;\;\lambda_{\alpha i} = \lambda_{\alpha 0i} = \left( {\lambda_{0i} } \right)^{\alpha } \\ \frac{{\left( {1 - x_{i} } \right)}}{{x_{i} }} & = \lambda_{\alpha i} \;a\left( {{}_{C}D_{{0^{ + } }}^{\alpha } \gamma } \right) \\ \end{aligned}$$
(23a\hbox{-}c)

leading to \(C_{\alpha }\) the shear viscosity expressed in the form

$$C_{\alpha } = \sum\limits_{i = 1}^{n} {C_{\alpha i} } = \sum\limits_{i = 1}^{n} {\lambda_{\alpha i} } G_{i}$$
(24)

where \(G_{0i}\) and \(\lambda_{\alpha 0i}\) are the equilibrium values of \(G_{{{\kern 1pt} i}}\) and \(\lambda_{\alpha i}\), evaluated through the procedure described in the next section.

It is worth underscoring that Eqs. (23) are the transformed equation of the model of non-linear viscoelasticity with relaxation times depending on structure, taking into account the presence of fractional Maxwell elements instead of classical ones.

It is apparent that the relevant result is that the empirical equation is no more present but all equations have been derived theoretically leading to a closed form solution for \(x_{i}\). At this point the fundamental step will be the validation of this proposed formulation through experimental data developed by Meissner and reported in [44, 45]. It is worth underscoring that, such experimental data are the same used for validating the classical formulation in [39, 40].

4 Best fitting of relaxation function: classical and fractional model

To obtain the equilibrium values \(G_{0i}\) and \(\lambda_{0i}\)(classical model) and/or \(G_{0i}\) and \(\lambda_{\alpha 0i}\) (fractional model) describing the mechanical behavior of the fluid in the limit of linear viscoelasticity it needs experimental data of the relaxation function such that the best fitting, through expressions (13) and (16a), for fractional and classical constitutive laws respectively, will return the main parameters of each model. Specifically, considering the experimental data of relaxation function \(\varPhi \left( t \right)\) of the IUPAC L.D polyethylene samples obtained by experimental tests performed by Meissner [44, 45], then to evaluate the aforementioned equilibrium values the same procedure adopted in [39, 40] has been considered for both classical and fractional models. In Fig. 3 both best fittings of experimental relaxation function, using five (n = 5) classical and five fractional Maxwell elements connected in parallel are shown. Each best fitting leads to the identification of Maxwell parameters whose values are reported in Table 1.

Fig. 3
figure 3

Best fitting of the experimental relaxation function: (red dotted line) through five classical Maxwell elements (black dashed line) and five fractional Maxwell elements (blue solid line). (Color figure online)

Full size image
Table 1 Values of viscoelastic parameters obtained from best fitting
Full size table

In particular for classical Maxwell elements ten parameters (spring’s and dashpot’s parameters: \(G_{0i}\) and \(\lambda_{0i}\)) have been identified, considering the relaxation function expressed in the form

$$\varPhi \left( t \right) = \sum\limits_{i = 1}^{n} {G_{0i} \exp \left( { - \frac{t}{{\lambda_{0i} }}} \right)}$$
(25)

being the relaxation function of a Maxwell element formulated through Eq. (16a).

While for fractional Maxwell elements considering the following expression in terms of relaxation function [6, 23]

$$\varPhi \left( t \right) = \sum\limits_{i = 1}^{n} {G_{0i} E_{\alpha } \left[ { - \left( {\frac{{t^{\alpha } }}{{\lambda_{\alpha 0i} }}} \right)} \right]}$$
(26)

it needs the identification of eleven parameters (five spring’s and five spring-pot’s parameters and a unique value of \(\alpha\)).

As expected from a theoretical point of view, spring’s parameters are equal for both cases while \(\lambda_{\alpha 0i} = \left( {\lambda_{0i} } \right)^{\alpha }\).

5 Validation of the proposed formulation

Finally, in this section, the experimental data on the shear viscosity of polyethylene samples as a function of shear rate have been considered to validate the theoretical results outlined in the previous section. In particular, Fig. 4 sketches the values of viscosity as a function of shear rate, where, the dots are experimental data of the shear viscosity taken in different laboratories and introduced in [44, 45]. Below \(\dot{\gamma } \simeq 10 \, s^{ - 1}\) they were obtained with cone and plate-type instruments, while for larger \(\dot{\gamma }\) values, the viscosity was obtained from capillary measurements. Starting from the common point at lowest value of \(\dot{\gamma }\) say \(\mu \left( {10^{ - 4} } \right) =\sum\limits_{i = 1}^{n} {\lambda_{0i} } G_{0i} = C_{\alpha } \left( {10^{ - 4} } \right) = \sum\limits_{i = 1}^{n} {\lambda_{\alpha 0i} } G_{0i}\), after solving Eqs. (19) and (20) for classical procedure or Eqs. (23) and (24) for proposed procedure, the shear viscosity of polyethylene samples as a function of shear rate, is obtained and plotted in Fig. 4, having fixed the \(a\) parameter at 0.4.

Fig. 4
figure 4

Shear viscosity of polyethylene samples as a function of shear rate: experimental data (dots), theoretical results obtained with fractional model α = 0.97 (blue solid line), theoretical results obtained with classical model α = 1 (black dashed line). (Color figure online)

Full size image

As apparent from Fig. 4, results obtained from both methods highly match the experimental results assessing that the proposed procedure is reliable. More, the relative errors obtained using fractional constitutive law are lower than those evaluated through classical constitutive law, as shown in Table 2. Further, it is worth underscoring that for values of \(\dot{\gamma }\) pertaining a viscoelastic behavior the proposed model is the best model to predict the response, while, when \(\dot{\gamma }\) assumes higher values, since the material tends to behave as pure liquid, then classical procedure turns out more appropriate.

Table 2 Shear viscosity relative errors
Full size table

6 Conclusions

The main aim of this paper is to transform the equation of the model of non-linear viscoelasticity with relaxation times depending on material, introduced in [39, 40], taking into account the presence of fractional Maxwell element instead of classical ones.

An advanced model for capturing the non-linear trend of the shear viscosity of polymer melts as function of the shear rate has been proposed. Results obtained with the fractional model are compared with those obtained using a classical model which involves classical Maxwell elements. The good match among experimental data, results from classical theoretical formulation and proposed ones, underscores that that fractional model is proper for studying viscoelasticity, even if the material exhibits a non-linear behavior.