Fractional Tajimi–Kanai model for simulating earthquake ground motion

Abstract

The ground acceleration is usually modeled as a filtered Gaussian process. The most common model is a Tajimi–Kanai (TK) filter that is a viscoelastic Kelvin–Voigt unit (a spring in parallel with a dashpot) carrying a mass excited by a white noise (acceleration at the bedrock). Based upon the observation that every real material exhibits a power law trend in the creep test, in this paper it is proposed the substitution of the purely viscous element in the Kelvin Voigt element with the so called springpot that is an element having an intermediate behavior between purely elastic (spring) and purely viscous (dashpot) behavior ruled by fractional operator. With this choice two main goals are reached: (i) The viscoelastic behavior of the ground may be simply characterized by performing the creep (or the relaxation) test on a specimen of the ground at the given site; (ii) The number of zero crossing of the absolute acceleration at the free field that for the classical TK model is $\infty$ for a true white noise acceleration, remains finite for the proposed model.

1 Introduction

The classical Tajimi–Kanai (TK) to model earthquake ground motion (Tajimi 1960; Kanai 1957) is often used for the analysis of structures subjected to earthquakes. The TK model is a linear oscillator attached to the bedrock that, during the earthquake, moves with an acceleration modeled as a Gaussian white noise process. Studies of the TK filter and generalizations to take into account the non-stationatity may be found in Liu and Jhaveni (1969); Ahmadi and Fan (1990); Rofooei et al. (2001). The parameters of the TK model (damping ratio $\zeta _g$ and frequency $\omega _g$ of the soil deposit) are calibrated by the observation of zero crossings and other statistics of the historical earthquakes. In spite the studies and revisitations on this model two main questions remain unsolved: (i) If there is no previous time histories on the given site, how may we evaluate the relevant parameters of the TK model? (ii)As the classical TK model is assumed, the number of zero crossing of the acceleration at the free field is $\infty$ if the oscillator is enforced by a true white noise (power spectral density (PSD) constant at overall frequencies). The latter aspect remains hidden during the generation of artificial earthquakes starting from the TK filter since a cut-off frequency (80–100 rad/s) is usually performed. We preliminarly observe that the TK model is a Kelvin Voigt viscoelastic element that is a spring whose stiffness is $\omega _g^2$ and a dashpot characterized by the damping coefficient $2\zeta _g\omega _g$ carrying an unitary mass. Some authors give informations on calibration of the TK parameter, see e.g. Ellingwood and Batts (1982); Ellingwood et al. (1983); Rezaeian and Der Kiureghian (2008); Hindy and Novak (1979); Zerva and Harada (1997); Zerva and Stephenson (2011). Then the viscoelastic characteristics of the soil deposit are connected with such parameters. However Nutting (1921) observed that every real material (rubber, bitumen, cheramics, steel, $\ldots$) experiences a power law trend in the creep function. Based upon this observation in the second part of the last century many research works have been devoted to the correct constitutive laws of viscoelastic materials. And now it is widely recognized that the stress strain relationship involves fractional derivative rather than first order one, like it happens by assuming a constitutive law with integer order derivative (dashpot). Many papers have been focused on this theoretical aspect of fractional viscoelastic constitutive law and its numerical aspects (Blair and Caffyn 1949; Slonimsky 1961; Bagley and Torvik 1984; Schiessel and Blumen 1993; Schiessel et al. 1995; Bagley and Torvik 1983, 1986; Bagley 1989; Schmidt and Gaul 2002; Spanos and Evangelatos 2010; Yuan and Agrawal 2002; Schmidt and Gaul 2006a, b; Podlubny 1999; Di Paola et al. 2012; Di Paola and Zingales 2012; Di Paola et al. 2013), and others devoted to creep tests on real materials (Yang and Cheng 2011; Nian et al. 2012; Ter-Matirosyan and Ter-Matirosyan 2013; Li and Xia 2000; Di Paola et al. 2011; Zbiciak 2013; Grzesikiewiz et al. 2013). This new element, usually called springpot in literature, exhibits an intermediate behavior between purely elastic element (SPRING) and a purely viscous fluid (dashPOT). The qualitative viscoelastic behavior is characterized by the order $\beta$ of the fractional derivative (Di Paola and Zingales 2012), that for every material has the limitation $0\le \beta \le 1$. In particular the values $\beta =0$ and $\beta =1$ correspond to a purely elastic behavior and a purely viscous material, respectively.

From all these observations in this paper, a novel model of TK filter is proposed, that consists in assuming that the link between the bedrock and the free field is composed by a spring and a springpot in order to capture the correct viscoelastic behavior of the soil deposit. Then because of the presence of the fractional operator such a modified TK model will be termed as fractional Tajimi–Kanai (FTK) model. With this choice two main goals are reached: (i) The viscoelastic behavior of the ground may be simply characterized by performing the creep (or the relaxation) test on a specimen of the ground at the given site; (ii) The number of zero crossing of the absolute acceleration at the free field that for the TK filter is $\infty$ for a true white noise acceleration, remains finite for the FTK one confirming the robustness of the model. The paper is organized as follows: in Sect. 2 some preliminaries remarks on the fractional viscoelasticity is presented. In Sect. 3 the FTK model and the characterization of the parameters based upon experimental data available in literatures are proposed, while in Sect. 4 a wide discussion of the zero crossing of both TK and FTK is presented.

2 Preliminary concept on fractional viscoelasticity

In order to capture the viscoelastic behavior of any real material as a first step a creep or a relaxation function on a specimen of the given material has to be performed. In particular the creep function $J(t)$ is the strain history for an unitary imposed stress, while the relaxation function $G(t)$ is the stress history for an unitary imposed strain.

The constitutive law may be obtained in a linear viscoelastic range by using the Boltzmann superposition principle in the dual form (Flugge 1967)

$$\begin{aligned} \tau (t)&= G(t)\gamma (0)+\int \limits _0^t G(t-\bar{t})\dot{\gamma }(\bar{t})d\bar{t} \end{aligned}$$

(1)

$$\begin{aligned} \gamma (t)&= J(t)\tau (0)+\int \limits _0^t J(t-\bar{t})\dot{\tau }(\bar{t})d\bar{t} \end{aligned}$$

(2)

where $\tau (0)$, $\gamma (0)$ are the initial condition in terms of shear stress and shear strain, respectively. From Eqs. (1) and (2) we may affirm that in general the constitutive laws are ruled by convolution integrals whose kernels are the relaxation and creep function. Consider, without loss of generality, that the initial conditions are zero, that is $\gamma (0)=0$, $\tau (0)=0$, then by making the Laplace transform of Eqs. (1) and (2) we get a fundamental relationship between $\hat{G}(s)$ and $\hat{J}(s)$ in the form

$$\begin{aligned} \hat{G}(s) \hat{J}(s)=\frac{1}{s^2} \end{aligned}$$

(3)

being $s$ the Laplace (complex) parameter and $\hat{G}(s)$, $\hat{J}(s)$ the Laplace transform of $G(t)$ and $J(t)$, respectively. In the last part of the last century Nutting (1921) observed that the creep test performed on real materials like rubber, ceramics, steel, bitumen and many others are well fitted by a power law, that is

$$\begin{aligned} J(t)=\frac{t^\beta }{C_\beta \Gamma (1+\beta )}\quad 0\le \beta \le 1 \end{aligned}$$

(4)

where $\beta$ and $C_\beta$ are characteristic of the material at hand and $\Gamma (\cdot )$ is the Euler Gamma function. Further consider that the creep is given as in Eq. (4) by using Eq. (3) and making the inverse Laplace transform of $\hat{G}(s)=(\hat{J}(s) s^2)^{-1}$ we obtain that the relaxation function is given in the form

$$\begin{aligned} G(t)=\frac{C_\beta }{\Gamma (1-\beta )}t^{-\beta }\quad 0\le \beta \le 1 \end{aligned}$$

(5)

By inserting Eqs. (4) and (5) into Eqs. (1) and (2) we obtain

$$\begin{aligned} \tau (t)&= C_\beta \frac{1}{\Gamma (1-\beta )}\int \limits _0^t (t-\bar{t})^{-\beta } \dot{\gamma }(\bar{t})d\bar{t} \end{aligned}$$

(6)

$$\begin{aligned} \gamma (t)&= \frac{1}{C_\beta }\frac{1}{\Gamma (1+\beta )}\int \limits _0^t (t-\bar{t})^{\beta } \dot{\tau }(\bar{t})d\bar{t} \end{aligned}$$

(7)

Now we recognize that $\tau (t)/C_\beta$ in Eq. (6) is the Caputo’s fractional derivative of $\gamma (t)$ and $\gamma (t)C_\beta$ in Eq. (7) is the Riemann Liouville fractional integral of $\tau (t)$, that is the constitutive law may be written in the dual form

$$\begin{aligned} \tau (t)&= C_\beta \left( ^CD_{0^+}^\beta \gamma \right) (t) \end{aligned}$$

(8a)

$$\begin{aligned} \gamma (t)&= C_\beta ^{-1} \left( I_{0^+}^\beta \tau \right) (t) \end{aligned}$$

(8b)

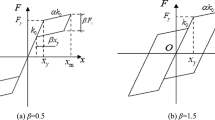
Eqs. (8) shows that as we assume for the creep (or relaxation) function a power law trend, then the fractional operators appear whose order of fractional derivative (or integral) is the exponent of the power law. Moreover because of the limitation on $\beta$ we recognize that for $\beta =0$ the purely elastic behavior is recovered, for $\beta =1$ the purely viscous behavior is obtained (see Eq. (2)). Intermediate values of $\beta$ take into account the viscoelastic behavior of the material.

3 Tajimi–Kanai model and its fractional counterpart

In this section the FTK model will be introduced in detail. For clarity’s sake the classical TK model is first discussed.

3.1 Classical TK filter

The TK model for the earthquake ground motion is based on the observation that the absolute acceleration of the ground may be sought as a white noise process (acceleration at bedrock) filtered through superimposed soil deposit modeled as a single degree of freedom oscillator as depicted in Fig. 1.

Fig. 1

Tajimi–Kanai model

Let us denote as $M_g$ the mass of the oscillator, $K_g$ the stiffness and $C_g$ the damping coefficient of the dashpot connecting the mass $M_g$ and the bedrock, $U(t)$ is the absolute displacement of the mass $M_g$, $W(t)$ the absolute displacement of the bedrock and $X_g(t)$ the relative displacement between the mass $M_g$ and the bedrock ($X_g(t)=U(t)-W(t)$). Based on the above considerations, the dynamic equilibrium equation of the mass $M_g$ is given as:

$$\begin{aligned} M_g(\ddot{X}_g(t)+\ddot{W}(t))+C_g \dot{X}_g(t)+K_g X(t)=0 \end{aligned}$$

(9)

and dividing by $M_g$ we get

$$\begin{aligned} \ddot{X}_g(t)+2\zeta _g \omega _g\dot{X}_g(t)+\omega _g^2 X(t)=-\ddot{W}(t) \end{aligned}$$

(10)

where $\zeta _g$ and $\omega _g$ are the damping ratio and the circular natural frequency of the ground, respectively, whose values are generally $\omega _g=5\pi$ (rad/s), $\zeta _g=0.6$. Then since we are interested in absolute acceleration of the free field we may write

$$\begin{aligned} \ddot{U}(t)=\ddot{X}_g(t)+\ddot{W}(t)=-2\zeta _g\omega _g \dot{X}_g-\omega _g^2X_g(t) \end{aligned}$$

(11)

Now let us suppose that $\ddot{W}(t)$ is a normal white noise process characterized by the PSD level $S_0$ (constant at overall frequencies), then the PSD for $\ddot{U}(t)$ is given as

$$\begin{aligned} S_{\ddot{U}}(\omega )=2\pi S_0\frac{\omega _g^4+4\zeta _g^2\omega _g^2\omega ^2}{(\omega _g^2-\omega ^2)^2+4\zeta _g^2\omega _g^2\omega ^2} \end{aligned}$$

(12)

Close inspection of Fig. 1 reveals that the classical TK filter is neither else than a Kelvin–Voigt element carrying a mass $M_g$ in which the elastic and the viscous elements take into account the viscoelastic property of the soil deposit. In order to overcome the unrealistic value of $S_{\ddot{U}}(\omega )$ at $\omega =0$ ($S_{\ddot{U}}(0)=2\pi S_0$) in Clough and Penzien (1995) is proposed a modification of the classical TK by inserting another oscillator (like a filter) avoiding the physical inconsistency.

On the other hand in the previous section it has been shown that the correct interpretation of the viscoelastic property of the soil is a spring (like in the classical TK filter) and a fractional element characterized by the coefficients $\beta$ and $C_\beta$. This issue will be addressed in the following.

3.2 Fractional Tajimi–Kanai model

Once we know the local constitutive law of the ground, by knowing the depth and the local characteristics of the soil deposit by using a shear type beam model the acceleration at the free field may be obtained. However since our goal is to find a simplified model like the TK filter we assume that the dashpot in the TK is substituted by a fractional element characterized by $\beta$ and $C_g^{(\beta )}$, as depicted Fig. 2.

Fig. 2

a FTK model, b Springpot

Inspection of the above model reveals that the dashpot characterized by $C_g$ in the classical TK is substituted by a fractional element (Fig. 2b), usually termed as springpot because it is an element with an intermediate behavior between the purely elastic (SPRING) and a purely viscous one (dashPOT). As we assume that the term $C_g\dot{X}_g(t)$ in Eq. (9) is substituted by $C_g^{(\beta )}\left( ^CD_{0^+}^{\beta }X_g\right) (t)$ the equation of motion in canonical form is written as

$$\begin{aligned} \ddot{X}_g(t)+2\bar{\zeta }_g\omega _g\left( ^CD_{0^+}^{\beta }X_g\right) (t)+\omega _g^2X_g(t)=-\ddot{W}(t) \end{aligned}$$

(13)

where $\bar{\zeta }_g$ is an anomalous damping coefficient $[\bar{\zeta }_g]=[\hbox {s}^{\beta -1}]$.

Since the Fourier transform of the Caputo’s fractional derivative is given as

$$\begin{aligned} \fancyscript{F}\left\{ \left( ^CD_{0^+}^{\beta }X_g\right) (t);\omega \right\}&= (i\omega )^\beta \hat{X}_g(\omega )\nonumber \\&= |\omega |^\beta \left( \cos \left( \frac{\beta \pi }{2}\right) +i\, sgn(\omega )\sin \left( \frac{\beta \pi }{2}\right) \right) \hat{X}_g(\omega ) \end{aligned}$$

(14)

where $i=\sqrt{-1}$, $sgn(\omega )$ is the signum function and $\hat{X}_g(\omega )$ is the Fourier transform of $X_g(t)$, then after some algebra we get the PSD of the absolute ground acceleration in the form

$$\begin{aligned} S_{\ddot{U}}(\omega )=2 \pi S_0 \frac{\omega _g^4+4 \bar{\zeta }_g^2 \omega _g^2 \omega ^{2\beta }+4\bar{\zeta }_g\omega ^\beta \omega _g^3\cos \left( {\frac{\beta \pi }{2}}\right) }{(\omega _g^2-\omega ^2)^2+4 \bar{\zeta }_g^2\omega _g^2\omega ^{2\beta }+4\bar{\zeta }_g\omega ^\beta \omega _g\cos \left( {\frac{\beta \pi }{2}}\right) (\omega _g^2-\omega ^2) } \end{aligned}$$

(15)

It is worth stressing that as soon as we assume $\beta =1$, then $\bar{\zeta }_g=\zeta _g$, and since $\cos (\beta \pi /2)=0$ Eq. (15) reverts to Eq. (12).

Also in the proposed model there is a physical inconsistency at $\omega =0$, that is $S_{\ddot{U}}(0)=2\pi S_0$ like in the classical filter. To avoid this problem, a similar strategy, like that one used in Clough and Penzien (1995), may be also used for the FTK system. However for the sake of simplicity hereinafter this problem is not considered. To select the parameters $k_g$, $C_g^{(\beta )}$ and $\beta$ it is possible to perform a best fitting of experimental shear creep tests on sample of real ground. It can be easily demonstrated that for a fractional Kelvin–Voigt model the creep function is given in the form

$$\begin{aligned} J(t)=t^\beta E_{\beta ,\beta +1}\left( -\frac{k_g}{C_g^{(\beta )}}t^\beta \right) \end{aligned}$$

(16)

where $E_{\beta ,\beta +1}(\cdot )$ is the Mittag-Leffler function defined as (Podlubny 1999)

$$\begin{aligned} E_{\alpha ,\gamma }(z)=\sum _{k=0}^\infty \frac{z^k}{\Gamma (\alpha k+\gamma )} \end{aligned}$$

(17)

Inserting Eq. (16) into Eq. (2) it leads to

$$\begin{aligned} \gamma (t)=\sum _{k=0}^\infty \frac{k_g}{C_g^{(\beta )}}\left( I_{0^+}^{\beta k+1}\tau \right) (t) \end{aligned}$$

(18)

The creep function for the ground are rare as in fact the tests performed on the specimen of ground are usually performed only to assess the ultimate load for the ground at hands and not for the characterization of the viscoelastic behavior. However recently Yang and Cheng (2011) for shale located in Lougtan Hydropower project of China using shale sample size of 150 mm $\times$ 150 mm $\times$ 150 mm the creep test are reported. Such a test have been performed for various shear stress levels and the results are depicted in Fig. 3a

Fig. 3

a Typical visco-elastic shear test (Yang and Cheng 2011), b shear creep test: experimental data (dots), theoretical result (solid line)

A best fitting between experimental creep and theoretical ones obtained by Eq. (16) returns the parameters $k_g=55\cdot 10^6$ N/m, $C_g^{(\beta )}=\gamma _1\, k_g\,\hbox {N\, s}^\beta /\hbox {m}$, $\beta =0.4$, for the minimum level stress $\tau =0,45$ MPa. The selection of the minimum stress level is made in order to ensure us that the ground behaves in the viscoelastic zone. The parameter $\gamma _1$ is a dimensional factor useful to give a numerical relation between $k_g$ and $C_g^{(\beta )}$; for the ground at hands it is $\gamma _1=20\,\hbox {s}^\beta$. Like in the classical TK then the main assumption is that the ground deposit behaves linearly. This is reflected from the fact that the equation of the filter is ruled by Caputo’s fractional operators that are in fact linear ones. If the magnitude of earthquake grows then the Nutting law requires the dependence on the level of stress as well. As in fact the Nutting law is $\gamma (t)\propto \tau ^\alpha t^{-\beta }$ (being $\alpha$ an indicator of nonlinearity) and the equation of the filter is non linear. Hereinafter the dependence on the stress level is eliminated in order to work with a linear model as the classical TK is. Once the parameters have been obtained by the best fitting the shear creep test curve obtained from experimental data is contrasted with the theoretical one expressed in Eq. 16 and plotted in Fig. 3b.

From the figures some considerations may be withdrawn: (i) From the experimental tests it is apparent that the correct way to describe the soil constitutive law is involving power law in the kernel of Eqs. (1) and/or (2). (ii) As a consequence of (i) the proper constitutive model of soil deposit is not a classical Kelvin–Voigt or Maxwell element or more complex combination of such elementary units since a fractional constituitive law may be represented by $\infty$ Kelvin–Voigt elements (see Di Paola and Zingales (2012); Di Paola et al. (2013)).

Now to study the PSD of the FTK the values of $\bar{\zeta }_g$ and $\omega _g$ have to be found; in order to do this, first a relation between $\bar{\zeta }_g$ and $\omega _g$ is found thanks to the relation between $k_g$ and $C_g^{(\beta )}$ as

$$\begin{aligned} \frac{C_g^{(\beta )}}{M_g}=\frac{\gamma _1\, k_g}{M}=2 \bar{\zeta }_g \omega _g \end{aligned}$$

(19)

and since

$$\begin{aligned} \frac{k_g}{M_g}=\omega _g^2 \end{aligned}$$

(20)

we obtain

$$\begin{aligned} \bar{\zeta }_g=\frac{\gamma _1}{2}\,\omega _g \end{aligned}$$

(21)

The values of $\bar{\zeta }_g$ and $\omega _g$ are then calibrated in order to have the PSD peak of the FTK at almost the same frequency of the peak of the TK PSD obtaining $\omega _g=2\,\hbox {rad/s}$ and $\bar{\zeta }_g=20$. In Fig. 4 the PSD for the classical TK filter is contrasted with that of the proposed FTK filter.

Fig. 4

Power spectral densities; classical TK (solid line): $\omega _g=5\pi$, $\zeta _g=0.6$, $S_0=1$; FTK (dashed line): $\omega _g=2$, $\bar{\zeta }_g=20$, $\beta =0.4$, $S_0=1$

From Fig. 4 at first glance it seems that no substantial difference between the two PSD distributions is evidenced. It follows that up to now the only reason to prefer using the FTK is that it models the viscoelastic property of the soil in a more realistic way. As in fact the parameters $\zeta _g$ and $\omega _g$ of the classical TK are mainly determined by the zero crossing of historical data and other specific characteristics based upon the probability theory of stochastic processes. However there is another reason to prefer the FTK from a theoretical point of view that is not explicitely claimed in literature. This issue will be adressed in the next section.

4 Zero crossings for TK and FTK model

The PSDs of the absolute acceleration $\ddot{U}(t)$ of TK and of FTK model are given in Eqs. (12) and (15), respectively. In order to match experimental data coming from historical earthquake model the zero crossings of the absolute acceleration at the free field has to be evaluated. It is well known that the mean number of zero crossings $\nu$ of the stationary Gaussian stochastic process $\ddot{U}(t)$ is given as (Lin 1967)

$$\begin{aligned} \nu =\frac{1}{\pi }\left[ \frac{\int _0^\infty S_{\dddot{U}}(\omega )d\omega }{\int _0^\infty S_{\ddot{U}}(\omega )d\omega }\right] ^{1/2}=\frac{1}{\pi }\frac{\sigma _{\dddot{U}}}{\sigma _{\ddot{U}}} \end{aligned}$$

(22)

where $S_{\dddot{U}}(\omega )$ is the PSD of the rate of acceleration $\dddot{U}$, $\sigma _{\dddot{U}}$ and $\sigma _{\ddot{U}}$ are the standard deviation of $\dddot{U}$ and $\ddot{U}$, respectively.

On the other hand since $S_{\dddot{U}}(\omega )=\omega ^2 S_{\ddot{U}}(\omega )$, the number of zero crossings for the TK model and the FTK model is given by inserting the corresponding PSDs obtained by Eq. (12) (TK model) or Eq. (15) (FTK model). We preliminary observe that $S_{\dddot{U}}(\omega )$ for classical TK model is depicted in Fig. 5 (solid line), in the same figure the $S_{\dddot{U}}(\omega )$ is plotted for FTK model (dashed line) for the selected parameters reported in previous sections and $S_0=1\,\hbox {cm}^2/\hbox {s}$.

Fig. 5

Power spectral densities of $\dddot{U}(t)$; classical TK solid line; FTK dashed line

From this figure it is evident that for $\beta =1$ (classical TK) the PSD of $\dddot{U}(t)$ for $\omega \rightarrow \infty$ is constant (for the case under exam the asymptotic value is $355\,\hbox {cm}^2/\hbox {s}^5$). This may also be captured by making the limit for $\omega \rightarrow \infty$ of Eq. (12) multiplied by $\omega ^2$. This means that as we assume that the PSD is that given in Eq. (12) the mean number of zero crossing per unit time is $\infty$. This fact is ignored in literature since usually people say that for $\omega >$80–100 rad/s the PSD is negligible. This means de facto that the stochastic process of input is band limited. If this assumptions is made then also the mean number of zero crossing does not diverge. In Fig. 6 two sample functions of $\ddot{U}(t)$ are plotted with different clipping on the PSD of the classical TK filter. In Fig. 6a the cut off frequency $\omega _C$ is 80 rad/s and the number of zero crossings $\nu \simeq 8\,\hbox {s}^{-1}$, in Fig. 6b the cut off frequency is 5,000 rad/s and $\nu \simeq 60\, \hbox {s}^{-1}$. By increasing the cut off frequency $\nu$ increase without limit.

Fig. 6

Sample functions of $\ddot{U}(t)$ for various values of the cut off frequency $\omega _c$ in the TK filter ($\omega _g=5\pi$, $\zeta _g=0.6$)

In Fig. 5 something different happens for the FTK filter, that is the PSD of $\dddot{U}(t)$ goes to zero for $\omega \rightarrow \infty$. Moreover if $0<\beta <0.5$ also the area of the PSD reamains finite and then the mean number of zero crossings is finite. That is the FTK model may be enforced by a true white noise process, obtaining, for $\omega _c\rightarrow \infty$, a number of zero crossings $\nu \simeq 7.6\,\hbox {s}^{-1}$. In Fig. 7 two sample functions of $\ddot{U}(t)$ for the FTK with different values of $\omega _c$; in Fig. 7a the cut off frequency $\omega _C$ is 80 rad/s and the number of zero crossings $\nu \simeq 5.7\,\hbox {s}^{-1}$, in Fig. 7b the cut off frequency is 5,000 rad/s and $\nu \simeq 7\,\hbox {s}^{-1}$. This value remain stable also for higher values of the cut-off frequency and is $\nu \simeq 7.6\,\hbox {s}^{-1}$ for $\omega _c\rightarrow \infty$. From the above considerations it follows that by using the FTK one may take profit of all tools of $\mathrm{It}{\hat{o}}'s$ calculus that remains valid only if the input is a true white noise.

Fig. 7

Sample functions of $\ddot{U}(t)$ for various values of the cut off frequency in the FTK filter ($\omega _g=2$, $\bar{\zeta }_g=20$, $\beta =0.4$)

5 Conclusions

In this paper a modification of the TK model has been proposed, that is the dashpot in the mechanical model is substituted by a springpot. The latter element is a fractional viscoelastic model whose constitutive law involves the Caputo’s fractional derivative instead of the first derivative as in the classical dashpot. The behavior of the springpot is intermediate between pure solid phase and pure Newtonian fluid. The main motivations, for using such an element instead of the dashpot, are twofold: (i) the creep test performed on specimen of ground (as in all other materials like rubber, bitumen, bones ceramics and so on) are power law type and not exponential ones. This leads to the fractional operators in the constitutive law; (ii) the zero crossing of the FTK model here proposed leads to a finite number, while in the classical TK filter the number of zero crossing is $\infty$. This relevant fact remains hidden in literature since usually a band limited (pink noise) is used, disregarding the PSD for $\omega >$80–100 rad/s. There is another motivation that has not been developed in this paper, that is, if we know the constitutive law obtained by the creep test on the ground at hand, by knowing the depth of the soil deposit a correct model for determining the absolute acceleration of the free field may be easily derived. Usually the creep test on grounds is performed by using triaxial machine that returns only the relationship between normal stress and corresponding axial deformation. However ti may be useful to perform creep shear test in order to define the proper fractional constitutive laws. On the other hand the ground is considered as isotropic then with the parameters of axial stress and axial strain the shear behavior may be easily obtained. It is hoped that, the proposed approach can be used for simulating earthquake ground motion. Then since the soil is viscoelastic in nature, therefore the better characterization is one for which determining the relevant features of viscoelasticity that are creep and relaxation. Then creep and or relaxation tests should be the standard tests to perform on soils. Extensions to model non-stationary records is straightforward and may be handled like for the classical TK filter.