1 Introduction

FGMs are the new class of composite materials which have spatially varying material properties. The earliest FGMs were introduced by Japanese scientists in the mid-1980s as ultra-high temperature-resistant materials for aerospace applications. Recently, these materials have found other uses in electrical devices, energy transformation, biomedical engineering, optics, etc. [1].

In the study of Wattanasakulpong et al. [2], a multi-step sequential infiltration technique was used to fabricate FGM beams for vibration testing. An elaborate discussion on FGM fabrication, microstructure and material volume fraction analysis as well as vibration experimental set up was presented in the study. Kapuria et al. [3, 4] created ceramic-metal FGM beams via powder metallurgy and thermal spray techniques in order to test bending and vibration behaviour. For theoretical investigation on vibration response of FGM beams, there were several reports dealing with the topic; for example, Sina et al. [5] presented a new beam theory based on the first order shear deformation theory (FSDT) to obtain frequency results of FGM beams which have uniform cross section throughout the whole length. Simsek [6] used the Lagrange multiplier method to solve a fundamental frequency analysis of FGM beams, applying different beam theories. The vibration response of FGM beams which have cracks at the edge was investigated in Refs. [7, 8]. An improved third order shear deformation theory (TSDT) was applied to analyse thermal buckling and elastic vibration of FGM beams using the Ritz method [9, 10]. On the basic of Euler-Bernonulli beam theory, nonlinear governing differential equation was constructed by Fallah and Aghdam [11] in order to solve the problems of thermo-mechanical buckling and vibration analyses of FGM beams resting on elastic foundation. To obtain the analytical solutions of the nonlinear governing equation, He’s variational method was employed to carry out the results of critical bucking temperatures and natural frequencies of such beams. By using refined shear deformation theory, Vo et al. [12] provided static and vibration results of FGM beams using finite element method with two-noded Hermite-cubic element. Buckling and vibration of FGM beams which have axially varying material compositions were presented in Refs. [13, 14].

Stepped beam structures are widely used in various engineering fields in order to economize on the beam materials and to lighten the beams. They are also found in engineering structures due to fabrication, assembly and space constraint. On the investigations of vibration of stepped beams, there were a number of reports dealing with the topic [15–18]. However, the stepped beams selected to investigate free vibration characteristics in the past are made from isotropic and laminated composite materials, using different theories and methodologies.

The DTM is an effective mathematical tool used to solve ordinary and partial differential equation. By using the DTM to solve vibration problem, fundamental and higher frequencies as well as their corresponding mode shapes can be obtained accurately without any frequency missing. Malik and Dang [19] had successfully implemented the DTM to deal with vibration analysis of isotropic beams supported by several end conditions. Kaya and Ozgumus [20–22] applied the DTM to solve many cases of vibration problems. Pradhan et al. [23] also used the DTM to find out the buckling results of a single walled carbon nanotube. It was reported that the DTM results in vibrational prediction of beams agree very well with exact solutions, while using the Ritz method, an error occurs in calculation [24]. Moreover, Salehi et al. [25] confirmed that the DTM can give more accurate results in prediction large deformation behaviour of cantilever beams under point load, compared to those obtained from the variational iteration method (VIM) and Adomain decomposition method (ADM). Ni et al. [26] also concluded that the DTM is a semi-analytical approach which has high precision and computational efficiency in vibration analysis.

Among previous investigations on vibration response of FGM beams, it is found that most researchers have analysed and presented only the vibration of uniform cross section FGM beams. Therefore, in this current investigation, free vibration analysis of stepped FGM beams is chosen to consider their behaviour associated with various general boundary conditions. The DTM is applied to solve the governing equations of the stepped FGM beams in order to obtain accurate frequency results and mode shapes. Several important aspects such as step ratio, step location, boundary conditions as well as the material volume fraction index which have impacts on natural frequencies of such beams are investigated and discussed in details.

2 Stepped FGM beams

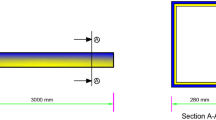
Two types of stepped FGM beams made of ceramic-metal are chosen to investigate vibration problem in this study. The geometries and descriptions of the FGM beam types are shown in Fig. 1.

Fig. 1
figure 1

Geometries and descriptions of two types of stepped FGM beams

Full size image

It can be seen in Fig. 1 that the material compositions at points p 1 and p 2 are the same for the FGM Type-I. However for FGM Type-II, the material at p 1 consists of the mixture of ceramic and metal whereas the material at p 2 is pure ceramic. It is also defined that the thickness of the stepped beams at Section 1 is given as h 1 = h and at Section 2 is h 2 = ξh in which ξ is the step ratio parameter (0 < ξ ≤ 1).

Based on the rule of mixture, the effective material properties, P j , can be written as

$$ P_{j} = P_{mj} V_{mj} + P_{cj} V_{cj} \quad (j = 1,2) $$
(1)

where the subscript j = 1 and 2 denote respectively the Section 1 and 2 of the stepped FGM beams. P mj , P cj , V mj and V cj are material properties and the volume fraction of the metal and ceramic corresponding to each beam section, respectively, with the relation

$$ V_{mj} + V_{cj} = 1\quad (j = 1,2). $$
(2)

According to the power law distribution, the volume fraction of ceramic (V cj ) in each section of the stepped beams can be seen in Table 1.

Table 1 The volume fractions of ceramic based on the power law distribution of the stepped FGM beams
Full size table

It is defined that N and n are the power law or volume fraction indexes of the stepped FGM beams for Sections 1 and 2, respectively. The range of these indexes is 0 ≤ N, n ≤ ∞. The FGM beam becomes a fully ceramic beam when N = n are set to zero. From the above relationship, the material properties, in terms of Young’s modulus and mass density in each section are expressed as

$$ E_{j} (z) = (E_{cj} - E_{mj} )\;V_{cj} + E_{mj} ,\quad (j = 1,2), $$
(3)
$$ \rho_{j} (z) = (\rho_{cj} - \rho_{mj} )\;V_{cj} + \rho_{mj} ,\quad (j = 1,2). $$
(4)

However for the material property of Poisson’s ratio (ν), it is assumed to be a constant value due to small difference between the ratio of ceramic and metal.

To investigate vibration analysis of the stepped FGM beams, the material stiffness components are obtained from \( (A_{11} ,B_{11} ,D_{11} )_{j} = \int {\frac{{E_{j} (z)}}{{[1 - \nu^{2} ]}}} (1,z,z^{2} )dz \) and the mass density can be calculated by using I 0j  = ∫ ρ j (z)dz. The upper and lower limits of the integrals are set according to the thickness of considered beam section. Therefore, the integral results of material stiffness components and the mass density in each beam section can be written in the function of the volume fraction indexes (N and n) as:

FGM Beam Section 1: (for Section 1, FGM Type-I and FGM Type II give the same results)

$$ A_{11} = \frac{h}{{1 - \nu^{2} }}\left[ {\frac{{E_{cm} }}{(N + 1)} + E_{m} } \right];\quad B_{11} = \frac{{E_{cm} h^{2} }}{{1 - \nu^{2} }}\left[ {\frac{N}{2(N + 1)(N + 2)}} \right] $$
(5a)
$$ D_{11} = \frac{{h^{3} }}{{1 - \nu^{2} }}\left[ {\frac{{E_{cm} (N^{2} + N + 2)}}{4(N + 1)(N + 2)(N + 3)} + \frac{{E_{m} }}{12}} \right];\quad I_{01} = h\left[ {\frac{{\rho_{cm} }}{(N + 1)} + \rho_{m} } \right] $$
(5b)

FGM Beam Section 2: (for FGM Type-I)

$$ A_{11} = \frac{h}{{1 - \nu^{2} }}\left[ {\frac{{E_{cm} \left( {\Xi_{1}^{n + 1} - \Xi_{2}^{n + 1} } \right)}}{(n + 1)} + \xi E_{m} } \right] $$
(6a)
$$ B_{11} = \frac{{E_{cm} h^{2} }}{{1 - \nu^{2} }}\left[ {\frac{{\frac{\xi }{2}\left( {\Xi_{1}^{n + 1} + \Xi_{2}^{n + 1} } \right)}}{(n + 1)} + \frac{{\Xi_{2}^{n + 2} - \Xi_{1}^{n + 2} }}{(n + 1)(n + 2)}} \right] $$
(6b)
$$ D_{11} = \frac{{h^{3} }}{{1 - \nu^{2} }}\left[ {E_{cm} \left( {\frac{{\frac{{\xi^{2} }}{4}\left( {\Xi_{1}^{n + 1} - \Xi_{2}^{n + 1} } \right)}}{(n + 1)} - \frac{{\xi \left( {\Xi_{1}^{n + 2} + \Xi_{2}^{n + 2} } \right)}}{(n + 1)(n + 2)} + \frac{{2\left( {\Xi_{1}^{n + 3} - \Xi_{2}^{n + 3} } \right)}}{(n + 1)(n + 2)(n + 3)}} \right) + \frac{{\xi^{3} E_{m} }}{12}} \right] $$
(6c)
$$ I_{02} = h\left[ {\frac{{\rho_{cm} \left( {\Xi_{1}^{n + 1} - \Xi_{2}^{n + 1} } \right)}}{(n + 1)} + \xi \rho_{m} } \right] $$
(6d)

where \( \Xi_{1} = \left( {\frac{\xi }{2} + \frac{1}{2}} \right) \); \( \Xi_{2} = \left( {\frac{ - \xi }{2} + \frac{1}{2}} \right) \) and E cm  = (E c  − E m ); ρ cm  = (ρ c  − ρ m ) in each section.

FGM Beam Section 2: (for FGM Type-II)

$$ A_{11} = \frac{\xi h}{{1 - \nu^{2} }}\left[ {\frac{{E_{cm} }}{(n + 1)} + E_{m} } \right];\quad B_{11} = \frac{{\xi^{2} E_{cm} h^{2} }}{{1 - \nu^{2} }}\left[ {\frac{n}{2(n + 1)(n + 2)}} \right] $$
(7a)
$$ D_{11} = \frac{{\xi^{3} h^{3} }}{{1 - \nu^{2} }}\left[ {\frac{{E_{cm} (n^{2} + n + 2)}}{4(n + 1)(n + 2)(n + 3)} + \frac{{E_{m} }}{12}} \right];\quad I_{02} = \xi h\left[ {\frac{{\rho_{cm} }}{(n + 1)} + \rho_{m} } \right] $$
(7b)

3 Application of DTM to vibration of stepped FGM beams

Consider a classical beam theory (CBT) based on the Kirchhoff–Love hypothesis, the partial differential equation used to describe the free vibration in each section of the FGM beams can be expressed as [18, 27]:

$$ \frac{{\partial^{4} w_{j} (x_{j} ,t)}}{{\partial x_{j}^{4} }} + \frac{{I_{0j} }}{{\lambda_{j} }}\frac{{\partial^{2} w_{j} (x_{j} ,t)}}{{\partial t^{2} }} = 0;\quad x_{j} \in [0,L]\,\,\,(j = 1,2). $$
(8)

It is defined that I 0j is the mass density, \( \lambda_{j} = \left( {D_{11} - \frac{{B_{11}^{2} }}{{A_{11} }}} \right)_{j} \) is the material stiffness coefficient corresponding to each section of such beams. By using the decoupling procedure for coupled governing equations of FGM beams as presented in Ref. [27], the parameter lambda (λ j ) is obtained from bending moment resultant when the axial inertia effect is neglected. Substituting harmonic vibration, w j (x j , t) = W j (x j )e iωt into Eq. (8), one can obtain a time independent governing equation as follows,

$$ \frac{{d^{4} W_{j} (x_{j} )}}{{dx_{j}^{4} }} - \frac{{I_{0j} }}{{\lambda_{j} }}\omega^{2} W_{j} (x_{j} ) = 0 $$
(9)

where ω is the natural frequency.

The DTM can be applied to solve vibration problem of stepped FGM beams. The principle of the DTM is to transform the ordinary and partial differential equations into algebraic equations. The brief detail of the method can be described as follows.

By considering rth-order differential transformation of a function f = f(x) at a point of x = x 0 , which can be defined as,

$$ F_{j} [r] = \frac{1}{r!}\left[ {\frac{{d^{r} f_{j} (x_{j} )}}{{dx_{j}^{r} }}} \right]_{{x = x_{0} }} $$
(10)

where f j (x j ) is the original function and F j [r] is the transformed function.

The function f j (x j ) can be expressed in the form of F j [r] as the following equation,

$$ f_{j} (x_{j} ) = \sum\limits_{r = 0}^{\infty } {(x_{j} - x_{j0} )^{r} F_{j} [r]} . $$
(11)

From the relationship between Eqs. (10) and (11), one can write

$$ f_{j} (x_{j} ) = \sum\limits_{r = 0}^{\infty } {\frac{{(x_{j} - x_{j0} )^{r} }}{r!}} \left[ {\frac{{d^{r} f_{j} (x_{j} )}}{{dx_{j}^{r} }}} \right]_{{x = x_{0} }} $$
(12)

which is known as the Taylor series expansion of f j (x j ) at a point x j  = x j0. To solve vibration problem of beams using the DTM, the governing differential equation and boundary condition equations as well as the continuity conditions are transformed into a set of algebraic equations using transformation rules. The basic operations required in differential transformation for the governing differential equations, boundary conditions, and the continuity conditions are shown in Tables 2 and 3, respectively [20–22].

Table 2 Basic operations of DTM for the governing equations
Full size table
Table 3 Basic operations of DTM for the boundary conditions and continuity conditions
Full size table

The general function, f j (x j ), in Tables 2 and 3 is considered as the transverse displacement W j (x j ). Apply the basic operations of DTM in Table 2 with the fundamentals of the DTM presented above and in Refs. [17–19] to the governing differential equation, Eq. (9), one can obtain the recurrence equation associated with the number of terms (r) for approximating solutions as:

$$ W_{j} [r + 4] = \frac{{I_{0j} \omega^{2} }}{{\lambda_{j} (r + 1)(r + 2)(r + 3)(r + 4)}}W_{j} [r] $$
(13)

In order to demonstrate the application of the DTM to vibration response of the stepped FGM beam, let us consider the beam with clamped-free (C–F) boundary condition. The governing equation in the form of the recurrence equation for the Section 1 of the beam can be expressed as:

$$ W_{1} [r + 4] = \frac{{I_{01} \omega^{2} }}{{\lambda_{1} (r + 1)(r + 2)(r + 3)(r + 4)}}W_{1} [r]. $$
(14)

The beam is clamped at the left end (x 1 = 0), hence the deflection W 1 = 0 and slope \( \frac{{dW_{1} }}{{dx_{1} }} = 0 \) at that end. The non-zero values of the bending moment and shear force at x 1 = 0 are represented by C 1 and C 2 respectively. Applying the basic operations of DTM for the boundary condition at x 1 = 0, using Table 3, one obtains

$$ W_{1} [0] = 0,\quad W_{1} [1] = 0,\quad W_{1} [2] = C_{1} ,\quad W_{1} [3] = C_{2} . $$
(15)

By using Eq. (15) with the recurrence equation, Eq. (14), this leads to W 1[r] for all values of r as follows:

$$ W_{1} [4r] = 0\quad r = 0,1,2,3 \ldots . $$
(16a)
$$ W_{1} [4r + 1] \,= \,0\quad r\, =\, 0,1,2,3 \ldots . $$
(16b)
$$ W_{1} [4r + 2] = \frac{{2!I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r + 2)!}}C_{1} \quad r\, =\, 0,1,2,3 \ldots . $$
(16c)
$$ W_{1} [4r + 3] = \frac{{3!I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r + 3)!}}C_{2} \quad r \,= \,0,1,2,3 \ldots . $$
(16d)

Next procedure is given for considering the Section 2 of the beam, therefore, the governing recurrence equation of the Section 2 is

$$ W_{2} [r + 4] = \frac{{\mu I_{01} \omega^{2} }}{{\lambda_{1} (r + 1)(r + 2)(r + 3)(r + 4)}}W_{2} [r], $$
(17)

where \( \mu = \frac{{I_{02} }}{{I_{01} }}\frac{{\lambda_{1} }}{{\lambda_{2} }}. \)

To consider the boundary condition at the right end (x 2 = 0) of the beam having free (F) condition, the bending moment \( \frac{{d^{2} W_{2} }}{{d^{2} x_{2} }} = 0 \) and shear force \( \frac{{d^{3} W_{2} }}{{d^{3} x_{2} }} = 0 \), the non-zero values of the deflection and slope account for C 3 and C 4 respectively. Again, applying the basic operations of DTM for the boundary condition at x 2 = 0, using Table 3, one obtains

$$ W_{2} [0] = C_{3} ,\quad W_{2} [1] = C_{4} ,\quad W_{2} [2] = 0,\quad W_{2} [3] = 0 $$
(18)

Again, by using Eq. (18) with Eq. (17), the expressions of W 2[r] for all values of r can be written as follows:

$$ W_{2} [4r] = \frac{{\mu^{r} I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r)!}}C_{3} \quad r = 0,1,2,3. \ldots $$
(19a)
$$ W_{2} [4r + 1] = \frac{{\mu^{r} I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r + 1)!}}C_{4} \quad r = 0,1,2,3 \ldots . $$
(19b)
$$ W_{2} [4r + 2] = 0\quad r = 0,1,2,3 \ldots . $$
(19c)
$$ W_{2} [4r + 3] = 0\quad r = 0,1,2,3 \ldots . $$
(19d)

It is assumed that, for a FGM beam having discontinuous cross-section, stress concentration at the interchange or the step location of the beam can be neglected [14, 15]. Hence, the continuity conditions are

$$ W_{1} (L_{1} ) = W_{2} (L_{2} ),\quad \frac{{dW_{1} (L_{1} )}}{{dx_{1} }} = - \frac{{dW_{2} (L_{2} )}}{{dx_{2} }} $$
(20a)
$$ \frac{{d^{2} W_{1} (L_{1} )}}{{d^{2} x_{1} }} = \frac{{\lambda_{2} }}{{\lambda_{1} }}\frac{{d^{2} W_{2} (L_{2} )}}{{d^{2} x_{2} }},\quad \frac{{d^{3} W_{1} (L_{1} )}}{{d^{3} x_{1} }} = - \frac{{\lambda_{2} }}{{\lambda_{1} }}\frac{{d^{3} W_{2} (L_{2} )}}{{d^{3} x_{2} }} $$
(20b)

According to the principle of the DTM, the continuity conditions are transformed into algebraic equations using Table 3. The results of the transformation can be expressed as,

$$ W_{1} [r]L_{1}^{(r)} - W_{2} [r]L_{2}^{(r)} = 0 $$
(21)
$$ W_{1} [r]rL_{1}^{(r - 1)} + W_{2} [r]rL_{2}^{(r - 1)} = 0 $$
(22)
$$ W_{1} [r]r(r - 1)L_{1}^{(r - 2)} - \delta W_{2} [r]r(r - 1)L_{2}^{(r - 2)} = 0 $$
(23)
$$ W_{1} [r]r(r - 1)(r - 2)L_{1}^{(r - 3)} + \delta W_{2} [r]r(r - 1)(r - 2)L_{2}^{(r - 3)} = 0 $$
(24)

where \( \delta = \frac{{\lambda_{2} }}{{\lambda_{1} }} \)

Using the components in Eqs. (16) and (19) to substitute into the transformed continuity conditions in Eqs. (21–24), the results of the substitution can be arranged and presented in the matrix form as follows,

$$ \left[ {\begin{array}{*{20}c} {e_{11} } & {e_{12} } & {e_{13} } & {e_{14} } \\ {e_{21} } & {e_{22} } & {e_{23} } & {e_{24} } \\ {e_{31} } & {e_{32} } & {e_{33} } & {e_{34} } \\ {e_{41} } & {e_{42} } & {e_{43} } & {e_{44} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {C_{1} } \\ {C_{2} } \\ {C_{3} } \\ {C_{4} } \\ \end{array} } \right] = 0. $$
(25)

Where the elements in the matrix are:

$$ e_{11} = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r + 2)} }}{{\lambda_{1}^{r} (4r + 2)!}}} ,\quad e_{12} = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r + 3)} }}{{\lambda_{1}^{r} (4r + 3)!}}} , $$
$$ e_{13} = - \sum\limits_{r = 0}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r)} }}{{\lambda_{1}^{r} (4r)!}}} ,\quad e_{14} = - \sum\limits_{r = 0}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r + 1)} }}{{\lambda_{1}^{r} (4r + 1)!}}} , $$
$$ e_{21} = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r + 1)} }}{{\lambda_{1}^{r} (4r + 1)!}}} ,\quad e_{22} = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r + 2)} }}{{\lambda_{1}^{r} (4r + 2)!}}} , $$
$$ e_{23} = \sum\limits_{r = 1}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r - 1)} }}{{\lambda_{1}^{r} (4r - 1)!}}} ,\quad e_{24} = \sum\limits_{r = 0}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r)} }}{{\lambda_{1}^{r} (4r)!}}} , $$
$$ e_{31} = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r)} }}{{\lambda_{1}^{r} (4r)!}}} ,\quad e_{32} = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r + 1)} }}{{\lambda_{1}^{r} (4r + 1)!}}} , $$
$$ e_{33} = - \delta \sum\limits_{r = 1}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r - 2)} }}{{\lambda_{1}^{r} (4r - 2)!}}} ,\quad e_{34} = - \delta \sum\limits_{r = 1}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r - 1)} }}{{\lambda_{1}^{r} (4r - 1)!}}} , $$
$$ e_{41} = \sum\limits_{r = 1}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r - 1)} }}{{\lambda_{1}^{r} (4r - 1)!}}} ,\quad e_{42} = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} L_{1}^{(4r)} }}{{\lambda_{1}^{r} (4r)!}}} , $$
$$ e_{43} = \delta \sum\limits_{r = 1}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r - 3)} }}{{\lambda_{1}^{r} (4r - 3)!}}} ,\quad e_{44} = \delta \sum\limits_{r = 1}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} L_{2}^{(4r - 2)} }}{{\lambda_{1}^{r} (4r - 2)!}}} , $$
(26)

To obtain a non-trivial solution, the determinant of coefficient matrix in Eq. (25) could be set equal to zero. For practical calculation, the finite number of terms in each element of the matrix in Eq. (26) from r to R should be applied. It is noted that r is the lower limit and R is the upper limit of the sum operator. An appropriate number of R can be determined from convergence studies which will be shown in the following section.

Mode shapes of the step FGM beams can be plotted by setting C 1 to unity in Eq. (25) so that the remaining nonzero constants (C 2, C 3,, C 4) are solved. Thus, the mode shapes corresponding to any frequency can be expressed as the function of W j (x j ) = ∑  ∞ r=0 x r j W j [r]. To obtain the mode shapes with the whole length coordinate (x), for example in the case of CF beam, its mode shape functions are:

$$ W(x) = \left\{ \begin{array}{ll} W_{1} (x) = \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r + 2)}}x^{(4r + 2)} + C_{2} \sum\limits_{r = 0}^{\infty } {\frac{{I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r + 3)}} x^{(4r + 3)}} }& \quad x \in [0,L_{1} ] \hfill \\ W_{2} (L - x) = C_{3} \sum\limits_{r = 0}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r)}}(L - x)^{4r} + C_{4} \sum\limits_{r = 0}^{\infty } {\frac{{\mu^{r} I_{01}^{r} \omega^{2r} }}{{\lambda_{1}^{r} (4r + 1)}}(L - x)^{(4r + 1)}} }&\quad x \in [L_{1} ,L] \\ \end{array} \right. $$
(27)

By following the same procedure, one can solve the vibration problem of the stepped FGM beams with other kinds of boundary conditions. The matrix elements for other boundary conditions that are simply supported at both ends (S–S), clamped-clamed (C–C) and clamped-simply supported (C–S) are presented in Table 8 in Appendix 1. The mode shape functions of these boundary conditions are also provided in Appendix 2.

4 Numerical results and discussions

In this present study, stepped FGM beams made of Alumina (Al2O3) and Aluminum (Al); whose material properties are: E c  = 380 GPa, ρ c  = 3,960 kg/m3, ν = 0.3 for Al2O3 and E m  = 70 GPa, ρ m  = 2,702 kg/m3, ν = 0.3 for Al; are chosen for investigation throughout the paper.

Using the DTM for solving vibration analysis of stepped FGM beams, it is important to first carry out convergence studies. The results of the studies are presented in Table 4 with various types of boundary conditions. The stepped FGM beams in this table are specialised to pure Al2O3 stepped beams by setting N = n=0 in which some available results were adopted to compare with the present results. The available results of Mao and Pietrzko [18] were computed from the ADM. Based on the numerical results, it is observed that the DTM gives rapid convergence for the first to fifth frequencies using only R = 10, and it also demonstrates computational stability as well as accuracy for every boundary condition.

Table 4 Convergence studies and comparisons of frequency results (rad/s) of isotropic stepped beams with various boundary conditions (L/h = 30; L 1 = 0.25 L; ξ = 0.5)
Full size table

Table 5 gives dimensionless fundamental frequencies of stepped FGM beams. The expression of the dimensionless form is \( \Omega = ({{\omega L^{2} } \mathord{\left/ {\vphantom {{\omega L^{2} } h}} \right. \kern-0pt} h})\sqrt {({{\rho_{m} } \mathord{\left/ {\vphantom {{\rho_{m} } {E_{m} )}}} \right. \kern-0pt} {E_{m} )}}}. \) The new frequency results of such beams related to different boundary conditions and beam types are investigated by varying the values of step ratio. As shown in the table, the trends of frequency changes for the cases of C–C, S–S and C–S are the same in which the frequency results increase with the increasing step ratio. However, for the case of C–F, the trend is different and the highest frequency is obtained at ξ = 0.5with L 1 = 0.5L. By setting ξ = 1.0, the frequency results can account for the results of uniform FGM beams, which their accuracy are confirmed by comparing with the available results presented in the brackets. In general, the natural frequency is higher when the system becomes stiffer with the increase of elastic properties. By increasing of step ratio, the beam has larger size and becomes stronger; therefore, its frequency is found to increase accordingly.

Table 5 Dimensionless fundamental frequencies of stepped FGM beams with different step ratios (L/h = 20; L 1 = 0.5 L; N = n = 0.5)
Full size table

To study the influences of step location (L 1 /L) and step ratio (ξ) on fundamental frequencies, the dimensionless frequency results are tabulated in Table 6. Again, the trend of frequency changes of C–F beams shows different patterns compared to others when using different step locations. It is also seen that FGM Type-I provides higher frequency results than those of FGM Type-II for every boundary condition. This is because the FGM Type-I has much higher material stiffness coefficient compared to that of the FGM Type-II, while, the difference between the mass of the two beam types are relatively small. Hence, according to the above discussion, the stronger beam has higher frequency. In order to clearly understand the relationship between the step location and the step ratio, Fig. 2 shows the relationship of these aspects to the fundamental frequencies of FGM-Type I beams with C–F and C–C boundary conditions. It is seen that the frequency results change considerably when the aspects are varied for both boundary conditions. It is also found that the greatest frequency of C–F beam is at around L 1 /L = 0.7 and ξ = 0.2, whereas for C–C beam, it is around L 1 /L = 0.9 and ξ = 0.9.

Table 6 Dimensionless fundamental frequencies of stepped FGM beams with different step ratios and step locations (L = 30; N = n = 0.5)
Full size table
Fig. 2
figure 2

Dimensionless fundamental frequencies of stepped FGM beams: a C–F, b C–C

Full size image

Table 7 presents the first three modes of frequency results of stepped FGM beams by varying the values of the volume fraction index (n = N). Increasing the values leads to reduction in frequency results for all types of beams and boundary conditions. Within a range of 0 < n=N ≤ 1, the frequency results of stepped FGM-Type I beams are higher than those of the FGM-Type II beams for every boundary condition. However, this phenomenon is reversed when n = N>1. Similarly, the material volume fraction indexes (n and N) are the important parameters that lead to the change in material stiffness coefficient of the stepped beam made from FGM. In case of n = N = 0, the stepped beam is made from fully ceramic and it is classified as the strongest beam which has the greatest frequency. When the indexes are increased, n = N>0, this means that the beam is made from the mixture of ceramic and metal and the frequency of the beam is reduced according to the increase of percentage of metal. In addition, it is noted that n = N<1 means that the beams are made from more percentage of ceramic than that of metal, whereas for n = N>1 the beam has less ceramic. Therefore, the vibration responses of the beams with these two ranges are different.

Table 7 Dimensionless frequency results of stepped FGM beams with different values of the volume fraction index (L = 30; L 1 = 0.5 L; ξ = 0.5)
Full size table

Figure 3 illustrates a 3-D plot of fundamental frequencies of stepped FGM beams associated with variations of the volume fraction index in Sections 1 and 2. The frequency results are obtained from FGM-Type II with C–F boundary condition. It is seen that substantial changes in the frequency results are observed at the values of the volume fraction index varied from 0 to 3 for both sections. In Fig. 4, mode shapes from the first to third mode of stepped FGM-Type I beams are illustrated with various boundary conditions. The volume fraction index is fixed to be the same for Sections 1 and 2 (N = n = 0.5).

Fig. 3
figure 3

Dimensionless fundamental frequencies of stepped FGM beams with variations of the volume fraction index in Sections 1 and 2 (L = 20; L 1 = 0.5 L; ξ = 0.5)

Full size image
Fig. 4
figure 4

The 1st to 3th mode shapes of stepped FGM beams with various boundary conditions (L = 30; L 1 = 0.5 L; ξ = 0.5)

Full size image

5 Conclusions

In this paper, the DTM is applied to solve the governing differential equations for predicting vibration characteristics of stepped FGM beams supported by various boundary conditions. According to some previous researches in the open literature, the method yields accurate frequency results and mode shape of the beams with small computational efforts. Two main types of FGM are chosen to make the stepped beams, for investigating vibration characteristics. According to the numerical results, the concluding remarks are revealed as follows:

  • Step ratio, step location, the volume fraction index and boundary conditions show significant effects on frequency results for every mode.

  • As step ratio increases, the frequencies detected in C–C, S–S and C–S boundary conditions follow the same increasing trend. However, the frequency changes detected in C–F case is dependent on step location.

  • FGM-Type I beam gives higher frequency results than those of FGM-Type II beam for every mode and boundary condition.

  • Increasing the values of the volume faction index leads to reduction in frequency results for every boundary condition and beam type.

The methodology, discussion and numerical results that are presented in this paper are supposed to be useful for further development and validation. The DTM can be extended to deal with various engineering problems. For example, to design piezoelectric modal senor for uniform and non-uniform cross section beams, this can be achieved by using structural mode shape functions obtained from the DTM. Additionally, to calculate mode characteristics for piezoelectromechanical beams [28] and to identify damages on cracked beams [29, 30], these topics can be analysed by using the DTM.