Static and free vibration analyses of carbon nanotube-reinforced composite plate using differential quadrature method

Abstract

This work presents bending and free vibration behaviour of carbon nanotubes reinforced composite (CNTRC) plates using the three dimensional theory of elasticity. The single-walled carbon nanotubes reinforcement is either uniformly distributed or functionally graded (FG) along the thickness direction indicated with FG-V, FG-O and FG-X. In the present study the effective material properties of CNTRC plates, are estimated according to the rule of mixture along with considering the CNT efficiency parameters. For the plate with simply supported edges we used Fourier series expansion across the in plane coordinates as well as the state space technique across the thickness direction to obtain closed form solution. Since in the case of plate with non-simply supported boundary conditions it is not possible to use Fourier series along the longitudinal and width directions, therefore it should be employed numerical method along the above mentioned coordinates. In this investigation we used semi analytical technique, differential quadrature method along the in-plane coordinates and state-space technique across the thickness direction. Present approach is validated by comparing the numerical results with those published results. Furthermore, effect of types of CNT distributions in the polymer matrix, volume fraction of CNT, edges boundary conditions and width-to-thickness ratio on the bending and free vibration behaviour of FG-CNTRC plate are discussed.

1 Introduction

The special mechanical, thermal and electrical properties of CNT cause to use it as a reinforcing constituent instead of conventional fibers in composite structures. Introduction of CNT into polymer matrix increases the application of reinforcing composite elements. Due to these exceptional properties of the CNT, analysis of the static and dynamic behaviour of carbon nanotubes reinforced composite (CNTRC) beam, plate and shell structures has been considered by many researchers in recent years.

Wuite and Adali [1], presented a multi-scale analysis of the deflection and stress behavior of CNTRC beams. Vodenitcharova and Zhang [2] investigated pure bending and bending-induced local buckling of a nanocomposite beam reinforced by a SWNT computationally as well as experimentally using Airy stress-function technique. Shen [3] discussed nonlinear bending behavior of simply supported, FG composite plates reinforced by single-walled carbon nanotubes (SWCNTs) and subjected to transverse uniform or sinusoidal load in thermal environments. Nonlinear free vibration of beam reinforced by SWCNTs was studied by Ke et al. [4] based on Timoshenko beam theory along with a von Kármán-type of kinematic nonlinearity. Shen and Zhang [5] presented an analytical solution consists of two steps perturbation technique for thermal buckling and post-buckling behavior of functionally graded CNT reinforced composite plates. Shen [6] used higher order shear deformation theory as well as a von Karman-type of kinematic nonlinearity to investigate the post-buckling behavior of CNTRC cylindrical shells subjected to axial compression in thermal environments. Based on a micromechanical model and multiscale approach, Shen [7] discussed post buckling behavior of functionally graded (FG)-CNTRC cylindrical shells subjected to mechanical load in thermal environments. Based on a higher order shear deformation plate theory, Wanga and Shen [8] used an improved perturbation technique to investigate nonlinear vibration of FG-SWCNT plates rested on elastic foundation in thermal environments. Arani et al. [9] investigated buckling behavior of laminated CNTRC plates analytically based on the CLPT and numerically based on the TSDT. Yas and Heshmati [10] used Timoshenko beam theory to analyze vibration of nanocomposite beams reinforced by randomly oriented straight SWCNTs subjected to moving load. Based on three dimensional theory of elasticity, Sobhani et al. [11] used Ashelby–Mori–Tanaka approach to analyses of vibration characteristic of cylindrical panel. Wang and Shen [12] investigated nonlinear vibration and bending of sandwich plates with nanotube-reinforced composite face sheets resting on an elastic foundation in thermal environments. Shen and Xiang [13] discussed nonlinear free vibration of cylindrical shells reinforced by SWCNTs in thermal environments using higher order shear deformation theory as well as a von Karman-type of kinematic nonlinearity. Wang and Shen [14] used the higher order shear deformation theory along with a von Kármán-type of kinematic nonlinearity to study non-linear dynamic response of CNTRC plate rested on elastic foundations in thermal environments. Mehrabadi et al. [15] discussed mechanical buckling behavior of FG-CNTRC plate using Mindlin plate theory and first-order shear deformation theory (FSDT). Alibeigloo [16] presented an analytical solution for bending behavior of FG-CNTRC rectangular plate embedded in piezoelectric layers by using theory of elasticity. Based on first-order shear deformation theory, Malekzadeh and Shojaee [17] derived Buckling response of quadrilateral laminated CNTRC plate using differential quadrature method (DQM). Free vibration analysis of FG-CNTRC plate based on first-order shear deformation theory was investigated by Lei et al. [18] using the Ritz method. Bending and free vibration analysis of thin-to-moderately thick composite plates reinforced by SWCNTs was presented by Zhu et al. [19] using the FEM and FSDT. Alibeigloo and Liew [20] used three-dimensional theory of elasticity to discuss thermo elastic behavior of FG-CNTRC rectangular plate with simply supported boundary condition. According to the above mention survey it was found that three-dimensional free vibration and static analysis of FG-CNTRC rectangular plate with various edges boundary conditions has not yet been reported. In this paper, elasticity solution of FG-CNTRC plate for free vibration and bending behavior of FG-CNTRC rectangular plate subjected to uniform pressure with different edges boundary condition was presented by using differential quadrature method (DQM) along in-plane coordinates and state-space analytical approach in transverse direction.

2 Problem formulation

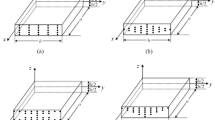
Consider a CNTRC rectangular plate with length a, width b and thickness h as shown in Fig. 1. The SWCNT reinforcement is either uniformly distributed (UD) or FG in the thickness direction which are specified as FG-V, FG-O and FG-X. Displacements component along the x-, y- and z- directions are denoted by U, V and W, respectively.

Fig. 1

Geometry of the CNTRC plates

Effective material properties of CNTRC plates are according to the rule of mixture with considering the CNT efficiency parameters [19];

$$ E_{11}^{{}} = \eta_{1} \,V_{CNT} E_{11}^{CNT} + V_{m} E^{m} $$

(1a)

$$ \frac{{\eta_{2} }}{{E_{22}^{{}} }} = \frac{{V_{CNT} }}{{E_{22}^{CNT} }} + \frac{{V_{m} }}{{E^{m} }}\; $$

(1b)

$$ \frac{{\eta_{3} }}{{G_{12} }} = \frac{{V_{CNT} }}{{G_{22}^{CNT} }} + \frac{{V_{m} }}{{G^{m} }} $$

(1c)

Relation between CNT and polymer matrix volume fractions, is as the follow;

$$ V_{CNT} + V_{m} = 1 $$

(2)

The uniform and three types of functionally graded distributions of the carbon nanotubes along the plate thickness depicted in Fig. 1 are assumed to be

$$ \left\{ \begin{gathered} V_{CNT} (z) = V_{CNT}^{*} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad (UD) \hfill \\ V_{CNT} (z) = 2(1 + \frac{2z}{h})\,V_{CNT}^{*} \quad \quad \quad \quad \quad \quad \quad \;\;(FG - V) \hfill \\ V_{CNT} (z) = (\frac{4\left| z \right|}{h})\,V_{CNT}^{*} \quad \quad \quad \quad \quad \quad \;\quad \quad \;\;(FG - X) \hfill \\ V_{CNT} (z) = 2(1 - \frac{2\left| z \right|}{h})\,V_{CNT}^{*} \quad \quad \quad \;\;\quad \quad \quad \;\;(FG - O) \hfill \\ \end{gathered} \right. $$

(3)

Effective Poisson ratio, ν ₁₂ and material density, ρ of the CNTRC plates are, respectively [19]

$$ \nu_{12} = V_{CNT}^{*} \nu_{11}^{CNT} + V_{m} \nu^{m} $$

(4a)

$$ \rho = V_{CNT}^{{}} \rho_{{}}^{CNT} + V_{m} \rho^{m} $$

(4b)

And the other effective mechanical properties are [6]

$$ E_{33} = E_{22} \;,\;G_{13} = G_{12} ,{\text{G}}_{23} = 1.2G_{12} \;,\;\,\nu_{13} = \nu_{12} \;,\;\,\nu_{31} = \nu_{21} \;,\;\,\nu_{32} = \nu_{23} = \nu_{21} \;,\;\,\nu_{21} = \frac{{E_{22} }}{{E_{11} }}\nu_{12} $$

(5)

The constitutive equations for anisotropic composite layer can be shown as

$$ \sigma = Q\varepsilon $$

(6)

where

$$ \sigma = \left[ {\sigma_{x} \;\,\sigma_{y} \,\;\sigma_{z} \;\,\tau_{yz} \;\,\tau_{xz} \;\tau_{xy} } \right]^{T} ,\quad \varepsilon = \left[ {\varepsilon_{x} \;\,\varepsilon_{y} \,\;\varepsilon_{z} \;\,\gamma_{yz} \;\,\gamma_{xz} \;\gamma_{xy} } \right]^{T} $$

$$ Q = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & {Q_{13} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & {Q_{23} } & 0 & 0 & 0 \\ {Q_{13} } & {Q_{23} } & {Q_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {Q_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {Q_{66} } \\ \end{array} } \right] $$

Relation between the stiffness elements, Q _ij and engineering constants, E _ij , G _ij and v _ij are described in Appendix.

In the absence of body forces, governing differential equations of motion are

$$ \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} + \frac{{\partial \tau_{xz} }}{\partial z} = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }} $$

$$ \frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \sigma_{y} }}{\partial y} + \frac{{\partial \tau_{yz} }}{\partial z} = \rho \frac{{\partial^{2} v}}{{\partial t^{2} }} $$

(7)

$$ \frac{{\partial \tau_{xz} }}{\partial x} + \frac{{\partial \tau_{yz} }}{\partial y} + \frac{{\partial \sigma_{z} }}{\partial z} = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }} $$

Three dimensional linear strain–displacement relations are

$$ \varepsilon_{x} = \frac{\partial u}{\partial x}\;,\; \, \varepsilon_{y} = \frac{\partial v}{\partial y}\;,\; \, \varepsilon_{z} = \frac{\partial w}{\partial z}\;,\; \, \gamma_{xy} = \frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}\;,\; \, \gamma_{xz} = \frac{\partial w}{\partial x} + \frac{\partial u}{\partial z}\;,\; \, \gamma_{yz} = \frac{\partial w}{\partial y} + \frac{\partial v}{\partial z} $$

(8)

By using Eqs. (6)–(8), governing state-space equations can be written as follow

$$ \frac{d}{dz}\delta = G\delta $$

(9)

Where δ = {σ _z uvwτ _xz τ _yz }^T is the state variable vector, and G is the coefficients matrix (see Appendix).

The in-plane stresses in term of state variables can be derived as

$$ \sigma_{x} = \frac{{Q_{13} }}{{Q_{33} }}\sigma_{z} + \left( {Q_{11} - \frac{{Q_{13}^{2} }}{{Q_{33} }}} \right)\frac{\partial u}{\partial x} + \left( {Q_{12} - \frac{{Q_{13} Q_{23} }}{{Q_{33} }}} \right)\frac{\partial v}{\partial y} $$

$$ \sigma_{y} = \frac{{Q_{23} }}{{Q_{33} }}\sigma_{z} + \left( {Q_{12} - \frac{{Q_{13} Q_{23} }}{{Q_{33} }}} \right)\frac{\partial u}{\partial x} + \left( {Q_{22} - \frac{{Q_{23}^{2} }}{{Q_{33} }}} \right)\frac{\partial v}{\partial y}\quad \quad $$

(10)

$$ \tau_{xy} = Q_{66} \left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right) $$

3 Analytical solution

In this section we use 3D theory of elasticity to derive exact solution of simply supported CNTRC rectangular plate.

Relations for simply supported edges boundary condition maybe written as

$$ \sigma_{x} = 0\;,\quad v = w = 0\;\quad \;at\quad x = 0,a $$

$$ \sigma_{y} = 0\;,\quad u = w = 0\;\quad \;at\quad y = 0,b $$

(11)

Following assumed solutions which satisfy the simply supported boundary conditions are introduced

$$ \sigma_{x} = \sigma_{x}^{ * } \,\sin (p_{m} x)\,\sin (p_{n} y)e^{i\omega t} \,,\; \, \sigma_{y} = \sigma_{y}^{ * } \,\sin (p_{m} x)\,\sin (p_{n} y)e^{i\omega t} \, $$

$$ \sigma_{z} = \sigma_{z}^{ * } \sin (p_{m} x)\,\sin (p_{n} y)e^{i\omega t} , \, \;\tau_{xz} = \tau_{xz}^{ * } \,\cos (p_{m} x)\,\sin (p_{n} y)e^{i\omega t} $$

$$ \,\tau_{yz} = \tau_{yz}^{ * } \,\sin (p_{m} x)\,\cos (p_{n} y)e^{i\omega t} \,, \, \;\tau_{xy} = \tau_{xy}^{ * } \,\cos (p_{m} x)\,\sin (p_{n} y)e^{i\omega t} $$

$$ u = U\,\cos (p_{m} x)\,\sin (p_{n} y)e^{i\omega t} \,,\; \, v = V\,\sin (p_{m} x)\,\cos (p_{n} y)e^{i\omega t} $$

$$ \,w = W\,\sin (p_{m} x)\,\sin (p_{n} y)e^{i\omega t} $$

(12)

where $p_{m} = \frac{m\pi }{a}\;,\quad p_{n} = \frac{n\pi }{b}$

It is convenient to define following dimensionless quantities for the plate

$$ \begin{gathered} \bar{\sigma }_{ij} = \frac{{\sigma_{ij}^{ * } }}{Y}\;,\;\bar{P}_{o} = \frac{{P_{o} }}{Y}, \, \;\bar{Q}_{ij} = \frac{{Q_{ij} }}{Y}\;,\;\;Y = 1Gpa\;,\;\;\bar{U}_{i} = \frac{{U_{i} }}{h}\;,\;\;\bar{z} = \frac{z}{h}\;,\;\;\bar{p}_{m} = \;ap_{m} \;,\;\;\bar{p}_{n} = \;bp_{n} \;,\;\; \hfill \\ \bar{\omega } = \omega h\sqrt {\frac{\rho }{Y}} \hfill \\ \end{gathered} $$

(13)

Upon substitution of Eqs. (13) and (12) into Eq (9), following dimensionless state space equations can be derived

$$ \frac{d}{{d\bar{z}}}\bar{\delta } = \bar{G}\bar{\delta } $$

(14)

where $\bar{\delta } = \left\{ {\bar{\sigma }_{z} \;\;\bar{U}\;\;\bar{V}\;\;\bar{W}\;\;\bar{\tau }_{xz} \;\;\bar{\tau }_{yz} } \right\}^{T}$ and $\bar{G}$ is defined in Appendix.

Since the coefficient matrix $\bar{G}$ is not constant, it is difficult to solve Eq (14) directly. It is possible to solve such differential equations by using layer wise technique via dividing the FGM layer into N fictitious thin layers. Thus, the coefficient matrix $\bar{G}$ can be assumed constant within each layer. General solution to Eq (14) for k-th fictitious layer is

$$ \bar{\delta }_{k} = expm(\bar{G}^{k - 1} h_{k - 1} )\bar{\delta }_{k - 1} $$

(15)

By applying the continuity and equilibrium interface conditions, relation between surface traction at the top and bottom surface can written as the follow

$$ \bar{\delta }( + 0.5) = \bar{G}^{*} \bar{\delta }( - 0.5) $$

(16)

where $\bar{G}^{*} = \mathop \varPi \limits_{i = 1}^{N} e^{{\left( {\frac{1}{N}\bar{G}_{i} } \right)}}$, $z_{i} = 0.5 - \frac{2i - 1}{2N}$

Non-dimensional in-plane stresses can be derived from Eqs. (10), (12) and (13) as

$$ \bar{\sigma }_{x} = \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}\bar{\sigma }_{z} - \left( {\bar{Q}_{11} - \frac{{\bar{Q}_{13}^{2} }}{{\bar{Q}_{33} }}} \right)\frac{h}{a}\bar{p}_{m} \bar{U} - \left( {Q_{12} - \frac{{Q_{13} Q_{23} }}{{Q_{33} }}} \right)\frac{h}{b}\bar{p}_{n} \bar{V} $$

$$ \bar{\sigma }_{y} = \frac{{\bar{Q}_{23} }}{{Q_{33} }}\bar{\sigma }_{z} - \left( {\bar{Q}_{12} - \frac{{\bar{Q}_{13} \bar{Q}_{23} }}{{\bar{Q}_{33} }}} \right)\frac{h}{a}\bar{p}_{m} \bar{U} - \left( {\bar{Q}_{22} - \frac{{\bar{Q}_{23}^{2} }}{{\bar{Q}_{33} }}} \right)\frac{h}{b}\bar{p}_{n} \bar{V} $$

$$ \bar{\tau }_{xy} = \bar{Q}_{66} \left( {\frac{h}{a}\bar{p}_{m} \bar{V} + \frac{h}{b}\bar{p}_{n} \bar{U}} \right) $$

(17)

The top and bottom surfaces of plate in the state of free vibration are tractions free as

$$ \bar{\sigma }_{z} = \;\bar{\tau }_{xz} = \bar{\tau }_{yz} = 0\;,\quad at\;\;\bar{z} = - 0.5 \, , \, 0.5 $$

(18)

Applying Eq (18) to Eq (16), following eigenfrequency equation can be obtained

$$ \left| {\bar{G}_{ij}^{*} } \right| = 0,\quad (i = 1,5,6\,j = 2,3,4) $$

(19)

Solving Eq (19) yields the natural frequencies. By setting ω = 0 in Eq (12) and using the following surface boundary condition, it is possible to consider bending behavior of CNTRC plate

$$ \;\bar{\sigma }_{z} = \;\bar{p}_{mn} \;,\quad \bar{\tau }_{xz} = \bar{\tau }_{yz} = 0\; \, at\;\;\bar{z} = 0.5 $$

(20a)

$$ \;\bar{\sigma }_{z} = \bar{\tau }_{xz} = \bar{\tau }_{yz} = 0\; \, at\;\;\bar{z} = - 0.5 $$

(20b)

where $\;\;\bar{p}_{mn} \; = \frac{{16\bar{p}_{o} }}{{mn\pi^{2} }}$

Imposing surface traction at the top and bottom surface of the plate [Eq (20)–Eq (16)] along with ω = 0 yields

$$ \left[ {\bar{G}_{ij}^{*} } \right]\left\{ {\bar{\delta }_{j} ( - 0.5)} \right\} = \left\{ {\bar{p}_{mn} \;\;0\;\;\;0} \right\}\;,\quad (i = 1,5,6\quad j = 2,3,4) $$

(21)

Solving Eq (21) for $\left\{ {\bar{\delta }_{j} } \right\}$, yields displacements at the bottom surface. Using state vector $\bar{\delta }( - 0.5)$ and Eq (15), the state variables in three dimensions will be obtained. Finally, inserting the obtained state variables into the induced variable, Eq (17), the in-plane stresses can be determined.

4 Semi-analytical solution

It is impossible to obtain analytical solution for plats with non-simply supports boundary condition. A semi-analytical procedure with the aids of DQ technique was developed by Chen et al. [21]. In this method, the r-th order partial derivative of a continuous function f(x,y,z) with respect to x and y at a given point (x _i , y _j ) can be approximated as a linear sum of weighted function values at all of the discrete points in the domain of x and y, i.e.

$$ \left. {\frac{{\partial^{r} f(x,y,z)}}{{\partial x^{r} }}} \right|_{{(x_{i} ,y_{j} )}} = \sum\limits_{m = 1}^{{N_{x} }} {A_{im}^{r} \;f(} x_{m} ,y_{j} ,z)\quad for\;i = 1, \ldots ,N_{i} ,\quad j = 1, \ldots ,N_{j} ,\quad r = 1, \ldots ,N - 1 $$

(22a)

$$ \left. {\frac{{\partial^{r} f(x,y,z)}}{{\partial y^{r} }}} \right|_{{(x_{i} ,y_{j} )}} = \sum\limits_{n = 1}^{{N_{y} }} {B_{jn}^{r} \;f(} x_{i} ,y_{n} ,z)\quad for\;i = 1, \ldots ,N_{i} ,\quad j = 1, \ldots ,N_{j} ,\quad r = 1, \ldots ,N - 1 $$

(22b)

$$ \left. {\frac{{\partial^{r} f(x,y,z)}}{{\partial x^{r - t} \partial y^{t} }}} \right|_{{(x_{i} ,y_{j} )}} = \sum\limits_{n = 1}^{{N_{y} }} {B_{jn}^{t} } \sum\limits_{m = 1}^{{N_{x} }} {A_{im}^{r - t} \;f(} x_{m} ,y_{n} ,z)\quad for\;i = 1, \ldots ,N_{i} ,\quad i = 1, \ldots ,N_{j} ,\quad r = 1, \ldots ,N - 1 $$

(22c)

where N _x , N _y are the number of sampling points in x- and y- directions, respectively, and A ^r _im , B ^r _jn are the weight coefficients in x- and y- directions, respectively [22].

Applying Eqs. (22a)–(22c) and (13) to Eq (9), following state equations at an arbitrary sampling point are then obtained

$$ \frac{{\partial \bar{\sigma }_{{z_{ij} }} }}{{\partial \bar{z}}} = - \sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;\bar{\tau }_{{xz_{mj} }} - } \sum\limits_{m = 1}^{{N_{y} }} {\bar{B}_{jm}^{{}} \;\bar{\tau }_{{yz_{im} }} } - \bar{\omega }^{2} \bar{w}_{ij} $$

$$ \frac{{\partial \bar{u}_{ij} }}{{\partial \bar{z}}} = - \sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;\bar{w}_{mj} - \frac{1}{{\bar{Q}_{55} }}} \bar{\tau }_{{xz_{ij} }} $$

$$ \frac{{\partial \bar{v}_{ij} }}{{\partial \bar{z}}} = - \sum\limits_{m = 1}^{{N_{y} }} {\bar{B}_{jm}^{{}} \;\bar{w}_{im} - \frac{1}{{\bar{Q}_{44} }}} \bar{\tau }_{{yz_{ij} }} $$

$$ \frac{{\partial \bar{w}_{ij} }}{{\partial \bar{z}}} = \frac{{\bar{\sigma }_{{z_{ij} }} }}{{\bar{Q}_{33} }} - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;\bar{u}_{mj} - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}} \sum\limits_{m = 1}^{{N_{y} }} {\bar{B}_{jm}^{{}} \;} \bar{v}_{im} $$

$$ \begin{aligned} \frac{{\partial \bar{\tau }_{{xz_{ij} }} }}{{\partial \bar{z}}} & = - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \bar{\sigma }_{{z_{mj} }} } + \left( {\frac{{\bar{Q}_{13}^{2} }}{{\bar{Q}_{33} }} - \bar{Q}_{11} } \right)\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{2} \;\bar{u}_{mj} - \bar{Q}_{66} } \sum\limits_{m = 1}^{{N_{y} }} {\bar{B}_{jm}^{2} \;} \bar{u}_{im} \\ & \quad - \left( {\bar{Q}_{12} + \bar{Q}_{66} - \frac{{\bar{Q}_{13} \bar{Q}_{23} }}{{\bar{Q}_{33} }}} \right)\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;} \sum\limits_{s = 1}^{{N_{y} }} {\bar{B}_{js}^{{}} \;\bar{v}_{ms} } - \bar{\omega }^{2} \bar{u}_{ij} \\ \end{aligned} $$

$$ \begin{aligned} \frac{{\partial \bar{\tau }_{{yz_{ij} }} }}{{\partial \bar{z}}} & = - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}\sum\limits_{m = 1}^{{N_{y} }} {\bar{B}_{jm}^{{}} \bar{\sigma }_{{z_{im} }} } - \left( {\bar{Q}_{12} + \bar{Q}_{66} - \frac{{\bar{Q}_{13} \bar{Q}_{23} }}{{\bar{Q}_{33} }}} \right)\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;} \sum\limits_{s = 1}^{{N_{y} }} {\bar{B}_{js}^{{}} \;\bar{u}_{ms} } \\ & \quad + \left( {\frac{{\bar{Q}_{23}^{2} }}{{\bar{Q}_{33} }} - \bar{Q}_{22} } \right)\sum\limits_{m = 1}^{{N_{y} }} {\bar{B}_{im}^{2} \;\bar{v}_{im} - \bar{Q}_{66} } \sum\limits_{m = 1}^{{N_{y} }} {\bar{A}_{im}^{2} \;} \bar{v}_{mj} - \bar{\omega }^{2} \bar{v}_{ij} \\ \end{aligned} $$

(23)

Similarly the induced variables, Eq (10), after applying the DQM are;

$$ \bar{\sigma }_{{x_{ij} }} = \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}\bar{\sigma }_{{z_{ij} }} - \left( {\bar{Q}_{11} - \frac{{\bar{Q}_{13}^{2} }}{{\bar{Q}_{33} }}} \right)\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;\bar{u}_{mj} - \left( {\bar{Q}_{12} - \frac{{\bar{Q}_{13} \bar{Q}_{23} }}{{\bar{Q}_{33} }}} \right)} \sum\limits_{n = 1}^{{N_{y} }} {\bar{B}_{jn}^{{}} \;} \bar{v}_{in} $$

$$ \bar{\sigma }_{{y_{ij} }} = \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}\bar{\sigma }_{{z_{ij} }} - \left( {\bar{Q}_{12} - \frac{{\bar{Q}_{13} \bar{Q}_{23} }}{{\bar{Q}_{33} }}} \right)\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;\bar{u}_{mj} - \left( {\bar{Q}_{22} - \frac{{\bar{Q}_{23}^{2} }}{{\bar{Q}_{33} }}} \right)} \sum\limits_{n = 1}^{{N_{y} }} {\bar{B}_{jn}^{{}} \;} \bar{v}_{in} $$

$$ \bar{\tau }_{{xy_{ij} }} = \bar{Q}_{66} \left( {\sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im}^{{}} \;\bar{v}_{mj} + } \sum\limits_{n = 1}^{{N_{y} }} {\bar{B}_{jn}^{{}} \;} \bar{u}_{in} } \right) $$

(24)

By assembling of Eq (23) at all sampling points lead to the following global state equation in matrix form;

$$ \frac{d}{{d\bar{z}}}{\bar{\Delta }} = \bar{M}{\bar{\Delta }} $$

(25)

where

$$ {\bar{\Delta }} = \left\{ {\bar{\sigma }_{z} \;\;\bar{u}\;\;\bar{v}\;\;\bar{w}\;\;\bar{\tau }_{xz} \;\;\bar{\tau }_{yz} } \right\}^{T} \;,\quad \bar{\sigma }_{z} = \left\{ {\bar{\sigma }_{{z_{1} }} ,\bar{\sigma }_{{z_{2} }} ,\, \ldots \,,\,\bar{\sigma }_{{z_{N} }} } \right\}^{T} $$

(26)

And the other of sub-vectors in Eq (25) are defined in the same manner as Eq (26). The partitioned matrix $\bar{M}$ is described in Appendix.

Applying the boundary conditions at x = 0, a to Eq (25) the unique solution for the state variables,${\bar{\Delta }}$, will be derived. Relations of boundary conditions for Simply (S) support, Clamped (C) support, Free (F) from supported at the x = 0,a edges are assumed

$$ S\;:\; \, v = w = \sigma_{x} = 0 $$

$$ C\;: \, \;u = v = w = 0 $$

$$ F\;:\; \, \tau_{xz} = \tau_{yz} = \sigma_{x} = 0 $$

(27)

After applying the boundary conditions, Eq (25) becomes;

$$ \frac{d}{{d\bar{z}}}{\bar{\Delta }}_{b} = \bar{M}_{b} {\bar{\Delta }}_{b} $$

(28)

Where, the subscript, b, denotes that the state equation contains the boundary conditions and the matrix $\bar{M}_{b}$ according to each boundary condition type are given in Appendix. Applying the same procedure used in Eq (14) to Eq (28), stresses and displacements due to static loading as well as natural frequencies are obtained.

5 Results and discussion

For numerical illustration, three-dimensional static and free vibration analysis for UD-CNT and three type of FG-CNT with the following material properties for the CNT and matrix polymer is carried out [6]

$$ E_{11}^{CNT} = 5.6466\;Tpa\;,\;\;E_{22}^{CNT} = 7.08\;Tpa\;,\;\;G_{12}^{CNT} = 1.9445\;Tpa\;,\;\;\nu_{12}^{CNT} = 0.175\;\; $$

$$ \rho^{CNT} = 1.4\;g/cm^{3} \;\;,\quad E^{m} = 2.1\,Gpa\;\;,\quad \nu^{m} = 0.34\;\;,\quad \rho^{m} = 1.5\;g/cm^{3} \;,\quad \eta_{3} = 0.7\;\eta_{2} $$

$$ V_{CNT}^{*} = 0.11\quad :\quad \eta_{1} = 0.149\;\;,\quad \eta_{2} = 0.934 $$

$$ V_{CNT}^{*} = 0.14\quad :\quad \eta_{1} = 0.150\;\;,\quad \eta_{2} = 0.941 $$

$$ V_{CNT}^{*} = 0.17\quad :\quad \eta_{1} = 0.149\;\;,\quad \eta_{2} = 1.381 $$

In DQM procedure, following sampling points along the x- coordinate [22] are used:

$$ x_{i} = \frac{L}{2}\left[ {1 - \cos \left( {\frac{{\left( {i - 1} \right)\pi }}{{N_{x} - 1}}} \right)} \right]\quad \quad \quad i = 1,2,3, \ldots ,N_{x} $$

It is noted that sampling points along the y-coordinate are defined the same as x-direction. At first, we presente numerical results in Table 1 for CNTRC square plate to show the convergence of DQM. From the table it can be observed that, regardless of case of CNT distribution, at sampling point N _x  = N _y  = 11 numerical results converge to the analytical results. Further investigation is to show the validity of the present approach. For this purpose, numerical results for the square plate with various kind of CNT distributions as well as different kind of edges boundary conditions are presented in Table 2 and compared with the results obtained by Zhu et al. [19]. As the Table shows, the results of present approach for the thin plate are nearly the same as the results of Ref. [19] and for the thick plate some discrepancy can be observed which is due to the conventional two dimensional theory that has been used in Ref. [19]. To validate the frequency behaviour of CNTRC square plate, Non-dimensional frequency parameters are presented numerically in Tables 3 and 4. Table 3 shows analytical results for the first three dimensionless frequencies of thin and thick plates with different case of CNT distributions. From comparison good agreement can be observed especially for the thin plate. In addition, we present numerical results for the plate with clamped edges conditions as well as different case of CNT distributions in Table 4. As the table shows, increase the CNT volume fraction causes to increase the frequency parameter. Further conclusion is that in the case of FG − X _CNT distribution, fundamental frequencies are greater than that for the other case of CNT distributions. As expected, it is also seen that non-dimensional frequency for the plate with four edges clamped conditions is maximum where as it is minimum for the plate with four edges simply supported conditions. Effect of SCSC edges conditions on first three nondimensional frequencies of thin and thick CNTRC square plate with three CNT volume fraction is depicted in Table 5. According to the table, CNT volume fraction affects the frequency parameter at higher modes significantly. Further conclusion is that the frequency parameter, regardless of case of CNT distribution, for the plate with SCSC condition is greater than that for the plate with SSSS conditions and is smaller than that for the plate with CCCC conditions. For further discussion numerical results for CNTRC plate are obtained and plotted in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15. Figure 2 depicts the convergence of the analytical solution. According to the figure, by increasing the half wave number in longitudinal and width direction up to m = n = 21 exact solution can be achieved. Figures 3, 4, 5 and 6 shows the effect of different cases of CNT distribution in polymer matrix on the longitudinal normal stress and displacements distribution of CNTRC square plate. The symmetric distribution of CNT in the cases of UD, FG-X and FG-O cause the distribution of stress as well as displacements to be symmetry. Also from Figs. 4, 5 and 6 it is seen that displacement components at a point in the FG-X distribution is smaller than that the other cases of CNT distribution at the same point, therefore the numerical results for parametric study is for the case of FG-X CNT distribution. Influence of edges boundary conditions on through the thickness distribution of transverse displacement and longitudinal normal stress are presented in Figs. 7 and 8. According to figures, transverse displacement as well as longitudinal normal stress in the case of CCCC boundary condition has minimum value in comparison with the other edge conditions. Further conclusion is that the effect of CCCC edges boundary condition on the stress and displacements is more significant. Distribution of transverse and width displacements along the thickness for thin and thick CNTRC square plate is depicted in Figs. 9 and 10. Thickness to length ratio affects transverse displacement as well as latitudinal displacement significantly. In addition, it is seen that regardless of plate thickness, transverse displacement is independent of transverse coordinate whereas the width displacement varies linearly along the thickness direction. Effect of CNT volume fraction on through the thickness distribution of transverse and longitudinal displacements is presented in Figs. 11 and 12. Increases CNT volume fraction causes to increase transverse displacement (Fig. 11). From Fig. 12 it can be observed that increase the CNT volume fraction decreases the longitudinal displacement. Since the axial stiffness of CNT is greater than the radial stiffness, so when CNT increases the stiffness of the plate in the longitudinal direction increases and consequently the longitudinal displacement decreases. Besides, it is seen that the rate of decreasing the width displacement decreases with increasing the CNT volume fraction. Effect of aspect ratio, a/b, on fundamental frequency of CNTRC rectangular plate for three volume fraction of CNT is shown in Fig. 13. Fundamental frequency of the plate with aspect ratio a/b = 2.5 is more affected by CNT volume fraction in comparison with the other aspect ratio. Influence of edges boundary conditions on dimensionless fundamental frequency for thin and thick CNTRC square plate is presented in Fig. 14. As expected and it is observed from this figure, regardless of thickness to length ratio, fundamental frequency for the plate with CCCC boundary conditions has maximum value and it is minimum for the plate with SSSS boundary conditions. Moreover it can be concluded that the CNT affects the fundamental frequency in higher CNT volume fraction significantly. Figure 15 depicts the effect of thickness to length ratio on dimensionless fundamental frequency of CNTRC square plate with various CNT volume fractions. According to the figure, influence of CNT in thick plate is more significant and it is nearly negligible in thin plate. Also it can be concluded that the effect of CNT in higher CNT volume fraction is greater than that in lower volume fraction.

Table 1 Dimensionless longitudinal normal stress at top surface of CNTRC square plate with $x = y = \frac{a}{2}$, V ^* = 0.11, h/a = 0.02

Table 2 Non-dimensional central deflection in top surface of square plate with V ^* = 0.17, h/a = 0.02

Table 3 Effects of CNT volume fraction on the dimensionless natural frequency, $\bar{\omega }^{*} = \omega \,a^{2} /h\sqrt {\frac{{\rho^{m} }}{{E^{m} }}}$, of thin and thick plate with SSSS condition

Table 4 Effects of CNT volume fraction on the dimensionless natural frequency, $\bar{\omega }^{*} = \omega \,a^{2} /h\sqrt {\frac{{\rho^{m} }}{{E^{m} }}}$, of thin and thick plate with CCCC condition

Table 5 Effects of CNT volume fraction on the dimensionless natural frequency, $\bar{\omega }^{*} = \omega \,a^{2} /h\sqrt {\frac{{\rho^{m} }}{{E^{m} }}}$, of thin and thick plate with SCSC condition

Fig. 2

Convergence study for plate with simply supported condition, V ^* = 0.11, h/a = 0.02 and UD

Fig. 3

Effect of case of CNT distribution on the axial normal stress of plate with V ^* = 0.17, h/a = 0.02, CCCC

Fig. 4

Effect of case of CNT distribution on central deflection of plate with V ^* = 0.17, h/a = 0.02, CCCC

Fig. 5

Effect of case of CNT distribution on the longitudinal displacements of plate with V ^* = 0.17, h/a = 0.02, CCCC

Fig. 6

Effect of case of CNT distribution on the latitudinal displacements of plate with V ^* = 0.17, h/a = 0.02, CCCC

Fig. 7

Effect of edge conditions on the deflection of plate with V ^* = 0.17, h/a = 0.02, FG-X

Fig. 8

Effect of edge condition on the longitudinal stress of plate with V ^* = 0.17, h/a = 0.02, FG-X

Fig. 9

Effect of thickness to length ratio on the deflection of plate with V ^* = 0.17, FG-X, CCCC

Fig. 10

Effect of thickness to length ratio on the latitudinal displacements of plate with V ^* = 0.17, FG-X, CCCC

Fig. 11

Effect of CNT volume fractions on the deflection of plate with h/a = 0.02, FG-X, CCCC

Fig. 12

Effect of CNT volume fractions on the longitudinal displacements of plate with h/a = 0.02, FG-X, CCCC

Fig. 13

Effect of length to width ratio on central deflection of rectangular plate with various CNT volume fraction and FG-X, SSSS

Fig. 14

First natural frequency parameter ($\bar{\omega } = \omega h\sqrt {\frac{\rho }{Y}}$) of plate with FG-X

Fig. 15

Effect of length to width ratio on dimensionless fundamental frequency,$\bar{\omega } = \omega h\sqrt {\frac{\rho }{Y}}$, of plate with various CNT volume fraction and FG-X

6 Conclusions

We presented a three-dimensional static and vibration analysis of FG-CNTRC rectangular plate with four cases of CNT distribution. Material properties are assumed to vary through the thickness. Analytical solution is presented for the plate with simply supported edges by using Fourier series along the in-plane axis and state space method in thickness direction. Furthermore, a semi analytical solution for the plate with non-simply supported boundary conditions is carried out by using DQM along the longitudinal and width direction instead of Fourier series. Effectiveness of the method in predicting the exact behaviour of FG-CNTRC plate was checked by comparing its numerical results with the related published results in literature. From the study, it is concluded that

• Case of CNT distribution affects the bending behaviour of CNTRC plate significantly and in this investigation FG-X CNT distribution has minimum displacement and maximum fundamental frequency.

• The numerical results reveal that the variations of material properties along the thickness direction affect the response of FG-CNTRC plate.

• Absolute distribution of axial normal stress across the thickness of FG-CNTRC plate would be symmetric with respect to the mid plane when the CNT distribution is symmetric.

• Axial normal stresses and transverse displacement in the case of CCCC, at a point are always smaller in magnitude than those at the corresponding points in the other three cases of boundary condition.

• Increases the CNT volume fraction causes to decrease the transverse and longitudinal displacements and the rate of decreasing the transverse displacement decreases by increasing the CNT volume fraction.

• Non-dimensional natural frequencies strongly depend on the case of CNT distribution CNT volume fraction.

• Effect of CNT volume fraction in thick plate is more significant.

• Influence of CNT volume fraction in clamped edges is greater than that for the other edges conditions.

Appendix

$$ Q_{11} = \frac{{E_{11} }}{\Delta }\left( {1 - \nu_{23} \nu_{32} } \right)\;,\quad Q_{22} = \frac{{E_{22} }}{\Delta }\left( {1 - \nu_{31} \nu_{13} } \right)\;,\quad Q_{33} = \frac{{E_{33} }}{\Delta }\left( {1 - \nu_{21} \nu_{12} } \right)\;,\quad Q_{12} = \frac{{E_{11} }}{\Delta }\left( {\nu_{21} + \nu_{23} \nu_{31} } \right)\; $$

$$ Q_{13} = \frac{{E_{11} }}{\Delta }\left( {\nu_{31} + \nu_{21} \nu_{32} } \right),\quad Q_{23} = \frac{{E_{22} }}{\Delta }\left( {\nu_{32} + \nu_{12} \nu_{31} } \right),\quad Q_{44} = G_{23} \;,\quad Q_{55} = G_{13} \;,\quad Q_{66} = G_{12} \;,\quad $$

$$ \Delta = 1 - \nu_{12} \nu_{21} - \nu_{23} \nu_{32} - \nu_{31} \nu_{13} - 2\nu_{12} \nu_{32} \nu_{13} $$

$$ G = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & {\rho \frac{{\partial^{2} }}{{\partial t^{2} }}} & { - \frac{\partial }{\partial x}} & { - \frac{\partial }{\partial y}} \\ 0 & 0 & 0 & { - \frac{\partial }{\partial x}} & {a_{1} } & 0 \\ 0 & 0 & 0 & { - \frac{\partial }{\partial y}} & 0 & {a_{2} } \\ {a_{3} } & {a_{4} \frac{\partial }{\partial x}} & {a_{5} \frac{\partial }{\partial y}} & 0 & 0 & 0 \\ {a_{4} \frac{\partial }{\partial x}} & {a_{6} \frac{{\partial^{2} }}{{\partial y^{2} }} + a_{7} \frac{{\partial^{2} }}{{\partial x^{2} }} + \rho \frac{{\partial^{2} }}{{\partial t^{2} }}} & {a_{9} \frac{{\partial^{2} }}{\partial x\partial y}} & 0 & 0 & 0 \\ {a_{5} \frac{\partial }{\partial y}} & {a_{9} \frac{{\partial^{2} }}{\partial x\partial y}} & {a_{6} \frac{{\partial^{2} }}{{\partial x^{2} }} + a_{9} \frac{{\partial^{2} }}{{\partial y^{2} }} + \rho \frac{{\partial^{2} }}{{\partial t^{2} }}} & 0 & 0 & 0 \\ \end{array} } \right] $$

$$ \begin{gathered} a_{1} = \frac{1}{{Q_{55} }}\;,\;\;a_{2} = \frac{1}{{Q_{44} }}\;,\;\;a_{3} = \frac{1}{{Q_{33} }}\;,\;\;a_{4} = - \frac{{Q_{13} }}{{Q_{33} }}\;,\;\;a_{5} = - \frac{{Q_{23} }}{{Q_{33} }}\;,\;\;a_{6} = - Q_{66} \; \hfill \\ \;a_{7} = \frac{{Q_{13}^{2} }}{{Q_{33} }} - \;Q_{11} ,\;\;\;\;a_{8} = \frac{{Q_{13} Q_{23} }}{{Q_{33} }} - \;Q_{12} - \;Q_{66} ,\;\;\;a_{9} = \frac{{Q_{23}^{2} }}{{Q_{33} }} - \;Q_{22} \hfill \\ \end{gathered} $$

$$ \bar{G} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - \bar{\omega }^{2} } & {\left( \frac{h}{a} \right)\bar{p}_{m} } & {\left( \frac{h}{b} \right)\bar{p}_{n} } \\ 0 & 0 & 0 & { - \left( \frac{h}{a} \right)\bar{p}_{m} } & {\bar{a}_{1} } & 0 \\ 0 & 0 & 0 & { - \left( \frac{h}{b} \right)\bar{p}_{n} } & 0 & {\bar{a}_{2} } \\ {\bar{a}_{3} } & {\bar{a}_{4} } & {\bar{a}_{5} } & 0 & 0 & 0 \\ { - \bar{a}_{4} } & {\bar{a}_{6} - \bar{\omega }^{2} } & {\bar{a}_{7} } & 0 & 0 & 0 \\ { - \bar{a}_{7} } & { - \bar{a}_{7} } & {\bar{a}_{8} - \bar{\omega }^{2} } & 0 & 0 & 0 \\ \end{array} } \right] $$

$$ \bar{a}_{1} = \frac{1}{{\bar{Q}_{55} }}\;,\;\;\bar{a}_{2} = \frac{1}{{\bar{Q}_{44} }}\;,\;\;\bar{a}_{3} = \frac{1}{{\bar{Q}_{33} }}\;,\;\;\bar{a}_{4} = \bar{p}_{m} \left( \frac{h}{a} \right)\frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}\;,\;\;\bar{a}_{5} = \bar{p}_{n} \left( \frac{h}{a} \right)\frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}\; $$

$$ \bar{a}_{6} = \left( \frac{h}{a} \right)^{2} \bar{p}_{m}^{2} \left( {\bar{Q}_{11} - \frac{{\bar{Q}_{13}^{2} }}{{\bar{Q}_{33} }}} \right)\; + \bar{Q}_{66} \left( \frac{h}{a} \right)^{2} \bar{p}_{n}^{2} \;,\;\;a_{7} = \frac{{h^{2} }}{ab}\bar{p}_{m} \bar{p}_{n} \left( {\bar{Q}_{12} + \;\bar{Q}_{66} - \frac{{\bar{Q}_{13} \bar{Q}_{23} }}{{\bar{Q}_{33} }}} \right),\;\;\; $$

$$ \;a_{8} = \bar{Q}_{66} \left( \frac{h}{a} \right)^{2} \bar{p}_{m}^{2} - \left( {\frac{{\bar{Q}_{23}^{2} }}{{\bar{Q}_{33} }} - \bar{Q}_{22} } \right)\left( \frac{h}{b} \right)^{2} \bar{p}_{n}^{2} $$

$$ \bar{M} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - \bar{\omega }^{2} I_{{N_{x} \times N_{y} }} } & {C_{ij} } & {D_{ij} } \\ 0 & 0 & 0 & {C_{ij} } & { - \frac{{I_{{N_{x} \times N_{y} }} }}{{\bar{Q}_{55} }}} & 0 \\ 0 & 0 & 0 & {D_{ij} } & 0 & { - \frac{{I_{{N_{x} \times N_{y} }} }}{{\bar{Q}_{44} }}} \\ {\frac{{I_{{N_{x} \times N_{y} }} }}{{\bar{Q}_{33} }}} & { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{ij} } & { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{ij} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{ij} } & {\bar{Q}_{52} C_{ij}^{2} - \bar{Q}_{66} D_{ij}^{2} - \bar{\omega }^{2} I_{{N_{x} \times N_{y} }} } & {\bar{Q}_{53} C_{ij} D_{ij} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{ij} } & {\bar{Q}_{53} C_{ij} D_{ij} } & {\bar{Q}_{63} D_{ij}^{2} - \bar{Q}_{66} C_{ij}^{2} - \bar{\omega }^{2} I_{{N_{x} \times N_{y} }} } & 0 & 0 & 0 \\ \end{array} } \right] $$

$$ \;\bar{Q}_{52} = \frac{{\bar{Q}_{13}^{2} }}{{\bar{Q}_{33} }} - \;\bar{Q}_{11} \;,\;\;\;\;\bar{Q}_{53} = - \left( {\bar{Q}_{12} + \bar{Q}_{66} - \frac{{\bar{Q}_{13} \,\bar{Q}_{23} }}{{\bar{Q}_{33} }}} \right)\;\;,\quad \bar{Q}_{63} = \frac{{\bar{Q}_{23}^{2} }}{{\bar{Q}_{33} }} - \;\bar{Q}_{22} $$

C _ij and D _ij are coefficients Matrix in The series respectively $\left( { - \sum\limits_{m = 1}^{{N_{x} }} {\bar{A}_{im} \,\bar{\tau }_{{xz_{mj} }} } } \right)$ and $\left( { - \sum\limits_{m = 1}^{{N_{y} }} {\bar{B}_{jm} \,\bar{\tau }_{{yz_{im} }} } } \right)$

SSSS:

$$ \bar{M}_{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - \bar{\omega }^{2} I_{1} } & {C_{1} } & {D_{1} } \\ 0 & 0 & 0 & {C_{2} } & { - \frac{{I_{2} }}{{\bar{Q}_{55} }}} & 0 \\ 0 & 0 & 0 & {D_{3} } & 0 & { - \frac{{I_{3} }}{{\bar{Q}_{44} }}} \\ {\frac{{I_{1} }}{{\bar{Q}_{33} }}} & { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{1} } & { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{1} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{2} } & {\bar{Q}_{52} C_{2}^{2} - \bar{Q}_{66} D_{2}^{2} - \bar{\omega }^{2} I_{2} } & {\bar{Q}_{53} C_{2} D_{2} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{3} } & {\bar{Q}_{53} C_{3} D_{3} } & {\bar{Q}_{66} C_{3}^{2} - \bar{Q}_{63} D_{3}^{2} - \bar{\omega }^{2} I_{3} } & 0 & 0 & 0 \\ \end{array} } \right] $$

$$ C_{1} = C_{ij} \left( {i = 2, \ldots ,N_{x} - 1\;;\;j = 2, \ldots ,N_{y} - 1} \right) $$

$$ D_{1} = D_{ij} \left( {i = 2, \ldots ,N_{x} - 1\;;\;j = 2, \ldots ,N_{y} - 1} \right) $$

$$ I_{1} = I_{ij} \left( {i = 2, \ldots ,N_{x} - 1\;;\;j = 2, \ldots ,N_{y} - 1} \right) $$

$$ C_{2} = C_{ij} \left( {i = 1, \ldots ,N_{x} \;;\;j = 2, \ldots ,N_{y} - 1} \right) $$

$$ D_{2} = D_{ij} \left( {i = 1, \ldots ,N_{x} \;;\;j = 2, \ldots ,N_{y} - 1} \right) $$

$$ I_{2} = I_{ij} \left( {i = 1, \ldots ,N_{x} \;;\;j = 2, \ldots ,N_{y} - 1} \right) $$

$$ C_{3} = C_{ij} \left( {i = 2, \ldots ,N_{x} - 1\;;\;j = 1, \ldots ,N_{y} } \right) $$

$$ D_{3} = D_{ij} \left( {i = 2, \ldots ,N_{x} - 1\;;\;j = 1, \ldots ,N_{y} } \right) $$

$$ I_{3} = I_{ij} \left( {i = 2, \ldots ,N_{x} - 1\;;\;j = 1, \ldots ,N_{y} } \right) $$

CCCC:

$$ \bar{M}_{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - \bar{\omega }^{2} I_{1} } & {C_{1} } & {D_{1} } \\ 0 & 0 & 0 & {C_{1} } & { - \frac{{I_{1} }}{{\bar{Q}_{55} }}} & 0 \\ 0 & 0 & 0 & {D_{1} } & 0 & { - \frac{{I_{1} }}{{\bar{Q}_{44} }}} \\ {\frac{{I_{1} }}{{\bar{Q}_{33} }}} & { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{1} } & { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{1} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{1} } & {\bar{Q}_{52} C_{1}^{2} - \bar{Q}_{66} D_{1}^{2} - \bar{\omega }^{2} I_{1} } & {\bar{Q}_{53} C_{1} D_{1} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{1} } & {\bar{Q}_{53} C_{1} D_{1} } & {\bar{Q}_{66} C_{1}^{2} - \bar{Q}_{63} D_{1}^{2} - \bar{\omega }^{2} I_{1} } & 0 & 0 & 0 \\ \end{array} } \right] $$

SCSC:

$$ \bar{M}_{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - \bar{\omega }^{2} I_{1} } & {C_{1} } & {D_{1} } \\ 0 & 0 & 0 & {C_{2} } & { - \frac{{I_{2} }}{{\bar{Q}_{55} }}} & 0 \\ 0 & 0 & 0 & {D_{1} } & 0 & { - \frac{{I_{1} }}{{\bar{Q}_{44} }}} \\ {\frac{{I_{1} }}{{\bar{Q}_{33} }}} & { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{1} } & { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{1} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{2} } & {\bar{Q}_{52} C_{2}^{2} - \bar{Q}_{66} D_{2}^{2} - \bar{\omega }^{2} I_{2} } & {\bar{Q}_{53} C_{2} D_{2} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{1} } & {\bar{Q}_{53} C_{1} D_{1} } & {\bar{Q}_{66} C_{1}^{2} - \bar{Q}_{63} D_{1}^{2} - \bar{\omega }^{2} I_{1} } & 0 & 0 & 0 \\ \end{array} } \right] $$

SFSF:

$$ \bar{M}_{b} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - \bar{\omega }^{2} I_{3} } & {C_{3} } & {D_{3} } \\ 0 & 0 & 0 & {C_{ij} } & { - \frac{I}{{\bar{Q}_{55} }}} & 0 \\ 0 & 0 & 0 & {D_{1} } & 0 & { - \frac{{I_{1} }}{{\bar{Q}_{44} }}} \\ {\frac{{I_{3} }}{{\bar{Q}_{33} }}} & { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{3} } & { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{3} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{13} }}{{\bar{Q}_{33} }}C_{ij} } & {\bar{Q}_{52} C_{ij}^{2} - \bar{Q}_{66} D_{ij}^{2} - \bar{\omega }^{2} I} & {\bar{Q}_{53} C_{2} D_{2} } & 0 & 0 & 0 \\ { - \frac{{\bar{Q}_{23} }}{{\bar{Q}_{33} }}D_{1} } & {\bar{Q}_{53} C_{1} D_{1} } & {\bar{Q}_{66} C_{1}^{2} - \bar{Q}_{63} D_{1}^{2} - \bar{\omega }^{2} I_{1} } & 0 & 0 & 0 \\ \end{array} } \right] $$