Content-Dependent Nonlinear Vibration of Composite Plates Reinforced with Carbon Nanotubes

Abstract

Purpose

In this paper, the nonlinear vibration behavior of functionally graded carbon nanotube reinforced composite (FG-CNTRC) plates is investigated by meshless method.

Methods

The efficiency parameters, which clearly affect the mechanical properties of the composite materials, are characterized by polynomial expressions for different CNT contents, and applied as the inputs in the vibration analysis of plate structure. Four distributions of CNTs along the thickness of composite plate are considered, namely, the uniform distribution (UD), FG-O, FG-X and FG-V. Based on the classical plate theory and von Karman strain-displacement relation, the governing equations of motion are derived by the virtual displacement principle. Based on the reproducing kernel particle method (RKPM), the discrete governing equations for the vibration of the FG-CNTRC plates are derived. The linearized updated mode (LUM) method is adopted to solve the iteration process of governing equations.

Results

Numerical results are employed to investigate the effects of boundary condition, aspect ratio, volume fraction and arrangement of CNT on the nonlinear vibration characteristics of composite plates.

Introduction

Composite with nano-reinforcement is widely used in engineering applications such as aerospace, marine, automotive owing to the high strength and stiffness. As an ideal reinforcement for composite structures, carbon nanotubes (CNTs) demonstrate the excellent mechanical, electrical and thermal properties [1,2,3,4]. Scientists and engineers have raised huge interest to promote the development of CNT-based composites in fundamental research and application [5,6,7]. Functionally graded materials (FGMs) were proposed by Bever and Duwez [8], in which the volume fraction of reinforcement was changed by layers along the thickness direction of composite structures, and the resulting material properties were changed smoothly and effectively [9, 10]. By introducing the concept of the FGMs into the CNT-based composites, Shen [11] proposed functionally graded carbon nanotube reinforced composite (FG-CNTRC), and the further study about nonlinear bending behavior and large amplitude vibration demonstrated the effect of CNT distribution on the frequency and deflection of FG-CNTRC plates [12].

Composite materials can be custom tailored to meet the specific requirements of particular structures. In the process of design, it is necessary to analyze and predict the mechanical property with scale effect taken into account [13]. Wang et al. [14] investigated the thermal vibration and buckling of FG-CNTRC quadrilateral plates, and presented the effects of CNT volume fraction and distribution on the natural frequency and critical buckling load. Chiker et al. [15] studied the influence of CNT distribution on the vibrational behavior of nanocomposite plates, and the results indicated that compared with the FG-based plates with uniform CNT distribution, the natural frequencies of FG-X and FG-O CNTRC plates were increased and decreased, respectively. Tang and Dai [16] established the mechanical model of CNTRC plates with different CNT distributions to discuss the effects of geometrical size, volume fraction and damping coefficient on the nonlinear vibration behaviors.

The effective material parameters of composites are of great significance to study the mechanical behavior of structures, which are generally evaluated by Halpin-Tsai micromechanics model or the rule of mixtures. Nevertheless, the difference between the homogenization approach and molecular dynamics (MD) simulation could not be neglected due to the nano-scale effect. Shen and Zhang [17] incorporated the CNT efficiency parameters under a specific CNT volume fraction by matching Young’s moduli of CNTRC via the rule of mixtures with the MD results obtained by Han and Elliott [18]. It is noticed that the value of CNT efficiency parameter may be variable according to different CNT volume fractions. Wang et al. [19] derived the polynomial expression of efficiency parameters for composites with different CNT volume fractions, and extended to the vibration analysis of composite plates. Based on that, the adjacent macro- and micro-scale of material properties are connected, and the quantitative transfer across scales are achieved.

A considerable number of experimental and numerical methods have been developed rapidly and applied successfully to investigate the mechanical behaviors of CNTRC plates. Mehar et al. [20, 21] carried out three-point bending test and impact hammer test to analyze the bending and vibration behaviors of CNTRC plate, respectively. Fantuzzi et al. [22] performed the free vibration of arbitrarily shaped FG-CNTRC plates by generalized differential quadrature (GDQ) method. Gupta and Talha [23] discussed the effects of geometrical parameter and boundary condition on the vibration response of FG plates with finite element method (FEM). Mesh distortion problem is usually encountered when dealing with large deformations, and lead to reduced accuracy and expensive computational effort because of the additional error during remeshing procedure [24, 25]. Meshless method was proposed to eliminate the above-mentioned problem, which has been widely used in the vibration analysis of composite plates [26,27,28,29,30]. Esfahani et al. [31] incorporated the reproducing kernel particle method (RKPM) into finite strip method (FSM) to study the free vibration of rectangular FG plates. Shukla et al. [32] used the radial basis function (RBF) to analyze the free vibration of angular laminates. Wang et al. [33] adopted the solution of the RKPM to study the nonlinear vibration of composite rectangular plates. Kazemi et al. [34] carried out the nonlinear dynamic analysis of FG-CNTRC cylinders by the meshless local Petrov Galerkin (MLPG) method.

The present work is focused on the nonlinear free vibration of FG-CNTRC plates by meshless method. The effective material parameters including Young’s and shear moduli are derived by the extended rule of mixtures. Based on the classical plate theory and nonlinear strain-displacement relation, the governing equations of motion are derived by the virtual displacement principle. The numerical results demonstrate the effects of boundary condition, aspect ratio, volume fraction and the distribution of CNTs on the nonlinear vibration characteristics of FG-CNTRC plates.

Formulations for FG-CNTRC Plates

According to the classical plate theory, the displacements of FG-CNTRC plates along the x, y and z directions are defined as

$$u(x,y,z,t) = u_{0} (x,y,t) - zw_{0,x} (x,y,t),$$

(1a)

$$v(x,y,z,t) = v_{0} (x,y,t) - zw_{0,y} (x,y,t),$$

(1b)

$$w(x,y,z,t) = w_{0} (x,y,t),$$

(1c)

where u, v, and w are the displacements of an arbitrary point along x, y, and z directions, respectively, and u₀, v₀, and w₀ are the mid-plane displacements in the FG-CNTRC plate. The strain-displacement relation is defined as

$$\varepsilon_{x}^{{0}} = u_{,x} + \frac{1}{2}\left( {w_{,x} } \right)^{2} ,$$

(2a)

$$\varepsilon_{y}^{{0}} = v_{,y} + \frac{1}{2}\left( {w_{,y} } \right)^{2} ,$$

(2b)

$$\varepsilon_{xy}^{0} = u_{,y} + v_{,x} + w_{,x} w_{,y} .$$

(2c)

$$\kappa_{x} = - w_{,xx} ,$$

(3a)

$$\kappa_{y} = - w_{,yy} ,$$

(3b)

$$\kappa_{z} = - 2w_{,xy} .$$

(3c)

Therefore, the in-plane and shear strains are expressed as

$${\varvec{\varepsilon}} = \left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{y}^{0} } \\ {\varepsilon_{xy}^{0} } \\ \end{array} } \right] + z\left[ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{z} } \\ \end{array} } \right] = {\varvec{\varepsilon}}^{{0}} + z{\varvec{\kappa}},$$

(4)

where ɛ⁰ is the mid-plane strain, and κ is the curvature. The constitutive relation of CNTRC plates is expressed as

$${\varvec{\sigma}} = \left[ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{y} } \\ {\sigma_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Q_{{{11}}} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\varepsilon_{xy} } \\ \end{array} } \right]{ = }\varvec{Q\varepsilon },$$

(5)

where Q_ij are given as

$$Q_{11} = \frac{{E_{11} }}{{1 - \nu_{12} \nu_{21} }},Q_{22} = \frac{{E_{22} }}{{1 - \nu_{12} \nu_{21} }},Q_{12} = \frac{{\nu_{21} E_{22} }}{{1 - \nu_{12} \nu_{21} }} = \frac{{\nu_{21} E_{11} }}{{1 - \nu_{12} \nu_{21} }},Q_{66} = G_{12} ,$$

(6)

and E₁₁, E₂₂, and G₁₂ are the effective longitudinal, transverse and shear moduli, respectively. The moduli are determined by

$$E_{11} = \eta_{1} V_{{{\text{CNT}}}} E_{{{\text{CNT}}}}^{11} + V_{{\text{m}}} E_{{\text{m}}} ,$$

(7a)

$$\frac{{\eta_{2} }}{{E_{22} }} = \frac{{V_{{{\text{CNT}}}} }}{{E_{{{\text{CNT}}}}^{{{22}}} }} + \frac{{V_{{\text{m}}} }}{{E_{{\text{m}}} }},$$

(7b)

$$\frac{{\eta_{3} }}{{G_{12} }} = \frac{{V_{{{\text{CNT}}}} }}{{G_{{{\text{CNT}}}}^{{{12}}} }} + \frac{{V_{{\text{m}}} }}{{G_{{\text{m}}} }},$$

(7c)

where $E_{{{\text{CNT}}}}^{11}$, $E_{{{\text{CNT}}}}^{{{22}}}$ and $G_{{{\text{CNT}}}}^{{{12}}}$ indicate Young’s moduli of CNT along the longitudinal and transverse directions and shear modulus, $\eta_{1}$, $\eta_{2}$ and $\eta_{3}$ are the corresponding efficiency parameters, E_m and G_m represent Young’s and shear moduli of the matrix.

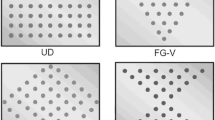
The FG-CNTRC plates with four distributions of CNT are shown in Fig. 1, and the dimensions are length a, width b and thickness h. The effective volume fractions of FG-CNTRC plates are expressed as

$$V_{{{\text{CNT}}}}^{*} = V_{{{\text{CNT}}}} {\text{, UD,}}$$

(8a)

$$V_{{{\text{CNT}}}}^{*} \left( z \right) = \left( {1 + \frac{2z}{h}} \right)V_{{{\text{CNT}}}} {\text{, FG - V,}}$$

(8b)

$$V_{{{\text{CNT}}}}^{*} \left( z \right) = 2\left( {1 - \frac{2\left| z \right|}{h}} \right)V_{{{\text{CNT}}}} {\text{, FG - O,}}$$

(8c)

$$V_{{{\text{CNT}}}}^{*} \left( z \right) = \left( {\frac{4\left| z \right|}{h}} \right)V_{{{\text{CNT}}}} {\text{, FG - X,}}$$

(8d)

Fig. 1

Configurations of carbon nanotube reinforced composite plates including a UD; b FG-O; c FG-X; d FG-V

where $V_{{{\text{CNT}}}}^{*}$ is the corresponding CNT volume fraction of each layer, $V_{{{\text{CNT}}}}$ is the total CNT volume fraction of composite plate. The volume fractions of composite components are denoted as

$$V_{{{\text{CNT}}}} + V_{{\text{m}}} = 1,$$

(9)

where $V_{{\text{m}}}$ is the volume fraction of matrix. The material parameters including Poisson’s ratio and density are determined by volume fractions as

$$\nu_{12} = V_{{{\text{CNT}}}} \nu_{{{\text{CNT}}}}^{{{12}}} + V_{{\text{m}}} \nu_{{\text{m}}} ,$$

(10)

$$\rho = V_{{{\text{CNT}}}} \rho_{{{\text{CNT}}}} + V_{{\text{m}}} \rho_{{\text{m}}} ,$$

(11)

where $\rho_{{\text{m}}}$ and $\rho_{{{\text{CNT}}}}$ are the densities of matrix and CNT, respectively. The in-plane and transverse shear force resultants are defined as

$$\left( {{\varvec{N}},{\varvec{M}}} \right) = \int_{{z_{k - 1} }}^{{z_{k} }} {\left( {1,z} \right){\varvec{\sigma}}} {\text{d}}z{.}$$

(12)

By substituting Eq. (5) into Eq. (12), the stress and moment resultants are obtained as follows

$${\varvec{N}} = \varvec{A\varepsilon }^{0} + \varvec{B\kappa },$$

(13)

$${\varvec{M}} = \varvec{B\varepsilon }^{0} + \varvec{D\kappa }.$$

(14)

where A, B, and D are the in-plane, coupled bending-stretching, and bending stiffness matrices, respectively, which are given by

$$\left( {{\varvec{A}}, {\varvec{B}}, {\varvec{D}}} \right) = \int_{{z_{k - 1} }}^{{z_{k} }} {\left( {1,z,z^{2} } \right){\varvec{Q}}{\text{d}}z} .$$

(15)

According to the principle of virtual work

$$\delta W_{{{\text{in}}}} + \delta W_{{{\text{ex}}}} = 0,$$

(16)

$$\delta W_{{{\text{ex}}}} = \int_{\Omega } {\rho h\left( {\delta u_{0} \ddot{u} + \delta v_{0} \ddot{v} + \delta w_{0} \ddot{w}} \right){\text{d}}\Omega } ,$$

(17)

$$\delta W_{{{\text{in}}}} = \int_{\Omega } {\left( {\delta {\varvec{N}}^{\text{T}} {\varvec{\varepsilon}}^{0} + \delta {\varvec{M}}^{\text{T}} {\varvec{\kappa}}} \right)} {\text{d}}\Omega ,$$

(18)

where $\delta W_{{{\text{in}}}}$ and $\delta W_{{{\text{ex}}}}$ are the work done by the inertial force and the elastic restoring force, respectively.

After that, the motion equation of composite plate is derived by setting the sum of virtual works as zero. Based on the von Karman strain–displacement relation and the principle of virtual work, we get

$$\int_{\Omega } {\rho h\left( {\delta u_{0} \ddot{u} + \delta v_{0} \ddot{v} + \delta w_{0} \ddot{w}} \right){\text{d}}\Omega } + \int_{\Omega } {\left( {\delta {\varvec{N}}^{\text{T}} {\varvec{\varepsilon}}^{0} + \delta {\varvec{M}}^{\text{T}} {\varvec{\kappa}}} \right)} {\text{d}}\Omega = 0.$$

(19)

Solution Procedure

By introducing a correction function in the reproduction formula of the smooth particle hydrodynamics, RKPM is proposed to modify the kernel function and enhance the accuracy [35]. The whole domain $\Omega$ is assumed to be discretized by the particles (x₁, x₂, …, x_N), and the approximation of displacement is expressed as

$$\left[ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ \end{array} } \right] = \sum\limits_{{{\text{I = }}1}}^{\text{N}} {\psi_{{\text{I}}} \left( {\varvec{x}} \right)\left[ {\begin{array}{*{20}c} {{\varvec{d}}_{{{\text{pI}}}} } \\ {{\varvec{d}}_{{{\text{wI}}}} } \\ \end{array} } \right]} ,$$

(20)

where $\psi_{{\text{I}}} \left( {\varvec{x}} \right)$ is the shape function associated with node x_I, N denotes the number of nodes, and the in-plane and transverse displacements are expressed as ${\varvec{d}}_{\text{pI}} = [u_{{0{\text{I}}}} \ v_{{0{\text{I}}}} ]^{\text{T}}$, and ${\varvec{d}}_{{{\text{wI}}}} = [w_{{0{\text{I}}}} ]$, respectively. The shape function is written as

$$\psi_{{\text{I}}} \left( {\varvec{x}} \right){ = }C({\varvec{x}};{\varvec{x}} - {\varvec{x}}_{{\text{I}}} )\Phi ({\varvec{x}} - {\varvec{x}}_{{\text{I}}} ),$$

(21)

where $\Phi ({\varvec{x}} - {\varvec{x}}_{{\text{I}}} )$ denotes the kernel function, and the coefficient function $C({\varvec{x}};{\varvec{x}} - {\varvec{x}}_{{\text{I}}} )$ is expressed as

$$C({\varvec{x}};{\varvec{x}} - {\varvec{x}}_{{\text{I}}} ){ = }{\varvec{H}}^{\text{T}} ({\varvec{x}} - {\varvec{x}}_{{\text{I}}} ){\varvec{K}}({\varvec{x}}),$$

(22)

$${\varvec{H}}^{\text{T}} ({\varvec{x}} - {\varvec{x}}_{{\text{I}}} ){ = }\left[ {1,x - x_{{\text{I}}} ,y - y_{{\text{I}}} ,\left( {x - x_{{\text{I}}} } \right)\left( {y - y_{{\text{I}}} } \right),\left( {x - x_{{\text{I}}} } \right)^{2} ,\left( {y - y_{{\text{I}}} } \right)^{2} } \right],$$

(23)

$${\varvec{K}}\left( {\varvec{x}} \right) = \left[ {k_{0} \left( {x,y} \right),k_{1} \left( {x,y} \right),k_{{2}} \left( {x,y} \right),k_{3} \left( {x,y} \right),k_{4} \left( {x,y} \right),k_{5} \left( {x,y} \right)} \right]^{\text{T}} ,$$

(24)

where ${\varvec{H}}^{\text{T}} ({\varvec{x}} - {\varvec{x}}_{{\text{I}}} )$ and ${\varvec{K}}\left( {\varvec{x}} \right)$ denote the quadratic basis and undetermined coefficient vectors, respectively. Then, the shape function is expressed as

$$\psi ({\varvec{x}};{\varvec{x}} - {\varvec{x}}_{{\text{I}}} ){ = }{\varvec{K}}^{\text{T}} \left( {\varvec{x}} \right){\varvec{H}}({\varvec{x}} - {\varvec{x}}_{{\text{I}}} )\Phi ({\varvec{x}} - {\varvec{x}}_{{\text{I}}} ).$$

(25)

When the shape function satisfies the reproduction conditions

$$\sum\limits_{{\text{I = 1}}}^{{\text{N}}} {\psi_{{\text{I}}} \left( {\varvec{x}} \right)\left( {{\varvec{x}} - {\varvec{x}}_{{\text{I}}} } \right)^{i} } = \delta_{i0} ,i = 0,1,2,3, \ldots ,n,$$

(26)

and

$${\varvec{K}}\left( {\varvec{x}} \right) = {\varvec{M}}^{ - 1} \left( {\varvec{x}} \right){\varvec{H}}\left( {\mathbf{0}} \right),$$

(27)

where

$${\varvec{M}}\left( {\varvec{x}} \right) = \sum\limits_{\text{I} = 1}^{\text{N}} {{\varvec{H}}\left( {{\varvec{x}} - {\varvec{x}}_{{\text{I}}} } \right)} {\varvec{H}}^{\text{T}} \left( {{\varvec{x}} - {\varvec{x}}_{{\text{I}}} } \right)\Phi \left( {{\varvec{x}} - {\varvec{x}}_{{\text{I}}} } \right),$$

(28)

$${\varvec{H}}\left( {\mathbf{0}} \right) = \left[ {1,0,0,0, \cdot \cdot \cdot ,0} \right]^{\text{T}} ,$$

(29)

the shape function is expressed as

$$\psi_{\text{I}} \left( {\varvec{x}} \right) = {\varvec{H}}^{\text{T}} \left( {\mathbf{0}} \right){\varvec{M}}^{ - 1} \left( {\varvec{x}} \right){\varvec{H}}\left( {{\varvec{x}} - {\varvec{x}}_{\text{I}} } \right)\Phi \left( {{\varvec{x}} - {\varvec{x}}_{\text{I}} } \right).$$

(30)

In the application of meshless method, the commonly used weight functions are cubic spline weight function, quartic spline weight function, exponential weight function, Gaussian weight function, etc. The choice of weight function depends on the problem, and the cubic spline function is generally adopted for the mechanical behavior of composite plates [13, 28,29,30, 33], which is given by

$$\Phi \left( r \right) = \left\{ {\begin{array}{*{20}c} {\frac{2}{3} - 4r^{2} + 4r^{3} {,}} & {{0} \le r < \frac{1}{2}} \\ {\frac{4}{3} - 4r + 4r^{2} - \frac{4}{3}r^{3} {,}} & {\frac{1}{2} \le r \le 1} \\ {0,} & {r > 1} \\ \end{array} } \right.$$

(31)

where $r\varvec{ = }{{\left\| {{\varvec{x}} - {\varvec{x}}_{\text{I}} } \right\|} \mathord{\left/ {\vphantom {{\left\| {{\varvec{x}} - {\varvec{x}}_{\text{I}} } \right\|} {a_{{\text{I}}} }}} \right. \kern-\nulldelimiterspace} {a_{{\text{I}}} }}$, and $a_{{\text{I}}}$ represents the radii of influence domain corresponding to the particle x_I, which should be appropriate to involve sufficient particles to ensure the invertible matrix and avoid the ill-conditioned system. Therefore, $a_{{\text{I}}}$ is defined as d_maxc_I, in which d_max denotes the scaling parameter ranging from 2 to 4, and c_I denotes the longest distance between the particle x_I and neighbor points.

By substituting Eq. (20) into Eq. (19), the matrix form of discretized equations of composite plate is

$$\left[ {\begin{array}{*{20}c} {{\varvec{M}}_{\text{p}} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{M}}_{\text{w}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varvec{\ddot{d}}_{\text{p}} } \\ {\varvec{\ddot{d}}_{\text{w}} } \\ \end{array} } \right] + \left( {\left[ {\begin{array}{*{20}c} {{\varvec{K}}_{\text{p}} } & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{\text{w}} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {{\varvec{K}}_{2} } \\ {\mathbf{0}} & {\mathbf{0}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {{\varvec{K}}_{3} } & {\mathbf{0}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\varvec{K}}_{4} } \\ \end{array} } \right]} \right)\left[ {\begin{array}{*{20}c} {{\varvec{d}}_{\text{p}} } \\ {{\varvec{d}}_{\text{w}} } \\ \end{array} } \right] = {\mathbf{0}},$$

(32)

where

$$\left[ {{\varvec{M}}_{\text{p}} } \right]_{{{\text{IJ}}}} = \int_{\Omega } {{\varvec{B}}_{\text{pI}}^{\text{T}} I_{0} {\varvec{B}}_{\text{pJ}} {\text{d}}\Omega } ,$$

(33)

$${\kern 1pt} {\kern 1pt} \left[ {{\varvec{M}}_{\text{w}} } \right]_\text{IJ} = \int_{\Omega } {\psi_{{\text{I}}} I_{0} \psi_{{\text{J}}} {\text{d}}\Omega ,}$$

(34)

$$\left[ {{\varvec{K}}_{\text{p}} } \right]_{{{\text{IJ}}}} = \int_{\Omega } {{\varvec{B}}_{{{\text{lI}}}}^{\text{T}} {\varvec{AB}}_{{{\text{lJ}}}} {\text{d}}\Omega } ,$$

(35)

$$\left[ {{\varvec{K}}_{\text{w}} } \right]_{{{\text{IJ}}}} = \int_{\Omega } {{\varvec{B}}_{{{\text{bI}}}}^{{\text{T}}} {\varvec{DB}}_{{{\text{bJ}}}} {\text{d}}\Omega ,}$$

(36)

$$\left[ {{\varvec{K}}_{2} } \right]_{{{\text{IJ}}}} = \frac{1}{2}\int_{\Omega } {{\varvec{B}}_{{{\text{lI}}}}^{{\text{T}}} {\varvec{AB}}_{{{\text{nJ}}}} {\text{d}}\Omega ,} {\kern 1pt}$$

(37)

$$\left[ {{\varvec{K}}_{3} } \right]_{{{\text{IJ}}}} = \frac{1}{2}\int_{\Omega } {{\varvec{B}}_{{{\text{nI}}}}^{{\text{T}}} {\varvec{AB}}_{{{\text{lJ}}}} {\text{d}}\Omega ,{\kern 1pt} }$$

(38)

$$\left[ {{\varvec{K}}_{4} } \right]_{{{\text{IJ}}}} = \frac{1}{4}\int_{\Omega } {{\varvec{B}}_{{{\text{nI}}}}^{{\text{T}}} {\varvec{AB}}_{{{\text{nJ}}}} {\text{d}}\Omega ,}$$

(39)

$${\varvec{B}}_{{{\text{pI}}}} = \left[ {\begin{array}{*{20}c} {\psi_{\text{I}} } & 0 \\ 0 & {\psi_{\text{I}} } \\ \end{array} } \right],{\varvec{B}}_\text{lI} = \left[ {\begin{array}{*{20}c} {\psi_{{\text{I},x}} } & 0 \\ 0 & {\psi_{{\text{I},y}} } \\ {\psi_{{\text{I},y}} } & {\psi_{{\text{I},x}} } \\ \end{array} } \right],{\varvec{B}}_\text{bI} = \left[ {\begin{array}{*{20}c} { - \psi_{{\text{I},xx}} } \\ { - \psi_{{\text{I},yy}} } \\ { - 2\psi_{{\text{I},xy}} } \\ \end{array} } \right],{\varvec{B}}_\text{nI} = \left[ {\begin{array}{*{20}c} {w_{0,x} } & 0 \\ 0 & {w_{0,y} } \\ {w_{0,y} } & {w_{0,x} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\psi_{{\text{I},x}} } \\ {\psi_{{\text{I},y}} } \\ \end{array} } \right].$$

(40)

Furthermore, Eq. (32) is divided into two parts as

$${\varvec{M}}_{\text{p}} \varvec{\ddot{d}}_{\text{p}} + {\varvec{K}}_{\text{p}} {\varvec{d}}_{\text{p}} + {\varvec{K}}_{2} {\varvec{d}}_{\text{w}} = {\mathbf{0}},$$

(41)

$${\varvec{M}}_{\text{w}} \varvec{\ddot{d}}_{\text{w}} + {\varvec{K}}_{3} {\varvec{d}}_{\text{p}} + ({\varvec{K}}_{\text{w}} + {\varvec{K}}_{4} ){\varvec{d}}_{\text{w}} = {\mathbf{0}}.$$

(42)

By substituting Eq. (41) into Eq. (42), we get

$${\varvec{M}}_{\text{w}} \varvec{\ddot{d}}_{\text{w}} + ({\varvec{K}}_{\text{w}} + {\varvec{K}}_{4} - {\varvec{K}}_{3} {\varvec{K}}_{\text{p}}^{ - 1} {\varvec{K}}_{2} ){\varvec{d}}_{\text{w}} = {\mathbf{0}}.$$

(43)

The transverse displacement is assumed as

$${\varvec{d}}_{{{\text{w}}{\text{I}}}} = \psi_{{\text{I}}} \overline{\varvec{d}}_{{{\text{w}}{\text{I}}}} \sin \omega t.$$

(44)

By substituting Eq. (44) into Eq. (43), the equations of motion are expressed as

$$\left[ { - \omega^{2} {\varvec{M}}_{\text{w}} \sin \omega t + {\varvec{K}}_{\text{w}} \sin \omega t + ({\varvec{K}}_{4} - {\varvec{K}}_{3} {\varvec{K}}_{\text{p}}^{ - 1} {\varvec{K}}_{2} )(\sin \omega t)^{3} } \right]\overline{\varvec{d}}_{\text{w}} = {\mathbf{0}}.$$

(45)

The weighted residual is taken along the time path [0, T/4] to consider the complete displacement path [0, $\overline{\varvec{d}}_{{{\text{w}}{\text{max}}}}$], and the above equation is written as

$$\int_{0}^{T/4} {\left[ { - \omega^{2} {\varvec{M}}_{\text{w}} \sin \omega t + {\varvec{K}}_{\text{w}} \sin \omega t + ({\varvec{K}}_{4} - {\varvec{K}}_{3} {\varvec{K}}_{\text{p}}^{ - 1} {\varvec{K}}_{2} )(\sin \omega t)^{3} } \right]\overline{\varvec{d}}_{\text{w}} \sin \omega t {\text{d}}t= {\mathbf{0}}} .$$

(46)

The discretized nonlinear vibration equation without the time term is expressed as

$$\left[ {{\varvec{K}}_{\text{w}} + \frac{3}{4}({\varvec{K}}_{4} - {\varvec{K}}_{3} {\varvec{K}}_{\text{p}}^{ - 1} {\varvec{K}}_{2} ) - \omega^{2} {\varvec{M}}_{\text{w}} } \right]\overline{\varvec{d}}_{\text{w}} = {\mathbf{0}}.$$

(47)

The linearized updated mode (LUM) method is adopted to solve the nonlinear vibration equation of the composite plates. The following linear equations are solved to obtain linear eigenvalue and eigenvector via

$$\left( { - \omega^{2} {\varvec{M}}_{\text{w}} + {\varvec{K}}_{\text{w}} } \right)\overline{\varvec{d}}_{\text{w}} = {\mathbf{0}}.$$

(48)

The linear eigenvalue λ_L and eigenvector ω_L are normalized to obtain the initial input data by the assumed amplitude αh as

$$\omega_{{\text{i}}} = \frac{\alpha h}{{\left( {\omega_{\text{L}} } \right)_{\max } }}\omega_{\text{L}} ,$$

(49)

where $\left( {\omega_{\text{L}} } \right)_{\max }$ denotes the amplitude of linear eigenvector, and α is the amplitude parameter. The normalized eigenvector is substituted into the following equation to solve the nonlinear stiffness matrix as

$${\varvec{K}}_{\text{NL}} = \,{\varvec{K}}_{\text{w}} + \frac{3}{4}\left( {{\varvec{K}}_{4} - {\varvec{K}}_{3} {\varvec{K}}_{\text{p}}^{ - 1} {\varvec{K}}_{2} } \right)$$

(50)

$$\left( { - \omega^{2} {\varvec{M}}_{\text{w}} + {\varvec{K}}_{{{\text{NL}}}} } \right)\overline{\varvec{d}}_{\text{w}} = {\mathbf{0}}.$$

(51)

Afterwards, Eq. (51) is solved to regenerate the eigenvalue λ_i and eigenvector $\omega_{{\text{i}}}$, where i denotes the i-th iteration.

The amplitude αh in Eq. (49) is used to normalize the new eigenvalue λ_i and eigenvector $\omega_{{\text{i}}}$

$$\omega_{{\text{i}}} = \frac{\alpha h}{{\left( {\omega_{{\text{i}}} } \right)_{\max } }}\omega_{{\text{i}}} .$$

(52)

Then, the nonlinear stiffness matrix is calculated, and the new eigenvalues λ_i+1 and eigenvectors ω_i+1 are generated.

Finally, the convergence is checked by

$$\left| {\frac{{\lambda_{{\text{i + 1}}} - \lambda_{{\text{i}}} }}{{\lambda_{{{\text{i}} + 1}} }}} \right| < C_{\text{r}} ,$$

(53)

where C_r ranges between 10⁻⁴ and 10⁻⁶. If the condition is satisfied, the nonlinear frequency ratios versus amplitude parameter are recorded, otherwise, it is returned to Eq. (52).

Results and Discussion

In this section, the nonlinear free vibration of CNTRC plate is analyzed. The material parameters of FG-CNTRC plates are quoted from the MD simulation of our previous study [19]. The Poly (methyl methacrylate), referred to as PMMA, is considered as the matrix. Long CNT is used as reinforcement throughout the polymer matrix along the axial direction, and the material parameters of matrix and CNT reinforcement are listed in Table 1. The considered CNT volume fraction and corresponding efficiency parameters of (5, 5) SWCNT are shown in Table 2. Different boundary conditions are considered, where “S” represents simply supported, and “C” represents clamped boundary conditions. Three combined boundary conditions are adopted including four edges simply supported (SSSS), a pair of opposite edges clamped and left edges simply supported (CSCS), and four edges fully clamped (CCCC). Unless otherwise mentioned, the plate is considered with all edges simply supported.

Table 1 The material properties of PMMA matrix and CNT reinforcement

Table 2 The efficiency parameters of elastic moduli for composite with different CNT volume fraction reinforcement

For convenience, the linear and nonlinear frequencies of FG-CNTRC plates are nondimensionalized using the formula $\overline{\omega } = \omega \left( {a^{2} /h} \right)\sqrt {\rho_{{\text{m}}} /E_{{\text{m}}} }$. The nonlinear frequency ratio is defined as $\omega_{{{\text{NL}}}} /\omega_{{\text{L}}}$, where $\omega_{{\text{L}}}$ and $\omega_{{{\text{NL}}}}$ represent the linear and nonlinear frequencies, respectively. The non-dimensional maximum amplitude of the composite plate is $W_{{{\text{max}}}} /h$, which is also called as amplitude parameter. The CNTRC plates are considered with four distributions, namely UD, FG-O, FG-X and FG-V, and the thickness is taken as h = 0.001 m.

Convergence and Validation Study

The convergence study is carried out, and the errors of the nonlinear frequency ratios with different node numbers for the UD CNTRC plates are illustrated under three boundary conditions (SSSS, CSCS and CCCC) with $W_{{{\text{max}}}} /h{ = }0.2$ in Fig. 2. The aspect ratio a/b is 1, width to thickness ratio a/h is 10, and CNT volume ratio is V_CNT = 2%. It is observed that the error decreases as the node number increases for all boundary conditions. When the number of nodes increases from 18 × 18 to 24 × 24, the error remains stable around 0, and hence, the mesh consists of 18 × 18 nodes is adopted in the following studies.

Fig. 2

Convergence curves of nonlinear frequency ratio for different node numbers with three boundary conditions

The nonlinear frequency ratios of square simply supported plates are compared with FEM in Table 3. The nonlinear frequency ratios of UD and FG-V CNTRC plates are depicted, and the amplitude ratios are set as $W_{\max } /h$ = 0.2, 0.4, 0.6, 0.8 and 1.0, respectively. The present results are in good agreements with Refs. [34] and [35], which demonstrate that the nonlinear frequency ratio increases with the increase of amplitude parameter.

Table 3 Comparison of the nonlinear to linear frequency ratios for CNTRC plates (a/b = 1, b/h = 100, V_CNT = 0.17)

Parametric Studies

The influence of CNT distribution on the fundamental frequency is shown in Fig. 3a, which indicates that among the four CNT distributions of CNTRC plates including UD, FG-X, FG-O and FG-V, FG-X has the highest frequency, and FG-O CNTRC plates have the lowest one. The composite plate with the reinforcement distributions close to the top and bottom surfaces are more efficient in increasing the stiffness of CNTRC plate than those distributions near the mid-plane. Meanwhile, the nonlinear frequency ratios of the composite plate are displayed in Fig. 3b. With the increase of amplitude parameter, the nonlinear frequency ratio increases obviously. When the composite plate has a high dimensionless fundamental frequency, the corresponding nonlinear frequency ratio is low relatively. The nonlinear frequency ratio of the composite plates decreases with the increase of the stiffness, because of the transverse deformation of the composite plate and that the influence of geometrical nonlinearity decrease with the increase of stiffness. Figure 4 presents the influence of aspect ratio (a/b = 1.0, 1.2, 1.4, 1.6 and 1.8) on the nonlinear frequency ratio of four FG-CNTRC square plates, which reveals that the nonlinear frequency ratio of CNTRC plates decreases gradually with the increase of aspect ratio.

Fig. 3

Comparison of a fundamental frequencies and b nonlinear frequency ratios of UD, FG-O, FG-X, and FG-V of square composite plate (a/b = 1, b/h = 10, V_CNT = 2%)

Fig. 4

Nonlinear frequency ratio–amplitude curve of FG-CNTRC plates including a UD; b FG-O; c FG-X; d FG-V with different aspect ratios (b/h = 10, V_CNT = 4%)

The influence of boundary condition on the nonlinear frequency ratio of UD and FG-X CNTRC plates with different CNT volume fractions are shown in Figs. 5 and 6, respectively. The nonlinear frequency ratios of CNTRC plates with SSSS boundary condition are generally higher than those with CSCS boundary condition, and the nonlinear frequency ratios with CCCC boundary condition are usually lower than those with CSCS boundary condition. The similar nonlinear vibration behaviors of FG-O and FG-V CNTRC plates are consistent with UD and FG-X CNTRC plates for the above three boundary conditions.

Fig. 5

Nonlinear frequency ratio–amplitude curve of square UD CNTRC plates under different boundary conditions with CNT volume fraction a V_CNT = 2%; b V_CNT = 4%; c V_CNT = 6%; d V_CNT = 8% (a/b = 1, b/h = 10)

Fig. 6

Nonlinear frequency ratio–amplitude curve of square FG-X CNTRC plates under different boundary conditions with CNT volume fraction a V_CNT = 2%; b V_CNT = 4%; c V_CNT = 6%; d V_CNT = 8% (a/b = 1, b/h = 10)

Figures 7 and 8 depict the effects of reinforcement content and amplitude parameter on the nonlinear vibration of the FG-CNTRC plates, respectively, in which the variation range of CNT volume fractions are 1%, 2%, 3%,4%, 5%, 6%, 7%, 8% and 9%, and the scope of amplitude parameters are from 0.2 to 1. The effect of the amplitude parameter on nonlinear frequency ratio of square CNTRC plates is demonstrated in Fig. 7, which indicate that the nonlinear frequency ratio increases with the amplitude parameter increases, furthermore, the downward trend of curve declines apparently with the increase of amplitude parameters. Figure 8 illustrates that as the CNT volume fraction increases from 1 to 9% and the amplitude parameter is taken as 1, the stiffness of the plate increases correspondingly resulting in the decrease of the nonlinear frequency ratio. For the four distribution patterns, the decline amplitude of nonlinear frequency ratio curve almost decreases gradually, which demonstrates that the reinforcement effect of CNT on the stiffness of composite plate is not linearly related to the CNT volume fraction.

Fig. 7

Nonlinear frequency ratio of square CNTRC plates with different amplitude parameters under the boundary condition a SSSS; b CSCS; c CCCC (a/b = 1, b/h = 10)

Fig. 8

Nonlinear frequency ratio of CNTRC plates with the increase of CNT volume fraction with the aspect ratio a a/b = 1; b a/b = 1.5

Conclusions

The nonlinear vibration behavior for CNTRC plate is presented, and a parametric study of CNTRC plates with different boundary conditions, aspect ratios, CNT volume fractions and distributions is carried out in detail. The comparison analysis proves that the nonlinear frequency ratio of FG-CNTRC plates obtained by RKPM is consistent with FEM. Numerical results reveal that the nonlinear frequency ratio is increased by increasing the amplitude parameter. Among the four distributions, FG-X CNTRC plates have the highest frequency, and FG-O CNTRC plates have the lowest. On the contrary, FG-X CNTRC plates have the lowest nonlinear frequency ratio, and FG-O CNTRC plates have the highest. Hence, the composite plate with the reinforcement close to the top and bottom surfaces are more efficient in increasing the stiffness of CNTRC plates than those near the mid-plane. The nonlinear frequency ratio is reduced by increasing the CNT volume fraction. As the aspect ratio increases, the nonlinear frequency ratio decreases slowly. The present results indicate that the nonlinear frequency ratio decreases with the increase of boundary constraint of the FG-CNTRC plates.