1 Introduction

The earliest theories for face gear drives are found in book [1], and developed in the decade because face gear drives have many advantages such as [2]: (i) reduced sensitivity of bearing contact to gear misalignment, (ii) a reduced level of noise due to the very low level of transmission errors, (iii) more favorable conditions for the transfer of load from one pair of teeth to the next pair of teeth. Face gear drives have found an important application in helicopter transmissions explored by Litvin [2], in 1994, which is the possibility of the split of the torque and the reduction of the weight of the transmission system [2, 3].

Most previous researches are devoted to developing the analytical geometry of face-gear drives [4–6], static contact analysis about the localization of bearing contact and the influence of assemble errors on the shift of bearing contact and static transmission errors [7–12]. Their main targets are to optimize the localization of contact, avoid edge contact and reduce transmission errors.

Litvin et al. [8] developed a modified geometry of face gear drives with reduced stresses and low transmission errors. The application of a double crowned pinion generated by a grinding disk in mesh with a face gear is introduced. In this case, the localization of bearing contact of the face gear drive was achieved by crowning the surface of the pinion teeth in longitudinal direction by plunging. And profile crowning of the pinion was provided by the application of parabolic rack cutters. It was also indicated that the application of a double crowned pinion is favorable for the stabilization of bearing contact. But the face gear drive for an asymmetric gear drive with an involute pinion and an involute shaper applied for the generation of face gear is sensitive to the error of shaft angle. A double crowned pinion is favorable for the stabilization of bearing contact but stresses are increased, which is preferable for low loaded gear drives. Subsequently, Zanzi and Pedrero [3] developed the crowning method to achieve a uniform set of contact ellipses, reduce the sensitivity to misalignment and avoid the edge contact.

As for the dynamic characteristics of the face gear drive system, especially the nonlinear dynamic behaviors should attract more and more attention. Firstly, the crowning modification can avoid the edge contact and improve the localization of the contact. But the distance between the meshing point and rotation axis varies during the meshing process. Moreover, the meshing stiffness and backlash are considered in the face gear drive system. Then the control equation of the face gear drive system is a nonlinear parametric excitation system. Dynamic characteristics based on the nonlinear theory are unavoidable for the design and manufacture of the face gear drive system.

Up to now, there have been few papers relative to the dynamic characteristics of the face gear drive. Peng et al. [13] investigated the parametric instability behavior of the face-gear drives with periodically time-varying gear tooth mesh stiffness variation by using Floquet theory. Yang et al. [14] and Jin [15] investigated the chaotic and periodic responses of a face gear transmission system numerically. The meshing stiffness functions of the face gear drive system are proposed similar to spur gear pair but without any theoretical definition [14, 15]. Additionally, researches on the effects of modification on the dynamic characteristics of the face gear drive are blank. The main motivation of the present paper is to study the dynamic characteristics of the face gear drive system combining with time varying stiffness, backlash with and without modification.

The subsequent sections are structured as follows: in Sect. 2, a 6 degrees of freedom (6DOF) system combining with time varying stiffness, backlash, time varying arm of meshing force and supporting stiffness is modeled. The arm of meshing force is deduced based on tooth contact analysis (TCA). In Sect. 3, the dynamic characteristics of the face gear drive system are performed by using numerical simulation. Comparisons for the face gear drive system with and without modification are illustrated at the same time. A short remark concludes this paper in the final section.

2 Gear system model

2.1 System model

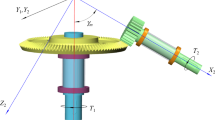
The gear transmission system is illustrated in Fig. 1. The driving motor and load are indicated by two cycle blocks with moment of inertia J i (i=1,2) respectively. And θ i is the rotation angle displacement of the driving motor and load. They are connected with pinion and gear with shafts, which are indicated by two shafts torsional stiffness \(k_{\theta_{i}}\). Each gear is supported with two bearings and the combination supporting stiffness is k jn (j=p,g,n=x,y) for gear j at n direction and the corresponding displacements are x j (i=1,2) and y j respectively. J j ,m j and θ j are the moment of inertia, mass and rotation angle displacement of the gear and pinion.

Fig. 1
figure 1

Illustration of face gear transmission system combined with motor and load

Full size image

Beginning to the analysis, one can let q be a vector of degrees of freedom as,

$$ \mathbf{q} = [ \theta_{p},x_{p},y_{p}, \theta_{g},z_{g},y_{g} ]^{T} $$
(1)

As shown in Fig. 1 the kinetic energy, T, and the potential (strain) energy V of the system can be written as,

$$\begin{aligned} &{T = \frac{1}{2}J_{p}\dot{\theta}_{p}^{2} + \frac{1}{2}m_{p}\dot{x}_{p}^{2} + \frac{1}{2}m_{p}\dot{y}_{p}^{2} + \frac{1}{2}J_{g}\dot{\theta }_{g}^{2}} \\ &{\phantom{T=}{} + \frac{1}{2}m_{g}\dot{z}_{g}^{2} + \frac{1}{2}m_{g}\dot{y}_{g}^{2}} \end{aligned}$$
(2)
$$\begin{aligned} &{V = \frac{1}{2}k_{m}\delta^{2} + \frac{1}{2}\sum_{{ j = p,g \atop n = x,y}} k_{jn}n_{j}^{2}} \end{aligned}$$
(3)

here δ is the displacement along the line of action, which is expressed as,

$$\begin{aligned} \delta ( t ) =& ( x_{p} - y_{g} + R_{p} \theta_{p} - r_{m}\theta_{g} )\cos a \\ &{} + ( y_{p} - z_{g} )\sin a \end{aligned}$$
(4)

and a is the normal pressure angle of gear pairs. And the expression (4) can again be written as,

$$ \delta ( t ) = \varGamma\mathbf{q} $$
(5)

and

$$ \boldsymbol{\varGamma} = \biggl[ \frac{\partial\delta}{\partial \theta_{p}},\frac{\partial\delta}{\partial x_{p}}, \frac{\partial \delta}{ \partial y_{p}},\frac{\partial\delta}{\partial \theta_{g}},\frac{\partial\delta}{\partial z_{g}},\frac{\partial \delta}{ \partial y_{g}} \biggr] $$
(6)

Using Lagrange’s equation,

$$ \frac{\partial}{\partial t} \biggl( \frac{\partial T}{\partial\dot{q}_{i}} \biggr) - \frac{\partial T}{\partial q_{i}} + \frac{\partial V}{\partial q_{i}} = Q_{i} $$
(7)

The equations of motion without proportional damping matrix C can be written as,

$$ \mathbf{M}\ddot{\mathbf{q}} + \mathbf{Kq} + \mathbf{NF}1 ( \mathbf{q},\dot{ \mathbf{q}} ) =\mathbf{F}_{ex} $$
(8)

Here M represents the mass matrix given by

$$ \mathbf{M} = \operatorname{diag} ( J_{p},m_{p},m_{p},J_{g},m_{g},m_{g} ) $$
(9)

And stiffness matrix is given by,

$$ \mathbf{K} = \operatorname{diag} ( 0,k_{px},k_{py},0,k_{gz},k_{gy} ) $$
(10)

And the nonlinear meshing force component NF1 is represented as,

$$ \mathbf{NF}1 ( \mathbf{q},\dot{\mathbf{q}} ) = k_{m} \varGamma^{T}\delta+ c_{m}\varGamma^{T}\dot{\delta} $$
(11)

And the external torque vector F ex is

$$ \mathbf{F}_{ex} = [ T_{1},0,0, - T_{2},0,0 ]^{T} $$
(12)

According to the meshing theory of gear system, two other factors must be included in the dynamic analysis, i.e., time varying contact pattern and gear backlash. The first one can be described as time varying stiffness in previous studies [16–20] and will be discussed in the following section. Here we just show the formative expression as,

$$ k_{m} ( t ) = k_{0} + \sum_{i = 1}^{N} k_{i}\sin \biggl( \frac{z_{p}\varOmega i}{60}2\pi t + \varphi_{i} \biggr) $$
(13)

Here k 0 is mean stiffness and k i and φ i are the amplitude and phase of ith component of time varying stiffness respectively. For the gear backlash, a piecewise linear function is proposed as,

$$ f ( \delta ) = \left \{ \begin{array}{l@{\quad}l} \delta- B & \delta> B \\ 0 & \vert \delta \vert \le B \\ \delta+ B & \delta< - B \end{array} \right . $$
(14)

And the contact damping c m between the two meshing teeth is also introduced. Then the nonlinear contact force (11) can be rewritten as,

$$ \mathbf{NF}1 ( t,\delta,\dot{\delta} ) = k_{m} ( t ) \varGamma^{T}f ( \delta ) + c_{m}\varGamma^{T}\dot{ \delta} $$
(15)

The whole equation of the gear transmission system with motor and load is an six degrees of freedom system as,

$$ \mathbf{M}\ddot{\mathbf{q}} + \mathbf{Kq} + \mathbf{NF}1 ( t,\delta,\dot{\delta} ) =\mathbf{ F}_{ex} $$
(16)

Now working with expression (5) and twice derivative to time t, one gets,

$$\begin{aligned} \frac{d^{2}\delta ( t )}{dt^{2}} = \varGamma \frac{d^{2}\mathbf{q}}{dt^{2}} =& \varGamma \mathbf{M}^{ - 1}\mathbf {F}_{ex} - \varGamma \mathbf{M}^{ - 1}\mathbf{Kq} \\ &{}- \varGamma\mathbf{M}^{ - 1} \mathbf{NF}1 ( t,\delta,\dot{\delta} ) \end{aligned}$$
(17)

Formally, the value θ j is still included in the right hand of Eq. (17). But one should bear in mind, that the stiffness matrix is a diagonal K with two zero and the θ j will disappear theoretically. Then with the new variations,

$$\begin{aligned} \mathbf{q} =& [ \theta_{p},x_{p},y_{p}, \theta_{g},z_{g},y_{g} ]^{T} \to [ \delta,x_{p},y_{p},z_{g},y_{g} ]^{T} \\ =& \mathbf{x} \end{aligned}$$
(18)

And the equation of motion can be written as,

$$ \{ \mathbf{M} \}\ddot{\mathbf{x}} + \{ \mathbf{K} \}\mathbf{x} + \mathbf{NF} ( t,\delta,\dot{\delta} ) = \mathbf{F} $$
(19)

Here,

$$\begin{aligned} &{ \{ \mathbf{M} \} = \operatorname{diag} ( m_{p},m_{p},m_{g},m_{g},1 )} \end{aligned}$$
(20)
$$\begin{aligned} &{ \{ \mathbf{K} \} = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} k_{px} & 0 & 0 & 0 & 0 \\ 0 & k_{py} & 0 & 0 & 0 \\ 0 & 0 & k_{gz} & 0 & 0 \\ 0 & 0 & 0 & k_{gy} & 0 \\ \frac{\partial\varPsi}{\partial x_{p}} & \frac{\partial\varPsi}{\partial y_{p}} & \frac{\partial\varPsi}{\partial z_{g}} & \frac {\partial \varPsi}{\partial y_{g}} & 0 \end{array} \right ]} \end{aligned}$$
(21)
$$\begin{aligned} &{\mathbf{NF} ( t,\delta,\dot{\delta} ) = \bigl[ \varGamma ( 2 ), \varGamma ( 3 ),\varGamma ( 5 ),\varGamma ( 6 ),\varGamma\mathbf{M}^{ - 1} \varGamma^{T} \bigr]^{T}} \\ &{\phantom{\mathbf{NF} ( t,\delta,\dot{\delta} ) =}{}\times \bigl( k_{m}f ( \delta ) + c_{m}\dot{\delta} \bigr)} \end{aligned}$$
(22)
$$\begin{aligned} &{\mathbf{F} = \bigl[ 0,0,0,0,\varGamma\mathbf{M}^{ - 1} \mathbf{F}_{ex} \bigr]^{T}} \end{aligned}$$
(23)
$$\begin{aligned} &{\varPsi ( x_{p},y_{p},z_{g},y_{g} ) = \varGamma\mathbf{M}^{ - 1}\mathbf{Kq}} \end{aligned}$$
(24)

Additionally, a proportional damping matrix expressed by

$$ \mathbf{C} = \alpha \{ \mathbf{M} \} + \beta \{ \mathbf{K} \} $$
(25)

is proposed based on Eq. (19) in this study.

For convenience of numerical analysis, nondimension time τ=ϖt is introduced and the differential and time symbol are still the same without losing generality. The second order differential equation (16) can be written as a state equation

$$ \dot{\mathbf{X}}= \{ \mathbf{A} \}\mathbf{X }+ \{ \mathbf{B} \} ( \mathbf{F} - \mathbf{NF} ) $$
(26)

by introducing a new state variable

$$ \mathbf{X} = ( \mathbf{x},\dot{\mathbf{x}} )^{T} $$
(27)

And here,

$$ \begin{aligned} {}&\{ \mathbf{A} \} = \left [ \begin{array}{c@{\quad}c} \mathbf{0} & \mathbf{I} \\ - \frac{ \{ \mathbf{M} \}^{ - 1} \{ \mathbf{K} \}}{\varpi^{2}} & - \frac{ \{ \mathbf{M} \}^{ - 1} \{ \mathbf{C} \}}{\varpi} \end{array} \right ],\\ &\{ \mathbf{B} \} = \left [ \begin{array}{c} 0 \\ - \frac{ \{ \mathbf{M} \}^{ - 1}}{\varpi^{2}} \end{array} \right ] \end{aligned} $$
(28)

2.2 Generation of face gear

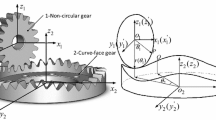
For the convenience of understanding the detailed mesh pattern of the face gear drive system, a face gear transmission system with a spur pinion gear and its coordinate of generation process is shown in Fig. 2. The pitch cone angle of the face gear drive is γ=90 deg in this study (Fig. 2(a)). In Fig. 2(b), the generation process of the face gear with a spur tool is illustrated. The main generation method adopted in this study is based on previous work in Refs. [4, 21] Coordinate systems S m (x m ,y m ,z m ) and S p (x p ,y p ,z p ) are fixed. And movable coordinate systems S s (x s ,y s ,z s ) and S 2(x 2,y 2,z 2) are connected to the shaper (pinion) and the face gear respectively. During the generation process, the rotation angles of the shaper and the face-gear along axes z a and z m are related as follows,

$$ \varphi_{s} / \varphi_{2} = N_{g} / N_{s} $$
(29)

The equation of the shaper at coordinate system S m (x m ,y m ,z m ) is represented as,

$$\begin{aligned} &{\vec{r}_{s}(u_{s},\theta_{s})} \\ &{\quad = \left [ \begin{array}{c} \pm r_{bs}[\sin (\theta_{os} + \theta_{s}) - \theta_{s}\cos(\theta_{os} + \theta_{s})] \\ - r_{bs}[\cos(\theta_{os} + \theta_{s}) + \theta_{s}\sin(\theta_{os} + \theta_{s})] \\ u_{s} \\ 1 \end{array} \right ]} \end{aligned}$$
(30)

and the unit normal of \(\vec{r}_{s}(u_{s},\theta_{s})\) is

$$ \vec{n}= \frac{\frac{\partial\vec{r}}{\partial\theta_{s}} \times\frac{\partial\vec{r}_s}{\partial u_{s}}}{|\frac{\partial\vec{r}_s}{\partial\theta_{s}} \times \frac{\partial\vec{r}_s}{\partial u_{s}}|} = \left [ \begin{array}{c} - \cos (\theta_{os} + \theta_{s}) \\ \mp\sin(\theta_{os} + \theta_{s}) \\ 0 \end{array} \right ] $$
(31)

Here r bs is the radius of the shaper’s base circle, and θ os determines half of the width of the space of the shaper on the base circle especially for a standard shaper θ os is represented by,

$$ \theta_{os} = \frac{\pi}{2N_{s}} - \operatorname{inv} \alpha_{n} $$
(32)

where α n is the pressure angle. The surface of face gear is determined as the envelope to the family of the shaper tooth surface and combined with the equation of meshing, as

$$ \left \{ \begin{array}{l} \vec{r}_{{2}}(u_{s},\theta_{s},\varphi_{s}) = M_{2s}(\varphi_{s})\vec{r}_{s}(u_{s},\theta_{s}) \\ \vec{n}_s\cdot\vec{\nu}_{s2} = f(u_{s},\theta_{s},\varphi_{s}) = 0 \end{array} \right . $$
(33)

Here

$$\begin{aligned} &{M_{2s}(\varphi_{s})} \\ &{\quad = M_{2p}M_{pm}M_{ms}} \\ &{\quad = \left [ \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \cos \varphi_{s}\cos\varphi_{2} & - \sin\varphi_{s}\cos\varphi_{2} & - \sin\varphi_{2} & 0 \\ - \cos\varphi_{s}\sin\varphi_{2} & \sin \varphi_{s}\sin\varphi_{2} & - \cos\varphi_{2} & 0 \\ \sin\varphi_{s} & \cos\varphi_{s} & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right ]} \end{aligned}$$
(34)
Fig. 2
figure 2

Illustration (a) and coordinate (b) of the face gear generation process

Full size image

2.3 Time varying arm of meshing process

Based on the tooth contact analysis (TCA) program in Ref. [21], the contact point of a face gear drive without assemble error can be determined numerically based on Sect. 2.2. With a standard spur gear shaper, the contact points of a meshing tooth cycle are illustrated in Fig. 3(a) by a red line. As seen in this figure, the meshing point is almost a line perpendicular to x-axis (tooth width direction). The edge contact may occur at the top of the face gear tooth. To avoid edge contact, many researchers adopt the tooth modification strategy such as profile and longitudinal modification in terms of linear or parabola type to improve the meshing performance of the gear transmission system. In this paper, firstly, a profile modification with parabola type is adopted. The contact points are listed in Fig. 3(a) by a blue line. The TCA result indicates that the proposed method can effectively avoid edge contact. All these considerations are the levels in the static design view, and the effect of modification on the dynamic performances is still an unavoidable problem in practical engineering. For example, the arm r m of meshing force

$$ r_{m} = \sqrt{x_{s}^{2} + y_{s}^{2}} $$
(35)

relative to face gear is almost constant. In Eq. (35) (x s ,y s ) are the meshing points obtained from TCA as shown in Fig. 4. The value of r m is varying from r LMP ≈488 mm to r LMP ≈560 mm when modification is applied to the gear pair as shown in Fig. 3(b). Then the arm of force r m can be represented with N terms Taylor series as,

$$ r_{m} ( t ) = \bar{r}_{m} + \sum _{i = 1}^{N} \bar{r}_{mvi}\sin \biggl( \frac{N_{p}\varOmega i}{60}2\pi t \biggr) $$
(36)

Here Ω is input shaft speed at rpm, \(\bar{r}_{m}\) is the mean part of the arm of force and \(\bar{r}_{mvi}\) is the amplitude of ith component.

Fig. 3
figure 3

(a) Contact points of the face gear drive and (b) distance of contact points and rotation axis. Red and blue lines/points are denoted for unmodified and modified condition respectively

Full size image
Fig. 4
figure 4

Sketch of arm of meshing force

Full size image

2.4 Time varying meshing stiffness

To construct the time varying meshing stiffness, the contact ratio of the face gear drive must be determined. Firstly, a so-called Tregold’s approximation for contact ratio, as mentioned in Ref. [13], is proposed. The pitch cone angles of pinion and face-gear are,

$$ \begin{aligned} \gamma_{p} &= \operatorname{arc} \cot \biggl( \frac{m_{12} + \cos\gamma}{ \sin\gamma} \biggr), \\ \gamma_{g} &= \operatorname{arc} \cot \biggl( \frac {1 + m_{12}\cos\gamma}{m_{12}\sin\gamma} \biggr) \end{aligned} $$
(37)

Here, m 12=N g /N p and γ is the pitch cone angle of face-gear drive, then the numbers of teeth for the formative spur pinion and the formative spur gear are,

$$ N_{vp} = N_{p} / \cos\gamma_{p},\qquad N_{vg} = N_{g} / \cos\gamma_{g} $$
(38)

Then the analytical formula for the contact ratio of gears is

$$ \begin{aligned} {}&\mathit{ICR} = \frac{N_{vp} ( \tan\alpha_{ap} - \tan\alpha ) + N_{vg} ( \tan\alpha_{ag} - \tan\alpha )}{2\pi},\\ &\cos\alpha_{ai} = \frac{r_{bi}}{r_{ai}},\quad ( i = p,g ) \end{aligned} $$
(39)

here, α is pressure angle, r bi is base circle radius and r ai is addendum circle radius.

The time varying meshing stiffness of the face gear is assumed to be rectangular. Recalling the definition of gear tooth meshing stiffness k m in literature [22, 23], one can simplify it as

$$ \begin{aligned} {}&k_{m} = k_{0} + k ( t ) = k_{0} + \sum_{r = 1}^{N} k_{r}\cos ( 2\pi rf_{m}t - \varphi_{r} ) \\ &\frac{k_{0}}{k_{tp}} = \mathit{ICR}, \\ &\frac{k_{r}}{k_{tp}} = \frac{\sqrt{2 - 2\cos ( 2\pi r ( \mathit{ICR} - 1 ) )}}{\pi r}, \\ &\varphi_{r} = \frac{1 - \cos ( 2\pi r ( \mathit{ICR} - 1 ) )}{\sin ( 2\pi r ( \mathit{ICR} - 1 ) )} \end{aligned} $$
(40)

for the contact ratio less than 2.

2.5 Supporting stiffness

A single gear supported by two bearings is illustrated in Fig. 5. Here the bearings are denoted by two stiffnesses and the bending stiffnesses of shafts are determined by,

$$ k_{bx} = k_{by} = 3EI\frac{L_{l} + L_{r}}{ ( L_{l}L_{r} )^{3}} \bigl[ ( L_{l} - L_{r} )^{2} + L_{l}L_{r} \bigr] $$
(41)

here \(I = \pi r_{l}^{4} / 4\) and E is the Young’s modulus. Generally the shaft of a gear transmission system is a stepped shaft. And the radius r l in I can be substituted by the equivalent radius r e

$$ ( r_{e} )^{4} = l \Big/ \sum_{i = 1}^{n} \frac{l_{i}}{D_{i}^{4}} $$
(42)

where l=L l +L r ,l i and D i are length and diameter at i step.

Fig. 5
figure 5

Illustration of supporting stiffness

Full size image

And the stiffnesses of the bearing at parallel direction (x,y) are assumed to be the same as

$$ k_{Bx} = k_{By} = 2 \times10^{10}~ ( \mathrm{N} / \mathrm{m} ) $$
(43)

Then the combined supporting stiffness can be obtained

$$ k_{x} = k_{y} = \frac{k_{bx}k_{Bx}}{k_{bx} + k_{Bx}} $$
(44)

2.6 Torsional stiffness of shaft

As for the bending stiffness of the shaft, the equivalent idea is still adopted to calculate the length as

$$ k_{\theta_{1}} = k_{\theta_{1}} = \sum_{i = 1}^{n} \frac{\pi GD_{i}^{4}}{32l_{i}} $$
(45)

Here G is shear modulus of shaft materials.

2.7 Unloaded transmission error excitation

The excitations of the gear transmission system have two parts: internal displacement excitation and external torque fluctuation excitation, generally. The internal displacement excitation is presented as effect of the unloaded transmission error, which is the major source of the spur/helical and bevel gears’ vibration. In this paper, the external torque fluctuation excitation is neglected and the internal displacement excitation is modeled as,

$$ F_{in} = \rho \bigl( \varGamma\mathbf{M}^{ - 1} \mathbf{F}_{ex} \bigr)\sin ( 2\pi f_{m}t ) $$
(46)

Here ρ is the load ratio and combining with Eq. (23), the excitation of the gear transmission system is,

$$ \mathbf{F} = \bigl[ 0,0,0,0,\varGamma\mathbf{M}^{ - 1} \mathbf{F}_{ex} \bigl( 1 + \rho\sin ( 2\pi f_{m}t ) \bigr) \bigr]^{T} $$
(47)

3 Numerical analysis

The main design data of the face gear drive and system parameters are listed in Table 1 and Table 2 respectively. Before the numerical analysis is made, the natural frequencies of corresponding 5DOF face gear drive system without damping are listed in Table 3. Substituting system parameters into Eq. (26), one can solve the nonlinear dynamic system by the Runge-Kutta method. The initial states of the numerical calculation are set to zeros and the transient response is neglected.

Table 1 Design data of face gear
Full size table
Table 2 System parameters
Full size table
Table 3 Natural frequency of 5DOF face gear drive system
Full size table

3.1 Dynamic characteristics without modification

When the standard face gear drive system is performed, the arm of meshing force is constant. The bifurcation map under two different load conditions, lightly load 10 Nm and highly load 600 Nm, are shown in Figs. 6 and 7 respectively. When lightly load is applied, the face gear drive system undergoes periodic motion when the rotation speed of the pinion is less than 2500 rpm. When the rotation speed is around 3000 rpm, approximate 3000z p /60=950 Hz, the system resonates with the first natural frequency (as shown in Table 3) and the periodic and chaotic motion are detected. The spectrum of the response is dominated by the first five harmonic components of mesh frequency as shown in Fig. 8. When the rotation speed overruns 6000 rpm, the system still undergoes chaotic motion but the frequencies of the responses are below the first mesh frequency.

Fig. 6
figure 6

Bifurcation map of unmodified face gear drive system with 10 Nm load applied on the pinion

Full size image
Fig. 7
figure 7

Bifurcation map of unmodified face gear drive system with 600 Nm load applied on the pinion

Full size image
Fig. 8
figure 8

Frequency spectrum of the face gear drive system with 10 Nm load applied on the pinion

Full size image

When load 600 Nm is applied on the pinion, the responses frequency spectrum of the face gear drive system is shown in Fig. 9. The responses frequency spectrum in the resonance region is almost the same as that in Fig. 8 but the amplitude increases obviously. When the pinion runs above 6000 rpm, for light load condition, the system undergoes chaotic motion. However, for high load condition, the system undergoes periodic motion. The results indicate that the increased load may restrict the chaotic motion and the peak values of frequency spectrum are occurring at the mesh frequencies.

Fig. 9
figure 9

Frequency spectrum of the face gear drive system with 600 Nm load applied on the pinion

Full size image

3.2 Dynamic characteristics with modification

In this subsection, we consider the case when the modification is applied in the face gear drive system as mentioned in Sect. 2.3. Mathematically, the time varying arm of meshing force is represented as parametric excitation e.g. Eqs. (15) and (17). Therefore Γ(t) is a function of meshing position or a time varying function. Equation (17) shows that although the applied torque load is constant, the meshing force will be time varying. The transmission force for the face gear drive system is fluctuation, see the first term of right hands of Eq. (17), Γ M −1 F ex . And the time varying coefficient is included in the linear stiffness force term Γ M −1 Kq and nonlinear stiffness force term Γ M −1 NF1 even if the stiffness is constant during the meshing process.

The numerical simulation is performed as previous subsection. To illustrate the difference of modification on the face gear drive system, the maximum and minimum contact force relative to unmodified and modified case with 600 Nm load applied on the pinion is shown in Fig. 10. The figure shows that the modification strategy can improve the static mesh pattern, but it influences the nonlinear characteristic of the face gear drive system in some sort. This may be caused by the time varying meshing stiffness, for the modification can also induce the time varying coefficient and couple with time varying meshing stiffness.

Fig. 10
figure 10

Maximum (a) and minimum (b) contact force comparison relative to unmodified and modified face gear drive with 600 Nm load applied on the pinion

Full size image

Theoretically, in what follows, the effects of the time varying mesh characteristic on the dynamic responses are compared. Before that, the constant arm (unmodified face gear drive) and constant meshing stiffness are indicated by Case 1, the time varying arm (modified face gear drive) and constant meshing stiffness by Case 2, and the time varying arm and time varying meshing stiffness by Case 3. The equivalent root-mean-square (rms) values [24] and mean values of the dynamic responses x 5 (which means y g and it is fifth variation of dimensionless Eq. (26)) with respect to the rotation speed of the pinion from 100 rpm to 10000 rpm are illustrated in Fig. 11. The figure shows that the predicted responses of the time varying system are slightly smaller than the time-invariant system at a lower rotation speed of the pinion (<6000 rpm), totally. Moreover, the results are different from the case of the hypoid gear drive system, which is similar to the face gear drive system, but the time varying mesh characteristics enlarge the response amplitude [25].

Fig. 11
figure 11

Comparisons of the effects of time varying characteristics within face gear drive system

Full size image

On the other hand, the 3rd–8th harmonic components of the dynamic responses for the three cases are illustrated in Fig. 12 serially. The figure shows that the first harmonic is found to dominate the vibration spectra more than other higher harmonics and the time varying mesh characteristics influence the first harmonic slightly. But the higher harmonics are affected by the time varying mesh characteristic obviously as shown in Fig. 12. Especially, the 4th, 6th and 8th harmonics of case 3 and case 2 are much higher than those of case 1 at a lower rotation speed (<6000 rpm) except the main resonant region (around 3000 rpm).

Fig. 12
figure 12

Comparisons of the effects of time varying characteristics within face gear drive system. Ampl. is shorten of Amplitude, which indicates the amplitude of each harmonic components

Full size image

3.3 Discussion

The presence of gear backlash and time varying meshing stiffness leads to the strong nonlinear interaction in the system dynamic equation. And the nonlinear characteristics such as bifurcations, different kinds of periodic solutions, limit cycles behaviour, super- and sub-resonances, multiple coexisting stable solutions and chaotic motions in the gear dynamics (especially the spur gear, helical gear, hypoid gear) have been studied [16, 18, 25–32]. Although there is a general agreement about the nature of the phenomenon in gear dynamics, the current research rarely involves the face gear drive system. Therefore in the following subsection, the period doubling bifurcation, multiple coexisting stable motion and the jump phenomena of the steady-state response in the face gear drive system are analyzed for Case 2. Here noted that the final steady-state response at a particular input speed is used as the initial condition for the next speed in the numerical calculation.

3.3.1 Jump phenomena and coexisting stable solutions

The rms values and mean are calculated in the speed region (5500, 7500) rpm and shown in Fig. 13 respectively. A nonlinear jump phenomenon is detected in region (5631, 5701) rpm. The rms response jumps up as the input speed is increased and jumps down at a lower speed when the input speed is decreased. Moreover, when the input speed is lower than 5631 rpm, namely before the jump occurring, the system undergoes period-1 solution without lossing contact. With the increase of the input speed, the mesh teeth separate and the single side impact motion and jump phenomenon occur. In view of the non-smooth dynamics [33], the grazing bifurcation may be one of the reasons for the jump phenomenon in the gear dynamic with backlash. When the input speed is larger than 6000 rpm the jump phenomenon still occurs, but the jump region is small and the grazing bifurcation does not occur.

Fig. 13
figure 13

Steady-state rms value \(x_{5}^{rms}\) and mean \(x_{5}^{mean}\) of the face gear drive system in speed region (5500, 7500) rpm. Note: red ‘- - -’ line for increasing speed, blue ‘–’ line for decreasing speed, ‘→’ denoting the sweep direction. (◯)—no impact motion, (△)—single side impact, (□)—double side impact

Full size image

On the other hand, multiple coexisting stable solutions are possible in the speed region between the jump down and jump up speed. For example, the three kinds of multiple coexisting stable solutions are detected at 5651 rpm, 5781 rpm and 6585 rpm respectively as shown in Fig. 14. In Fig. 14-(1), the phase portrait and their corresponding spectra of the two coexisting period-1 solutions (denotes by one Poincare point at phase portrait) are illustrated, (a) and (b) are corresponding with the upper and lower branch in Fig. 13 around 5651 rpm. The phase portrait twists with different patterns and the first mesh harmonic dominates the gear response, their main differences occur at higher mesh harmonics. Moreover, the period-1 solution in the lower branch is close to the grazing bifurcation and the portrait is tangent with the discontinuous boundary induced by backlash, approximately. In Fig. 14-(2), coexisting of period-2 (a) and period-1 (b) solutions are illustrated, both solutions indicate that the system undergoes single side impact motion. In Fig. 14-(3), the system undergoes double side impact motion and the coexisting of period-1 (a) and period-3 (b) solutions are shown. The one third mesh frequency appears at higher mesh frequency and the amplitude at mesh order is almost identical.

Fig. 14
figure 14

Three kinds of multiple coexisting periodic stable solutions in the face gear drive system. Note: in each column the upper one subplot (a, b) is phase portrait and another one is corresponding spectra (c, d). The cycles denote the Poincare point at each phase portrait map

Full size image

3.3.2 Period doubling bifurcation

Period doubling bifurcation is a main route to chaos in a nonlinear system. The type of nonlinear behaviour appears to occur in the face gear drive system as shown in Fig. 7. In this subsection, the enlarged bifurcation of Fig. 7 in speed region (5500, 7500) rpm is shown in Fig. 15. In this region, the first period doubling bifurcation (PD) is detected around \(\varOmega_{1}^{PD} = 5762~\mathrm{rpm}\), then the period-1 solution transfers to period-2 solution and finally to chaos with the increase of the input speed. Around \(\varOmega_{1}^{PD}\), the system undergoes single side impact motion. When the speed is around \(\varOmega_{2}^{PD} = 6545~\mathrm{rpm}\) with the decrease of the input speed, the period-1 solution transfers to period-3 solution, then transfers from the period-3 solution to chaos directly and the system undergoes double side impact motion. Around \(\varOmega_{3}^{PD} = 6947~\mathrm{rpm}\) and \(\varOmega_{4}^{PD} = 7068~\mathrm{rpm}\), the PD bifurcation is observed but it does not lead to chaos. On the other hand, intermittency or sudden change to chaotic behaviour is reached in the vicinity of \(\varOmega_{1}^{C} = 6033~\mathrm{rpm}\) and \(\varOmega_{2}^{C} = 6143~\mathrm{rpm}\).

Fig. 15
figure 15

Enlarged bifurcation map of Fig. 7 in speed region (5500, 7500) rpm

Full size image

4 Conclusions

A 6DOF face gear drive system combining with time varying stiffness, backlash, time varying arm of meshing force and supporting stiffness is used to analyze the nonlinear dynamics of the face gear drive system with and without modification. The main works of the present paper are concluded as follows:

  1. (1)

    The mesh pattern of the face gear drive system is analyzed when the modification strategy is applied. To analyze the effect of modification on the dynamics response, the time varying arm of meshing force based on the TCA is deduced for the case with and without modification simply.

  2. (2)

    The modification influences the system vibration response such as resonance, rms and meshing force slightly. Jump phenomena are detected in the steady-state response, but they do not occur near primary and higher harmonic resonance. But the multiple coexisting stable solutions are observed in the jump region. Three kinds of coexisting solutions, two period-1 solutions, period-1 and period-2 solution, period-1 and period-3 solution are detected in the steady-state response.

  3. (3)

    Other nonlinear phenomena common in systems have backlash type nonlinearity and time varying coefficient such as chaos and period doubling bifurcation are analyzed.

  4. (4)

    From an engineering point of view, the modification can improve the mesh characteristic in previous static analysis. Moreover, from our analysis, the system response do not sensitize to the time varying mesh arm deduced by the modification.