1 Introduction

Orthogonal curve-face gear transmission is a new type of variable transmission ratio gear pair between the intersecting axes based on the noncircular bevel gear pair, which combines the common transmission characteristics of noncircular gears, bevel gears and face gears [1]. It can be used to transmit motion and power between intersecting axes. Orthogonal curve-face gear transmission has some unique advantages and transmission characteristics. It has the variable transmission ratio characteristics of noncircular gear [2], can also transmit motion between orthogonal axes and has the characteristics of face gear such as better uniform load performance, larger coincidence ratio and no anti-dislocation design [3–5]. The major characteristic of curve-face gear is variable transmission ratio and the specific transmission ratio can be designed to meet the demands of practical application. When the transmission ratio changes, the geometry of the gear also changes. It has potentially broad application prospects in agricultural machinery, textile machinery and other fields. Its design principle and processing method are easier than noncircular bevel gear.

The dynamic characteristics of the gear transmission system will directly affect the stability and reliability of the transmission system. Scholars have done a lot of research on this topic and the dynamic model considering time-varying mesh stiffness, gear backlash and static transmission error was established [6–10]. With regard to intersecting axis gear transmission, the study on bevel gear and orthogonal face gear transmission dynamics is more extensive and in-depth. However, existing related literature about orthogonal curve-face gear dynamics has not yet been found. Research on the orthogonal curve-face gear currently concentrates on tooth profile, measurement, error, strength, kinematic properties, manufacturing and other fields [1, 11]. This paper uses the lumped parameter theory to establish a twisting vibration model of orthogonal curve-face gear pair. In the model, internal excitation, such as time-varying mesh stiffness of the face gear pair, statics transmission error and backlash, and external excitation, such as input rotational speed and load torque, are considered. Twisting vibration was converted to displacement vibration on the meshing line. Using fourth-order Runge–Kutta numerical integration method to solve the dynamics differential equation, the dynamics response of the system was obtained. The research also provides a theoretical basis for the engineering applications of orthogonal curve-face gear.

2 Dynamics model of the transmission system

2.1 Transmission system model

The transmission model of orthogonal curve-face gear transmission system is shown in Fig. 1.

Fig. 1
figure 1

Orthogonal curve-face gear transmission model

Full size image

The pitch curve of a noncircular gear is high-order elliptic. The pitch curve of a curve-face gear is conjugated with the pitch curve of a noncircular gear, so it can be calculated according to the principle of gear engagement [1]. When the orthogonal curve-face gear transmission system works, the center distance remains constant, the pitch curves maintain pure rolling and the transmission ratio changes with time.

According to the relationships of noncircular gear and curve-face gear, the coordinate of the gear system was established. As shown in Fig. 1, the coordinate \(o_{1} x_{1} y_{1} z_{1}\) is fixed to the frame and the coordinate \(o_{1} x_{1}^{'} y_{1}^{'} z_{1}^{'}\) is fixed to the noncircular gear. In the initial state, the two coordinates are coincident when the system works, and the noncircular gear rotates counterclockwise about the \(o_{1} y_{1}\). The coordinate \(o_{2} x_{2} y_{2} z_{2}\) is fixed to the frame, and the coordinate \(o_{2} x_{2}^{'} y_{2}^{'} z_{2}^{'}\) is fixed to the curve-face gear. In the initial state, the two coordinates are coincident when the system works, and the curve-face gear rotates clockwise about \(o_{2} z_{2}\). When the noncircular gear turns an angle \(\theta_{1}\), the curve-face gear turns an angle \(\theta_{2}\). Point \(P\) and point \(Q\) are the meshing point on a noncircular gear and a curve-face gear when the noncircular gear turns an angle \(\theta_{1}\).

The pitch curve of a noncircular gear is expressed in polar coordinates as Eq. (1):

$$r(\theta_{1} ) = \frac{{a(1 - k^{2} )}}{{1 - k\cos (n_{1} \theta {}_{1})}},$$
(1)

where \(a\) represents the semi-major axis, \(k\) is the eccentricity ratio, and \(n_{1}\) and \(\theta_{1}\) are the order and the rotation angle of the noncircular gear.

According to the coordinate transformation theory, the pitch curve of the curve-face gear was obtained:

$$\left\{ {\begin{array}{*{20}c} {x = - R\cos (\theta_{2} )} \\ {y = - R\sin (\theta_{2} )} \\ {z = r(0) - r(\theta_{1} )} \\ \end{array} } \right..$$
(2)

The transmission ratio of the gear pair \(i_{12}\) is expressed as:

$$i_{12} = \frac{{R(1 - k\cos (n_{1} \theta_{1} ))}}{{a(1 - k^{2} )}},$$
(3)

where \(R\) is the radius of the curve-face gear pitch curve.

2.2 Dynamics model of the transmission system

The dynamics model of the orthogonal curve-face gear transmission system is shown in Fig. 2.

Fig. 2
figure 2

Orthogonal curve-face gear transmission twisting vibration dynamics model

Full size image

In the model, only considering the twisting vibration, cabinet bearing seat is regarded as a rigid support. Point \(P\) is the meshing point on the noncircular gear, point \(Q\) the meshing point on the curve-face gear, \(PQ\) the meshing line, \(\theta_{1}\) the rotation angle of noncircular gear, \(\theta_{2}\) the rotation angle of curve-face gear, \(C_{\text{m}}\) the meshing damping, \(k_{\text{m}} (t)\) the time-varying meshing stiffness and \(e(t)\) the static transmission error of normal direction. In this paper, the model of the vibration on the meshing line is represented by the \(M - C - K\) system.

2.3 Analysis of excitation

Excitation of the vibration of the gear transmission includes external excitation and internal excitation [9]. External excitation includes input speed and load torque; internal excitation includes time-varying meshing stiffness of the gear, static transmission error and backlash. For the orthogonal curve-face gear transmission, excitation also includes the change of input shaft torque caused by the change of output shaft angular acceleration.

The load of the orthogonal curve-face gear \(T_{2}\) is constant, and the angular velocity of the drive shaft \(\omega_{1}\) is also constant. The transmission ratio of the system \(i_{12}\) is time varying, so the angular acceleration of the driven shaft \(\beta_{2}\) is time varying and the drive shaft torque \(T_{1}\) is also time varying. The relationship between the drive shaft torque and the driven shaft torque is expressed as Eq. (4),

$$T_{1} = \frac{{T_{2} - I_{2} \beta_{2} }}{{i_{12} }}$$
(4)
$$\beta_{2} = \frac{{{\text{d}}\omega_{2} }}{{{\text{d}}t}} = \frac{{{\text{d}}(\omega_{1} /i_{12} )}}{{{\text{d}}t}} = \frac{{n_{1} a\omega_{1}^{2} k(1 - k^{2} )\sin (n_{1} \omega_{1} t)}}{{R(1 - k\cos (n_{1} \omega_{1} t))^{2} }},$$
(5)

where \(\beta_{2}\) is the angular acceleration of the driven shaft.

The drive shaft torque can be obtained by solving Eq. 4 with 5. The torque variation is expressed in the upper right corner of Fig. 2. In the figure, the driven gear torque \(T_{2}\) was taken as 20 N m.

In the actual transmission, because of the error in processing and installation, backlash must exist to ensure smooth engagement, which leads to the existence of shock of mesh in, mesh out and mesh apart. This is an important nonlinear factor of gear dynamics. Gear backlash function can be expressed as:

$$f(x) = \left\{ {\begin{array}{*{20}c} {x_{\text{n}} - b\;\;x_{\text{n}} > b} \\ {0\;\;\;\;\;\;\;\;\left| {x_{\text{n}} } \right| \le b} \\ {x_{\text{n}} + b\;\;x_{\text{n}} < - b} \\ \end{array} } \right.$$
(6)

where b is the half of the total backlash. The backlash function is shown in Fig. 3 [12].

Fig. 3
figure 3

The backlash function

Full size image

Because of the processing and installation errors, there must exist static transmission errors in the meshing process. Static transmission errors can be approximately expressed by harmonic function as:

$$e(t) = e_{0} + e_{1} \cos (\omega_{e} t + \phi_{1} ),$$
(7)

where \(e_{0}\) is the constant of gear static transmission error, \(e_{1}\) the magnitude of gear static transmission error, \(\omega_{1}\) the meshing angular frequency of the transmission system and \(\phi_{1}\) the initial phase of static transmission error.

In the gear’s meshing process, when the coincidence degree \(1 < \varepsilon < 2\), there are single-tooth meshing zones and double-tooth meshing zones. A meshing cycle experiences three processes of double-tooth meshing, single-tooth meshing and double-tooth meshing. When the gear meshes between the single-tooth meshing zone and double-tooth meshing zone, meshing stiffness steps, which lead to the time-varying of meshing stiffness. Time-varying meshing stiffness is an important internal excitation of the gear system dynamics.

For curve-face gear, each tooth shape varies in a cycle and single-tooth stiffness also varies, which also have an impact on the time-varying meshing stiffness of the orthogonal curve-face gear transmission system. In this paper, the tooth stiffness formula is used in the ISO formula draft to approximate the solving tooth stiffness of the curve-face gear [13]. The approximation of tooth stiffness of unit tooth width is:

$$C^{'} \approx \frac{1}{q}\cos \alpha \cos \beta_{\text{g}} N/({\text{mm}}\;\mu {\text{m}}),$$
(8)
$$\begin{gathered} q = 0.04723 + \frac{0.15551}{{z_{v1} }} + \frac{0.25791}{{z_{v2} }} - 0.00635x_{1} - 0.11654\frac{{x_{1} }}{{z_{v1} }} - 0.00193x_{2} \hfill \\ \;\;\;\;\; - 0.24188\frac{{x_{2} }}{{z_{v2} }} + 0.00529x_{1}^{2} + 0.00182x_{2}^{2} , \hfill \\ \end{gathered}$$
(9)

where \(\alpha\) is the pressure angle of the gear transmission system, \(\beta_{\text{g}}\) is the helix angle of helical gears which is taken as 0, \(z{}_{v1}\) and \(z_{v2}\) are the number of teeth in the noncircular gear and curve-face gear, and \(x_{1}\) and \(x_{2}\) are the modification coefficients of the noncircular gear and curve-face gear, taken as 0.

The pressure angle of the orthogonal curve-face gear transmission is shown in Eq. (10) [2]:

$$\alpha_{\text{m}} = \alpha_{\text{u}} + \frac{\pi }{2} - \mu$$
(10)
$$\mu = \arctan \frac{{r(\theta_{1} )}}{{r^{'} (\theta_{1} )}} = \arctan \frac{{ - (1 - k\cos (n_{1} \omega_{1} t))}}{{n_{1} k\sin (n_{1} \omega_{1} t)}},$$
(11)

where \(\alpha_{\text{u}}\) is the pressure angle of the tool, \(\mu\) is the angle between the radius vector of the noncircular gear pitch curve and the tangent of the noncircular gear pitch curve.

Therefore, the tooth stiffness of the curve-face gear is also time varying. Considering the factor of tooth width, tooth stiffness of the curve-face gear is:

$$k_{2} = \frac{1}{q}B\cos \alpha_{\text{m}} .$$
(12)

Because the coincidence degree of orthogonal curve-face gear transmission \(\varepsilon\) is larger than normal gears, the meshing stiffness can be approximated as meshing stiffness of the double-tooth meshing zone. Meshing stiffness can be expressed as:

$$k_{\text{m}} (t) = 1.5k^{'} = 1.5\frac{{k_{1} k_{2} }}{{k_{1} + k_{2} }},$$
(13)

where \(k_{1}\) is the tooth stiffness of the noncircular gear, \(k_{2}\) is the tooth stiffness of the curve-face gear and \(k_{1} = k_{2}\), \(k^{'}\) is the meshing stiffness of the single-tooth meshing zone. Taking into account the problem of uneven load distribution, generally we take 1.5 times the meshing stiffness of single-tooth meshing zone as the meshing stiffness of the double-tooth meshing zone.

3 Solving and analysis of dynamics equation

3.1 Solving the differential equations

According to Newton’s law of motion, the dynamics equations of two degrees of twisting vibration are listed as follows:

$$I_{1} \ddot{\theta }_{1} + Cr_{\text{b1}} [r_{\text{b1}} \dot{\theta }_{1} - r_{\text{b2}} \dot{\theta }_{2} - \dot{e}(t)] + r_{\text{b1}} k(t)f(r_{\text{b1}} \theta_{1} - r_{\text{b2}} \theta_{2} - e(t)) = T_{1} ,$$
(14)
$$I_{2} \ddot{\theta }_{2} - Cr_{\text{b2}} [r_{\text{b1}} \dot{\theta }_{1} - r_{\text{b2}} \dot{\theta }_{2} - \dot{e}(t)] - r_{\text{b2}} k(t)f(r_{\text{b1}} \theta_{1} - r_{\text{b2}} \theta_{2} - e(t)) = - (T_{2} - I_{2} \beta_{2} ),$$
(15)

where \(I_{1}\) and \(I_{2}\) are the moment of inertia of the drive gear and driven gear, and \(r_{\text{b1}}\) and \(r_{\text{b2}}\) are the distance between the meshing point and the center of rotation of the drive gear and driven gear.

Let A1 be the result of Eq. (14) multiplied by \(I_{2} r_{\text{b1}}\) and A2 be the result of Eq. (15) multiplied by \(I_{1} r_{\text{b2}}\); subtract the A1 and A2 and then divided by \(I_{1} r_{\text{b2}}^{2} + I_{2} r_{\text{b1}}^{ 2}\). The combined results of the two equations are:

$$m_{\text{e}} (r_{\text{b1}} \ddot{\theta }_{1} - r_{\text{b2}} \ddot{\theta }_{2} ) + C[r_{\text{b1}} \dot{\theta }_{1} - r_{\text{b2}} \dot{\theta }_{2} - \dot{e}(t)] + k(t)f(r_{\text{b1}} \theta_{1} - r_{\text{b2}} \theta_{2} - e(t)) = F_{\text{m}} (t),$$
(16)

where \(m_{\text{e}} = \frac{{I_{1} I_{2} }}{{I_{1} r_{\text{b2}}^{ 2} + I_{2} r_{\text{b1}}^{2} }}\) is the equivalent mass, and \(F_{\text{m}} (t) = \frac{{T_{1} I_{2} r_{\text{b1}} + I_{1} r_{\text{b2}} (T_{2} - I_{2} \beta_{2} )}}{{I_{1} r_{\text{b2}}^{ 2} + I_{2} r_{\text{b1}}^{ 2} }}\) is the equivalent excitation force.

Let \(x = r_{\text{b1}} \theta_{1} - r_{\text{b2}} \theta_{2} - e(t)\), then the above Eq. (16) can be written as:

$$m_{e} \textit{\"{x}}(t) + C\dot{x}(t) + k(t)f(x) = F_{m} (t) - m_{e} \textit{\"{e}}(t).$$
(17)

On nondimensionalization of Eq. (17), \(l = 10^{ - 6}\); let \(\tau = \omega_{0} t\), \(x(t) = lu(\tau )\), then

$$\textit{\"{u}}(\tau ) + 2\xi \dot{u}(\tau ) + f(u(\tau ))\frac{{k_{\text{m}} (t)}}{{k_{\text{m}} }} = \frac{{F_{\text{m}} }}{{k_{\text{m}} l}} - \frac{{\textit{\"{e}}(t)}}{{l\omega_{0}^{2} }},$$
(18)

where \(\zeta\) is the damping coefficient, \(\zeta = \frac{C}{{2m_{\text{e}} \omega_{0} }}\) and \(k_{\text{m}}\) is the average meshing stiffness.

Substitute the parameters of Table 1 for the calculations. The above dynamics equation has nonlinear factors and analytical solutions cannot be solved; therefore, we use the numerical method. Solving the equation requires the introduction of state variables \(\nu (\tau )\). Using the fourth-order Runge–Kutta method and solving by MATLAB programming, we get the vibration response of the orthogonal curve-face gear transmission system.

Table 1 Parameters of gear transmission
Full size table

3.2 Vibration analysis

Analysis of the impact of different meshing frequencies on the dynamics of orthogonal curve-face gear system is performed by changing the frequency ratio \(\varOmega = \frac{{\omega_{\text{e}} }}{{\omega_{0} }}\) to observe the vibration response of the system.

As seen in Fig. 4, when \(\varOmega = 0.1\), the system shows chaotic response. When the value of \(\varOmega\) is in the range of 0.01–0.38, the vibration response of the system is similar to that in Fig. 4. On enlarging the displacement response graph, there are small oscillations of high frequency in each of the peaks and troughs. Phase plane graph is a complex closed curve, which corresponds to the high-frequency oscillation of the displacement response.

Fig. 4
figure 4

Dynamic response when \(\varOmega = 0.1\). a Displacement response graph, b phase graph

Full size image

As seen in Fig. 5, when \(\varOmega = 0.8\), the system shows vibration response of nine cycles. When the value of \(\varOmega\) is in the range of 0.38–0.96, the vibration response of the system is similar to that in Fig. 5. After dimensionless time 100, the vibration response of the system tends to be stabilized. After being stabilized, the displacement response graph presents a high-frequency wave superimposed on a low-frequency wave. There are nine peaks in a cycle which correspond to nine teeth of half cycle of the noncircular gear. The phase plane graph is a closed curve consisting of nine approximate ellipses, which also correspond to the nine peaks of each cycle in the displacement response graph.

Fig. 5
figure 5

Dynamic response when \(\varOmega = 0.8\). a Displacement response graph, b phase graph

Full size image

As seen in Fig. 6, when \(\varOmega = 1\), the system shows vibration response of nine cycles, but it is significantly different from the vibration response of the nine cycles in Fig. 5. When the value of \(\varOmega\) is in the range of 0.96–3, the vibration response of the system is similar to that in Fig. 6. Its phase graph is a closed curve consisting of nine approximately elliptical, so the system response is vibration response of nine cycles. Its displacement response graph presents periodicity, but the vibration characteristics in each cycle are quite complex and there is no regularity in each cycle.

Fig. 6
figure 6

Dynamic response when \(\varOmega = 1\). a Displacement response graph, b phase graph

Full size image

As seen in Fig. 7, when \(\varOmega = 5\), the system shows single-cycle vibration response. When the value of \(\varOmega\) is in the range of 3–5, the vibration response of the system is similar to that in Fig. 7. Greater meshing frequency has no practical significance, so it will not be discussed. After the vibration is stabilized, the displacement response graph is significantly cyclical, like simple harmonic. Its phase graph is a irregular closed curve, which means that the system response is a single-cycle vibration.

Fig. 7
figure 7

Dynamic response when \(\varOmega = 5\). a Displacement response graph, b phase graph

Full size image

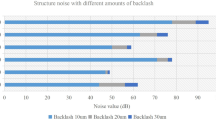
The impact of different gear backlashes on the orthogonal curve-face gear transmission system is analyzed, keeping the meshing frequency ratio \(\varOmega = 0.8\) unchanged, to observe the vibration response of the system.

Figure 8a, b shows the displacement response graphs of the system when the backlash 2b values are 20 and 100 μm. As we can see, the larger the backlash, the greater is the amplitude of the displacement response and the longer the time needed to be stabilized. When the total backlash is large enough to exceed a certain range, the system presents chaotic response.

Fig. 8
figure 8

Impact on the dynamic response of gear backlash. a Displacement response when \(2b = 20\;\mu {\text{m}}\), b displacement response when \(2b = 100\;\mu {\text{m}}\)

Full size image

4 Conclusion

In this paper, the nonlinear dynamics model of an orthogonal curve-face gear system considering time-varying meshing stiffness, statics transmission error and backlash was established, approximate time-varying meshing stiffness of the orthogonal curve-face gear pair was obtained and vibration characteristics of the gear system at different mesh frequencies were also obtained.

The main results of the study are:

  1. 1.

    With the changing of meshing frequency, the gear system shows single-cycle harmonic response, nine-cycle response, quasi-periodic and chaotic response. When the meshing frequency is in the range of 0.38–0.96, the twisting vibration characteristics are most suitable for stable operation of the gear system. Based on the results, the gear system must operate much above or below its resonance range for stable operation.

  2. 2.

    With the increase of total backlash, the vibration amplitude also increases and the time to be stabilized also increases. When the total backlash is too large, the system shows chaotic response.