3D elasticity solution for uniformly loaded elliptical plates of functionally graded materials using complex variables method

Abstract

Based on the generalized England’s method, the three-dimensional elastic response in a transversely isotropic functionally graded elliptical plate with clamped edge subject to uniform load is investigated. The material properties can arbitrarily vary along the thickness direction of the plate. The expressions of the mid-plane displacements of the plate are constructed to meet the clamped boundary conditions in which the unknown constants are determined from the governing equations. The expressions of four analytic functions $\alpha (\zeta )$, $\beta (\zeta )$, $\phi (\zeta )$ and $\psi (\zeta )$ corresponding to this problem are then obtained using the complex variables method. As a result, the three-dimensional elasticity solution of a functionally graded elliptical plate with clamped boundary subject to uniform load is derived. Finally, numerical examples are presented to verify the proposed method and discuss the effects of different factors on the deformation and stresses in the plate.

1 Introduction

Elliptical plates are frequently encountered in many engineering fields. The bending of elliptical plate has long been one of the important classical topics in the theory of elasticity [1]. Meanwhile, functionally graded materials (FGMs) are a novel type of microscopically inhomogeneous composites in which the material composition and mechanical properties exhibit gradient change in one or more directions. Therefore, a large number of research activities have been directed to the study of elastic responses of FGM plates under various conditions [2].

There are several methods that have been adopted to analyze the bending problem of FGM plates, most of which are based on certain simplified plate theories. For example, Reddy et al. [3] studied the axisymmetric bending of FGM circular and annular plates and presented the relationships between the solutions of the classical plate theory (CPT) and the first-order shear deformation plate theory (FSDT). Various higher-order shear deformation theories were used to model the FGM rectangular plates by Xiang and Kang [4], and a meshless method based on thin plate spline radial function was suggested. Based on the extended Kantorovich method combined with the FSDT, Aghdam et al. [5] and Fallah and Khakbaz [6] presented highly accurate bending solutions for moderately thick functionally graded (FG) fully clamped sector plates and functionally graded annular sector plates with arbitrary boundary conditions, respectively.

As we all know, only a relatively few problems can be solved to obtain the exact analytical solutions based on the elasticity theory. However, these analytical solutions can be used as benchmarks to access the validity of various plate theories or numerical methods. Based on the three-dimensional (3D) elasticity theory, Cheng and Batra [7] used an asymptotic expansion method to analyze the isotropic FGM elliptic plate with clamped edge. Li et al. [8] obtained the solution of pure bending of FGM circular plates using stress function method. Wang et al. [9] investigated the axisymmetric bending of transversely isotropic FGM circular plates subject to arbitrarily transverse loads. Alibeigloo [10] presented 3D thermoelastic solution of a simply supported sandwich panel with FG core using Fourier series expansions and state-space technique. Numerical or semi-analytical methods based on elasticity theory have also been used in the literature. For instance, Adineh and Kadkhodayan [11] recently carried out a thermoelastic analysis of a multi-directional functionally graded thick rectangular plate with different boundary conditions. To the authors’ knowledge, however, no closed-form solution has been reported for the bending of transversely isotropic FGM elliptical plates based on 3D theory of elasticity.

In the authors’ previous work [13,14,15,16], based on a generalization of the England’s theory [12], equilibrium problems of transversely isotropic FGM plates with circular and elliptical holes, sectorial plates and annular sectorial plates were investigated based on 3D elasticity, respectively. In the present study, the generalized England’s theory is further utilized to study the bending of transversely isotropic FGM elliptical plates with clamped boundary subject to uniform load. Inspired by the skill of solving clamped elliptical plate in the classical book by Timoshenko and Woinowsky-Krieger [17], the expressions of the mid-plane displacements of the clamped elliptical plate are explicitly constructed firstly. Using the complex variables method, four analytic functions $\alpha (\zeta )$, $\beta (\zeta )$, $\phi (\zeta )$ and $\psi (\zeta )$ are then determined to express the 3D elasticity solution. Finally, the proposed method is verified in the numerical examples, and the effects of different factors on the deformation and stress distributions in the plate are investigated in detail through a comprehensive parametric study.

Fig. 1

Schematic diagram of FGM elliptical plate and the coordinates: a 3D model, b front view and c mid-plane

2 Theoretical formulations

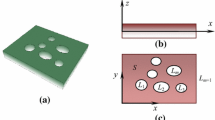
For a transversely isotropic FGM elliptical plate with thickness h, and semimajor and semiminor axes a and b, respectively, we employ a system of rectangular Cartesian coordinates (x, y, z). As shown in Fig. 1, the z-axis coincides with the material axis of symmetry and is perpendicular to the mid-plane (i.e., the $x-y$ plane) of the plate.

In the absence of body forces, the equations of equilibrium are

$$\begin{aligned} \sigma _{ij,j} =0, \end{aligned}$$

(1)

where the subscript comma denotes differentiation with respect to the coordinate variable that follows.

The relations of stresses and displacements for transversely isotropic materials can be expressed as [18]:

$$\begin{aligned} \sigma _x= & {} c_{11} u_{,x} +c_{12} v_{,y} +c_{13} w_{,z} , \quad \sigma _y =c_{12} u_{,x} +c_{11} v_{,y} +c_{13} w_{,z} , \quad \sigma _{zx} =c_{44} ( {w_{,x} +u_{,z} }),\nonumber \\ \sigma _z= & {} c_{13} u_{,x} +c_{13} v_{,y} +c_{33} w_{,z} , \quad \sigma _{yz} =c_{44} ( {v_{,z} +w_{,y} } ), \quad \sigma _{xy} =c_{66} ( {u_{,y} +v_{,x} } ), \end{aligned}$$

(2)

where $c_{ij}$ with $2c_{66} =c_{11} -c_{12}$ denotes the elastic coefficients, which are functions of z, i.e., $c_{ij} =c_{ij} (z)$ for FGMs. If $c_{11} =c_{33}$, $c_{12} =c_{13}$, and $c_{44} =c_{66}$, the material becomes isotropic.

We express the displacement field as [12]

$$\begin{aligned} u( {x,y,z} )= & {} {\bar{u}}+R_1 \Delta _{,x} +R_0 {\bar{w}}_{,x} +R_2 \nabla ^{2}{\bar{w}}_{,x} +R_3 \nabla ^{4}{\bar{w}}_{,x} +R_4 \nabla ^{6}{\bar{w}}_{,x},\nonumber \\ v( {x,y,z})= & {} {\bar{v}}+R_1 \Delta _{,y} +R_0 {\bar{w}}_{,y} +R_2 \nabla ^{2}{\bar{w}}_{,y} +R_3 \nabla ^{4}{\bar{w}}_{,y} +R_4 \nabla ^{6}{\bar{w}}_{,y},\nonumber \\ w( {x,y,z})= & {} {\bar{w}}+T_1 \Delta +T_2 \nabla ^{2}{\bar{w}}+T_3 \nabla ^{4}{\bar{w}}+T_4 \nabla ^{6}{\bar{w}}, \end{aligned}$$

(3)

where $R_j \;( {j=0,\ldots ,4} )$ and $T_{k}(k=1,\ldots ,4)$ are functions of z; ${\bar{u}}={\bar{u}}(x,y)$, ${\bar{v}}={\bar{v}}(x,y)$ and ${\bar{w}}={\bar{w}}(x,y)$ are the mid-plane displacements; and

$$\begin{aligned} \Delta =\bar{u}_{,x}+\bar{v}_{,y}, \quad \nabla ^{2}=\frac{\partial ^{2}}{\partial x^{2}}+\frac{\partial ^{2}}{\partial y^{2}}, \quad \nabla ^{4}=\nabla ^{2}\nabla ^{2},\quad \nabla ^{6}=\nabla ^{2}\nabla ^{4}. \end{aligned}$$

(4)

The expressions of the z-dependent functions $R_j \;( {j=0,\ldots ,4})$ and $T_k \;( {k=1,\ldots ,4})$ can be determined from the stress boundary conditions on the top and bottom surfaces of the plate; they can be readily found in Yang et al. [12]. The governing equations of the mid-plane displacements are

$$\begin{aligned}&S_{1} ( {h/2})\nabla ^{{4}}{\bar{w}}=-p( {x,y})+S_{21} \nabla ^{2}p( {x,y} ). \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial E( {x,y})}{\partial x}-\frac{\partial \Omega }{\partial y}=0, \quad \frac{\partial E( {x,y})}{\partial y}+\frac{\partial \Omega }{\partial x}=0. \end{aligned}$$

(6)

where $S_{21} ={S_2 (h/2)}/{S_1 (h/2)}$, p(x, y) is an arbitrary biharmonic load applied on the surface $z=h/2$ of the plate, and

$$\begin{aligned}&E( {x,y})=\kappa _1 \Delta +\kappa _2 \nabla ^{2}{\bar{w}}+\kappa _3 \nabla ^{4}{\bar{w}}+\kappa _4 \nabla ^{6}{\bar{w}}, \quad \Omega ={\bar{v}}_{,x} -{\bar{u}}_{,y} . \end{aligned}$$

(7)

$$\begin{aligned}&S_1 ( z)=c_{33} {T}'_3 +c_{13} \left( {R_2 -\frac{\kappa _2 }{\kappa _1 }R_1 } \right) , \quad S_2 ( z)=c_{33} {T}'_4 +c_{13} \left( {R_3 -\frac{\kappa _3 }{\kappa _1 }R_1 } \right) . \end{aligned}$$

(8)

in which $\kappa _1$, $\kappa _2$, $\kappa _3$ and $\kappa _4$ are constants defined in Yang et al. [12].

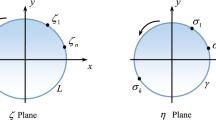
According to Yang et al. [12], the mid-plane displacements of the plate can be expressed by four complex functions $\alpha ( \zeta )$, $\beta ( \zeta )$, $\phi ( \zeta )$ and $\psi ( \zeta )$ as:

$$\begin{aligned} {\bar{w}}= & {} \alpha ( \zeta )+\overline{\alpha ( \zeta )} +{\bar{\zeta }}\beta ( \zeta )+\zeta \overline{\beta ( \zeta )} +W( {\zeta ,{\bar{\zeta }}}). \end{aligned}$$

(9)

$$\begin{aligned} D= & {} {\bar{u}}+i{\bar{v}}=\frac{\kappa _1 +1}{\kappa _1 -1}\phi ( \zeta )-\zeta \overline{{\phi }'( \zeta )} -\overline{\psi ( \zeta )} -2\frac{\kappa _2 }{\kappa _1 }\left[ {\beta ( \zeta )+\zeta \overline{{\beta }'( \zeta )} } \right] \nonumber \\&-\frac{2}{\kappa _1 }\left( {\kappa _2 +\kappa _3 \nabla ^{2}+\kappa _4 \nabla ^{4}} \right) \frac{\partial W}{\partial {\bar{\zeta }}}. \end{aligned}$$

(10)

where $W(\zeta ,{\bar{\zeta }})$ is a particular solution related to load in Eq. (5) and

$$\begin{aligned} \zeta =x+iy, \quad {\bar{\zeta }}=x-iy, \quad 2\frac{\partial }{\partial \zeta }=\frac{\partial }{\partial x}-i\frac{\partial }{\partial y}, \quad 2\frac{\partial }{\partial {\bar{\zeta }}}=\frac{\partial }{\partial x}+i\frac{\partial }{\partial y}. \end{aligned}$$

(11)

It should be noted that the two analytic functions $\phi ( \zeta )$ and $\psi ( \zeta )$ are related to the in-plane deformation and two analytic functions $\alpha ( \zeta )$ and $\beta ( \zeta )$ are associated with the bending deformation of the plate. The corresponding 3D displacement and stress components can then be given as

$$\begin{aligned} w( {x,y,z})= & {} {\bar{\zeta }}\beta ( \zeta )+\zeta \overline{\beta ( \zeta )} +\alpha ( \zeta )+\overline{\alpha ( \zeta )} +W( {\zeta ,{\bar{\zeta }}}) \nonumber \\&+\, \frac{2T_1 }{\kappa _1 -1}\left[ {{\phi }'( \zeta )+\overline{{\phi }'( \zeta )} } \right] +4\left( {T_2 -\frac{\kappa _2 }{\kappa _1 }T_1 } \right) \left[ {{\beta }'( \zeta )+\overline{{\beta }'( \zeta )} } \right] \nonumber \\&+\left( {T_2 -\frac{\kappa _2 }{\kappa _1 }T_1 } \right) \nabla ^{2}W+\left( {T_3 -\frac{\kappa _3 }{\kappa _1 }T_1 } \right) \nabla ^{4}W+\left( {T_4 -\frac{\kappa _4 }{\kappa _1 }T_1 } \right) \nabla ^{6}W. \end{aligned}$$

(12)

$$\begin{aligned} u\left( {x,y,z} \right) +iv\left( {x,y,z} \right)= & {} \frac{\kappa _1 +1}{\kappa _1 -1}\phi ( \zeta )-\zeta \overline{{\phi }'( \zeta )} -\overline{\psi \left( \zeta \right) } +\frac{4}{\kappa _1 -1}R_1 \overline{{\phi }''( \zeta )} \nonumber \\&+\, 2\left( {R_0 -\frac{\kappa _2 }{\kappa _1 }} \right) \left[ {\beta ( \zeta )+\zeta \overline{{\beta }'( \zeta )} } \right] +2R_0 \overline{{\alpha }'( \zeta )} \nonumber \\&+\, 8\left( {R_2 -\frac{\kappa _2 }{\kappa _1 }R_1 } \right) \overline{{\beta }''( \zeta )} \nonumber \\&+\, 2\frac{\partial }{\partial {\bar{\zeta }}}\left[ {\left( {R_0 -\frac{\kappa _2 }{\kappa _1 }} \right) W+\left( {R_2 -\frac{\kappa _2 }{\kappa _1 }R_1 -\frac{\kappa _3 }{\kappa _1 }} \right) \nabla ^{2}W} \right. \nonumber \\&+\,\left. {\left( {R_3 -\frac{\kappa _3 }{\kappa _1 }R_1 -\frac{\kappa _4 }{\kappa _1 }} \right) \nabla ^{4}W+\left( {R_4 -\frac{\kappa _4 }{\kappa _1 }R_1 } \right) \nabla ^{6}W} \right] . \end{aligned}$$

(13)

$$\begin{aligned} \sigma _x +\sigma _y= & {} \left( {c_{11} +c_{12} -2\frac{c_{13}^2 }{c_{33} }} \right) \left\{ {\frac{2}{\kappa _1 -1}\left[ {{\phi }'( \zeta )+\overline{{\phi }'( \zeta )} } \right] } \right. \nonumber \\&-\, 4\left( {z+\frac{\kappa _2 }{\kappa _1 }} \right) \left[ {{\beta }'( \zeta )+\overline{{\beta }'( \zeta )} } \right] +\left. {\left( {z+\frac{\kappa _2 }{\kappa _1 }} \right) \nabla ^{2}W} \right\} \nonumber \\&+\, \left[ {\left( {c_{11} +c_{12} } \right) \left( {R_2 -\frac{\kappa _2 }{\kappa _1 }R_1 } \right) +2c_{13} {T}'_3 -\left( {c_{11} +c_{12} -2\frac{c_{13}^2 }{c_{33} }} \right) \frac{\kappa _3 }{\kappa _1 }} \right] \nabla ^{4}W \nonumber \\&+\, \left[ {\left( {c_{11} +c_{12} } \right) \left( {R_3 -\frac{\kappa _3 }{\kappa _1 }R_1 } \right) +2c_{13} {T}'_4 -\left( {c_{11} +c_{12} -2\frac{c_{13}^2 }{c_{33} }} \right) \frac{\kappa _4 }{\kappa _1 }} \right] \nabla ^{6}W.\nonumber \\ \end{aligned}$$

(14)

$$\begin{aligned} \sigma _y -\sigma _x +2i\sigma _{xy}= & {} 4c_{66} \left[ {{\bar{\zeta }}{\phi }''( \zeta )+{\psi }'\left( \zeta \right) } \right] -\frac{16c_{66} }{\kappa _1 -1}R_1 {\phi }'''( \zeta )\nonumber \\&+\, 8c_{66} \left( {z+\frac{\kappa _2 }{\kappa _1 }} \right) {\bar{\zeta }}{\beta }''( \zeta )+8c_{66} z{\alpha }''( \zeta ) \nonumber \\&-\,32c_{66} \left( {R_2 -\frac{\kappa _2 }{\kappa _1 }R_1 } \right) {\beta }'''( \zeta )\nonumber \\&+\, 8c_{66} \frac{\partial ^{2}}{\partial \zeta ^{2}}\left[ {\left( {z+\frac{\kappa _2 }{\kappa _1 }} \right) W-\left( {R_2 -\frac{\kappa _2 }{\kappa _1 }R_1 -\frac{\kappa _3 }{\kappa _1 }} \right) \nabla ^{2}W} \right. \nonumber \\&-\,\left. {\left( {R_3 -\frac{\kappa _3 }{\kappa _1 }R_1 -\frac{\kappa _4 }{\kappa _1 }} \right) \nabla ^{4}W-\left( {R_4 -\frac{\kappa _4 }{\kappa _1 }R_1 } \right) \nabla ^{6}W} \right] . \end{aligned}$$

(15)

$$\begin{aligned} \sigma _{{xz}} - i\sigma _{{yz}}= & {} \frac{{4c_{{44}} }}{{\kappa _{1} - 1}}\left( {R^{\prime }_{1} + T_{1} } \right) \phi ^{\prime \prime }\left( \zeta \right) + 8c_{{44}} \left[ {T_{2} + R^{\prime }_{2} - \frac{{\kappa _{2} }}{{\kappa _{1} }}\left( {T_{1} + R^{\prime }_{1} } \right) } \right] \beta ^{\prime \prime }\left( \zeta \right) \nonumber \\&+\,2c_{{44}} \frac{\partial }{{\partial \zeta }}\left\{ {\left[ {T_{2} + R^{\prime }_{2} - \frac{{\kappa _{2} }}{{\kappa _{1} }}\left( {T_{1} + R^{\prime }_{1} } \right) } \right] \nabla ^{2} W} \right. \nonumber \\&+\,\left[ {T_{3} + R^{\prime }_{3} - \frac{{\kappa _{3} }}{{\kappa _{1} }}\left( {T_{1} + R^{\prime }_{1} } \right) } \right] \nabla ^{4} W \nonumber \\&+\,\left. {\left[ {T_{4}+ R^{\prime }_{4} - \frac{{\kappa _{4} }}{{\kappa _{1} }}\left( {T_{1} + R^{\prime }_{1} } \right) } \right] \nabla ^{6} W} \right\} . \end{aligned}$$

(16)

$$\begin{aligned} \sigma _{z}= & {} S_{1} \left( z \right) \nabla ^{4} \bar{w} + S_{2} \left( z \right) \nabla ^{6} \bar{w}. \end{aligned}$$

(17)

3 An FGM elliptical plate with clamped edge subject to uniform load

Now consider an elliptical plate subject to a uniform load $p(x,y)=q$. The shape of the plate can be defined by the equation

$$\begin{aligned} \left( {\frac{x}{a}} \right) ^{2}{+}\left( {\frac{y}{b}} \right) ^{2}=1. \end{aligned}$$

(18)

The cylindrical boundary conditions at the clamped edge of the plate are approximated by

$$\begin{aligned} {\bar{u}}={\bar{v}}={\bar{w}}=0, \quad \frac{\partial {\bar{w}}}{\partial n}=0 \end{aligned}$$

(19)

here n denotes the outward unit normal to the edge of the elliptical plate.

Inspired by the skill of solving clamped elliptical plate in Timoshenko and Woinowsky-Krieger [17], we may take the following forms for the mid-plane displacements

$$\begin{aligned} {\bar{w}}=C\left( {1-\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}} \right) ^{2}, \quad {\bar{u}}=A\left( {1-\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}} \right) x, \quad {\bar{v}}=B\left( {1-\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}} \right) y, \end{aligned}$$

(20)

where the first equation is taken as that in the book [17] and A, B and C are constants to be determined.

By substituting Eq. (20)$_{1}$ into Eq. (5), we get

$$\begin{aligned} C=-\frac{qa^{4}b^{4}}{8S_1 \left( {h/2} \right) \left( {3a^{4}+3b^{4}+2a^{2}b^{2}} \right) }. \end{aligned}$$

(21)

which is the same as that in Timoshenko and Woinowsky-Krieger [17].

Substituting Eq. (20) into Eq. (7), we obtain

$$\begin{aligned} E\left( {x,y} \right)= & {} \kappa _1 \left[ {A+B-\left( {3A+B} \right) \frac{x^{2}}{a^{2}}-\left( {3B+A} \right) \frac{y^{2}}{b^{2}}} \right] \nonumber \\&+\,\kappa _2 C\left[ {-4\left( {\frac{1}{a^{2}}+\frac{1}{b^{2}}} \right) +4\left( {\frac{3}{a^{4}}+\frac{1}{a^{2}b^{2}}} \right) x^{2}+4\left( {\frac{1}{a^{2}b^{2}}+\frac{3}{b^{4}}} \right) y^{2}} \right] \nonumber \\&+\,8\kappa _3 C\left[ {\frac{3}{a^{4}}+\frac{2}{a^{2}b^{2}}+\frac{3}{b^{4}}} \right] . \end{aligned}$$

(22)

$$\begin{aligned} \Omega \left( {x,y} \right)= & {} 2\left( {\frac{A}{b^{2}}-\frac{B}{a^{2}}} \right) xy. \end{aligned}$$

(23)

Substituting Eqs. (22) and (23) into Eq. (6) gives

$$\begin{aligned}&\left( {\frac{3\kappa _1 }{a^{2}}+\frac{1}{b^{2}}} \right) A+\left( {\frac{\kappa _1 -1}{a^{2}}} \right) B=4\kappa _2 C\left( {\frac{3}{a^{4}}{+}\frac{1}{a^{2}b^{2}}} \right) . \end{aligned}$$

(24)

$$\begin{aligned}&\left( {\frac{\kappa _1 -1}{b^{2}}} \right) A+\left( {\frac{3\kappa _1 }{b^{2}}+\frac{1}{a^{2}}} \right) B=4\kappa _2 C\left( {\frac{1}{a^{2}b^{2}}{+}\frac{3}{b^{4}}} \right) . \end{aligned}$$

(25)

By solving Eqs. (24) and (25), we obtain

$$\begin{aligned} A=\frac{4\kappa _2 C}{a^{2}\kappa _1 }, \quad B=\frac{4\kappa _2 C}{b^{2}\kappa _1 }. \end{aligned}$$

(26)

As can be found in Yang et al. [12], the expression of the constant $\kappa _2$ is

$$\begin{aligned} \kappa _2 =-\frac{h_1^0 \left( {h/2} \right) }{g_6 \left( {h/2} \right) }. \end{aligned}$$

(27)

where

$$\begin{aligned} g_6 \left( z \right) =\int _{-\frac{h}{2}}^z {c_{66} \left( \xi \right) } \hbox {d}\xi , \quad h_1^0 \left( z \right) =\int _{-\frac{h}{2}}^z {\xi \left[ {c_{11} \left( \xi \right) -\frac{c_{13}^2 \left( \xi \right) }{c_{33} \left( \xi \right) }} \right] \;} \hbox {d}\xi . \end{aligned}$$

(28)

For a homogeneous material, it can be found from Eq. (27) that $\kappa _2 =0$. As a result, constants A and B and hence ${\bar{u}}={\bar{v}}$ are all equal to zero, which are consistent with those in simplified plate theories for homogeneous materials.

By integrating Eq. (5), we have

$$\begin{aligned} W\left( {\zeta ,{\bar{\zeta }}} \right) =-\,\frac{q}{64S_1 \left( {h/2} \right) }\zeta ^{2}{\bar{\zeta }}^{2}, \end{aligned}$$

(29)

which is a particular solution of Eq. (5).

Equation (20)$_{1}$ is represented by the complex variables $\zeta$ as

$$\begin{aligned} {\bar{w}}= & {} C\left[ {1+\left( {\frac{1}{16a^{4}}+\frac{1}{16b^{4}}-\frac{1}{8a^{2}b^{2}}} \right) \zeta ^{4}+\left( {\frac{1}{2b^{2}}-\frac{1}{2a^{2}}} \right) \zeta ^{2}} \right. \nonumber \\&+\,\left( {\frac{1}{16a^{4}}+\frac{1}{16b^{4}}-\frac{1}{8a^{2}b^{2}}} \right) {\bar{\zeta }}^{4}+\left( {\frac{1}{2b^{2}}-\frac{1}{2a^{2}}} \right) {\bar{\zeta }}^{2}+{\bar{\zeta }}\zeta ^{3}\left( {\frac{1}{4a^{4}}-\frac{1}{4b^{4}}} \right) \nonumber \\&-\,\left. {{\bar{\zeta }}\zeta \left( {\frac{1}{a^{2}}+\frac{1}{b^{2}}} \right) +\zeta {\bar{\zeta }}^{3}\left( {\frac{1}{4a^{4}}-\frac{1}{4b^{4}}} \right) +\zeta ^{2}{\bar{\zeta }}^{2}\left( {\frac{1}{4a^{2}b^{2}}+\frac{3}{8a^{4}}+\frac{3}{8b^{4}}} \right) } \right] . \end{aligned}$$

(30)

By comparing Eq. (30) with Eq. (9), we obtain

$$\begin{aligned} \alpha ( \zeta )= & {} \frac{C}{2}\left[ {1+\frac{1}{8}\left( {\frac{1}{b^{2}}-\frac{1}{a^{2}}} \right) ^{2}\zeta ^{4}+\left( {\frac{1}{b^{2}}-\frac{1}{a^{2}}} \right) \zeta ^{2}} \right] . \end{aligned}$$

(31)

$$\begin{aligned} \beta ( \zeta )= & {} \frac{C}{2}\left[ {\frac{1}{2}\left( {\frac{1}{a^{4}}-\frac{1}{b^{4}}} \right) \zeta ^{3}-\left( {\frac{1}{a^{2}}+\frac{1}{b^{2}}} \right) \zeta } \right] . \end{aligned}$$

(32)

The expressions of the mid-plane displacements can be rewritten in complex forms based on Eqs. (20)$_{2,3}$

$$\begin{aligned} D= & {} {\bar{u}}+i{\bar{v}} \nonumber \\= & {} \frac{1}{2}\left( {A+B} \right) \zeta +\frac{1}{2}\left( {A-B} \right) {\bar{\zeta }}+\frac{1}{8}\left( {A+B} \right) \left( {\frac{1}{b^{2}}-\frac{1}{a^{2}}} \right) \zeta ^{3} \nonumber \\&+\,\frac{1}{8}\left( {A-B} \right) \left( {\frac{1}{b^{2}}-\frac{1}{a^{2}}} \right) {\bar{\zeta }}^{3}+\left[ {\frac{1}{8}\left( {A-B} \right) \left( {\frac{1}{b^{2}}-\frac{1}{a^{2}}} \right) -\frac{1}{4}\left( {A+B} \right) \left( {\frac{1}{a^{2}}+\frac{1}{b^{2}}} \right) } \right] {\bar{\zeta }}\zeta ^{2} \nonumber \\&+\,\left[ {\frac{1}{8}\left( {A+B} \right) \left( {\frac{1}{b^{2}}-\frac{1}{a^{2}}} \right) -\frac{1}{4}\left( {A-B} \right) \left( {\frac{1}{a^{2}}+\frac{1}{b^{2}}} \right) } \right] \zeta {\bar{\zeta }}^{2}. \end{aligned}$$

(33)

Substituting Eqs. (29), (31) and (32) into Eq. (10) leads to

$$\begin{aligned} D= & {} \frac{\kappa _1 +1}{\kappa _1 -1}\phi ( \zeta )-\zeta \overline{{\phi }'( \zeta )} -\overline{\psi \left( \zeta \right) } \nonumber \\&-\,\frac{\kappa _2 C}{\kappa _1 }\left[ {\frac{1}{2}\left( {\frac{1}{a^{4}}-\frac{1}{b^{4}}} \right) \zeta ^{3}+\frac{3}{2}\left( {\frac{1}{a^{4}}-\frac{1}{b^{4}}} \right) \zeta {\bar{\zeta }}^{2}-2\left( {\frac{1}{a^{2}}+\frac{1}{b^{2}}} \right) \zeta } \right] \nonumber \\&+\,\frac{\kappa _2 }{\kappa _1 }\frac{q}{16S_1 }\zeta ^{2}{\bar{\zeta }}+\frac{\kappa _3 }{\kappa _1 }\frac{q}{2S_1 }\zeta . \end{aligned}$$

(34)

By comparing Eq. (33) with Eq. (34), we obtain

$$\begin{aligned} \phi ( \zeta )= & {} \left[ {\frac{\kappa _1 -1}{4}\left( {A+B} \right) -\frac{\kappa _1 -1}{\kappa _1 }\kappa _2 C\left( {\frac{1}{a^{2}}{+}\frac{1}{b^{2}}} \right) -\frac{\kappa _1 -1}{4\kappa _1 S_1 }\kappa _3 q} \right] \zeta . \end{aligned}$$

(35)

$$\begin{aligned} \psi ( \zeta )= & {} \frac{1}{2}\left( {B-A} \right) \zeta +\frac{1}{8}\left( {B-A} \right) \left( {\frac{1}{b^{2}}-\frac{1}{a^{2}}} \right) \zeta ^{3}. \end{aligned}$$

(36)

So far, the expressions of four complex functions $\alpha \left( \zeta \right)$, $\beta ( \zeta )$, $\phi \left( \zeta \right)$ and $\psi ( \zeta )$ have been determined. Then, all 3D displacement and stress components of the plate can be obtained from Eqs. (12)–(17).

4 Numerical examples

4.1 Validation study

In order to validate the present method, an isotropic FGM circular plate with clamped boundary is considered by letting $a=b$ in an elliptical plate. We take $a=b=0.1~\hbox {m}$, $h=0.02~\hbox {m}$ and $q=10^{6}~\hbox {N}/\hbox {m}^{2}$. The elastic coefficients vary along the thickness of the plate according to the following power function model [3, 19, 20]

$$\begin{aligned} E=E^{T}\left( {0.5-z/h} \right) ^{\lambda }+E^{Z}\left[ {1-\left( {0.5-z/h} \right) ^{\lambda }} \right] ,\quad \upsilon =\hbox {const}, \end{aligned}$$

(37)

where $\lambda$ is the gradient index, $E^{T}=110.25~\hbox {GP}a$ and $E^{Z}=278.41~\hbox {GPa}$ are Young’s moduli of Titanium at $z={-\,h}/2$ and Zirconium at $z=h/2$, respectively, and $\upsilon =0.288$ is Poisson’s ratio. It is clearly shown that $\lambda =0$ or $\lambda \rightarrow \infty$ corresponds to a homogeneous material of Titanium or Zirconium.

Table 1 The deflection factor $w_0$ of the clamped circular plate subject to uniform load

The deflection factor $w_0 ={w(0,\;0,\;0)}/{w_1 }$ is introduced in this example where $w_1 ={qa^{4}}/{64D_Z }$ is the central deflection of a uniformly loaded isotropic homogeneous circular plate with clamped edge and $D_Z ={E^{Z}h^{3}}/{12(1-\upsilon ^{2})}$ is the bending stiffness of the plate [17]. Table 1 gives the deflection factor $w_0$ of the FGM circular plate with clamped edge, where comparison is made with the existing results. It can be found that the present solution agrees well with those predicted by the FSDT [3] and those by the elasticity theory [19]. Just as commented by Li et al. [19], the deflection of the plate with this kind of clamped boundary condition is independent of the thickness-to-radius ratio h / a, that is the deflection of the clamped plate is similar to that based on the CPT which is illustrated by Eqs. (20) and (21).

4.2 Parametric study

A parametric study is then carried out to investigate the influences of the gradient index, thickness-to-radius ratio and semiminor axis ratio on the deformation and stress fields in the transversely isotropic FGM elliptical plate with clamped edge. Unless stated otherwise, we take $a=0.1~\hbox {m}$, $b=0.05~\hbox {m}$ and $h=0.02~\hbox {m}$ and choose the point at $x=0$ and $y=0$ for calculating the values of the deflection and normal stress. The following FG model is adopted

$$\begin{aligned} c_{ij} =c_{ij}^{0\left( A \right) } \left( {0.5-z/h} \right) ^{\lambda }+c_{ij}^{0\left( T \right) } \left[ {1-\left( {{0.5-z}/h} \right) ^{\lambda }} \right] \quad \left( {i,\;j=1,2,3,4,5,6} \right) \end{aligned}$$

(38)

where $c_{ij}^{0(A)}$ are those of $\hbox {Al}_{2}\hbox {O}_{3}$ at $z={-\,h}/2$ and $c_{ij}^{0(T)}$ are those of Titanium at $z=h/2$, both given in Table 2 [18, 21].

Table 2 Elastic constants of $\hbox {Al}_{2}\hbox {O}_{3}$ and Titanium (Unit: GPa) [18, 21]

Table 3 Dimensionless deflection and stress of the clamped elliptical plate subject to uniform load

Table 3 gives the dimensionless deflection ${w(0,0,-\,h/2)}/h$, normal stresses ${\sigma _x (0,0,-\,h/2)}/q$ and ${\sigma _y (0,0,-\,h/2)}/q$ in the FGM elliptical plate with different values of $\lambda$. The thickness-to-radius ratio is fixed at $\beta =h/a=0.2$. The following observations can be obtained from the results:

• (1) The deflection increases with $\lambda$. The reason is that the bending rigidity of the FGM plate decreases with $\lambda$. Such an amplitude of increasing is obviously large at first and then becomes small when $\lambda$ increases.

• (2) At the plane of $z=-\,h/2$ where it is in a state of being stretched, the normal stresses are all positive. With the increase of $\lambda$, the value of the normal stresses increases gradually. The value of normal stress ${\sigma _x }/q$ is smaller than that of normal stress ${\sigma _y }/q$ for a given $\lambda$. This is attributed to a bigger size in the x direction than that in the y direction of the plate.

Fig. 2

Variation of elastic constant $c_{11}$ along the thickness with $\lambda$ in power function model

Figure 2 shows the variation of elastic coefficient $c_{11}$ along the thickness direction of the elliptical plate with $\lambda$ in power function model. It is clearly shown that $\lambda =0$ corresponds to a homogeneous material of $\hbox {Al}_{2}\hbox {O}_{3}$. The bending stiffness of the plate decreases when $\lambda >0$ and the constant $c_{11}$ falls faster along the thickness direction of the plate with the increase of $\lambda$.

Fig. 3

Distribution of dimensionless deflection $w/h\times 10^{5}$ along the thickness direction of the plate with different values of $\lambda$

Figure 3 displays the dimensionless deflection $w/h\times 10^{5}$ along the thickness direction of the clamped elliptical plate. The deflection is roughly a constant throughout the thickness direction when $\lambda =0,4$, whereas for $\lambda =10$, it is more clearly a symmetric and nonlinear curve. It should be emphasized that the real deflection distribution in the thickness direction can be naturally captured by the 3D elasticity theory, while in most plate theories (classical, first-order and higher-order), the deflection is usually assumed to be constant along the thickness direction.

Fig. 4

Distribution of dimensionless normal stress ${\sigma _x }/q$ along the thickness direction of the plate with different values of $\lambda$

Figure 4 illustrates the through-thickness distribution of dimensionless normal stress ${\sigma _x }/q$ of the clamped elliptical plate. The normal stress in the homogeneous plate changes linearly and antisymmetrically along the thickness direction, while that for the two inhomogeneous plates changes nonlinearly. In addition, it is observed that the difference in normal stress on the top surface is smaller than that on the bottom surface for the three kinds of elliptical plate.

Fig. 5

Distribution of dimensionless deflection $w/h\times 10^{4}$ in the x-direction of the plate with different values of $\beta$

Fig. 6

Distribution of dimensionless normal stress ${\sigma _x }/q$ in the x-direction of the plate with different values of $\beta$

Figures 5 and 6 depict the distributions of the dimensionless deflection $w/h\times 10^{4}$ and normal stress ${\sigma _x }/q$ at $z=h/2$ of the clamped elliptical plate along the x direction with $\lambda =2$ and different values of the thickness-to-radius ratio $\beta$. Here, the radius a keeps unchanged and the plate thickness h varies with $\beta$. Consequently, the bending stiffness increases with $\beta$ and the deflection corresponding to $\beta =0.1$ shows the biggest value. It can be found from Fig. 6 that the distribution of the dimensionless normal stress displays a symmetric and parabolic characteristic which is the same as that of the dimensionless deflection. It is also noted that for $\beta =0.1$, the maximum value occurs both at the center and the boundary among the three kinds of plate.

Fig. 7

Effects of geometric dimension and gradient factor on the dimensionless deflection $w/h\times 10^{4}$ of the plate

Fig. 8

Effects of geometric dimension and gradient factor on the dimensionless normal stress ${\sigma _x }/q$ of the plate

Figures 7 and 8 draw the effects of geometric dimension and gradient factor on the dimensionless deflection $w/h\times 10^{4}$ and normal stress ${\sigma _x }/q$ at $z=h/2$ in the elliptical plate. Here, the major radius a keeps constant and the minor radius b varies. It can be understood that the bending stiffness increases with a / b and the deflection eventually approaches to a small value for the three kinds of plate. For the dimensionless normal stress shown in Fig. 8, there is a little difference among the three kinds of plate, except for the case of a circular plate which shows a relatively large difference.

In order to show the material properties can arbitrarily vary along the thickness direction of the plate, the following FG exponential function model is adopted [8, 9]

$$\begin{aligned} c_{ij} =c_{ij}^{0\left( A \right) } e^{\frac{\left( {z+h/2} \right) }{h}\lambda } \quad \left( {i,\;j=1,2,3,4,5,6} \right) \end{aligned}$$

(39)

where $c_{ij}^{0(A)}$ are those of $\hbox {Al}_{2}\hbox {O}_{3}$ at $z={-\,h}/2$.

Fig. 9

Variation of elastic constant $c_{11}$ along the thickness with $\lambda$ in exponential function model

Figure 9 shows the variation of elastic coefficient $c_{11}$ along the thickness direction of the elliptical plate with $\lambda$ in exponential function model. It is verified again that $\lambda =0$ corresponds to a homogeneous material of $\hbox {Al}_{2}\hbox {O}_{3}$. The bending stiffness along the thickness direction decreases when $\lambda <0$, and increases for $\lambda >0$.

Fig. 10

Distribution of dimensionless deflection $w/h\times 10^{5}$ along the thickness direction of the plate with different values of $\lambda$

Figure 10 displays the dimensionless deflection $w/h\times 10^{5}$ along the thickness direction of the clamped elliptical plate. The deflection is roughly a constant throughout the thickness direction when $\lambda =0,5$, whereas for $\lambda =-\,5$, it is more clearly a nonlinear curve. Among three kinds of FGM plate, the dimensionless deflection is the smallest for $\lambda =5$ which corresponds to the largest bending stiffness of the plate and that is the largest for $\lambda =-\,5$ which corresponds to the smallest bending stiffness of the plate.

Fig. 11

Distribution of dimensionless normal stress ${\sigma _x }/q$ along the thickness direction of the plate with different values of $\lambda$

Figure 11 illustrates the through-thickness distribution of dimensionless normal stress ${\sigma _x }/q$ of the clamped elliptical plate. The normal stress in the homogeneous plate changes linearly and antisymmetrically along the thickness direction, while that for the two inhomogeneous plates changes nonlinearly. In addition, it is observed that the maximum compressive stress occurs on the top surface when $\lambda =5$ and the maximum tensile stress occurs on the bottom surface when $\lambda ={-}\,5$.

Fig. 12

Distribution of dimensionless shear stress ${\sigma _{xz} }/q$ along the thickness direction of the plate with different values of $\lambda$

Figure 12 draws the through-thickness distribution of dimensionless shear stress ${\sigma _{xz} }/q$ of the clamped elliptical plate at $x=a/2$ and $y=0$. As for $\lambda =0$, the dimensionless shear stress is parabolic distribution and symmetric about the mid-plane of the plate. As for FGM plates, the shear stress grows quickly and reaches the maximum value near the bottom surface when $\lambda ={-}\,5$ and decreases quickly from the maximum value occurred near the top surface when $\lambda =5$.

5 Conclusions

This paper studies the bending of a transversely isotropic FGM elliptical plate with clamped edge subject to uniform load based on a generalization of the England’s theory. The material coefficients can vary arbitrarily and continuously along the thickness of the plate. The simplified boundary conditions in the CPT at the cylindrical boundary are employed. By constructing explicitly the expressions of the mid-plane displacements to meet the clamped boundary conditions and the governing equations, the 3D closed-form solution of a transversely isotropic FGM elliptical plate with clamped edge subject to uniform load is successfully derived.

The validity and accuracy of the present method is verified by comparing the numerical results for a circular plate with the available FSDT solution and the elasticity solution. Numerical results show that the gradient index, thickness-to-radius ratio and semiminor axis ratio have important effects on the response of the FGM elliptical plate. Therefore, the bending behavior of FGM elliptical plates can be optimized by adjusting properly the factors mentioned above in engineering applications.

We finally emphasize that the present closed-form solutions exactly satisfy the 3D equilibrium equations and the traction boundary conditions on the top and bottom surfaces of the plate. The cylindrical boundary conditions in the plate are satisfied in the Saint-Venant sense. Thus, the proposed elasticity solutions can serve as a benchmark for the mechanical bending solutions of FGM elliptical plates with clamped edge based on various simplified plate theories or numerical methods.