Transverse Vibration of Thin Rectangular Orthotropic Plates on Translational and Rotational Elastic Edge Supports: A Semi-analytical Approach

Abstract

The free vibration analysis of thin orthotropic plates with elastically constrained edges is presented using the energy-based Rayleigh–Ritz (RR) method. Various edge conditions are modeled with rotational and translational linear springs. The complete set of admissible functions, which is a combination of (1) trigonometric functions, (2) the unit function, (3) the linear function, and (4) the lowest order polynomial, has been used in the RR method. It has been demonstrated that the use of a combination of the lowest order polynomial and the cosine series results in a rapid convergence of the solution, without any ill-conditioning of the admissible functions upon expansion. In particular, this work proposes a simple guideline for determining a set of trial functions that can be universally utilized for the vibration analysis of plates with non-classical boundary conditions. The convergence and exactness of this approach have been demonstrated through several examples. The results indicate that the elastically restrained stiffness and the plate aspect ratio impact the frequency parameters considerably.

1 Introduction

Orthotropic plates, due to their high strength-to-weight ratio, have wide applications in various structural engineering fields like civil constructions, aerospace structures, and marine constructions. The extensive use of orthotropic plates requires the precise vibration characteristics for long-lasting engineering design. In the industry, the finite element method-based softwares are used for vibration analysis, leading to the natural frequencies, mode shapes, and dynamic responses of the structure. However, the non-classical boundary conditions may be often difficult to model. Also, repeatedly changing the non-classical boundary conditions during the design iterations becomes a long-drawn out process in the commercial software. Therefore, during the initial design stage, when the boundary conditions (along with the geometric and material properties) are yet to be finalized, it is useful to have a reliable and fast analytical/semi-analytical methodology to benchmark the vibration parameters of the structure.

The free vibration of orthotropic plates with classical boundary conditions has been extensively studied in recent decades. Hearmon (1959) studied the free vibration of orthotropic plates considering beam functions as the trial functions in the Rayleigh–Ritz method. The beam functions were expressed as linear combinations of trigonometric and hyperbolic functions, with unknown coefficients which are to be determined for each set of boundary conditions by solving a system of four coupled ordinary differential equations. This makes the use of beam functions a very tedious process. In addition, a set of trial functions using hyperbolic and trigonometric functions are prone to numerical instability when more terms are incorporated in the solution. The Rayleigh–Ritz method is one of the suitable and convenient methods to calculate the eigenvalues of rectangular orthotropic plates due to its conceptual simplicity (Meirovitch 1975). Dickinson and Di Blasio (1986) used orthogonal polynomials as admissible functions in the Rayleigh–Ritz method to study the transverse vibration and buckling of orthotropic and isotropic rectangular plates for classical boundary conditions. Bapat et al. (1988) investigated the effects of the elastic edge support stiffness and its distribution on the natural frequencies, shear force, and bending moment of the thin plate. Gorman (1982) applied the superposition method to study free vibration of the isotropic plate and then extended it for the application to completely free orthotropic plates (Gorman 1993), clamped orthotropic plates (Gorman 1990), and point-supported orthotropic plates (Gorman 1994). Dalaei and Kerr (1996) investigated the free vibration of thin rectangular orthotropic plates with fully fixed edges using the extended Kantorovich method. Rossi et al. (1998) studied the vibration of orthotropic plates with free edges using an optimized Rayleigh–Ritz method. The results were compared with those calculated using the finite element method. Hurlebaus et al. (2001) studied the modal characteristics of a completely free orthotropic thin plate by an exact solution method. Ahmadian and Zangeneh (2002) applied efficient superelements to study the fundamental frequencies of isotropic and orthotropic plates with various classical boundaries. Li (2004) studied the vibration of isotropic plates with elastic edge supports using Rayleigh–Ritz method. The displacement functions are a combination of cosine Fourier series and fourth-order Legendre polynomial. The coefficients of the Legendre polynomial functions are required to be calculated for every boundary condition. In addition, it was reported that the use of polynomials in higher-order analysis led to numerically unstable solutions due to round-off errors. Biancolini et al. (2005) studied the free vibration of thin orthotropic rectangular plates with classical edges by an approximate solution technique and validated them with the finite element method.

Li and Cheng (2005) studied the nonlinear vibration of orthotropic plates using the differential quadrature method (DQM). Huang et al. (2005) investigated the free vibration of orthotropic rectangular plates with variable thickness in one or two directions, using a discrete method, for only the classical boundary conditions. Xing and Liu (2009) presented an exact solution technique for the free vibration of thin orthotropic plates having combinations of simply supported and clamped conditions only. Hsu (2010) investigated the vibration of a thin plate resting on an elastic foundation using the Rayleigh–Ritz method. Jafari and Eftekhari (2011) calculated the non-dimensional frequency parameters and critical bucking loads of thin orthotropic plates for classical boundary conditions, using the efficient mixed Ritz-differential quadrature method. Shi et al. (2014) investigated the free vibration of thin orthotropic plate with arbitrary elastic supports using the Spectro-Geometric Method. Xing and Xu (2013) investigated the free vibration of rectangular thin plates with at least two adjacent clamped edges and others as arbitrary combinations of the simply supported, guided, and clamped type. Datta and Verma (2018) studied the influence of the rigid-body modes on the vibration modes of thin plates. Verma and Datta (2018) investigated the free vibration of the Kirchhoff’s plate having edges supported only by variable translational springs, by using the Rayleigh–Ritz method. Zhang et al. (2019) recently investigated the free transverse vibration of the rotationally restrained rectangular orthotropic plates using the method of finite integral transform.

The past investigations on orthotropic plates are mostly limited to classical boundary conditions and their possible combinations. However, the realistic non-classical boundary conditions are often encountered in practical engineering applications, where the edge supports can be modeled as uniformly distributed translational and/or rotational springs. This work presents a new complete set of orthogonal admissible functions, satisfying all the beam boundary conditions, as well as the rigid-body mode shapes for free–free and sliding–sliding beams. Only four simple functions are shown to be sufficient to together act as admissible functions, proving to be versatile for the vibration analysis of thin orthotropic/isotropic plates with any classical/non-classical boundary conditions, for any aspect ratio. This greatly reduces the tedious process of choosing the correct admissible functions of individual classical boundary conditions and the exponentially cumbersome process of choosing the admissible functions for non-classical boundary conditions. The availability of admissible functions bypasses the cumbersome numerical analyses for non-classical boundary conditions, giving the results with speed and accuracy.

2 Orthotropic Rectangular Plate Vibration

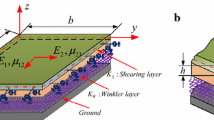
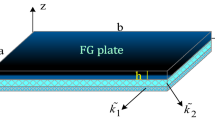
A thin, orthotropic, homogenous, rectangular plate is shown in Fig. 1. The edge constraints are non-classical, and thus, they are modeled as translational and rotational springs distributed uniformly over the edges. The stiffness distribution for both translational and rotational springs can be specified independently with respect to the flexural rigidity of the plate, such that they can represent non-classical boundary conditions (of practical interest) and all classical boundary conditions (when spring stiffness equals either infinity or zero). The free edge (F) refers to a special case of elastic support when the stiffness values of both rotational and translational springs are set to zero. Similarly, for the clamped edge (C), stiffness values for both the springs are set to infinity (represented by $10^{8}$ in the analysis). The simple supported (S) case can be represented by setting an infinite stiffness for the translational spring and a zero stiffness for the rotational spring. The opposite is done for the sliding case (G).

Fig. 1

Rectangular plate elastically restrained along edges

The governing differential equation of free transverse vibration of a thin orthotropic rectangular plate is given as Hsu (2010) follows:

$$D_{11} \frac{{\partial^{4} Z\left( {x,y,t} \right)}}{{\partial x^{4} }} + 2\left( {D_{12} + 2D_{66} } \right)\frac{{\partial^{4} Z\left( {x,y,t} \right)}}{{\partial x^{2} \partial y^{2} }} + D_{22} \frac{{\partial^{4} Z\left( {x,y,t} \right)}}{{\partial y^{4} }} + \rho h\frac{{\partial^{2} Z\left( {x,y,t} \right)}}{{\partial t^{2} }} = 0$$

(1)

The transverse displacement can be expressed as:

$$Z\left( {x,y,t} \right) = W\left( {x,y} \right){\text{e}}^{i\omega t}$$

(2)

Substituting Eq. (2) in Eq. (1), the spatial component of Eq. (1) can be rewritten as

$$D_{11} \frac{{\partial^{4} W\left( {x,y} \right)}}{{\partial x^{4} }} + 2\left( {D_{12} + 2D_{66} } \right)\frac{{\partial^{4} W\left( {x,y} \right)}}{{\partial x^{2} \partial y^{2} }} + D_{22} \frac{{\partial^{4} W\left( {x,y} \right)}}{{\partial y^{4} }} = \rho h\omega^{2} W\left( {x,y} \right)$$

(3)

where $W\left( {x,y} \right)$ is the space-wise flexural displacement, $D_{ij}$ are the flexural rigidities, $\rho$ is the density of the plate material, $h$ is the plate thickness, and $\omega$ is the circular frequency of vibration. For an orthotropic plate, the bending stiffness coefficients are given by:

$$D_{ij} = \mathop \int \limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} P_{ij} z^{2} {\text{d}}z\quad {\text{for}}\; i,j = 1,2, 6$$

(4)

$$\begin{aligned} & {\text{where}}\;P_{11} = \frac{{E_{1} }}{{1 - \upsilon_{12} \upsilon_{21} }},P_{12} = \frac{{E_{2} \upsilon_{12} }}{{1 - \upsilon_{12} \upsilon_{21} }}, P_{21} = \frac{{E_{1} \upsilon_{21} }}{{1 - \upsilon_{12} \upsilon_{21} }} , \\ & \quad P_{22} = \frac{{E_{2} }}{{1 - \upsilon_{12} \upsilon_{21} }}\;{\text{and}}\;D_{66} = G_{12} \frac{{h^{3} }}{12} \\ \end{aligned}$$

(5–9)

where $E_{1 }$ and $E_{2}$ are Young’s modulus of the material in 1 and 2 directions, respectively, $\upsilon_{12}$ is the Poisson’s ratio for transverse strain in the second direction due to applied stress in the first direction, $\upsilon_{21}$ is the Poisson’s ratio for transverse strain in the first direction due to applied stress in the second direction, and $G_{12}$ is the shear modulus in the 1–2 plane. For orthotropic materials, the elastic properties have two perpendicular planes of symmetry, and thus, they are characterized by four independent elastic constants $E_{1} ,E_{2} ,G_{12}$, and $\nu_{12}$, with $E_{2} \nu_{12} = E_{1} \nu_{21}$.

The bending moment, the twisting moment, and the shear force are, respectively, expressed in terms of the transverse displacement as follows:

$$M_{x } = - D_{11} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }} - D_{12} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }} ;\quad M_{y } = - D_{22} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }} - D_{12} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }}$$

(10–11)

$$M_{xy} = - 2D_{66} \frac{{\partial^{2} W\left( {x,y} \right)}}{\partial x\partial y}$$

(12)

$$Q_{x} = - D_{11} \frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x^{3} }} - \left( {D_{12} + 4D_{66} } \right)\frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x\partial y^{2} }}$$

(13)

$$Q_{y} = - D_{22} \frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial y^{3} }} - \left( {D_{12} + 4D_{66} } \right)\frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x^{2} \partial y}}$$

(14)

Here, the edge is elastically constrained with translational and rotational springs. Thus, the shear force developed at the edges is balanced by the translational spring force generated due to the deflection. Similarly, the bending moment at the edges is balanced by the moment generated by rotational spring due to the slope. The boundary conditions for an elastically restrained plate are expressed as:

$$k_{{{\text{T}}x0}} W\left( {x,y} \right) = Q_{x} = - D_{11} \frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x^{3} }} - \left( {D_{12} + 4D_{66} } \right)\frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x\partial y^{2} }}\;{\text{at}}\;x = 0$$

(15)

$$k_{{{\text{R}}x0}} \frac{{\partial W\left( {x,y} \right)}}{\partial x} = - M_{x} = D_{11} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }} + D_{12} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }}\;{\text{at}}\;x = 0$$

(16)

$$k_{{{\text{T}}x1}} W\left( {x,y} \right) = - Q_{x} = D_{11} \frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x^{3} }} + \left( {D_{12} + 4D_{66} } \right)\frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x\partial y^{2} }}\;{\text{at}}\;x = a$$

(17)

$$k_{{{\text{R}}x1}} \frac{{\partial W\left( {x,y} \right)}}{\partial x} = M_{x} = - D_{11} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }} - D_{12} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }}\;{\text{at}}\;x = a$$

(18)

$$k_{{{\text{T}}y0}} W\left( {x,y} \right) = Q_{y} = - D_{22} \frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial y^{3} }} - \left( {D_{12} + 4D_{66} } \right)\frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x^{2} \partial y}}\;{\text{at}}\;y = 0$$

(19)

$$k_{{{\text{R}}y0}} \frac{{\partial W\left( {x,y} \right)}}{\partial y} = - M_{y} = D_{22} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }} + D_{12} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }}\;{\text{at}}\;y = 0$$

(20)

$$k_{{{\text{T}}y1}} W\left( {x,y} \right) = - Q_{y} = D_{22} \frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial y^{3} }} + \left( {D_{12} + 4D_{66} } \right)\frac{{\partial^{3} W\left( {x,y} \right)}}{{\partial x^{2} \partial y}}\;{\text{at}}\;y = b$$

(21)

$$k_{{{\text{R}}y1}} \frac{{\partial W\left( {x,y} \right)}}{\partial y} = M_{y} = - D_{22} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }} - D_{12} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }}\;{\text{at}}\;y = b$$

(22)

where $k_{{{\text{T}}x0}}$ and $k_{{{\text{T}}x1}}$ ($k_{{{\text{T}}y0}}$ and $k_{{{\text{T}}y1}}$) are the translational spring stiffness per unit length and $k_{{{\text{R}}x0}}$ and $k_{{{\text{R}}x1}}$ ($k_{{{\text{R}}y0}}$ and $k_{{{\text{R}}y1}}$) are the rotational spring stiffness per unit length, located along edges of the plate at $(x = 0,x = a,y = 0\;{\text{and}}\;y = b)$, respectively. Classical boundary conditions can be obtained by setting appropriate extreme values to the spring constants. Generally, an exact analytical solution for plates with non-classical [Eq. (15–22)] is not possible. Therefore, to obtain the approximate solutions, the energy-based Rayleigh–Ritz method (RRM) has been used with the complete set of admissible functions, efficiently converging to the exact solution.

The strain potential energy (U) of orthotropic Kirchhoff’s plates with elastically restrained against translational and rotational edges is given as

$$\begin{aligned} U & = \frac{1}{2}\mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \left( {D_{11} \left( {\frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }}} \right)^{2} + 2D_{12} \frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial x^{2} }}\frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }} + 4D_{66} \left( {\frac{{\partial^{2} W\left( {x,y} \right)}}{\partial x\partial y}} \right)^{2} } \right. \\ & \quad \left. { + D_{22} \left( {\frac{{\partial^{2} W\left( {x,y} \right)}}{{\partial y^{2} }}} \right)^{2} } \right){\text{d}}x{\text{d}}y + \frac{1}{2}\mathop \int \limits_{0}^{a} k_{{{\text{R}}y0}} \left( {\frac{{\partial W\left( {x,0} \right)}}{\partial y}} \right)^{2} {\text{d}}x + \frac{1}{2}\mathop \int \limits_{0}^{a} k_{{{\text{R}}y1}} \left( {\frac{{\partial W\left( {x,b} \right)}}{\partial y}} \right)^{2} {\text{d}}x \\ & \quad + \frac{1}{2}\mathop \int \limits_{0}^{b} k_{{{\text{R}}x0}} \left( {\frac{{\partial W\left( {0,y} \right)}}{\partial x}} \right)^{2} {\text{d}}y + \frac{1}{2}\mathop \int \limits_{0}^{b} k_{{{\text{R}}x1}} \left( {\frac{{\partial W\left( {a,y} \right)}}{\partial y}} \right)^{2} {\text{d}}y + \frac{1}{2}\mathop \int \limits_{0}^{a} k_{{{\text{T}}y0}} \left( {W\left( {x,0} \right)} \right)^{2} {\text{d}}x \\ & \quad + \frac{1}{2}\mathop \int \limits_{0}^{a} k_{{{\text{T}}y1}} \left( {W\left( {x,b} \right)} \right)^{2} {\text{d}}x + \frac{1}{2}\mathop \int \limits_{0}^{b} k_{{{\text{T}}x0}} \left( {W\left( {0,y} \right)} \right)^{2} {\text{d}}y + \frac{1}{2}\mathop \int \limits_{0}^{b} k_{{{\text{T}}x1}} \left( {W\left( {a,y} \right)} \right)^{2} {\text{d}}y \\ \end{aligned}$$

(23)

The kinetic energy (T) of the orthotropic plate is given as

$$T = \frac{1}{2}\rho h\omega^{2} \mathop \int \limits_{0}^{a} \mathop \int \limits_{0}^{b} \left( {W\left( {x,y} \right)} \right)^{2} {\text{d}}x{\text{d}}y$$

(24)

The amplitude of the transverse deflection of the plate is expressed as the weighted superposition of the admissible functions in either direction as:

$$W\left( {x,y} \right) = \mathop \sum \limits_{i = 1}^{\text{modex}} \mathop \sum \limits_{j = 1}^{\text{modey}} A_{ij} \emptyset_{i} \left( x \right)\emptyset_{j} \left( y \right)$$

(25)

where ‘modex’ and ‘modey’ are the number of trial functions considered in $x$ direction and $y$ direction, respectively, and $A_{ij}$ are the unknown coefficients. $\emptyset_{j} \left( x \right)$ and $\emptyset_{j} \left( y \right)$ are the set of admissible beam functions in x and y directions, respectively. To investigate a wide range of aspect ratio, it is required to non-dimensionalize the system of equations with the non-dimensional spatial coordinates of the plate $\xi = \frac{x}{b}$, $\eta = \frac{y}{b}$ and aspect ratio ($\alpha$) = $\frac{a}{b}$. Thus, the above strain energy (Eq. 23) and kinetic energy (Eq. 24) expressions can be rewritten as:

$$\begin{aligned} U_{\text{Plate}} & = \frac{{D_{11} }}{2}\frac{b}{{a^{3} }}\mathop \int \limits_{0}^{1} \mathop \int \limits_{0}^{1} \left[ {\left( {\frac{{\partial^{2} W}}{{\partial \xi^{2} }}} \right)^{2} + 2\frac{{D_{12} }}{{D_{11} }}\frac{{a^{2} }}{{b^{2} }}\frac{{\partial^{2} W}}{{\partial \xi^{2} }}\frac{{\partial^{2} W}}{{\partial \eta^{2} }} + 4\frac{{D_{66} }}{{D_{11} }}\frac{{a^{2} }}{{b^{2} }}\left( {\frac{{\partial^{2} W}}{\partial \xi \partial \eta }} \right)^{2} + \frac{{D_{22} }}{{D_{11} }}\frac{{a^{4} }}{{b^{4} }}\frac{{\partial^{4} W}}{{\partial \eta^{4} }}} \right]\partial \xi \partial \eta \\ & \quad + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{R}}x0}} \frac{b}{{a^{2} }}\left( {\frac{{\partial W\left( {0,\eta } \right)}}{\partial \xi }} \right)^{2} {\text{d}}\eta + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{R}}x1}} \frac{b}{{a^{2} }}\left( {\frac{{\partial W\left( {1,\eta } \right)}}{\partial \xi }} \right)^{2} {\text{d}}\eta + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{R}}y0}} \frac{a}{{b^{2} }}\left( {\frac{{\partial W\left( {\xi ,0} \right)}}{\partial \eta }} \right)^{2} {\text{d}}\xi \\ & \quad + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{R}}y1}} \frac{a}{{b^{2} }}\left( {\frac{{\partial W\left( {\xi ,1} \right)}}{\partial \eta }} \right)^{2} {\text{d}}\xi + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{T}}y0}} a\left( {W\left( {\xi ,0} \right)} \right)^{2} {\text{d}}\xi + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{T}}y1}} a\left( {W\left( {\xi ,1} \right)} \right)^{2} {\text{d}}\xi \\ & \quad + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{T}}x0}} b\left( {W\left( {0,\eta } \right)} \right)^{2} {\text{d}}\eta + \frac{1}{2}\mathop \int \limits_{0}^{1} k_{{{\text{T}}x1}} b\left( {W\left( {1,\eta } \right)} \right)^{2} {\text{d}}\eta \\ \end{aligned}$$

(26)

$$T_{\text{Plate}} = \frac{1}{2}\rho h\omega^{2} ab\mathop \int \limits_{0}^{1} \mathop \int \limits_{0}^{1} W\left( {\xi ,\eta } \right)^{2} {\text{d}}\xi {\text{d}}\eta$$

(27)

The RRM is used to minimize the energy functional (i.e., the difference of total strain energy and total kinetic energy) with respect to unknown coefficients, which leads to a set of linear homogeneous equations:

$$\left( {\frac{\partial }{{\partial A_{ij} }}} \right)\left[ {U_{\text{Plate}} - T_{\text{Plate}} } \right] = 0$$

(28)

This generates a non-dimensional eigenvalue problem:

$$\left( {\left[ \varvec{K} \right] -\Omega ^{2} \left[ \varvec{M} \right]} \right)\left\{ \varvec{A} \right\} = 0$$

(29)

$$\begin{aligned} K_{ijkp} & = A_{ik}^{{\left( {2,2} \right)}} B_{jp}^{{\left( {0,0} \right)}} + 2\frac{{D_{12} }}{{D_{11} }}\alpha^{2} \left[ {A_{ik}^{{\left( {0,2} \right)}} B_{jp}^{{\left( {2,0} \right)}} + A_{ik}^{{\left( {2,0} \right)}} B_{jp}^{{\left( {0,2} \right)}} } \right] + 4\frac{{D_{66} }}{{D_{11} }}\alpha^{2} A_{ik}^{{\left( {1,1} \right)}} B_{jp}^{{\left( {1,1} \right)}} + \frac{{D_{22} }}{{D_{11} }}\alpha^{4} A_{ik}^{{\left( {0,0} \right)}} B_{jp}^{{\left( {2,2} \right)}} \\ & \quad + K_{{{\text{R}}1}} \frac{{\partial \emptyset_{i} \left( 0 \right)}}{\partial \xi }\frac{{\partial \emptyset_{k} \left( 0 \right)}}{\partial \xi }B_{jp}^{{\left( {0,0} \right)}} + K_{{{\text{R}}3}} \frac{{\partial \emptyset_{i} \left( 1 \right)}}{\partial \xi }\frac{{\partial \emptyset_{k} \left( 1 \right)}}{\partial \xi }B_{jp}^{{\left( {0,0} \right)}} + \alpha^{4} K_{R4} \frac{{\partial \emptyset_{i} \left( 0 \right)}}{\partial \eta }\frac{{\partial \emptyset_{k} \left( 0 \right)}}{\partial \eta }A_{ik}^{{\left( {0,0} \right)}} \\ & \quad + \alpha^{4} K_{{{\text{R}}2}} \frac{{\partial \emptyset_{i} \left( 1 \right)}}{\partial \eta }\frac{{\partial \emptyset_{k} \left( 1 \right)}}{\partial \eta }A_{ik}^{{\left( {0,0} \right)}} + K_{{{\text{T}}1}} \phi_{i} \left( 0 \right)\phi_{k} \left( 0 \right)B_{jp}^{{\left( {0,0} \right)}} + K_{{{\text{T}}3}} \phi_{i} \left( 1 \right)\phi_{k} \left( 1 \right)B_{jp}^{{\left( {0,0} \right)}} \\ & \quad + \alpha^{4} K_{{{\text{T}}4}} \phi_{j} \left( 0 \right)\phi_{p} \left( 0 \right)A_{ik}^{{\left( {0,0} \right)}} + \alpha^{4} K_{{{\text{T}}2}} \phi_{j} \left( 1 \right)\phi_{p} \left( 1 \right)A_{ik}^{{\left( {0,0} \right)}} \\ \end{aligned}$$

(30)

$$\varvec{M}_{ijkp} = A_{i,k}^{{\left( {0,0} \right)}} B_{j,p}^{{\left( {0,0} \right)}}$$

(31)

$$\begin{aligned} & {\text{where}}\; K_{{{\text{R}}1}} = \frac{{k_{{{\text{R}}x0}} a}}{{D_{11} }} ,K_{{{\text{R}}2}} = \frac{{k_{Ey0} b}}{{D_{11} }}, K_{{{\text{R}}3}} = \frac{{k_{{{\text{R}}x1}} a}}{{D_{11} }}, K_{{{\text{R}}4}} = \frac{{k_{{{\text{R}}y1b}} }}{{D_{11} }}, K_{{{\text{T}}1}} = \frac{{k_{{{\text{T}}x0}} a^{3} }}{{D_{11} }} ,K_{T2} = \frac{{k_{{{\text{T}}y0}} b^{3} }}{{D_{11} }}, \\ & \quad K_{{{\text{T}}3}} = \frac{{k_{{{\text{T}}x1}} a^{3} }}{{D_{11} }},K_{{{\text{T}}4}} = \frac{{k_{{{\text{T}}y1}} b^{3} }}{{D_{11} }};\quad A_{i.k}^{m,n} = \mathop \int \limits_{0}^{1} \frac{{{\text{d}}^{m} \phi_{i} \left( \xi \right)}}{{{\text{d}}\xi^{m} }}\frac{{{\text{d}}^{m} \phi_{k} \left( \xi \right)}}{{{\text{d}}\xi^{n} }}{\text{d}}\xi ;\quad B_{j,p}^{m,n} = \mathop \int \limits_{0}^{1} \frac{{{\text{d}}^{m} \phi_{j} \left( \eta \right)}}{{{\text{d}}\eta^{m} }}\frac{{{\text{d}}^{n} \phi_{p} \left( \eta \right)}}{{{\text{d}}\eta^{n} }}{\text{d}}\eta \\ \end{aligned}$$

where $m, n = 0, 1, 2$ and $i, k, j, p = 1, 2, 3 \ldots , n$. $\left[ \varvec{K} \right]$ and $\left[ \varvec{M} \right]$ are the non-dimensional stiffness matrix and mass matrix, respectively; $\left\{ \varvec{A} \right\}$ denotes the unknown coefficients in the series expansion. Here, $\Omega ^{2} = \frac{{\rho h\omega^{2} a^{2} b^{2} }}{{D_{11} }}$ stands for the non-dimensional frequency parameter, where $\omega^{2}$ is the dimensional frequency parameter (rad/s). The natural frequencies and corresponding eigenvectors are determined by solving Eq. (29). The mode shapes can be found by using Eq. (25).

3 Building a Set of Admissible Functions

Several researchers have specified the guidelines to select a set of admissible functions for plate vibration analysis, e.g., Oosterhout et al. (1995) as follows:

• (a) The set of admissible functions must satisfy the geometric boundary conditions.

• (b) The admissible functions must be linearly independent of each other.

• (c) The second-order derivatives of the admissible functions must exist (required to capture flexural modes).

• (d) The set of admissible functions should be able to represent all the modes of vibration.

Based on the above guidelines, this work presents a complete set of admissible functions to model an unconstrained (FFFF) plate, whose RRM analysis converges fast without numerical instabilities. The complex boundary conditions can be modeled by adding appropriate translational and rotational spring stiffness at the edges. The set of admissible functions should include the translational and rotational rigid-body modes of the beam and should also satisfy the essential boundary conditions as a complete series of functions, rather than each individual function. The rigid-body modes of the beam have been included in the set of admissible functions by a unit term and a linear function. The unit term represents the translational rigid mode or the heave mode of the beam, and the linear function represents the rotational rigid mode or the pitch mode. To keep the solution free from numerical instabilities, the minimum number of possible lowest order polynomial functions is to be included in the complete set of admissible functions. Next, to satisfy all the geometrical boundary conditions, it is necessary to include an additional term which satisfies a second nonzero slope at the end of the beam; thus, the lowest order polynomial has been added to the series. Monterrubio and Ilanko (2015) stated that for most of the boundary conditions, the convergence rates are faster with cosine series as compared to the sine series. Actually, the cosine series show their rapid rate of convergence for sliding-type boundary condition, while the sine series is suitable for the simply supported conditions. Cosine functions satisfy the orthogonality properties which makes the mass and stiffness matrix sparser or diagonally dominant, leading to higher computational efficiency and faster convergence of the solution. Therefore, the cosine series has been selected to complete the set of admissible functions. The selection of proper admissible functions has a major role in the present energy-based method because the exactness of the solution is largely influenced by them. The final set of admissible functions are:

$$\phi_{1} \left( x \right) = 1; \phi_{2} \left( x \right) = \left( {1 - \frac{2x}{L}} \right); \phi_{3} \left( x \right) = \left( {\frac{x}{L}} \right)^{2} ; \phi_{i} \left( x \right) = \cos \frac{{\left( {i - 1} \right)\pi x}}{L},\quad {\text{for}}\;i = 4,5 \ldots ,n$$

(32(a–d))

The admissible functions $\emptyset_{i} \left( x \right)$ used in the present study are given in Eq. (32), and the first five admissible functions are shown in Fig. 2. It clearly indicates that the admissible functions selected for the present study permit nonzero displacement and translation at both ends of the beam. The complete set of admissible functions satisfies the geometric boundary conditions at both ends of the free–free beam. In this study, the set of admissible functions is the same for both $x$ and $y$ directions.

Fig. 2

First five admissible functions

4 Results and Discussion

The above analysis has been performed for a wide range of edge conditions of thin orthotropic rectangular plates, in order to demonstrate the versatility and stability of the proposed set of admissible functions. The accuracy and convergence of the present method have also been investigated and presented. The material properties of the thin orthotropic rectangular plate are specified in Table 1. Two types of material have been used.

Table 1 Material properties of the orthotropic plate

First, the most challenging classical boundary condition for vibration analysis, i.e., a completely free square orthotropic plate (FFFF), is considered. The convergence behavior for first ten non-dimensional frequency parameters of the square FFFF plate is reported in Table 2 and verified with Shi et al. (2014). It is seen that the first 20 terms in the set of admissible functions (in either direction) are sufficient for the convergence.

Table 2 Convergence study of frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ square F–F–F–F orthotropic plates M1

The convergence study for the square CCCC isotropic and orthotropic plates is presented in Table 3 and Fig. 3a, b. For the isotropic plate (Fig. 3a), the first 13 terms of the proposed set of admissible functions give an error of less than 0.1% from the exact frequency parameter. The error reduces to less than 0.01% with 25 terms. For the orthotropic plate (Fig. 3b), this error is less than 0.1% with the first 28 terms of admissible functions and reduces to less than 0.01% with 38 terms. The convergence of the frequency parameter up to the second decimal place is achieved with only 20 terms.

Table 3 Convergence study of the fundamental frequency of square CCCC isotropic and orthotropic plates M1

Fig. 3

Convergence study: a isotropic square plate and b orthotropic square plate M1

The influence of the plate aspect ratio on the non-dimensional frequency parameters (having classical boundary conditions) are given in Tables 4, 5, 6, 7, 8, 9, and 10 for the orthotropic plate of material M1, and in Tables 11, 12, and 13 for the orthotropic plate of material M2. The calculated non-dimensional frequencies shown are for the first ten modes of free vibration with five different aspect ratios and verified with the literature.

Table 4 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular F–F–F–F orthotropic plates M1

Table 5 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular S–S–S–S orthotropic plates M1

Table 6 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular C–S–C–F orthotropic plates M1

Table 7 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular C–F–F–F orthotropic plates M1

Table 8 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular C–C–C–C orthotropic plates M1

Table 9 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular C–C–C–G orthotropic plates M1

Table 10 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular G–G–C–C orthotropic plates M1

Table 11 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular C–C–C–G orthotropic plates M2

Table 12 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular S–G–C–C orthotropic plates M2

Table 13 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for rectangular G–G–C–C orthotropic plates M2

All the above results presented in Tables 4, 5,6, 7, 8, 9, 10, 11, 12, and 13 have been limited to plates with classical boundary conditions, which are the extreme cases of the non-classical elastically constrained edges.

This study is further extended to the free vibration analysis of non-classical boundary conditions, using a wide range of spring constants $K_{\text{T}} , K_{\text{R}}$ for modeling the edge support. First, we consider a simply supported thin rectangular plate for various rotational stiffness parameters $K_{\text{R}}$. Table 14 shows the frequency parameters of the orthotropic SSSS plate with varying elastic rotational spring stiffness, for four different aspect ratios of 1, 0.8, 0.6, and 0.4. It is seen that non-dimensional frequency parameters are significantly affected by the edge conditions and the plate aspect ratio. A lower edge spring constant leads to a lower frequency (approaching an SSSS plate), while making the edge stiffer increases the natural frequency (approaching a CCCC plate). This is consistently seen for all aspect ratios and all modes of vibration. A squarish plate (aspect ratio ~ 1) has a higher frequency than a more rectangular plate. This is because the beam mode shapes from the longer side dominate the vibration, neglecting the same from the shorter side. There is less density of nodal lines, leading to lower strain potential energy.

Table 14 Non-dimensional frequency parameter $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ for orthotropic plates M1 versus $K_{\text{R}}$, with $K_{\text{T}} = 10^{8}$

Figure 4 shows that the frequency parameters $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D _{11} }}$ are functions of the rotational spring constant. Square orthotropic plate edges are modeled with a very large translational spring constant $K_{\text{T}} = 10^{8}$ and varying rotational spring constant $K_{\text{R}}$. It is observed that with an increase in rotational spring constant, the non-dimensional frequency parameters also increase. When rotational spring constant ($K_{\text{R}}$) is ~ 10⁻⁶, the plate appears to vibrate as a simply supported (SSSS) plate. When $K_{\text{R}}$ ~ 10⁶, the plate behaves like a fully clamped (CCCC) plate. Therefore, the fundamental natural frequency of the SSSS plate is observed to deviate to the fundamental frequency of CCCC plate with the increase in rotational spring constant $K_{\text{R}}$. The conspicuous transition of SSSS plate behavior to CCCC plate behavior occurs at $10^{1} < K_{\text{R}} < 10^{3}$. The transition region separates the ranges of edged spring constants where the non-classical plate can be assumed to behave like for practical engineering analysis. It helps in taking a time-bound engineering decision without having to resort to the complicated non-classical analysis (which may not be possible in several commercial CAD tools).

Fig. 4

Frequency parameter of orthotropic plate $\left( {M_{1} } \right)$ with various values of rotational spring constant

Figure 5 shows the frequency parameters $\Omega = \sqrt[4]{{\omega^{2} \rho ha^{2} b^{2} /D_{11} }}$ of a square orthotropic plate with the edges constrained with rotational and translational spring stiffness. It is noticed that when both stiffnesses are very small in magnitude (10⁻⁶ order), the plate vibrates like a completely free plate (FFFF) and exhibits three rigid-body modes. When both the stiffnesses increase, the trivial frequency parameters of FFFF plate bifurcate to the frequency characteristics of the CCCC plate. The conspicuous transition of FFFF plate behavior to the CCCC plate behavior occurs at $10^{ - 3} < K_{\text{T}} , K_{\text{R}} < 10^{3}$.

Fig. 5

Frequency parameter of orthotropic plate $\left( {M_{1} } \right)$ with variable translational and rotational spring constant

The present method is capable of analyzing the free vibration of orthotropic and isotropic plates for a wide range of non-classical boundary conditions. In order to demonstrate this approach for isotropic plates, all the 55 possible classical boundary conditions [the combination of clamped (C), free (F), sliding (G), and simply supported (S)] have been analyzed by the Rayleigh–Ritz method with the proposed set of admissible functions. The first ten non-dimensional frequency parameters are shown in Table 15. The results show that in most cases, the non-dimensional frequency parameters of isotropic plates converge to the exact results (where these are available) to at least four significant numbers for any geometric edge condition. This establishes the efficacy of the present set of trial functions.

Table 15 Non-dimensional frequency parameter $\Omega = \sqrt[2]{{\omega^{2} \rho ha^{2} b^{2} /D}}$ for square isotropic plates $\left( {D = Eh^{3} /12\left( {1 - \nu^{2} } \right)} \right)$

The non-dimensional frequency parameters for a square isotropic plate have rotationally restrained edges. The effect of the $K_{\text{R}}$ is investigated for the first six modes and compared with those by Zhang et al. (2019), as mentioned in Table 16. Next, the rectangular orthotropic plates with three edges simply supported and one edge restrained with rotational spring of variable stiffness are investigated. The effect of the aspect ratio and rotational spring constant on the non-dimensional fundamental frequency parameter is tabulated in Table 17 and compared with the results of Zhang et al. (2019). Finally, the magnitudes of spring constants (for both translational and rotational springs) used for modeling various classical boundary conditions of the plate are summarized in Table 18.

Table 16 First six non-dimensional frequency parameters for a square isotropic plate with all edges rotationally restrained (RRRR)

Table 17 Fundamental frequency parameter $\Omega = \sqrt {\omega^{2} \rho ha^{2} b^{2} /D_{11} }$ for the rectangular orthotropic plates with three edges simply supported and one edge rotationally restrained (SRRR) with $D_{11} /H = D_{11} /H = 0.5$, $H = D_{12} + 2D_{66}$

Table 18 Non-dimensional translational and rotational spring constants for various edge conditions of plate

5 Conclusion

A new complete set of admissible functions has been proposed to be incorporated in the energy-based Rayleigh–Ritz method for determining the frequency parameters of rectangular plates for arbitrary (non-classical) boundary conditions. The non-classical edge conditions are modeled as translational and rotational spring stiffness on the edges. The complete set of admissible functions (consisting of unit function, linear function, the lowest order polynomial, and trigonometric functions) shows an excellent convergence capability for various boundary conditions, aspect ratios, and modes of vibration, without ill-conditioning. This efficacy is seen for both isotropic and orthotropic plates. The accuracy and convergence of the present method are shown through examples of various boundary conditions with both isotropic and orthotropic materials. The non-dimensional frequency parameters have been shown to converge to the exact value up to the third decimal place for most of the boundary conditions. The effects of elastic support stiffness and plate aspect ratio on the frequency parameters have also been studied. The present work establishes an efficient method for selecting a set of admissible functions that can be invariably implemented to plate with any classical and non-classical boundary conditions. This work provides an easy and quick technique to obtain a wide range of frequency parameters for both isotropic and orthotropic rectangular plates.