1 Introduction

The boundary layer flow and heat transfer of a viscous fluid over a continuous moving surface has applications in number of technological processes such as metal and polymer extrusion, continuous casting, glass-fiber production, manufacturing of plastic and rubber sheets, paper production, cable coating etc. In these processes, the quality of the final product depends very much on the rate of heat and mass transfer of the system. Sakiadis [1, 2] was the first to recognize this different class of boundary layer flow adjacent to continuous surface moving with a constant velocity. The thermal behavior corresponding to this problem was examined by Erickson et al. [3]. He found out that for large values of the Prandtl number the local Nusselt number can be approximated by \(\mathit{Nu}_{x} = 0.53\sqrt{\mathrm{Re}_{x}\mathrm{Pr}}\). Later, Tsou et al. [4] showed experimentally that such a flow is physically realizable. Fox et al. [5] extended this problem to include the effects of suction and injection on heat and mass transfer coefficients of a moving isothermal surface through a fluid medium at rest. Soundalgekar and Murthy [6] studied the thermal boundary layer on a continuous plate with uniform motion. These studies were limited to a continuous surface moving with a constant velocity, which is not appropriate for the problem of continuous extrusion of polymer sheets and filaments from a dye. Since the polymer is a flexible material, the sheet and the filament surfaces may stretch during the course of ejection and therefore the surface velocity may be expected to deviate from being uniform. Crane [7] was the first among the others to formulate this problem to study a steady two-dimensional boundary layer flow caused by stretching of a sheet that moves in its plane with a velocity which varies linearly with the distance from a fixed point on the sheet. Thereafter various aspects of the above boundary layer problem on continuous moving surface were considered by many researchers (Grubka and Bobba [8], Chen [9], Gupta and Gupta [10], Chen and Char [11], Ali [12], and Vajravelu [13]).

All the above investigators restricted their analyses to flow and heat transfer in the absence of magnetic field. But in recent years, we find several applications in polymer industry (where one deals with stretching of plastic sheets) and metallurgy where hydro-magnetic techniques are being used. To be more specific, it may be pointed out that many metallurgical processes involve the cooling of continuous strips or filaments by drawing them through a quiescent fluid and that in the process of drawing, these strips are sometimes stretched. Mention may be made of drawing, annealing, and thinning of copper wires. In all these cases, the properties of final product depend to a great extent on the rate of cooling: By drawing such strips in an electrically conducting fluid one may achieve the desired characteristics of the final product. In view of these applications Pavlov [14] investigated the flow of an electrically conducting fluid caused solely by the stretching of an elastic sheet in the presence of a uniform magnetic field. Chakrabarti and Gupta [15] considered the flow and heat transfer of an electrically conducting fluid past a porous stretching sheet and presented analytical solution for the flow and numerical solution for the heat transfer problem. In these studies the fluid was assumed to be Newtonian. However, many industrial fluids are non-Newtonian or rheological in their flow characteristics (such as molten plastics, polymers, suspension, foods, slurries, paints, glues, printing inks, blood). That is, they might exhibit dynamic deviation from Newtonian behavior depending upon the flow configuration and/or the rate of deformation. These fluids often obey non-linear constitutive equations and the complexity in the equations is the main culprit for the lack of exact analytical solutions. For example, visco-elastic and Walters’ models are simple models (Char [16], Wen-Dong-Chang [17], Andersson [18], and Vajravelu and Rollins [19]) which are known to be accurate only for weakly elastic fluids subject to slowly varying flows. These two models are known to violate certain rules of thermodynamics. Therefore the significance of the results reported in the above works is limited as far as the polymer industry is concerned. Obviously for the theoretical results to be of any industrial importance, more general visco-elastic fluid models such as upper convected Maxwell model (UCM fluid) or Oldroyd B model should be invoked. Indeed these two fluid models are being used recently to study the visco-elastic fluid flow above stretching and non-stretching sheets with or without heat transfer (Bhatnagar et al. [20], Renardy [21], Sadeghy et al. [22], Hayat et al. [23], Aliakbar et al. [24], Vajravelu et al. [25], Hayat and Qasim [26]). Recently, Hayat et al. [25] investigated the mass transfer in the MHD flow of an upper-convected Maxwell (UCM) fluid over a porous shrinking sheet with chemically reactive species and solved the nonlinear system of ordinary differential equations by using homotopy analysis method. We mention also the papers by Hayat et al. [27], Abbas et al. [28], Sadeghy et al. [29], Mamaloukas et al. [30], Kumari and Nath [31] and Hayat et al. [32, 33], on UCM fluids.

Most of the above mentioned papers are based on the constant thermo-physical properties of the fluid. However, it is well known that (Herwig and Wickern [34], Lai and Kulacki [35], Takhar et al. [36], Pop et al. [37], Hassanien [38], Abel et al. [39], Seedbeck [40], Ali [41], Andersson and Aarseth [42] Prasad et al. [43]) the thermo-physical properties rather vary with temperature, especially the fluid viscosity and the thermal conductivity. For lubricating fluids, heat generated by internal friction and the corresponding rise in the temperature affects the physical properties of the fluid, and the properties of the fluid are no longer assumed to be constant. The increase in temperature leads to increase in the transport phenomena and thereby changing the physical properties across the thermal boundary layer; and hence the heat transfer at the wall is affected. Therefore to predict the flow and heat transfer rates, it is necessary to take into account the variable fluid properties.

In view of this, the problem studied here extends the work of Sadeghy et al. [24] by considering the temperature dependent variable fluid properties. Thus in the present paper, the authors envisage the effects of the variable viscosity and the variable thermal conductivity on the hydro-magnetic flow and heat transfer of a UCM fluid over a linear stretching sheet in the presence of internal heat generation/absorption. Highly non-linear, coupled partial differential equations governing the momentum and heat transfer equations are reduced to a system of coupled non-linear ordinary differential equations by applying a suitable similarity transformation. These non-linear coupled ordinary differential equations are solved numerically by Keller-Box method for different values of the parameters. The effects of various parameters on the velocity and temperature fields as well as the skin friction coefficient and the Nusselt number are presented in graphical and tabular forms. It is believed that the results obtained from the present investigation will provide useful information for application and also serve as a complement to the previous studies.

2 Mathematical formulation

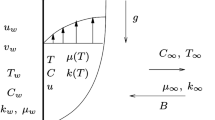
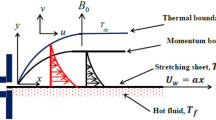
Consider a steady, two-dimensional incompressible and electrically conducting UCM fluid flow over a stretching sheet of stretching velocity U w (x)=bx, where b>0 is the stretching velocity rate (see Fig. 1). The thermo-physical fluid properties are assumed to be isotropic and constant, except for the fluid viscosity and the fluid thermal conductivity which are assumed to vary as a function of temperature in the following forms:

(1)
(2)

where μ ∞ and K ∞ are the ambient fluid dynamic viscosity and thermal conductivity respectively. ε is a small parameter known as variable thermal conductivity parameter, T is the temperature of the fluid and ΔT=(T w −T ∞). Equation (1) can be written as,

$$ \frac{1}{\mu} = a( T - T_{r} ) ,$$
(3)

where

$$ a = \frac{\gamma}{\mu _{\infty}}\quad \mbox{and}\quad T_{r} = T_{\infty} -\frac{1}{\gamma} .$$
(4)

Both a and T r are constants and their values depend on the reference state and the thermal property of the fluid, i.e. γ (a constant). In general, a>0 for liquids and a<0 for gases, respectively. Also, let θ r be the constant which is defined by

$$ \theta_{r} = \frac{T_{r} - T_{\infty}}{\Delta T} = - \frac{1}{\gamma \Delta T}.$$
(5)

It is worth mentioning here that for γ→0 i.e. μ=μ ∞ (constant), θ r →∞. It is also important to note that θ r is negative for liquids and positive for gases. This is due to the fact that viscosity of a liquid usually decreases with increasing temperature while it increases for gases. The reference temperatures selected here for the correlations are very useful for most applications [44]. The flow region is exposed under uniform transverse magnetic field B=(0,B 0,0) and the imposition of such magnetic filed stabilize the boundary layer flow (Hayat et al. [32, 33]). It is assumed that the flow is generated by stretching of an elastic sheet from a slit by imposing two equal and opposite forces in such a way that velocity of the boundary sheet is of linear order of the flow. It is also assumed that the magnetic Reynolds number is very small and the electric field due to polarization of charges is negligible. It is assumed that the boundary layer approximation is applicable (Gupta and Wineman [45]). Therefore, the first step would be to derive the boundary layer equations for our fluid of interest, and this can be done starting from Cauchy equations of motion in which a source term due to the magnetic field should also be included (Bird et al. [46]). For a two-dimensional flow, the equation of continuity, the equations of motion (with no pressure gradient) and the equation of energy can be written as,

(6)
(7)
(8)
(9)

where u and v are the velocities components along the x and y axes respectively, ρ ∞ is the fluid density, σ is the electrical conductivity, B 0 is the uniform magnetic field, c p is the specific heat at constant pressure, K(T) is the thermal conductibility of the fluid and Q s is the temperature dependent volumetric rate of heat source when Q s >0 and heat sink when Q s <0. These heat sources and sinks deal with the situations of exothermic and endothermic chemical reactions respectively. As mentioned above, the fluid of interest in the present work obeys upper convected Maxwell model. For a Maxwell fluid the extra tensor τ ij can be related to the deformation rate tensor d ij by an equation of the form:

$$ \tau_{ij} + \lambda\frac{\Delta}{\Delta t}\tau_{ij} = 2\delta d_{ij},$$
(10)

where δ is the coefficient of viscosity and λ is the relaxation time of the period. The time derivative \(\frac{\Delta}{\Delta t}\) appearing in the above equation is the so called upper convected time derivative devised to satisfy the requirements of the continuum (i.e., material objectivity and frame difference). This time derivative when applied to stress tensor reads as follows (Bird et al. [46]),

$$ \frac{\Delta}{\Delta t}\tau_{ij} = \frac{D}{Dt}\tau_{ij} -L_{jk}\tau_{ik} - L_{ik}\tau_{kj},$$
(11)

where L ij is the velocity gradient tensor. For an incompressible fluid obeying Upper convected Maxwell model, the x-momentum equation and the energy equation can be simplified using the usual boundary layer theory approximations as (see Sadeghy et al. [24]),

(12)
(13)

It may be pointed out here that there is an additional term \(\frac{\sigma B_{0}^{2}}{\rho _{\infty}} \lambda v \frac{\partial u}{\partial y} \) in the momentum equation (12) as in Refs. [32, 33]. It is assumed that the normal stress is of the same order of magnitude as that of the shear stress in addition to the usual boundary layer approximation for deriving the x-component of the momentum boundary layer equation (12). The appropriate boundary condition on velocity and temperature are appropriate

$$ \begin{array}{l}u = U_{w}(x) = bx,\quad v = 0,\quad T = T_{w}\quad \mbox{at}\ y =0, \\u \to 0,\quad T \to T_{\infty}\quad \mbox{as}\ y \to\infty.\end{array}$$
(14)
Fig. 1
figure 1

Physical model and coordinate system

Full size image

3 Similarity equations

From the numerical solutions of the forced convection flow and heat transfer, it is observed that the thermal and momentum boundary layers exist along a horizontal impermeable surface whenever the wall temperature differs from that of the surrounding fluid temperature. Using the boundary layer approximations and the above mentioned variable fluid properties the governing equations (12) and (13) in terms of stream function ψ can be written as,

(15)
(16)

The stream function ψ automatically satisfies the continuity equation (6) and is given by (u,v)=(∂ψ/∂y,−∂ψ/∂x). With a properly chosen similarity variables, the above equation can be transformed into ordinary differential equations: The suitable similarity transformations for the problem are,

(17)

In terms of the new variables, the velocity components can be written as,

$$ u = bx f'\left( \eta\right),\quad v = - ( b\nu_{\infty})^{1 / 2} f\left( \eta\right).$$
(18)

The governing equations (15) and (16) in terms of the new variables f and θ are,

(19)
(20)

Here primes denote differentiation with respect to η, \(\mathit{Mn} = \sigma B_{0}^{2}/(\rho_{\infty} b)\) is the magnetic parameter, β=λb is the Maxwell parameter, Pr=ν ∞/α ∞ is the Prandtl number and β 1=Q s /(ρ ∞ c p b) is the heat source/sink parameter. In view of the above transformations, the boundary conditions (14) can be written as

$$ \begin{array}{l}f(0) = 0,\quad f'(0) = 1,\quad \theta(0) = 1, \\f'(\eta) \to 0,\quad \theta(\eta) \to 0\quad \mbox{as}\ \eta\to\infty. \end{array}$$
(21)

We noticed that in the absence of fluid viscosity parameter and the variable thermal conductivity parameter the equations reduce to those of Sadeghy et al. [29], while in the absence of Maxwell parameter the equations reduce to those of Chen and Char [11], Grubka and Bobba [8] and Crane [7] under different physical situations. Further with constant physical properties i.e. θ r →∞, β=0, ε=0 and β 1=0 the equations reduce to those of Andersson et al. [47] for a special case of n=1 (Newtonian fluid). From the engineering point of view, the important flow and heat transfer characteristics are the skin friction coefficient C f and the local Nusselt number Nu x , which are defined as

$$ C_{f} = \frac{\tau _{w}}{\rho _{\infty} U_{w}^{2}/2},\quad \mathit{Nu}_{x} =\frac{xq_{w}}{K_{\infty} \Delta T},$$
(22)

where the skin friction τ w and the heat transfer from the surface q w are given by

$$ \tau_{w} = \mu_{\infty} \left( \frac{\partial u}{\partial y} \right)_{y= 0},\quad q_{w} = - K_{\infty} \left( \frac{\partial T}{\partial y}\right)_{y = 0}.$$
(23)

Using (17), (22) and (23), we get

$$ \mathrm{Re} _{x}^{1/2}C_{f} =2f''(0),\quad \mathrm{Re} _{x}^{ - 1/2}\mathit{Nu}_{x} = - \theta '(0),$$
(24)

where Re x =U w (x)x/ν ∞ is the local Reynolds number.

4 Numerical procedure

Equations (19) and (20) are highly non-linear, coupled ordinary differential equations of third-order and second-order, respectively. Exact analytical solutions are not possible for the complete set of equations and therefore we use the efficient numerical method with second order finite difference scheme known as Keller-Box method. The coupled boundary value problem (19,20) of third order in f(η) and second order in θ(η), respectively, has been reduced to a system of five simultaneous ordinary differential equations of first order for five unknowns following the method of superposition (Na [48]) by assuming f=f 1, f′=f 2, f″=f 3, θ=θ 1, θ′=θ 2. To solve this system of equations we require five initial conditions whilst we have only two initial conditions f(0),f′(0) on f(η) and one initial condition θ(0) on θ(η). There are two initial condition f″(0) and θ′(0) which are not prescribed, however the values of f′(η) and θ(η) are known at η→∞. Now, we employ numerical Keller-Box scheme where these two boundary conditions are utilized to produce two unknown initial conditions at η=0. To select η ∞, we begin with some initial guess values and solve the boundary value problem with some particular set of parameters to obtain f″(0) and θ′(0). Thus we start with the initial approximation as f 3(0)=α 0 and θ 2(0)=β 0. Let α ∗ and β ∗ be the correct values of f 3(0) and θ 2(0). We integrate the resulting system of five ordinary differential equations using fourth order Runge-Kutta method and denote the values of f 3(0) and θ 2(0). The solution process is repeated with another larger value of η ∞ until two successive values of f″(0) and θ′(0) differ only after desired digit signifying the limit of the boundary along η. The last value of η ∞ is chosen as appropriate value for that particular set of parameters. Finally the problem has been solved numerically using a second order finite difference scheme known as Keller-Box method [49, 50]. The numerical solutions are obtained in four steps as follows:

  • reduce (19) and (20) to a system of first-order equations;

  • write the difference equations using central differences;

  • linearize the algebraic equations by Newton’s method, and write them in matrix-vector form; and

  • solve the linear system by the block tri-diagonal elimination technique.

For numerical calculations, a uniform step size of Δη=0.01 is found to be satisfactory and the solutions are obtained with an error tolerance of 10−6 in all the cases. To assess the accuracy of the present method, comparison of the skin friction f″(0) and the wall temperature gradient θ′(0) between the present results and previously published results are made, for several special cases in which the Maxwell parameter and thermo physical fluid properties are neglected (see Tables 1 and 2).

Table 1 Comparison of skin friction f″(0) for different values of the magnetic parameter when θ r →∞,ε=0.0,β=0, and β 1=0.0
Full size table
Table 2 Comparison of wall temperature gradient θ′(0) for different values of Prandtl number and magnetic parameter when θ r →∞,ε=0.0,β=0, and β 1=0.0
Full size table

5 Results and discussion

The influence of the temperature- dependent fluid properties on MHD boundary layer flow and heat transfer of a UCM fluid over a stretching sheet is investigated numerically. Analytical solutions are obtained for the special case when θ r →∞,β=0 and ε=0. Numerical solution is warranted for the general case which is achieved by using a second order finite difference scheme known as the Keller-Box method (Prasad et al. [43]). In order to have an understanding of the mathematical model, we present the numerical results, graphically for the horizontal velocity and the temperature fields, respectively in Figs. 2a, 2b and 3 and in Figs. 4a, 4b to 8; the skin friction f″(0) and the wall temperature gradient θ′(0) are presented in Table 3.

Fig. 2a
figure 2

Velocity profiles for different values of β-with β 1=0.1, ε=0.1, Pr=1.0, 1/θ r =0.0

Full size image
Fig. 2b
figure 3

Velocity profiles for different values of β-with β 1=0.0, ε=0.0, θ r =−1.0, Pr=1.0

Full size image
Fig. 3
figure 4

Velocity profiles for different values of θ r when (a) Mn=0.0 and (b) Mn=0.5 with β 1=0.0, ε=0.0, Pr=1.0

Full size image
Fig. 4a
figure 5

Temperature profiles for different values of β with β 1=0.1, ε=0.1, Pr=1.0, 1/θ r =0.0

Full size image
Fig. 4b
figure 6

Temperature profiles for different values of β with β 1=0.0, ε=0.0, θ r =−1.0, Pr=1.0

Full size image
Table 3 Values of f″(0) and θ′(0) for different values of pertinent parameters
Full size table

Figures 2a and 2b present, respectively, the effects of constant fluid viscosity (θ r →∞) and non-zero fluid viscosity parameter (θ r =−1.0) on the horizontal velocity profile f′(η) for different values of the Maxwell parameter β and the magnetic parameter Mn. It is noticed that the velocity f′(η) is unity at the wall and tends asymptotically to zero as the distance increases from the boundary. The effect of increasing values of the Maxwell parameter β is to reduce the velocity f′(η) and thereby reduce the boundary layer thickness, and hence an increase in the absolute value of the surface velocity gradient. This is true for zero/non-zero values of the magnetic parameter and the variable viscosity parameter [see Fig. 2b]. From Fig. 2a, it is also noticed that the velocity f′(η) decreases with an increase in the magnetic parameter Mn due to the fact that the transverse magnetic field normal to the flow direction has a tendency to produce a drag force known as the Lorentz force which tends to resist the flow. The effects of fluid viscosity parameter θ r on the velocity f′(η) for the cases Mn=0.0 (without magnetic field) and Mn=0.5 (with magnetic field) are depicted respectively in Figs. 3a and 3b. It is observed that the velocity f′(η) decreases with increasing values of the variable viscosity parameter θ r : This is due to the fact that for a given fluid, when δ is fixed, smaller θ r implies higher temperature difference between the wall and the ambient fluid. The results presented in this paper demonstrate clearly that θ r the indicator of the variable viscosity with temperature has a substantial effect on the velocity component f′(η) and hence on the skin friction. This is true for non-zero values of the magnetic parameter Mn. The results for non-zero values of the magnetic parameter are qualitatively similar to those of Mn=0.0 case, but quantitatively reduced (see Fig. 3b).

Temperature profiles θ(η) are shown graphically in Figs. 4a, 4b, to 8 for different values of the pertinent parameters. The general trend is that the temperature distribution is unity at the wall and with the changes in the physical parameters tends asymptotically to zero in the free stream region. Figure 4a shows the effect of the Maxwell parameter β and the magnetic parameter Mn on the temperature θ(η) for the case θ r →∞. The effect of increasing values of the Maxwell parameter β is to increase the temperature distribution in the flow region. This is in conformity with the fact that an increase in the Maxwell parameter β leads to an increase in the thermal boundary layer thickness. This is true even for non-zero values of the magnetic parameter Mn. Also, as explained above, the introduction of transverse magnetic filed to an electrically conducting fluid gives rise to a resistive force known as the Lorentz force. This force makes the fluid experience a resistance by increasing the friction between its layers and thereby increases the temperature. This behavior is true even for non-zero values of the fluid viscosity parameter θ r , shown in Fig. 4b. Figure 5a depicts the effect of fluid viscosity parameter θ r on the temperature θ(η) for zero and non-zero values of Maxwell parameter β From the graphical representation, we see that the combined effect of increasing value of the variable viscosity parameter θ r and the Maxwell parameter β is to enhance the temperature. This is because of the fact that an increase in the fluid viscosity parameter θ r results in an increase in the thermal boundary layer thickness. This is even true for non-zero values of magnetic parameter (see Fig. 5b). The variations in temperature for different values of the Prandtl number Pr and the Maxwell parameter β are displayed respectively in Figs. 6a and 6b for θ r →∞, and θ r =−5.0. Both figures demonstrate that an increase in the Prandtl number Pr (means decrease in the thermal conductivity K ∞) leads to a decrease in the temperature. Hence the thermal boundary layer thickness decreases as the Prandtl number increases.

Fig. 5
figure 7

Temperature profiles for different values of θ r when (a) Mn=0.0 and (b) Mn=0.5 with β 1=0.0, ε=0.0, Pr=1.0

Full size image
Fig. 6
figure 8

Temperature profiles for different values of Pr when (a) 1/θ r =0.0 and (b) θ r =−5.0 with β 1=0.0, ε=0.1, Mn=1.0

Full size image

The effect of variable thermal conductivity parameter ε on the temperature profile θ(η) for increasing values of the Maxwell parameter β is shown graphically in Figs. 7a and 7b for both the cases of θ r →∞ and θ r =−5.0. It is observed that the temperature distribution increases with an increase in the value of the variable thermal conductivity parameter ε. This is due to the fact that the temperature dependent thermal conductivity induces a reduction in the magnitude of the transverse velocity by a quantity ∂K(T)/∂y which can be seen from (18). Figures 8a and 8b exhibit the changes in the temperature distribution θ(η) for different values of the heat source/sink parameter β 1 for θ r →∞ and θ r =−5.0, respectively. From these figures we observe that the temperature distribution is being reduced throughout the boundary layer for negative values of β 1 compared to the positive values of β 1. Physically, β 1>0 implies T w >T ∞ (that is, the case of supply of heat to the flow region form the wall). Similarly β 1<0 implies T w <T ∞ (the transfer of heat is from flow to the wall). The effect of increasing values of heat source/sink parameter β 1 is to increase the temperature profile when θ r →∞ and θ r =−5.0.

Fig. 7
figure 9

Temperature profiles for different values of ε when (a) 1/θ r =0.0 and (b) θ r =−5.0 with β 1=0.0, Mn=1.0, Pr=1.0

Full size image
Fig. 8
figure 10

Temperature profiles for different values of β 1, when (a) 1/θ r =0.0 and (b) θ r =−5.0 with ε=0.1, Mn=1.0, Pr=1.0

Full size image

The impact of all the physical parameters on the skin friction and the wall-temperature gradient may be analyzed from Table 2. Analysis of the tabular data shows that the Maxwell parameter, the magnetic parameter and the variable viscosity parameter decrease the skin friction: But quite the opposite is true with the rate of heat transfer. This observation is even true in the presence of the variable thermal conductivity parameter. However the effect of heat source/sink parameter or the variable thermal conductivity parameter is to enhance the rate of heat transfer. But the effect of the Prandtl number is to decrease the wall-temperature gradient for zero and non-zero values of the Maxwell parameter.

6 Conclusions

In this paper we have theoretically studied the effects of the temperature-dependent thermo-physical properties on the MHD boundary layer flow and heat transfer of a UCM fluid over a stretching sheet in the presence of internal heat generation/absorption. Here, the flow is generated, due to the stretching of an elastic sheet caused by the simultaneous application of two equal and opposite forces along the x-axis, keeping the origin fixed: The sheet is then stretched with a speed varying linearly with distance from the slit. The governing partial differential equations are transformed into ordinary differential equations by using an appropriate similarity transformation and then the resulting boundary value problem is solved numerically by a second order finite difference scheme. A systematic study to assess the effects of variable viscosity and other physical parameters controlling the flow and heat transfer characteristics is carried out. The following conclusions are drawn from the computed numerical values:

  • In the presence of temperature dependent thermo-physical properties, the effect of increasing Maxwell parameter and the magnetic parameter is to decrease the velocity throughout the boundary layer. However, quite the opposite is true with the thermal boundary layer.

  • The effect of Prandtl number is to decrease the thermal boundary layer thickness and the wall temperature gradient.

  • The effects of variable thermal conductivity parameter and the heat source/sink parameter are to enhance the temperature in the flow region.

  • Of all the parameters, the variable thermo-physical property parameters have the strong effects on the drag, heat transfer characteristics, the horizontal velocity and the temperature fields in the MHD flow of UCM fluid over a stretching sheet.