1 Introduction

In Various manufacturing processes the heat and fluid flow past a moving/stretching surfaces plays a vital role in designing a product of desired shape, size and quality, for example, manufacturing of rubber and plastic sheet, glass blowing, polymer sheets and filaments, cooling of metallic plates, etc. Thus, understanding the characteristics of fluid flows induced by a moving or elongating sheet owes a great importance in industrial applications. Sakiadis [1] pioneered the boundary layer flow induced by a continuous moving surface. Crane [2] extended Sakiadis’s [1] idea to extensible surface with linearly stretching speed. In his investigation, he modeled the stretching velocity as a linear function of distance measured from the origin. These pioneering research works are being followed by numerous researches considering different aspects of stretching rate of deforming surface viz. nonlinear stretching [3], exponentially stretching [4], unsteady stretching [5] and oscillatory stretching with rotation [6].

Most of the fluids which are important in various industries viz. metallurgical, petroleum, chemical, agricultural, biomedical, automobile, electronics, etc. do not obey the Newton’s linear viscosity model. Unlike the Newtonian fluids the rheological behavior of non-Newtonian fluids are very different and knowledge of their flow characteristics is very important for industrial application purpose. Many researchers investigated the flow characteristics of various fluids obeying non-Newtonian constitutive equations viz. Power Law or Ostwald de Waele fluids [7] Casson fluids [8], Oldroyd-B fluids [9], Walter’s liquid B fluids [10, 11], Sisko fluid [12], Jeffrey fluid [13], Eyring-Powell fluid [14] etc.

MHD boundary layer flows have numerous application in various industries. These flows can be realized in the liquid metal flows or plasma flows where transverse magnetic fields are used to control the flow. Pavlov [15] obtained the solution of MHD flow caused by deforming plane surface. A closed form solution of MHD viscoelastic fluid is obtained by Anderson [16]. Liu [17] investigated the heat transfer aspect in a second grade fluid past a stretching sheet in the presence of transverse magnetic field in a porous medium considering the effect of viscous dissipation and internal heat generation and arrived at the same expression for the solution of momentum equation as obtained by Anderson [16] with combined effect of magnetic field and porous medium. He also obtained solution for fluid temperature analytically in terms of Kummer’s function and presented the heat transfer gradient at the surface for prescribed surface temperature (PST) case and prescribed heat flux (PHF) case corresponding to different flow parameters. The Bionic study of variable viscosity on MHD peristaltic flow of non-Newtonian (Pseudoplastic) fluid in an asymmetric channel is carried out by Khan et al. [18]. There may be the cases where a variable magnetic field is applied to control the flow motion. Study of variable magnetic field on the peristaltic flow of Jeffrey fluid is presented by Bhatti et al. [19]. Further, Bhatti et al. [20] analyzed sinusoidal motion of two-phase flow (particle–fluid suspension) with heat and mass transfer through a planar channel in the presence of transverse magnetic field. The effect of induced magnetic field due to the motion of electrically conducting fluid in presence of an applied transverse magnetic field is studied by Sheikholeslami et al. [21]. Bhatti et al. [22] applied an inclined magnetic field instead of transverse magnetic field in a peristaltically induced fluid motion. Knowledge of thermal radiation characteristics for heat transfer problems, mainly the problems dealing at high temperature, viz., nuclear power plants, solar power, gas turbines and various propulsion devices for aircraft, missiles, satellites and space vehicles, metallurgical industries, etc. is indispensable [23]. This fact leads many researcher to investigate thermal radiation effect on fluid flow. Chen [24] obtained an analytic solution for MHD viscoelastic fluid flow, incorporating the thermal radiation term. To obtain the solution he linearized the thermal radiation term by employing Rosseland approximation. The nonlinear thermal radiation is considered by Bhatti et al. [25] in a sinusoidal motion of dusty fluid with magnetic solid particles. Zeeshan et al. [26] investigated the magnetic dipole effect on ferro-fluid past a stretching sheet with thermal radiation. Magyari and Pantokratoras [27] observed in their research paper that the solution of the radiation problem for optically thick media in view of the linearized Rosseland approximation does not require any additional numerical or analytical effort compared to the same problem without radiation. To simplify the radiation problem they gave the concept of “effective Prandtl number”.

Natural or free or buoyant convection heat and fluid flows arise due to the interaction of gravitational force and temperature difference. The mechanism of free convection is important in variety of engineering and industrial applications viz. Oceanography, convection in Earth’s Mantle, Nuclear Reactor, etc. Abel et al. [28] analyzed the effect of thermal buoyancy force on MHD boundary layer flow of Walter’s B viscoelastic liquid under the PST and PHF surface boundary conditions. Hayat et al. [29] investigated the Soret and Dufour effects on heat and mass transfer in a MHD viscoelastic fluid filled in porous medium using HAM. Some recent studies on natural convective flow of viscoelastic fluids are due to Rashidi et al. [30], Jena et al. [31], etc.

An understanding of the boundary slip has significant implications in the designing of various microfluidic systems, red blood flow through capillaries and in many technological processes such as lubrication and permeability of micro-porous media. The above mentioned studies have been carried out assuming no-slip velocity at the solid–fluid interface, however, this assumption is not appropriate for various situation such as micro\nano-scale flows, and low pressure (rarefied) flows. The non-adherence phenomena of fluids has been confirmed analytically [32, 33] as well as experimentally [34]. It was found that the velocity slip at the fluid–surface interface is a function of shear stress and the property of surface [35]. Thus, consideration of boundary slip condition in case of non-Newtonian fluid flows have more importance than Newtonian fluid flow. Ariel et al. [36], Megahed [37] and Anand [38] presented the studies which explored the effect of partial velocity slip in viscoelastic fluid flow induced by stretching sheet.

Most of the research studies on heat transfer were carried out under the assumption of either Dirichlet’s (PST) or Neumann’s (PHF) boundary conditions, however, the Robin (convective) boundary conditions are more realistic and occurrent in nature. Bataller [39] analyzed Blasius and Sakiadis flows under the influence of radiation and convective boundary condition (Robin condition). Aziz [40] deduced that a similarity solution is possible if heat transfer coefficient varies inversely proportional to the square root of distance from the origin in the direction of stretching, since then several research studies have been carried out considering the convective thermal boundary condition [41,42,43].

The present article investigates the two-dimensional magnetohydromagnetic, natural convective flow of an optically thick radiating, electrically conducting and viscoelastic fluid past a vertically upward linearly stretching sheet considering the effect of partial velocity slip at the sheet-fluid interface. The analysis presented in this article is relatively original and does not seem to be reported in the literature till now. The physical model investigated in the present article finds its application in polymer and melting metal industries.

2 Mathematical formulation of the problem

2.1 Governing equations

The Cauchy stress tensor \(\varUpsilon\) for the viscoelastic fluids (Walters liquid B’ model) with short relaxation time can be written in the form [10]

$$\varUpsilon = - {\text{pI}} + S,$$
(1)

where

$$S = 2\mu A - 2k_{0} \frac{DA}{Dt},$$
(2a)
$$2A = (\nabla V) + (\nabla V)^{*} ,$$
(2b)
$$\frac{DA}{Dt} = \frac{\partial A}{\partial t} + (V \bullet \nabla )A - (\nabla V)A - A(\nabla V)^{*} ,$$
(2c)
$$V = (u,v,0)\;{\text{and }}(\nabla V) = \left( {\begin{array}{*{20}c} {\frac{\partial u}{\partial x}} & {\frac{\partial u}{\partial y}} & 0 \\ {\frac{\partial v}{\partial x}} & {\frac{\partial v}{\partial y}} & 0 \\ 0 & 0 & 0 \\ \end{array} } \right),$$
(2d)

where superscript * stands for matrix transpose.

The equations of motion for steady two-dimensional incompressible viscoelastic fluid satisfying Eq. (1) and including body force \(b = (b_{x} ,b_{y} ,0)\) become

$$\begin{aligned} \rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) & = - \frac{\partial p}{\partial x} + \mu \nabla^{2} u - k_{0} \left[ {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)\nabla^{2} u - \frac{\partial u}{\partial x}\nabla^{2} u - \frac{\partial u}{\partial y}\nabla^{2} v} \right] \\ & \quad + 2k_{0} \left[ {\left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)\frac{{\partial^{2} u}}{\partial x\partial y} + \frac{\partial v}{\partial y}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial x^{2} }}} \right] + \rho b_{x} \\ \end{aligned}$$
(3)
$$\begin{aligned} \rho \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right) & = - \frac{\partial p}{\partial y} + \mu \nabla^{2} v - k_{0} \left[ {\left( {u\frac{\partial }{\partial x} + v\frac{\partial }{\partial y}} \right)\nabla^{2} v - \frac{\partial v}{\partial x}\nabla^{2} u - \frac{\partial v}{\partial y}\nabla^{2} v} \right] \\ & \quad + 2k_{0} \left[ {\left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)\frac{{\partial^{2} v}}{\partial x\partial y} + \frac{\partial v}{\partial y}\frac{{\partial^{2} v}}{{\partial y^{2} }} + \frac{\partial u}{\partial x}\frac{{\partial^{2} v}}{{\partial x^{2} }}} \right] + \rho b_{y} , \\ \end{aligned}$$
(4)

and equation of continuity is given by

$$\frac{\partial u}{\partial x} + \frac{\partial u}{\partial x} = 0,$$
(5)

Examples of fluids satisfying Eq. (1) are the dilute polymer solutions, e.g., 5.4% polyisobutylene in cetane and 0.83% ammonium alginate in water, which are mobile and not highly elastic hence the usual concepts of boundary layer theory is valid for the given model [10]. Thus, on applying boundary layer approximation, Eqs. (3) and (4) reduce to

$$\rho \left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right) = - \frac{\partial p}{\partial x} + \mu \frac{{\partial^{2} u}}{{\partial y^{2} }} - k_{0} \left\{ {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + v\frac{{\partial^{3} u}}{{\partial y^{3} }} + \frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\partial u}{\partial y}\frac{{\partial^{2} v}}{{\partial y^{2} }}} \right\} + \rho b_{x} ,$$
(6)
$$- \frac{\partial p}{\partial y} = 0.$$
(7)

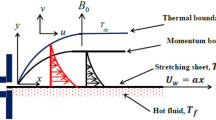
The present problem deals with two-dimensional steady hydromagnetic natural convective flow of an electrically conducting, incompressible and optically thick radiating viscoelastic fluid past a vertically upward stretching sheet. Physical sketch depicting the flow configuration and coordinate system of the problem is presented in Fig. 1. Leading edge of the sheet is kept fixed at origin O and the flow is confined within the region \(y \ge 0\). The left side surface of the sheet is convectively heated with temperature \(T_{s}\) and heat transfer coefficient \(h_{f}\). A uniform transverse magnetic field of intensity \(B\) is applied in a direction parallel to \(y\)-axis. The induced magnetic field is ignored by assuming magnetic Reynolds number very small [44].

Fig. 1
figure 1

Geometry of the problem

Full size image

Under the Prandtl’s boundary layer and Boussinesq approximations, governing equations for described model [28, 36, 45] are given by

$$\rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = \mu \frac{{\partial^{2} u}}{{\partial y^{2} }} - k_{0} \left( {\frac{\partial u}{\partial x}\frac{{\partial^{2} u}}{{\partial y^{2} }} + u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + \frac{\partial u}{\partial y}\frac{{\partial^{2} v}}{{\partial y^{2} }} + v\frac{{\partial^{3} u}}{{\partial y^{3} }}} \right) + \rho g\beta \left( {T - T_{\infty } } \right) - \sigma B^{2} u,$$
(8)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{m} \frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\left( {\rho C_{p} } \right)}}\frac{{\partial q_{r} }}{\partial y},$$
(9)

where \(b_{x} = \beta \left( {T - T_{\infty } } \right)g - \sigma B^{2} u\) is the term due to body force acting on the fluid.

For the described model, the boundary conditions are:

$$u = u_{s} + u_{\text{slip}} ,\,\,v = 0,\,\,k\frac{\partial T}{\partial y} = - h_{f} \left( {T_{s} - T_{\infty } } \right)\,\,\,{\text{at}}\,\,y = 0,$$
(10a)
$$u \to 0,\,\,\frac{\partial u}{\partial y} \to 0,\,\,T \to T_{\infty } ,\,\,\,\,\,\,\,\,\,{\text{as}}\,\,y \to \infty ,$$
(10b)

where \(u_{s} = ax\,\,\,\,\,{\text{and}}\,\,\,\,\,u_{\text{slip}} = N\left[ {\frac{\partial u}{\partial y} - \frac{{k_{0} }}{\mu }\left( {2\frac{\partial u}{\partial x}\frac{\partial u}{\partial y} + u\frac{{\partial^{2} u}}{\partial x\partial y} + v\frac{{\partial^{2} u}}{{\partial y^{2} }}} \right)} \right].\)

It may be noted from Eq. (7) that pressure \(p\) is independent of \(y\) and fluid flow is induced due to the stretching sheet so the pressure gradient term \(- \frac{\partial p}{\partial x}\) is not considered in the present problem.

Applying Rosseland approximation, the radiative heat flux \(q_{r}\) [27] is given as

$$q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y}.$$
(11)

One can linearize the nonlinear term \(\,T^{4}\) occurring in Eq. (11) with the help of Taylor series by assuming a small variation between the fluid temperature within the boundary layer and ambient fluid temperature, retaining terms up to first order only. Thus, \(\,T^{4}\) can be represented as:

$$T^{4} \cong 4T_{\infty }^{3} T - 3T_{\infty }^{4} .$$
(12)

The energy Eq. (9), after incorporating Eqs. (11) and (12), becomes

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{m} \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{1}{{\left( {\rho C_{p} } \right)}}\frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}.$$
(13)

2.2 Similarity transformation

To obtain similarity solution of equations (5), (8) and (13) subjected to the boundary conditions (10a) and (10b), following similarity transforms are introduced

$$\eta = y\sqrt {\frac{{u_{s} }}{\upsilon x}} ,\,\,\psi = \sqrt {u_{s} \upsilon x} f\left( \eta \right),\,\,\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{s} - T_{\infty } }}$$
(14)

With these assumptions, continuity equation (5) is automatically satisfied.

Using (14) in Eqs. (8) and (13), we obtain

$$f^{\prime\prime\prime} + ff^{\prime\prime} - f^{\prime 2} + \lambda \theta - Mf^{\prime} + \alpha \left( { - 2f^{\prime}f^{\prime\prime\prime} + f^{\prime \prime 2} + ff^{{\left( {\text{iv}} \right)}} } \right) = 0,$$
(15)
$$\theta^{\prime\prime} + { \Pr }_{eff} \, f\theta^{\prime} = 0.$$
(16)

The boundary conditions (10a) and (10b), in non-dimensional form, are given by

$$\left. \begin{array}{ll} f\left( \eta \right) = 0,\,\,\,f^{\prime}\left( \eta \right) = 1 + \gamma f^{\prime\prime}\left( \eta \right)\left( {1 - 3\alpha f^{\prime}\left( \eta \right)} \right), \theta^{\prime}\left( \eta \right) = {\text{Bi}}\left( {1 - \theta \left( \eta \right)} \right),& {\text{at}}\,\,\eta = 0, \\ f^{\prime}\left( \eta \right) \to 0,\quad f^{\prime\prime}\left( \eta \right) \to 0,\quad \theta \left( \eta \right) \to 0, & {\text{as}}\,\,\eta \to \infty \\ \end{array} \right\}$$
(17)

where \(\alpha = \frac{{k_{0} a}}{\mu }\), \(\lambda = \frac{{Gr_{x} }}{{\text{Re}_{x}^{2} }}\), \(Gr_{x} = \frac{{g\beta \left( {T_{s} - T_{\infty } } \right)x^{3} }}{{\upsilon^{2} }}\), \(\text{Re}_{x} = \frac{{u_{s} x}}{\upsilon }\), \(M = \frac{{\sigma B^{2} }}{\rho a}\), \(\Pr = \frac{\upsilon }{{\alpha_{m} }}\), \(R = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3kk^{*} }}\), \(\Pr_{eff} = \frac{\Pr }{(1 + R)}\) [27], \({\text{Bi}} = \frac{{h_{f} \,x}}{k}\text{Re}_{x}^{ - 1/2}\) and \(\gamma = N\sqrt {\frac{a}{\upsilon }}\) are dimensionless parameters.

It may be noted that here \(\alpha > 0\) represents the second order viscoelastic designated Walters liquid \(B^{\prime}\) model [10], whereas \(\alpha < 0\) represents the second grade viscoelastic fluid model proposed by Coleman and Noll [46] [17 and 29].

2.3 Physical quantities of engineering interests

The local skin friction or frictional drag coefficient \(Cf_{x}\) and local Nusselt number \(Nu_{x}\) which stimulates the stress at the surface and heat transfer rate from surface to fluid, respectively, are defined by

$$Cf_{x} = \frac{{\tau_{s} }}{{\rho \,u_{s}^{2} }} \quad {\text{ and }}\quad Nu_{x} = \frac{{xq_{s} }}{{k(T_{s} - T_{\infty } )}},$$
(18)

Where

$$\tau_{s} = \left[ {\mu \frac{\partial u}{\partial y} - k_{0} \left( {u\frac{{\partial^{2} u}}{\partial x\partial y} + 2\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}} \right)} \right]_{y = 0} {\text{ and}}\,\,\,q_{s} = - \left[ {\left( {k + \frac{{16\sigma T^{3} }}{{3k^{*} }}} \right)\frac{\partial T}{\partial y}} \right]_{y = 0} .$$
(19)

With the help of (14) and (19), (18) can be expressed in dimensionless form as

$$Cf_{x} \text{Re}_{x}^{1/2} = (1 - 3\alpha )f^{\prime\prime}(0)\quad{\text{and }} \quad Nu_{x} \text{Re}_{x}^{ - 1/2} = - (1 + R)\theta^{\prime}(0),$$
(20)

where, \(f^{\prime\prime}(0)\,\,{\text{and}}\, - \theta^{\prime}(0)\) are, respectively, dimensionless wall velocity gradient and wall temperature gradient.

3 Numerical implementation

To ease our computation we have reduced the order of Eq. (15) by introducing a new variable as

$$f' = t.$$
(21)

Thus, the Eq. (15) and (16) together with (17) are transformed into

$$t^{\prime\prime} + ft^{\prime} - t^{2} + \lambda \theta - Mt + \alpha \left( {t^{\prime 2} - 2tt^{\prime\prime} + ft^{\prime\prime\prime}} \right) = 0,$$
(22)
$$\theta^{\prime\prime} + \Pr_{eff} f\theta^{\prime} = 0,$$
(23)
$$\left. \begin{aligned} f\left( \eta \right) = 0,\,\,\,t\left( \eta \right) = 1 + \gamma t^{\prime}\left( \eta \right)\left( {1 - 3\alpha t\left( \eta \right)} \right),\,\,\,\theta^{\prime}\left( \eta \right) = {\text{Bi}}\left( {1 - \theta \left( \eta \right)} \right),\,\,\,\,\,\,\,\,{\text{at}}\,\,\eta = 0, \hfill \\ t\left( \eta \right) \to 0,\,\,t^{\prime}\left( \eta \right) \to 0,\,\,\,\theta \left( \eta \right) \to 0,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{as}}\,\,\eta \to \infty . \hfill \\ \end{aligned} \right\}$$
(24)

Equations (21)–(23) along with (24) are extremely non-linear and coupled. Thus, obtaining an exact solution is almost impossible. Therefore, a numerical scheme must be utilized to solve this system. We have employed the finite element method [47] to get an approximate solution of the above-mentioned system of equations.

The essential steps involved in a typical finite element analysis are summarized below:

  1. a.

    Generation of finite element mesh: like any other numerical technique this method also involves the process of discretization of entire physical domain into a finite set of sub-domains in such a non-overlapping manner that they entirely cover the whole flow domain of the problem. Each such sub-domain is termed as an element.

  2. b.

    Derivation of the element equations: Over a typical element from the discretized domain (i.e., finite element mesh) the variational (weak) formulation of the differential equation is constructed. An approximate solution of the unknowns, i.e., dependent variables assumed in the forms of \(U = \sum\limits_{i = 1}^{n} {U_{i} } \varphi_{i}\) is selected, where \(\varphi_{i}\) are the element interpolation function or basis function and \(U_{i}\) are the unknowns to be computed at the nodal points of the element. Substituting these approximate solutions into the variational formulation of the differential equation, the element equation over the typical element are obtained.

  3. c.

    Global finite element model: to constitute the global finite element model representing whole physical domain, the element (algebraic) equations obtained in previous step are assembled by imposing the inter-element continuity and balance conditions.

  4. d.

    Solution of the finite element model: to get the solution of the global finite element model any of the direct or iterative methods of solving a system of algebraic equations can be used after employing the boundary conditions.

The similarity solution of the flow variables \(f,\,\,t\,\,{\text{and }}\theta\) have been obtained over 2001 nodes of 1000 uniform quadratic elements created from the physical domain of the concerned problem. Since there are three unknowns to be calculated at each nodes, therefore, the step (c) produces a system of 6003 nonlinear algebraic equations of the form

$$\left[ {K\left( {\left\{ U \right\}} \right)} \right]\left\{ U \right\} = \left\{ F \right\},$$
(25)

where \(K\left( {\left\{ U \right\}} \right)\) is the stiffness matrix and \(F\) is the source vector.

After employing the boundary conditions, system of Eqs. (25) reduces into \(5999\) nonlinear algebraic equations which is solved by direct iterative procedure also known as Picard iterative method of successive substitution [47]. The convergence criteria for the iterative procedure which is based on absolute difference of two recent iterative solutions is employed with an accuracy of \(O\,(10^{ - 6} )\). A numerical method requires a finite domain, thus the free stream (i.e., \(\eta \to \infty\)) boundary conditions of the problem are replaced with a finite quantity as \(\eta_{\hbox{max} }\) which has been selected \(\eta_{\hbox{max} } = 6\). The value of \(\eta_{\hbox{max} }\) is chosen in such a manner that it satisfies all the free stream boundary conditions asymptotically.

3.1 Validation of numerical solution

For the validation of the developed code, the approximate solution obtained from the used scheme are compared with the solution obtained by Anderson [16] for various values of \(\alpha\) and \(M\) by taking \(\gamma = \lambda = 0\). As one can see from Figs. 2 and 3 that there is good agreement with the solution of Anderson [16] and the approximate solution computed with the developed code of finite element method.

Fig. 2
figure 2

Velocity variation when \(\gamma = 0\,\,\,{\text{and}}\,\,\,\,\lambda = 0\)

Full size image
Fig. 3
figure 3

Velocity variation when \(\gamma = 0\,\,\,{\text{and}}\,\,\,\,\lambda = 0\)

Full size image

4 Results and discussion

To highlight the perspective of the physics of the flow regime, the influence of all the physical parameters on the flow-field characteristics have been analyzed. The quantities of engineering interests, i.e., local skin friction coefficient, local Nusselt number, fluid velocity and temperature have been computed for various regulatory parameters of flow-field. For better-understanding all the computed results are presented in a graphical form. The numerical computations have been carried out by adopting the default values \(\alpha = 0.1,\,\,\gamma = 0.5,\,\,\lambda = 2,\,\,M = 0.5,\,\,\Pr_{eff} = 10\,\,\,{\text{and}}\,\,{\text{Bi}} = 0.5\), until otherwise specified particularly.

The variation of skin friction coefficient \(Cf_{x} \text{Re}_{x}^{1/2}\) and Nusselt number \(Nu_{x} \text{Re}_{x}^{ - 1/2}\) with \(\alpha\) for various values of \(\lambda\) is presented for the case of no-slip effect (\(\gamma = 0\)) and partial slip effect (\(\gamma = 0.5\)) in Figs. 4 and 5. Since \(\lambda\) represents the relative importance of buoyancy force to viscous force, therefore, an increase in \(\lambda\) stimulates in increased buoyancy force which assists the fluid motion and reduces the shear stress. Figure 4 reveals that \(Cf_{x} \text{Re}_{x}^{1/2}\) is a decreasing function of \(\lambda\) in both the cases, i.e., for \(\gamma = 0\,\,\,{\text{and }}\gamma { = 0} . 5\). It can be seen that in the absence of slip effect the value of \(Cf_{x} \text{Re}_{x}^{1/2}\) decreases almost linearly with \(\alpha\) for all the values of \(\lambda\), whereas presence of slip causes a dramatic change in decreasing behavior of the \(Cf_{x} \text{Re}_{x}^{1/2}\). It may be noted that as \(\alpha \to 1/3\) the Skin friction coefficient tends to vanish and then changes its sign for \(\alpha > 1/3\) which is also in agreement with the Eq. (20), which states that flow separation occurs when \(\alpha = 1/3\). However, this situation may not occur as the momentum Eq. (8) is valid for \(\alpha < < 1\). Figure 5 indicates that the Nusselt number, in absence of velocity slip, varies almost linearly and has diminishing trend with increasing value of \(\alpha\), but presence of velocity slip changes the nature of \(Nu_{x} \text{Re}_{x}^{ - 1/2}\) drastically. First with increase in \(\alpha\), it increases up to \(\alpha = 1/3\) and then it decreases very rapidly for \(\alpha > 1/3\). The buoyancy parameter \(\lambda\) represents the effect of free convection in the governing equations thus an increases in \(\lambda\) leads a higher temperature variation and high convection rate in the flow regime. An increased heat convection rate downgrades the temperature throughout the boundary layer and enhances the temperature gradient at the surface, which is clearly evident from Figs. 5. Figure 6 has been drawn to exhibit the behavior of Nusselt number corresponding to \({\text{Bi}}\,\,\,{\text{and}}\,\,\,M\). It is seen from the figure that corresponding to \(M\) there is a decline in \(Nu_{x} \text{Re}_{x}^{ - 1/2}\). The trend observed in Fig. 6 is due to the Lorentz force generated by movement of conducting fluid in the presence of magnetic field which acts as a resistive force against fluid motion and slows down the flow-velocity and the heat convection rate too. Thus, magnetic field acts as a moderator for heat transfer. The rate of heat transfer at the surface corresponding to Biot number Bi gets enhanced and its effect is quite prominent which is in agreement with the boundary condition (17).

Fig. 4
figure 4

Local skin friction coefficient against \(\alpha\) for \(\lambda \,\,\,{\text{and }}\gamma\)

Full size image
Fig. 5
figure 5

Nusselt number against \(\alpha\) for \(\lambda \,\,\,{\text{and }}\gamma\)

Full size image
Fig. 6
figure 6

Nusselt number against \({\text{Bi}}\) for \(\lambda \,\,\,{\text{and }}M\)

Full size image

Effect of viscoelasticity on fluid velocity is presented in Fig. 7. In absence of partial slip and buoyancy force, Anderson [16] observed that velocity of the fluid shows a decreasing nature for increasing strength of viscoelasticity in whole momentum boundary layer. However, present study reveals completely different phenomena. The strengthening of viscoelasticity effect leads the fluid to move faster close to the surface and with a slower speed away from the sheet. It was also observed that for higher values of \(\gamma\), the crossover point shifts towards free stream within the momentum boundary layer. Figure 8 is plotted to analyze the effect of slip on the velocity field. The nature of velocity distribution corresponding to slip is just opposite to the behavior corresponding to the viscoelasticity, i.e., the increase in magnitude of slip parameter slows down the velocity near the surface and opposite trend is observed away from the surface. The momentum boundary layer gets thicker as more and more fluid gets slipped over the sheet.

Fig. 7
figure 7

Velocity profiles with respect to \(\alpha .\)

Full size image
Fig. 8
figure 8

Velocity profiles with respect to \(\gamma\)

Full size image

Effect of buoyancy force arising due to temperature difference on velocity field is characterized in Fig. 9. A higher curve in Fig. 9 corresponds to the higher values of buoyancy parameter \(\lambda\), which represents the free convection term of the momentum equation. An increase in the value of \(\lambda\) enhances the buoyancy force which acts as a positive force term for velocity and accelerates the fluid velocity. This results in an increased velocity, however, the nature of velocity field turns opposite, as fluid moves towards the boundary layer. The externally applied transverse magnetic field has a tendency to control momentum boundary layer and the velocity of fluid due to the retarding nature of Lorentz force, which acts in perpendicular direction of the fluid motion and applied magnetic field. The phenomena described above is clearly visible in Fig. 10.

Fig. 9
figure 9

Velocity profiles with respect to \(\lambda\)

Full size image
Fig. 10
figure 10

Velocity profiles with respect to \(M\)

Full size image

The temperature field within the thermal boundary layer corresponding to the various values of \(\alpha ,\,\,\,\gamma ,\,\,\,M\), \({\text{Bi}}\) and \(\Pr_{\text{eff}}\) have been analyzed in Figs. 11, 12, 13, 14 and 15. The curves in Fig. 11 are plotted to depict the influence of viscoelasticity on temperature field. It is concluded that the temperature field is a decreasing function of viscoelastic parameter \(\alpha\). Effect of slip of fluids at the stretching surface over fluid temperature is shown in Fig. 12 with different curves plotted for different values of \(\gamma\). The decreasing behavior of temperature distribution is more prominent for the slip parameter \(\gamma\) as compared to \(\alpha\). The physics behind the enhancement of fluid temperature due to increased slip parameter is that, as we noticed from Fig. 8 that the fluid velocity is getting reduced owing to enhanced slip between fluid and surface. Thus, continuous deformation in the surface against the fluid motion produces a frictional heat. As a result, an increased thermal boundary layer thickness as well as enhanced temperature distribution is noticed throughout the boundary layer.

Fig. 11
figure 11

Temperature profiles with respect to \(\alpha\)

Full size image
Fig. 12
figure 12

Temperature profiles with respect to \(\gamma\)

Full size image
Fig. 13
figure 13

Temperature profiles with respect to \(M\)

Full size image
Fig. 14
figure 14

Temperature profiles with respect to \({\text{Bi}}\)

Full size image
Fig. 15
figure 15

Temperature profiles with respect to \(\Pr_{\text{eff}}\)

Full size image

Variation of temperature distribution corresponding to the magnetic parameter \(M\) is elucidated in Fig. 13. It describes that temperature is an increasing function of magnetic field. The trend observed in Fig. 13 is due to the Lorentz force which acts as a resistive force against fluid motion. Consecutively heat is generated and it results in an enhanced temperature within the boundary layer. Figure 14 exhibits the influence of convective heat transfer from the surface to the fluid controlled by Biot number \({\text{Bi}}\). It can be seen from this figure that the fluid temperature at the surface as well as within the thermal boundary layer rises sharply with increasing value of \({\text{Bi}}\). Biot number represents the diffusive resistance within the sheet to the convective resistance at the surface of sheet. Thus, a small \({\text{Bi}}\) represents a high convective resistance at the surface leading to a low heat transfer from the sheet to fluid which is indeed true from this figure. Effect of \(\Pr_{\text{eff}}\) for fixed value of radiation parameter \(R\) which stimulates the relative strengths of viscous and thermal diffusivities is presented in Fig. 15. Since the thermal diffusivity is inversely proportional to \(\Pr_{\text{eff}}\), for a fluid of fixed viscosity, an increment in \(\Pr_{eff}\) results in a weak thermal diffusion which ultimately turns in the reduction of fluid temperature. This phenomena is also validated in Fig. 15. It can also be concluded from this figure that for the fixed value of \(\Pr\), the fluid temperature increases for strengthening effect of radiation.

5 Conclusions

Investigation of two dimensional hydromagnetic natural convection flow of an electrically conducting, incompressible and optically thick radiating viscoelastic fluid past a vertically upward stretching sheet is carried out. Significant findings are summarized below:

  • Partial slip effect and viscoelasticity of the fluid have opposite nature on the velocity field. It is interesting to report that, for smaller values of slip parameter, the nature of velocity field corresponding to viscoelasticity changes quickly near the sheet, whereas as magnitude of slip parameter enhances the turning point moves away from the sheet.

  • Buoyancy force acts as a favorable factor for the velocity field and with its strengthening effect, it enhances the velocity of the fluid.

  • Temperature distribution slows down with increasing magnitude of viscoelasticity and thermal diffusivity, whereas the opposite nature is observed for strengthening effects of partial velocity Slip, magnetic field, convective heat transfer and thermal radiation.