Abstract
As mentioned in Biondini et al. (Commun Math Phys 348:475–533, 2016), the complete theory of the inverse scattering transform for the multi-component focusing nonlinear Schrödinger equation with nonzero boundary conditions still remains open. In this paper, we attempt to investigate the above problem with a particular class of nonzero boundary conditions. The direct problem is shown to be well posed for potential \({\textbf{q}}\) such that \({\textbf{q}}(\cdot ,t)-{\textbf{q}}_\pm \) lies in the \(L^{1,1}({\mathbb {R}}^\pm )\) space. By introducing two modified Lax pairs and generalized cross product operations in \({\mathbb {C}}^{N+1}\), the analyticity properties and the symmetries of a complete set of eigenfunctions and scattering data are obtained. The inverse problem is characterized in terms of a \(3\times 3\) block matrix Riemann–Hilbert problem, whose solution exists uniquely due to the growth conditions at branch points and the symmetries of jump matrices, residue conditions and asymptotics at two infinities of Riemann surface. In the reflectionless case, some special solutions including soliton and breather are displayed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As one of the most important theories in the nonlinear integrable PDEs over the last 50 years, the inverse scattering transform (IST) was pursued mostly for the zero boundary conditions (ZBCs), i.e., the potentials vanish for large spatial variable. However, recent studies have shown that the nonzero boundary conditions (NZBCs) are relevant to the research of modulation instability and the generation mechanism of rogue wave [1,2,3,4]. From a mathematical viewpoint, such problems are less well characterized. Following that, a nature issue is to formulate the IST in the NZBCs cases. Specifically, we focus on the N-component nonlinear Schrödinger (NLS) equation
where \(\kappa =\pm 1\) means the focusing (resp. defocusing) case. It is well known that the scalar version is referred to as the celebrated NLS equation and the 2-component case as the Manakov system. There are two main motivations for studying the multi-component case.
On the one hand, the N-component NLS equation not only possesses some remarkably rich symmetries but also arises in many physical fields such as nonlinear optics, fluid mechanics, plasmas physics and multi-component Bose-Einstein condensates [5,6,7,8]. On the other hand, let us recall the research works about the IST for the N-component NLS equation. The scalar case with ZBCs was developed in Ref. [9] (see also Refs. [10,11,12,13]), the 2-component case was dealt in Ref. [7], and the theory can be extended to any multi-component NLS equations with ZBCs in a straightforward way [14, 15]. Unlike the case of ZBCs, the IST with NZBCs is more complicated because the spectral parameter lies in the two-sheeted Riemann surface rather than the complex plane. The early work for the NLS equation with NZBCs was shown in Refs. [16, 17] and was revisited in Refs. [18,19,20,21]. The work about the defocusing Manakov system was accomplished in Ref. [22] and developed in Ref. [23]. The focusing Manakov system with NZBC was studied in Ref. [24] using similar methods. By generalizing the tensor approach, important advance in the multi-component defocusing NLS equation with NZBCs was outlined in Ref. [25]. Recently, a more rigorous analysis of the IST for the 3-component defocusing NLS equation with NZBC was presented in Ref. [26], and it was pointed out that for the multi-component focusing NLS equation with NZBCs, the complete theory of the inverse scattering transformation is still open. Unfortunately, the above methods can not be applied directly to the arbitrary N-component focusing NLS equation with NZBCs. Despite several development has been established in Refs. [23,24,25,26], there are still some crucial problems, in which the most important ones are the symmetry of jump matrix, the existence and uniqueness of the solution for Riemann–Hilbert (RH) problem, the verification of reconstruction formula. Furthermore, it is well known that the focusing NLS equation and the defocusing NLS equation are fundamentally different, the IST for the focusing case is much more involved than the defocusing case because there are four different fundamental domains of analyticity instead of two.
The purpose of this work is to overcome some challenging difficulties and to present a characterization of the IST for the N-component focusing NLS equation
with NZBCs for large \(\vert x\vert \):
where \({\textbf{q}}_0\) is a constant complex valued vector of modulus \(q_0 \), \(\theta _\pm \in [0,2\pi )\). Indeed, by two gauge transformations \({\textbf{q}}(x,t)\rightarrow {\textbf{q}}(x,t)\textrm{e}^{-2\textrm{i}q_0^2t}\) and \({\textbf{q}}(x,t)\rightarrow q_0 {\textbf{q}}( q_0x, q_0^2 t)\), Eq. (1.2) can be converted into the N-component focusing NLS equation (1.1) and the multi-component Gross–Pitaevskii equation \( \textrm{i}{\textbf{q}}_t+{\textbf{q}}_{xx}+2{\textbf{q}}{\textbf{q}}^\dag {\textbf{q}}-2{\textbf{q}}={\textbf{0}}\), respectively. In addition, given the U(N) invariance of Eq. (1.2), without loss of generality, \({\textbf{q}}_0\) can be chosen to be the form \({\textbf{q}}_0=(\underbrace{0,\ldots ,0}_{N-1},q_0)^T\).
As it will be shown, when it comes to focusing the N-component focusing NLS equation with NZBCs, the analysis process becomes extremely difficult, so we have to introduce some new concepts and new tools. The innovation of this paper is mainly reflected in the following aspects: (i) Instead of the method in Ref. [18], two modified Lax pairs are first used to set up the Volterra integral equations and investigate the analyticity properties of the scattering matrix entries. In addition, compared with Ref. [18], a slightly weaker nonzero boundary condition is required in this context. (ii) Instead of the tensor approach, a generalized cross product operation in \({\mathbb {C}}^{N+1}\), consistent with the common cross product operation in \({\mathbb {R}}^3\), is introduced to generate the auxiliary eigenfunctions. The decompositions of the auxiliary eigenfunctions and the symmetries of a complete set of eigenfunctions are established by virtue of the adjugate matrix. Especially, some essential identities, which may be also useful to the ISTs, are proved for the first time. (iii) Unlike the cases with ZBCs or the scalar cases with NZBCs, it does not seem obvious for the multi-component cases with NZBCs that the inverse problem can be solved uniquely. In this paper, the existence and the uniqueness of the solution for the inverse problem are proved by virtue of Zhou’s vanishing Lemma (see Refs. [27, 28]), and the reconstruction formula is verified by the dressing method (see Ref. [29]).
The organization of this paper is as follows: In Sect. 2, we prove that the direct scattering problem is well defined for potential \({\textbf{q}}\) such that \({\textbf{q}}(\cdot ,t)-{\textbf{q}}_\pm \) lies in the appropriate functional space. As a consequence, we obtain the integral representations for the scattering data and establish the analyticity of the eigenfunctions and the scattering data. In Sect. 3, we prove that the solution of the N-component focusing NLS equation with NZBCs can be expressed in terms of the unique solution of a \(3\times 3\) block matrix RH problem, which is directly formulated by a combination of the eigenfunctions and the scattering data. In the reflectionless case, some exact solutions are obtained in Sect. 4.
The following basic notations will be used throughout this paper: We denote by \({\bar{z}}\) the complex conjugate of a complex number z, and denote \({\hat{z}}=-\frac{q_0^2}{z}\). When used with a matrix \({\textbf{A}}\), \(\bar{{\textbf{A}}}\) denotes the element-wise complex conjugate, \({\textbf{A}}^T\) denotes the transpose, \({\textbf{A}}^\dag \) denotes the conjugate transpose. In addition, we use \({\textbf{A}}^*\) to denote the adjugate of a square matrix \({\textbf{A}}\). We use \({\textbf{I}}\) and \({\textbf{0}}\) to denote an appropriately sized identity and zero matrix, respectively. For any (matrix-valued) function f(z), we denote \({\tilde{f}}(z)=\overline{f({\bar{z}})}\). Let
Furthermore, for a set D in the complex plane \({\mathbb {C}}\), \({\bar{D}}\) represents its closure. For an \((N+1)\)-order square matrix \({\textbf{A}}\), without otherwise specified, we write it in block form as \({\textbf{A}}=({\textbf{A}}_1,{\textbf{A}}_2,{\textbf{A}}_3)\), where \({\textbf{A}}_1\) represents the first column, \({\textbf{A}}_3\) represents the last column, and \({\textbf{A}}_2\) represents the rest of columns. The notation \({\textbf{A}}(z)\) holds for \(z\in ({\mathcal {D}}_1,{\mathcal {D}}_2,{\mathcal {D}}_3)\), means that \( {\textbf{A}}_1(z)\), \({\textbf{A}}_2(z)\) and \({\textbf{A}}_3(z)\) hold for \(z\in {\mathcal {D}}_1\), \({\mathcal {D}}_2\) and \({\mathcal {D}}_3\), respectively. Also, sometimes, \({\textbf{A}}\) is rewritten in another block form as
where \({\textbf{A}}_{11}\) and \({\textbf{A}}_{33}\) are scalar.
2 Direct problem
2.1 Lax pair, Riemann surface and uniformization
The N-component focusing NLS equation (1.2) admits the Lax pair:
with
where \({\textbf{q}}=(q_1,\ldots ,q_N)^T\), and k is a constant spectral parameter. In order to introduce the Jost solutions, it is necessary to study the asymptotic spectral problems
with
The eigenvalues of \({\textbf{U}}_\pm \) are \(\pm \textrm{i}\lambda \) and \(\textrm{i}k\) (with multiplicity \(N-1\)), the eigenvalues of \({\textbf{V}}_\pm \) are \(\pm 2\textrm{i}k\lambda \) and \(-\textrm{i}(k^2+\lambda ^2)\) (with multiplicity \(N-1\)), where
We fix the branch cut \([-\textrm{i}q_0,\textrm{i}q_0]\), from which \(\sqrt{k^2+q_0^2}\) is well defined by setting \(\arg (k\pm \textrm{i}q_0)\in [-\frac{\pi }{2},\frac{3\pi }{2})\). The two branches,  , do not get mixed up with each other, but are interchanged in passing from one edge of the cut \([-\textrm{i}q_0,\textrm{i}q_0]\) to the other. By gluing the two copies with cut, it can be compactified a two-sheeted Riemann surface \(\Upsilon =\left\{ (k,\lambda )\in {\mathbb {C}}^2|\lambda ^2=k^2+q_0^2\right\} \), where
, do not get mixed up with each other, but are interchanged in passing from one edge of the cut \([-\textrm{i}q_0,\textrm{i}q_0]\) to the other. By gluing the two copies with cut, it can be compactified a two-sheeted Riemann surface \(\Upsilon =\left\{ (k,\lambda )\in {\mathbb {C}}^2|\lambda ^2=k^2+q_0^2\right\} \), where  represents the first (resp. second) sheet. The multi-valued function \(\lambda =\lambda (k)\) becomes a single valued function \(\lambda = \lambda ({\textbf{P}})\) of a point \({\textbf{P}}\) on the Riemann surface \(\Upsilon \): if \({\textbf{P}}=(k,\lambda )\in \Upsilon \), then \(\lambda ({\textbf{P}})=\lambda \) (the projection on the the \(\lambda \)-axis). Define the uniformization map \(z:\Upsilon \mapsto {\mathbb {C}}\),
represents the first (resp. second) sheet. The multi-valued function \(\lambda =\lambda (k)\) becomes a single valued function \(\lambda = \lambda ({\textbf{P}})\) of a point \({\textbf{P}}\) on the Riemann surface \(\Upsilon \): if \({\textbf{P}}=(k,\lambda )\in \Upsilon \), then \(\lambda ({\textbf{P}})=\lambda \) (the projection on the the \(\lambda \)-axis). Define the uniformization map \(z:\Upsilon \mapsto {\mathbb {C}}\),
whose inverse map is
where \({\hat{z}}=-\frac{q_0^2}{z}\). Note that, the branch cut is mapped onto \(C_0\), the first (resp. second) sheet is mapped onto the exterior (resp. interior) of \(C_0\),  ,
,  ,
,  , where
, where  represents the point at infinity in sheet
represents the point at infinity in sheet  (see [19, 24] for further details).
(see [19, 24] for further details).
It is easy to see that two solution matrices of the asymptotic spectral problems (2.4) read
where
and \({\varvec{\Theta }}(x,t;z)\) is an \((N+1)\times (N+1)\) matrix defined by
Indeed, each column of \({\textbf{E}}_{\pm }(z)\) is a common eigenvector of \({\textbf{U}}_\pm \) and \({\textbf{V}}_\pm \), respectively, and
2.2 Jost solutions and scattering matrix
We look for two fundamental solution matrices \(\psi _\pm (x,t;z)\), which also known as Jost solutions, of (2.1) that satisfies the boundary conditions
The reason we are interested especially in \((\Gamma _\pm ,{\mathbb {R}},\Gamma _\pm )\) is that \(\psi _\pm (x,t;z)\) are oscillatory rather than exponentially decreasing or increasing for large \(\vert x\vert \).
Introduce the modified eigenfunctions
by which two equivalent forms are obtained as follows:
where \({\varvec{\Lambda }}(z)={\text {diag}}(-\lambda ,\underbrace{k,\ldots ,k}_{N-1},\lambda )\), \(\Delta {\textbf{Q}}_\pm ={\textbf{Q}}- {\textbf{Q}}_\pm \), the (x, t; z)-dependence is omitted for brevity. Equation (2.17) is equivalent to
Integrating (2.18a) from \(\pm \infty \) to x, and noting the asymptotics
we find that \(\mu _\pm \) satisfy the Volterra integral equations
Also, integrating (2.18b) from 0 to x, we state
Splicing (2.20) and (2.21) together, we arrive at
where \(\mu (0,t;z)\) obtained from (2.22a) is used at the initial condition in (2.22b).
Remark 2.1
The reason we introduce two equivalent modified Lax pairs or Volterra integral equations is that \(\Delta {\textbf{Q}}_\pm \notin L^1({\textbf{R}})\), which presents some difficulties for investigating the analyticities of \(\mu _{\pm }(x,t;z)\) for \(x\in {\mathbb {R}}\). In Refs. [23, 24], only considering the integral equation (2.20), one needs another method in Ref. [18] to analyze the analyticity properties of the scattering matrix entries. However, one can avoid such a problem by combining two equivalent modified Lax pairs.
Remark 2.2
For all \(x\in {\mathbb {R}}\),
At \(z=\pm \textrm{i}q_0\), although the matrices \({\textbf{E}}_\pm (z)\) are degenerate, the expressions \({\textbf{E}}_\pm (z)\textrm{e}^{\textrm{i}x{\varvec{\Lambda }}(z)}{\textbf{E}}_\pm ^{-1}(z)\) remain finite as \(z\rightarrow \pm \textrm{i}q_0\),
In the following, we must prove that the Jost solutions or the modified ones are well defined. Set
and \(\Vert \cdot \Vert _1\) is the \(L^1\) vector norm.
Theorem 2.3
Suppose that \({\textbf{q}}(\cdot ,t)-{\textbf{q}}_\pm \in L^{1,1}({\mathbb {R}}^{\pm })\), \(\mu _+(x,t;z)\) is analytic for \(z\in (D_2,{\mathbb {C}}^+,D_3)\) and \(\mu _-(x,t;z)\) is analytic for \(z\in (D_1,{\mathbb {C}}^-,D_4)\). Meanwhile, \(\mu _+(x,t;z)\) is continuous up to \((\Gamma _+,{\mathbb {R}},\Gamma _+)\) and \(\mu _-(x,t;z)\) is continuous up to \((\Gamma _-,{\mathbb {R}},\Gamma _-)\).
Proof
We only give the proofs about \(\mu _{-1}(x,t;z)\) and \(\mu _{-2}(x,t;z)\), the rest of the theorem is proved similarly. Firstly, we consider \(\mu _{-1}(x,t;z)\). Let
Case i: \(x\in {\mathbb {R}}^-\). It follows from (2.22a) that
We introduce a Neumann series \(\mu _{-1}(x,t;z)=\sum _{n=0}^\infty \mu _n(x,t;z)\) for the solution of (2.25), where
As \(z\in D_1\), \({\textbf{G}}_-(x-y;z)\) is analytic and continuous up to the boundary \(\partial D_1\). In the integrand \(y\leqslant x\), so if \( z\in D_1\cup \Gamma _-\), by maximum modulus principle, we conclude that
Consequently,
By induction, we can prove that
It follows that the infinite series converges absolutely and uniformly by comparison with an exponential series,
It is easy to use the uniform convergence of the Neumann series to prove that \(\mu _{-1}(x,t;z)\) is in fact a solution of the Volterra equation (2.25) whenever \(z\in D_1\cup \Gamma _-\). The uniqueness of this solution follows by the fact that a certain power of the operator \(\int _{-\infty }^x{\textbf{K}}_1(x,y,t;z)(\cdot )\textrm{d}y\) is a contraction operator. Note that, \(\mu _0(x,t;z)\) is analytic for \(z\in D_1\) and continuous up to the boundary \(\partial D_1\). As \(n\geqslant 1\), for \(z\in \bar{D}_1\),
by Lebesgue dominated convergence theorem,
This proves \(\mu _n(x,t;z)\) is a continuous function of z in \(\bar{D}_1\). Suppose that \(\mu _{n-1}(x,t;z)\) is analytic for \(z\in D_1\), let C be a piecewise-smooth closed curve contained in \(D_1\). Thus,
The estimate (2.31) yields the above integrand lies in \(L^1({\mathbb {R}}^-\times C)\). By Fubini’s theorem and Cauchy’s integral theorem, we have
By Morera’s theorem, \(\mu _n(x,t;z)\) is analytic for \(z\in D_1\). Since a uniformly convergent series of analytic functions converges to an analytic function, \(\mu _{-1}(x,t;z)\) is analytic for \(z\in D_1\). Also, \(\mu _{-1}(x,t;z)\) is continuous in \(\bar{D}_1\) respect to z.
Case ii: \(x\in {\mathbb {R}}^+\). It follows from (2.22b) that
We introduce a Neumann series \( \frac{\mu _{-1}(x,t;z)}{1+\vert x\vert }=\sum _{n=0}^\infty \nu _n(x,t;z)\) for the solution of (2.35), where
As \(z\in D_1\cup \Gamma _-\), similar to (2.27), we have
Therefore,
For all \(x\in {\mathbb {R}}^+\), \(z\in D_1\cup \Gamma _-\), we obtain the uniform convergence
Similarly, \(\mu _{-1}(x,t;z)\) is well defined in \(D_1\cup \Gamma _-\) respect to z, analytic for \(z\in D_1\) and continuous up to the boundary \(\partial D_1\).
Secondly, we consider \(\mu _{-2}(x,t;z)\). Let
Note that,
as \(z\in {\mathbb {R}}\),
Case i: \(x\in {\mathbb {R}}^-\). It follows from (2.22a) that
We introduce a Neumann series \(\mu _{-2}(x,t;z)=\sum _{n=0}^\infty {\hat{\mu }}_n(x,t;z)\) for the solution of (2.45), where
\(\hat{{\textbf{G}}}_-(x-y;z)\) is analytic for \(z\in {\mathbb {C}}^-\backslash \{-\textrm{i}q_0\}\) and continuous in \({\mathbb {C}}^-\cup {\mathbb {R}}\). In the integrand \(y\leqslant x\), so if \( z\in {\mathbb {C}}^-\cup {\mathbb {R}}\), by maximum modulus principle, we conclude that
Consequently,
By induction, we can prove that
It follows that the infinite series converges absolutely and uniformly by comparison with an exponential series,
It is easy to use the uniform convergence of the Neumann series to prove that \(\mu _{-2}(x,t;z)\) is a solution matrix of the Volterra equation (2.45) whenever \(z\in {\mathbb {C}}^-\cup {\mathbb {R}}\). The uniqueness of this solution follows by the fact that a certain power of the operator \(\int _{-\infty }^x\hat{{\textbf{K}}}_1(x,y,t;z)(\cdot )\textrm{d}y\) is a contraction operator. Note that, \({\hat{\mu }}_0(x,t;z)\) is analytic for \(z\in {\mathbb {C}}^-\) and continuous up to the boundary \({\mathbb {R}}\). As \(n\geqslant 1\), for \(z\in {\mathbb {C}}^-\cup {\mathbb {R}}\),
by Lebesgue dominated convergence theorem,
This proves \({\hat{\mu }}_n(x,t;z)\) is a continuous function of z in \({\mathbb {C}}^-\cup {\mathbb {R}}\). Suppose that \({\hat{\mu }}_{n-1}(x,t;z)\) is analytic for \(z\in {\mathbb {C}}^-\), let C be a piecewise-smooth closed curve contained in \({\mathbb {C}}^-\). Thus,
The estimate (2.51) yields the above integrand lies in \(L^1({\mathbb {R}}^-\times C)\). By Fubini’s theorem and Cauchy’s integral theorem, we have
By Morera’s theorem, \({\hat{\mu }}_n(x,t;z)\) is analytic for \(z\in {\mathbb {C}}^-\). Since a uniformly convergent series of analytic functions converges to an analytic function, \(\mu _{-2}(x,t;z)\) is analytic for \(z\in {\mathbb {C}}^-\). Also, \(\mu _{-2}(x,t;z)\) is continuous in \({\mathbb {C}}^-\cup {\mathbb {R}}\) respect to z.
Case ii: \(x\in {\mathbb {R}}^+\). It follows from (2.22b) that
We introduce a Neumann series \( \mu _{-2}(x,t;z)=\sum _{n=0}^\infty {\hat{\nu }}_n(x,t;z)\) for the solution of (2.55), where
As \(z\in {\mathbb {C}}^-\cup {\mathbb {R}}\), similar to (2.47), we have
Therefore,
For all \(x\in {\mathbb {R}}^+\), \(z\in {\mathbb {C}}^-\cup {\mathbb {R}}\), we obtain the uniform convergence
Similarly, \(\mu _{-2}(x,t;z)\) is well defined in \({\mathbb {C}}^-\cup {\mathbb {R}}\) respect to z, analytic for \(z\in {\mathbb {C}}^-\) and continuous up to the boundary \({\mathbb {R}}\). \(\square \)
Remark 2.4
Unlike what happens for the defocusing case, the defect of analyticity for the focusing N-component NLS equation does not increase with the number of components. In fact, for any \(N\geqslant 2\), one has exactly N analytic eigenfunctions in each of the domains \(D_1,\ldots , D_4\), and hence, only one additional eigenfunction per each of the domain is required to obtain a fundamental set of analytic solutions.
Lemma 2.5
Under the same hypotheses as in Theorem 2.3, for all z in the interior of their corresponding domains of analyticity, \(\mu _{\pm 2}(x,t;z)\) are bounded for all \(x\in {\mathbb {R}}\), \(\mu _{\pm 1}(x,t;z)\) and \(\mu _{\pm 3}(x,t;z)\) are bounded for \(x\in {\mathbb {R}}^\pm \), \(\frac{\mu _{\pm 1}(x,t;z)}{1+\vert x\vert }\) and \(\frac{\mu _{\pm 3}(x,t;z)}{1+\vert x\vert }\) are bounded for \(x\in {\mathbb {R}}^\mp \).
Proof
The first column of \(\mu _-(x,t;z)\) follows from (2.30) and (2.40), and \(\mu _{-2}(x,t;z)\) follows from (2.50) and (2.60). The rest of this lemma is obtained similarly. \(\square \)
Theorem 2.3 shows that \(\mu _\pm (x,t;z)\) are continuous up to \((\Gamma _\pm ,{\mathbb {R}},\Gamma _\pm )\), respectively. Moreover, formally differentiating the Volterra integral equation (2.22) with respect to z and performing a similar Neumann series analysis, one can show the following:
Corollary 2.6
Under the same hypotheses as in Theorem 2.3, \(\partial _z\mu _\pm (x,t;z)\) are continuous for \(z\in (\Gamma _\pm ,{\mathbb {R}},\Gamma _\pm )\).
Remark 2.7
It follows trivially from the above theorem that the columns of \(\psi _\pm (x,t;z)\) have the same analyticity properties as \(\mu _\pm (x,t;z)\). Moreover, if \({\textbf{q}}(\cdot ,t)-{\textbf{q}}_\pm \in L^1({\mathbb {R}}^\pm )\), the modified eigenfunctions \(\mu _{\pm }(x,t;z)\) are also are analytic for \(z\in (D_2,{\mathbb {C}}^+,D_3)\), \((D_1,{\mathbb {C}}^-,D_4)\), respectively. However, \(\mu _{\pm 1}(x,t;z)\) and \(\mu _{\pm 3}(x,t;z)\) are not continuous at the branch points \(\pm \textrm{i}q_0\). Furthermore, noting that \({\textbf{q}}(\cdot ,t)-{\textbf{q}}_\pm \) is needed to be lied in \( L^{1,2}({\mathbb {R}}^\pm )\) in Ref. [18], in this context, we require a slightly weaker condition \({\textbf{q}}(\cdot ,t)-{\textbf{q}}_\pm \in L^{1,1}({\mathbb {R}}^\pm )\).
In the following, we will introduce the scattering matrix. Observing the traceless nature of \({\textbf{Q}}(x,t)-{\textbf{Q}}_\pm \), by Abel’s Theorem, we arrive at \(\partial _x\det ( {\textbf{E}}_\pm ^{-1}(z)\mu _\pm (x,t;z))=0\). Therefore, we may compute the determinant of \( {\textbf{E}}_\pm ^{-1}(z)\mu _\pm (x,t;z)\) with the limit \(x\rightarrow \pm \infty \). Consequently, equation (2.19) implies
i.e.,
Since both \(\psi _+(x,t;z)\) and \(\psi _-(x,t;z)\) are the fundamental solutions of the Lax pair (2.1), there exists a \((N+1)\times (N+1)\) matrix \({\textbf{s}}(z)\) independent of x and t such that
where
is usually referred to as the scattering matrix. Taking the determinants of both sides of (2.63) and recalling (2.62), we state
Let
thus,
Evaluating (2.63) at \((+\infty ,0)\), recalling (2.16) and (2.22), we conclude that
Similarly,
From Theorem 2.3, Lemma 2.5 and the above integral representations (2.68)–(2.69), we can obtain the following theorem obviously.
Corollary 2.8
Under the same hypotheses as in Theorem 2.3, \({\textbf{s}}_{11}(z), {\textbf{s}}_{13}(z), {\textbf{s}}_{31}(z)\) and \({\textbf{s}}_{33}(z)\) are well defined in \(\Gamma _-\backslash \{\textrm{i}q_0\}\), \({\textbf{S}}_{11}(z), {\textbf{S}}_{13}(z), {\textbf{S}}_{31}(z)\) and \({\textbf{S}}_{33}(z)\) are well defined in \(\Gamma _+\backslash \{-\textrm{i}q_0\}\), the remainder of scattering coefficients are well defined in \({\mathbb {R}}\). Furthermore, the following scattering coefficients can be analytically continued to the corresponding regions:
2.3 Auxiliary eigenfunctions
In order to pose the inverse problem, that is, to formulate an \((N+1)\times (N+1)\) matrix RH problem, we need to have a complete set of analytic eigenfunctions in any given domain \(D_j\), \(j=1,\ldots ,4\). However, only N of the columns of \(\mu _+(x,t;z)\) and \(\mu _-(x,t;z)\) are analytic in \(D_j\). To offset the incompleteness of analyticity, we introduce a “generalized cross product" for vectors in \({\mathbb {C}}^{N+1}\) as follows:
Definition 2.9
(Generalized cross product) For all \({\textbf{u}}_1,\ldots ,{\textbf{u}}_{N}\in {\mathbb {C}}^{N+1}\), let
where \(\{{\textbf{e}}_1,\ldots ,{\textbf{e}}_{N+1}\}\) represents the standard basis for \({\mathbb {R}}^{N+1}\).
Specially, as \(N=2\), \({\mathcal {G}}[{\textbf{u}}_1,{\textbf{u}}_2]={\textbf{u}}_1\times {\textbf{u}}_2\), represents the common cross product in \({\mathbb {R}}^3\). Like this case, \({\mathcal {G}}[\cdot ]\) is also multi-linear and totally antisymmetric.
Lemma 2.10
For any \({\textbf{A}}\in {\mathbb {C}}^{(N+1)\times (N+1)}\), \({\textbf{B}}\in {\mathbb {C}}^{n\times n}(n\leqslant N)\), \(1\leqslant l\leqslant N-n+1\), then
Proof
Set
Since \(\det ({\textbf{I}}+t{\textbf{A}})\) is continuous for \(t\in {\mathbb {R}}\), there exists a positive number \(\delta \) such that \({\textbf{I}}+t{\textbf{A}}\) is non-degenerate for \(|t|<\delta \). The definition of \({\mathcal {G}}[\cdot ]\) yields the left-hand side of (2.72a)
On the other hand, for \(| t | < \delta \),
Indeed,
The right-hand side of (2.72a)
In addition, the identity (2.72b) is the trivial result of Definition 2.9. \(\square \)
Remark 2.11
In Refs. [23, 24, 26], four identities always are introduced to construct the auxiliary eigenfunctions in \({\mathbb {C}}^3\) or \({\mathbb {C}}^4\). However, verifying four similar identities directly in higher dimensional space will bring us a heavy calculation burden. Fortunately, combining with the differential operation of determinant function, we have proved the identity (2.72a), which is essential to construct the auxiliary eigenfunctions, especially in the arbitrary N-component case. In addition, those identities in Refs. [23, 24, 26] are the special cases of (2.72a).
Indeed, observing that \({\textbf{Q}}^T=-\bar{{\textbf{Q}}}\), by virtue of the identity (2.72a), we can directly verify the following fact.
Proposition 2.12
Suppose that \(\psi _1(x,t;z),\ldots ,\psi _N(x,t;z)\) are N arbitrary solution vectors of the Lax pair (2.1), then
is a solution vector of the Lax pair (2.1), where \({\tilde{\psi }}_j(x,t;z)=\overline{\psi _j(x,t;{\bar{z}})}\) for \(j=1,\ldots ,N\).
The above functions \({\tilde{\psi }}_j(x,t;z)\ (j=1,\ldots , N+1)\) are also called the adjoint Jost solutions, the analyticity of which can be derived obviously by Riemann–Schwarz symmetry principle. Note that, a simple relation exists between the adjoint Jost solutions and the Jost solutions of the original Lax pair (2.1):
Lemma 2.13
Under the same hypotheses as in Theorem 2.3, as \(z\in {\mathbb {R}}\),
where
and \((j_1,\ldots ,j_{N+1})\) is an even permutation of \((1,\ldots ,N+1)\), \(\psi _{\pm ,j}\) and \({\tilde{\psi }}_{\pm ,j}\) represent the j-th columns of \(\psi _{\pm }\) and \({\tilde{\psi }}_{\pm }\), respectively.
Definition 2.14
Introducing four new solutions of the original Lax pair (2.1):
we called \(\chi _1(x,t;z),\ldots , \chi _4(x,t;z)\) the auxiliary eigenfunctions. Analogous to the Jost eigenfunctions, the auxiliary eigenfunctions have a modified form
Considering the \(\psi _\pm \)’s corresponding domains of analyticity, by Riemann–Schwarz symmetry principle, we state
Lemma 2.15
Under the same hypotheses as in Theorem 2.3, as \(j=1,\ldots ,4\), the auxiliary eigenfunction \(\chi _j(x,t;z)\) and the modified form \({\textbf{m}}_j(x,t;z)\) are analytic for \(z\in D_j\) and continuous up to the boundary \(\partial D_j\), respectively.
2.4 Symmetries
Similar to the scalar case and the 2-component case, the scattering problem admits two symmetries corresponding to the involutions: \((k,\lambda )\rightarrow ({\bar{k}},{\bar{\lambda }})\) and \((k,\lambda )\rightarrow (k,-\lambda )\), i.e., in terms of uniformization variable z: \(z\rightarrow {\bar{z}}\) and \(z\rightarrow {\hat{z}}\). Indeed, there is also another symmetry corresponding to \({\bar{z}}\rightarrow {\hat{z}}\) or \(z\rightarrow \hat{{\bar{z}}}\), which can be obtained by combining the first two symmetries.
2.4.1 First symmetry: \(z\rightarrow {\bar{z}}\)
Proposition 2.16
If \(\psi (x,t;z)\) is a matrix solution of the Lax pair (2.1), then
The above statement is a straightforward consequence of the symmetries of the Lax pair (2.1). Considering the asymptotic conditions as in (2.15) for \(\psi _\pm (x,t;z)\), we deduce
Especially,
According to (2.63) and (2.67), we state
Consequently, the scattering matrices \({\textbf{s}}(z)\) and \({\textbf{S}}(z)\) satisfy the symmetry
Componentwise,
Particularly,
2.4.2 Second symmetry: \(z\rightarrow {\hat{z}}\)
Proposition 2.17
If \(\psi (x,t;z)\) is a matrix solution of the Lax pair (2.1), so is \(\psi (x,t;{\hat{z}})\).
Considering the asymptotic conditions in (2.15) for \(\psi _\pm (x,t;z)\), we find
where
In particular,
which implies the auxiliary eigenfunctions satisfy the symmetries
Combining (2.63), (2.67) with (2.91), we find
Componentwise,
A similar set of relations obviously holds for the components of \({\textbf{S}}(z)\),
2.4.3 Combined symmetry
In the inverse problem, the following reflection coefficients will appear,
Considering the transform \(z\rightarrow {\hat{z}}\), we have
From (2.87)–(2.90), it follows that
The above expressions together with Corollary 2.6 give the following
Corollary 2.18
Under the same hypotheses as in Theorem 2.3, and suppose that none of the zeros of \({\textbf{s}}_{11}(z)\) and \(\det ({\textbf{s}}_{22}(z))\) occurs on \(\Gamma _-\), then \(\rho _1(z)\), \(\rho _3(z)\in C^1({\mathbb {R}})\) and \(\rho _2(z)\in C^1(\Gamma _-)\).
Remark 2.19
For \(z\in {\mathbb {R}}\), it follows trivially from \({\textbf{S}}(z){\textbf{s}}(z)={\textbf{I}}\) that
the subtraction of which yields
Equations (2.98) and (2.99) allow us to conclude
which implies the scattering coefficients \(\rho _1(z)\), \(\rho _2(z)\) and \(\rho _3(z)\) are not independent.
2.5 Behavior at branch points
In order to properly specify growth conditions for the RH problem, we should analyze the behaviors of the eigenfunctions and the scattering data near the branch points. It follows from Theorem 2.3 and Lemma 2.15 that \(\mu _{-1}(x,t;z)\), \(\mu _{+2}(x,t;z)\), \(\mu _{-3}(x,t;z)\), \({\textbf{m}}_1(x,t;z)\) and \({\textbf{m}}_4(x,t;z)\)are well defined and continuous at the branch point \(z=\textrm{i}q_0\), \(\mu _{+1}(x,t;z)\), \(\mu _{-2}(x,t;z)\), \(\mu _{+3}(x,t;z)\), \({\textbf{m}}_2(x,t;z)\) and \({\textbf{m}}_3(x,t;z)\) are well defined and continuous at the branch point \(z=-\textrm{i}q_0\). Furthermore, it follows from (2.15) that all of the above eigenfunctions are nonzero at the branch points.
From (2.87), it follows that the scattering coefficients \({\textbf{s}}_{11}(z)\), \({\textbf{s}}_{13}(z)\), \({\textbf{s}}_{31}(z)\) and \({\textbf{s}}_{33}(z)\) have a pole at the branch point \(z=\textrm{i}q_0\).
Corollary 2.20
Under the same hypotheses as in Theorem 2.3, as \(z\rightarrow \textrm{i}q_0\),
Similarly, the scattering coefficients \({\textbf{S}}_{11}(z)\), \({\textbf{S}}_{13}(z)\), \({\textbf{S}}_{31}(z)\) and \({\textbf{S}}_{33}(z)\) have a pole at the branch point \(z=-\textrm{i}q_0\).
Corollary 2.21
Under the same hypotheses as in Theorem 2.3, as \(z\rightarrow -\textrm{i}q_0\),
Considering the asymptotics for the columns of \(\psi _\pm (x,t; \mp \textrm{i}q_0)\) as \(x\rightarrow \pm \infty \), respectively, we state
It follows trivially from (2.87), (2.98) and (2.106) that
which implies that the jump matrices in Sect. 3 are not singular at \(\pm \textrm{i}q_0\).
2.6 Asymptotic behavior as \(z\rightarrow \infty \) and \(z\rightarrow 0\)
In the context of IST with ZBCs, we need to investigate the asymptotic behaviors of the eigenfunctions and the scattering data as the spectral parameter approaches infinity. However, since two points \(\infty _{1}\) and \(\infty _2\) at infinity on the Riemann surface \(\Upsilon \) are mapped to infinity and zero in the complex z plane, respectively, we should consider the asymptotics both as \(z\rightarrow \infty \) and \(z\rightarrow 0\). Substituting the Wentzel–Kramers–Brillouin expansions of the columns of the modified Jost solutions into (2.17) and collecting the terms \(O(z^j)\) as in Ref. [18], or substituting the formal expansions \(\mu _\pm (x,t;z)=\sum _{j=1}^\infty \mu _\pm ^{(j)}(x,t;z)\) into the Volterra integral equation (2.22) as in Ref. [21], we obtain the following asymptotics:
Lemma 2.22
Suppose that \({\textbf{q}}(\cdot ,t)-{\textbf{q}}_\pm \in L^{1,1}({\mathbb {R}}^{\pm })\) and \({\textbf{q}}(\cdot ,t)\) is continuously differentiable with \({\textbf{q}}_x(\cdot ,t)\in L^{1}({\mathbb {R}}^{\pm })\), as \(z\rightarrow \infty \) in the appropriate regions that each column is well defined,
Similarly, as \(z\rightarrow 0\) in the appropriate regions that each column is well defined,
where \(\{{{\epsilon }}_1,\ldots ,{\epsilon }_{N}\}\) represents the standard basis for \({\mathbb {R}}^{N}\).
Consequently, we can calculate the asymptotics of \({\textbf{m}}_j\ (j=1,\ldots ,4)\) by the definitions (2.14) and (2.14) of the auxiliary eigenfunctions and the modified ones, respectively.
Corollary 2.23
Under the same hypotheses as in Lemma 2.22, as \(z\rightarrow \infty \) in the appropriate regions that each column is well defined,
Similarly, as \(z\rightarrow 0\) in the appropriate regions that each column is well defined,
Remark 2.24
Indeed, by virtue of the symmetries (2.93) and (2.94), Eqs. (2.109) and (2.23) can be obtained directly from Eqs. (2.108) and (2.23), respectively.
Next, it follows from the asymptotics in Lemma 2.22 and the scattering relation (2.90) that the scattering matrix entries have the asymptotic behaviors:
Corollary 2.25
Under the same hypotheses as in Lemma 2.22, as \(z\rightarrow \infty \) in the appropriate regions that each column is well defined,
Similarly, as \(z\rightarrow 0\) in the appropriate regions that each column is well defined,
Lemma 2.22 together with (2.100) immediately implies the following:
Corollary 2.26
Under the same hypotheses as in Lemma 2.22, as \(z\rightarrow \infty \),
3 Inverse problem
For \(z\in D_j,\ j=1,\ldots ,4\), an extra analytic eigenfunction \(\chi _j(x,t;z)\) is generated by virtue of the generalized cross product. Therefore, \(\mu _\pm (x,t;z)\) and \(\{\chi _j(x,t;z)\}_1^4\) make up a complete set of analytic eigenfunctions for solving the inverse problem. In the following, we will introduce a new operator and several identities, which play a key role in decomposing the auxiliary eigenfunctions and expressing symmetries.
3.1 Decomposition of the auxiliary eigenfunctions
Definition 3.1
For all \({\textbf{u}}_1,\ldots ,{\textbf{u}}_{N+1}\in {\mathbb {C}}^{N+1}\), define
where \({\textbf{u}}=({\textbf{u}}_1,\ldots ,{\textbf{u}}_{N+1})\). Consequently, the l-th column of \({\mathscr {G}}[{\textbf{u}}_1,\ldots ,{\textbf{u}}_{N+1}]\) reads \(l=1,\ldots ,N+1\),
By direct calculations, it is easy to verify the following relation among the adjugate matrix \((\cdot )^*\), the generalized cross product \({\mathcal {G}}[\cdot ]\) and the operator \({\mathscr {G}}[\cdot ]\),
Lemma 3.2
For all \({\textbf{u}}\in {\mathbb {C}}^{(N+1)\times (N+1)}\),
Lemma 3.3
For all \({\textbf{u}}_1,\ldots ,{\textbf{u}}_{N},{\textbf{v}}_1,\ldots ,{\textbf{v}}_{N}\in {\mathbb {C}}^{N+1}\),
where \({\textbf{v}}=({\textbf{v}}_1,\ldots ,{\textbf{v}}_{N})\), \({\textbf{u}}_{(1)}=({\textbf{u}}_1,\ldots ,{\textbf{u}}_{N})\).
Proof
Firstly, we give the proof of (3.5a). Since
we need to prove the remaining part
If \({\textbf{v}}_1,\ldots ,{\textbf{v}}_N\) are linear dependent, the identities \({\mathcal {G}}[{\textbf{v}}_1,\ldots ,{\textbf{v}}_N]={\textbf{0}}\) and \({\textbf{v}}({\textbf{u}}^T_{(1)}{\textbf{v}})^*={\textbf{0}}\) yield (3.7). If not, there exists \({\textbf{v}}_{N+1}\in {\mathbb {C}}^{N+1}\) such that \({\textbf{v}}_{(1)}=({\textbf{v}}_1,\ldots ,{\textbf{v}}_{N+1})\) is nonsingular. According to (3.3), we obtain \({\mathcal {G}}[{\textbf{v}}_1,\ldots ,{\textbf{v}}_N]=({\textbf{v}}^*_{(1)})^T{\textbf{e}}_{N+1}\). Indeed,
where \(\{{\epsilon }_1,\ldots ,{{\epsilon }}_{N}\}\) represents the standard basis for \({\mathbb {R}}^{N}\). The identity (3.5b) is proved similarly. \(\square \)
Consequently, the relation (3.3) yields the following repeated cross product identity
which generalizes the triple cross product formula \({\textbf{u}}_1\times ({\textbf{v}}_1\times {\textbf{v}}_2)=({\textbf{u}}_1^T{\textbf{v}}_2){\textbf{v}}_1-({\textbf{u}}_1^T{\textbf{v}}_1){\textbf{v}}_2\) in \({\mathbb {R}}^3\).
Lemma 3.4
Under the same hypotheses as in Theorem 2.3, the auxiliary eigenfunctions have the following decompositions:
where the (x, t)-dependence is suppressed for brevity.
Proof
We suppress the (x, t; z)-dependence for simplicity. As \(z\in \Gamma _-\backslash \{\textrm{i}q_0\}\),
As \(z\in {\mathbb {R}}\),
Indeed,
Therefore,
The remainder of Lemma 3.4 is proved similarly. \(\square \)
In the following, we will consider the inverse scattering transformation, which can be characterized in terms of a \(3\times 3\) block matrix RH problem.
3.2 Riemann–Hilbert problem
In order to coincide with the focusing Manakov system with NZBCs in Ref. [24], we define the piecewise meromorphic function \({\textbf{M}}(x,t;z)\) as
By virtue of Lemma 3.3, we prove that
Lemma 3.5
Under the same hypotheses as in Theorem 2.3, as \(z\in {\mathbb {C}}\backslash \Gamma \),
Proof
We suppress the (x, t; z)-dependence for simplicity. As \(z\in D_1\),
Similarly, we can prove
which means
For \(z\in D_1\), the (1, 1)-entry of \({\textbf{M}}^T(x,t;z){\mathscr {G}}[{\textbf{M}}(x,t;z)]=\det ({\textbf{M}}(x,t;z)){\textbf{I}}\) implies
Similarly, \(\det ({\textbf{M}}(x,t;z))=\gamma (z)\) holds for \(z\in D_2,D_3,D_4\). \(\square \)
The above lemma, together with the relation (3.3) and the symmetries (2.90), (2.93), (2.94) and (2.96), implies that the piecewise meromorphic function \({\textbf{M}}(x,t;z)\) satisfies two symmetries:
Lemma 3.6
Under the same hypotheses as in Theorem 2.3, as \(z\in {\mathbb {C}}\backslash \Gamma \),
Set
and “ \(\overset{\angle }{\lim }\)" means non-tangential limit, \(D_+=D_1\cup D_3\), \(D_-=D_2\cup D_4\). From Theorem 2.3, Lemma 2.15 and Corollary 2.20, 2.21, it follows that \({\textbf{M}}_{\pm }(x,t;z)\) is well defined for \(z\in \Gamma \).
Furthermore, \({\textbf{M}}(x,t;z)\) satisfies the growth conditions near the branch points \(\pm \textrm{i}q_0\):
Lemma 3.7
Under the same hypotheses as in Theorem 2.3,
The piecewise meromorphic function \({\textbf{M}}(x,t;z)\) has the jump across the oriented contour \(\Gamma \) as follows:
Lemma 3.8
Under the same hypotheses as in Theorem 2.3,
with
where the oriented contours \(\Gamma _l\ (l=1,\ldots ,4)\) are depicted in Fig. 1, \(\rho _1(z)\), \(\rho _2(z)\) and \(\rho _3(z)\) are defined in (2.98). Meanwhile, the jump matrix \({\textbf{J}}(x,t;\cdot )\in C^1(\Gamma ) \) and tends to identity matrix both as \(z\rightarrow \infty \) and \(z\rightarrow 0\).
Proof
For \(z\in \Gamma _1\), denote \({\textbf{J}}_1(z)=\begin{pmatrix} \textbf{J}_{11}(z) &{} \textbf{J}_{12}(z)&{} \textbf{J}_{13}(z) \\ \textbf{J}_{21}(z) &{} \textbf{J}_{22}(z)&{} \textbf{J}_{23}(z) \\ \textbf{J}_{31}(z) &{} \textbf{J}_{32}(z)&{} \textbf{J}_{33}(z) \end{pmatrix}\). The jump (3.24) implies that
Substituting (2.63), (2.67), (3.10a) and (3.10b) into (3.27), we find
Since \(\det (\psi _\pm )\ne 0\) for \(z\in \Gamma _1\), all columns of \(\psi _{\pm }\) are linearly independent. Comparing the coefficients yields
Recalling (2.98), (2.99) and the fact \({\textbf{s}}(z){\textbf{S}}(z)={\textbf{S}}(z){\textbf{s}}(z)={\textbf{I}}\) for \(z\in \Gamma _1\), we derive (3.26a) obviously. One can obtain (3.26b)-(3.26d) by a similar way, so we omit the rest of proofs. The statement that the jump matrix \({\textbf{J}}(x,t;\cdot )\in C^1(\Gamma ) \) and tends to identity matrix both as \(z\rightarrow \infty \) and \(z\rightarrow 0\), follows by Corollary 2.18 and 2.26. \(\square \)
Remark 3.9
For \(z\in \Gamma \), note that,
which exactly coincide with the symmetries (3.21a) and (3.21b) of \({\textbf{M}}(x,t;z)\). These symmetries play a key role in ensuring the existence and uniqueness of the solution for the RH problem, and the correctness of the reconstruction formula.
Substituting the asymptotics (2.108)−(2.25) of the eigenfunctions and the scattering coefficients into (3.15), we state
Lemma 3.10
Under the same hypotheses as in Lemma 2.22, the piecewise meromorphic function \({\textbf{M}}(x,t;z)\) has the following asymptotic behaviors as \(z\in {\mathbb {C}}\backslash \Gamma \),
It follows from (2.90) and (2.96) that
Lemma 3.11
Under the same hypotheses as in Theorem 2.3, as \(z_0\in D_1\), then
The definition (3.15) implies that \({\textbf{M}}_1(x,t;z)\) can only have singularities at the zeros of \({\textbf{s}}_{11}(z)\) and \(\det ({\textbf{S}}_{22}(z))\). Similarly, \({\textbf{M}}_2(x,t;z)\) can only have singularities at the zeros of \({\textbf{S}}_{11}(z)\) and \(\det ({\textbf{s}}_{22}(z))\), etc. Lemma 3.11 implies that these zeros appear in symmetric quartets: \(z_0\), \({\bar{z}}_0\), \({\hat{z}}_0\), \(\hat{{\bar{z}}}_0\). Therefore, we only need to study the zeros of \({\textbf{s}}_{11}(z)\) and \(\det ({\textbf{S}}_{22}(z))\) for \(z\in D_1\).
Assumption 3.12
Assume that \({\textbf{s}}_{11}(z)\) has \(N_1+N_2\) simple zeros \(\{w_l\}_1^{N_1}\) and \(\{y_m\}_1^{N_2}\) in \(D_1\), \(\det ({\textbf{S}}_{22}(z))\) has \(N_2+N_3\) simple zeros \(\{y_m\}_1^{N_2}\) and \(\{z_n\}_1^{N_3}\) in \(D_1\), where \(\{w_l\}_1^{N_1}\cap \{z_n\}_1^{N_3}=\emptyset \), \(\{y_m\}_1^{N_2}\) are the common zeros of \({\textbf{s}}_{11}(z)\) and \(\det ({\textbf{S}}_{22}(z))\). Assume that none of these zeros occurs in \(\Gamma \).
Lemma 3.13
Under the same hypotheses as in Theorem 2.3, if w is the simple pole of \({\textbf{M}}(x,t;z)\), then
Furthermore, suppose that there exists a matrix \({\textbf{A}}\) such that \(\underset{ w}{{\text {Res}}} {{\textbf{M}}}(x,t;z)={{\textbf{M}}}(x,t;w){\textbf{A}}\), then
Proof
Since the pole is simple,
Suppose
Indeed,
The symmetry (3.21a) implies that
Substituting (3.36) into (3.39), we obtain
Setting \(z={\bar{w}}\), combining (3.21a) with (3.37), we obtain
\(\square \)
Lemma 3.14
Suppose \({\textbf{A}}(z)\) is a s-order square matrix, w is the simple zero of \(\det ({\textbf{A}}(z))\), then
Proof
The lemma follows trivially from the fact
where “\(\cdot {}\)" represents the differential operator respect to z. If not, i.e., \({\text {rank}}({\textbf{A}}(w))\leqslant s-2\), which implies \({\dot{\det }} ({\textbf{A}}(w))=0\), this a contradiction. \(\square \)
Lemma 3.15
Under the same hypotheses as in Theorem 2.3, and suppose that the set of the singularities are as in Assumption 3.12, the following residue conditions hold:
where \({\textbf{M}}(x,t;z)=({\textbf{M}}_1(x,t;z),{\textbf{M}}_2(x,t;z),{\textbf{M}}_3(x,t;z))\), \(a_l\), \({\textbf{B}}_m\), \({\textbf{C}}_n\) are constants or \((N-1)\) dimensional constant vectors, \(l=1,\ldots , N_1\), \(m=1,\ldots , N_2\), \(n=1,\ldots , N_3\).
Proof
By virtue of Lemma 3.13 and the symmetry (3.21b), we only need to prove (3.44a), (3.45a) and (3.46a). In the following proofs, we omit the (x, t; z)-dependence for brevity.
As \(z=\omega _l\). It follows from (3.15) and (3.16) that
Consequently, \({\text {rank}}(\tilde{\mu }_{+1},\tilde{\mu }_{-2}\tilde{{\textbf{s}}}^{-1}_{22},\tilde{{\textbf{m}}}_2)\leqslant N\) and \(\frac{{\textbf{m}}_1}{\det ({\textbf{S}}_{22})}\ne {\textbf{0}}\) (if not, \(\tilde{\mu }_{+1}={\textbf{0}}\), this is a contradiction). Combining with Lemma 3.2 yields \({\text {rank}}\left( \mu _{-1},{\textbf{0}},\frac{{\textbf{m}}_1}{\det ({\textbf{S}}_{22})}\right) =1\), i.e., there exists a constant \(b_l\) independent of (x, t; z) such that \(\mu _{-1}=b_l\textrm{e}^{-2\textrm{i}\theta _1}\frac{{\textbf{m}}_1}{\det ({\textbf{S}}_{22})}\). Setting \(a_l=\frac{b_l}{\dot{{\textbf{s}}}_{11}}\), we complete the proof of (3.44a).
As \(z=y_m\). It follows from (3.15) and (3.16) that
Since \(\mu _{+2}\) and \(\tilde{\mu }_{-2}\) are full column rank, combining with Lemma 3.2 and Lemma 3.14 yields
i.e., there exists a constant vector \(\alpha _m\) independent of (x, t; z) such that \(\mu _{-1}=\textrm{e}^{\textrm{i}(\theta _2-\theta _1)}\mu _{+2}{\textbf{S}}^*_{22}\alpha _m\). Furthermore, (3.49) and (3.53) imply \({\textbf{m}}_1={\textbf{0}}\). Setting \({\textbf{B}}_m=\frac{{\textbf{S}}^*_{22}\alpha _m}{\dot{{\textbf{s}}}_{11}}\), we complete the proof of (3.45a).
As \(z=z_n\), it follows from (3.15) and (3.16) that
Since \(\mu _{+2}\) is full column rank, combining with Lemma 3.2 and Lemma 3.14 yields
i.e., there exists a constant vector \(\beta _n\) independent of (x, t; z) such that \({\textbf{m}}_1=\textrm{e}^{\textrm{i}(\theta _1+\theta _2)}\mu _{+2}{\textbf{S}}^*_{22}\beta _n\). Setting \({\textbf{C}}_n=\frac{{\textbf{S}}^*_{22}\beta _n}{{\dot{\det }}({\textbf{S}}_{22})}\), we complete the proof of (3.46a). \(\square \)
The inverse problem can be formulated in terms of the following:
Riemann–Hilbert Problem 3.16
Find a matrix-valued function \({\textbf{M}}(x,t;z)\) which is sectionally meromorphic in \({\mathbb {C}}\backslash \Gamma \), has simple poles as in Assumption 3.12, satisfies the growth conditions as in Lemma 3.7, the jump conditions as in Lemma 3.8, the asymptotic behaviors as in Lemma 3.10 and the residue conditions as in Lemma 3.15.
Theorem 3.17
Under the same hypotheses as in Lemma 2.22, the matrix \({\textbf{M}}(x,t;z)\) defined by (3.15) satisfies Riemann–Hilbert problem 3.16.
3.3 Reconstruction of potential
Lemma 3.18
(Vanishing Lemma) The regular RH problem for \({\textbf{M}}(x,t;z)\) obtained from RH problem 3.16 by replacing the asymptotic conditions in Lemma 3.10 with
has only the zero solution.
Proof
Let \({\mathcal {H}}(x,t;z)={\textbf{M}}(x,t;z){\textbf{H}}^{-1}(z){\textbf{M}}^\dag (x,t;{\bar{z}})\), it follows from the growth conditions (3.23) that \({\mathcal {H}}(x,t;z)\) is well defined at \(z=\pm \textrm{i}q_0\). Also,
where \({\textbf{J}}_{n}(x,t;z)={\textbf{J}}(x,t;z)\vert _{\Gamma _n}\), \(n=1,\ldots ,4\). The above equations imply \({\mathcal {H}}(x,t;z)\) has no jump across \(\Gamma _1\cup \Gamma _4\), similarly for \(\Gamma _2\cup \Gamma _3\). Since \({\mathcal {H}}(x,t;z)\) is analytic for \(z\in {\mathbb {C}}\backslash \Gamma \), also approaches \({\textbf{0}}\) as \(z\rightarrow \infty \), by Liouville’s theorem, we state
From (3.26) and (3.30), we find \({\textbf{J}}_1(x,t;z){\textbf{H}}^{-1}(z)\) is positive definite for \(z\in \Gamma _1\). Combining with (3.57a3.57b3.57c3.57d) implies \({\textbf{M}}_-(x,t;z)={\textbf{0}}\) for \(z\in \Gamma _1\), similarly for \(z\in \Gamma _3\). As a consequence, \({\textbf{M}}(x,t;z)={\textbf{0}}\) for \(z\in {\mathbb {R}}\), which implies \({\textbf{M}}(x,t;z)\) has no jump across \({\mathbb {R}}\). As is known to all, the zeros of the analytic function are isolated, thus \({\textbf{M}}(x,t;z)\equiv {\textbf{0}}\). \(\square \)
Now, we rewrite any \((N+1)\times (N+1)\) matrix \({\textbf{A}}\) in the following block form
where \({\textbf{A}}_{11}\) and \({\textbf{A}}_{13}\) are scalar.
Theorem 3.19
(Reconstruction formula) The solution \({\textbf{M}}(x,t;z)\) of RH problem 3.16 exists uniquely, thus
solves the N-component focusing NLS equation (1.2).
Proof
As we know that \({\textbf{M}}(x,t;z)\) may have some poles, however, this singular RH problem can be mapped to a regular one (see Ref. [30]). The solution of the regular RH problem 3.16 (has no singularities) exists uniquely if and only if Vanishing Lemma 3.18 holds (see Refs. [27, 28]). In absence of the possible poles, based on the symmetry properties of the jump matrix \({\textbf{J}}(x,t;z)\), one obtains that \({\textbf{M}}(x,t;z)\), \(({\textbf{M}}^\dag (x,t;{\bar{z}}))^{-1}{\textbf{H}}(z)\) and \({\textbf{M}}(x,t;{\hat{z}})\varvec{\Pi }_+(z)\) satisfy the same RH problem. Taking into account the uniqueness, we conclude
In the following, we shall prove that \({\textbf{q}}(x,t)\) defined by (3.60) solves the N-component focusing NLS (1.2) by virtue of the dressing method [29]. Set
where \({\textbf{U}}(x,t;z)\) and \({\textbf{V}}(x,t;z)\) are defined by (2.2), \({\varvec{\Omega }}(z)={\text {diag}}(-2k\lambda ,\underbrace{k^2+\lambda ^2,\ldots ,k^2+\lambda ^2}_{N-1},2k\lambda )\). Suppose \({\textbf{q}}(x,t)\) is defined by (3.60), and \({\textbf{M}}(x,t;z)\) has the asymptotic expansion forms
combining with the symmetries in (3.61), we conclude
Direct calculations yield \({\mathscr {A}}(x,t;z)\) satisfies the homogeneous RH problem
which by Lemma 3.18 implies
Furthermore, substituting the asymptotic expansion (3.633.64) into (3.67), and comparing the coefficients of \(O(z^{-1})\), we obtain
It follows from (3.65) and (3.68) that \({\mathscr {B}}(x,t;z)\) satisfies the homogeneous RH problem
which also by Lemma 3.18 implies that
The compatibility condition of Eqs. (3.67) and (3.70) yields the function \({\textbf{q}}(x,t)\) defined by (3.60) and solves the N-component focusing NLS equation (1.2). \(\square \)
Remark 3.20
In general, if the symmetries of jump matrix, the residue conditions and the asymptotic conditions are sufficient, the above theorem holds naturally by (3.15). In order to verify those symmetries that have been found are adequate, one must prove the reconstruction formula. In other words, the potential also can be expressed in terms of \({\textbf{M}}_{12}(x,t;z)\), the consistency of two reconstructions should be ensured by symmetries.
Indeed, RH problem 3.16 can be regularized by subtracting any pole contributions and the leading order asymptotic behavior at infinity and zero:
Consequently, the piecewise holomorphic function \({\mathcal {M}}(x,t;z)\) satisfies
Using the Plemelj–Sokhotski formula, we get
Equivalently, RH problem 3.16 can be solved by the system of algebraic-integral equations:
Corollary 3.21
The solution of the N-component focusing NLS equation (1.2) with NZBCs (1.3) is reconstructed as
4 Reflectionless potential and exact solutions
We now reconstruct the potential \({\textbf{q}}(x,t)\) explicitly in the reflectionless case, i.e., \(\rho _1(z)={\textbf{0}}\) and \(\rho _2(z)=0\). In this case, there is no jump across the contour \(\Gamma \). As a consequence, the inverse problem reduces to an algebraic system
where
4.1 Reconstruction
It follows trivially from (3.76) that
Theorem 4.1
In the reflectionless case, the solution of the N-component focusing NLS (1.2) with NZBCs (1.3) can be expressed by
Substituting (4.1a) into (4.1b) and (4.1c), we get the following algebraic system for \(\{\alpha _j{\textbf{M}}_3(\omega _j)\}_1^{2N_1}\) and \(\{{\textbf{M}}_2(\lambda _n){\mathcal {B}}_n\}_1^{N_2+N_3}\):
Solving this system, combining with Theorem 4.1, we find
Corollary 4.2
In the reflectionless case, the solution of the N-component focusing NLS (1.2) with NZBCs (1.3) can be written
where the \({\mathscr {N}}\times {\mathscr {N}}\) matrix-valued function \({\textbf{G}}(x,t)=(g_{mn})_{{\mathscr {N}}\times {\mathscr {N}}}\), the \(N\times {\mathscr {N}}\) matrix-valued function \({\textbf{F}}(x,t)=({\textbf{F}}_1,\ldots ,{\textbf{F}}_{{\mathscr {N}}})\), the \({\mathscr {N}}\)-dimensional column vector \({\textbf{1}}_{{\mathscr {N}}}=(1,\ldots ,1)^T\), \({\mathscr {N}}=2N_1+N_2+N_3\),
Remark 4.3
As \(N_2=N_3=0\), i.e., \({\mathscr {N}}=2N_1\), it follows from (4.10) that the (m, n)-element of the matrix \({\textbf{F}}(x,t)\) is zero for \(m=1,\ldots ,N-1\). Consequently, \(q_1=\cdots =q_{N-1}=0\).
4.2 Special exact solution
In the following, we explore the different possibilities for the reflectionless solution in the 3-component case. Without loss of generality, we consider \(q_+=1\), \(q_-=-1\), i.e., \({\textbf{q}}_+=(0,0,1)^T\), \({\textbf{q}}_-=(0,0,-1)^T\). In the reflectionless case, similar to the Manakov system [24], we find that
Setting \(z\rightarrow 0\) in the above equation, and comparing the asymptotics in (2.25) yields
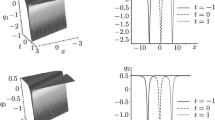
Case (i) \(N_2=0\), \(N_3=0\) (Fig. 2); Since \(q_1=q_2=0\), we only consider the dynamical evolutions of \(q_3\).
Case (ii) \(N_1=1\), \(N_2=1\), \(N_3=0\) (Fig. 3);
Case (iii) \(N_1=0\), \(N_2=1\), \(N_3=1\) (Fig. 4);
Case (iv) \(N_1=1\), \(N_2=1\), \(N_3=1\) (Fig. 5);
Remark 4.4
By virtue of the numerical software “Mathematica,” we have verified that all the expressions for \({\textbf{q}}(x,t)\) in cases \(\mathbf {(i)}-\mathbf {(iv)}\) solve the 3-component focusing NLS equation (1.2) with \(\lim _{x\rightarrow \pm \infty }{\textbf{q}}(x,t)=(0,0,\pm 1)^T\).
5 Conclusion and outlook
As it has shown that this work is more involved than the scalar case and the 2-component case, mainly in understanding the algebraic structure thoroughly. In this paper, we have introduced the idea of “block" and the generalized cross product in multi-dimensional space to develop the IST for the N-component focusing NLS with NZBCs and have characterized the inverse problem in terms of a \(3\times 3\) block matrix RH problem. Moreover, by virtue of the symmetries of the scattering data, we have verified the existence and uniqueness of solution for the above RH problem and have proved that the reconstruction potential \({\textbf{q}}(x,t)\) solves the N-component focusing NLS. We expect these ideas to be useful in investigating the other multi-component integrable equations. However, due to lacking \(N-1\) analytic eigenfunctions rather than one in each sector, those ideas in this work can not be applied to the IST for the N-component defocusing NLS equation with NZBCs in a straightforward way. We should remark that the IST for the multi-component defocusing NLS equation with NZBCs was recently established in Ref. [25, 26]. In spite of some ideas can be extended to the N-component case, a detailed treatment of the symmetries is still open. We believe that the idea of “block” would be useful to characterize the symmetries. In this paper, we consider the case of a solution that tends to \({\textbf{q}}_0 \textrm{e}^{i\theta _\pm }\) as \(x \rightarrow \pm \infty \), where \({\textbf{q}}_0\) is a fixed vector. This is a special case, the problem with general nonzero boundary condition is left as a topic for future work.
Once the long-time asymptotics for the focusing NLS with NZBCs have been analyzed in Refs. [31,32,33,34] by virtue of the nonlinear steepest descend method [35], one could try to investigate the 2-component case. Therefore, it would be an interesting subject to relate our previous work [36] on the 2-component coupled case with ZBCs to the techniques in this paper and Refs. [31,32,33].
Data availability statements
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
Zakharov, V.E., Ostrovsky, L.A.: Modulation instability: the beginning. Phys. D 238, 540–548 (2009)
Kibler, B., Fatome, J., Finot, C., et al.: The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 6, 790–795 (2010)
Biondini, G., Fagerstrom, E.: The integrable nature of modulational instability. SIAM J. Appl. Math. 75, 136–163 (2015)
Biondini, G., Li, S., Mantzavinos, D., Trillo, S.: Universal behavior of modulationally unstable media. SIAM Rev. 60, 888–908 (2018)
Chiao, R.Y., Garmire, E., Townes, C.H.: Self-trapping of optical beams. Phys. Rev. Lett. 13, 479–482 (1964)
Zakharov, V.E.: Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194 (1968)
Manakov, S.V.: On the theory of two-dimensional stationary self-focusing of electromagnetic waves. Soviet Phys. JETP 38, 248–253 (1974)
Busch, T., Anglin, J.R.: Dark-bright solitons in inhomogeneous Bose-Einstein condensates. Phys. Rev. Lett. 87, 010401 (2001)
Zakharov, V.E., Shabat, A.B.: Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Soviet Phys. JETP 34, 62–69 (1972)
Ablowitz, M.J., Segur, H.: Solitons and the Inverse Scattering Transform. SIAM Studies in Applied Mathematics, vol. 4. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (1981)
Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. London Mathematical Society Lecture Note Series, vol. 149. Cambridge University Press, Cambridge (1991)
Beals, R., Coifman, R.R.: Scattering and inverse scattering for first order systems. Commun. Pure Appl. Math. 37, 39–90 (1984)
Beals, R., Deift, P., Tomei, C.: Direct and Inverse Scattering on the Line. Mathematical Surveys and Monographs, vol. 28. American Mathematical Society, Providence (1988)
Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Discrete and Continuous Nonlinear Schrodinger Systems. London Mathematical Society Lecture Note Series, vol. 302. Cambridge University Press, Cambridge (2004)
Ablowitz, M.J., Prinari, B., Trubatch, A.D.: Soliton interactions in the vector NLS equation. Inverse Prob. 20, 1217 (2004)
Zakharov, V.E., Shabat, A.B.: Interaction between solitons in a stable medium. Soviet Phys. JETP 37, 823 (1973)
Kawata, T., Inoue, H.: Inverse scattering method for the nonlinear evolution equations under nonvanishing conditions. J. Phys. Soc. Jpn. 44, 1722–1729 (1978)
Demontis, F., Prinari, B., van der Mee, C., Vitale, F.: The inverse scattering transform for the defocusing nonlinear Schrödinger equations with nonzero boundary conditions. Stud. Appl. Math. 131, 1–40 (2013)
Biondini, G., Kovačič, G.: Inverse scattering transform for the focusing nonlinear Schrödinger equation with nonzero boundary conditions. J. Math. Phys. 55, 031506 (2014)
Bilman, D., Miller, P.D.: A robust inverse scattering transform for the focusing nonlinear Schrödinger equation. Commun. Pure Appl. Math. 72, 1722–1805 (2019)
Biondini, G., Lottes, J., Mantzavinos, D.: Inverse scattering transform for the focusing nonlinear Schrödinger equation with counterpropagating flows. Stud. Appl. Math. 146, 371–439 (2021)
Prinari, B., Ablowitz, M.J., Biondini, G.: Inverse scattering transform for the vector nonlinear Schrödinger equation with nonvanishing boundary conditions. J. Math. Phys. 47, 063508 (2006)
Biondini, G., Kraus, D.: Inverse scattering transform for the defocusing Manakov system with nonzero boundary conditions. SIAM J. Math. Anal. 47, 706–757 (2015)
Kraus, D., Biondini, G., Kovačič, G.: The focusing Manakov system with nonzero boundary conditions. Nonlinearity 28, 3101–3151 (2015)
Prinari, B., Biondini, G., Trubatch, A.D.: Inverse scattering transform for the multi-component nonlinear Schrödinger equation with nonzero boundary conditions. Stud. Appl. Math. 126, 245–302 (2011)
Biondini, G., Kraus, D., Prinari, B.: The three-component defocusing nonlinear Schrödinger equation with nonzero boundary conditions. Commun. Math. Phys. 348, 475–533 (2016)
Zhou, X.: The Riemann-Hilbert problem and inverse scattering. SIAM J. Math. Anal. 20, 966–986 (1989)
Ablowitz, M.J., Fokas, A.S.: Complex Variables: Introduction and Applications. Cambridge Texts in Applied Mathematics, 2nd edn. Cambridge University Press, Cambridge (2003)
Fokas, A.S.: A Unified Approach to Boundary Value Problems. CBMS-NSF Regional Conference Series in Applied Mathematics, vol. 78. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2008)
Fokas, A.S., Its, A.R.: The linearization of the initial-boundary value problem of the nonlinear Schröinger equation. SIAM J. Math. Anal. 27, 738–764 (1996)
Buckingham, R., Venakides, S.: Long-time asymptotics of the nonlinear Schrödinger equation shock problem. Commun. Pure Appl. Math. 60, 1349–1414 (2007)
Biondini, G., Mantzavinos, D.: Long-time asymptotics for the focusing nonlinear Schrödinger equation with nonzero boundary conditions at infinity and asymptotic stage of modulational instability. Commun. Pure Appl. Math. 70, 2300–2365 (2017)
Biondini, G., Li, S., Mantzavinos, D.: Long-time asymptotics for the focusing nonlinear Schrödinger equation with nonzero boundary conditions in the presence of a discrete spectrum. Commun. Math. Phys. 382, 1495–1577 (2021)
Boutet de Monvel, A., Lenells, J., Shepelsky, D.: The focusing NLS equation with step-like oscillating background: scenarios of long-time asymptotics. Commun. Math. Phys. 383, 893–952 (2021)
Deift, P., Zhou, X.: A steepest descent method for oscillatory Riemann-Hilbert problems. Asymptotics for the MKdV equation. Ann. Math. 137, 295–368 (1993)
Geng, X.G., Liu, H.: The nonlinear steepest descent method to long-time asymptotics of the coupled nonlinear Schrödinger equation. J. Nonlinear Sci. 28, 739–763 (2018)
Acknowledgements
We thank Qingping Liu and Yonghui Kuang for many helpful discussions and thank the anonymous referees for their comments and corrections. This work was supported by National Natural Science Foundation of China (Grant Nos. 12171439, 12101190, 11871440, 11931017) and Henan Youth Talent Support Project of China (Grant No. 2021HYTP001).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, H., Shen, J. & Geng, X. Inverse scattering transformation for the N-component focusing nonlinear Schrödinger equation with nonzero boundary conditions. Lett Math Phys 113, 23 (2023). https://doi.org/10.1007/s11005-023-01643-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11005-023-01643-5
Keywords
- Multi-component nonlinear Schrödinger equation
- Nonzero boundary conditions
- Generalized cross product
- Riemann–Hilbert problem