The focusing coupled modified Korteweg–de Vries equation with nonzero boundary conditions: the Riemann–Hilbert problem and soliton classification

Abstract

The focusing coupled modified Korteweg–de Vries equation with nonzero boundary conditions is investigated by the Riemann–Hilbert approach. Three symmetries are formulated to derive compact exact solutions. The solutions include six different types of soliton solutions and breathers, such as dark–dark, bright–bright, kink–dark–dark, kink–bright–bright solitons, and a breather–breather solution.

1. Introduction

The modified Korteweg–de Vries (mKdV) equation was first introduced by Miura [1] as a natural extension of the KdV equation. It appears in many physical contexts, such as meandering ocean currents [2], acoustic waves in a certain anharmonic lattice [3], the Alfvén waves in a cold collision-free plasma [4], and so on. As a consequence, the equation has been studied extensively and many important results have been obtained [5]–[12].

In recent years, multicomponent integrable models have attracted considerable attention because of their physical significance in many fields such as optical fibers [13], [14], Bose–Einstein condensate [15], [16], and nonlinear optics [13]. An extension to the multicomponent equations is needed to describe different physical phenomena. For example, we know that the scalar nonlinear Schrödinger (NLS) equation controls the propagation of light pulses with fixed polarization, but when we consider the polarization effect in the pulse propagation along an optical fiber [17], we should use its two-component version. And when it comes to the effects of polarization or anisotropy in birefringent fibers [18], the short-pulse equation characterizing the propagation of ultrashort optical pulses in nonlinear media should be replaced by its two-component counterpart to describe the propagation of ultrashort pulses in birefringent fibers. Moreover, multicomponent integrable systems are rich in mathematical structures, and therefore their studies from different standpoints offer completely different experiences and challenges. Generalizations of the mKdV equation to the multicomponent case have been proposed and studied by several authors [19]–[24].

In this paper, we consider the focusing coupled modified Korteweg–de Vries (fcmKdV) equation

$$\mathbf q_t+\mathbf q_{xxx}+3\|\mathbf q\|^2\mathbf q_x +3\mathbf q^{\mathrm T}\mathbf q_x\mathbf q=\boldsymbol 0,\qquad \mathbf q=(q_1,q_2)^{\mathrm T}, $$

(1.1)

where the superscripts $\mathrm T$ and $\|\cdot\|$ represent the matrix transpose and the standard Euclidean norm, and $\boldsymbol 0$ denotes a zero matrix of the appropriate size. In 2017, multisoliton solutions of the fcmKdV equation decaying rapidly for large $|x|$ were obtained in [25] by using the inverse scattering transform (IST) method. In 2020, Wang et al. [26] obtained the nonlinear stability of breather solutions of the fcmKdV equation.

To better understand nonlinear phenomena of integrable systems, it is important to use various methods to find their exact solutions, among which the Riemann–Hilbert approach is always considered as an effective tool for solving initial-value problems. The Riemann–Hilbert approach is the modern version of the IST method. It has become evident that this method is also applicable to the long-time asymptotics of solutions to a wide range of integrable systems [27]–[29]. In addition, integrable nonlinear systems with nonzero boundary conditions (NZBCs) have numerous applications. Recent experiments with Bose–Einstein condensates have shown a proliferation of dark–dark vector solitons in the dynamics of two miscible superfluids experiencing fast counterflow in a narrow (cigar-shaped) condensate [16]. Problems with NZBCs are also relevant for the modulational instability in optics and the generation of rogue waves [30], [31]. In this paper, we use IST to solve the fcmKdV equation with the NZBCs

$$\lim_{x\to\pm\infty}{\mathbf q(x,t)}=\mathbf q_{\pm},\qquad \|\mathbf q_{\pm}\|=q_0>0, $$

(1.2)

where $\mathbf q_{\pm}=(q_{1\pm},q_{2\pm})^{\mathrm T}$. We note that the defocusing cmKdV equation with NZBCs was considered in [19]. Compared with the latter problem, we show that the focusing one in this paper has a more complicated spectral structure and richer classification of the discrete spectrum, leading to abundance of soliton solutions. We also want to explore the soliton classification for this problem.

This paper is organized as follows. In Sec. 2, for the potential $\mathbf q(x,t)$ such that $\mathbf q(\,\cdot\,,t)-\mathbf q_\pm\in L^1(\mathbb R)$, the Jost eigenfunctions and scattering coefficients are defined in the direct problem. The auxiliary eigenfunctions that can comprise a complete set of analytic eigenfunctions are given. The symmetries and asymptotic behavior of the eigenfunctions and scattering coefficients are systematically obtained. In Sec. 3, a matrix Riemann–Hilbert problem (RHP) for the inverse problem is formulated, and the trace formula and the asymptotic phase difference are given. In Sec. 4, a compact matrix-form formula for general soliton solutions is derived in the reflectionless case, including an arbitrary combination of six different types of solitons. The conclusions are given in Sec. 5.

2. Direct problem

The Lax pair for Eq. (1.1) is given by

$$\begin{alignedat}{2} &\varphi_x=\mathbf X\varphi,&\qquad &\mathbf X(x,t,k)=ik\boldsymbol\sigma+\mathbf Q, \\ &\varphi_t=\mathbf T\varphi,&\qquad &\mathbf T(x,t,k) =4k^2\mathbf Q+2ik(2k^2\boldsymbol\sigma+\boldsymbol\sigma\mathbf Q^2 +\mathbf Q_x\boldsymbol\sigma)+2\mathbf Q^3-[\mathbf Q,\mathbf Q_x]-\mathbf Q_{xx}, \end{alignedat} $$

(2.1)

where

$$\boldsymbol\sigma=\operatorname{diag}(-1,1,1),\qquad \mathbf Q(x,t)=\begin{pmatrix} 0 &\mathbf q^{\mathrm T} \\ -\mathbf q &\boldsymbol 0 \end{pmatrix}, $$

(2.2)

and $[\,\cdot\,{,}\,\cdot\,]$ denotes matrix commutator.

2.1. Jost eigenfunctions and the scattering matrix

To introduce Jost solutions, we must first study the asymptotic spectral problem for (2.1) as $x\to\pm\infty$,

$$\begin{alignedat}{2} &\phi_{\pm,x}=\mathbf X_{\pm}\phi_{\pm}, &\qquad &\mathbf X_{\pm}=ik\boldsymbol\sigma+\mathbf Q_{\pm}, \\ &\phi_{\pm,t}=\mathbf T_{\pm}\phi_{\pm}, &\qquad &\mathbf T_{\pm}=4k^2\mathbf Q_{\pm} +2ik(2k^2\boldsymbol\sigma +\boldsymbol\sigma\mathbf Q^2_{\pm})+2\mathbf Q^3_\pm, \end{alignedat} $$

(2.3)

where

$$\mathbf Q_\pm=\begin{pmatrix} 0 &\mathbf q^{\mathrm T}_\pm \\ -\mathbf q_\pm &\boldsymbol 0 \end{pmatrix}.$$

The eigenvalues of $\mathbf X_\pm$ are $ik$ and $\pm i\lambda$, where

$$\lambda(k)=\sqrt{k^2+q_0^2}. $$

(2.4)

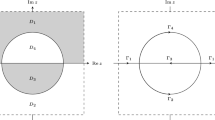
We note that $\lambda(k)$ is multivalued. As usual, this situation can be obviated by introducing the two-sheeted Riemann surface defined by (2.4). Its branch points are the values of $k$ for which $\lambda(k)=0$, i.e., $k={\pm}iq_0$. This Riemann surface is constructed by gluing two copies along the branch cut $i[-q_0,q_0]$. We define $\lambda(k)$ such that $\operatorname{Im}\lambda(k)>0$ is the upper-half plane on the sheet $\mathrm I$ and the lower-half plane on the sheet $\mathrm{II}$, and $\operatorname{Im}\lambda(k)<0$ is the lower-half plane on the sheet $\mathrm I$ and the upper-half plane on the sheet $\mathrm{II}$.

For convenience, we introduce the uniformization variable as

$$z=k+\lambda, $$

(2.5)

whose inverse map is given by

$$k=\frac{1}{2}(z-\hat z),\qquad \lambda=\frac{1}{2}(z+\hat z), $$

(2.6)

where $\hat z:=q_0^2/z$. Let $C_0$ be the circle of radius $q_0$ centered at the origin in the complex $z$ plane. Then the branch cut on either sheet is mapped onto $C_0$: the first sheet $\mathbb C_{\mathrm I}$ is mapped onto the exterior of $C_0$, and the second sheet $\mathbb C_{\mathrm{II}}$ is mapped onto the interior of $C_0$. We also have $z(k,\lambda_{\mathrm I})z(k,\lambda_{\mathrm{II}})=q_0^2$.

We next perform the IST on the complex $z$ plane. On either sheet of the Riemann surface, we can take the asymptotic eigenvector matrices in the form

$$\mathbf E_\pm(z)=\begin{pmatrix} 1 &0 &-iq_0/z \\ -i\mathbf q_\pm/z &\mathbf q_\pm^{\perp}/q_0 &\mathbf q_\pm/q_0 \end{pmatrix}, $$

(2.7)

whence

$$\begin{alignedat}{2} &\mathbf E_\pm^{-1}\mathbf X_\pm\mathbf E_\pm=i\boldsymbol\Lambda_1, &\qquad &\boldsymbol\Lambda_1(z)=\operatorname{diag}(-\lambda,k,\lambda), \\ &\mathbf E_\pm^{-1}\mathbf T_\pm\mathbf E_\pm =i\boldsymbol\Lambda_2,&\qquad &\boldsymbol\Lambda_2(z) =\operatorname{diag}(-2\lambda(2k^2-q_0^2),4k^3,2\lambda(2k^2-q_0^2)), \end{alignedat} $$

(2.8)

where $\mathbf q_\pm^{\perp}=(q_{2\pm},-q_{1\pm})^{\mathrm T}$. For future reference, we note that

$$\operatorname{det}\mathbf E_\pm(z)=1+\frac{q_0^2}{z^2}:=\gamma(z). $$

(2.9)

The continuous spectrum $k\in(\mathbb R\cup i[-q_0,q_0])$ consists of all values of $k$ (on either sheet) such that $\lambda(k)\in\mathbb R$. The corresponding set is $\Sigma=\mathbb R\cup C_0$ in the complex $z$ plane. In that way, for $z \in \Sigma$, we can define $\varphi_\pm(x,t,z)$ as the Jost eigenfunctions with the boundary conditions

$$\varphi_\pm(x,t,z)=\mathbf E_\pm(z)e^{i\boldsymbol\Theta(x,t,z)}+o(1),\qquad x\to\pm\infty, $$

(2.10)

where $\boldsymbol\Theta(x,t,z)=\boldsymbol\Lambda_1(z)x+\boldsymbol\Lambda_2(z)t =\operatorname{diag}(\theta_1(x,t,z),\theta_2(x,t,z),-\theta_1(x,t,z))$. As usual, we introduce the modified Jost eigenfunctions

$$\mu_\pm(x,t,z)=\varphi_\pm(x,t,z)e^{-i\boldsymbol\Theta(x,t,z)}, $$

(2.11)

such that

$$\lim_{x\to\pm\infty}\mu_\pm(x,t,z)=\mathbf E_\pm(z),\qquad z\in\Sigma. $$

(2.12)

The spectral problem for $\mu_\pm(x,t,z)$ is defined by

$$\begin{aligned} \, (\mathbf E_\pm^{-1}\mu_\pm)_x+i[\mathbf E_\pm^{-1}\mu_\pm, \boldsymbol\Lambda_1]&=\mathbf E_\pm^{-1}\Delta\mathbf Q_\pm\mu_\pm, \\ (\mathbf E_\pm^{-1}\mu_\pm)_t+i[\mathbf E_\pm^{-1}\mu_\pm, \boldsymbol\Lambda_2]&=\mathbf E_\pm^{-1}\Delta\mathbf T_\pm \mu_\pm, \end{aligned} $$

(2.13)

where $\Delta\mathbf Q_\pm=\mathbf Q-\mathbf Q_\pm$ and $\Delta\mathbf T_\pm=\mathbf T-\mathbf T_\pm$. Using these linear equations, it can be proved that $\mu_\pm(x,t,z)$ are well defined.

Theorem 2.1.

Let $\mathbf q(\,\cdot\,,t)-\mathbf q_\pm\in L^1(\mathbb R)$. Then the columns of $\mu_\pm(x, t, z)$ can be analytically extended to the corresponding domains in the complex $z$ plane,

$$\begin{alignedat}{3} &\mu_{-,1}:D_1, &\qquad &\mu_{-,2}:\mathbb C_-, &\qquad &\mu_{-,3}:D_4, \\ &\mu_{+,1}:D_2, &\qquad &\mu_{+,2}:\mathbb C_+, &\qquad &\mu_{+,3}:D_3, \end{alignedat} $$

(2.14)

where the analytic domains $D_1,\dots,D_4$ and $\mathbb C_+$, $\mathbb C_-$ are

$$\begin{alignedat}{3} &D_1=\{z\mid\operatorname{Im}z>0,\,|z|>q_0\},&\quad &D_2=\{z\mid\operatorname{Im}z<0,\,|z|>q_0\}, \\ &D_3=\{z\mid\operatorname{Im}z<0,\,|z|<q_0\},&\quad &D_4=\{z\mid\operatorname{Im}z>0,\,|z|<q_0\},\\ &\mathbb C_-=\{z\mid\operatorname{Im}z<0\}, &\qquad &\mathbb C_+=\{z\mid\operatorname{Im}z>0\}. \end{alignedat} $$

(2.15)

We next introduce the scattering matrix in a standard way. Because $\operatorname{tr}\mathbf X=ik$ and $\operatorname{tr}\mathbf T=4ik^3$, it follows from the Abel theorem that

$$\frac{\partial}{\partial x}\operatorname{det} [\varphi_\pm(x,t,z)e^{-i\boldsymbol\Theta(x,t,z)}] =\frac{\partial}{\partial t}\operatorname{det} [\varphi_\pm(x,t,z)e^{-i\boldsymbol\Theta(x,t,z)}]=0, $$

(2.16)

which implies that

$$\operatorname{det}\varphi_\pm(x,t,z) =\gamma(z)e^{i\theta_2(x,t,z)},\qquad z\in\Sigma. $$

(2.17)

As a result, for $z\in\Sigma_0:=\Sigma\setminus\{\pm iq_0\}$, $\varphi_+(x,t,z)$ and $\varphi_-(x,t,z)$ are two fundamental solutions of linear system (2.1), and hence a $3 \times 3$ scattering matrix $\mathbf A(z)$ must exist such that

$$\varphi_-(x,t,z)=\varphi_+(x,t,z)\mathbf A(z). $$

(2.18)

Because of the explicit time dependence of boundary condition (2.10), $\mathbf A(z)$ is independent of time. Combining (2.18) with (2.17) yields

$$\operatorname{det}\mathbf A(z)=1,\qquad z\in\Sigma_0. $$

(2.19)

We set $\mathbf B(z):=\mathbf A^{-1}(z)=(b_{ij}(z))$ for convenience. Furthermore, we obtain the following theorem.

Theorem 2.2.

Under the same hypotheses as in Theorem 2.1, the scattering coefficients can be analytically extended to the corresponding domains in the complex $z$ plane:

$$\begin{alignedat}{3} &a_{11}(z):D_1, &\qquad &a_{22}(z):\mathbb C_-, &\qquad &a_{33}(z):D_4, \\ &b_{11}(z):D_2, &\qquad &b_{22}(z):\mathbb C_+, &\qquad &b_{33}(z):D_3. \end{alignedat} $$

(2.20)

2.2. Auxiliary eigenfunctions

To formulate a complete RHP, four more eigenfunctions for (2.1) that are respectively analytic in four fundamental domains must be constructed. For this, as in [32], we turn to the adjoint problem

$$\tilde\varphi_x=\widetilde{\mathbf X}(z)\tilde{\varphi},\qquad \tilde\varphi_t=\widetilde{\mathbf T}(z)\tilde\varphi, $$

(2.21)

where $\widetilde{\mathbf X}(z)=\mathbf X^*(z^*)$ and $\widetilde{\mathbf T}(z)=\mathbf T^*(z^*)$. As before, for $z\in\Sigma$, we define the adjoint Jost eigenfunctions $\tilde\varphi_\pm(x,t,z)$ for (2.21) satisfying boundary conditions

$$\tilde\varphi_\pm(x,t,z) =\mathbf E_\pm^*(z^*)e^{-i\boldsymbol\Theta(x,t,z)}+o(1),\qquad x\to\pm\infty. $$

(2.22)

Under the same assumption as in Theorem 2.1, by introducing the modified adjoint Jost eigenfunctions $\tilde\mu_\pm(x,t,z)=\tilde\varphi_\pm(x,t,z)e^{i\boldsymbol\Theta(x,t,z)}$, it can be shown that the columns of $\tilde\mu_\pm(x,t,z)$ can be analytically extended to the corresponding domains:

$$\begin{alignedat}{3} &\tilde\mu_{-,1}:D_2, &\qquad &\tilde\mu_{-,2}:\mathbb C_+, &\qquad &\tilde\mu_{-,3}:D_3, \\ &\tilde\mu_{+,1}:D_1, &\qquad &\tilde\mu_{+,2}:\mathbb C_-, &\qquad &\tilde\mu_{+,3}:D_4. \end{alignedat} $$

(2.23)

For $z\in\Sigma$, we have $\operatorname{det}\tilde\varphi_\pm(x,t,z)=\gamma(z)e^{-i\theta_2(x,t,z)}$. Consequently, for $z\in\Sigma_0$, we introduce the corresponding scattering matrix as

$$\tilde\varphi_-(x,t,z)=\tilde\varphi_+(x,t,z)\widetilde{\mathbf A}(z). $$

(2.24)

By simple calculation, we can obtain the following fact.

Proposition 2.1.

If $\tilde{\mathbf p}(x,t,z)$ and $\tilde{\mathbf q}(x,t,z)$ are any two solutions to adjoint problem (2.21), then

$$\mathbf r(x,t,z)=e^{i\theta_2(x,t,z)} [\tilde{\mathbf p}\times\tilde{\mathbf q}](x,t,z) $$

(2.25)

is a solution of the original Lax pair (2.1), where $\times$ denotes the usual cross product.

Recalling the definition of the adjoint problem, we conclude that

$$\tilde\varphi_\pm(x,t,z)=\varphi_\pm^*(x,t,z^*),\qquad z\in\Sigma. $$

(2.26)

By the above results, we can build four new solutions of the original spectral problem (2.1), referred to as the auxiliary eigenfunctions, as

$$\begin{alignedat}{2} &\chi_1(x,t,z)=e^{i\theta_2(x,t,z)}[\varphi_{+,1}^*\times\varphi_{-,2}^*](x,t,z^*), &\qquad &z\in D_1, \\ &\chi_2(x,t,z)=e^{i\theta_2(x,t,z)}[\varphi_{-,1}^*\times\varphi_{+,2}^*](x,t,z^*), &\qquad &z\in D_2, \\ &\chi_3(x,t,z)=e^{i\theta_2(x,t,z)}[\varphi_{+,2}^*\times\varphi_{-,3}^*](x,t,z^*), &\qquad &z\in D_3, \\ &\chi_4(x,t,z)=e^{i\theta_2(x,t,z)}[\varphi_{-,2}^*\times\varphi_{+,3}^*](x,t,z^*), &\qquad &z\in D_4. \end{alignedat} $$

(2.27)

The corresponding modified auxiliary eigenfunctions are defined as

$$\begin{alignedat}{3} &m_j(x,t,z)=\chi_j(x,t,z)e^{i\theta_1(x,t,z)}, &\qquad &z\in D_j,&\quad &j=1,2, \\ &m_l(x,t,z)=\chi_l(x,t,z)e^{-i\theta_1(x,t,z)}, &\qquad &z\in D_l,&\quad &l=3,4. \end{alignedat} $$

(2.28)

By using above results again, we establish the following relation in a straightforward way.

Lemma 2.1.

For all cyclic permutations of the indices $j$, $l$, and $m$ with $z\in\Sigma$,

$$\varphi_{\pm,j}(x,t,z)=e^{i\theta_2(x,t,z)} \frac{[\varphi_{\pm,l}^*\times\varphi_{\pm,m}^*](x,t,z^*)}{\gamma_j(z)}\,, $$

(2.29)

where $\gamma_1(z)=\gamma_3(z)=1$ and $\gamma_2(z)=\gamma(z)$.

It is useful to note that

$$(\operatorname{det}\varphi_\pm)\mathbf I =(\varphi_{\pm,2}\times\varphi_{\pm,3},\varphi_{\pm,3}\times\varphi_{\pm,1}, \varphi_{\pm,1}\times\varphi_{\pm,2})\varphi_\pm^{\mathrm T},\qquad z\in\Sigma_0, $$

(2.30)

where $\mathbf I$ denotes the $3\times 3$ identity matrix. Thanks to this identity and scattering relation (2.18), we have the following corollary.

Corollary 2.1.

The scattering matrices $\mathbf A(z)$ and $\widetilde{\mathbf A}(z)$ satisfy the relation

$$\widetilde{\mathbf A}(z)=\boldsymbol\Gamma(z) [\mathbf A^{-1}(z)]^{\mathrm T}\boldsymbol\Gamma^{-1}(z),\qquad z\in\Sigma_0, $$

(2.31)

where $\boldsymbol\Gamma(z)=\operatorname{diag}(1,\gamma(z),1)$.

Applying scattering relation (2.24) and relation (2.29) to the auxiliary eigenfunctions (2.27) and then using (2.31) yields the following statement.

Corollary 2.2.

For $z\in\Sigma_0$, the Jost eigenfunctions $\varphi_{\pm,1}(x,t,z)$, $\varphi_{\pm,3}(x,t,z)$ have the decompositions

$$\begin{aligned} \, &\varphi_{-,1}(x,t,z)=\frac{1}{a_{22}(z)}[\chi_3(z)+a_{21}(z)\varphi_{-,2}(z)] =\frac{1}{a_{33}(z)}[\chi_4(z)+a_{31}(z)\varphi_{-,3}(z)], \\ &\varphi_{-,3}(x,t,z)=\frac{1}{a_{11}(z)}[\chi_1(z)+a_{13}(z)\varphi_{-,1}(z)] =\frac{1}{a_{22}(z)}[\chi_2(z)+a_{23}(z)\varphi_{-,2}(z)], \\ &\varphi_{+,1}(x,t,z)=\frac{1}{b_{33}(z)}[\chi_3(z)+b_{31}(z)\varphi_{+,3}(z)] =\frac{1}{b_{22}(z)}[\chi_4(z)+b_{21}(z)\varphi_{+,2}(z)], \\ &\varphi_{+,3}(x,t,z)=\frac{1}{b_{11}(z)}[\chi_2(z)+b_{13}(z)\varphi_{+,1}(z)] =\frac{1}{b_{22}(z)}[\chi_1(z)+b_{23}(z)\varphi_{+,2}(z)]. \end{aligned} $$

(2.32)

2.3. Symmetries

Symmetries of the eigenfunctions and scattering coefficients determine the distribution of the discrete spectrum, degrees of freedom of the soliton parameters, and solvability of the problem.

2.3.1. First symmetry

We first consider the transformation $z\mapsto z^*$. The following result is a straightforward consequence of the fact that $\mathbf Q^\dagger=-\mathbf Q$ and $\boldsymbol\sigma\mathbf Q=-\mathbf Q\boldsymbol\sigma$, where $\dagger$ denotes the conjugate transpose.

Lemma 2.2.

The Jost eigenfunctions $\varphi_\pm(x,t,z)$ admit the symmetry relation

$$\varphi_\pm^\dagger(x,t,z^*)=\mathbf C(z)\varphi_\pm^{-1}(x,t,z),\qquad z\in\Sigma, $$

(2.33)

where $\mathbf C(z)=\operatorname{diag}(\gamma(z),1,\gamma(z))$.

Using identity (2.30) and symmetry (2.33), substituting the (2.32) into it, and applying the Schwartz reflection principle, we obtain the following lemma.

Lemma 2.3.

The Jost eigenfunctions satisfy the symmetry relations

$$\begin{alignedat}{2} &\varphi_{-,1}^*(z^*)=\frac{e^{-i\theta_2(x,t,z)}}{a_{22}(z)} [\varphi_{-,2}\times\chi_2](x,t,z), &\qquad & z\in D_2, \\ &\varphi_{-,2}^*(z^*)= \begin{cases} \dfrac{e^{-i\theta_2(x,t,z)}}{\gamma(z)a_{11}(z)} [\chi_1\times\varphi_{-,1}](x,t,z),& z\in D_1, \vphantom{\Biggl\}} \\ \dfrac{e^{-i\theta_2(x,t,z)}}{\gamma(z)a_{33}(z)} [\varphi_{-,3}\times\chi_4](x,t,z), & z\in D_4, \end{cases} \\ &\varphi_{-,3}^*(z^*)=\frac{e^{-i\theta_2(x,t,z)}}{a_{22}(z)} [\chi_3\times \varphi_{-,2}](x,t,z), &\qquad & z\in D_3, \\ &\varphi_{+,1}^*(z^*)=\frac{e^{-i\theta_2(x,t,z)}}{b_{22}(z)} [\varphi_{+,2}\times\chi_1](x,t,z), &\qquad & z\in D_1, \\ &\varphi_{+,2}^*(z^*)=\begin{cases} \dfrac{e^{-i\theta_2(x,t,z)}}{\gamma(z)b_{33}(z)} [\varphi_{+,3}\times\chi_3](x,t,z) &z\in D_3, \vphantom{\Biggl\}} \\ =\dfrac{e^{-i\theta_2(x,t,z)}}{\gamma(z)b_{11}(z)} [\chi_2\times\varphi_{+,1}](x,t,z), &z\in D_2, \end{cases} \\ &\varphi_{+,3}^*(z^*)=\frac{e^{-i\theta_2(x,t,z)}}{b_{22}(z)} [\chi_4\times\varphi_{+,2}](x,t,z), &\qquad & z\in D_4. \end{alignedat} $$

(2.34)

We now explore the impact of the first symmetry on the scattering matrix. The next lemma follows from symmetry (2.33) and scattering relation (2.18).

Lemma 2.4.

For $z\in\Sigma_0$, the relation between the scattering matrices $\mathbf A(z)$ and $\mathbf B(z)$ is

$$\mathbf A^\dagger(z^*)=\mathbf C(z)\mathbf B(z)\mathbf C^{-1}(z). $$

(2.35)

Recalling the analyticity of the scattering coefficients, we conclude from the Schwartz reflection principle that

$$\begin{alignedat}{2} &b_{11}(z)=a_{11}^*(z^*),&\qquad &z\in D_2, \\ &b_{22}(z)=a_{22}^*(z^*),&\qquad &z\in\mathbb C_+, \\ &b_{33}(z)=a_{33}^*(z^*),&\quad &z\in D_3. \end{alignedat} $$

(2.36)

2.3.2. Second symmetry

We next discuss the transformation $z\mapsto -z^*$. It is easy to prove the following lemma.

Lemma 2.5.

The Jost eigenfunctions $\varphi_\pm(x,t,z)$ have the symmetry

$$\varphi_\pm(x,t,z)=\varphi^*_\pm(x,t,-z^*),\qquad z\in\Sigma. $$

(2.37)

We now discuss the symmetry of the scattering matrix in the context of the second symmetry. Substituting (2.37) in scattering relation (2.18), we obtain the following statement.

Lemma 2.6.

For $z\in\Sigma_0$, the scattering matrices satisfy the symmetries

$$\mathbf A(z)=\mathbf A^*(-z^*),\qquad \mathbf B(z)=\mathbf B^*(-z^*). $$

(2.38)

Then the Schwartz reflection principle allows us to conclude that

$$\begin{alignedat}{2} &a_{11}(z)=a_{11}^*(-z^*),&\qquad &z\in D_1, \\ &a_{22}(z)=a_{22}^*(-z^*),&\qquad &z\in\mathbb C_-, \\ &a_{33}(z)=a_{33}^*(-z^*),&\qquad &z\in D_4. \end{alignedat} $$

(2.39)

Finally, we combine symmetries (2.37) with definitions (2.27) of the auxiliary eigenfunctions to arrive at the following lemma.

Lemma 2.7.

The auxiliary eigenfunctions admit the symmetry relations

$$\chi_j(x,t,z)=\chi_j^*(x,t,-z^*),\qquad z\in D_j,\quad j=1,\dots,4. $$

(2.40)

2.3.3. Third symmetry

Finally, we study the transformation $z\mapsto-\hat z$.

Lemma 2.8.

The Jost eigenfunctions $\varphi_\pm(x,t,z)$ satisfy the symmetry

$$\varphi_\pm(x,t,z)=\varphi_\pm(x,t,-\hat z)\boldsymbol\Pi(z), \qquad z\in\Sigma, $$

(2.41)

where

$$\boldsymbol\Pi(z)=\begin{pmatrix} 0 &0 &-iq_0/z \\ 0 &1 &0 \\ -iq_0/z &0 &0 \end{pmatrix}.$$

Combining symmetry (2.41) with scattering relation (2.18) yields the following lemma.

Lemma 2.9.

For $z\in\Sigma_0$, the scattering matrices $\mathbf A(z)$ and $\mathbf B(z)$ admit the symmetries

$$\mathbf A(-\hat z)=\boldsymbol\Pi(z)\mathbf A(z)\boldsymbol\Pi^{-1}(z),\qquad \mathbf B(-\hat z)=\boldsymbol\Pi(z)\mathbf B(z)\boldsymbol\Pi^{-1}(z). $$

(2.42)

Using the Schwartz reflection principle, we conclude that

$$\begin{alignedat}{2} &a_{11}(z)=a_{33}(-\hat z),&\qquad &z\in D_1, \\ &a_{22}(z)=a_{22}(-\hat z),&\qquad &z\in\mathbb C_-. \end{alignedat} $$

(2.43)

To see how the third symmetry affects the symmetry of the auxiliary eigenfunctions, we substitute (2.41) in (2.27).

Lemma 2.10.

The auxiliary eigenfunctions obey the symmetries

$$\begin{alignedat}{2} &\chi_1(x,t,z)=-\frac{iq_0}{z}\,\chi_4(x,t,-\hat z),&\qquad &z\in D_1, \\ &\chi_2(x,t,z)=-\frac{iq_0}{z}\,\chi_3(x,t,-\hat z),&\qquad &z\in D_2. \end{alignedat} $$

(2.44)

2.3.4. Reflection coefficients

We note that we cannot exclude the possible existence of zeros for $a_{11}(z)$ and $b_{22}(z)$ along $\Sigma$. To solve the RHP, we focus on the potentials without spectral singularities [33]. For $z\in \Sigma$, there are three reflection coefficients in the inverse problem, which are given by

$$\rho_1(z)=\frac{a_{21}(z)}{a_{11}(z)}\,,\qquad \rho_2(z)=\frac{a_{31}(z)}{a_{11}(z)}\,,\qquad \rho_3(z)=\frac{a_{32}(z)}{a_{22}(z)}\,. $$

(2.45)

They have the following symmetries. We first consider the effect from the first symmetry:

$$\rho_1(z)=\gamma(z)\frac{b_{12}^*(z^*)}{b_{11}^*(z^*)}\,,\qquad \rho_2(z)=\frac{b_{13}^*(z^*)}{b_{11}^*(z^*)}\,,\qquad \rho_3(z)=\frac{1}{\gamma(z)}\frac{b_{23}^*(z^*)}{b_{22}^*(z^*)}\,. $$

(2.46)

Next, the second symmetry leads to the relations

$$\rho_j(z)=\rho_j^*(-z^*),\qquad j=1,2,3. $$

(2.47)

Finally, due to the third symmetry, we obtain that

$$\begin{aligned} \, &\rho_1(-\hat z)=\frac{iz}{q_0}\frac{a_{23}(z)}{a_{33}(z)} =\frac{iz\gamma(z)}{q_0}\frac{b_{32}^*(z^*)}{b_{33}^*(z^*)}\,,\qquad \rho_2(-\hat z)=\frac{a_{13}(z)}{a_{33}(z)} =\frac{b_{31}^*(z^*)}{b_{33}^*(z^*)}\,, \\ &\rho_3(-\hat z)=-\frac{iq_0}{z}\frac{a_{12}(z)}{a_{22}(z)} =-\frac{iq_0}{z\gamma(z)}\frac{b_{21}^*(z^*)}{b_{22}^*(z^*)}\,. \end{aligned} $$

(2.48)

2.4. Asymptotic behavior

We next study the asymptotic behavior of the eigenfunctions and scattering coefficients as $k\to\infty$. Because $z(\infty_{\mathrm I})=\infty$ and $z(\infty_{\mathrm{II}})=0$, we discuss the asymptotics both as $z\to\infty$ and as $z\to 0$. Specifically, substituting the corresponding standard Wentzel–Kramers–Brillouin expansions in differential equations (2.13) with boundary conditions (2.12) leads to the following lemma.

Lemma 2.11.

As $z\to\infty$, the columns of the modified Jost eigenfunctions $\mu_\pm(x,t,z)$ in the corresponding analyticity domains have the following asymptotic behavior:

$$\mu_{\pm,1}(x,t,z)=\begin{pmatrix} 1+\dfrac{1}{z}\displaystyle \int_{\pm\infty}^xi[q_0^2-\|\mathbf q(y,t)\|^2]\,dy \\ -i\mathbf q(x,t)/z \end{pmatrix}+o(z^{-2}),$$

(2.49a)

$$(\mu_{\pm,2}(x,t,z),\mu_{\pm,3}(x,t,z))=\begin{pmatrix} 0 &0 \\ \mathbf q_\pm^\perp/q_0 &\mathbf q_\pm/q_0 \end{pmatrix}+o(z^{-1}).$$

(2.49b)

Using the last two terms in (2.49a), we obtain the following proposition.

Proposition 2.2.

The solution $\mathbf q(x,t)=(q_1(x,t),q_2(x,t))^{\mathrm T}$ of the fcmKdV equation with NZBCs can be expressed as

$$q_j(x,t)=i\lim_{z\to\infty}[z\mu_\pm(x,t,z)]_{(j+1)1}. $$

(2.50)

Lemma 2.12.

As $z\to 0$, the columns of the modified Jost eigenfunctions $\mu_\pm(x,t,z)$ in the corresponding analyticity domains have the following asymptotic behavior:

$$\begin{aligned} \, &(\mu_{\pm,1}(x,t,z),\mu_{\pm,3}(x,t,z))=\begin{pmatrix} 0 &-iq_0/z \\ -i\mathbf q_\pm/z &\boldsymbol 0 \end{pmatrix}+o(1), \\ &\mu_{\pm,2}(x,t,z)=\begin{pmatrix} 0\\ \mathbf q_\pm^{\perp}/q_0 \end{pmatrix}+o(z). \end{aligned} $$

(2.51)

Substituting the above asymptotics in representations (2.28) for the modified auxiliary eigenfunctions yields the following corollary.

Corollary 2.3.

The modified auxiliary eigenfunctions $m_j(x,t,z)$ ($j=1,\dots,4$) in the corresponding analyticity domains have the following asymptotics:

$$\begin{aligned} \, \begin{aligned} \, &(m_1,m_2,m_3,m_4)=\begin{pmatrix} 0 &0 &\mathbf q_+^{\mathrm T}\mathbf q_-/q_0^2 &\mathbf q_+^{\mathrm T}\mathbf q_-/q_0^2 \\ \mathbf q_-/q_0 &\mathbf q_+/q_0 &\boldsymbol 0 &\boldsymbol 0 \end{pmatrix}+o(z^{-1}),& z\to\infty, \\ &(m_1,m_2,m_3,m_4)=\begin{pmatrix} -i\mathbf q_+^{\mathrm T}\mathbf q_-/(zq_0) &-i\mathbf q_+^{\mathrm T}\mathbf q_-/(zq_0) &0 &0 \\ \boldsymbol 0 &\boldsymbol 0 &-i\mathbf q_+/z &-i\mathbf q_-/z \end{pmatrix}+o(1),&z\to 0. \end{aligned} \end{aligned}$$

(2.52)

Next, we investigate the asymptotic behavior of the scattering coefficients. Combining the asymptotics of the Jost eigenfunctions in Lemmas 2.11 and 2.12 with scattering relation (2.18), we arrive at the following statements.

Corollary 2.4.

As $z\to\infty$, the scattering coefficients in the corresponding analyticity domains have the asymptotic behavior

$$ \begin{alignedat}{3} &a_{11}(z)=1+o(z^{-1}), &\qquad &a_{22}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z^{-1}), &\qquad &a_{33}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z^{-1}), \\ &b_{11}(z)=1+o(z^{-1}), &\qquad &b_{22}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z^{-1}), &\qquad &b_{33}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z^{-1}). \end{alignedat}$$

(2.53)

Corollary 2.5.

As $z\to 0$, the scattering coefficients in the corresponding analyticity domains have the asymptotics

$$a_{11}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z), \qquad a_{22}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z), \qquad a_{33}(z)=1+o(z),$$

(2.54a)

$$b_{11}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z), \qquad b_{22}(z)=\frac{\mathbf q_+^{\mathrm T}\mathbf q_-}{q_0^2}+o(z), \qquad b_{33}(z)=1+o(z).$$

(2.54b)

3. Inverse problem

In what follows, we formulate the corresponding RHP and then obtain a reconstruction formula and the trace formula.

3.1. Riemann–Hilbert problem

We start by introducing the piecewise meromorphic function

$$\begin{alignedat}{2} &\mathbf M(x,t,z)=\biggl(\frac{\mu_{-,1}(x,t,z)}{a_{11}(z)}\,,\mu_{+,2}(x,t,z), \frac{m_1(x,t,z)}{b_{22}(z)}\biggr), &\qquad &z\in D_1, \\ &\mathbf M(x,t,z)=\biggl(\mu_{+,1}(x,t,z),\frac{\mu_{-,2}(x,t,z)}{a_{22}(z)}\,, \frac{m_2(x,t,z)}{b_{11}(z)}\biggr), &\qquad &z\in D_2, \\ &\mathbf M(x,t,z)=\biggl(\frac{m_3(x,t,z)}{b_{33}(z)}\,, \frac{\mu_{-,2}(x,t,z)}{a_{22}(z)}\,,\mu_{+,3}(x,t,z)\biggr), &\qquad &z\in D_3, \\ &\mathbf M(x,t,z)=\biggl(\frac{m_4(x,t,z)}{b_{22}(z)}\,,\mu_{+,2}(x,t,z), \frac{\mu_{-,3}(x,t,z)}{a_{33}(z)}\biggr), &\quad &z\in D_4. \end{alignedat} $$

(3.1)

We next study the jump conditions of the matrix function $\mathbf M(x,t,z)$ across the contour $\Sigma$. Thus, we set

$$\mathbf M_\pm(x,t,z)=\lim_{\substack{\acute z\to z\\ \acute z\in D_\pm}} \mathbf M(x,t,\acute z),\qquad z\in\Sigma,$$

where $D_+=D_1\cup D_3$, $D_-=D_2\cup D_4$. Here, $\Sigma=\Sigma_1\cup\Sigma_2\cup\Sigma_3\cup\Sigma_4$, where $\Sigma_j$ is the boundary of $\overline D_j\cap\overline D_{(j+1)\mod 4}$. We define the orientation of the boundary $\Sigma_j$, $j=1,\dots,4$, such that $D_+$ is always on its left side. Then by combining scattering relation (2.18) with decompositions (2.32), we conclude that the following lemma holds.

Lemma 3.1.

The function $\mathbf M(x,t,z)$ satisfies the jump conditions

$$\mathbf M_+(x,t,z)=\mathbf M_-(x,t,z)\mathbf G(x,t,z),\qquad z\in\Sigma, $$

(3.2)

where

$$\mathbf G(x,t,z)=e^{i\boldsymbol\Theta(x,t,z)}\mathbf G_j(z) e^{-i\boldsymbol\Theta(x,t,z)},\qquad z\in\Sigma_j, \quad j=1,\dots,4, $$

(3.3)

with

$$\begin{aligned} \, &\mathbf G_1(z)=\begin{pmatrix} 1+\dfrac{1}{\gamma(z)}|\rho_1(z)|^2+|\rho_2(z)|^2 &\dfrac{1}{\gamma(z)}\rho_1^*(z) &\rho_2^*(z)-\rho_1^*(z)\rho_3^*(z) \\ \rho_1(z) &1 &-\gamma(z)\rho_3^*(z) \\ \rho_2(z)-\rho_1(z)\rho_3(z) &-\rho_3(z)&1+\gamma(z)|\rho_3(z)|^2 \end{pmatrix},\qquad z\in\Sigma_1, \nonumber \\ &\mathbf G_2(z)=\begin{pmatrix} 1-\rho_2^*(z^*)\rho_2(\hat z) &0 &\rho_2^*(z^*) \\ 0 &1 &0 \\ -\rho_2(\hat z) &0 &1 \end{pmatrix},\qquad z\in\Sigma_2,\nonumber\\[-5mm] \\ &\mathbf G_3(z)=\begin{pmatrix} 1+|\rho_2(\hat z)|^2 &-\dfrac{b_{12}(z)}{a_{22}(z)a_{33}(z)} &-\rho_2^*(\hat z) \\ -\dfrac{a_{21}(z)}{b_{22}(z)b_{33}(z)} &\dfrac{1}{a_{22}(z)b_{22}(z)} &\gamma(z)\rho_3^*(z) \\ -\rho_2(\hat z) &\rho_3(z) &1 \end{pmatrix},\qquad z\in\Sigma_3, \nonumber \\ &\mathbf G_4(z)=\begin{pmatrix} 1-\rho_2(z)\rho_2^*(\hat z^*) &0 &-\rho_2^*(\hat z^*) \\ 0 &1 &0 \\ \rho_2(z) &0 &1 \end{pmatrix},\qquad z\in\Sigma_4. \nonumber \end{aligned}$$

(3.4)

The following symmetry holds:

$$\mathbf G(x,t,z)=\mathbf C^{-1}(z)\mathbf G^\dagger(x,t,z^*)\mathbf C(z),\qquad z\in\Sigma. $$

(3.5)

Moreover, using the asymptotics of the eigenfunctions and scattering coefficients with the restriction that $\mathbf q_+$ is parallel to $\mathbf q_-$, we derive the following result.

Lemma 3.2.

The matrix $\mathbf M(x,t,z)$ admits the normalization conditions

$$\begin{alignedat}{2} &\mathbf M(x,t,z)=\mathbf M_\infty+o(z^{-1}), &\qquad &z\to\infty, \\ &\mathbf M(x,t,z)=-\frac{i}{z}\mathbf M_0+o(1), &\quad &z\to 0, \end{alignedat} $$

(3.6)

where

$$\mathbf M_\infty=\begin{pmatrix} 1 &0 &0 \\ \boldsymbol 0 &\mathbf q_+^\perp/q_0 &\mathbf q_+/q_0 \end{pmatrix},\qquad \mathbf M_0=\begin{pmatrix} 0 &0 &q_0 \\ \mathbf q_+ &\boldsymbol 0 &\boldsymbol 0 \end{pmatrix}. $$

(3.7)

The next lemma follows from (2.36), (2.39), and (2.43).

Lemma 3.3.

If $z_0\in D_1$, then

$$\begin{aligned} \, &b_{22}(z_0)=0\Longleftrightarrow a_{22}(z_0^*)=0\Longleftrightarrow a_{22}(-\hat z_0^*) =0\Longleftrightarrow b_{22}(-\hat z_0)=0\Longleftrightarrow b_{22}(-z_0^*)=0\Longleftrightarrow \\ &\hphantom{b_{22}(z_0)=0{}}\Longleftrightarrow a_{22}(-z_0)=0\Longleftrightarrow a_{22}(\hat z_0) =0\Longleftrightarrow b_{22}(\hat z_0^*)=0, \\ &a_{11}(z_0)=0\Longleftrightarrow b_{11}(z_0^*)=0\Longleftrightarrow b_{33}(-\hat z_0^*) =0\Longleftrightarrow a_{33}(-\hat z_0)=0\Longleftrightarrow a_{11}(-z_0^*)=0\Longleftrightarrow \\ &\hphantom{a_{11}(z_0)=0{}}\Longleftrightarrow b_{11}(-z_0)=0\Longleftrightarrow b_{33}(\hat z_0) =0\Longleftrightarrow a_{33}(\hat z_0^*)=0. \end{aligned} $$

(3.8)

These relations indicate that it suffices to study the zeros of $a_{11}(z)$ and $b_{22}(z)$ for $z\in D_1$. In this paper, we consider the zeros in the simple cases. Hence, there are six possible types of discrete eigenvalues:

• 1. $\{\xi_n\}_{n=1}^{N_1}$ is the set of all type-I eigenvalues; $a_{11}(\xi_n)=0$ and $b_{22}(\xi_n)\ne 0$ for $\operatorname{Re}\xi_n=0$;

• 2. $\{\omega_n\}_{n=1}^{N_2}$ is the set of all type-II eigenvalues; $a_{11}(\omega_n)=0$ and $b_{22}(\omega_n)\ne 0$ for $\operatorname{Re}\omega_n\ne 0$;

• 3. $\{\eta_n\}_{n=1}^{N_3}$ is the set of all type-III eigenvalues; $a_{11}(\eta_n)\ne 0$ and $b_{22}(\eta_n)=0$ for $\operatorname{Re}\eta_n=0$;

• 4. $\{z_n\}_{n=1}^{N_4}$ is the set of all type-IV eigenvalues; $a_{11}(z_n)\ne 0$ and $b_{22}(z_n)=0$ for $\operatorname{Re}z_n\ne 0$;

• 5. $\{\nu_n\}_{n=1}^{N_5}$ is the set of all type-V eigenvalues; $a_{11}(\nu_n)=b_{22}(\nu_n)=0$ for $\operatorname{Re}\nu_n=0$;

• 6. $\{\zeta_n\}_{n=1}^{N_6}$ is the set of all type-VI eigenvalues; $a_{11}(\zeta_n)=b_{22}(\zeta_n)=0$ for $\operatorname{Re}\zeta_n\ne 0$.

Lemma 3.4.

The meromorphic matrix $\mathbf M(x,t,z)$ satisfies the residue conditions

$$\begin{alignedat}{2} &\operatorname{Res}_{z=\xi_n}\mathbf M(x,t,z) =A_n(\mathbf M_3(\xi_n),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=-\hat\xi_n^*}\mathbf M(x,t,z) =-\frac{q_0^2}{(\xi_n^*)^2}\, A_n^*(\mathbf M_3(-\hat\xi_n^*),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=\xi_n^*}\mathbf M(x,t,z) =-A_n^*(\boldsymbol 0,\boldsymbol 0,\mathbf M_1(\xi_n^*)), \\ &\operatorname{Res}_{z=-\hat\xi_n}\mathbf M(x,t,z) =\frac{q_0^2}{\xi_n^2}A_n(\boldsymbol 0,\boldsymbol 0,\mathbf M_1(-\hat\xi_n)); \end{alignedat} $$

(3.9)

$$\begin{alignedat}{2} &\operatorname{Res}_{z=\omega_n}\mathbf M(x,t,z) =B_n(\mathbf M_3(\omega_n),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=-\widehat\omega_n^*}\mathbf M(x,t,z) =-\frac{q_0^2}{(\omega_n^*)^2}\, B_n^*(\mathbf M_3(-\widehat\omega_n^*),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=\omega_n^*}\mathbf M(x,t,z) =-B_n^*(\boldsymbol 0,\boldsymbol 0,\mathbf M_1(\omega_n^*)),\\ &\operatorname{Res}_{z=-\widehat\omega_n}\mathbf M(x,t,z) =\frac{q_0^2}{\omega_n^2}B_n(\boldsymbol 0,\boldsymbol 0,\mathbf M_1(-\widehat\omega_n)), \\ &\operatorname{Res}_{z=-\omega_n^*}\mathbf M(x,t,z) =-B_n^*(\mathbf M_3(-\omega_n^*),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=\widehat\omega_n}\mathbf M(x,t,z) =\frac{q_0^2}{\omega_n^2}B_n(\mathbf M_3(\widehat\omega_n),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=-\omega_n}\mathbf M(x,t,z) =B_n(\boldsymbol 0,\boldsymbol 0,\mathbf M_1(-\omega_n)),\\ &\operatorname{Res}_{z=\widehat\omega_n^*}\mathbf M(x,t,z) =-\frac{q_0^2}{(\omega_n^*)^2}\, B_n^*(\boldsymbol 0,\boldsymbol 0,\mathbf M_1(\widehat\omega_n^*)); \end{alignedat} $$

(3.10)

$$\begin{alignedat}{2} &\operatorname{Res}_{z=\eta_n}\mathbf M(x,t,z) =C_n(\boldsymbol 0,\boldsymbol 0,\mathbf M_2(\eta_n)), \\ &\operatorname{Res}_{z=-\hat\eta_n^*}\mathbf M(x,t,z) =\frac{iq_0^3}{(\eta_n^*)^3}\frac{C_n^*}{\gamma(\eta_n^*)} (\boldsymbol 0,\mathbf M_1(-\hat\eta_n^*),\boldsymbol 0), \\ &\operatorname{Res}_{z=\eta_n^*}\mathbf M(x,t,z) =-\frac{C_n^*}{\gamma(\eta_n^*)} (\boldsymbol 0,\mathbf M_3(\eta_n^*),\boldsymbol 0),\\ &\operatorname{Res}_{z=-\hat{\eta}_n}\mathbf M(x,t,z) =\frac{iq_0}{\eta_n}\,C_n(\mathbf M_2(-\hat\eta_n),\boldsymbol 0,\boldsymbol 0); \end{alignedat} $$

(3.11)

$$\begin{alignedat}{2} &\operatorname{Res}_{z=z_n}\mathbf M(x,t,z) =D_n(\boldsymbol 0,\boldsymbol 0,\mathbf M_2(z_n)), \\[-0.2mm] &\operatorname{Res}_{z=-\hat z_n^*}\mathbf M(x,t,z) =\frac{iq_0^3}{(z_n^*)^3}\frac{D_n^*}{\gamma(z_n^*)} (\boldsymbol 0,\mathbf M_1(-\hat z_n^*),\boldsymbol 0), \\[-0.2mm] &\operatorname{Res}_{z=z_n^*}\mathbf M(x,t,z) =-\frac{D_n^*}{\gamma(z_n^*)}(\boldsymbol 0,\mathbf M_3(z_n^*),\boldsymbol 0),\\[-0.2mm] &\operatorname{Res}_{z=-\hat z_n}\mathbf M(x,t,z) =\frac{iq_0}{z_n}\,D_n(\mathbf M_2(-\hat z_n),\boldsymbol 0,\boldsymbol 0), \\[-0.2mm] &\operatorname{Res}_{z=-z_n^*}\mathbf M(x,t,z) =-D_n^*(\boldsymbol 0,\boldsymbol 0,\mathbf M_2(-z_n^*)), \\[-0.2mm] &\operatorname{Res}_{z=\hat z_n}\mathbf M(x,t,z) =\frac{iq_0^3}{z_n^{3}}\frac{D_n}{\gamma(z_n)} (\boldsymbol 0,\mathbf M_1(\hat z_n),\boldsymbol 0), \\[-0.2mm] &\operatorname{Res}_{z=-z_n}\mathbf M(x,t,z) =\frac{D_n}{\gamma(z_n)}(\boldsymbol 0,\mathbf M_3(-z_n),\boldsymbol 0),\\[-0.2mm] &\operatorname{Res}_{z=\hat z_n^*}\mathbf M(x,t,z) =\frac{iq_0}{z_n^*}\,D_n^*(\mathbf M_2(\hat z_n^*),\boldsymbol 0,\boldsymbol 0); \end{alignedat} $$

(3.12)

$$\begin{alignedat}{2} &\operatorname{Res}_{z=\nu_n}\mathbf M(x,t,z) =E_n(\mathbf M_2(\nu_n),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=-\hat\nu_n^*}\mathbf M(x,t,z) =\frac{iq_0^3}{(\nu_n^*)^3}\frac{E_n^*}{\gamma(\nu_n^*)} (\boldsymbol 0,\mathbf M_3(-\hat\nu_n^*),\boldsymbol 0), \\ &\operatorname{Res}_{z=\nu_n^*}\mathbf M(x,t,z) =-\frac{E_n^*}{\gamma(\nu_n^*)} (\boldsymbol 0,\mathbf M_1(\nu_n^*),\boldsymbol 0), \\ &\operatorname{Res}_{z=-\hat\nu_n}\mathbf M(x,t,z) = \frac{iq_0}{\nu_n}\,E_n(\boldsymbol 0,\boldsymbol 0,\mathbf M_2(-\hat{\nu}_n)); \end{alignedat} $$

(3.13)

$$\begin{alignedat}{2} &\operatorname{Res}_{z=\zeta_n}\mathbf M(x,t,z) =F_n(\mathbf M_2(\zeta_n),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=-\hat\zeta_n^*}\mathbf M(x,t,z) =\frac{iq_0^3}{(\zeta_n^*)^3}\frac{F_n^*}{\gamma(\zeta_n^*)} (\boldsymbol 0,\mathbf M_3(-\hat{\zeta}_n^*),\boldsymbol 0), \\ &\operatorname{Res}_{z=\zeta_n^*}\mathbf M(x,t,z) =-\frac{F_n^*}{\gamma(\zeta_n^*)} (\boldsymbol 0,\mathbf M_1(\zeta_n^*),\boldsymbol 0),\\ &\operatorname{Res}_{z=-\hat\zeta_n}\mathbf M(x,t,z) =\frac{iq_0}{\zeta_n}\, F_n(\boldsymbol 0,\boldsymbol 0,\mathbf M_2(-\hat{\zeta}_n)), \\ &\operatorname{Res}_{z=-\zeta_n^*}\mathbf M(x,t,z) =-F_n^*(\mathbf M_2(-\zeta_n^*),\boldsymbol 0,\boldsymbol 0), \\ &\operatorname{Res}_{z=\hat\zeta_n}\mathbf M(x,t,z) =\frac{iq_0^3}{\zeta_n^3}\frac{F_n}{\gamma(\zeta_n)} (\boldsymbol 0,\mathbf M_3(\hat\zeta_n),\boldsymbol 0), \\ &\operatorname{Res}_{z=-\zeta_n}\mathbf M(x,t,z) =\frac{F_n}{\gamma(\zeta_n)} (\boldsymbol 0,\mathbf M_1(-\zeta_n),\boldsymbol 0), \\ &\operatorname{Res}_{z=\hat\zeta_n^*}\mathbf M(x,t,z) =\frac{iq_0}{\zeta_n^*}\, F_n^*(\boldsymbol 0,\boldsymbol 0,\mathbf M_2(\hat\zeta_n^*)) \end{alignedat} $$

(3.14)

with the normalization constants

$$\begin{alignedat}{3} &A_n=\frac{a_nb_{22}(\xi_n)}{a'_{11}(\xi_n)}e^{-2i\theta_1(\xi_n)}, &\qquad &B_n=\frac{b_nb_{22}(\omega_n)}{a'_{11}(\omega_n)}\,e^{-2i\theta_1(\omega_n)}, &\qquad &C_n=\frac{c_n}{b'_{22}(\eta_n)}\,e^{i(\theta_1+\theta_2)(\eta_n)}, \\ &D_n=\frac{d_n}{b'_{22}(z_n)}\,e^{i(\theta_1+\theta_2)(z_n)}, &\qquad &E_n=\frac{e_n}{a'_{11}(\nu_n)}\,e^{i(\theta_2-\theta_1)(\nu_n)}, &\qquad &F_n=\frac{f_n}{a'_{11}(\zeta_n)}\,e^{i(\theta_2-\theta_1)(\zeta_n)}, \end{alignedat}$$

where $a_n$, $b_n$, $c_n$, $d_n$, $e_n$, and $f_n$ are constants satisfying

$$a_n=a_n^*, \quad c_n=c_n^*,\quad e_n=e_n^*, $$

(3.15)

and where $n=1,\dots,N_1$ for equations involving $\xi_n$, $n=1,\dots,N_2$ for equations involving $\omega_n$, $n=1,\dots,N_3$ for equations involving $\eta_n$, $n=1,\dots,N_4$ for equations involving $z_n$, $n=1,\dots,N_5$ for equations involving $\nu_n$, and $n=1,\dots,N_6$ for equations involving $\zeta_n$.

When there are no zeros of $a_{11}(z)$ and $b_{22}(z)$, that is, the RHP is regular, the uniqueness of its solution is equivalent to the vanishing Lemma [34], [35].

Lemma 3.5.

Suppose that no discrete spectrum is present, or the RHP has no poles. Then the RHP defined in (3.1)–(3.7) has a unique solution.

However, the RHP defined in (3.1)–(3.15) has many singularities. According to [36], the RHP with poles can be mapped into a regular one. This RHP can be regularized by subtracting the leading terms of the asymptotic behavior and the pole contributions from the jump conditions. Then by the Plemelj’s formula [37], we obtain the following theorem.

Theorem 3.1.

The general solution of the RHP is given by

$$\begin{aligned} \, \mathbf M(x,t,z)={}&\mathbf E_+(z)+\sum_{n=1}^{N_1} \biggl(\frac{\operatorname*{Res}_{z=\xi_n}\mathbf M}{z-\xi_n} +\frac{\operatorname*{Res}_{z=\xi_n^*}\mathbf M}{z-\xi_n^*} +\frac{\operatorname*{Res}_{z=-\hat\xi_n^*}\mathbf M}{z+\hat\xi_n^*} +\frac{\operatorname*{Res}_{z=-\hat\xi_n}\mathbf M}{z+\hat\xi_n}\biggr)+{} \nonumber \\ &{}+\sum_{n=1}^{N_2} \biggl(\frac{\operatorname*{Res}_{z=\omega_n}\mathbf M}{z-\omega_n} +\frac{\operatorname*{Res}_{z=-\omega_n^*}\mathbf M}{z+\omega_n^*} +\frac{\operatorname*{Res}_{z=\omega_n^*}\mathbf M}{z-\omega_n^*} +\frac{\operatorname*{Res}_{z=-\omega_n}\mathbf M}{z+\omega_n}+{} \nonumber \\ & {}+\frac{\operatorname*{Res}_{z=-\widehat\omega_n^*}\mathbf M} {z+\widehat\omega_n^*} +\frac{\operatorname*{Res}_{z=\widehat\omega_n}\mathbf M}{z-\widehat\omega_n} +\frac{\operatorname*{Res}_{z=-\widehat\omega_n}\mathbf M}{z+\widehat\omega_n} +\frac{\operatorname*{Res}_{z=\widehat\omega_n^*}\mathbf M}{z-\widehat\omega_n^*}\biggr)+{} \nonumber \\ &{}+\sum_{n=1}^{N_3} \biggl(\frac{\operatorname*{Res}_{z=\eta_n}\mathbf M}{z-\eta_n} +\frac{\operatorname*{Res}_{z=\eta_n^*}\mathbf M}{z-\eta_n^*} +\frac{\operatorname*{Res}_{z=-\hat\eta_n^*}\mathbf M}{z+\hat\eta_n^*} +\frac{\operatorname*{Res}_{z=-\hat\eta_n}\mathbf M}{z+\hat\eta_n}\biggr)+{} \nonumber \\ &{}+\sum_{n=1}^{N_4} \biggl(\frac{\operatorname*{Res}_{z=z_n}\mathbf M}{z-z_n} +\frac{\operatorname*{Res}_{z=-z_n^*}\mathbf M}{z+z_n^*} +\frac{\operatorname*{Res}_{z=z_n^*}\mathbf M}{z-z_n^*} +\frac{\operatorname*{Res}_{z=-z_n}\mathbf M}{z+z_n}+{} \nonumber \\ & {}+\frac{\operatorname*{Res}_{z=-\hat z_n^*}\mathbf M}{z+\hat z_n^*} +\frac{\operatorname*{Res}_{z=\hat z_n}\mathbf M}{z-\hat z_n} +\frac{\operatorname*{Res}_{z=-\hat z_n}\mathbf M}{z+\hat z_n} +\frac{\operatorname*{Res}_{z=\hat z_n^*}\mathbf M}{z-\hat z_n^*}\biggr)+{} \nonumber \\ &{}+\sum_{n=1}^{N_5} \biggl(\frac{\operatorname*{Res}_{z=\nu_n}\mathbf M}{z-\nu_n} +\frac{\operatorname*{Res}_{z=\nu_n^*}\mathbf M}{z-\nu_n^*} +\frac{\operatorname*{Res}_{z=-\hat\nu_n^*}\mathbf M}{z+\hat\nu_n^*} +\frac{\operatorname*{Res}_{z=-\hat\nu_n}\mathbf M}{z+\hat\nu_n}\biggr)+{} \nonumber \\ &{}+\sum_{n=1}^{N_6} \biggl(\frac{\operatorname*{Res}_{z=\zeta_n}\mathbf M}{z-\zeta_n} +\frac{\operatorname*{Res}_{z=-\zeta_n^*}\mathbf M}{z+\zeta_n^*} +\frac{\operatorname*{Res}_{z=\zeta_n^*}\mathbf M}{z-\zeta_n^*} +\frac{\operatorname*{Res}_{z=-\zeta_n}\mathbf M}{z+\zeta_n}+{} \nonumber \\ & {}+\frac{\operatorname*{Res}_{z=-\hat\zeta_n^*}\mathbf M}{z+\hat\zeta_n^*} +\frac{\operatorname*{Res}_{z=\hat\zeta_n}\mathbf M}{z-\hat\zeta_n} +\frac{\operatorname*{Res}_{z=-\hat\zeta_n}\mathbf M}{z+\hat\zeta_n} +\frac{\operatorname*{Res}_{z=\hat\zeta_n^*}\mathbf M}{z-\hat\zeta_n^*}\biggr)+{} \nonumber \\ &+\frac{1}{2\pi i}\int_\Sigma \frac{\mathbf M_-(x,t,\zeta)(\mathbf G(x,t,\zeta)-\mathbf I)}{\zeta-z}\,d\zeta,\quad z\in\mathbb C\setminus\Sigma. \end{aligned}$$

(3.16)

Using the symmetries of the eigenfunctions, we can simplify the columns of $\mathbf M(x,t,z)$ as

$$\begin{aligned} \, \mathbf M_1(z)&=\mathbf E_{+,1}(z)+\sum_{n=1}^{\mathcal N_1} \frac{K_n\mathbf M_3(k_n)}{z-k_n}+\sum_{n=1}^{\mathcal N_2} \frac{L_n\mathbf M_2(l_n)}{z-l_n}+\frac{1}{2\pi i} \int_\Sigma\frac{\mathbf M_-(\mathbf G-\mathbf I)_1(\zeta)}{\zeta-z}\,d\zeta, \nonumber \\ \mathbf M_2(z)&=\mathbf E_{+,2}(z)-\sum_{n=1}^{\mathcal N_2} \frac{L_n^*\mathbf M_1(l_n^*)}{z+\hat{l}_n^*-\hat z-{l}_n^*} +\frac{1}{2\pi i} \int_\Sigma\frac{\mathbf M_-(\mathbf G-\mathbf I)_2(\zeta)}{\zeta-z}\,d\zeta, \nonumber \\[-4mm] \\ \mathbf M_3(z)&=\mathbf E_{+,3}(z)-\sum_{n=1}^{\mathcal N_1} \frac{K_n^*\mathbf M_1(k_n^*)}{z-k_n^*}+\sum_{n=1}^{\mathcal N_2} \frac{iq_0L_n\mathbf M_2(l_n)}{l_n(z+\hat l_n)}+{} \nonumber \\ &\hphantom{={}}+\frac{1}{2\pi i} \int_\Sigma\frac{\mathbf M_-(\mathbf G-\mathbf I)_3(\zeta)}{\zeta-z}\,d\zeta, \nonumber \end{aligned}$$

(3.17)

where $k_n$, $K_n$ and $l_n$, $L_n$ are given in Appendix A.1 with $\mathcal N_1=2N_1+4N_2$ and $\mathcal N_2=N_3+2N_4+N_5+2N_6$.

From formula (2.50), we deduce the following theorem.

Theorem 3.2 (reconstruction formula).

The solution $\mathbf q(x,t)=(q_1(x,t),q_2(x,t))^{\mathrm T}$ of the fcmKdV equation (1.1) with NZBCs (1.2) is reconstructed as

$$\begin{aligned} \, q_j(x,t)=q_{j+}+i\sum_{n=1}^{\mathcal N_1}K_n\mathbf M_{(j+1)3}(k_n)+i\sum_{n=1}^{\mathcal N_2}L_n\mathbf M_{(j+1)2}(l_n) -\frac{1}{2\pi}\int_\Sigma[\mathbf M_-(\mathbf G-\mathbf I)]_{(j+1)1}(z)\,dz. \end{aligned}$$

(3.18)

3.2. Trace formula and the asymptotic phase difference

We next reconstruct the analytic scattering coefficients in terms of scattering data. Thus can be achieved by constructing another RHP, as shown in Appendix A.2.

Lemma 3.6 (trace formula).

The analytic scattering coefficients $a_{11}(z)$ and $b_{22}(z)$ can be expressed as

$$\begin{aligned} \, b_{22}(z)&=\delta\prod_{n=1}^{N_3} \frac{(z-\eta_n)(z+\hat\eta_n)}{(z-\eta_n^*)(z+\hat\eta_n^*)} \prod_{n=1}^{N_4} \frac{(z-z_n)(z+z_n^*)(z+\hat z_n)(z-\hat z_n^*)} {(z-z_n^*)(z+z_n)(z+\hat z_n^*)(z-\hat z_n)}\times{} \nonumber \\ &\qquad{}\times\prod_{n=1}^{N_{5}}\frac{(z-\nu_n)(z+\hat\nu_n)}{(z-\nu_n^*)(z+\hat\nu_n^*)} \prod_{n=1}^{N_6}\frac{(z-\zeta_n)(z+\zeta_n^*)(z+\hat\zeta_n)(z-\hat\zeta_n^*)} {(z-\zeta_n^*)(z+\zeta_n)(z+\hat\zeta_n^*)(z-\hat\zeta_n)}\times{} \nonumber \\ &\qquad{}\times\exp\biggl[-\frac{1}{2\pi i}\int_{\mathbb R} \frac{J_0(\zeta)}{\zeta-z}\,d\zeta\biggr],\qquad z\in\mathbb C_+, \end{aligned}$$

(3.19a)

$$\begin{aligned} \, a_{11}(z)&=\prod_{n=1}^{N_1}\frac{(z-\xi_n)(z+\hat\xi_n^*)}{(z-\xi_n^*)(z+\hat\xi_n)} \prod_{n=1}^{N_2}\frac{(z-\omega_n)(z+\omega_n^*)(z+\widehat\omega_n^*)(z-\widehat\omega_n)} {(z-\omega_n^*)(z+\omega_n)(z+\widehat\omega_n)(z-\widehat\omega_n^*)}\times{} \nonumber \\ &\qquad{}\times\prod_{n=1}^{N_3}\frac{z+\hat\eta_n}{z+\hat\eta_n^*} \prod_{n=1}^{N_4}\frac{(z+\hat z_n)(z-\hat z_n^*)}{(z+\hat z_n^*)(z-\hat z_n)} \prod_{n=1}^{N_5}\frac{z-\nu_n}{z-\nu_n^*}\prod_{n=1}^{N_6} \frac{(z-\zeta_n)(z+\zeta_n^*)}{(z-\zeta_n^*)(z+\zeta_n)}\times{} \nonumber \\ &\qquad{}\times\exp\biggl[\frac{1}{2\pi i} \int_\Sigma\frac{J(\zeta)}{\zeta-z}\,d\zeta\biggr],\quad z\in D_1, \end{aligned}$$

(3.19b)

where $\delta=\pm 1$ and the matrices $J_0(z)$ and $J(z)$ are respectively defined in (A.5b) and (A.9a)–(A.9d).

Next, comparing the asymptotic behavior of the trace formula for $a_{11}(z)$ as $z\to 0$ with the result in (2.54a), we obtain that

$$\delta=(-1)^{N_3+N_5}\exp\biggl[\frac{1}{2\pi i}\int_\Sigma\frac{J(z)}{z}\,dz\biggr]. $$

(3.20)

Furthermore, we decompose the above integral term into

$$\begin{alignedat}{2} &H_1=\int_{-\infty}^{-q_0}\frac{J_1(z)}{z}\,dz,&\qquad &I_1=\int_{-\pi}^{-\pi/2}iJ_2(q_0e^{i\alpha})\,d\alpha, \\ &H_3=\int^0_{q_0}\frac{J_3(z)}{z}\,dz,&\qquad &I_3=\int^{\pi/2}_{\pi}iJ_4(q_0e^{i\alpha})\,d\alpha, \\ &H_2=\int^\infty_{q_0}\frac{J_1(z)}{z}\,dz, &\qquad &I_2=\int^0_{-\pi/2}iJ_2(q_0e^{i \alpha})\,d\alpha, \\ &H_4=\int^{-q_0}_0\frac{J_3(z)}{z}\,dz, &\qquad &I_4=\int^0_{\pi/2}iJ_4(q_0e^{i\alpha})\,d\alpha. \end{alignedat} $$

(3.21)

Applying the symmetries of the reflection coefficients to the jump matrices $J_j(z)$ shows that $H_1=-H_2$, $H_3=-H_4$, $I_1=-I_4$, and $I_2=-I_3$. It hence follows that

$$\delta=(-1)^{N_3+N_5}. $$

(3.22)

Corollary 3.1 (asymptotic phase difference).

The potential $\mathbf q(x,t)$ has the same boundary condition $\mathbf q_+=\mathbf q_-$ at infinity when $N_3+N_5$ is even. The potential $\mathbf q(x,t)$ has the opposite boundary condition $\mathbf q_+=-\mathbf q_-$ at infinity when $N_3+N_5$ is odd.

4. Reflectionless potential and soliton solutions

We now explicitly construct the potential $\mathbf q(x,t)$ in the case of a reflectionless potential, that is, $\rho_1(z)=\rho_2(z)=\rho_3(z)=0$. In this case, there is no jump across the contour $\Sigma$ in the RHP, allowing the solution $\mathbf q(x,t)$ to be found from a closed algebraic system (3.17).

Theorem 4.1.

In the case of a reflectionless potential, the solution $\mathbf q(x,t)$ of the fcmKdV equation (1.1) with NZBCs (1.2) can be expressed as

$$\mathbf q(x,t)=\frac{1}{\operatorname{det}\mathbf G} \begin{pmatrix} \operatorname{det}\mathbf G_1^{\mathrm{aug}} \\ \operatorname{det}\mathbf G_2^{\mathrm{aug}} \end{pmatrix},\qquad \mathbf G_k^{\mathrm{aug}}=\begin{pmatrix} q_{k+} &\mathbf Y^{\mathrm T} \\ \mathbf B_k &\mathbf G \end{pmatrix},\qquad k=1,2, $$

(4.1)

with the $(\mathcal N_1+\mathcal N_2)\times(\mathcal N_1+\mathcal N_2)$ matrix $\mathbf G=\mathbf I+\mathbf F$, $\mathbf B_k=(B_{k1},\dots,B_{k(\mathcal N_1+\mathcal N_2)})^{\mathrm T}$, $\mathbf Y=(Y_1,\dots,Y_{(\mathcal N_1+\mathcal N_2)})^{\mathrm T}$ and

$$Y_n=\begin{cases} iK_n, &n=1,\dots,\mathcal N_1, \\ iL_{n-\mathcal N_1}, &n=\mathcal N_1+1,\dots,\mathcal N_1+\mathcal N_2, \end{cases}$$

(4.2)

$$B_{kn}=\begin{cases} \dfrac{q_{k+}}{q_0}+\sum_{m=1}^{\mathcal N_1} \dfrac{iq_{k+}K_m^*}{k_m^*(k_n-k_m^*)}, \qquad n=1,\dots,\mathcal N_1, \vphantom{\Biggl\}} \\ \dfrac{(-1)^{\bar k}q_{\bar k+}}{q_0}+\sum_{m=1}^{\mathcal N_2} \dfrac{iq_{k+}L_m^*}{l_m^*(l_{n-\mathcal N_1}+\hat l_m^*-\hat l_{n-\mathcal N_1}-l_m^*)}, \vphantom{\Biggl\}}\\ n=\mathcal N_1+1,\dots,\mathcal N_1+\mathcal N_2, \end{cases}$$

(4.3)

$$F_{nj}=\begin{cases} \sum_{m=1}^{\mathcal N_1}\dfrac{K_m^*K_j}{(k_n-k_m^*)(k_m^*-k_j)}, \qquad n,j=1,\dots,\mathcal N_1, \vphantom{\biggl\}} \\ -\dfrac{iq_0L_{j-\mathcal N_1}}{l_{j-\mathcal N_1}(k_n+\hat l_{j-\mathcal N_1})} +\sum_{m=1}^{\mathcal N_1} \dfrac{K_m^*L_{j-\mathcal N_1}}{(k_n-k_m^*)(k_m^*-l_{j-\mathcal N_1})}\,, \vphantom{\Biggl\}} \\ \; n=1,\dots,\mathcal N_1,\quad j=\mathcal N_1+1,\dots,\mathcal N_1+\mathcal N_2, \\ \sum_{m=1}^{\mathcal N_2} \dfrac{L_m^*K_j}{(l_{n-\mathcal N_1}+\hat l_m^*-\hat l_{n-\mathcal N_1}-l_m^*)(l_m^*-k_j)}, \vphantom{\Biggl\}} \\ \; n=\mathcal N_1+1,\dots,\mathcal N_1+\mathcal N_2,\quad j=1,\dots,\mathcal N_1, \\ \sum_{m=1}^{\mathcal N_2} \dfrac{L_m^*L_{j-\mathcal N_1}} {(l_{n-\mathcal N_1}+\hat l_m^*-\hat l_{n-\mathcal N_1}-l_m^*)(l_m^*-l_{j-\mathcal N_1})}\,, \vphantom{\Biggl\}} \\ \; n,j=\mathcal N_1+1,\dots,\mathcal N_1+\mathcal N_2, \end{cases}$$

(4.4)

where $\bar k=3-k$.

Next, we focus on the soliton solutions corresponding to the six different types of discrete eigenvalues and explore their properties.

4.1. Type-I solitons

In the case $N_1=1$ and $N_2=N_3=N_4=N_5=N_6=0$, in general, we take the discrete eigenvalue and the proportionality constant in the form

$$\xi_1=iZ,\quad a_1=e^{\xi+i(m-1)\pi},\quad Z>q_0, \quad \xi\in\mathbb R, \quad m=0,1.$$

Substituting these quantities in the general formula (4.1) yields the explicit one-soliton solution

$$\mathbf q(x,t)=\frac{\cosh\chi+(-1)^m\operatorname{sech}(\ln(Z/q_0))\cosh(2\ln(Z/q_0))} {\cosh\chi+(-1)^m\operatorname{sech}(\ln(Z/q_0))}\,\mathbf q_+, $$

(4.5)

where

$$\chi=-\frac{q_0^6}{Z^3}t+\biggl(Z-\frac{q_0^2}{Z}\biggr)(3q_0^2t-x)+Z^3t+\xi.$$

The solutions are completely determined by $m$ and the vector $\mathbf q_+$. Some examples of such one-soliton solutions describing the dark–dark and bright–bright solitons are shown in Figs. 1 and 2. The soliton classification in this case is given in detail in Sec. 4.7.

4.2. Type-II solitons

In the case $N_2=1$ and $N_1=N_3=N_4=N_5=N_6=0$, in general, we take the soliton parameters in the form

$$\omega_1=Ze^{i\theta},\quad b_1=e^{\alpha+i\beta},\quad Z>q_0, \quad\theta\in\biggl(0,\frac{\pi}{2}\biggr) \cup\biggl(\frac{\pi}{2}\,,\pi\biggr), \quad \alpha,\beta\in\mathbb R.$$

From (4.1), we can obtain the breather–breather solutions of the fcmKdV equation. An example of such a solution is plotted in Fig. 3.

4.3. Type-III solitons

In the case $N_3=1$ and $N_1=N_2=N_4=N_5=N_6= 0$, in general, we take the discrete eigenvalue and proportionality constant in the form

$$\eta_1=iZ, \quad c_1=e^{\eta+i(m-1)\pi}, \quad Z>q_0, \quad \eta\in\mathbb R,\quad m=0,1.$$

Substituting these parameters in the general formula (4.1) generates the one-soliton solution

$$\begin{aligned} \, {} \mathbf q(x,t)=-\tanh\biggl(\chi+\ln\frac{Z\sqrt{Z^2+q_0^2}}{Z^2-q_0^2}\biggr) \mathbf q_+-(-1)^m\frac{\sqrt{Z^2+q_0^2}}{Z} \operatorname{sech} \biggl(\chi+\ln\frac{Z\sqrt{Z^2+q_0^2}}{Z^2-q_0^2}\biggr)\mathbf q_+^\perp, \end{aligned}$$

(4.6)

where

$$\chi=\frac{q_0^6}{Z^3}\,t+\frac{q_0^2}{Z}(3q_0^2t-x)+\eta.$$

The solutions are also completely determined by $m$ and $\mathbf q_+$. Some examples of such solitons describing the kink–bright–dark and kink–dark–bright solitons are given in Figs. 4 and 5. In this paper, the pair of a kink–bright soliton for the component $q_1(x,t)$ and a kink–dark soliton for the component $q_2(x,t)$ is simply referred to as the kink–bright–dark soliton, and so on. The soliton classification is given in detail in Sec. 4.7.

4.4. Type-IV solitons

In the case $N_4=1$ and $N_1=N_2=N_3=N_5=N_6=0$, in general, we take the soliton parameters in the form

$$z_1=Ze^{i\theta}, \quad d_1=e^{\alpha+i\beta}, \quad Z>q_0, \quad \theta\in\biggl(0,\frac{\pi}{2}\biggr)\cup\biggl(\frac{\pi}{2}\,,\pi\biggr), \quad \alpha,\beta\in\mathbb R.$$

From (4.1), we can obtain the W (type)–S (type) or the breather–breather solutions for the fcmKdV equation. Examples of such solutions are shown in Figs. 6 and 7.

4.5. Type-V solitons

In the case $N_5=1$ and $N_1=N_2=N_3=N_4=N_6=0$, in general, we take the discrete eigenvalue and proportionality constant in the form

$$\nu_1=iZ, \quad e_1=e^{\nu+i(m-1)\pi}, \quad Z>q_0, \quad \nu\in\mathbb R, \quad m=0,1.$$

Substituting these quantities in (4.1) yields the explicit one-soliton solution

$$\mathbf q(x,t)=-\tanh\biggl(\chi+\ln\frac{Z}{\sqrt{Z^2+q_0^2}}\biggr) \mathbf q_++(-1)^m\frac{\sqrt{Z^2+q_0^2}}{q_0} \operatorname{sech}\biggl(\chi+\ln\frac{Z}{\sqrt{Z^2+q_0^2}}\biggr)\mathbf q_+^\perp, $$

(4.7)

where

$$\chi=Z^3t+Z(3q_0^2t-x)+\nu.$$

The type-V solitons are similar to those of type-III, and are also determined by $m$ and $\mathbf q_+$. Some examples of such soliton solutions describing the kink–dark–dark and kink–bright–bright solitons are plotted in Figs. 8 and 9. The soliton classification is given in Sec. 4.7.

Fig. 1.

One dark–dark soliton of the fcmKdV equation with NZBCs obtained by taking $m=1$, $Z=3/2$, $\xi=\ln 2$, $\mathbf q_+=(\sqrt{3}/2,1/2)^{\mathrm T}$, and $q_0=1$.

Fig. 2.

One bright–bright soliton of the fcmKdV equation with NZBCs obtained by taking $m=0$, $Z=3/2$, $\xi=\ln 2$, $\mathbf q_+=(\sqrt{3}/2,1/2)^{\mathrm T}$, and $q_0=1$.

Fig. 3.

One breather–breather solution of the fcmKdV equation with NZBCs obtained by taking $\omega_1=2+i/2$, $\alpha=0$, $\beta=\pi/4$, $\mathbf q_+=(\sqrt{2}/2,\sqrt{2}/2)^{\mathrm T}$, and $q_0=1$.

Fig. 4.

One kink–bright–dark soliton of the fcmKdV equation with NZBCs obtained by taking $m=1$, $Z=3/2$, $\eta=\ln3$, $\mathbf q_+=(\sqrt{2}/2,\sqrt{2}/2)^{\mathrm T}$, and $q_0=1$.

Fig. 5.

One kink–dark–bright soliton of the fcmKdV equation with NZBCs obtained by taking $m=0$, $Z=3/2$, $\eta=\ln 3$, $\mathbf q_+=(\sqrt{2}/2,\sqrt{2}/2)^{\mathrm T}$, and $q_0=1$.

Fig. 6.

One W (type)–S (type) soliton of the fcmKdV equation with NZBCs obtained by taking $z_1=2+2i$, $\alpha=\beta=0$, $\mathbf q_+=(1, 0)^{\mathrm T}$, and $q_0=1$.

Fig. 7.

One breather–breather solution of the fcmKdV equation with NZBCs obtained by taking $z_1=1+i/2$, $\alpha=\beta=0$, $\mathbf q_+=(1,0)^{\mathrm T}$, and $q_0=1$.

Fig. 8.

One kink–dark–dark soliton of the fcmKdV equation with NZBCs obtained by taking $m=1$, $Z=3/2$, $\nu=\ln 2$, $\mathbf q_+=(-\sqrt{3}/2,1/2)^{\mathrm T}$, and $q_0=1$.

Fig. 9.

One kink–bright–bright soliton of the fcmKdV equation with NZBCs obtained by taking $m=0$, $Z=3/2$, $\nu=\ln 2$, $\mathbf q_+=(-\sqrt{3}/2,1/2)^{\mathrm T}$, and $q_0=1$.

Fig. 10.

One breather–breather solution of the fcmKdV equation with NZBCs obtained by taking $\zeta_1=3/2+i/4$, $\alpha=\beta=0$, $\mathbf q_+=(\sqrt{3}/2,1/2)^{\mathrm T}$, and $q_0=1$.

4.6. Type-VI solitons

In the case $N_6=1$ and $N_1=N_2=N_3=N_4=N_5=0$, in general, we take the soliton parameters in the form

$$\zeta_1=Ze^{i\theta}, \quad f_1=e^{\alpha+i\beta}, \quad Z>q_0, \quad \theta\in\biggl(0,\frac{\pi}{2}\biggr) \cup\biggl(\frac{\pi}{2}\,,\pi\biggr),\qquad \alpha,\beta\in\mathbb R.$$

From (4.1), we can obtain the breather–breather solution for the fcmKdV equation. An example of such a solution is shown in Fig. 10.

4.7. Discussions

First, the results for the soliton solutions admit the asymptotic phase difference, that is, only when $N_3+N_5$ is odd, there are kink solitons. The soliton classification of type-I, III, and V discrete eigenvalues in terms of $m$ and $\mathbf q_+$ is summarized in respective Tables 1, 2, and 3. In addition, the similarities between type-III and V solitons can be traced to their expressions in (4.6) and (4.7): their bright-soliton part always follows an orthogonal polarization to that of the dark-soliton part. And their solutions are any combinations of kink–dark or kink–bright solitons, where kink–dark solitons have rich complex soliton dynamics in Bose–Einstein condensates [38], [39] and nano-optical fibers [40]. Thus, we expect that our results could be beneficial to the development of the one-dimensional two-component Bose–Einstein condensate systems. Finally, type-II, IV, and VI solutions all have breather–breather solutions.

Table 1. Soliton classification of type I

Table 2. Soliton classification of type III

Table 3. Soliton classification of type V

Of course, (4.1) allows us to easily generate the multisoliton solutions by including any combinations of any number of the six types of solitons. For example, Fig. 11 shows the interaction between two dark–dark solitons, Fig. 12 shows the interaction between two bright–bright solitons, Fig. 13 shows the interaction between kink–dark–bright and W (type)–S (type) solitons, and Fig. 14 describes the interaction between kink–dark–bright and breather–breather solutions.

Fig. 11.

One two-dark–dark soliton of the fcmKdV equation with NZBCs obtained by taking $N_1=2$, $N_2=N_3=N_4=N_5=N_6=0$, $\xi_1=3i/2$, $\xi_2=4i/3$, $a_1=2$, $a_2=-3$, $\mathbf q_+=(\sqrt{3}/2,1/2)^{\mathrm T}$, and $q_0=1$.

Fig. 12.

One two-bright–bright soliton of the fcmKdV equation with NZBCs obtained by taking $N_1=2$, $N_2=N_3=N_4=N_5=N_6=0$, $\xi_1=3i/2$, $\xi_2=4i/3$, $a_1=-2$, $a_2=3$, $\mathbf q_+=(\sqrt{3}/2,1/2)^{\mathrm T}$, and $q_0=1$.

Fig. 13.

One kink–dark-bright, W (type)–S (type) soliton of the fcmKdV equation with NZBCs obtained by taking $N_3=N_4=1$, $N_1=N_2=N_5=N_6=0$, $\eta_1=2i$, $c_1=-1$, $z_1=1+2i$, $d_1=1$, $\mathbf q_+=(\sqrt{2}/2,\sqrt{2}/2)^{\mathrm T}$, and $q_0=1$.

Fig. 14.

One kink–dark-bright, breather–breather soliton of the fcmKdV equation with NZBCs obtained by taking $N_{5}=N_{6}=1$, $N_1=N_2=N_3=N_4=0$, $\nu_1=3i/2$, $e_1=1$, $\zeta_1=3/2+i$, $f_1=1$, $\mathbf q_+=(\sqrt{2}/2,\sqrt{2}/2)^{\mathrm T}$, and $q_0=1$.

5. Conclusions

In this paper, we applied the IST to the fcmKdV equation with NZBCs. This problem has three symmetries, resulting in six different types of discrete eigenvalues. Thus, six types of soliton solutions are obtained. Furthermore, the soliton classification for the types I, III, and V are constructed. Several two-soliton solutions having interesting structures are displayed.

We note that this paper is more involved than the defocusing counterpart in [19] due to the four fundamental domains of analyticity instead of two. Specifically, four new auxiliary eigenfunctions and a more complex RHP including four jump relations had to be formulated. In addition, although they both have three symmetries, the focusing case has more discrete eigenvalues, which leads to more diverse solutions. Within the framework of the IST method with NZBCs, we also note that the differences between the focusing Manakov system [41] and the fcmKdV equation are mainly manifested in four aspects: 1) the Jost eigenfunctions of the fcmKdV equation have three symmetries, with a total of $4N_1+8N_2+4N_3+8N_4+4N_5+8N_6$ discrete eigenvalues; 2) the fcmKdV equation has a simpler asymptotic phase difference, which is direct information to characterize solitons; 3) the potential of the fcmKdV equation is real, and the formula of its exact solutions is more compact; 4) the fcmKdV equation has richer soliton solutions and breathers, including dark–dark, bright–bright, W (type)–S (type), kink solitons, and breather–breather solutions.

Appendix A

A.1. The RHP solution

The coefficients $k_n$, $K_n$, and $l_n$, $L_n$ appearing in Theorem 3.1 are defined as follows:

$$\begin{aligned} \, &\text{for}\quad n=1,\dots,N_1 \nonumber \\ &\qquad k_n=\xi_n,\qquad K_n=A_n, \end{aligned}$$

(A.1a)

$$\begin{aligned} \, &\text{for}\quad n=N_1+1,\dots,2N_1 \nonumber \\[-2mm] &\qquad k_n=-\hat\xi^*_{n-N_1},\qquad K_n=-\frac{q_0^2}{(\xi_{n-N_1}^*)^2}A_{n-N_1}^*, \end{aligned}$$

(A.1b)

$$\begin{aligned} \, &\text{for}\quad n=2N_1+1,\dots,2N_1+N_2 \nonumber \\ &\qquad k_n=\omega_{n-2N_1}, \qquad K_n=B_{n-2N_1}, \end{aligned}$$

(A.1c)

$$\begin{aligned} \, &\text{for}\quad n=2N_1+N_2+1,\dots,2N_1+2N_2 \nonumber \\[-2mm] &\qquad k_n=-\widehat\omega_{n-2N_1-N_2}^*,\qquad K_n=-\frac{q_0^2}{(\omega_{n-2N_1-N_2}^*)^2}B_{n-2N_1-N_2}^*, \end{aligned}$$

(A.1d)

$$\begin{aligned} \, &\text{for}\quad n=2N_1+2N_2+1,\dots,2N_1+3N_2 \nonumber \\ &\qquad k_n=-\omega^*_{n-2N_1-2N_2},\qquad K_n=-B_{n-2N_1-2N_2}^*, \end{aligned}$$

(A.1e)

$$\begin{aligned} \, &\text{for}\quad n=2N_1+3N_2+1,\dots,\mathcal N_1 \nonumber \\ &\qquad k_n=\widehat\omega_{n-2N_1-3N_2},\qquad K_n=\frac{q_0^2}{\omega_{n-2N_1-3N_2}^2}B_{n-2N_1-3N_2}, \end{aligned}$$

(A.1f)

$$\begin{aligned} \, &\text{for}\quad n=1,\dots,N_3 \nonumber \\ &\qquad l_n=-\hat\eta_n,\qquad L_n=-\frac{il_n}{q_0}C_n, \end{aligned}$$

(A.2a)

$$\begin{aligned} \, &\text{for}\quad n=N_3+1,\dots,N_3+N_4 \nonumber \\ &\qquad l_n=-\hat z_{n-N_3},\qquad L_n=-\frac{il_n}{q_0}D_{n-N_3}, \end{aligned}$$

(A.2b)

$$\begin{aligned} \, &\text{for}\quad n=N_3+N_4+1,\dots,N_3+2N_4 \nonumber \\ &\qquad l_n=\hat z_{n-N_3-N_4}^*,\qquad L_n=\frac{il_n}{q_0}D_{n-N_3-N_4}^*, \end{aligned}$$

(A.2c)

$$\begin{aligned} \, &\text{for}\quad n=N_3+2N_4+1,\dots, N_3+2N_4+N_5 \nonumber \\ &\qquad l_n=\nu_{n-N_3-2N_4},\qquad L_n=E_{n-N_3-2N_4}, \end{aligned}$$

(A.2d)

$$\begin{aligned} \, &\text{for}\quad n=N_3+2N_4+N_5+1,\dots,N_3+2N_4+N_5+N_6 \nonumber \\ &\qquad l_n=\zeta_{n-N_3-2N_4-N_{5}},\qquad L_n=F_{n-N_3-2N_4-N_5}, \end{aligned}$$

(A.2e)

$$\begin{aligned} \, &\text{for}\quad n=N_3+2N_4+N_5+N_6+1,\dots,\mathcal N_2 \nonumber \\ &\qquad l_n=-\zeta_{n-N_3-2N_4-N_5-N_6}^*,\qquad L_n=-F_{n-N_3-2N_4-N_5-N_6}^*. \end{aligned}$$

(A.2f)

A.2. Trace formula

The scattering coefficients $a_{22}(z)$ and $b_{22}(z)$ has a jump across $\mathbb R$. We recall that $a_{22}(z)$ is analytic in $\mathbb C_-$ and has simple zeros

$$\{\eta_n^*,-\hat\eta_n^*\}_{n=1}^{N_3},\qquad \{z_n^*,-z_n,-\hat z_n^*,\hat z_n\}_{n=1}^{N_4},\qquad \{\nu_n^*, -\hat\nu_n^*\}_{n=1}^{N_5},\qquad \{\zeta_n^*,-\zeta_n,-\hat\zeta_n^*,\hat\zeta_n\}_{n=1}^{N_6},$$

while $b_{22}(z)$ is analytic in $\mathbb C_+$ and has simple zeros

$$\{\eta_n,-\hat\eta_n\}_{n=1}^{N_3},\qquad \{z_n,-z_n^*,-\hat z_n,\hat z_n^*\}_{n=1}^{N_4},\qquad \{\nu_n,-\hat\nu_n\}_{n=1}^{N_5},\qquad \{\zeta_n,-\zeta_n^*,-\hat\zeta_n,\hat\zeta_n^*\}_{n=1}^{N_6}.$$

We therefore define

$$\begin{aligned} \, \beta(z)={}&\delta b_{22}(z)\prod_{n=1}^{N_3} \frac{(z-\eta_n^*)(z+\hat\eta_n^*)}{(z-\eta_n)(z+\hat\eta_n)} \prod_{n=1}^{N_4}\frac{(z-z_n^*)(z+z_n)(z+\hat z_n^*)(z-\hat z_n)} {(z-z_n)(z+z_n^*)(z+\hat z_n)(z-\hat z_n^*)}\times{} \nonumber \\ &\times\prod_{n=1}^{N_5} \frac{(z-\nu_n^*)(z+\hat\nu_n^*)}{(z-\nu_n)(z+\hat\nu_n)} \prod_{n=1}^{N_6} \frac{(z-\zeta_n^*)(z+\zeta_n)(z+\hat\zeta_n^*)(z-\hat\zeta_n)} {(z-\zeta_n)(z+\zeta_n^*)(z+\hat\zeta_n)(z-\hat{\zeta}_n^*)},\quad z\in\mathbb C_+,\, \end{aligned}$$

(A.3a)

$$\begin{aligned} \, \beta(z)={}&\delta a_{22}(z)\prod_{n=1}^{N_3} \frac{(z-\eta_n)(z+\hat\eta_n)}{(z-\eta_n^*)(z+\hat\eta_n^*)} \prod_{n=1}^{N_4} \frac{(z-z_n)(z+z_n^*)(z+\hat z_n)(z-\hat z_n^*)} {(z-z_n^*)(z+z_n)(z+\hat z_n^*)(z-\hat z_n)}\times{} \nonumber \\ &\times\prod_{n=1}^{N_5} \frac{(z-\nu_n)(z+\hat\nu_n)}{(z-\nu_n^*)(z+\hat\nu_n^*)} \prod_{n=1}^{N_6} \frac{(z-\zeta_n)(z+\zeta_n^*)(z+\hat\zeta_n)(z-\hat\zeta_n^*)} {(z-\zeta_n^*)(z+\zeta_n)(z+\hat\zeta_n^*)(z-\hat\zeta_n)},\quad z\in\mathbb C_-.\, \end{aligned}$$

(A.3b)

It is easy to find that $\beta(z)\to 1$ as $z\to\infty$ and has no poles. Combining the fact that $\beta_+(z)\beta_-(z)=a_{22}(z)b_{22}(z)$ with the $2,2$ element of the identity $\mathbf B(z)\mathbf A(z)=\mathbf I$, we obtain that

$$\ln\beta_+(z)+\ln\beta_-(z)=-J_0(z),\qquad z\in\mathbb R, $$

(A.4)

where

$$\beta_\pm(x,t,z)=\lim_{\substack{\acute z\to z\\ \acute z\in\mathbb C_\pm}} \beta(x,t,\acute z),\qquad z\in\mathbb R,$$

(A.5a)

$$J_0(z)=\ln\biggl[1+\gamma(z)\rho_3(z)\rho_3(-z) +\frac{z^2\gamma(z)}{q_0^2}\rho_3(\hat z)\rho_3(-\hat z)\biggr].$$

(A.5b)

Then applying the Plemelj formula to (A.4) yields

$$\beta(z)=\exp\biggl[-\frac{1}{2\pi i}\int_{\mathbb R} \frac{J_0(\zeta)}{\zeta-z}\,d\zeta\biggr],\qquad z\in\mathbb C_+. $$

(A.6)

The first half of the proof is completed by substituting (A.6) in (A.3a).

We recall that $a_{11}(z)$, $b_{11}(z)$, $b_{33}(z)$, and $a_{33}(z)$ are respectively analytic in $D_1$, $D_2$, $D_3$, and $D_4$. For this reason, we can solve the problem by establishing a RHP as in Sec. 3.1. Based on the jump conditions, we see from the identity $\mathbf B(z)\mathbf A(z)=\mathbf I$ that

$$\begin{aligned} \, \begin{aligned} \, &b_{31}(z)a_{13}(z)+b_{32}(z)a_{23}(z)+b_{33}(z)a_{33}(z)&=1, \\ &b_{11}(z)a_{11}(z)+b_{12}(z)a_{21}(z)+b_{13}(z)a_{31}(z)&=1, \\ &b_{22}(z)=a_{11}(z)a_{33}(z)-a_{31}(z)a_{13}(z), \\ &a_{22}(z)=b_{11}(z)b_{33}(z)-b_{31}(z)b_{13}(z). \end{aligned} \end{aligned}$$

It is worth noting that $b_{22}(z)$ and $a_{22}(z)$ are involved in the last two relations. Thus, the $a_{11}(z)$ trace formula is related to the type-III and IV discrete eigenvalues.

Recalling the definition of the oriented contour $\Sigma$, we define

$$\begin{aligned} \, \tilde{\beta}(z)={}&a_{11}(z)\prod_{n=1}^{N_1} \frac{(z-\xi_n^*)(z+\hat\xi_n)}{(z-\xi_n)(z+\hat\xi_n^*)} \prod_{n=1}^{N_2} \frac{(z-\omega_n^*)(z+\omega_n)(z+\widehat\omega_n)(z-\widehat\omega_n^*)} {(z-\omega_n)(z+\omega_n^*)(z+\widehat\omega_n^*)(z-\widehat\omega_n)} \prod_{n=1}^{N_3}\frac{z+\hat\eta_n^*}{z+\hat\eta_n}\times{} \nonumber \\ &\times\prod_{n=1}^{N_4} \frac{(z+\hat z_n^*)(z-\hat z_n)}{(z+\hat z_n)(z-\hat z_n^*)} \prod_{n=1}^{N_5}\frac{z-\nu_n^*}{z-\nu_n} \prod_{n=1}^{N_6} \frac{(z-\zeta_n^*)(z+\zeta_n)}{(z-\zeta_n)(z+\zeta_n^*)},\quad z\in D_1, \end{aligned}$$

(A.7a)

$$\begin{aligned} \, \tilde\beta(z)={}&b_{11}(z)\prod_{n=1}^{N_1} \frac{(z-\xi_n)(z+\hat\xi_n^*)}{(z-\xi_n^*)(z+\hat\xi_n)} \prod_{n=1}^{N_2} \frac{(z-\omega_n)(z+\omega_n^*)(z+\widehat\omega_n^*)(z-\widehat\omega_n)} {(z-\omega_n^*)(z+\omega_n)(z+\widehat\omega_n)(z-\widehat\omega_n^*)} \prod_{n=1}^{N_3}\frac{z+\hat\eta_n}{z+\hat\eta_n^*}\times{} \nonumber \\ &\times\prod_{n=1}^{N_4} \frac{(z+\hat z_n)(z-\hat z_n^*)}{(z+\hat z_n^*)(z-\hat z_n)} \prod_{n=1}^{N_5}\frac{z-\nu_n}{z-\nu_n^*} \prod_{n=1}^{N_6} \frac{(z-\zeta_n)(z+\zeta_n^*)}{(z-\zeta_n^*)(z+\zeta_n)},\quad z\in D_2, \end{aligned}$$

(A.7b)

$$\begin{aligned} \, \tilde\beta(z)={}&\delta b_{33}(z)\prod_{n=1}^{N_1} \frac{(z-\xi_n^*)(z+\hat\xi_n)}{(z-\xi_n)(z+\hat\xi_n^*)} \prod_{n=1}^{N_2} \frac{(z-\omega_n^*)(z+\omega_n)(z+\widehat\omega_n)(z-\widehat\omega_n^*)} {(z-\omega_n)(z+\omega_n^*)(z+\widehat\omega_n^*)(z-\widehat\omega_n)} \prod_{n=1}^{N_3}\frac{z-\eta_n}{z-\eta_n^*}\times{} \nonumber \\ &\times\prod_{n=1}^{N_4}\frac{(z+z_n^*)(z-z_n)}{(z+z_n)(z-z_n^*)} \prod_{n=1}^{N_5}\frac{z+\hat{\nu}_n}{z+\hat{\nu}_n^*} \prod_{n=1}^{N_6} \frac{(z+\hat{\zeta}_n)(z-\hat{\zeta}_n^*)} {(z+\hat{\zeta}_n^*)(z-\hat{\zeta}_n)},\quad z\in D_3, \end{aligned}$$

(A.7c)

$$\begin{aligned} \, \tilde\beta(z)={}&\delta a_{33}(z)\prod_{n=1}^{N_1} \frac{(z-\xi_n)(z+\hat\xi_n^*)}{(z-\xi_n^*)(z+\hat\xi_n)} \prod_{n=1}^{N_2} \frac{(z-\omega_n)(z+\omega_n^*)(z+\widehat\omega_n^*)(z-\widehat\omega_n)} {(z-\omega_n^*)(z+\omega_n)(z+\widehat\omega_n)(z-\widehat\omega_n^*)} \prod_{n=1}^{N_3}\frac{z-\eta_n^*}{z-\eta_n}\times{} \nonumber \\ &\times\prod_{n=1}^{N_4}\frac{(z+z_n)(z-z_n^*)}{(z+z_n^*)(z-z_n)} \prod_{n=1}^{N_5}\frac{z+\hat\nu_n^*}{z+\hat\nu_n} \prod_{n=1}^{N_6} \frac{(z+\hat\zeta_n^*)(z-\hat\zeta_n)} {(z+\hat\zeta_n)(z-\hat\zeta_n^*)},\quad z\in D_4. \end{aligned}$$

(A.7d)

Thus, $\tilde\beta(z)\to 1$ as $z\to\infty$ and has no poles. Also, the following jump conditions hold:

$$\ln\tilde\beta_+(z)+\ln\tilde\beta_-(z)=J(z),\quad z\in\Sigma, $$

(A.8)

where the jump matrices $J_j(z)=J(z)|_{z\in\Sigma_j}$ are

$$J_1(z)=-\ln\biggl[1+\frac{1}{\gamma(z)}\rho_1(z)\rho_1(-z) +\rho_2(z)\rho_2(-z)\biggr], \qquad z\in\Sigma_1,$$

(A.9a)

$$J_2(z)=\frac{1}{2\pi i} \int_{\mathbb R}\frac{J_0(\zeta)}{\zeta-z}\,d\zeta -\ln[1-\rho_2(-z)\rho_2(\hat z)], \qquad z \in \Sigma_2,$$

(A.9b)

$$J_3(z)=-\ln\biggl[1+\frac{q_0^2}{z^2\gamma(z)}\rho_1(\hat z)\rho_1(-\hat z) +\rho_2(\hat z)\rho_2(-\hat z)\biggr], \qquad z\in\Sigma_3,$$

(A.9c)

$$J_4(z)=-\frac{1}{2\pi i} \int_{\mathbb R}\frac{J_0(\zeta)}{\zeta-z}\,d\zeta -\ln[1-\rho_2(-\hat z)\rho_2(z)], \qquad z\in\Sigma_4.$$

(A.9d)

Applying the Plemelj formula to (A.8), we obtain the solutions of the RHP in the form

$$\tilde\beta(z)=\exp\biggl[\frac{1}{2\pi i} \int_\Sigma\frac{J(\zeta)}{\zeta-z}\,d\zeta\biggr],\qquad z\in D_1\cup D_3. $$

(A.10)

Substituting the above result in (A.7a) yields Eq. (3.19a).