The study of the behavior of stresses in elastic materials with temperature-dependent properties is of importance for many engineering applications. Some elastic materials change their mechanical moduli under the influence of temperature. In these cases, the application of Hookean strain-stress relations is not appropriate to describe stress distributions. The theory of thermoelasticity of materials with temperature-dependent properties seems to be the most adjusted for modeling of the interaction between mechanical and thermal fields. One of the first researchers who considerably developed the theoretical basis for the investigation of elastic bodies with temperature-dependent modulus was J. L. Nowiński (see [1–3] and the monograph [4]). Many experimental results on the determination of the mechanical properties of solids as functions of temperature are presented in the monograph [5] (mainly for metals), as well as in the papers [6–11]. Some theoretical investigations of solid mechanics with temperature-dependent properties can be found in [12–15].

In the present paper, we consider the antiplane strain state for an elastic layer with temperature-dependent properties. The boundary planes are assumed to be kept at given constant temperatures, which leads to a linear temperature distribution in the considered layer. The lower boundary plane is loaded by a concentrated force and the upper boundary plane is free of loading. The shear modulus μ as a function of temperature θ is taken into account in the form of a linear function. The assumption connected with the temperature dependence of the shear modulus leads to the problem of FGM layer in which the material properties continuously depend on the space variables. It can be observed that, in the case of classical thermoelasticity for homogeneous isotropic bodies in the antiplane strain state, the distributions of stresses are independent of temperature, unlike the analyzed problem.

Formulation and Solution of the Problem

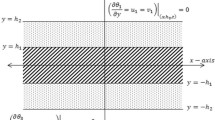
Consider an isotropic elastic layer with thickness h. Let (x 1, x 2, x 3) be a Cartesian coordinate system such that the planes x 2 = 0 and x 2 = h are boundaries of the body, and the 0x 3 -axis is perpendicular to the boundaries. Let the lower and upper boundary planes be kept at given constant temperatures θ0 and θ1, respectively.

Moreover, the investigated layer is loaded by forces linearly distributed along the 0x 3 -axis and concentrated forces with intensity P acting in the direction of the 0x 3 -axis. The shear modulus μ is assumed to be a function of temperature θ of the following form:

$$ \mu \left( \theta \right)={\mu_0}\left( {1-A\theta } \right), $$
(1)

where μ0 and A are constant. The form of the dependence of shear modulus (1) agrees with the experimental results presented in [5].

The assumptions made above lead to the antiplane strain state described by the displacement vector u(x 1, x 2) = (0, 0, u 3 (x 1, x 2)), and the considered problem is stationary and independent of x 3. The temperature θ = θ (x 1, x 2) satisfies the following equation:

$$ \frac{{{\partial^2}\theta }}{{\partial x_1^2}}+\frac{{{\partial^2}\theta }}{{\partial x_2^2}}=0,\quad {x_1}\in R,\quad {x_2}\in \left( {0,h} \right), $$

and boundary conditions

$$ \theta \left( {{x_1},0} \right)={\theta_0},\quad \theta \left( {{x_1},h} \right)={\theta_1},\quad {x_1}\in R, $$

causing the distribution of temperature

$$ \theta \left( {{x_1},{x_2}} \right)=\frac{{\left( {{\theta_1}-{\theta_0}} \right){x_2}}}{h}+{\theta_0},\quad {x_1}\in R,\quad {x_2}\in \left\langle {0,h} \right\rangle . $$
(2)

It follows from Eqs. (1) and (2) that

$$ \mu \left( {{x_1},{x_2}} \right)={\mu_0}\left( {{\alpha_0}+{\alpha_1}{x_2}} \right),\quad {\alpha_0}=1-A{\theta_0},\quad {\alpha_1}=-\frac{{A\left( {{\theta_1}-{\theta_0}} \right)}}{h}. $$
(3)

The stress state is described by the nonzero components σ13 and σ23 of the form

$$ {\sigma_{13 }}\left( {{x_1},{x_2}} \right)={\mu_0}\left( {{\alpha_0}+{\alpha_1}{x_2}} \right)\frac{{\partial {u_3}}}{{\partial {x_1}}},\quad {\sigma_{23 }}\left( {{x_1},{x_2}} \right)={\mu_0}\left( {{\alpha_0}+{\alpha_1}{x_2}} \right)\frac{{\partial {u_3}}}{{\partial {x_2}}}. $$
(4)

The equilibrium equation in the case of stresses given by relations (4) can be written as

$$ \frac{{{\partial^2}{u_3}}}{{\partial x_1^2}}+\frac{{{\partial^2}{u_3}}}{{\partial x_2^2}}+\frac{{{\alpha_1}}}{{{\alpha_0}+{\alpha_1}{x_2}}}\frac{{\partial {u_3}}}{{\partial {x_2}}}=0,\quad {x_1}\in R,\quad {x_2}\in \left( {0,h} \right). $$
(5)

The boundary conditions have the form

$$ {\sigma_{23 }}\left( {{x_1},0} \right)=P\delta \left( {{x_1}} \right),\quad {\sigma_{23 }}\left( {{x_1},h} \right)=0,\quad {x_1}\in R, $$
(6)

where δ(∙) is the Dirac delta function. We now use the Fourier integral transform [16] with respect to variable x 1 and denote

$$ {{\tilde{u}}_3}\left( {s,{x_2}} \right)=\frac{1}{{\sqrt{{2\pi }}}}\int\limits_{{-\infty}}^{\infty } {{u_3}\left( {{x_1},{x_2}} \right){e^{{-is{x_1}}}}d{x_1}} . $$

Thus, it follows from Eq. (5) that

$$ \frac{{{d^2}{{\tilde{u}}_3}\left( {s,{x_2}} \right)}}{{dx_2^2}}+\frac{{{\alpha_1}}}{{{\alpha_0}+{\alpha_1}{x_2}}}\frac{{d{{\tilde{u}}_3}\left( {s,{x_2}} \right)}}{{d{x_2}}}-{s^2}{{\tilde{u}}_3}\left( {s,{x_2}} \right)=0. $$
(7)

The linear ordinary second-order differential equation (7) is reduced to the form

$$ \frac{{{d^2}{{\tilde{u}}_3}}}{{d{\omega^2}}}+\frac{1}{\omega}\frac{{d{{\tilde{u}}_3}}}{{d\omega }}-\frac{{{s^2}}}{{\alpha_1^2}}{{\tilde{u}}_3}=0, $$
(8)

where

$$ \omega ={\alpha_0}+{\alpha_1}{x_2}. $$
(9)

The general solution of Eq. (8) can be written as [17]

$$ {{\tilde{u}}_3}\left( {s,\omega } \right)={C_1}{J_0}\left( {\frac{{i\omega s}}{{{\alpha_1}}}} \right)+{C_2}{Y_0}\left( {\frac{{i\omega s}}{{{\alpha_1}}}} \right) $$
(10)

where C 1 and C 2 are constants and J 0 (x) and Y 0 (x) are Bessel functions of the first and the second kind, respectively. In view of relations [8]

$$ {J_0}\left( {ix} \right)={I_0}(x),\quad {Y_0}\left( {ix} \right)={K_0}(x),\quad x\in R, $$

where I 0 (∙) and K 0 (∙) are modified Bessel functions, and relations (9) and (10), the general solution of equation (7) can be written as follows:

$$ {{\tilde{u}}_3}\left( {s,{x_2}} \right)={C_1}{I_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]+{C_2}{K_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]. $$
(11)

The constants C 1 and C 2 are determined from the boundary conditions (6). By using Eqs. (4), (6), (11) and the following relations [19]:

$$ \frac{d}{dz }{I_0}(z)={I_1}(z),\quad \frac{d}{dz }{K_0}(z)=-{K_1}(z), $$
(12)

where I 1(x) and K 1(x) are modified Bessel functions, we conclude that a 1 and a 2 must satisfy the following system of algebraic equations:

$$ {a_1}{I_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]-{a_2}{K_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]=0,\quad {a_1}{I_1}\left( {\frac{{s{\alpha_0}}}{{{\alpha_1}}}} \right)-{a_2}{K_1}\left( {\frac{{s{\alpha_0}}}{{{\alpha_1}}}} \right)=\frac{P}{{\sqrt{{2\pi }}s{\mu_0}{\alpha_0}}}. $$
(13)

where ω* = α0 + α1 h.

In view of Eqs. (13) and (11), by applying the inverse Fourier transformation [16], we rewrite the displacement u 3 in the following form:

$$ {u_3}\left( {{x_1},{x_2}} \right)=-\frac{P}{{\pi {\alpha_0}{\mu_0}}}\int\limits_0^{\infty } {\frac{1}{sW}\left\{ {{K_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{I_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]+{I_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{K_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]} \right\}\cos \left( {s{x_1}} \right)ds,} $$
(14)

where

$$ W={I_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{K_1}\left( {\frac{s}{{{\alpha_1}}}{\alpha_0}} \right)-{K_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{I_1}\left( {\frac{{s{\alpha_0}}}{{{\alpha_1}}}} \right).. $$

The components of stresses σ13 and σ23 are computed from relations (4) and (14).

Substituting (14) in (4), we find

$$ {\sigma_{13 }}\left( {{x_1},{x_2}} \right)=\frac{{P\omega }}{{\pi {\alpha_0}}}\int\limits_0^{\infty } {\frac{1}{W}\left\{ {{K_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{I_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]+{I_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{K_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]} \right\}\sin \left( {s{x_1}} \right)ds,} $$
(15)
$$ {\sigma_{23 }}\left( {{x_1},{x_2}} \right)=\frac{{P\omega }}{{\pi {\alpha_0}}}\int\limits_0^{\infty } {\frac{1}{W}\left\{ {-{K_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{I_1}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]+{I_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{K_1}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]} \right\}\cos \left( {s{x_1}} \right)ds.} $$
(16)

Relations (14)–(16) give the fundamental solution (Green’s function) for the considered problem in the integral form.

From the viewpoint of mechanics, it is necessary to study the singularities of stresses at the point of action of the concentrated forces. For this purpose, we analyze the asymptotic behavior of the integrand functions in (15) and (16).

Singularities of Stresses

By using relations (see [19])

$$ {I_{\nu }}(x)\mathop{\approx}\limits_{{x\to \infty }}\frac{{{e^x}}}{{\sqrt{{2\pi x}}}},\quad {K_{\nu }}(x)\mathop{\approx}\limits_{{x\to \infty }}\sqrt{{\frac{\pi }{2x }}}{e^{-x }},\quad {I_0}(x)\mathop{\approx}\limits_{{x\to 0}}1, $$
$$ {I_1}(x)\mathop{\approx}\limits_{{x\to 0}}\frac{1}{2}x,\quad {K_1}(x)\mathop{\approx}\limits_{{x\to 0}}\frac{1}{x},\quad {K_0}(x)\mathop{\approx}\limits_{{x\to 0}}\ln \frac{2}{x}, $$
(17)

and Eq.(14), we conclude that

$$ W\mathop{\approx}\limits_{{s\to 0}}\frac{{{\alpha_1}h\left( {2{\alpha_0}+{\alpha_1}h} \right)}}{{2{\alpha_0}\left( {{\alpha_0}+{\alpha_1}h} \right)}}=\mathrm{const},\quad W\mathop{\approx}\limits_{{s\to \infty }}\frac{{{\alpha_1}}}{{\sqrt{{{\alpha_0}\left( {{\alpha_0}+{\alpha_1}h} \right)}}}}\frac{{\sinh \left( {sh} \right)}}{s}. $$
(18)

Denote

$$ {L_0}\equiv {K_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{I_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]+{I_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{K_0}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right], $$
$$ {L_1}\equiv -{K_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{I_1}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]+{I_1}\left[ {\frac{{s{\omega^{*}}}}{{{\alpha_1}}}} \right]{K_1}\left[ {\frac{{s\omega }}{{{\alpha_1}}}} \right]. $$
(19)

Thus, by using (17) and (18) we obtain

$$ \frac{{{L_0}}}{W}\mathop{\approx}\limits_{{s\to \infty }}\sqrt{{\frac{{{\alpha_0}}}{\omega }}}{e^{{-s{x_2}}}},\quad \frac{{{L_1}}}{W}\mathop{\approx}\limits_{{s\to \infty }}\sqrt{{\frac{{{\alpha_0}}}{\omega }}}{e^{{-s{x_2}}}}. $$
(20)

In view of Eqs. (15), (16), (19), and (20), the singularities of the stress components can be represented in the form

$$ {\sigma_{13 }}\left( {{x_1},{x_2}} \right)=\frac{P}{\pi}\sqrt{{\frac{\omega }{{{\alpha_0}}}}}\frac{{{x_1}}}{{x_1^2+x_2^2}}+0(1),\quad {\sigma_{23 }}\left( {{x_1},{x_2}} \right)=\frac{P}{\pi}\sqrt{{\frac{\omega }{{{\alpha_0}}}}}\frac{{{x_2}}}{{x_1^2+x_2^2}}+0(1). $$
(21)

Equation (21) now implies that the order of singularities of the stress components σ13 and σ23 is the same as in the elastic homogeneous isotropic layer. However, the difference is observed in the coefficients of singularities.

The integrals in expressions (15) and (16) for the stresses σ13 and σ23 can be found numerically. For this purpose, we use the following dimensionless variables:

$$ {{{\overset{\scriptscriptstyle\smile}{x}}}_1}=\frac{{{x_1}}}{h},\quad {{{\overset{\scriptscriptstyle\smile}{x}}}_2}=\frac{{{x_2}}}{h},\quad {\overset{\scriptscriptstyle\smile}{s}}=sh, $$

The physical data taken into account are the same as in [20], where the copper material is investigated. In Fig. 1, we observe the influence of the parameter A and the difference between the boundary temperatures θ0 and θ1 on the stresses θ23. The dimensionless stresses σ23 at the point \( {{{\overset{\scriptscriptstyle\smile}{x}}}_1} \) = 0.0, \( {{{\overset{\scriptscriptstyle\smile}{x}}}_2} \) = 0.1 as a function of the ratio θ1/θ0 are presented in Fig. 1 for three values of the parameter A. It is easy to see that the component of stresses is a linear function of the ratio θ1/θ0 and, for θ1/θ0, the solutions are reduced to the case of a homogeneous body with constant material properties.

Fig. 1
figure 1

Dimensionless stresses σ23(\( {{{\overset{\scriptscriptstyle\smile}{x}}}_1},{{{\overset{\scriptscriptstyle\smile}{x}}}_2} \))h/P as a function of the parameter θ1/θ0 for θ0 = 819°K, \( {{{\overset{\scriptscriptstyle\smile}{x}}}_1} \) = 0.0, and \( {{{\overset{\scriptscriptstyle\smile}{x}}}_2} \) = 0.1: (1) A = 0.00051K−1; (2) 0.00025 K−1; (3) 0.000125 K−1.

Full size image

In Fig. 2 the cases A = 0 are adequate for the homogeneous elastic body. Small variations of the stresses σ23 with respect to the boundary temperatures near the boundary plane loaded by a concentrated force can be observed for the following three values of A:A = 0.00051K−1, A = 0.00025 K−1, and A = 0.

Fig. 2
figure 2

Dimensionless stresses as a function of the parameter A:(a) σ23 h/P; (b) σ13 h/P:θ0 = 819°K, θ1 = 0.5θ0, \( {{{\overset{\scriptscriptstyle\smile}{x}}}_2} \) = 0.25.

Full size image

The stresses σ13 change their sign at \( {{{\overset{\scriptscriptstyle\smile}{x}}}_1} \) = 0 (the curve representing σ13 is antisymmetric but the curve representing σ23 is symmetric). The maximal values of σ23 are attained at the point of action of the concentrated force.

Conclusions

The problem of distribution of stresses in the thermoelastic layer with temperature-dependent properties loaded by a concentrated force in the boundary plane is solved under the conditions of antiplane strain state. It is assumed that the shear modulus is a linear function of temperature. The obtained results for stresses at the point of action of the concentrated force are characterized by the singularity of the same order as in the case of an isotropic homogeneous body with constant material properties. The singularities observed for the two mentioned materials differ by the singularity coefficients. Moreover, we can emphasize that, for the case of ordinary elasticity (when the shear modulus is constant), the boundary temperatures affect the stresses σ13 and σ23. In the considered problem of the layer with temperature-dependent properties, the temperature is coupled with the displacement u 3 .