Free vibration frequency of thick FGM spherical shells with simply homogeneous equation by using TSDT

Abstract

The effects of third-order shear deformation theory (TSDT) and varied shear correction coefficient on the free vibration frequency of thick functionally graded material (FGM) spherical shells are investigated with simply homogeneous equation under thermal environment. The nonlinear coefficient term of displacement field of TSDT is included to derive the simply homogeneous equation with the assumed reasonable simplifications in the elements of homogeneous matrix under free vibration of thick FGM spherical shells. The determinant of the coefficient matrix in dynamic equilibrium differential equations under free vibration can be represented into the simply five-degree polynomial equation; thus, the natural frequency can be obtained. For the preliminary FGM spherical shell study, the effects of nonlinear coefficient term and meridional angle on the varied shear correction coefficient calculation are not considered. The calculated values of shear correction coefficient are increasing with the increase in power law index. Three parametric effects of nonlinear coefficient term, environment temperature and power law index on the frequency of thick FGM spherical shells are computed and investigated for a given meridional angle in the spherical shells. Data in underestimated or overestimated are also investigated in the frequency parameters under free vibration with and without the effects of nonlinear coefficient term, respectively.

1 Introduction

There are some investigations with shear deformation effect and experimental studies in the shells. Lei and Tong [1] presented the low-velocity impact of graphene-reinforced composite functionally graded material (FGM) cylindrical shells by using the Reddy’s third-order shear deformation theory (TSDT). Biswal and Mohanty [2] presented the free vibration of multilayer sandwich spherical shell panels including the elastic face layers and viscoelastic material core layers by using the first-order shear deformation theory (FSDT); some effects on the result of the natural frequencies are investigated, e.g., thickness of the core layers, viscoelastic material and aspect ratios. Ghavanloo et al. [3] used the experimental method and the numerical method to study the free vibrations in the momentless spherical shell with Legendre functions. Hasrati et al. [4] used the variational differential quadrature (VDQ) technique and the six-parameter shell theory of displacement to obtain the numerical results for the nonlinear free vibration of spherical shells. Huang et al. [5] presented the wave superposition modeling method to study the vibration of an elastic spherical shell considering the effects of fluid–structure interaction vibration, acoustic radiation and propagations. Sayyad and Ghugal [6] presented the results of static bending and free vibration by using a generalized higher-order shell theory for the laminated spherical shells. Li et al. [7] presented the free vibration analysis of combined paraboloidal, cylindrical and spherical shells based on a semi-analytical approach with Flügge thin shell theory. Lee [8] presented the matched Fourier–Chebyshev expansions and used the free vibration analyses for the joined spherical cylindrical shells. Duc et al. [9] presented nonlinear vibration analyses of the sigmoid power law distribution in functionally graded material (S-FGM) shallow spherical shells including the effects of elastic foundations and environment temperature. Sepiani et al. [10] presented the numerical free vibration and buckling results by using the FSDT formulation for the FGM shells without considering the thermal effect. The above investigations did not consider the varied effects of shear correction coefficient on the frequency results.

The author also has some free vibration frequency computational experience in the composite FGM circular cylindrical shells. Hong [11] used the thin displacement approach of Love’s theory to present the frequency results for the thin laminated magnetostrictive FGM shells with the value effects of velocity feedback and control gain subjected to thermal vibration. It is interesting to investigate the natural frequency in the TSDT approach of thick FGM spherical shells under free vibration with simply homogeneous equation and four edges in simply supported boundary conditions. Three parametric effects of nonlinear coefficient c₁ term, environment temperature and power law index on the natural frequency of thick FGM spherical shells are investigated under the angle of the direction of z axis and the direction of radius in the spherical shells. The main novelty of this study is to provide the frequency solutions of free vibration in FGM thick spherical shells by considering the varied effects of shear correction coefficient and nonlinear coefficient c₁ term of TSDT.

2 Formulation

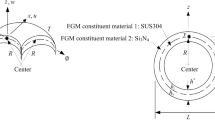
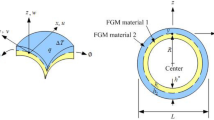
Two-material thick FGM spherical shells in thermal environment are shown in Fig. 1 with inner layer thickness h₁ of FGM material 1 and outer layer thickness h₂ of FGM material 2. A point in the coordinates of spherical axes $\left( {r, \theta , \emptyset } \right)$ corresponds to Cartesian coordinates $\left( {x, y, z} \right)$, in which r is the radius, $\theta$ denotes the angle of circumferential direction, ∅ denotes the meridional angle of direction of z axis and the direction of radius in the spherical shells. The material properties of power law function of FGM spherical shells are considered with Young’s modulus E_fgm of FGM in standard variation form of power-law index R_n; the others are assumed in the simple average form [12]. The properties P_i of individual constituent material of FGM spherical shells are functions of environment temperature T that can be provided as follows [13]:

$$ P_{i} = P_{0} (P_{ - 1} T^{ - 1} + 1 + P_{1} T + P_{2} T^{2} + P_{3} T^{3} ), $$

(1)

where $P_{0} ,\,P_{ - 1} ,\,P_{1} ,\,P_{2}$ and P₃ are the temperature coefficients.

Fig. 1

Two-material thick FGM spherical shell

The time dependent nonlinear displacements u, v and w of thick FGM spherical shells under vibration for a given ∅ angle are assumed in the nonlinear coefficient c₁ term of TSDT equations [14] as follows:

$$ \begin{aligned} u & = u_{0} \left( {x,\theta ,t} \right) + z\phi_{x} \left( {x,\theta ,t} \right) - c_{1} z^{3} \left( {\phi_{x} + \frac{\partial w}{\partial x}} \right), \\ v & = v_{0} \left( {x,\theta ,t} \right) + z\phi_{\theta } \left( {x,\theta ,t} \right) - c_{1} z^{3} \left( {\phi_{\theta } + \frac{\partial w}{R\partial \theta }} \right), \\ w & = w\left( {x,\theta ,t} \right) \\ \end{aligned} $$

(2)

where u₀ and v₀ are the tangential displacements in the in-surface coordinates x and $\theta$ axes direction, respectively, w is the transverse displacement in the out-of-surface coordinates z axis direction of the middle plane of shells, $\phi_{x}$ and $\phi_{\theta }$ are the shear rotations, R is the radius of middle surface of FGM spherical shells, and t is the time. Coefficient for $c_{1} = 4/(3h^{*2} )$ is given as in TSDT approach, in which $h^{*}$ is the total thickness of spherical shells.

The constitutive equations of normal stresses ($\sigma_{xx}$ and $\sigma_{\theta \theta }$) and the shear stresses ($\sigma_{x\theta }$, $\sigma_{\theta z}$ and $\sigma_{xz}$) in the thick FGM spherical shells for a given ∅ angle and temperature difference $\Delta T$ can be obtained as function of stiffness and strains as follows [15, 16]:

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}_{\left( k \right)} & = \left[ {\begin{array}{*{20}c} {\bar{Q}_{11} } & {\bar{Q}_{12} } & {\bar{Q}_{16} } \\ {\bar{Q}_{12} } & {\bar{Q}_{22} } & {\bar{Q}_{26} } \\ {\bar{Q}_{16} } & {\bar{Q}_{26} } & {\bar{Q}_{66} } \\ \end{array} } \right]_{\left( k \right)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} - \alpha_{x} \Delta T} \\ {\varepsilon_{\theta } - \alpha_{\theta } \Delta T} \\ {\varepsilon_{x\theta } - \alpha_{x\theta } \Delta T} \\ \end{array} } \right\}_{\left( k \right)} , \\ \left\{ {\begin{array}{*{20}c} {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ \end{array} } \right\}_{\left( k \right)} & = \left[ {\begin{array}{*{20}c} {\bar{Q}_{44} } & {\bar{Q}_{45} } \\ {\bar{Q}_{45} } & {\bar{Q}_{55} } \\ \end{array} } \right]_{\left( k \right)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{\theta z} } \\ {\varepsilon_{xz} } \\ \end{array} } \right\}_{\left( k \right)} , \\ \end{aligned} $$

(3)

where $\alpha_{x}$ and $\alpha_{\theta }$ are the coefficients of thermal expansion, $\alpha_{x\theta }$ is the coefficient of thermal shear, $\bar{Q}_{ij}$ is the stiffness of FGM shells. $\varepsilon_{x}$, $\varepsilon_{\theta }$ and $\varepsilon_{x\theta }$ are the in-plane strains, not negligible, and $\varepsilon_{\theta z}$ and $\varepsilon_{xz}$ are the shear strains. $\Delta T$ is the temperature difference between the FGM shell and curing area that can be considered about thermal loads and is given in the formula as follows:

$$ \Delta T = T_{0} \left( {x,\theta ,t} \right) + \frac{z}{{h^{*} }}T_{1} \left( {x,\theta ,t} \right), $$

(4)

where $T_{0}$ and $T_{1}$ are the temperature parameters.

The dynamic equations of motion with TSDT for a small element in the thick FGM spherical shells under vibration for a given ∅ angle can be obtained as follows [6] [17]:

$$ \frac{{\partial N_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial N_{x\theta } }}{\partial \theta } = I_{0} \frac{{\partial^{2} u_{0} }}{{\partial t^{2} }} + J_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} - c_{1} I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{\partial w}{\partial x}} \right), $$

$$ \begin{aligned} & \frac{{\partial N_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial N_{\theta \theta } }}{\partial \theta } = I_{0} \frac{{\partial^{2} v_{0} }}{{\partial t^{2} }} + J_{1} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }} - c_{1} I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{\partial w}{R\partial \theta }} \right), \\ & \frac{{\partial \bar{Q}_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial \bar{Q}_{\theta } }}{\partial \theta } + c_{1} \left( {\frac{{\partial^{2} P_{xx} }}{{\partial x^{2} }} + \frac{2}{R}\frac{{\partial^{2} P_{x\theta } }}{\partial x\partial \theta } + \frac{1}{{R^{2} }}\frac{{\partial^{2} P_{\theta \theta } }}{{\partial \theta^{2} }}} \right) \\ & \quad + q = I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - c_{1}^{2} I_{6} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right), \\ & \quad + c_{1} \left[ {I_{3} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial u_{0} }}{\partial x} + \frac{1}{R}\frac{{\partial v_{0} }}{\partial \theta }} \right) + J_{4} \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{1}{R}\frac{{\partial \phi_{\theta } }}{\partial \theta }} \right)} \right] \\ & \frac{{\partial \overline{M}_{xx} }}{\partial x} + \frac{1}{R}\frac{{\partial \overline{M}_{x\theta } }}{\partial \theta } - \bar{Q}_{x} = \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {J_{1} u_{0} + K_{2} \phi_{x} - c_{1} J_{4} \frac{\partial w}{\partial x}} \right), \\ & \frac{{\partial \overline{M}_{x\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial \overline{M}_{\theta \theta } }}{\partial \theta } - \bar{Q}_{\theta } = \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {J_{1} v_{0} + K_{2} \phi_{\theta } - c_{1} J_{4} \frac{\partial w}{R\partial \theta }} \right), \\ \end{aligned} $$

(5)

where $\overline{M}_{\alpha \beta } = M_{\alpha \beta } - c_{1} P_{\alpha \beta }$, $\bar{Q}_{\alpha } = Q_{\alpha } - 3c_{1} P_{\alpha }$, $\alpha ,\beta = x,\theta$,

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{\theta \theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} & = \mathop \smallint \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}dz,\left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{\theta \theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \mathop \smallint \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}zdz,\left\{ {\begin{array}{*{20}c} {P_{xx} } \\ {P_{\theta \theta } } \\ {P_{x\theta } } \\ \end{array} } \right\} = \mathop \smallint \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}z^{3} dz, \\ \left\{ {\begin{array}{*{20}c} {Q_{\theta } } \\ {Q_{x} } \\ \end{array} } \right\} & = \mathop \smallint \limits_{{ - \frac{{h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} \left\{ {\begin{array}{*{20}c} {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ \end{array} } \right\}dz, I_{i} = \mathop \sum \limits_{k = 1}^{{N^{*} }} \mathop \smallint \limits_{k}^{k + 1} \rho^{\left( k \right)} z^{i} dz,\left( {i = 0,1,2, \ldots ,6} \right), \\ \end{aligned} $$

where $N^{*}$ is the total number of layers, $\rho^{\left( k \right)}$ is the density of kth ply. $J_{i} = I_{i} - c_{1} I_{i + 2}$, (i = 1, 4), $K_{2} = I_{2} - 2c_{1} I_{4} + c_{1}^{2} I_{6}$.

The kinematical equations in the von Karman type of strain–displacement relations with $\frac{{\partial v_{0} }}{\partial z} = \frac{{ - v_{0} }}{R\sin \emptyset }$, $\frac{{\partial u_{0} }}{\partial z} = \frac{{ - u_{0} }}{R\sin \emptyset }$ assumed in the spherical shell and $\frac{\partial w}{\partial z} = \frac{{\partial \phi_{x} }}{\partial z} = \frac{{\partial \phi_{\theta } }}{\partial z} = 0$ for a given angle ∅ are as follows:

$$ \begin{aligned} \varepsilon_{x} & = \frac{\partial u}{\partial x} + \frac{1}{2}\left(\frac{\partial w}{\partial x}\right)^{2} = \frac{{\partial u_{0} }}{\partial x} + z\frac{{\partial \phi_{x} }}{\partial x} - c_{1} z^{3} \left( {\frac{{\partial \phi_{x} }}{\partial x} + \frac{{\partial^{2} w}}{{\partial x^{2} }}} \right) + \frac{1}{2}\left( {\frac{\partial w}{\partial x}} \right)^{2} , \\ \varepsilon_{\theta } & = \frac{1}{R}\frac{\partial v}{\partial \theta } + \frac{1}{2}\left(\frac{1}{R}\frac{\partial w}{\partial \theta }\right)^{2} = \frac{1}{R}\frac{{\partial v_{0} }}{\partial \theta } + z\frac{1}{R}\frac{{\partial \phi_{\theta } }}{\partial \theta } - c_{1} z^{3} \left( {\frac{1}{R}\frac{{\partial \phi_{\theta } }}{\partial \theta } + \frac{1}{{R^{2} }}\frac{{\partial^{2} w}}{{\partial \theta^{2} }}} \right) + \frac{1}{2}\frac{1}{{R^{2} }}\left( {\frac{\partial w}{\partial \theta }} \right)^{2} , \\ \varepsilon_{zz} & = 0, \\ \varepsilon_{x\theta } & = \frac{1}{R}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x} + \left( {\frac{\partial w}{\partial x}} \right)\left( {\frac{1}{R}\frac{\partial w}{\partial \theta }} \right) = \frac{1}{R}\left[ {\frac{{\partial u_{0} }}{\partial \theta } + z\frac{{\partial \phi_{x} }}{\partial \theta } - c_{1} z^{3} \left( {\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{{\partial^{2} w}}{\partial x\partial \theta }} \right)} \right] \\ & \quad + \frac{{\partial v_{0} }}{\partial x} + z\frac{{\partial \phi_{\theta } }}{\partial x} - c_{1} z^{3} \left( {\frac{{\partial \phi_{\theta } }}{\partial x} + \frac{1}{R}\frac{{\partial^{2} w}}{\partial x\partial \theta }} \right) + \left( {\frac{\partial w}{\partial x}} \right)\left( {\frac{1}{R}\frac{\partial w}{\partial \theta }} \right) \\ \varepsilon_{\theta z} & = \frac{\partial v}{\partial z} + \frac{1}{R}\frac{\partial w}{\partial \theta } = \frac{{ - v_{0} }}{R\sin \emptyset } + \phi_{\theta } - 3c_{1} z^{2} \left( {\phi_{\theta } + \frac{1}{R}\frac{\partial w}{\partial \theta }} \right) + \frac{1}{R}\frac{\partial w}{\partial \theta }, \\ \varepsilon_{xz} & = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} = \frac{{ - u_{0} }}{R\sin \emptyset } + \phi_{x} - 3c_{1} z^{2} \left( {\phi_{x} + \frac{\partial w}{\partial x}} \right) + \frac{\partial w}{\partial x}. \\ \end{aligned} $$

(6)

The dynamic equilibrium differential equations with TSDT of thick FGM spherical shells in terms of partial derivatives of five unknowns (3 displacements and 2 shear rotations) subjected to partial derivatives of thermal loads, mechanical loads and inertia terms can be obtained in matrix form of five equations. The coefficients of elements in the matrices contain stiffness integrals ($A_{{i^{s} j^{s} }} ,B_{{i^{s} j^{s} }} ,D_{{i^{s} j^{s} }} ,E_{{i^{s} j^{s} }} ,F_{{i^{s} j^{s} }} ,H_{{i^{s} j^{s} }} ,i^{s} j^{s} = 1,2,6$) ($A_{{i^{*} j^{*} }} ,B_{{i^{*} j^{*} }} ,D_{{i^{*} j^{*} }} ,E_{{i^{*} j^{*} }} ,F_{{i^{*} j^{*} }} ,H_{{i^{*} j^{*} }} ,i^{*} ,j^{*} = 4,5$) and c₁ terms, where

$$ \begin{aligned} & (A_{{i^{s} j^{s} }} ,B_{{i^{s} j^{s} }} ,D_{{i^{s} j^{s} }} ,E_{{i^{s} j^{s} }} ,F_{{i^{s} j^{s} }} ,H_{{i^{s} j^{s} }} ) \\ & \quad = \int_{{\frac{{ - h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} {\bar{Q}_{{i^{s} j^{s} }}^{{}} } \quad (1,z,z^{2} ,z^{3} ,z^{4} ,z^{6} ){\text{d}}z, \\ & (A_{{i^{*} j^{*} }} ,B_{{i^{*} j^{*} }} ,D_{{i^{*} j^{*} }} ,E_{{i^{*} j^{*} }} ,F_{{i^{*} j^{*} }} ,H_{{i^{*} j^{*} }} ) \\ & \quad = \int_{{\frac{{ - h^{*} }}{2}}}^{{\frac{{h^{*} }}{2}}} {k_{\alpha } \bar{Q}_{{i^{*} j^{*} }}^{{}} } \quad (1,z,z^{2} ,z^{3} ,z^{4} ,z^{5} ){\text{d}}z, \\ \end{aligned} $$

(7)

where $k_{\alpha }$ is the shear correction coefficient. $\bar{Q}_{{i^{s} j^{s} }}$ and $\bar{Q}_{{i^{*} j^{*} }}$ are the stiffness with $z/R$ terms which cannot be neglected [10] [18] and are used and assumed in the following simple terms containing $z/\left( {R\sin \emptyset } \right)$ for thick FGM spherical shells:

$$ \begin{aligned} \bar{Q}_{11} & = \bar{Q}_{22} = \frac{{E_{fgm} }}{{1 - \nu_{fgm}^{2} }},\quad \bar{Q}_{12} = \bar{Q}_{21} = \frac{{\nu_{fgm} E_{fgm} }}{{\left( {1 + \frac{z}{R\sin \emptyset }} \right)\left( {1 - \nu_{fgm}^{2} } \right)}}, \\ \bar{Q}_{44} & = \frac{{E_{fgm} }}{{2(1 + \nu_{fgm} )}},\quad \bar{Q}_{55} = \bar{Q}_{66} = \frac{{E_{fgm} }}{{2\left( {1 + \frac{z}{R\sin \emptyset }} \right)\left( {1 + \nu_{fgm} } \right)}}, \\ \bar{Q}_{16} & = \bar{Q}_{26} = \bar{Q}_{45} = 0, \\ \end{aligned} $$

(8)

where $\nu_{fgm} = \frac{{\nu_{1} + \nu_{2} }}{2}$ is the Poisson’s ratios of the FGM spherical shells, $E_{fgm} = (E_{2} - E_{1} )(\frac{{z + h^{ *} /2}}{{h^{ *} }})^{{R_{n} }} + E_{1}$ is the Young’s modulus of the FGM spherical shells, R_n is the power law exponent parameter, E₁ and E₂ are the Young’s modulus, and v₁ and v₂ are the Poisson’s ratios of the FGM constituent material 1 and 2, respectively. The A₁₂, E₁₁, F₁₁, H₁₁ and H₄₄ of thick FGM spherical shells can be given by using direct integration, by using the long division method for the integration of rational function and by taking the first five terms of quotient polynomials in the calculation approximately; the A₁₂, B₁₂, D₁₂, E₁₂, F₁₂, H₁₂, A₅₅, B₅₅, D₅₅, E₅₅, F₅₅ and H₅₅ of thick FGM spherical shells can be obtained for a given angle ∅ of the stiffness integrals.

The modified shear correction factor $k_{\alpha }$ can be derived usually based on the energy equivalence principle by equaling the equations of total strain energy due to transverse shears and due to shear forces with $k_{\alpha }$, respectively. For the preliminary study, the effects of c₁ and ∅ on the modified calculation are considered; thus, $k_{\alpha }$ can be obtained as follows [18]:

$$ k_{\alpha } = \frac{1}{{h^{*} }}\frac{\text{FGMZSV}}{\hbox{FGMZIV}}, $$

(9)

where FGMZSV and FGMZIV are the parameters of total strain energy that can be presented as functions of $\nu_{fgm}$, $h^{*}$, R_n, E₁ and E₂, respectively.

3 Some numerical results and discussion

The thick FGM spherical shells with layers in the stacking sequence $(0^\circ /0^\circ )$ are used to study the free vibration frequency results with the effects of T and $k_{\alpha }$ under four sides simply supported boundary condition, no thermal loads ($\Delta T$ = 0), no in-plane distributed forces ($p_{1} = p_{2} = 0$), and no external pressure load ($\,q = 0$). The free vibration frequency ($\omega_{mn}$ with mode shape numbers m and n) for four sides simply supported boundary condition can be derived by simply assuming that $I_{1} = I_{3} = J_{1} = 0$, $B_{ij} = E_{ij} = 0$, $A_{16} = A_{26} = 0$, $D_{16} = D_{26} = 0$ and $A_{45} = D_{45} = F_{45} = 0$ under the following time sinusoidal displacement and shear rotations forms with amplitudes $a_{mn}$, $b_{mn}$, $c_{mn}$, $d_{mn}$ and $e_{mn}$:

$$ \begin{aligned} u_{0} = a_{mn} \cos \left( {m\pi x/L} \right)\sin \left( {n\pi \theta /R} \right)\sin (\omega_{mn} t), \hfill \\ v_{0} = b_{mn} \sin \left( {m\pi x/L} \right)\cos \left( {n\pi \theta /R} \right)\sin (\omega_{mn} t), \hfill \\ w = c_{mn} \sin \left( {m\pi x/L} \right)\sin \left( {n\pi \theta /R} \right)\sin (\omega_{mn} t), \hfill \\ \phi_{x} = d_{mn} \cos \left( {m\pi x/L} \right)\sin \left( {n\pi \theta /R} \right)\sin (\omega_{mn} t), \hfill \\ \phi_{\theta } = e_{mn} \sin \left( {m\pi x/L} \right)\cos \left( {n\pi \theta /R} \right)\sin (\omega_{mn} t), \hfill \\ \end{aligned} $$

(10)

where m is the number of axial half-waves; n is the number of circumferential waves; L is the axial length of FGM shells. By substituting Eqs. (10) in dynamic equilibrium differential equations under free vibration, the fully homogeneous equation can be obtained as follows:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}l} {FH_{11} } \hfill & {FH_{12} } \hfill & {FH_{13} } \hfill & {FH_{14} } \hfill & {FH_{15} } \hfill \\ { - \frac{{I_{0} \lambda_{mn} }}{{I_{0} }}} \hfill & {} \hfill & { + \frac{{c_{1} I_{3} \left( {\frac{m\pi }{L}} \right)\lambda_{mn} }}{{I_{0} }}} \hfill & { - \frac{{J_{1} \lambda_{mn} }}{{I_{0} }}} \hfill & {} \hfill \\ {FH_{12} } \hfill & {FH_{22} - \frac{{I_{0} \lambda_{mn} }}{{I_{0} }}} \hfill & {FH_{23} } \hfill & {FH_{24} } \hfill & {FH_{25} } \hfill \\ {} \hfill & {}\hfill & { + \frac{{c_{1} I_{3} \left( {\frac{n\pi }{R}} \right)\lambda_{mn} }}{{I_{0} }}} \hfill & {} \hfill & { - \frac{{J_{1} \lambda_{mn} }}{{I_{0} }}} \hfill \\ {FH_{13} } \hfill & {FH_{23} } \hfill & {FH_{33} } \hfill & {FH_{34} } \hfill & {FH_{35} } \hfill \\ { + \frac{{c_{1} I_{3} \left( {\frac{m\pi }{L}} \right)\lambda_{mn} }}{{I_{0} }}} \hfill & { + \frac{{c_{1} I_{3} \left( {\frac{m\pi }{L}} \right)\lambda_{mn} }}{{I_{0} }}} \hfill & { - [I_{0} + c_{1}^{2} I_{6} \left( {\frac{m\pi }{L}} \right)^{2} } \hfill & { + \frac{{c_{1} J_{4} \left( {\frac{m\pi }{L}} \right)\lambda_{mn} }}{{I_{0} }} } \hfill & { + \frac{{c_{1} J_{4} \left( {\frac{n\pi }{R}} \right)\lambda_{mn} }}{{I_{0} }}} \hfill \\ {} \hfill & {} \hfill & { + c_{1}^{2} I_{6} \left( {\frac{n\pi }{R}} \right)^{2} ]\lambda_{mn} /I_{0} } \hfill & {} \hfill & {} \hfill \\ {FH_{14} }\hfill & {FH_{24} } \hfill & {FH_{34} } \hfill & {FH_{44} } \hfill & {FH_{45} } \hfill \\ { - \frac{{J_{1} \lambda_{mn} }}{{I_{0} }}} \hfill & {} \hfill & { + \frac{{c_{1} J_{4} \left( {\frac{m\pi }{L}} \right)\lambda_{mn} }}{{I_{0} }}} \hfill & { - \frac{{K_{2} \lambda_{mn} }}{{I_{0} }}} \hfill & {} \hfill \\ {FH_{15} } \hfill & {FH_{25} } \hfill & {FH_{35} } \hfill & {FH_{45} } \hfill & {FH_{55} } \hfill \\ {} \hfill & { - \frac{{J_{1} \lambda _{{mn}} }}{{I_{0} }} } \hfill & { + \frac{{c_{1} J_{4} \left( {\frac{n\pi }{R}} \right)\lambda_{mn} }}{{I_{0} }}} \hfill & {} \hfill & { - \frac{{K_{2} \lambda_{mn} }}{{I_{0} }}} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {a_{mn} } \hfill \\ {b_{mn} } \hfill \\ {c_{mn} } \hfill \\ {d_{mn} } \hfill \\ {e_{mn} } \hfill \\ \end{array} } \right\} \\ & \quad = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ 0 \hfill \\ \end{array} } \right\}. \\ \end{aligned} $$

(11)

For the traditional study with the assumed reasonable simplifications of terms FH₁₃ = FH₁₄ = FH₁₅ = FH₂₃ = FH₂₄ = FH₂₅ = 0 and I₃ = J₁ = I₆ = J₄ = 0 in the elements of homogeneous matrix (11), the simply homogeneous equation can be obtained as follows:

$$ \left[ {\begin{array}{*{20}l} {FH_{11} - \lambda_{mn} } \hfill & {FH_{12} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {FH_{12} } \hfill & {FH_{22} - \lambda_{mn} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {FH_{33} - \lambda_{mn} } \hfill & {FH_{34} } \hfill & {FH_{35} } \hfill \\ 0 \hfill & 0 \hfill & {FH_{34} } \hfill & {FH_{44} - \frac{{K_{2} }}{{I_{0} }}\lambda_{mn} } \hfill & {FH_{45} } \hfill \\ 0 \hfill & 0 \hfill & {FH_{35} } \hfill & {FH_{45} } \hfill & {FH_{55} - \frac{{K_{2} }}{{I_{0} }}\lambda_{mn} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {a_{mn} } \\ {b_{mn} } \\ {c_{mn} } \\ {d_{mn} } \\ {e_{mn} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\}, $$

(12)

where

$$ \begin{aligned} \lambda_{mn} & = I_{0} \omega_{mn}^{2} , \\ FH_{11} & = A_{11} \left( {m\pi /L} \right)^{2} + A_{66} \left( {n\pi /R} \right)^{2} , \\ FH_{12} & = \left( {A_{12} + A_{66} } \right)\left( {m\pi /L} \right)\left( {n\pi /R} \right), \\ FH_{22} & = A_{66} \left( {m\pi /L} \right)^{2} + A_{22} \left( {n\pi /R} \right)^{2} , \\ FH_{33} & = A_{55} \left( {m\pi /L} \right)^{2} + A_{44} \left( {n\pi /R} \right)^{2} \\ & \quad + c_{1}^{2} H_{11} \left( {m\pi /L} \right)^{4} + (2c_{1}^{2} H_{12} + 4c_{1}^{2} H_{66} )\left( {m\pi /L} \right)^{2} \left( {n\pi /R} \right)^{2} \\ & \quad + c_{1}^{2} H_{22} \left( {n\pi /R} \right)^{4} - 3c_{1} (2D_{55} - 3c_{1} F_{55} )\left( {m\pi /L} \right)^{2} \\ & \quad - 3c_{1} \left( {2D_{44} - 3c_{1} F_{44} } \right)\left( {n\pi /R} \right)^{2} , \\ FH_{34} & = A_{55} m\pi /L - (c_{1} F_{11} - c_{1}^{2} H_{11} ) \left( {m\pi /L} \right)^{3} \\ & \quad - (2c_{1} F_{66} - 2c_{1}^{2} H_{66} + c_{1} F_{12} - c_{1}^{2} H_{12} )\left( {m\pi /L} \right)\left( {n\pi /R} \right)^{2} \\ & \quad - (6c_{1} D_{55} - 9c_{1}^{2} F_{55} )\left( {m\pi /L} \right), \\ FH_{35} & = A_{44} n\pi /R - (c_{1}^{{}} F_{22} - c_{1}^{2} H_{22} )(n\pi /R)^{3} \\ & \quad - (2c_{1}^{{}} F_{66} - 2c_{1}^{2} H_{66} + c_{1}^{{}} F_{12} - c_{1}^{2} H_{12} )(m\pi /L)^{2} (n\pi /R) \\& \quad - (6c_{1}^{{}} D_{44} - 9c_{1}^{2} F_{44} )(n\pi /R), \\ FH_{44} & = (D_{11} - 2c_{1} F_{11} + c_{1}^{2} H_{11} )(m\pi /L)^{2} + (D_{66} - 2c_{1} F_{66} + c_{1}^{2} H_{66} )(n\pi /R)^{2} \\ & \quad + A_{55} - 6c_{1} D_{55} + 9c_{1}^{2} F_{55} , \\ FH_{45} & = (D_{12} + D_{66} - 2c_{1} F_{12} + c_{1}^{2} H_{12} - 2c_{1} F_{66} + c_{1}^{2} H_{66} )(m\pi /L)(n\pi /R), \\ FH_{55} & = (D_{66} - 2c_{1} F_{66} + c_{1}^{2} H_{66} )(m\pi /L)^{2} + (D_{22} - 2c_{1} F_{22} + c_{1}^{2} H_{22} )(n\pi /R)^{2} \\ & \quad + A_{44} - 6c_{1} D_{44} + 9c_{1}^{2} F_{44} . \\ \end{aligned} $$

The determinant of the coefficient matrix in Eq. (12) vanishes in obtaining non-trivial solution of amplitudes which can be represented in the simply five-degree polynomial equation as follows. Thus, $\omega_{mn}$ can be found for a given angle ∅ of thick FGM spherical shells under free vibration:

$$ A (1)\lambda_{mn}^{5} + A (2)\lambda_{mn}^{4} + A (3)\lambda_{mn}^{3} + A (4)\lambda_{mn}^{2} + A (5)\lambda_{mn}^{{}} + A (6) = 0, $$

(13)

where

$$ \begin{aligned} A (1) & = - sd, \\ A (2) & = (FH_{11} + FH_{22} )sd + sc, \\ A (3) & = - [(FH_{11} FH_{22} - FH_{12} FH_{12} )sd + (FH_{11} + FH_{12} )sc + sb], \\ A (4) & = (FH_{11} FH_{22} - FH_{12} FH_{12} )sc + (FH_{11} + FH_{22} )sb + sa, \\ A (5) & = - [(FH_{11} FH_{22} - FH_{12} FH_{12} )sb + (FH_{11} + FH_{22} )sa], \\ A (6) & = (FH_{11} FH_{22} - FH_{12} FH_{12} )sa, \\ \end{aligned} $$

where

$$ \begin{aligned} sd & = (K_{2} /I_{0} )^{2} , \\ sc & = FH_{33} sd + FH_{44} K_{2} /I_{0} , \\ sb & = \left( {FH_{33} FH_{55} + FH_{44} FH_{55} + FH_{33} FH_{44} - FH_{35} FH_{35} } \right. \\ & \quad \left. { - FH_{34} FH_{34} } \right)K_{2} /I_{0} - FH_{45} FH_{45} , \\ sa & = FH_{33} FH_{44} FH_{55} + FH_{44} FH_{34} FH_{35} + FH_{35} FH_{34} FH_{45} \\ & \quad - FH_{35} FH_{35} FH_{44} - FH_{34} FH_{34} FH_{55} - FH_{45} FH_{45} FH_{33} . \\ \end{aligned} $$

The composite thick FGM SUS304/Si₃N₄ material is used to implement the numerical computation of vibration under environment temperature T (free stress assumed). The FGM material 1 at inner position of spherical shells is SUS304 (stainless steel); the FGM material 2 at outer position of spherical shells is Si₃N₄ (silicon nitride), used for the free vibration frequency computations with simply homogeneous equation. For the preliminary thick FGM spherical shells study, the effects of nonlinear coefficient term of displacements and meridional angles on the calculation of varied shear correction coefficient are not considered. Thus, k_α of different c1 is the same, which means that k_α is not affected by c1. In the future work, the domain of integration would be used for calculating k_α and stated in total strain energy. In Table 1, the values of varied k_α for SUS304/Si₃N₄ on ∅ = 10° and 90° are given, respectively, without considering the effects of c₁ and ∅ on the preliminary FGM spherical shells study. The varied values of k_α are usually functions of h^*, R_n and T in the thick FGM spherical shells ($B_{ij} \ne 0$). For $L/R = 1$, $h_{1} = h_{2}$, h^* = 1.2 mm, calculated values of k_α are increasing with R_n (from 0.1 to 10). Thus, values of k_α are used for frequency calculations of the free vibration (no thermal loads under no temperature difference $\Delta T$ = 0) including the effects of nonlinear coefficient c₁ term.

Table 1 $k_{\alpha }$ for SUS304/Si₃N₄ on ∅ = 10°, 45° and 90°

Firstly, for the frequency parameter $f^{*} = 4\pi \omega_{11} R\sqrt {I_{2} /A_{11} }$, values under the effects of c₁ = 0.925925/mm² and c₁ = 0/mm² for L/h^* = 5, 8 and 10, respectively, on ∅ = 10°, 45° and 90° are shown in Table 2a–c, where ω₁₁ is the first natural frequency ($m = n = 1$). The f^* values at c₁ = 0/mm² of the ∅ = 10° and ∅ = 90° cases are overestimated. The f^* values at c₁ = 0/mm² for L/h^* = 8 and 10 of the ∅ = 45° case are also overestimated, but they are underestimated for L/h^* = 5. For SUS304/Si₃N₄ thick spherical shells under free vibration with h^* = 1.2 mm, the f^* values under T = 1 K, 100 K, 300 K, 600 K and 1000 K with varied k_α and c₁ effects are not greater than 354.31817 on ∅ = 10°, not greater than 24.799451 on ∅ = 45°, not greater than 13.538765 on ∅ = 90°. Values of another frequency parameter $\Omega = \left( {\omega_{11} L^{2} /h^{*} } \right)\sqrt {\rho_{1} /E_{1} }$ under the effects of c₁ = 0.925925/mm² and c₁ = 0/mm² for L/h^* = 5, 8 and 10, respectively, on ∅ = 10°, 45° and 90° are shown in Table 3a–c; $\rho_{1}$ is the density of FGM material 1; for SUS304/Si₃N₄ thick spherical shells under free vibration with h^* = 1.2 mm, the $\Omega$ values under T = 1 K, 100 K, 300 K, 600 K and 1000 K with varied k_α and c₁ effects are not greater than 764.17688 on ∅ = 10°, not greater than 82.240913 on ∅ = 45°, not greater than 32.380783 on ∅ = 90°. The $\Omega$ values at c₁ = 0/mm² of the ∅ = 10° and ∅ = 90° cases are overestimated. The $\Omega$ values at c₁ = 0/mm² for L/h^* = 8 and 10 of the ∅ = 45° case are also overestimated, but they are underestimated for L/h^* = 5.

Table 2 f^* for SUS304/Si₃N₄ on (a) ∅ = 10°, (b) ∅ = 45° and (c) ∅ = 90°

Table 3 $\varOmega$ for SUS304/Si₃N₄ on (a) ∅ = 10°, (b) ∅ = 45° and (c) ∅ = 90°

It is interesting to compare the present vibration values of frequency with some authors’ work as shown in Tables 4 and 5. The values of f^* versus h^* for SUS304/Si₃N₄ under L/h^* = 10 and T = 300 K with varied k_α and c₁ effects are shown in Table 4. The compared value f^* = 11.616583 at c₁ = 0.925925/mm², h^* = 1.2 mm, R_n= 1 is smaller than 11.8186 of non-dimensional frequencies of three-layer (0^o/90^o/0^o) laminated composite spherical shell, a/h = 10, R/a = 10, TSDT presented by Sayyad and Ghugal [6], in which a is the arc length in the x direction, h is the thickness in the z direction, and R is the principal radius in the x direction. The discrepancy between two versions of f^* values is seemly acceptable for the preliminary study of FGM spherical shells. The values of $\varOmega$ versus h^* for SUS304/Si₃N₄ under L/h^* = 10 and T = 1000 K with varied k_α and c₁ effects are shown in Table 5. The compared value $\varOmega$ = 69.988494 at c₁ = 0.925925/mm², h^* = 1.2 mm, R_n= 1 is greater than 69.520 of non-dimensional first frequencies of composite laminated spherical shell, h/R = 0.02, n = m=1, SS–SS (four sides simply supported) presented by Li et al. 2019 [19]. The discrepancy between two versions of $\varOmega$ values is seemly acceptable for the preliminary study of FGM spherical shells.

Table 4 Comparison of frequency f^* for SUS304/Si₃N₄ on ∅ = 10°

Table 5 Comparison of frequency $\varOmega$ for SUS304/Si₃N₄ on ∅ = 10°

Secondly, the natural frequency ω_mn values (unit 1/s) of free vibration ($\Delta T$ = 0) according to mode shape numbers m and n for the SUS304/Si₃N₄ FGM thick spherical shells are calculated. For the values of first (m = n=1) natural frequency $\omega_{11}$ versus R_n with h^* = 1.2 mm, varied k_α and the effects of c₁ = 0.925925/mm² and c₁ = 0/mm² for L/h^* = 5, 8 and 10, under T = 1 K, 100 K, 300 K, 600 K and 1000 K on ∅ = 10° are shown in Table 6. The values of ω₁₁ are overestimated without the values of c₁, e.g., ω₁₁ = 0.012401/s with c₁ = 0/mm² is greater than ω₁₁ = 0.004222/s with c₁ = 0.925925/mm² for L/h^* = 5, R_n = 0.5 under T = 1 K. For the values of natural frequency ω_mn versus m, n = 1,2,…,9 with R_n = 0.5, T = 300 K, h^* = 1.2 mm under varied k_α, the effects of c₁ = 0.925925/mm² and c₁ = 0/mm² for L/h^* = 5 and 10 on ∅ = 10° are shown in Table 7. The values of ω₁₁ are overestimated without the values of c₁, e.g., ω₁₁ = 0.012416/s with c₁ = 0/mm² is greater than ω₁₁ = 0.004492/s with c₁ = 0.925925/mm² for L/h^* = 5, R_n = 0.5 under T = 300 K. The values of ω₁₁ are all increasing with the increase in T for L/h^* = 5, 8 and 10, under R_n = 0.5, 1 and 2.

Table 6 Fundamental natural frequency ω₁₁ for $h^{*} = 1.2\;{\text{mm}}$ on ∅ = 10°

Table 7 ω_mn versus m and n under varied $k_{\alpha }$, c₁,$\,R_{n} = 0.5$ and T = 300 K on ∅ = 10°

Finally, the natural frequency ω_mn values (unit 1/s) versus R_n and T of free vibration ($\Delta T$ = 0) according to mode shape numbers m = 1 and n (from 1 to 9) for the SUS304/Si₃N₄ FGM thick spherical shells are calculated. Figure 2 shows the values of ω_1n versus R_n in FGM spherical shells for thick L/h^* = 5, 10, respectively, on ∅ = 10°, with the effects of varied k_α and c₁ = 0.925925/mm² under T = 300 K. Generally, the values of ω_1n are oscillating with values of n (from 1 to 9) for L/h^* = 5, R_n = 0.5; ω_1n are increasing firstly and then almost kept constant, increasing again and then decreasing finally with values of n (from 1 to 9) for L/h^* = 5, R_n = 1 and 10. The greatest value of ω₁₆ = 0.007623 (unit 1/s) is found for L/h^* = 5, R_n = 1. The values of ω_1n are affected with R_n for L/h^* = 5. The values of ω_1n are kept constant with values of n (from 1 to 9) for L/h^* = 10, R_n = 10; ω_1n are the higher constant with values of n (from 1 to 5) and then oscillating for L/h^* = 10, R_n = 0.5 and 1, respectively. The greatest value of ω₁₇ = 0.011711 (unit 1/s) is found for L/h^* = 10, R_n = 1. The values of ω_1n also are affected with R_n for L/h^* = 10. Figure 3 shows the values of ω_1n versus T in FGM spherical shells for thick L/h^* = 5, 10, respectively, on ∅ = 10°, under the effects of varied k_α, c₁ = 0.925925/mm² and R_n = 1. Generally, the values of ω_1n are oscillating with values of n (from 1 to 9) for L/h^* = 5, T = 300 K, 600 K and 1000 K. The greatest value of ω₁₆ = 0.007623 (unit 1/s) is found for L/h^* = 5, T = 300 K. The value of ω₁₅ only can stand for higher temperature T = 1000 K at L/h^* = 5. The values of ω_1n are almost kept constant with values of n (from 1 to 5) and then oscillating for L/h^* = 10, T = 300 K, 600 K and 1000 K, respectively. The greatest value of ω₁₇ = 0.012632 (unit 1/s) is found for L/h^* = 10, T = 600 K. The values of ω₁₇, ω₁₈ and ω₁₉ can stand for higher temperature T = 1000 K at L/h^* = 10. The values of ω_1n for n = 1–4 at L/h^* = 5 are found in the greater values than those at L/h^* = 10, respectively.

Fig. 2

ω_1n versus R_n for L/h^* = 5 and 10

Fig. 3

ω_1n versus T for L/h^* = 5 and 10

4 Conclusions

The values of natural frequency and frequency parameters, respectively, on ∅ = 10°, 45° and 90° are calculated and obtained by using the simply homogeneous equation with the polynomial equation in the fifth order of $\lambda_{mn}$ in the free vibration of thick FGM spherical shells. The three items of value effects are considered in the frequency calculation, e.g., nonlinear coefficient term c₁, shear correction coefficient k_α and environment temperature T. For the preliminary FGM spherical shell study, the effects of c₁ and ∅ on the varied k_α calculation were not considered. The calculated values of k_α are increasing with the increase in R_n. Some of the important results are found as follows. (a) Data are investigated in the frequency parameters under free vibration with and without the effects of c₁. The f^* and $\Omega$ values at c₁ = 0/mm² of the ∅ = 10° and ∅ = 90° cases are overestimated. The f^* and $\Omega$ values at c₁ = 0/mm² for L/h^* = 8 and 10 of the ∅ = 45° case are also overestimated, but they are underestimated for L/h^* = 5. (b) The values of natural frequency ω_mn versus R_n and T in free vibration according to mode shape numbers m and n for the thick SUS304/Si₃N₄ FGM spherical shells are calculated with the effects of c₁.