Modified and Trefftz unsymmetric finite element models

Abstract

The unsymmetric finite element method employs compatible test functions but incompatible trial functions. The pertinent 8-node quadrilateral and 20-node hexahedron unsymmetric elements possess exceptional immunity to mesh distortion. It was noted later that they are not invariant and the proposed remedy is to formulate the element stiffness matrix in a local frame and then transform the matrix back to the global frame. In this paper, a more efficient approach will be proposed to secure the invariance. To our best knowledge, unsymmetric 4-node quadrilateral and 8-node hexahedron do not exist. They will be devised by using the Trefftz functions as the trial function. Numerical examples show that the two elements also possess exceptional immunity to mesh distortion with respect to other advanced elements of the same nodal configurations.

1 Introduction

Tremendous efforts have been put on developing finite element (FE) models with excellent accuracy and low susceptibility to mesh distortion. In this regard, advanced FE techniques such as hybrid/mixed method (Pian and Sumihara 1984; Pian and Tong 1986; Yuan et al. 1993; Sze 2000; Qin 2003; Sze et al. 2004, 2010; Cen et al. 2011; Freitas and Moldovan 2011; Cao et al. 2012), incompatible displacement/enhanced assumed strain modes (Taylor et al. 1976; Simo and Rifai 1990; Liu and Sze 2010), reduced integration and stabilization (Hughes 1980; Bachrach 1987; Sze et al. 2004), assumed strain formulation (Macneal 1982; Kim et al. 2003; El-Abbasi and Meguid 2000; Cardoso et al. 2008) and discrete shear gap method (Bletzinger et al. 2000) have been developed. Many of them have yielded FE models with excellent accuracy when the mesh is regular. However, their accuracy often drops considerably when the mesh is distorted.

Rajendran et al. (Rajendran and Liew 2003; Ooi et al. 2004; Liew et al. 2006; Ooi et al. 2008) proposed the unsymmetric FE method (US-FEM), which belongs to the Petrov–Galerkin formulation. The incompatible metric interpolants expressed in the metric or Cartesian coordinates are employed as the trial functions to satisfy the quadratic completeness for the unsymmetric 8-node quadrilateral plane element (UQ8) and 20-node hexahedral element (UH20). On the other hand, the test functions are the conventional compatible parametric interpolants. UQ8 and UH20 possess exceptional immunity to mesh distortion. It was noted later that they are not invariant, i.e., the element predictions change when the inclination of the element with respect to the global coordinate frame changes (Sze et al. 1992; Ooi et al. 2008). The proposed remedy is to formulate the element stiffness matrix in a corotational Cartesian frame, which translates and rotates with the element, and then transform the matrix back to the global frame (Ooi et al. 2008). In this paper, a more efficient approach will be proposed to secure their invariance.

Researchers are more inclined to put efforts on improving the accuracy of lower order elements due to their low construction cost. For the conventional parametric 4-node quadrilateral plane element (Q4) and 8-node hexahedral element (H8), poor bending response caused by the excessive shear strain is a major shortcoming. To our best knowledge, unsymmetric 4-node quadrilateral and 8-node hexahedral elements do not exist. In this paper, they will be formulated. The test functions remain to be the compatible parametric interpolants. Among the trial functions, the constant and linear metric modes are retained. The higher order trial functions are mainly the bending modes expressed with respect to some chosen corotational metric frames. As the constant, linear and bending modes can be regarded as Trefftz functions (Herrera 2000), the resulting elements can be termed as Trefftz unsymmetric elements. From the benchmark tests, the proposed Trefftz unsymmetric 4-node quadrilateral element (TQ4) and 8-node hexahedral element (TH8) not only are invariant but also possess remarkable bending response and immunity to mesh distortion with respect to other advanced elements of the same nodal configurations. It is worth noting that an UQ8 element was also devised (Cen et al. 2012) by using analytical displacement functions which can be regarded as Trefftz functions (Herrera 2000).

In Sect. 2, US-FEM is reviewed. Existing UQ8 and UH20 are briefly reviewed in Sect. 3. The modified approaches to secure their invariance are presented in Sects. 4 and 5. The proposed Trefftz unsymmetric elements TQ4 and TH8 are presented in Sects. 6 and 7.

2 The unsymmetric finite element method

The 3D linear elasticity problem for domain Ω is considered. The domain boundary ∂Ω can be partitioned into Γ _u and Γ _t which are prescribed with displacement $\overline{{\mathbf{u}}}$ and traction ${\bar{\mathbf{t}}}$, respectively. Without loss of generality, we assume

$$ \Gamma_{u}^{{}} \cup \Gamma_{t} = \partial \Omega \quad{\text{and}}\quad\Gamma_{u} \cap \Gamma_{t} = \emptyset $$

(1)

When Ω is partitioned into elements Ω^e, the strong form of the boundary value problem can be stated as:

• (a) domain equilibrium: $\user2{L}^{T} {\varvec{\upsigma}} + {\overline{\mathbf{b}}} = {\mathbf{0}}$ in all Ω^e

• (b) traction boundary condition: $\user2{n}{\varvec{\upsigma}} = {\overline{\mathbf{t}}}$ on all $\Gamma_{t}^{e} \subset \Gamma_{t}^{{}}$

• (c) traction reciprocity condition: $\user2{n}^{a} {\varvec{\upsigma}}^{a} = \user2{n}^{b} {\varvec{\upsigma}}^{b}$ on all $\Gamma_{ab}^{{}}$

• (d) compatibility: ${\mathbf{u}}^{a} = {\mathbf{u}}^{b}$ on all $\Gamma_{ab}^{{}}$

• (e) displacement boundary condition: $\mathbf{u} = {\overline{\mathbf{u}}}$ on all $\Gamma_{u}^{e} \subset \Gamma_{u}^{{}}$

• (f) constitutive relation: ${\varvec{\upsigma}} = {\mathbf{C\varepsilon }}$ in all Ω^e

• (g) strain–displacement relation: ${\varvec{\upvarepsilon}} = \user2{L}{\mathbf{u}}$ in all Ω^e

where

$$ {\varvec{\upsigma}} = \{ \sigma_{xx} ,\sigma_{yy} ,\sigma_{zz} ,\sigma_{yz} ,\sigma_{zx} ,\sigma_{xy} \}^{T} , $$

$$ {\varvec{\upvarepsilon}} = \{ \varepsilon_{xx} ,\varepsilon_{yy} ,\varepsilon_{zz} ,2\varepsilon_{yz} ,2\varepsilon_{zx} ,2\varepsilon_{xy} \}^{T} , $$

u is the displacement vector, $\overline{{\mathbf{b}}}$ is the prescribed body force vector,

$$ \user2{L} = \left[ {\begin{array}{*{20}c} {\partial /\partial x} & 0 & 0 & 0 & {\partial /\partial z} & {\partial /\partial y} \\ 0 & {\partial /\partial y} & 0 & {\partial /\partial z} & 0 & {\partial /\partial x} \\ 0 & 0 & {\partial /\partial z} & {\partial /\partial y} & {\partial /\partial x} & 0 \\ \end{array} } \right]^{T} $$

and

$$ \user2{n} = \left[ {\begin{array}{*{20}c} {n_{x} } & 0 & 0 & 0 & {n_{z} } & {n_{y} } \\ 0 & {n_{y} } & 0 & {n_{z} } & 0 & {n_{x} } \\ 0 & 0 & {n_{z} } & {n_{y} } & {n_{x} } & 0 \\ \end{array} } \right] $$

In the expressions, ε _ij , σ _ij and n _i denote the components of strain, stress and unit outward normal vector of the element boundary, respectively. Γ _ab denotes the common boundary between the adjacent elements “a” and “b”. Thus, $\user2{n}_{a}$ = $-\user2{n}_{b}$. The element designation appearing as a superscript would be dropped unless ambiguity may arise. Following (1), the properties below on element boundary can be assumed:

$$ \begin{gathered} \mathop \cup \limits_{e} \Omega^{e} = \Omega ,\quad \mathop \cup \limits_{e} \Gamma_{u}^{e} = \Gamma_{u},\quad\mathop \cup \limits_{e} \Gamma_{t}^{e} = \Gamma_{t} ,\quad\Gamma_{u}^{e} \cup \Gamma_{t}^{e} \cup \Gamma_{m}^{e} = \partial \Omega^{e} \hfill \\ \Gamma_{u}^{e} \cap \Gamma_{t}^{e} = \Gamma_{t}^{e} \cap \Gamma_{m}^{e} = \Gamma_{m}^{e} \cap \Gamma_{u}^{e} = \emptyset \hfill \\ \end{gathered} $$

(2)

where $\Gamma_{m}^{e}$ denotes the portion of ∂Ω^e which is common to the adjacent element(s) of element “e”. The virtual work statement can be stated as:

$$ \sum\limits_{e} {\left(\int\limits_{{\Omega^{e} }} {({\varvec{\upsigma}}^{T} \delta {\varvec{\upvarepsilon}} - {\overline{\mathbf{b}}}^{T} \delta {\mathbf{u}})d\Omega - \int\limits_{{\Gamma_{t}^{e} }} {{\overline{\mathbf{t}}}^{T} \delta {\mathbf{u}}d\Gamma } }\right)} = 0 $$

(3)

in which δ is the virtual symbol. For the statement, (d)–(g) are auxiliary conditions. In the context of the weighted residual method, the displacement u leading to stress/strain and the virtual displacement δ u leading to virtual strain are the trial and the test functions, respectively. By substituting the following version of divergence theorem

$$ \int\limits_{{\Omega^{e} }} {(\;{\varvec{\upsigma}}^{T} \delta (\user2{L}{\mathbf{u}}) + (\user2{L}^{T} {\varvec{\upsigma}})^{T} \delta {\mathbf{u}}\;)d\Omega = \int\limits_{{\Gamma_{t}^{e} \cup \Gamma_{m}^{e} }} {(\user2{n}{\varvec{\upsigma}})^{T} \delta {\mathbf{u}}d\Omega } } $$

(4)

into (3), the latter becomes

$$ \sum\limits_{e} {\left({ -\int\limits_{{\Omega^{e} }} {(\user2{L}^{T} {\varvec{\upsigma}}+{\overline{\mathbf{b}}})^{T} \delta {\mathbf{u}}d\Omega\,+\,\int\limits_{{\Gamma_{t}^{e} }} {(\user2{n}{\varvec{\upsigma}}-{\overline{\mathbf{t}}})^{T} \delta {\mathbf{u}}d\Gamma\,+\,\int\limits_{{\Gamma_{m}^{e} }} {(\user2{n}{\varvec{\upsigma}})^{T} \delta {\mathbf{u}}d\Gamma } } } } \right) = 0} $$

(5)

The last integral after pairing up with those arising from the adjacent elements can be expressed as:

$$ \sum\limits_{e} {\int\limits_{{\Gamma_{m}^{e} }} {(\user2{n}{\varvec{\upsigma}})^{T} \delta {\mathbf{u}}d\Gamma } = \sum\limits_{a,b} {\int\limits_{{\Gamma_{ab}^{{}} }} {\;\left( {[(\user2{n}{\varvec{\upsigma}})^{a} ]^{T} \delta {\mathbf{u}}^{a} + [(\user2{n}{\varvec{\upsigma}})^{b} ]^{T} \delta {\mathbf{u}}^{b} } \right)\;d\Gamma } } } $$

(6)

Provided that the virtual displacement is compatible, i.e.

$$ \delta {\mathbf{u}}^{a} = \delta {\mathbf{u}}^{b} \quad{\text{on}}\;{\text{all}}\;\Gamma_{ab} $$

(7)

δ u ^a and δ u ^b on Γ _ab can simply be denoted as δ u. In this light, (5) becomes

$$ \sum\limits_{e} {\left( -{\int\limits_{{\Omega^{e} }} {(\user2{L}^{T} {\varvec{\upsigma}} + {\overline{\mathbf{b}}})^{T} \delta {\mathbf{u}}d\Omega + \int\limits_{{\Gamma_{t}^{e} }} {(\user2{n}{\varvec{\upsigma}} - {\overline{\mathbf{t}}})^{T} \delta {\mathbf{u}}d\Gamma } } } \right) + \sum\limits_{a,b} {\int\limits_{{\Gamma_{ab}^{{}} }} {\;[(\user2{n}{\varvec{\upsigma}})^{a} + (\user2{n}{\varvec{\upsigma}})^{b} ]^{T} \delta {\mathbf{u}}\;d\Gamma } } = 0} $$

(8)

which is the weak form of (a), (b) and (c).

2.1 Galerkin finite element method

In Galerkin FEM, the bases of the displacement and virtual displacement are the same. For element “e”, they can be expressed as:

$$ {\mathbf{u}}^{e} = {\mathbf{Nd}}^{e} \;{\text{and}}\;\delta {\mathbf{u}}^{e} = {\mathbf{N}}\delta {\mathbf{d}}^{e} $$

(9)

in which ${\mathbf{d}}^{e}$ is the element displacement vector embracing all displacement vectors of the element nodes and N is constructed using the parametric coordinates of the element and can be termed as the parametric interpolation matrix. The renowned property of parametric interpolation is that (d), (e) and (7) are strictly satisfied. By invoking (9), (3) becomes

$$ \sum\limits_{e} {(\delta {\mathbf{d}}^{e} )^{T} ({\mathbf{k}}_{s}^{e} \cdot {\mathbf{d}}^{e} - {\mathbf{f}}^{e} )} = 0 $$

(10)

in which

$$ {\mathbf{k}}_{s}^{e} = \int\limits_{{\Omega^{e} }} {(\user2{L}{\mathbf{\mathbf N}})^{T} {\mathbf{C}}(\user2{L}{\mathbf{\mathbf N}})d\Omega } $$

is the symmetric element stiffness matrix,

$$ {\mathbf{f}}^{e} = \int\limits_{{\Omega^{e} }} {{\mathbf{N}}^{T} {\overline{\mathbf{b}}}d\Omega } + \int\limits_{{\Gamma_{t}^{e} }} {{\mathbf{N}}^{T} {\overline{\mathbf{t}}}d\Gamma } $$

is the element force vector.

2.2 Unsymmetric finite element method

In US-FEM, which is based on the Petrov–Galerkin formulation, the displacement and the virtual displacement are different and they can be expressed as (Rajendran and Liew 2003):

$$ {\mathbf{u}}^{e} = {\mathbf{{\mathbf M}d}}^{e} \quad{\text{and}}\quad\delta {\mathbf{u}}^{e} = {\mathbf{N}}\delta {\mathbf{d}}^{e} $$

(11)

where M is constructed using metric or Cartesian coordinates and it can be termed as the metric interpolation matrix. As the chosen virtual displacement remains to be parametric and compatible, the virtual work statement remains to be the weak form of (a) to (c). Substitution of (11) into (3) gives

$$ \sum\limits_{e} {(\delta {\mathbf{d}}^{e} )^{T} ({\mathbf{k}}_{u}^{e} \cdot {\mathbf{d}}^{e} - {\mathbf{f}}^{e} )} = 0 $$

(12)

in which

$$ {\mathbf{k}}_{u}^{e} = \int\limits_{{\Omega^{e} }} {(\user2{L}{\mathbf{\mathbf N}})^{T} {\mathbf{C}}(\user2{L}{\mathbf{M}})d\Omega } $$

is the unsymmetric element stiffness matrix, and the element force vector has been defined under (10).

2.3 Patch tests for unsymmetric finite element models

Note worthily, the metric interpolated displacement is not compatible in general, i.e., it fails (d) and (e). While patch test fulfillment have been numerically demonstrated for US-FE models, it is not difficult to prove analytically that the generalized patch test (Taylor et al. 1986) can be fulfilled by US-FE models using the individual element test abbreviated as IET (Felippa et al. 1995).

For an arbitrary linear displacement field u _L which leads to a constant stress state σ _c  = C L u _L , the first requirement of IET is that when the element displacement vector ${\mathbf{d}}^{e}$ is prescribed to ${\mathbf{d}}_{L}^{e}$ obtained from u _L , σ _c can be reproduced in the element. It can be noted in the next section that the metric interpolation M is constructed such that the following is valid:

$$ {\mathbf{M}} \cdot {\mathbf{d}}_{L}^{e} = {\mathbf{u}}_{L} $$

(13)

By invoking the auxiliary conditions (f) and (g), the first requirement (σ _c  = C(L M)${\mathbf{d}}_{L}^{e}$) of IET can be met. The second requirement of the test is the pairwise cancellation of tractions among adjacent elements subjected to the same uniform stress. By invoking (13) and the divergence theorem,

$$ \begin{aligned} {\mathbf{k}}_{u}^{e} \cdot {\mathbf{d}}_{L}^{e} \; & = \;\int\limits_{{\Omega ^{e} }} {(\user2{L}{\mathbf{{\mathbf N}}})^{T} {\mathbf{C}}(\user2{L}{\mathbf{u}}_{L} )d\Omega } \\ & = \int\limits_{{\Omega ^{e} }} {(\user2{L}{\mathbf{{\mathbf N}}})^{T} {\mathbf{\varvec{\upsigma}}}_{c} d\Omega } = \int\limits_{{\partial \Omega ^{e} }} {{\mathbf{{\mathbf N}}}^{T} \user2{n}{\mathbf{\varvec{\upsigma}}}_{c} d\Omega } \\ \end{aligned} $$

(14)

Since N is compatible, N ^a and N ^b in the following expression are identical over the common boundary Γ _ab of elements “a” and “b”. Thus,

$$ \begin{gathered} \int\limits_{{\Gamma_{ab}^{{}} }} {\;[({\mathbf{N}}^{T} \user2{n}{\varvec{\upsigma}}_{c} )^{a} + ({\mathbf{N}}^{T} \user2{n}{\varvec{\upsigma}}_{c} )^{b} ]\;d\Gamma } \hfill \\ = \int\limits_{{\Gamma_{ab}^{{}} }} {\;{\mathbf{N}}^{T} [\user2{n}^{a} + \user2{n}^{b} ]{\varvec{\upsigma}}_{c} d\Gamma } = {\mathbf{0}} \hfill \\ \end{gathered} $$

and the pairwise cancellation is also met. The generalized patch test also tests the element stability which can be addressed by examining whether the element exhibits spurious zero energy mode(s). To conclude, US-FE models can pass the generalized patch test provided that (13) is met by the metric interpolation and the element model does not exhibit any spurious zero energy mode.

3 Existing US-FE models

UQ8 and UH20 are US-FE models devised in References (Rajendran and Liew 2003; Ooi et al. 2004). In this section, the trial or metric interpolated displacements of the two models and the existing measure to secure invariance are briefly reviewed.

3.1 UQ8—the unsymmetric 8-node quadrilateral plane element

In analogous to the parametric interpolation basis of the Q8 element, the metric interpolation can be constructed by first considering the basis below for the x-displacement component of the element:

$$ \begin{gathered} u(x,y) = \left[ {1,{\hat{x}} ,{\hat{y}} ,{\hat{x}}^{2} ,{\hat{x}} {\hat{y}} ,{\hat{y}}^{2} ,{\hat{x}}^{2} {\hat{y}} ,{\hat{x}} {\hat{y}}^{2} } \right]\left\{ {\begin{array}{*{20}c} {\alpha_{1} } \\ \vdots \\ {\alpha_{8} } \\ \end{array} } \right\} \hfill \\ \quad\quad\quad = {\mathbf{p}}_{Q} ({\hat{x}} ,{\hat{y}} )\left\{ {\begin{array}{*{20}c} {\alpha_{1} } \\ \vdots \\ {\alpha_{8} } \\ \end{array} } \right\} \hfill \\ \end{gathered} $$

(15)

in which $\hat{x} = x - x_{o}$, $\hat{y} = y - y_{o}$, ($x_{o}$, $y_{o}$) is commonly taken as the parametric origin of the element, α’s are the coefficients to be determined and the trial function matrix p _Q is self-defined. US-FEM imposes the nodal interpolation property for the trial displacement and leads to

$$ \left\{ {\begin{array}{*{20}c} {u_{1} } \\ \vdots \\ {u_{8} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{Q} ({\hat{x}}_{1} ,{\hat{y}}_{1} )} \\ \vdots \\ {{\mathbf{p}}_{Q} ({\hat{x}}_{8} ,{\hat{y}}_{8} )} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\alpha_{1} } \\ \vdots \\ {\alpha_{8} } \\ \end{array} } \right\} $$

(16)

where u _i and ($\hat{x}_{i}$, $\hat{y}_{i}$) are the x-displacement and the ($\hat{x}$, $\hat{y}$)-coordinates of the i-th node, respectively. Provided that the matrix in (16) is invertible, the requirement in (13) can be satisfied. Back-substituting (16) into (15) gives

$$ \begin{aligned} u(x,y) &= {\mathbf{p}}_{Q} ({\hat{x}} ,{\hat{y}} )\left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{Q} ({\hat{x}}_{1} ,{\hat{y}}_{1} )} \\ \vdots \\ {{\mathbf{p}}_{Q} ({\hat{x}}_{8} ,{\hat{y}}_{8} )} \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {u_{1} } \\ \vdots \\ {u_{8} } \\ \end{array} } \right\} \hfill \\ &= [M_{Q1} , \ldots ,M_{Q8} ]\left\{ {\begin{array}{*{20}c} {u_{1} } \\ \vdots \\ {u_{8} } \\ \end{array} } \right\} \hfill \\ \end{aligned} $$

(17)

in which the metric nodal interpolation functions M’s can be obtained. M’s are also applicable to other displacement components. Thus, the metric interpolated displacement can be expressed as:

$$ {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} u \\ v \\ \end{array} } \right\} = [M_{Q1} {\mathbf{I}}_{2} , \ldots ,M_{Q8} {\mathbf{I}}_{2} ]\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{1} } \\ \vdots \\ {{\mathbf{u}}_{8} } \\ \end{array} } \right\} = {\mathbf{M}}_{Q} \cdot {\mathbf{d}}^{e} $$

(18)

where I _m is the m-th order identity matrix.

3.2 UH20—the unsymmetric 20-node hexahedral element

In analogous to the parametric interpolation basis of the H20 element, the metric interpolation can be constructed by first considering the basis below for the x-displacement component of the element:

$$ u(x,y,z) = {\mathbf{p}}_{H} ({\hat{x}} ,{\hat{y}} ,{\hat{z}} )\left\{ {\begin{array}{*{20}c} {\alpha_{1} } \\ \vdots \\ {\alpha_{20} } \\ \end{array} } \right\} $$

(19)

where ${\mathbf{p}}_{H} ({\hat{x}} ,{\hat{y}} ,{\hat{z}} ) = [1,{\hat{x}} ,{\hat{y}} ,{\hat{z}} ,{\hat{x}}^{2} ,{\hat{y}}^{2} ,{\hat{z}}^{2} ,{\hat{y}} {\hat{z}} ,{\hat{z}} {\hat{x}} ,{\hat{x}} {\hat{y}} ,$ ${\hat{x}}^{2} {\hat{y}} ,{\hat{x}} {\hat{y}}^{2} ,{\hat{y}}^{2} {\hat{z}} ,{\hat{y}} {\hat{z}}^{2} ,{\hat{z}}^{2} {\hat{x}} ,{\hat{z}} {\hat{x}}^{2} ,{\hat{x}} {\hat{y}} {\hat{z}} ,{\hat{x}}^{2} {\hat{y}} {\hat{z}} ,{\hat{y}}^{2} {\hat{z}} {\hat{x}} ,{\hat{z}}^{2} {\hat{x}} {\hat{y}} ].$ By repeating what has been done for UQ8, the metric interpolated displacement for the present UH20 can be expressed as:

$$ {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right\} = [M_{H1} {\mathbf{I}}_{3} , \ldots ,M_{H20} {\mathbf{I}}_{3} ]\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{1} } \\ \vdots \\ {{\mathbf{u}}_{20} } \\ \end{array} } \right\} = {\mathbf{M}}_{H} \cdot {\mathbf{d}}^{e} $$

(20)

where

$$ [M_{H1} , \ldots ,M_{H20} ] = {\mathbf{p}}_{H} (x,y,z)\left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{H} ({\hat{x}}_{1} ,{\hat{y}}_{1} ,{\hat{z}}_{1} )} \\ \vdots \\ {{\mathbf{p}}_{H} ({\hat{x}}_{20} ,{\hat{y}}_{20} ,{\hat{z}}_{20} )} \\ \end{array} } \right]^{ - 1} . $$

3.3 Existing measure to secure the invariance of UQ8 model

The numerical tests in (Rajendran and Liew 2003; Ooi et al. 2004) show that UQ8 and UH20 possess good immunity to various mesh distortions and can exactly reproduce the quadratic, in x and y, displacement field. However, it was noted later that they are not invariant and the proposed remedy in Reference (Ooi et al. 2008) is to employ a corotational Cartesian frame (x′, y′) as shown in Fig. 1a in which the x′-axis is parallel to the line connecting nodes 4 and 8. The interim element stiffness matrix ${\mathbf{k}}_{ul}^{e}$ defined with respect to x′- and y′- displacements is firstly computed using p _Q (x′, y′). The one defined with respect to x- and y- displacements is then obtained from ${\mathbf{k}}_{ul}^{e}$ by transformation as:

Fig. 1

a The 8-node quadrilateral element. b The 20-node hexahedral element

$$ {\mathbf{k}}_{ua}^{e} = {\mathbf{Rk}}_{ul}^{e} {\mathbf{R}}^{T} $$

(21)

where R is the 16 × 16 block diagonal transformation matrix given as

$$ {\mathbf{R}} = diag.\{ {\mathbf{R}}_{\theta } ,{\mathbf{R}}_{\theta } ,{\mathbf{R}}_{\theta } ,{\mathbf{R}}_{\theta } ,{\mathbf{R}}_{\theta } ,{\mathbf{R}}_{\theta } ,{\mathbf{R}}_{\theta } ,{\mathbf{R}}_{\theta } \} $$

in which

$$ {\mathbf{R}}_{\theta } = \left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } \\ {\sin \theta } & {\cos \theta } \\ \end{array} } \right] $$

and θ is the inclination of the x′-axis to the x-axis, see Fig. 1a. The resulting unsymmetric Q8 would be abbreviated as UQ8m.

Although the invariance of UQ8 and UH20 can be secured by using a corotational Cartesian frame, the transformation induces quite a number of operations. Moreover, the resultant element models are not isotropic, i.e., the element predictions are sensitive to the chosen connectivity which defines the parametric coordinate axes. In the next two sections, more efficient measures are introduced to secure the invariance as well as the isotropy of UQ8 and UH20, respectively.

4 Securing the invariance and isotropy of UQ8

To secure the invariance and isotropy of an element, the bases of its variables should be invariant and isotropic, respectively (Sze et al. 1992). Using corotational coordinates (such as (x′, y′) and (ξ, η)) as the arguments of p _Q can automatically secure the invariance. To secure both for UQ8, the non-dimensional skew coordinates ($\overline{\xi }$, $\overline{\eta }$) of Yuan, Huang & Pian (Yuan et al. 1993) can be used as the arguments of p _Q . Starting from the parametric interpolation of the global coordinates, namely,

$$ \left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} = \sum\limits_{n = 1}^{8} {N_{i} (\xi ,\eta )\left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ \end{array} } \right\}} $$

(22)

in which N _i is the parametric interpolation function of the i-th node, one can derive

$$ \left[ {\begin{array}{*{20}c} {a_{\xi } } & {b_{\xi } } \\ {a_{\eta } } & {b_{\eta } } \\ \end{array} } \right] = \left. {\left[ {\begin{array}{*{20}c} {\partial x/\partial \xi } & {\partial y/\partial \xi } \\ {\partial x/\partial \eta } & {\partial y/\partial \eta } \\ \end{array} } \right]} \right|_{\xi = \eta = 0} $$

(23)

and the non-dimensional skew coordinates (Yuan et al. 1993) are:

$$ \left\{ {\begin{array}{*{20}c} {\overline{\xi }} \\ {\overline{\eta }} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {a_{\xi } } & {b_{\xi } } \\ {a_{\eta } } & {b_{\eta } } \\ \end{array} } \right]^{{ - T}} \left( {\left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\}_{{\xi = \eta = 0}} } \right) $$

(24)

in which “−T” is the compounded inverse and transpose matrix operator. It is trivial that ($\overline{\xi }$, $\overline{\eta }$) are corotational and, thus, p _Q ($\overline{\xi }$, $\overline{\eta }$) is invariant. To show that p _Q $\left( {\overline{\xi } ,\overline{\eta } } \right)$ is isotropic, one can first check that the new $\overline{\xi }$- and $\overline{\eta }$-axes would assume the existing positive/negative $\overline{\xi }$- and $\overline{\eta }$-axes when the element connectivity is changed. As p _Q is balanced in its two arguments, the basis of p _Q $\left( {\overline{\xi } ,\overline{\eta } } \right)$ would not change with the connectivity. Hence, p _Q $\left( {\overline{\xi } ,\overline{\eta } } \right)$ is also isotropic. The good immunity to mesh distortion is retained as p _Q ($\overline{\xi }$,$\overline{\eta }$) is second order complete in (x, y). The resulting element would be abbreviated as UQ8*. Of course, other corotational skew coordinates can also secure the invariance, isotropy and good immunity to mesh distortion.

The numerical tests including those with unevenly placed nodes and curved edges used by (Rajendran and Liew 2003) have been repeated for the three US Q8 elements, viz., UQ8, UQ8m and UQ8* described in Sects. 3.1, 3.3 and the present section, respectively. As their predictions are largely the same, only two sets of tests are further described here.

Patch Tests, Invariance tests and Isotropy Tests UQ8, UQ8m and UQ8* pass the patch test prescribed by Macneal and Harder (1985) for plane elements. To test whether they are invariant and isotropic, the element geometry used by (Sze et al. 1992) and shown in Fig. 2 is considered. The coordinates of A to D are given with respect to the global coordinates (x, y). The local Cartesian coordinate frame $\bar{x}$-$\bar{y}$ attached to nodes A and B is rotated about A. The angle between the x- and $\bar{x}$- axes is denoted as ϕ. All dofs of nodes A and D are restrained and 100 units of force is applied to node C along the $\bar{x}$-direction and the displacement of node C along the same direction are computed. To test whether the element models are invariant, ϕ equal to 0°, 30°, 60° and 90° are considered. To test whether the element models are isotropic, the first parametric coordinate ξ is taken to be ξ ₁ and then ξ ₂ as shown in the figure. It can be seen from Table 1 that UQ8 is isotropic but not invariant whilst UQ8m is invariant but not isotropic. Both Q8 and UQ8* are invariant and isotropic. Under the 2 × 2 integration rule, all elements possess the well-known incompatible spurious zero energy mode (Cook et al. 2002) which disappears when the 3 × 3 integration is employed.

Fig. 2

Two-dimensional single-element structure for testing invariance and isotropy

Table 1 The computed displacement of node C along the $\bar{x}$-direction, see Fig. 2

Cantilevers subject to Pure Bending Moment Tests using cantilevers of different aspect ratios modelled by regular and distorted meshes are considered by UQ8 (Rajendran and Liew 2003). The displacement solutions are quadratic in x and y. All the US Q8 models can reproduce the exact solution in these tests regardless whether the 2 × 2 or 3 × 3 integration rule is employed.

5 Securing the invariance and isotropy of UH20

An invariant and isotropic US H20 element can be formulated in way analogous to that of UQ8*. For the 20-node element as shown in Fig. 1b,

$$ \left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\} = \sum\limits_{n = 1}^{20} {N_{i} (\xi ,\eta ,\zeta )\left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}} $$

(25)

from which one can derive

$$ \left[ {\begin{array}{*{20}c} {a_{1} } & {b_{1} } & {c_{1} } \\ {a_{2} } & {b_{2} } & {c_{2} } \\ {a_{3} } & {b_{3} } & {c_{3} } \\ \end{array} } \right] = \left. {\left[ {\begin{array}{*{20}c} {\partial x/\partial \xi } & {\partial y/\partial \xi } & {\partial z/\partial \xi } \\ {\partial x/\partial \eta } & {\partial y/\partial \eta } & {\partial z/\partial \eta } \\ {\partial x/\partial \zeta } & {\partial y/\partial \zeta } & {\partial z/\partial \zeta } \\ \end{array} } \right]} \right|_{\xi = \eta = \zeta = 0} $$

(26)

The 3D non-dimensional skew coordinates analogous to the 2D ones expressed in (24) are:

$$ \left\{ {\begin{array}{*{20}c} {\bar{\xi }} \\ {\bar{\eta }} \\ {\bar{\zeta }} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {a_{1} } & {b_{1} } & {c_{1} } \\ {a_{2} } & {b_{2} } & {c_{2} } \\ {a_{3} } & {b_{3} } & {c_{3} } \\ \end{array} } \right]^{{ - T}} \left( {\left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\} - \left. {\left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\}} \right|_{{\xi = \eta = \zeta = 0}} } \right) $$

(27)

The new element employs the trial function matrix p _H ($\overline{\xi }$, $\overline{\eta }$, $\overline{\zeta }$) for u, v and w, see (19) for the definition of p _H . It should be remarked that p _H ($\overline{\xi }$, $\overline{\eta }$, $\overline{\zeta }$) is second order complete in x, y and z. This element will be abbreviated as UH20*. Though it should be trivial, (Ooi et al. 2008) did not discuss a US H20 counterpart of UQ8m, see Sect. 3.3.

The numerical tests in Reference (Ooi et al. 2004) for the 20-node elements have been repeated. Again, the predictions of UH20 and UH20* are largely the same. Only two tests are further described.

Patch tests, invariance tests and isotropy tests Both UH20 and UH20* pass the patch test in (Macneal and Harder 1985) for 3D elements. To test the invariance and isotropy, the problem in Fig. 3 is employed (Sze et al. 1992). The coordinates of A to D are given with respect to global coordinates (x, y, z). The local Cartesian frame $\overline{x}$–$\overline{y}$–$\overline{z}$ is attached to the base of the element and four corner nodes are fully restrained. Two forces of magnitudes 100 and 200 units are applied respectively to E and F along the $\overline{x}$-direction. The $\overline{x}$–$\overline{z}$ plane is rotated about $\overline{y}$ anti-clockwisely by angle ϕ. With the ζ-axis kept normal to the x–z-plane, the two connectivity settings leading to ξ ₁ and ξ ₂ being the ξ-axis of the element are considered. The predicted displacements along the $\overline{x}$-direction at E are computed and reported in Table 2 for different ϕ and ξ-axes. All elements are evaluated by the 3rd order quadrature as the supports are not adequate to suppress the zero energy modes induced by the 2nd order quadrature. It can be seen from Table 2 that H20 and UH20* are invariant and isotropic. Though UH20 is isotropic, it is not invariant. Isotropy for UH20* is further verified by other combinations of the parametric axes among which ζ-axis is not normal to the x–z-plane.

Fig. 3

Three-dimensional single-element structure for testing invariance and isotropy

Table 2 The computed displacement of node E along the $\bar{x}$-direction, see Fig. 3

Cantilevers subject to pure bending moment Tests using 3D cantilevers of different aspect ratios modelled by regular and distorted meshes are considered by UH20 in (Ooi et al. 2004). The displacement solutions are quadratic in x, y and z. Both UH20 and UH20* can reproduce the exact solution in these tests regardless the 2 × 2 or 3 × 3 integration rule is employed.

6 Unsymmetric Q4 based on Trefftz functions

In this section, the element formulation for an unsymmetric Q4 element will be described followed by a number of numerical examples on the proposed and other elements.

6.1 Unsymmetric Trefftz formulation for 4-node quadrilateral plane element

For the Q4 element shown in Fig. 4, the parametric interpolant for its i-th node at (ξ _i , η _i ) is N _i  = (1 + ξ _i ξ)(1 + η _i η)/4 which leads to the following interpolated coordinates (x, y) and test displacement, i.e.,

Fig. 4

The 4-node quadrilateral element, r _ξ and r _η are the neutral axes for the bending modes

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} x \\ y \\ \end{array} } \right\} = \sum\limits_{i = 1}^{4} {N_{i} \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ \end{array} } \right\}} = \left\{ {\begin{array}{*{20}c} {x_{0} + a_{\xi } \xi + a_{\xi \eta } \xi \eta + a_{\eta } \eta } \\ {y_{0} + b_{\xi } \xi + b_{\xi \eta } \xi \eta + b_{\eta } \eta } \\ \end{array} } \right\}, \hfill \\ \delta {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} {\delta u} \\ {\delta v} \\ \end{array} } \right\} = \sum\limits_{i = 1}^{4} {N_{i} \left\{ {\begin{array}{*{20}c} {\delta u_{i} } \\ {\delta v_{i} } \\ \end{array} } \right\}} \hfill \\ \end{gathered} $$

(28)

where

$$ \left[ {\begin{array}{*{20}c} {x_{0} } & {y_{0} } \\ {a_{\xi } } & {b_{\xi } } \\ {a_{\xi \eta } } & {b_{\xi \eta } } \\ {a_{\eta } } & {b_{\eta } } \\ \end{array} } \right] = \frac{1}{4}\left[ {\begin{array}{*{20}c} { + 1} & { + 1} & { + 1} & { + 1} \\ { - 1} & { + 1} & { + 1} & { - 1} \\ { + 1} & { - 1} & { + 1} & { - 1} \\ { - 1} & { - 1} & { + 1} & { + 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{1} } & {y_{1} } \\ {x_{2} } & {y_{2} } \\ {x_{3} } & {y_{3} } \\ {x_{4} } & {y_{4} } \\ \end{array} } \right] $$

(29)

As mentioned in Introduction, Trefftz solutions will be employed as the trial displacement functions. In this light, two local metric coordinate systems (r _ξ , s _ξ ) and (r _η , s _η ) both with origin at (x ₀, y ₀) are introduced. The r _ξ - and r _η -axes are parallel to ξ- and η-axes at (x ₀, y ₀), respectively, see Fig. 4. Thus,

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {r_{\xi } } \\ {s_{\xi } } \\ \end{array} } \right\} = \frac{1}{{\sqrt {a_{\xi }^{2} + b_{\xi }^{2} } }}\left\{ {\begin{array}{*{20}c} {a_{\xi } {\hat{x}} + b_{\xi } {\hat{y}} } \\ { - b_{\xi } {\hat{x}} + a_{\xi } {\hat{y}} } \\ \end{array} } \right\}, \hfill \\ \left\{ {\begin{array}{*{20}c} {r_{\eta } } \\ {s_{\eta } } \\ \end{array} } \right\} = \frac{1}{{\sqrt {a_{\eta }^{2} + b_{\eta }^{2} } }}\left\{ {\begin{array}{*{20}c} {a_{\eta } {\hat{x}} + b_{\eta } {\hat{y}} } \\ { - b_{\eta } {\hat{x}} + a_{\eta } {\hat{y}} } \\ \end{array} } \right\} \hfill \\ \end{aligned} $$

(30)

in which $\hat{x}$(ξ,η) = x − x ₀ = a _ξ ξ + a _ξη ξη + a _η η and $\hat{y}$(ξ,η) = y − y ₀ = b _ξ ξ + b _ξη ξη + b _η η.

In hybrid stress elements, the optimal or close to optimal non-constant stress modes for Q4 are the two bending modes (Pian and Sumihara 1984) $\left\{ {\sigma_{\xi } ,\sigma_{\eta } ,\sigma_{\xi \eta } } \right\} = \left\{ {\eta ,0,0} \right\}$ and $\left\{ {0,\xi ,0} \right\}$ defined with respect to the parametric coordinates. They are close to

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{{r_{\xi } }} } \\ {\sigma_{{s_{\xi } }} } \\ {\sigma_{{r_{\xi } s_{\xi } }} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {s_{\xi } } \\ 0 \\ 0 \\ \end{array} } \right\}\quad{\text{and}}\quad\left\{ {\begin{array}{*{20}c} {\sigma_{{r_{\eta } }} } \\ {\sigma_{{s_{\eta } }} } \\ {\sigma_{{r_{\eta } s_{\eta } }} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {s_{\eta } } \\ 0 \\ 0 \\ \end{array} } \right\} $$

(31)

which arise from the following displacement modes defined with respect to (r _ξ , s _ξ ) and (r _η , s _η )

$$ \left\{ {\begin{array}{*{20}c} {u_{{r_{\xi } }} } \\ {u_{{s_{\xi } }} } \\ \end{array} } \right\} = \frac{1}{{\bar{E}}}\left\{ {\begin{array}{*{20}c} {2r_{\xi } s_{\xi } } \\ { - ({\bar{\upsilon }}s_{\xi }^{2} + r_{\xi }^{2} )} \\ \end{array} } \right\}\quad{\text{and}}\quad\left\{ {\begin{array}{*{20}c} {u_{{r_{\eta } }} } \\ {u_{{s_{\eta } }} } \\ \end{array} } \right\} = \frac{1}{{\bar{E}}}\left\{ {\begin{array}{*{20}c} {2r_{\eta } s_{\eta } } \\ { - ({\bar{\upsilon} }s_{\eta }^{2} + r_{\eta }^{2} )} \\ \end{array} } \right\} $$

(32)

in which $\overline{E}$ and $\overline{\upupsilon}$ appear in the material stiffness matrix for isotropic materials, i.e.

$$ {\mathbf{C}} = \left[ {\begin{array}{*{20}c} {{\bar{E}}/(1 - {\bar{\upsilon} }^{2} )} & {{\bar{\upsilon }}{\bar{E}}/(1 - {\bar{\upsilon }}^{2} )} & 0 \\ {{\bar{\upsilon} }{\bar{E}}/(1 - {\bar{\upsilon }}^{2} )} & {{\bar{E}}/(1 - {\bar{\upsilon }}^{2} )} & 0 \\ 0 & 0 & G \\ \end{array} } \right] $$

where $\overline{E}$ = $E$ = elastic modulus, $\overline{\upupsilon}$ = $\upsilon$ = Poisson’s ratio for plane stress problems; $\overline{E}$ = $E$/(1 − $\upsilon^{2}$), $\overline{\upupsilon}$ = $\upsilon /(1 - \upsilon )$ for plane strain problems; G = E/2/(1 + υ) is the shear modulus. Now, the trial displacement is taken to be

(33)

where $\hat{x} = x - x_{o}$, $\hat{y} = y - y_{o}$, p _Q4 is self-defined and, from (30), the transformation matrices are

$$ \begin{gathered} {\mathbf{T}}_{\xi } = \frac{1}{{\sqrt {a_{\xi }^{2} + b_{\xi }^{2} } }}\left[ {\begin{array}{*{20}c} {a_{\xi } } & { - b_{\xi } } \\ {b_{\xi } } & {a_{\xi } } \\ \end{array} } \right], \hfill \\ {\mathbf{T}}_{\eta } = \frac{1}{{\sqrt {a_{\eta }^{2} + b_{\eta }^{2} } }}\left[ {\begin{array}{*{20}c} {a_{\eta } } & { - b_{\eta } } \\ {b_{\eta } } & {a_{\eta } } \\ \end{array} } \right] \hfill \\ \end{gathered} $$

(34)

The first six terms represent the rigid body and constant strain modes. A distinct difference between the trial displacement modes in the present and those of the previous US elements is that some of the former modes are coupled. It would be more involved to derive the relation between the coefficients α and the nodal dofs. By enforcing the interpolation requirement at the four nodes,

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{Q4} (\xi_{1} ,\eta_{1} )} \\ \vdots \\ {{\mathbf{p}}_{Q4} (\xi_{4} ,\eta_{4} )} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\alpha_{1} } \\ \vdots \\ {\alpha_{8} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{1} } \\ \vdots \\ {{\mathbf{u}}_{4} } \\ \end{array} } \right\}\;{\text{and}}\;{\mathbf{u}} = {\mathbf{p}}_{Q4} (\xi ,\eta )\left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{Q4} (\xi_{1} ,\eta_{1} )} \\ \vdots \\ {{\mathbf{p}}_{Q4} (\xi_{4} ,\eta_{4} )} \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{1} } \\ \vdots \\ {{\mathbf{u}}_{4} } \\ \end{array} } \right\} $$

(35)

in which u _i is the nodal displacement vector. As all the displacement modes in (33) leads to equilibrating stress, they can be regarded as Trefftz functions for isotropic elasticity. Accordingly, the present element can be termed as a Trefftz unsymmetric element and will be abbreviated as TQ4. It is worth mentioning that the present element is based on the single-field virtual work principle whereas hybrid and most Trefftz elements employ multiple-fields variational statement (Pian and Sumihara 1984; Pian and Tong 1986; Yuan et al. 1993; Sze 2000; Qin 2003; Sze et al. 2004, 2010; Cen et al. 2011; Freitas and Moldovan 2011; Cao et al. 2012).

6.2 Numerical examples

The following four-node quadrilateral element models will be compared in the benchmark problems.

Q4:

the standard isoparametric four-node quadrilateral plane element.

PS:

the hybrid-stress element of Pian and Sumihara (1984).

TQ4:

the present Trefftz unsymmetric element.

General speaking, PS is less susceptible to mesh distortion than the popular QM6-2D incompatible displacement element (Sze 1992) and therefore other enhanced assumed strain elements. It is also popularly used for benchmarking new elements. To simplify the presentation, only Q4, and PS are included in the comparison with TQ4. The readers would hit “H8” and “TH8” in the comparison. They are the 8-node hexahedral elements to be discussed in Sect. 7.

6.2.1 Patch tests, invariance tests and isotropy tests

The tests described in Sect. 4 are repeated for TQ4. TQ4 passes the patch test, and it is invariant and isotropic.

6.2.2 Two-element cantilever

The 10 × 2 cantilever commonly adopted to examine the susceptibility to mesh distortion of the four-node element is shown in Fig. 5. The beam is modelled by two identical trapezoidal elements. The load cases of (1) end bending and (2) end shear are considered. The elastic modulus E and Poisson’s ratio ν are taken to be 1500 and 0.25, respectively. Plane stress condition is assumed. The element distortion is characterized by the length parameter ‘e’ which is varied between 0 and 4. The normalized deflection at tip A, V _A, and the normalized bending stress at the midpoint of the horizontal element edge B, σ _XB, closest to the sliding support are computed. Under (1) the pure bending, the TQ4 is able to reproduce the exact displacement and stress predictions as seen in Fig. 6. Under (2) the end shear, the exact solutions cannot be reproduced by TQ4. However, the predictions of TQ4 are still considerably better than those of PS as seen in Fig. 7.

Fig. 5

Two-element cantilever

Fig. 6

Normalized a deflection V _A and b stress σ _XB for the problem in Fig. 5 when (1) end moment is applied

Fig. 7

Normalized a deflection V _A and b stress σ _XB for the problem in Fig. 5 when (2) end shear load is applied

6.2.3 Five-element cantilever

The cantilever problem in Fig. 5 is now modelled by five elements as shown in Fig. 8. The longitudinal stresses under the end bending are plotted along the upper and lower edge of the cantilever in Fig. 9. The same stresses under the end shear are plotted in Fig. 10. On the other hand, the normalized deflections at the end nodes are tabulated in Table 3. Same as the previous examples, TQ4 can reproduce the exact solutions when the cantilever is loaded with end bending. Under the end shear, the end deflection of TQ4 remains highly accurate whilst its stress prediction is still marginally better than that of PS.

Fig. 8

The 5-element mesh for the cantilever problem shown in Fig. 5

Fig. 9

The normalized stress along a the upper edge and b lower edge of the cantilever in Fig. 8 when (1) end moment is applied

Fig. 10

The normalized stress along a the upper edge and b lower edge of the cantilever in Fig. 8 when (2) end shear is applied

Table 3 Normalized end deflections for the 5-element cantilever problem, see Fig. 8

6.2.4 Slender cantilever modelled by trapezoidal elements

The mesh modelling this slender cantilever was proposed by Macneal and Harder (1985). All elements are trapezoids as depicted in Fig. 11 and this problem has coined a locking phenomenon known as trapezoidal locking. The same supporting and loading conditions in Fig. 5 are applied here and normalized end deflections are computed and listed in Table 4. The predictions of TQ4 are either exact or very accurate. It is clear that other elements suffer from the trapezoidal locking. This problem is also employed to test the dilatational locking by assuming the plane strain condition and setting the Poisson’s ratio to 0.4999. The accuracy of PS and TQ4 are basically unaffected by the nearly material incompressibility whilst the accuracy of Q4 drops by more than half.

Fig. 11

The slender cantilever modelled by trapezoidal elements, l/h = 5

Table 4 Normalized end deflections for the thin cantilever problem, see Fig. 11

6.2.5 Shear panel

This is another popular benchmark problem in which a plane stress trapezoidal panel of unit thickness is clamped along the left edge and loaded by a unit vertical traction along the free edge as shown in Fig. 12. Using different mesh densities, the predicted maximum principal stress at A “σ _A(max)”, the minimum principal stress at B “σ _B(min)” and vertical deflection at point C “v _C” are computed and normalized by the highly converged solutions 0.2362, −0.2023 and 23.96, respectively, reported by (Cen et al. 2011). The normalized predictions are listed in Table 5. One can see that TQ4 delivers the highest coarse mesh accuracy and this point is most obvious in the displacement prediction.

Fig. 12

The shear panel loaded by a unit vertical traction at the free end

Table 5 Normalized predictions for the shear panel problem, see Fig. 12

7 Unsymmetric H8 based on Trefftz functions

In this section, the element formulation for an unsymmetric H8 element will be described followed by a number of numerical examples on the proposed and other elements.

7.1 Unsymmetric Trefftz formulation for 8-node hexahedral element

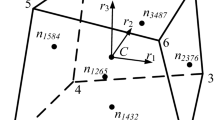
Figure 13 portrays the 8-node hexahedral element. The parametric interpolation function for i-th element node at (ξ _i , η _i , ζ _i ) is N _i  = (1 + ξ _i ξ)(1 + η _i η)(1 + ζ _i ζ)/8. Accordingly, the interpolated coordinates (x, y, z) can be expressed as:

Fig. 13

The 8-node hexahedral element

$$ \begin{gathered} {\mathbf{x}} = \left\{ {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right\} = \sum\limits_{i = 1}^{8} {N_{i} \left\{ {\begin{array}{*{20}c} {x_{i} } \\ {y_{i} } \\ {z_{i} } \\ \end{array} } \right\}} = \left\{ {\begin{array}{*{20}c} {x_{0} + a_{1} \xi + a_{2} \eta + a_{3} \zeta } \\ {y_{0} + b_{1} \xi + b_{2} \eta + b_{3} \zeta } \\ {z_{0} + c_{1} \xi + c_{2} \eta + c_{3} \zeta } \\ \end{array} } \right\} \hfill \\ \quad\quad + \left\{ {\begin{array}{*{20}c} {a_{4} \eta \zeta + a_{5} \zeta \xi + a_{6} \xi \eta + a_{7} \xi \eta \zeta } \\ {b_{4} \eta \zeta + b_{5} \zeta \xi + b_{6} \xi \eta + b_{7} \xi \eta \zeta } \\ {c_{4} \eta \zeta + c_{5} \zeta \xi + c_{6} \xi \eta + c_{7} \xi \eta \zeta } \\ \end{array} } \right\} \hfill \\ \end{gathered} $$

(36)

in which (x ₀, y ₀, z ₀) and (a _i , b _i , c _i )s are the average and linear combinations of (x _i , y _i , z _i )s, respectively. From (36), the basis vectors at ξ = η = ζ = 0 are

$$ \begin{aligned} [{\mathbf{g}}_{1} ,{\mathbf{g}}_{2} ,{\mathbf{g}}_{3} ] &= \left. {\left[ {\frac{{\partial {\mathbf{x}}}}{\partial \xi },\frac{{\partial {\mathbf{x}}}}{\partial \eta },\frac{{\partial {\mathbf{x}}}}{\partial \zeta }} \right]} \right|_{\xi = \eta = \zeta = 0}\\ &= \left[ {\begin{array}{*{20}c} {a_{1} } & {a_{2} } & {a_{3} } \\ {b_{1} } & {b_{2} } & {b_{3} } \\ {c_{1} } & {c_{2} } & {c_{3} } \\ \end{array} } \right]\\ \end{aligned} $$

(37)

In analogous to TQ4, three local Cartesian coordinate systems (r _i , s _i , t _i ) will be set up to express the Trefftz displacement functions. The unit vectors $\mathbf{e}_{{r}_{i}}$, $\mathbf{e}_{{s}_{i}}$ and $\mathbf{e}_{{t}_{i}}$ along r _i , s _i and t _i are taken to be

$$ {\mathbf{e}}_{{r_{i} }} = \frac{{{\mathbf{g}}_{i} }}{{|{\mathbf{g}}_{i} |}},\;{\mathbf{e}}_{{s_{i} }} = \frac{{{\mathbf{g}}_{j} \times {\mathbf{g}}_{i} }}{{|{\mathbf{g}}_{j} \times {\mathbf{g}}_{i} |}},\;{\mathbf{e}}_{{t_{i} }} = {\mathbf{e}}_{{r_{i} }} \times {\mathbf{e}}_{{s_{i} }} $$

(38)

where j = mod(i + 1,3) + 1. The projected lengths along the unit vectors are

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {r_{i} } \\ {s_{i} } \\ {t_{i} } \\ \end{array} } \right\} &= \left\{ {\begin{array}{*{20}c} {r(\xi ,\eta ,\zeta )} \\ {s(\xi ,\eta ,\zeta )} \\ {t(\xi ,\eta ,\zeta )} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{{r_{i} }}^{T} } \\ {{\mathbf{e}}_{{s_{i} }}^{T} } \\ {{\mathbf{e}}_{{t_{i} }}^{T} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\hat{x}} } \\ {{\hat{y}} } \\ {{\hat{z}} } \\ \end{array} } \right\} \hfill \\ &= \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{{r_{i} }}^{T} } \\ {{\mathbf{e}}_{{s_{i} }}^{T} } \\ {{\mathbf{e}}_{{t_{i} }}^{T} } \\ \end{array} } \right]\left( {\left\{ {\begin{array}{*{20}c} {a_{1} \xi + a_{2} \eta + a_{3} \zeta } \\ {b_{1} \xi + b_{2} \eta + b_{3} \zeta } \\ {c_{1} \xi + c_{2} \eta + c_{3} \zeta } \\ \end{array} } \right\}} \right. \hfill \\ &\quad+ \left. {\left\{ {\begin{array}{*{20}c} {a_{4} \eta \zeta + a_{5} \zeta \xi + a_{6} \xi \eta + a_{7} \xi \eta \zeta } \\ {b_{4} \eta \zeta + b_{5} \zeta \xi + b_{6} \xi \eta + b_{7} \xi \eta \zeta } \\ {c_{4} \eta \zeta + c_{5} \zeta \xi + c_{6} \xi \eta + c_{7} \xi \eta \zeta } \\ \end{array} } \right\}} \right) \hfill \\ \end{aligned} $$

(39)

In hybrid stress elements, it has been known that the twelve optimal or close to optimal non-constant stress modes for H8 (Pian and Tong 1986) defined with respect to the parametric coordinates are

(40)

Among them, the displacement modes pertinent to Groups 1, 2 and 3 will be mimicked by using (r ₁, s ₁, t ₁), (r ₂, s ₂, t ₂) and (r ₃, s ₃, t ₃), respectively. It can be shown that the following Trefftz displacement modes:

(41)

would lead to the following stress modes:

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{\xi } } \\ {\sigma_{\eta } } \\ {\sigma_{\zeta } } \\ {\sigma_{\eta \zeta } } \\ {\sigma_{\zeta \xi } } \\ {\sigma_{\xi \eta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {s_{i} } & {t_{i} } & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & {r_{i} } \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]\,{\mathbf{p}}_{i} \left\{ {\begin{array}{*{20}c} {\alpha_{3i + 4} } \\ {\alpha_{3i + 5} } \\ {\alpha_{3i + 6} } \\ \end{array} } \right\} $$

(42)

for isotropic materials. The trial displacement for the element is taken to be:

$$ \begin{aligned} {\mathbf{u}} = \left\{ {\begin{array}{*{20}c} u \\ v \\ w \end{array} } \right\} = \left[ {{\mathbf{I}}_{3} ,{\mathbf{I}}_{3} \hat{x},{\mathbf{I}}_{3} \hat{y},{\mathbf{I}}_{3} \hat{z},\left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{{r_{1} }}^{T} } \\ {{\mathbf{e}}_{{s_{1} }}^{T} } \\ {{\mathbf{e}}_{{t_{1} }}^{T} } \\ \end{array} } \right]^{{ - 1}} {\mathbf{p}}_{1} , \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{{r_{2} }}^{T} } \\ {{\mathbf{e}}_{{s_{2} }}^{T} } \\ {{\mathbf{e}}_{{t_{2} }}^{T} } \\ \end{array} } \right]^{{ - 1}} {\mathbf{p}}_{2} , \left[ {\begin{array}{*{20}c} {{\mathbf{e}}_{{r_{3} }}^{T} } \\ {{\mathbf{e}}_{{s_{3} }}^{T} } \\ {{\mathbf{e}}_{{t_{3} }}^{T} } \\ \end{array} } \right]^{{ - 1}} {\mathbf{p}}_{3} ,{\mathbf{I}}_{3} \xi \eta \zeta } \right]\left\{ {\begin{array}{*{20}c} {\alpha _{1} } \\ \vdots \\ {\alpha _{{24}} } \\ \end{array} } \right\} = {\mathbf{p}}_{{H8}} (\xi ,\eta ,\zeta )\left\{ {\begin{array}{*{20}c} {\alpha _{1} } \\ \vdots \\ {\alpha _{{24}} } \end{array} } \right\} \end{aligned} $$

(43)

where p _H8 is self-defined. In terms of the nodal displacement,

$$ {\mathbf{u}} = {\mathbf{p}}_{H8} (\xi ,\eta ,\zeta )\left[ {\begin{array}{*{20}c} {{\mathbf{p}}_{H8} (\xi_{1} ,\eta_{1} ,\zeta_{1} )} \\ \vdots \\ {{\mathbf{p}}_{H8} (\xi_{8} ,\eta_{8} ,\zeta_{8} )} \\ \end{array} } \right]^{ - 1} \left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{1} } \\ \vdots \\ {{\mathbf{u}}_{8} } \\ \end{array} } \right\}. $$

(44)

It should be remarked that Trefftz displacement functions mimicking the last three stress modes in (40) can also be derived as {$u_{{r_{i} }}$,$u_{{s_{i} }}$,$u_{{t_{i} }}$} = {$r_{i} s_{i} t_{i}$, $- s_{i}^{2} t_{i} /(6 - 4\upsilon )$, $- s_{i} t_{i}^{2} /(6 - 4\upsilon )$}. However, for highly distorted element, the square matrix in (44) can be ill-conditioned. The uncoupled ξηζ-modes in (43) do not lead to conditioning problem and are, thus, employed. To enhance the element accuracy, the last three columns in p _H8(ξ,η,ζ), immediately after the equal sign in (44) are scaled by 0.01. The predictions remain practically constant even if the factor is reduced to 0.0001. Here, the ξηζ-modes play the role of stabilizing the matrix. The element is abbreviated as TH8.

7.2 Numerical examples

In this part, benchmark problems are exercised to assess the performance of TH8. Element models to be included for comparison are listed below.

H8:

the standard isoparametric 8-node hexahedral element.

PT:

the hybrid-stress 8-node hexahedral element of Pian and Tong (1986).

OHB:

Bachrach’s hexahedral optimized with respect to bending response (Bachrach 1987).

TH8:

the unsymmetric Trefftz 8-node hexahedral element proposed in the last subsection.

While the predictions of OHB are extracted from Reference (Bachrach 1987), those of the other elements are computed using the second order quadrature. PT is less susceptible to mesh distortion than the popular QM6-3D incompatible displacement element (Sze 1992) and therefore other enhanced assumed strain elements. It is also popularly used for benchmarking new elements.

7.2.1 Patch test, invariance test and isotropy test

The tests in Sect. 5 are repeated. TH8 passes the patch test. It is also shown to be invariant and isotropic.

7.2.2 Two-element 3D cantilever

Figure 14 depicts a 2 × 2 × 10 cantilever beam modeled by two elements under two kinds of distortion characterized by length ‘e’. The deflection at A, V _A, and the bending stress at B, σ _XB, are computed and normalized by the exact solution. Under the first kind of distortion, the result yielded by H8, PT and TH8 are very close to those of Q4, PS and TQ4 presented

Fig. 14

A 10 × 2 × 2 two-element cantilever beam subjected to (1) end bending and (2) end shear with a mesh distortion 1 and b mesh distortion 2

in Figs. 6 and 7, respectively. Under the second kind of distortion, the normalized results are presented in Figs. 15 and 16 when end moment and end shear are applied, respectively. TH8 yields far better predictions than PT when the distortion comes in. In all cases, the exact solutions are reproduced by TH8 when end moment is applied.

Fig. 15

Normalized a deflection V _A and b stress σ _XB for the cantilever in Fig. 14 b under (1) end pure bending

Fig. 16

Normalized a deflection V _A and b stress σ _XB for the cantilever in Fig. 14 b under (2) end shear

7.2.3 Five-element cantilever and slender cantilever

The two cantilever problems shown in Figs. 8 and 11 are also considered by H8, PT and TH8. They are generalized into 3D cantilevers by extruding the mesh along the width direction and the width is taken to be the same as the thickness of the beam as in Fig. 14a. The results yielded by PT and TH8 are basically the same as those of PS and TQ4, respectively, see Figs. 9 and 10 and Tables 3 and 4. The difference between the predictions of Q4 and H8 are larger but their predictions are far less accurate than the others. Once again, the exact solutions are reproduced by TH8 when end moment is applied.

7.2.4 A thick plate problem

Figure 17 shows a quadrant of the fully clamped plate modeled by a single layer of sixteen elements. The irregular mesh is formed by shifting certain nodes by 1 unit in directions at π/4 to the coordinate axes on the x–y plane (Bachrach 1987). The plate is subjected to (1) a central point load of 4000 units and (2) the plate’s own weight of intensity 100 units per unit volume. The material parameters are E = 10⁷ and ν = 0.3. The reference solution is extracted from (Bachrach 1987) which is based on the thin plate solution. The normalized central deflections W _O as well as stresses σ _XO and σ _XB on the top face of the plate are listed in Tables 6 and 7 for regular and irregular meshes, respectively. Overall speaking, PT and TH8 are the most accurate and least susceptible to mesh distortion. Among them, TH8 is slightly less susceptible to mesh distortion.

Fig. 17

Bachrach’s thick plate problem using a regular mesh. b irregular mesh

Table 6 Normalized results for the thick plate problem in Fig. 17 (regular mesh)

Table 7 Normalized results for the thick plate problem in Fig. 17 (irregular mesh)

7.2.5 Shear panel problem

The shear panel problem in Fig. 12 is repeated by TH8, H8 and PT. Their predictions are very close to those of TQ4, Q4 and PS, respectively, see Table 5. The maximum difference is within 1 %. The predictions of the 3D elements are not separately reported for saving space.

8 Closure

The research community of the finite element method is always interested in elements with good accuracy and low susceptible to mesh distortion. Among the proposed methods, the unsymmetric finite element method is based on the Petrov–Galerkin formulation. It employs the compatible parametric interpolants as the test functions and incompatible metric interpolants as the trial functions. The first 8-node quadrilateral and 20-node hexahedron unsymmetric elements possess exceptional immunity to mesh distortion but are not invariant. In this paper, an efficient approach is proposed to secure the invariance and isotropy. It also develops the unsymmetric 4-node quadrilateral and 8-node hexahedral elements, which do not exist in the literature, by using the Trefftz displacement solutions defined with respect to selected local metric coordinates. Numerical examples show that the two elements also possess exceptional immunity to mesh distortion with respect to other advanced elements of the same nodal configurations.