Generalized modal element method: part-I—theory and its application to eight-node asymmetric and symmetric solid elements in linear analysis

Abstract

In this paper, a new finite element method, termed the generalized modal element method (GMEM), is proposed. In GMEM, the element stiffness is derived by decomposing element deformation patterns into individual element generalized modes, where different methods are used to construct the generalized modes. Specifically, three different modal construction methods, including analytical method, assumed displacement method and traditional finite element technique, are proposed for developing the element generalized modes. The concept of modal local coordinate systems is also proposed to ensure the element frame invariance when using polynomial displacement functions, which successfully enables one to use the analytical solutions derived from governing differential equations to develop high accuracy element formulations. An asymmetric hexahedral solid element and a symmetric hexahedral solid element are subsequently derived by using GMEM. The displacement functions of the elemental 24 generalized modes are expressed in terms of Cartesian coordinates so that the element behavior is independent of mesh distortions. Furthermore, the first 21 generalized modes are derived from analytical method making the element capable of avoiding common locking phenomena. Several benchmark problems are performed to demonstrate the accuracy and performance of the new element formulations in linear static and frequency analysis.

1 Introduction

In the engineering field, most of physical and mechanical problems are governed by differential equations with certain boundary conditions. Although the derivations of partial differential equations (PDEs) to describe various physical problems are usually straightforward, most of time it is difficult or even impossible to derive theoretical solutions for PDEs with complicated boundary conditions. In this context, the finite element method (FEM) was proposed and has been one of the most successful numerical methods in solving boundary value problems [1]. The key idea of FEM is to transform the differential equations into a finite number of algebraic equations for each element by using either Galerkin-weighted residual approach or variation principles. However, the element interpolation functions of FEM usually do not satisfy governing differential equations, which lead to various spurious deformation modes and locking phenomena [2, 3]. Indeed, there are numerous numerical methods that can describe the element deformation modes more precisely. For example, the theoretical solution of most locking deformation modes can be found by solving the governing differential equations. If the theoretical displacement fields can be used as the element displacement functions, the locking phenomenon can be automatically eliminated.

As different type of numerical methods has its own advantages to deal with a specific class of locking problems and none of the existing methods can combine the advantages of different numerical methods flexibly, a generalized modal element method is proposed in this paper to tackle with this problem. Specifically, three modal construction methods, including the analytical method, the assumed displacement method and traditional finite element technique, are presented for the derivation of element generalized modes. Comparing with the existing mode superposition methods, such as the assumed stress mode method [4], the Cosserat point element [5,6,7,8] and ANS method [9,10,11,12,13], each generalized mode defined in GMEM consists of a modal displacement vector and a corresponding modal force vector, making the present method totally different from the existing mode superposition methods. It should be noted that a natural mode finite element method introduced by Argyris [14, 15] is worked by separating the pure deformational modes (also called natural modes) from the rigid body movements of the element. The modes assumed in Argyris’ method are the stain modes so that no complex transformations or numerical integration are required in the construction of the elemental stiffness matrix, and the application of the natural mode method mainly focused on the triangular shell element. However, the generalized modal element method developed in this study directly constructs the elemental displacement modes which is more flexible and convenient, and in addition we have achieved the method using the solid elements and solid-shell elements. Furthermore, modal local coordinate systems are proposed to maintain the frame invariance of element stiffness if the element generalized modes are derived from the analytical method and the assumed displacement method, which makes the development of high accuracy low order hexahedral solid element using the analytical displacement functions possible.

In general, locking phenomena should be circumvented carefully in the construction of hexahedral elements. Various methods, such as the reduced integration (RI) and selective reduced integration (SRI) [16, 17], the incompatible modes method [18, 19], the Enhanced Assumed Strain method (EAS) [20,21,22,23] and the ANS method, were developed in the last decades and has been successfully reduced the influence of locking phenomena. Furthermore, the incompatibility between tension and bending deformations for irregular mesh is still one of the stumbling blocks in low order element design [24]. MacNeal [25] showed that the symmetric element will either lock in in-plane bending or fail to pass a C₀ patch test when the element’s shape is an isosceles trapezoid. To deal with this incompatibility, a family of asymmetrical elements, e.g. US-ATFQ4 [26], US-ATFH8 [27], TQ4, TH8 [28], were proposed in recent years, in which two types of shape functions were used to construct the element stiffness matrix. The developed elements are quite insensitive to variously severe mesh distortions and excellent performances for linear static analysis were obtained. But due to the asymmetrical element stiffness, these elements cannot be extended to the frequency analysis.

In this paper, two different hexahedral elements, an asymmetric hexahedral element US-MEM8S and a symmetric hexahedral element S-MEM8S, are presented as illustrations of GMEM. For the proposed low order solid element US-MEM8S, the elemental 24 generalized modes are divided into 21 basic deformation modes and 3 unphysical modes, in which the basic deformation modes of the present element, including tensile, shear, torsional and bending modes, are directly derived from three basic sets of equations of solid mechanics and the remaining 3 unphysical deformation modes are constructed by the assumed displacement method. Owing to the theoretical displacement functions used in basic deformation modes, the proposed element is insensitive to mesh distortions and can pass both the constant stress/strain patch test and the second-order bending patch test. However, as US-MEM8S is not suitable for structural frequency analysis, a symmetric hexahedral solid element named as S-MEM8S is proposed subsequently based on the displacement functions of US-MEM8S. A variety of popular numerical benchmark examples is performed to investigate the performance of the present elements.

2 Generalized modal element method

2.1 General formulation

2.1.1 Definition of generalized mode

In linear finite element method, the relationship between nodal force vector f and nodal displacement vector u is described by the element stiffness matrix

$$ {\mathbf{Ku}} = {\mathbf{f}} $$

(1)

For a finite element with r degrees of freedom, the deformation space prescribed by the element stiffness matrix includes r different deformation patterns, e.g. the rigid motion modes, the tensile modes, the shear modes, the bending modes and so on. In GMEM, the set of the nodal displacement vector Uⁱ and the corresponding nodal force vector Fⁱ of a specific deformation pattern is defined as a generalized mode ${\mathbf{M}}^{i} = \left[ {{\mathbf{F}}^{i} ,{\mathbf{U}}^{i} } \right]$, in which Uⁱ and Fⁱ are referred to as modal displacement vector and modal force vector, respectively. Since the element deformation space contains all possible deformations of the element, an arbitrary element displacement vector u can be expressed as a linear combination of the r modal displacement vectors

$$ {\mathbf{u}} = \sum\limits_{i = 1}^{r} {\beta_{i} {\mathbf{U}}^{i} } $$

(2)

where $\beta_{i}$ is the component of the node displacement vector u in the modal displacement vector Uⁱ. As the modal force vector corresponding to the modal displacement vector Uⁱ is defined as Fⁱ, the nodal force vector f corresponding to the nodal displacement vector u can be expressed as

$$ {\mathbf{f}} = \sum\limits_{i = 1}^{r} {\beta_{i} {\mathbf{F}}^{i} } $$

(3)

For simplicity, “generalized mode” is briefly referred to as “mode” in the following paper. For a given element, if the element modal force vector Fⁱ cannot approximates the equivalent nodal force of the modal displacement vector Uⁱ properly, the element may demonstrates locking phenomenon and reduces the element accuracy, such as the bending deformation mode simulated by the iso-parametric element. Therefore, the selection of element modes directly determines the element accuracy and performance.

2.1.2 Formulation of element stiffness

Assuming that the element node number is n and nodal degrees of freedom is m, then the number of element modes r should be consistent with element’s total degrees of freedom, i.e. r = mn. If the modal displacement function of i-th mode in j-th direction is defined as $R_{j}^{i} \left( {\mathbf{X}} \right)$, then the displacement of an arbitrary node X_a of mode i can be expressed as

$$ {\mathbf{H}}^{i} \left( {{\mathbf{X}}_{a} } \right) = \left[ {R_{1}^{i} \left( {{\mathbf{X}}_{a} } \right),R_{2}^{i} \left( {{\mathbf{X}}_{a} } \right), \ldots ,R_{m}^{i} \left( {{\mathbf{X}}_{a} } \right)} \right] $$

(4)

Substituting the coordinates of all nodes of the element into Eq. (4), the i-th modal displacement vector Uⁱ is given by

$$ {\mathbf{U}}^{i} = \left[ {{\mathbf{H}}^{i} \left( {{\mathbf{X}}_{1} } \right),{\mathbf{H}}^{i} \left( {{\mathbf{X}}_{2} } \right), \ldots ,{\mathbf{H}}^{i} \left( {{\mathbf{X}}_{n} } \right)} \right]^{T} $$

(5)

Similarly, the modal force vector Fⁱ represents the equivalent nodal force vector of i-th mode. Assuming ${\mathbf{L}}_{j}^{i}$ is the i-th modal equivalent force vector of node j, the modal force vector of i-th mode can be written as

$$ {\mathbf{F}}^{i} = \left[ {{\mathbf{P}}_{1}^{i} ,{\mathbf{P}}_{2}^{i} , \ldots ,{\mathbf{P}}_{n}^{i} } \right]^{T} $$

(6)

Equations (5) and (6) present the general formulations of modal displacement vector and modal force vector. Detailed modal construction procedures will be described in the following sections.

By constructing r linearly independent sets of element modal displacement vectors and corresponding modal force vectors, the element stiffness matrix K can be expressed as

$$ {\mathbf{K}} = {\mathbf{FU}}^{ - 1} $$

(7)

in which U = [U¹, U²,…,U^r] is referred to as the modal displacement matrix and F = [F¹, F²,…,F^r] is defined as the modal force matrix in GMEM.

From Eq. (7), it can be seen that the derivation of element stiffness in GMEM is highly different from the mainstream finite element techniques such as RI, EAS and ANS methods, in which the element stiffness is majorly computed by an integration of the element strain energy. Indeed, the nodal displacement vectors and nodal force vectors of element modes should be firstly calculated in GMEM, which makes the construction of the specified element mode completely independent of the other modes so that the construction of each mode can be very flexible. This difference will be more apparent in the construction of the out-of-plane modes of solid-shell element by using a plate bending element. Actually, GMEM is very similar to the ancient “displacement method”. In the displacement method [29], the matrix U in Eq. (7) is an identity matrix in which the element k_ij of stiffness matrix is defined as the force at coordinate i due to unit displacement in coordinate direction j, while the matrix U in GMEM is composed by r linear independent modal displacement vectors that represent special deformation modes. Therefore, GMEM can be regarded as an extension of the displacement method.

2.2 Modal construction methods

The GMEM can be constructed by applying different numerical methods. Generally, the selected modal construction method of a given deformation pattern should be able to approximate the element mechanical behavior efficiently. For some simple deformation modes that having analytical solutions, such as tensile, shear, torsion and bending deformation modes, the relationship between modal displacement vector and modal force vector can be obtained directly by solving the governing differential equations. However, for some complex deformation modes that don’t have the analytic solutions, this relationship can be approximated by other numerical methods. In general, the selected modes should meet the following criteria as much as possible:

• (1) The modes should be selected from the low order deformation modes to the high order deformation modes. Correspondingly, the element modal strain fields should be selected from the zero order strain fields (rigid body modes), constant strain fields (tensile modes, shear modes) to first and high order strain fields (torsion modes, bending modes and so on).

• (2) The selected modes or the boundary conditions of the element should reflect the elemental physical behavior as much as possible. For example, the upper and lower surfaces of thin-walled structures are rarely subjected to shear loads, which making the deformation modes of solid-shell element totally different from the deformation modes of solid element. Therefore, the shear stresses on the upper and lower surfaces of solid-shell elements should be equal to zero. Reasonable selection of element deformation modes can effectively improve the numerical accuracy of the constructed element.

• (3) The selected modes should satisfy the invertibility of the modal displacement matrix U so that the element stiffness matrix in Eq. (7) can be obtained correctly.

• (4) The element stiffness derived from the selected element modes must have the proper rank, i.e. the number of zero-frequencies modes should equal to the number of element rigid body modes.

The performance of the element stiffness matrix directly depends on the accuracy of the given modal displacement vectors and the modal force vectors as showed in Eqs. (5) and (6). In this section, we will present three common element modal construction methods, including analytic method, assumed displacement method and traditional finite element method.

2.2.1 Analytical method

For some physical problems with simple boundary conditions, the element displacement functions of these modes can be derived by simply solving the governing differential equations. Considering a finite body Ω with isotropic material, the equilibrium equations for this finite body can be expressed as

$$ \left\{ \begin{aligned} \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{yx} }}{\partial y} + \frac{{\partial \tau_{zx} }}{\partial z} = 0 \hfill \\ \frac{{\partial \sigma_{y} }}{\partial y} + \frac{{\partial \tau_{xy} }}{\partial x} + \frac{{\partial \tau_{zy} }}{\partial z} = 0 \hfill \\ \frac{{\partial \sigma_{z} }}{\partial z} + \frac{{\partial \tau_{xz} }}{\partial x} + \frac{{\partial \tau_{yz} }}{\partial y} = 0 \hfill \\ \end{aligned} \right. $$

(8)

and the strain–displacement equations are

$$ \left\{ {\begin{aligned} &{\varepsilon_{x} = \frac{\partial u}{\partial x},\varepsilon_{y} = \frac{\partial v}{\partial y},\varepsilon_{z} = \frac{\partial w}{\partial z} \, } \hfill \\ & {\gamma_{xy} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x},\gamma_{yz} = \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y},\gamma_{xz} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}} \hfill \end{aligned} } \right. $$

(9)

The constitutive equations or the stress and strain relations for linear elasticity are given as

$$ {\varvec{\upsigma}} = {\mathbf{D}}{\boldsymbol{\varepsilon }} $$

(10)

where D is the elasticity matrix.

By solving the governing differential equations, the analytical displacement functions with a specified boundary condition can be derived. Then the modal displacement vector, modal strain and stress distributions of this mode can be determined uniquely. The resulting modal force vector Fⁱ can be expressed as a surface integral of element surface traction,

$$ {\mathbf{F}}^{i} = \int_{{S^{e} }} {{\mathbf{N}}^{T} {\mathbf{T}}^{i} dS} $$

(11)

where N is referred to as stress weight matrix and Tⁱ is element surface traction. In General, the stress weight matrix N should be selected to ensure that the force and moment of distributed force Tⁱ on any side of element $S^{*}$ are equal to these of their equivalent nodal forces,

$$ \sum\limits_{i = 1}^{M} {{\mathbf{P}}_{i} } = \int_{{S^{ * } }} {{\mathbf{T}}^{i} dS} ,\sum\limits_{i = 1}^{M} {{\mathbf{P}}_{i} \times {\mathbf{R}}_{i} } = \int_{{S^{ * } }} {{\mathbf{T}}^{i} dS \times {\mathbf{R}}} $$

(12)

where M and ${\mathbf{P}}_{i}^{{}}$ are the number of nodes and the corresponding nodal force vector on side $S^{*}$, respectively, and R_i is the position vector of node i.

Since modal displacement functions are expressed in terms of Cartesian coordinates and satisfy governing differential equations, the elements derived from the analytical method are insensitive to mesh distortions.

2.2.2 Assumed displacement method

For some complex modes, it is difficult to find feasible displacement functions that satisfy the governing equations. However, these modes are inevitable to construct an invertible modal displacement matrix. In such cases, by defining proper modal displacement functions and modal strain distributions, the modal force vectors can be written as

$$ {\mathbf{F}}^{i} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\mathbf{D}}{\varvec{\varepsilon}}^{i} dV} $$

(13)

where B = LN is referred to as differential stress weight matrix and L is a differential operator matrix, ε = [ε_xε_yε_zγ_xyγ_yzγ_xz]^T is the assumed modal strain vector. Basically, B in Eq. (13) should satisfies the force and moment equilibrium conditions of the element,

$$ \sum\limits_{i = 1}^{n} {{\mathbf{P}}_{i} } = 0,\sum\limits_{i = 1}^{n} {{\mathbf{P}}_{i} \times {\mathbf{R}}_{i} } = 0 $$

(14)

The merit of the assumed displacement method is that its internal displacement functions can be expressed in terms of the Cartesian coordinate system, which can effectively improve the element behavior for distorted meshes.

2.2.3 Traditional finite element technique

In some special cases, the former two procedures are difficult to produce a desirable mode for some specified boundary conditions, whereas traditional finite element techniques may exhibit excellent performance. For example, the upper and lower surfaces of a solid-shell element are normally only subjected to zero or uniform pressure and rarely subjected to shear forces. In such a case, it is difficult or even impossible to obtain the displacement functions of some special modes, such as the torsional mode, using analytical method. In such cases, it is preferable for us to use shell element to approximate these specified modes of solid-shell elements as most shell elements have much better numerical accuracy and convergence rate than the existing solid-shell elements. In this context, GMEM enables to build up a connection between different element formulations and makes the construction of new elements more flexible.

When using traditional finite element technique, the referenced element may have the same modal DOF with the new developed element. Then the modal force vector of the new element F_g can be written as

$$ {\mathbf{F}}_{g} = {\mathbf{K}}_{r} {\mathbf{U}}_{g} $$

(15)

where K_r is the stiffness of the referenced element and U_g is the modal displacement vector of the new element. Equation (15) indicates that the construction of element mode is quite convenient when referenced element and new element have the same geometry description. This method will also be used in the following paper to derive the in-plane modes of a symmetric solid-shell element.

The problem will be more complicated if different nodal DOF are involved (for instance using a shell element to describe the out-of-plane modes of a solid-shell element). First, one has to use the nodal coordinates of the new developed element to ascertain the geometry description of the referenced element. Then, the transformation between the modal displacement vector of the new element and the referenced element should be established so that the modal displacement vector of the new element can be obtained from the modal displacement vector of the referenced element. Subsequently, the modal force vector of the referenced element can be derived from the modal displacement vector and element stiffness of the referenced element. Finally, the modal force vector of the new element can be computed from the modal force vector of the referenced element. With the computed modal displacement vector and modal force vector of the new element, one can uniquely express the element behavior of a specified deformation pattern. The detailed procedure of traditional finite element technique will be discussed in the construction of eight-node solid-shell elements in the following paper.

It is clear that the methods available for GMEM are far more than the above mentioned three methods as a mass of methods can describe or approximate the relationship between structural displacements and forces. Benefited from the diversity of modal construction method, high accuracy finite element formulations can be obtained by GMEM since it can make full use of the merits of different finite element design methods. It also should be noted that the element stiffness derived from GMEM is generally asymmetric. But with some special treatments, the element stiffness can also be converted into a symmetric form.

2.2.4 Selection of stress weight function

In the mainstream finite element methods such as EAS and ANS methods, the element displacement functions cannot be arbitrarily selected, e.g. the displacement fields of the solid-shell elements in the literatures are still limited to x² and y², while the items of x³ and y³ can be conveniently involved in shell elements [30]. In this section, we will present three relative theorems to demonstrate how to use an arbitrary displacement functions (including analytical solutions) to derive the corresponding modal force vectors in GMEM. These theorems will also be employed in the following sections to derive the modal force vector when using the analytical method and the assumed displacement method.

Theorem 1

Suppose the distributed traction forces on an element side $S^{*}$ are T , and the number of nodes on this side is M. Then the resultant force and moment between traction forces T and corresponding nodal forces are equivalent if iso-parametric shape functions are executed as stress weight functions,

$$ \sum\limits_{i = 1}^{M} {{\mathbf{P}}_{i}^{ *} } = \int_{{S^{ *} }} {{\mathbf{T}}dS} $$

(16)

$$ \sum\limits_{i = 1}^{M} {{\mathbf{P}}_{i}^{ *} \times {\mathbf{R}}_{i} } = \int_{{S^{ *} }} {{\mathbf{T}} \times {\mathbf{R}}dS} $$

(17)

Proof of Theorem 1

Using Eq. (11), the element nodal forces of this side can be expressed as

$$ {\mathbf{P}}_{i}^{ *} = \int_{{S^{ *} }} {{\mathbf{N}}_{i}^{T} {\mathbf{T}}dS} $$

(18)

Then we have

$$ \sum\limits_{i = 1}^{M} {{\mathbf{P}}_{i}^{ *} } = \sum\limits_{i = 1}^{M} {\int_{{S^{*} }} {{\mathbf{N}}_{i}^{T} {\mathbf{T}}dS} } = \int_{{S^{*} }} {\sum\limits_{i = 1}^{M} {{\mathbf{N}}_{i}^{T} {\mathbf{T}}dS} } { = }\int_{{S^{*} }} {{\mathbf{T}}dS} $$

(19)

$$ \begin{aligned} \sum\limits_{{i = 1}}^{M} {{\mathbf{P}}_{i}^{*} \times {\mathbf{R}}_{i} } & = \sum\limits_{{i = 1}}^{M} {\int {{\mathbf{N}}_{i}^{T} \left( {\mathbf{R}} \right){\mathbf{T}}dS \times {\mathbf{R}}_{i} } } \\ & = \int_{{S^{*} }} {{\mathbf{T}} \times \sum\limits_{{i = 1}}^{M} {{\mathbf{N}}_{i}^{T} \left( {\mathbf{R}} \right){\mathbf{R}}_{i} dS} } = \int_{{S^{*} }} {{\mathbf{T}} \times {\mathbf{R}}dS} \\ \end{aligned} $$

(20)

Theorem 2

Assume the displacement functions satisfy the equilibrium equations, and the surface tractions and stresses within the element are T and σ , respectively. If iso-parametric shape functions are executed as stress weight functions, then surface integrals of T and volume integrals of σ within the element are equivalent,

$$ \int_{{S^{e} }} {{\mathbf{N}}^{T} {\mathbf{T}}dS} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\varvec{\upsigma}}dV} $$

(21)

Proof of Theorem 2

For simplicity, the nodal forces in x-direction are considered independently. By applying Gauss’s theorem to the left component of Eq. (21), we have

$$ \begin{aligned} \int_{{S^{e} }} {{\mathbf{N}}_{1}^{T} T_{x} dS} & = \int_{{S^{e} }} {{\mathbf{N}}_{1}^{T} \left( {l\sigma _{x} + m\tau _{{xy}} + n\tau _{{xz}} } \right)dS} \\ & = \int_{{S^{e} }} {{\mathbf{N}}_{1}^{T} \left\{ {\left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right] \cdot d{\mathbf{S}}} \right\}} \\ & = \int_{{V^{e} }} {\left\{ {{\mathbf{N}}_{1}^{T} \left( {\frac{{\partial \sigma _{x} }}{{\partial x}} + \frac{{\partial \tau _{{xy}} }}{{\partial y}} + \frac{{\partial \tau _{{xz}} }}{{\partial z}}} \right)} \right.} \\ & \quad \left. { + \nabla {\mathbf{N}}_{1}^{T} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} } \right\}dV \\ \end{aligned} $$

(22)

where T_x is the x-direction component of T and N₁ is the first row of N. Since the displacement functions are assumed to satisfy the equilibrium differential equations, we have

$$ \frac{{\partial \sigma_{x} }}{\partial x} + \frac{{\partial \tau_{xy} }}{\partial y} + \frac{{\partial \tau_{xz} }}{\partial z} = 0 $$

(23)

Therefore, Eq. (22) is reduced to

$$ \int_{{S^{e} }} {{\mathbf{N}}_{1}^{T} T_{x} dS} = \int_{{V^{e} }} {\nabla {\mathbf{N}}_{1}^{T} \left[ {\begin{array}{*{20}c} {\sigma_{x} } & {\tau_{xy} } & {\tau_{xz} } \\ \end{array} } \right]^{T} dV} $$

(24)

The element nodal forces in other two directions follow the same lines and can be written as

$$ \int_{{S^{e} }} {{\mathbf{N}}_{2}^{T} T_{y} dS} = \int_{{V^{e} }} {\nabla {\mathbf{N}}_{2}^{T} \left[ {\begin{array}{*{20}c} {\tau_{xy} } & {\sigma_{y} } & {\tau_{{{\text{y}}z}} } \\ \end{array} } \right]^{T} dV} $$

(25)

$$ \int_{{S^{e} }} {{\mathbf{N}}_{3}^{T} T_{z} dS} = \int_{{V^{e} }} {\nabla {\mathbf{N}}_{3}^{T} \left[ {\begin{array}{*{20}c} {\tau_{xz} } & {\tau_{yz} } & {\sigma_{z} } \\ \end{array} } \right]^{T} dV} $$

(26)

Combination of Eqs. (24) (25) and (26) leads to

$$ \int_{{S^{e} }} {{\mathbf{N}}^{T} {\mathbf{T}}dS} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\varvec{\upsigma}}dV} $$

(27)

Theorem 3

If iso-parametric shape functions are performed as stress weight matrix, then the element nodal forces derived from volume integrals of stresses

$$ {\mathbf{P}} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\varvec{\upsigma}}dV} $$

(28)

satisfy the equilibrium of force and moment for arbitrary stress distributions σ no matter σ satisfies the equilibrium equations or not,

$$ \sum\limits_{i = 1}^{n} {{\mathbf{P}}_{i} = {\mathbf{0}}} ,\sum\limits_{i = 1}^{n} {{\mathbf{P}}_{i} \times {\mathbf{R}}_{i} = {\mathbf{0}}} $$

(29)

Proof of Theorem 3

Similarly to the proof of Theorem 2, we only investigate the resultant force and moment of nodal forces in x-direction at first. The nodal force of node i in x-direction in Eq. (28) can be expressed as

$$ P_{ix} = \int_{{V^{e} }} {\nabla N_{i} \left[ {\begin{array}{*{20}c} {\sigma_{x} } & {\tau_{xy} } & {\tau_{xz} } \\ \end{array} } \right]^{T} dV} $$

(30)

The sum of all nodal forces in x-directions is

$$ \begin{aligned} \sum\limits_{i = 1}^{n} {P_{ix} } & = \sum\limits_{i = 1}^{n} {\int_{{V^{e} }} {\nabla N_{i} \left[ {\begin{array}{*{20}c} {\sigma_{x} } & {\tau_{xy} } & {\tau_{xz} } \\ \end{array} } \right]^{T} dV} } \\ & = \int_{{V^{e} }} {\nabla \sum\limits_{i = 1}^{n} {N_{i} \left[ {\begin{array}{*{20}c} {\sigma_{x} } & {\tau_{xy} } & {\tau_{xz} } \\ \end{array} } \right]^{T} dV} } \\ & = \int_{{V^{e} }} {\nabla 1\left[ {\begin{array}{*{20}c} {\sigma_{x} } & {\tau_{xy} } & {\tau_{xz} } \\ \end{array} } \right]^{T} dV} \\ & = 0 \\ \end{aligned} $$

(31)

Similar results can be obtained for the other two directions, thus we have

$$ \sum\limits_{i = 1}^{n} {{\mathbf{P}}_{i} = {\mathbf{0}}} $$

(32)

For the moment equilibrium property,

$$\begin{aligned} & \sum\limits_{{i = 1}}^{n} {\left( {\left[ {\begin{array}{*{20}c} {P_{{ix}} } & 0 & 0 \\ \end{array} } \right] \times {\mathbf{R}}_{i} } \right)} \\ &\quad = \sum\limits_{{i = 1}}^{n} {\left[ {\begin{array}{*{20}c} {\int_{{V^{e} }} {\nabla N_{i} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} dV} } & 0 & 0 \\ \end{array} } \right]} \times\, {\mathbf{R}}_{i} \\ & = \sum\limits_{{i = 1}}^{n} {\left\{ { - R_{{iz}} \int_{{V^{e} }} {\nabla N_{i} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} dV} } \right.} \\ & \quad \left. { \times\,R_{{iy}} \int_{{V^{e} }} {\nabla N_{i} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} dV} } \right\} \\ & = \sum\limits_{{i = 1}}^{n} {\left[ {0 - \int_{{V^{e} }} {\nabla N_{i} R_{{iz}} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} dV} } \right.} \\&\quad \left. { \times \int_{{V^{e} }} {\nabla N_{i} R_{{iy}} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} dV} } \right] \\ & = \left[ {0 - \int_{{V^{e} }} {\nabla R_{z} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} dV} } \right. \\ & \quad \left. { \times \int_{{V^{e} }} {\nabla R_{y} \left[ {\begin{array}{*{20}c} {\sigma _{x} } & {\tau _{{xy}} } & {\tau _{{xz}} } \\ \end{array} } \right]^{T} dV} } \right] \\ & = \left[ {\begin{array}{*{20}c} 0 & { - \int_{{V^{e} }} {\tau _{{xz}} dV} } & {\int_{{V^{e} }} {\tau _{{xy}} dV} } \\ \end{array} } \right] \\ \end{aligned} $$

(33)

where ${\mathbf{R}}_{i} = \left[ {\begin{array}{*{20}c} {R_{ix} } & {R_{iy} } & {R_{iz} } \\ \end{array} } \right]$ and ${\mathbf{R}} = \left[ {\begin{array}{*{20}c} {R_{x} } & {R_{y} } & {R_{z} } \\ \end{array} } \right]$. Similarly,

$$ \sum\limits_{i = 1}^{n} {\left( {\left[ {\begin{array}{*{20}c} 0 & {P_{iy} } & 0 \\ \end{array} } \right] \times {\mathbf{R}}_{i} } \right)} = \left[ {\begin{array}{*{20}c} {\int_{{V^{e} }} {\tau_{yz} dV} } & 0 & { - \int_{{V^{e} }} {\tau_{xy} dV} } \\ \end{array} } \right] $$

(34)

$$ \sum\limits_{i = 1}^{n} {\left( {\left[ {\begin{array}{*{20}c} 0 & 0 & {P_{iz} } \\ \end{array} } \right] \times {\mathbf{R}}_{i} } \right)} = \left[ {\begin{array}{*{20}c} { - \int_{{V^{e} }} {\tau_{yz} dV} } & {\int_{{V^{e} }} {\tau_{xz} dV} } & 0 \\ \end{array} } \right] $$

(35)

By summing up Eqs. (33), (34) and (35), we have

$$ \sum\limits_{i = 1}^{n} {{\mathbf{P}}_{i} \times {\mathbf{R}}_{i} = {\mathbf{0}}} $$

(36)

By applying Theorem 2, Eq. (11) in the analytical method can be rewritten as

$$ {\mathbf{F}}^{i} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\varvec{\upsigma}}^{i} dV} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\mathbf{D}}{\varvec{\varepsilon}}^{i} dV} $$

(37)

Considering the integration of Eq. (37) using Gaussian numerical integration, it can be expressed as

$$ {\mathbf{F}}^{i} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\varvec{\upsigma}}^{i} dV = } \int_{ - 1}^{1} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {{\mathbf{B}}^{T} {\varvec{\upsigma}}^{i} \left| {\mathbf{J}} \right|d\xi d\eta d\zeta } } } $$

(38)

where J is the Jacobi matrix, and B is

$$ {\mathbf{B}} = \left[ {\begin{array}{l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l@{\quad}l} {N_{1,x} } & 0 & 0 & \cdots & {N_{n,x} } & 0 & 0 \\ 0 & {N_{1,y} } & 0 & \cdots & 0 & {N_{n,y} } & 0 \\ 0 & 0 & {N_{1,z} } & \cdots & 0 & 0 & {N_{n,z} } \\ {N_{1,y} } & {N_{1,x} } & 0 & \cdots & {N_{n,y} } & {N_{n,x} } & 0 \\ 0 & {N_{1,z} } & {N_{1,y} } & \cdots & 0 & {N_{n,z} } & {N_{n,y} } \\ {N_{1,z} } & 0 & {N_{1,x} } & \cdots & {N_{n,z} } & 0 & {N_{n,x} } \\ \end{array} } \right] $$

(39)

where N_i,x, N_i,y and N_i,z are the derivative of the iso-parametric function in the Cartesian coordinate system and satisfy

$$ \left[ {\begin{array}{*{20}c} {N_{i,x} } \\ {N_{i,y} } \\ {N_{i,z} } \\ \end{array} } \right] = {\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}c} {N_{i,\xi } } \\ {N_{i,\eta } } \\ {N_{i,\zeta } } \\ \end{array} } \right] = \frac{{Adj\left[ {\mathbf{J}} \right]}}{{\left| {\mathbf{J}} \right|}}\left[ {\begin{array}{*{20}c} {N_{i,\xi } } \\ {N_{i,\eta } } \\ {N_{i,\zeta } } \\ \end{array} } \right] $$

(40)

Substituting Eqs. (40) into (39), B can be rewritten as ${\mathbf{B}} = {\mathbf{B}}^{*} /\left| {\mathbf{J}} \right|$, then Eq. (38) becomes

$$\begin{aligned}{\mathbf{F}}^{i} &= \int_{ - 1}^{1} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {\frac{{{\mathbf{B}}^{*T} }}{{\left| {\mathbf{J}} \right|}}{\varvec{\upsigma}}^{i} \left| {\mathbf{J}} \right|d\xi d\eta d\zeta } } }\\ &= \int_{ - 1}^{1} {\int_{ - 1}^{1} {\int_{ - 1}^{1} {{\mathbf{B}}^{*T} {\varvec{\upsigma}}^{i} d\xi d\eta d\zeta } } }\end{aligned} $$

(41)

Since the inverse of the Jacobian matrix is eliminated in the Eq. (41), the resulting modal force vector can be precisely integrated by using the Gaussian numerical integration scheme, which makes the present element quite insensitive to server mesh distortions.

Although the analytic method and the assumed displacement method have the same expressions as shown in Eqs. (13) and (37), the mechanical mechanisms of these two methods are completely different. In the analytic method, the modal displacement functions satisfy the governing differential equations and the element equivalent modal force vector is obtained by an integration of the distribution force applied on the element surface, while the assumed displacement method is only an approximate mathematical method.

2.3 Modal local coordinate systems

In analytical method and assumed displacement method, the modal displacement functions of each mode should be firstly determined so that the corresponding modal displacement vector and modal force vector can be computed. As the same deformation pattern may have different directions, such as the tensile deformations in x and y directions, it is convenient to establish different modal local coordinate systems to describe the same deformation pattern in different directions. Furthermore, the frame invariance of element stiffness can also be guaranteed by using unique modal local coordinate system for different mode, which is essential to ensure the element numerical stability and consistence.

Using modal local coordinate systems, four different categories of element modes are given as follows:

Strong complete mode

If the displacement distribution function satisfies the governing differential equations and the exact structural deformation can be obtained for any selection of modal local coordinate system, then the modal is defined as a strong complete mode.

Weak complete mode

If the displacement distribution function doesn’t satisfy the governing differential equations, but the deformation specified by the displacement distribution function can be obtained for any selection of modal local coordinate system, then the modal is defined as a weak complete mode.

Strong incomplete mode

If the displacement distribution function satisfies the governing differential equations and the exact structural deformation can be obtained only for the direction specified by the modal local coordinate system, then the modal is defined as a strong incomplete mode.

Weak incomplete mode

If the displacement distribution function doesn’t satisfy the governing differential equations and the exact structural deformation can be obtained only for the direction specified by the modal local coordinate system, then the modal is defined as a weak incomplete mode.

From above definitions, we can see that whether a mode is “strong” or “weak” depends on whether the modal displacement functions satisfy the governing differential equations, and whether a mode is “complete” or “weak” is determined by whether unique element stiffness matrix can be obtained when using different modal local coordinate systems. For complete modes, different selection of modal local coordinate systems does not change the element stiffness, so the global coordinate system can be directly employed as the modal local coordinate systems of these modes. For incomplete modes, it is necessary to establish a unique modal local coordinate system for each mode to ensure the frame invariance of element stiffness. With the aid of the modal local coordinate, the analytic method and the assumed displacement method can be efficiently applied in developing new finite element formulations by using any desirable displacement functions.

3 Modes of eight-node solid element

Based on the modal construction criterions described in Sect. 2.2, the 24 modes of eight-node hexahedral element selected from low order to high order can be classified as: 6 rigid body motion modes, 3 tensile modes, 3 shear modes, 3 torsional modes, 6 bending modes and 3 unphysical modes. The detailed displacement functions of these modes will be given in the following section. For simplicity, the first 21 modes are referred to as basic deformation modes since all of them can be derived by solving basic governing differential equations of solid mechanics. As it is yet to find a feasible solution of unphysical modes that satisfies the governing equations, the assumed displacement method is adopted to construct unphysical modes to ensure the invertibility of the modal displacement matrix U.

3.1 Modal local coordinate systems

According to the modal completeness defined in Sect. 2.3, it can be verified that the rigid body motion modes, tensile modes and shear modes in the eight-node solid element are complete modes, i.e. any selection of the modal local coordinate systems for these modes doesn’t change the element behavior. For the remaining incomplete modes (including the torsional modes, bending modes and unphysical modes), different selection of modal local coordinate systems will produce different element stiffness. To tackle with this problem, unique modal local coordinate system is established for each incomplete mode to ensure the frame invariance of the developed hexahedral element.

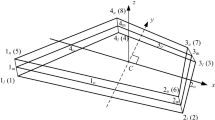
Considering an arbitrary eigh-node solid element illustrated in Fig. 1, the element centroid of the hexahedral element is determined by the cartesian coordinates of the element nodes:

$$ {\mathbf{X}}_{C} = \frac{1}{8}\sum\limits_{i = 1}^{8} {{\mathbf{X}}_{i} } $$

(42)

where ${\mathbf{X}}_{C}$ are the cartesian coordinates of the element centroid and ${\mathbf{X}}_{i}$ are the cartesian coordinates of node i. For the present element, 10 modal local coordinate systems are utilized for the construction of 24 modes. Specifically, the first modal local coordinate system $C_{1}$ is utilized for the construction of the 6 rigid body motion modes, 3 tensile modes, and 3 shear modes. As these modes are complete modes, the global coordinates can be selected as the local coordinates of these modes:

$$ C_{1} = \left\{ \begin{aligned} {\mathbf{r}} = \left[ {\begin{array}{l@{\quad}l@{\quad}l} 1 & 0 & 0 \\ \end{array} } \right] \hfill \\ {\mathbf{s}} = \left[ {\begin{array}{l@{\quad}l@{\quad}l} 0 & 1 & 0 \\ \end{array} } \right] \hfill \\ {\mathbf{t}} = \left[ {\begin{array}{l@{\quad}l@{\quad}l} 0 & 0 & 1 \\ \end{array} } \right] \hfill \\ \end{aligned} \right. $$

(43)

Fig. 1

Geometry of an eight node solid element

The second to the seventh modal local coordinate systems are used for the construction of 6 bending modes. For simplicity, the vectors passing through the midpoint of the opposite two surfaces are denoted as:

$$ {\mathbf{r}}_{1} = {\mathbf{n}}_{2376} - {\mathbf{n}}_{1584} ,{\mathbf{r}}_{1} = {\mathbf{r}}_{1} /\left\| {{\mathbf{r}}_{1} } \right\| $$

(44)

$$ {\mathbf{r}}_{2} = {\mathbf{n}}_{3487} - {\mathbf{n}}_{1265} ,{\mathbf{r}}_{2} = {\mathbf{r}}_{2} /\left\| {{\mathbf{r}}_{2} } \right\| $$

(45)

$$ {\mathbf{r}}_{3} = {\mathbf{n}}_{5678} - {\mathbf{n}}_{1432} ,{\mathbf{r}}_{3} = {\mathbf{r}}_{3} /\left\| {{\mathbf{r}}_{3} } \right\| $$

(46)

where n_abcd denotes for the midpoint of the surface S_abcd as shown in Fig. 1. Then the modal local coordinates of 6 bending modes are selected as:

$$ {\bar{\text{C}}}_{ij} = \left\{ {\begin{array}{*{20}l} {{\mathbf{r}} = {\mathbf{r}}_{i} /\left\| {{\mathbf{r}}_{i} } \right\|} \hfill \\ {{\mathbf{s}} = {\mathbf{r}} \times {\mathbf{r}}_{j} ,{\mathbf{s}} = {\mathbf{s}}/\left\| {\mathbf{s}} \right\|} \hfill \\ {{\mathbf{t}} = {\mathbf{r}} \times {\mathbf{s}},{\mathbf{t}} = {\mathbf{t}}/\left\| {\mathbf{t}} \right\|} \hfill \\ \end{array} } \right.\quad i = 1,2,3,j \ne i $$

(47)

where ${\bar{\text{C}}}_{ij}$ means that the bending mode is defined in the r-s plane or r_i–r_j plane. For the eighth to the tenth modal local coordinate systems:

$$ {\tilde{\text{C}}}_{l} = \left\{ {\begin{array}{*{20}l} {{\mathbf{r}} = {\mathbf{r}}_{l} /\left\| {{\mathbf{r}}_{l} } \right\|} \hfill \\ {{\mathbf{v}}_{1} = {\mathbf{r}} \times {\mathbf{r}}_{m} ,{\mathbf{v}}_{2} = {\mathbf{v}}_{1} \times {\mathbf{r}},{\mathbf{v}}_{3} = {\mathbf{v}}_{2} /\left\| {{\mathbf{v}}_{2} } \right\|} \hfill \\ {{\mathbf{v}}_{4} = {\mathbf{r}} \times {\mathbf{r}}_{n} ,{\mathbf{v}}_{5} = {\mathbf{v}}_{4} \times {\mathbf{r}},{\mathbf{v}}_{6} = {\mathbf{v}}_{5} /\left\| {{\mathbf{v}}_{5} } \right\|} \hfill \\ {{\mathbf{v}}_{7} = {\mathbf{v}}_{1} + {\mathbf{v}}_{4} ,{\mathbf{v}}_{8} = {\mathbf{v}}_{7} /\left\| {{\mathbf{v}}_{7} } \right\|} \hfill \\ {{\mathbf{v}}_{9} = {\mathbf{r}} \times \left( { - {\mathbf{v}}_{8} } \right),{\mathbf{v}}_{10} = {\mathbf{v}}_{9} + {\mathbf{v}}_{8} } \hfill \\ {{\mathbf{s}} = {\mathbf{v}}_{10} /\left\| {{\mathbf{v}}_{10} } \right\|} \hfill \\ {{\mathbf{t}} = {\mathbf{r}} \times {\mathbf{s}}} \hfill \\ \end{array} } \right.\begin{array}{*{20}l} {} \hfill \\ {} \hfill \\ {} \hfill \\ {\quad l = 1,2,3,m \ne l,n \ne l,m} \hfill \\ {} \hfill \\ {} \hfill \\ {} \hfill \\ \end{array} $$

(48)

here ${\tilde{\text{C}}}_{l}$ is utilized for the construction of the torsional and unphysical modes in the r or r_l axis and v₁ to v₁₀ are auxiliary vectors.

With the given modal local coordinate systems, the modal displacement vector u^g, strain tensor e^g and stress tensor ${\varvec{\upsigma}}^{g}$ in the global coordinate system can be expressed by the modal displacement vector u, strain tensor e and stress tensor ${\varvec{\upsigma}}$ in the local coordinate system as:

$$ {\mathbf{u}}^{g} = \left[ {\begin{array}{*{20}c} {\mathbf{R}} & \cdots & {\mathbf{0}} & {\mathbf{0}} \\ \vdots & \ddots & \vdots & \vdots \\ {\mathbf{0}} & \cdots & {\mathbf{R}} & {\mathbf{0}} \\ {\mathbf{0}} & \cdots & {\mathbf{0}} & {\mathbf{R}} \\ \end{array} } \right]{\mathbf{u}} $$

(49)

$$ {\mathbf{e}}^{g} = {\mathbf{R}}{\mathbf{eR}}^{T} $$

(50)

$$ {\varvec{\upsigma}}^{g} = {\mathbf{R}}{\mathbf{\sigma R}}^{T} $$

(51)

where ${\mathbf{R}}{ = }\left[ {{\mathbf{r}} \, \left| { \, {\mathbf{s}} \, \left| { \, {\mathbf{t}}} \right.} \right.} \right]$ is the rotation matrix between modal local coordinates and global coordinates shown in Eqs. (43), (47) and (48).

3.2 Modal displacement vectors

As mentioned above, the 21 basic deformation modes can be derived by solving the basic governing differential equations. Using Eqs. (8), (9) and (10) and applying suitable boundary conditions, the displacement functions of 21 basic deformation modes can be expressed by the modal local coordinate systems as:

• (i) three rigid translational modes:

  $$ \left\{ {\begin{array}{*{20}l} {M_{1} :u = 1;v = 0;w = 0;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{2} :u = 0;v = 1;w = 0;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{3} :u = 0;v = 0;w = 1;} \hfill & {\left( {C_{1} } \right)} \hfill \\ \end{array} } \right. $$

  (52)

• (ii) three rigid rotational modes:

  $$ \left\{ {\begin{array}{*{20}l} {M_{4} :u = 0;v = - z;w = y;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{5} :u = z;v = 0;w = - x;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{6} :u = - y;v = x;w = 0;} \hfill & {\left( {C_{1} } \right)} \hfill \\ \end{array} } \right. $$

  (53)

• (iii) three tensile modes:

  $$ \left\{ {\begin{array}{*{20}l} {M_{7} :u = x;v = - \nu y;w = - \nu z;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{8} :u = - \nu x;v = y;w = - \nu z;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{9} :u = - \nu x;v = - \nu y;w = z;} \hfill & {\left( {C_{1} } \right)} \hfill \\ \end{array} } \right. $$

  (54)

• (iv) three shear modes:

  $$ \left\{ {\begin{array}{*{20}l} {M_{10} :u = y;v = 0;w = 0;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{11} :u = 0;v = z;w = 0;} \hfill & {\left( {C_{1} } \right)} \hfill \\ {M_{12} :u = 0;v = 0;w = x;} \hfill & {\left( {C_{1} } \right)} \hfill \\ \end{array} } \right. $$

  (55)

• (v) three torsional modes:

  $$ \left\{ {\begin{array}{*{20}l} {M_{13} :u = 0;v = xz;w = - xy} \hfill & {\left( {\tilde{C}_{1} } \right)} \hfill \\ {M_{14} :u = 0;v = xz;w = - xy} \hfill & {\left( {\tilde{C}_{2} } \right)} \hfill \\ {M_{15} :u = yz;v = xz;w = xy} \hfill & {\left( {\tilde{C}_{3} } \right)} \hfill \\ \end{array} } \right. $$

  (56)

• (vi) six bending modes:

  $$ \begin{aligned}M_{16 - 21} :u &= { - }xy;v = \left[ {x^{2} - \nu \left( {z^{2} - y^{2} } \right)} \right]/2; \\ & \quad w = \nu yz;\quad \left( {\bar{C}_{ij} ,i = 1,2,3,j \ne i} \right)\end{aligned} $$

  (57)

In Eqs. (52–57), $M_{i}$ represents for the displacement functions of the i-th mode in its modal local coordinate system. The deformation shapes of 21 basic deformation modes are illustrated in Figs. 2, 3, 4, 5, 6 and 7. It should be mentioned that the torsional modes M_t :$u = 0;v = xz;w = - xy,\left( {\tilde{C}_{3} } \right)$ is linearly dependent to M₁₃ and M₁₄. Therefore, the third mode M₁₅ in Eq. (56) is selected as a supplementary of torsional modes to ensure the invertibility of the modal displacement matrix.

Fig. 2

Rigid translational modes

Fig. 3

Rigid rotational modes

Fig. 4

Tensile modes

Fig. 5

Shear modes

Fig. 6

Torsional modes

Fig. 7

Bending modes

As illustrated in Fig. 7, the present method enables to describe the bending deformation of the element surfaces accurately, while for traditional iso-parametric finite elements, such as EAS or ANS elements, the element surfaces derived from iso-parametric shape functions remain straight after bending deformation. Therefore, the present method can describe the element deformed geometry more precisely.

For the remaining three unphysical modes, since it is difficult to find a feasible solution that satisfies the governing differential equations, the assumed displacement method is adopted here. The assumed displacement functions of unphysical modes are selected as

$$ M_{22 - 24} :u = xyz;v = 0;w = 0;\quad \left( {\tilde{C}_{1 - 3} } \right) $$

(58)

The deformation shapes of the unphysical modes are shown in Fig. 8.

Fig. 8

Unphysical modes

Substituting the coordinates of element nodes into Eqs. (52–58) and using Eqs. (4), (5) and (49), we can get the modal displacement vectors of 24 modes. Then the element modal displacement matrix in the global coordinate system can be expressed as

$$ {\mathbf{U}} = \left[ {\begin{array}{*{20}c} {U_{1}^{1} } & {U_{1}^{2} } & {U_{1}^{3} } & \cdots & {U_{1}^{23} } & {U_{1}^{24} } \\ {V_{1}^{1} } & {V_{1}^{2} } & {V_{1}^{3} } & \cdots & {V_{1}^{23} } & {V_{1}^{24} } \\ {W_{1}^{1} } & {W_{1}^{2} } & {W_{1}^{3} } & \cdots & {W_{1}^{23} } & {W_{1}^{24} } \\ {U_{2}^{1} } & {U_{2}^{2} } & {U_{2}^{3} } & \cdots & {U_{2}^{23} } & {U_{2}^{24} } \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ {U_{8}^{1} } & {U_{8}^{2} } & {U_{8}^{3} } & \cdots & {U_{8}^{23} } & {U_{8}^{24} } \\ {V_{8}^{1} } & {V_{8}^{2} } & {V_{8}^{3} } & \cdots & {V_{8}^{23} } & {V_{8}^{24} } \\ {W_{8}^{1} } & {W_{8}^{2} } & {W_{8}^{3} } & \cdots & {W_{8}^{23} } & {W_{8}^{24} } \\ \end{array} } \right] $$

(59)

in which the subscript denotes the node number, and the superscript denotes the mode number.

For anisotropic materials, the Poisson ratio in Eqs. (52–58) should be set to zero. In such cases, all of the 24 modes are derived from the assumed displacement method since the displacement functions of the basic deformation modes are not theoretical solutions any more.

3.3 Modal force vectors

With the given modal displacement functions shown in Eqs. (52–57), the modal strain vector of first 21 modes in the global coordinates can be calculated using Eqs. (9) and (50):

$$ {\varvec{\upvarepsilon}}^{i} = \left[ {\begin{array}{*{20}c} {e_{11} } & {e_{22} } & {e_{33} } & {2e_{12} } & {2e_{23} } & {2e_{13} } \\ \end{array} } \right]^{T} \quad \left( {i = 1, \ldots ,21} \right) $$

(60)

The corresponding modal stress vector of i-th mode can be written as

$$ {\varvec{\upsigma}}^{i} = {\mathbf{D}}{\boldsymbol{\varepsilon }}^{i} $$

(61)

where D is the elasticity matrix. Then the corresponding distributed surface tractions Tⁱ at element surface can be expressed as

$$ {\mathbf{T}}^{i} = \left[ {\begin{array}{*{20}c} {T_{x}^{i} } & {T_{y}^{i} } & {T_{z}^{i} } \\ \end{array} } \right]^{T} = {\mathbf{n}}{\boldsymbol{\sigma }}^{i} $$

(62)

in which

$$ {\mathbf{n}} = \left[ {\begin{array}{*{20}c} {n_{1} } & 0 & 0 & 0 & {n_{3} } & {n_{2} } \\ 0 & {n_{2} } & 0 & {n_{3} } & 0 & {n_{1} } \\ 0 & 0 & {n_{3} } & {n_{2} } & {n_{1} } & 0 \\ \end{array} } \right] $$

(63)

where n₁, n₂ and n₃ are the cosines of the angles between the normal vector of the element surface and cartesian coordinates. Then the modal force vectors can be derived from a surface integral of the distributed surface tractions

$$ {\mathbf{F}}^{i} = \int_{{S^{e} }} {{\mathbf{N}}^{T} {\mathbf{T}}^{i} ds} \begin{array}{*{20}c} {} & {\left( {i = 1, \ldots ,21} \right)} \\ \end{array} $$

(64)

It is clear that different selections of stress weight matrix N leads to different modal force vectors. Basically, the equivalent modal force vectors must balance the forces and moments of the distributed surface tractions. Theorem 1 indicates that iso-parametric shape functions comply with this condition. Thus, the stress weight matrix of an eight node hexahedral element can be written as

$$ {\mathbf{N}} = \left[ {\begin{array}{*{20}c} {N_{1} \varvec{I}_{3} } & {N_{2} \varvec{I}_{3} } & {N_{3} \varvec{I}_{3} } & {N_{4} \varvec{I}_{3} } & {N_{5} \varvec{I}_{3} } & {N_{6} \varvec{I}_{3} } & {N_{7} \varvec{I}_{3} } & {N_{8} \varvec{I}_{3} } \\ \end{array} } \right] $$

(65)

in which

$$ N_{i} = \frac{1}{8}\left( {1 + \xi \xi_{i} } \right)\left( {1 + \eta \eta_{i} } \right)\left( {1 + \zeta \zeta_{i} } \right) $$

(66)

where ξ, η and ζ are the iso-parametric coordinates within the element.

The product of ${\mathbf{N}}^{T} {\mathbf{T}}^{i}$ in Eq. (64), for a constant elastic constitute matrix D, is a simple polynomial function of ξ, η and ζ, with the maximum polynomial order of 2. Therefore, it can be integrated exactly with a 2 × 2 point integration rule on each face. Therefore, a total number of 2 × 2 × 6 Gaussian integration points are required to accurately integrate Eq. (64). Using Theorem 2, a more efficient expression of Eq. (64) can be written as

$$ {\mathbf{F}}^{i} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\mathbf{D}}{\boldsymbol{\varepsilon }}^{i} dV} \quad \left( {i = \, 1, \ldots , \, 21} \right) $$

(67)

in which only 2 × 2 × 2 Gaussian integration points are required. We also tried one point integration schema to derive Eq. (67) for the consideration of computational efficiency. However, the numerical results are not so desirable.

For the unphysical modes in Eq. (58), the corresponding stress distribution functions are

$$ \left\{ {\begin{array}{*{20}l} {\sigma_{x} = yz\left( {\nu - 1} \right)/\left( {2\nu^{2} + \nu - 1} \right)} \hfill & {} \hfill \\ {\sigma_{y} = - \nu yz/\left( {2\nu^{2} + \nu - 1} \right)} \hfill & {} \hfill \\ {\sigma_{z} = - \nu yz/\left( {2\nu^{2} + \nu - 1} \right)} \hfill & {} \hfill \\ {\tau_{xy} = xz/\left( {2\nu + 2} \right)} \hfill & {\left( {\tilde{C}_{1 - 3} } \right)} \hfill \\ {\tau_{yz} = 0} \hfill & {} \hfill \\ {\tau_{xz} = xy/\left( {2\nu + 2} \right)} \hfill & {} \hfill \\ \end{array} } \right. $$

(68)

in which $\sigma_{x}$, $\sigma_{y}$, $\sigma_{z}$, $\tau_{xy}$ and $\tau_{xz}$ tends to infinite when $\nu \to 0.5$, leading to the well know Poisson locking effect under unphysical modes. In this paper, the assumed displacement method is applied to avoid this volumetric locking phenomenon, in which the assumed modal strain functions are:

$$ \left\{ {\begin{array}{l} {\varepsilon_{x} = yz \, } \\ {\varepsilon_{y} = - \nu yz} \\ {\varepsilon_{z} = - \nu yz} \\ {\gamma_{xy} = 0 \, } \\ {\gamma_{yx} = 0 \, } \\ {\gamma_{xz} = 0 \, } \\ \end{array} } \right. $$

(69)

and the corresponding modal stress functions are

$$ \left\{ {\begin{array}{l} {\sigma_{x} = yz} \\ {\sigma_{y} = 0} \\ {\sigma_{z} = 0} \\ {\tau_{yx} = 0} \\ {\tau_{yz} = 0} \\ {\tau_{xz} = 0} \\ \end{array} } \right. $$

(70)

The volume locking can be naturally eliminated as the corresponding stress distributions are only functions in terms of y and z. Then the modal force vectors of unphysical modes are given as

$$ {\mathbf{F}}^{i} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\mathbf{D}}{\boldsymbol{\varepsilon }}^{i} dV} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\varvec{\upsigma}}^{i} dV} \left( {i = \, 22, \, 23, \, 24} \right) $$

(71)

Interestingly, these assumed modal strain functions also consistent with the strain filed of Nastran’s HEXA element for cubic shape element. Combining Eqs. (67) and (71), the modal force matrix of the hexahedral element can be finally expressed as

$$ {\mathbf{F}} = \, \left[ {{\mathbf{F}}^{1} ,{\mathbf{F}}^{2} , \ldots ,{\mathbf{F}}^{24} } \right] $$

(72)

4 Element stiffness

Substituting Eqs. (59) and (72) into (7), the element stiffness matrix in the global coordinates can be given as

$$ {\mathbf{K}}{ = }{\mathbf{FU}}^{ - 1} = \int_{{V^{e} }} {{\mathbf{B}}^{T} {\mathbf{DE}}} dV{\mathbf{U}}^{ - 1} $$

(73)

where ${\mathbf{E}} = \left[ {\begin{array}{*{20}c} {{\varvec{\upvarepsilon}}^{1} } & {{\varvec{\upvarepsilon}}^{2} } & \cdots & {{\varvec{\upvarepsilon}}^{24} } \\ \end{array} } \right]$ is referred to as the modal strain matrix. Since the inverse of Jacobian matrix is eliminated during the integration of Eq. (73), the element stiffness can be precisely described by the element nodal displacement and nodal force vectors for the first 21 modes shown in Eqs. (52–57), i.e. the resulting elements are able to avoid common locking effects for these modes.

In this paper, the element obtained from Eq. (73) is named as US-MEM8S. For US-MEM8S, the element stiffness is an asymmetric matrix if element shape is non-cubic. This also implies that US-MEM8S can only be applied to structural static analysis and cannot be extended to frequency analysis. In view of this drawback, a symmetric eight-node element S-MEM8S is developed based on the displacement functions of US-MEM8S.

Using the same displacement functions of US-MEM8S as described in Eqs. (52–58), the element stiffness matrix of S-MEM8S is given as

$$ {\mathbf{K = }}\left[ {{\mathbf{U}}^{T} } \right]^{ - 1} \int_{{V^{e} }} {{\mathbf{E}}^{T} {\mathbf{DE}}} dV{\mathbf{U}}^{ - 1} $$

(74)

where ${\mathbf{EU}}^{ - 1}$ is similar to the B matrix in traditional finite element techniques and represents the relationship between element strain and displacement. Though the formulations of S-MEM8S and US-MEM8S are quite different, numerical results show that exactly the same element stiffness are obtained for US-MEM8S, S-MEM8S, and Nastran’s HEXA [31, 32] for cuboid shape elements. For non-cubic shape elements, as can be seen from the next section, the proposed solid elements are more insensitive to mesh distortion and obtain better performance in most cases. The major difference between HEXA and the proposed elements lies in the behavior of non-cuboid shape meshes.

5 Numerical tests

In this section, the static linear behavior of the two developed eight-node solid elements US-MEM8S and S-MEM8S and the frequency response of symmetric eight-node solid element S-MEM8S are investigated. All the elements possess the proper rank. The benchmark problems considered here are carefully selected to demonstrate some important features of the proposed elements, especially for the sensitivity to mesh distortion and locking effect. It also should be noted that the thin-walled structure problems are not considered here as the deformation patterns of solid and solid-shell element are totally different. Indeed, the computational efficiency of solid-shell elements is hundreds or even thousands of times faster than solid element when simulating thin-walled structures. Most of the results presented in tables and figures are normalized with respect to the reference solutions. A list of referenced elements used for comparison with MEM8S is outlined in Table 1.

Table 1 List of element models for comparison

5.1 Linear static analysis

5.1.1 Enginvalue and patch test

In this example, the eigenvalue analysis of a unit cubic solid element is first performed to evaluate the element behavior in the nearly incompressible limit. Because the element stiffness matrixes of S-MEM8S and US-MEM8S are symmetric and same for cubic shape element, both of these two elements are investigated in this test. The material properties of the cubic are defined as E = 1.0 and ν = 0.499999. Exactly the same eigenvalues, shown in Table 2, are obtained for S-MEM8S, US-MEM8S, HEXA and H1/E21 [33]. These results only include the eighteen non-zero eigenvalues, i.e. the six rigid body modes are excluded. The spectrum shows that only one eigenvalue tends to infinity as $\nu \to 0.5$. If any additional modes tend toward infinity, the element will exhibit volumetric locking.

Table 2 Eigenvalues for a nearly incompressible eight-node regular hexahedral element

Besides the cubic configuration, several different distorted configurations are also investigated for S-MEM8S and US-MEM8S. Complex eigenvalues are observed in severe distorted configurations for US-MEM8S. Nevertheless, in all of these tests, only one eigenvalue tends to infinity. Therefore, it can be stated that the proposed solid elements are free of volumetric locking [33].

Subsequently, the patch test for solids proposed by MacNeal and Harder [32] is carried out in this example to test the convergence of proposed element formulations. The geometry of a unit cubic with a discretization of seven irregular 8-node hexahedral elements is illustrated in Fig. 9. The material behavior is defined by Young’s modulus E = 1 × 10⁶ and Poisson ratio ν = 0.25. The displacements of the eight exterior nodes (four on the bottom surface and four on the top surface) are prescribed by the linear functions

Fig. 9

Patch test of a constant strain/stress problem

$$ \begin{aligned} u = 10^{ - 3} \left( {2x + y + z} \right)/2 \hfill \\ v = 10^{ - 3} \left( {x + 2y + z} \right)/2 \hfill \\ w = 10^{ - 3} \left( {x + y + 2z} \right)/2 \hfill \\ \end{aligned} $$

and the interior nodes are free of constraints, which results in a constant strain and stress state. The theoretical strain and stress solutions of this case is

$$ \begin{aligned} e_{11} = e_{22} = e_{33} = e_{12} = e_{23} = e_{13} = 10^{ - 3} \hfill \\ \sigma_{11} = \sigma_{22} = \sigma_{33} = \sigma_{12} = \sigma_{23} = \sigma_{13} = 400 \hfill \\ \end{aligned} $$

Since US-MEM8S is complete for constant strain modes (three tensile strain modes and three shear strain modes) and the stress weight functions are selected as iso-parametric shape functions, US-MEM8S enables to pass the patch test. Numerical results also verified this conclusion. For S-MEM8S, its behavior is quite similar to that of the HVCC8 element, which also cannot pass the patch test [34]. It should be noted that patch test is a sufficient condition but not a necessary condition of element convergence. Numerical results also show that the elements that cannot pass the patch test still can be convergent. Up to now, the necessary condition of element convergence still is an open question and needs to be studied in the future. The following examples test the accuracy and convergence of S-MEM8S further.

5.1.2 Element distortion

In order to evaluate the sensitivity of the proposed element formulation to mesh distortion in bending deformation patterns, the well-known cantilever beam test with two distorted elements [35] is investigated. The beam is subjected to a constant bending moment with F = 10 at the free tip as shown in Fig. 10. The length of the beam is 10, width and height are 2. Three different mesh divisions with vertical, horizontal and non-planar distortions are investigated. The parameter e is utilized to denote the magnitude of element distortions. When e = 0, the elements are cubic and regular. As e increased, the mesh will be more distorted. The Young’s modulus is E = 2.1 × 10⁵ and the Poisson ratio is ν = 0.0 and ν = 0.4999. The reference solution for the free tip deflection of the upper node A is

Fig. 10

Cantilever beam configuration: a vertical distortion; b horizontal distortion; c non-planar distortion

$$ w = \frac{15M}{E} $$

The normalized results of the tip deflection for three mesh distortions are given in Figs. 11, 12 and 13. US-MEM8S possesses the exact solutions for all distortions and shows totally free of element distortions. For the symmetric solid elements, S-MEM8S and HVCC8 obtain near the same performance for the vertical and horizon distortions, while S-MEM8S obtains better performance than HVCC8 for the non-planar distortion test. For other referenced element formulations, high sensitivity to element distortions are observed.

Fig. 11

Sensitivity test to vertical distortion. aν = 0.0; bν = 0.4999

Fig. 12

Sensitivity test to horizon distortion. aν = 0.0; bν = 0.4999

Fig. 13

Sensitivity test to non-plane distortion

5.1.3 MacNeal’s cantilever beam

The MacNeal’s straight cantilever beam test is another standard benchmark problem for evaluating the element sensitivity to mesh distortion. The cantilever beam is subjected to two different load cases: a unit in-plane shear force F₁ and a unit out-of-plane shear force F₂. Two different element shapes with trapezoidal and parallelogram shape elements are adopted with various skew angles θ, as depicted in Fig. 14. The length of the beam L = 6.0, width w = 0.2, depth d = 0.1. The elastic modulus is E = 1 × 10⁷ and Poisson ratio ν = 0.3. The theoretical solutions of the tip deflection in the loading directions are 0.1081 for in-plane shear load and 0.4321 for out-of-plane shear load [32]. In this test, the errors E of the tip deflection u are defined with respect to the theoretical solution u^*:

Fig. 14

MacNeal’s cantilever beam: a parallelogram shape elements; b trapezoidal shape elements

$$ E = \frac{{\left| {u - u^{*} } \right|}}{u} $$

Tables 3 and 4 report the errors of the tip deflection for different skew angles. As different boundary conditions are involved in the standard MacNeal’s cantilever beam test [32] and Li’s test [34], the results obtained from Li’s HVCC8 are not compared in this example. It can be seen that the accuracy of the referenced elements deteriorates severely as the increase of skew angle, especially for the trapezoidal mesh distortions. Compared with the other elements, US-MEM8S and S-MEM8S obtain excellent numerical results for different skew angles.

Table 3 Errors of MacNeal’s beam with in-plane shear force

Table 4 Errors of MacNeal’s beam with out of plane shear force

5.1.4 Curved beam test

In this example, a curved cantilever beam [32] is considered to test the element behavior for curved structures. The inner radius of the beam is taken as R_i = 4.12, the width is h = 0.2 and the thickness is t = 0.1. The beam is subjected to two load cases with a unit in-plane shear load F₁ and a unit out-of-plane shear load F₂, as shown in Fig. 15. The material behavior is defined as Young’s modulus E = 1 × 10⁷ and Poisson ratio ν = 0.25. Five different meshes with element number varied from 2 up to 10 are considered. The analytical solutions of the tip deflection for these two load cases are 0.08734 and 0.5022, respectively. The normalized displacements with respect to theoretical solutions are plotted in Fig. 16. For out-of-plane shear load, all elements cannot converge to the reference solutions as the mesh is only refined in one direction. In comparing convergence of different formulations, US-MEM8S and S-MEM8S generally appear to be more effective in simulating curved beam than other formulations.

Fig. 15

Curved beam test

Fig. 16

Normalized results of the curved beam. a In-plane shear load, b Out-of-plane shear load

5.1.5 Thick-walled cylinder

In this example, a thick-walled cylindrical tube as shown in Fig. 17 is considered to assess the performance of the proposed element formulation for a confined nearly incompressible state. The cylinder is subjected to a uniform pressure p at the inner radius. The top and bottom surfaces of the cylinder are clamped in the thickness direction. Young’s modulus is E = 1000 and six different Poisson ratio with ν = 0.0, ν = 0.1, ν = 0.2, ν = 0.3, ν = 0.4 and ν = 0.49999 is investigated. The analytical solution of the radial displacement at the inner radius is given by [32]:

Fig. 17

Thick-walled cylinder

$$ u = \frac{{\left( {1 + \nu } \right)pR_{1}^{2} }}{{E\left( {R_{2}^{2} - R_{1}^{2} } \right)}}\left[ {R_{1}^{2} /r + \left( {1 - 2\nu } \right)/r} \right] $$

where R₁ and R₂ is the inner and outer radius, respectively. The normalized displacements with respect to theoretical solutions are shown in Fig. 18. It should be pointed out that the numerical solutions given by [32] are not consistent with the analytical solution given by itself. In this paper, we use the analytical solution to normalize our results. The numerical results show that the normalized displacements of all elements are decreased as ν varies from 0 to 0.5. Generally, the present solid elements exhibit better convergence than other elements when ν is little than 0.4, while for other models, the results are close to the theoretical solution when ν approaches to 0.5.

Fig. 18

Normalized radial displacements of Thick-walled cylinder with different Poisson ratio

5.1.6 Straight cantilever beam under gravity

To investigate the behavior of the present element for problems involving body forces, a straight cantilever beam subjected to a uniform constant body force is considered in this example. The length of the beam is L = 4, height h = 0.5, width w = 0.5. The beam is composed of two materials with E₁ = 2 × 10⁸, E₂ = 4 × 10⁸ as shown in Fig. 19. The interface between the two materials is considered to be perfectly bonded. A constant body force of 10 in the vertical direction is applied to the beam. Four different distorted meshes: Mesh 1 (4 × 1 × 1), Mesh 2 (10 × 2 × 2), Mesh 3 (20 × 4 × 4), Mesh 4 (40 × 8 × 8), as shown in Fig. 20, are performed to investigate the convergence of the present element. The reference solution of the vertical displacement of the free tip obtained by Nastran with a mesh of 80 × 20 × 20 elements is given as 7.451 × 10⁻⁵. Figure 21 gives the normalized results for different meshes obtained by the proposed solid elements as well as the referenced formulations. It can be observed that all the elements converge to the benchmark value with the increasing of the mesh density. Compared with other referenced element formulations, the results again demonstrate the excellent convergence characteristics of the proposed element formulations.

Fig. 19

Straight cantilever beam with two materials

Fig. 20

Meshes of straight cantilever beam

Fig. 21

Convergence for the straight cantilever beam

5.1.7 Cook’s membrane test with an isotropic material

In this example, the famous Cook’s membrane problem is considered. The tapered panel is clamped on its left edge and subjected to a unit in-plane shear load on its right edge. The thickness of the panel is 1 and the detailed geometry parameters are shown in Fig. 22. The elastic modulus is taken as E = 1 and Poisson ration ν = 0.33. A finite element converged solution of the vertical tip displacement is taken as 23.91 in [36]. However, the solution derived from a more refined model with a total number of 154,141 HEXA elements is 24.48. A detailed convergence study for the vertical displacement of the free tip versus number of elements per side is plotted in Fig. 23. As can be seen, the responses from US-MEM8S and S-MEM8S show excellent convergence behavior even with a coarse mesh.

Fig. 22

Cook’s membrane test with an isotropic material

Fig. 23

Convergence rate of Cook’s membrane with an isotropic material

5.1.8 Cook’s test with an anisotropic material

The model in this example is like the model in the previous example, except that the material of the plate is changed into an anisotropic material. Furthermore, the meshes of this test are divided by assigning the size of the element length, which is more frequently used in engineering. Five different element sizes with L = 12, L = 8, L = 4, L = 2, L = 1 are investigated, as partly illustrated in Fig. 24. The anisotropic material behavior of this plate is defined as [31]:

Fig. 24

Cook’s membrane test with an anisotropic material. a Element length L = 12, b element length L = 4

$$ {\mathbf{D}} = \left[ {\begin{array}{*{20}c} { 10. 6 7} & { 6. 9 1} & { 6. 8 9} & { 1. 2 5} & { - 0.09} & {0.86} \\ { 6. 9 1} & { 1 9.0 3} & { 6. 90} & { 1. 2 7} & { - 0.12} & {0.83} \\ { 6. 8 9} & { 6. 90} & { 1 4. 2 8} & { 1. 2 3} & { - 0.15} & {0.82} \\ { 1. 2 5} & { 1. 2 7} & { 1. 2 3} & {5.27} & {0.21} & { - 0.11} \\ { - 0.09} & { - 0.12} & { - 0.15} & {0.21} & {4.63} & {0.52} \\ {0.86} & {0.83} & {0.82} & { - 0.11} & {0.52} & {5.72} \\ \end{array} } \right] \times 10^{6} $$

In this example, the shear load on the right edge of the tapered panel equals to 1.0 × 10⁶. The convergence rate of the present element is reported in Fig. 25. Nearly the same convergence rates are observed for US-MEM8S and S-MEM8S. Comparing with the referenced elements, the present elements show excellent performance for the simulation of anisotropic material as well as for the distorted meshes.

Fig. 25

Convergence rate of Cook’s membrane with an anisotropic material

5.1.9 Hemispheric shell with 18° hole

In this example, the pinched hemispherical shell problem with an 18° hole under the action of inward and outward orthogonal concentrated loads F = 1.0 is tested to assess the element performance for inextensional bending and complex membrane modes. The radius of the shell is R = 10.0 and the thickness is t = 0.04. Due to the symmetry property, only one quadrant is analyzed as shown in Fig. 26. The material behavior is defined as Young’s modulus E = 6.825 × 10⁷ and Poisson ratio ν = 0.3. The results reported in Table 5 for the radial displacement of Node A under the load are normalized with respect to the reference value 0.0941 derived from a model with 810,000 HEXA elements. It can be concluded that the new elements, especially for the asymmetric S-MEM8S, demonstrate excellent convergence characteristic and produce much better results than referenced element formulations.

Fig. 26

Hemispherical shell with 18° hole showing 8 × 8 mesh

Table 5 Normalized results of hemispherical shell with 18° hole

5.1.10 Pinced cylinder test

In this example, a thin pinched cylinder as illustrated in Fig. 27 is performed to investigate the element behavior for single curved structures. The inner radius of the cylinder is R = 298.5, thickness d = 3.0, and length L = 600. The elastic modulus is taken as E = 3.0 × 10⁶ and Poisson ration ν = 0.3. Two end edges of the cylinder are constrained in such a way that they can move only in the axial direction. One-eighth of the shell is modeled by an N × N mesh defined in cylindrical coordinates. The cylinder model is subjected to two diametrically opposite point loads of magnitude F = 1.0. The reference solution for the vertical displacement is taken as 1.82488 × 10⁻⁵ in [32]. In this paper, we use the value of 1.85427 × 10⁻⁵ that was obtained from a fine finite element model with 960,000 HEXA elements for normalization of our results. As demonstrated in Table 6, the proposed elements perform well for this test.

Fig. 27

Pinched cylinder with end diaphragms

Table 6 Normalized results of pinched cylinder

5.2 Frequency analysis

In this section, we investigate the performance of S-MEM8S for frequency analysis. All of the mass matrixes are selected as lumped mass matrixes, which is the default setting in NASTRAN and ABAQUS. The material density of all tested problems is set to 1 for simplicity.

5.2.1 Straight cantilever beam with vertical distortion

In this example, a straight cantilever beam is considered to test the element performance in frequency analysis. The length of the beam is L = 20, width d = 2, height w = 2. The elastic modulus is taken as E = 2.1 × 10⁵ and Poisson ration ν = 0.3. In order to evaluate the sensitivity of the proposed element formulation to mesh distortion, the finite element model as illustrated in Fig. 28 is investigated, in which parameter e denotes the magnitude of element distortion.

Fig. 28

Straight cantilever beam

Due to the structure symmetry, the first and second order frequencies are same and equal to 0.3706. Figure 29 presents the normalized first and second order frequencies of S-MEM8S and referenced elements. It can be observed that the error of the first and second order frequencies increased significantly as e increased for the referenced elements. As a comparison, S-MEM8S shows better numerical stability and accuracy for distorted meshes.

Fig. 29

Normalized first two order frequencies of straight cantilever beam. a First order, b second order

5.2.2 Simply supported beam

In this example, a simply supported beam as illustrated in Fig. 30 is considered. The length of the bean is L = 12, width d = 1, height w = 0.4. The material behavior is defined as Young’s modulus E = 1.74 × 10⁷ and Poisson ratio ν = 0.3. The simply supported beam is meshed by 16 eight-node solid elements (two elements in the thickness direction), in which parameter e denotes the magnitude of element distortions.

Fig. 30

Simply supported beam

For this structure, the first and second order frequencies equal to 5.2456 and 20.8795, respectively. The normalized frequencies of S-MEM8S and other referenced elements are illustrated in Fig. 31. The numerical results again show that S-MEM8S is low susceptible to mesh distortion.

Fig. 31

Normalized first two order frequencies of simply supported beam. a First order frequency, b second order frequency

5.2.3 Curved beam test

In this example, the element performance with a curved cantilever beam problem is investigated. The model geometry of this example is same as the model shown in Sect. 5.1.4. Five meshes with the number of elements varies from 2 up to 10 are considered. The reference solutions of first and second order frequencies obtained from a fine mesh with 16,950 HEXA elements are taken as 1.2389 and 2.4443, respectively. Figure 32 compares the normalized frequencies between S-MEM8S and referenced elements. For both tests, S-MEM8S obtains better numerical accuracy and convergence speed.

Fig. 32

Normalized first two order frequencies of curved beam. a First order frequency, b second order frequency

5.2.4 Thick-sphere shell problem

In this example, the thick-sphere shell problem proposed by Kasper and Taylor [33] is performed to investigate the element behavior of S-MEM8S for double curved structures. The inner radius of sphere shell is R_i = 7.5, outer radius is R_e= 10. The material behavior is defined as Young’s modulus E = 250 and Poisson ratio ν = 0.3. The geometry is discretized by m × m × n elements as depicted in Fig. 33, in which m is the element number in radial direction and n is the element number in thickness direction. The reference solution of the first order frequency obtained from 71,000 HEXA elements is taken as 0.2250. Figure 34 compares the numerical results of different element formulations for different meshes. All the tested elements obtain excellent performance for this problem. For S-MEM8S, a maximum error of 0.4% is derived even using a coarse 4 × 4 × 1 mesh.

Fig. 33

Thick sphere shell

Fig. 34

Normalized first order frequency of sphere shell

5.2.5 Pinced cylinder test

In this example, the frequency response of the present symmetric solid element in thin curved geometry is considered. The same structure given in Sect. 5.1.9 is investigated in this test. The reference solutions of first order frequencies obtained from a fine mesh with 60,000 HEXA elements is 0.1178. Figure 35 illustrates the normalized first order frequency of the cylinder for different element formulations. The numerical results show that S-MEM8S obtains better convergence rate than the referenced solid elements used in NASTRAN and ABAQUS.

Fig. 35

Normalized first order frequency of Pinced cylinder

6 Conclusion

In this paper, a generalized finite element method named as generalized modal element method (GMEM) is proposed to develop new finite element formulations using different finite element design methods. Furthermore, an asymmetric hexahedral element US-MEM8S and a symmetric hexahedral element S-MEM8S based on the GMEM are introduced in this paper. The highlights of this paper include the follows:

• 1. Three different element modal construction methods, including analytic method, assumed displacement method and traditional finite element technique are proposed in this paper. A more accurate finite element formulation can be obtained by GMEM since it is a generalized finite element method and can make full use of the merits of different finite element techniques, i.e. any of the existing finite element technique can be adopted in GEME to design new element formulations.

• 2. The concept of modal local coordinates systems is proposed, which effectively ensures the frame invariance of element stiffness and has been proved to be a useful tool to link the analytical method and the finite element technique. As the analytical method can be regarded as the most accurate method, the combination of modal local coordinates systems and analytical method can significantly improve the element behavior. Theoretically, this method can also be extended to other engineering fields such as heat transfer, fluid flow, electromagnetic radiation and so on.

• 3. Two eight-node hexahedral solid elements are proposed to demonstrate the use of analytical method and the assumed displacement method in developing new finite element formulations. The basic deformation modes of these two elements, such as tension, shear, torsional and bending deformation modes, are derived from basic governing equations of solid mechanics. Therefore, the proposed element formulations are insensitive to element distortions, and in addition the element can also avoid common locking phenomena, and obtain excellent performance for both thick and thin structures.

Due to the compatibility and diversity of modal construction methods, the elements using GMEM are able to achieve higher accuracy and has wider application fields than the existing finite element methods. The GMEM seems to open up exciting possibilities in designing new finite elements in various application fields. But a deeper theoretical and mathematical explanations of GMEM still need further studies.