Performance of goodness-of-fit tests for the Cox proportional hazards model with time-varying covariates

Abstract

There are few readily-implemented tests for goodness-of-fit for the Cox proportional hazards model with time-varying covariates. Through simulations, we assess the power of tests by Cox (J R Stat Soc B (Methodol) 34(2):187–220, 1972), Grambsch and Therneau (Biometrika 81(3):515–526, 1994), and Lin et al. (Biometrics 62:803–812, 2006). Results show that power is highly variable depending on the time to violation of proportional hazards, the magnitude of the change in hazard ratio, and the direction of the change. Because these characteristics are unknown outside of simulation studies, none of the tests examined is expected to have high power in real applications. While all of these tests are theoretically interesting, they appear to be of limited practical value.

1 Introduction

The proportional hazards (PH) regression model proposed by Cox (1972) is commonly used to analyze survival data in a variety of fields. The primary focus of the PH model is typically to estimate hazard ratios (HRs) that compare the hazard of event occurrence between groups defined by predictor variables.

Let a subject’s observed time be denoted as $T$. $T$ represents the minimum of the subject’s event time and the subject’s censoring time. The initial Cox PH model relates the hazard of event occurrence to constant covariates through the hazard function $\lambda (t|\mathbf{Z })$

$$\begin{aligned} \lambda (t|\mathbf{Z })= \lambda _0(t)e^{{\varvec{\beta }}' \mathbf{Z }}, \end{aligned}$$

where $\lambda _0(t)$ is an unspecified baseline hazard function, $e^{{\varvec{\beta }}'\mathbf{Z }}$ is the exponentiated linear predictor and $Z$ is a vector of fixed covariates. The covariates are fixed in the sense that their values do not change over the time period of observation. The PH model has been extended to accommodate covariates which change over time, known as time-dependent or time-varying covariates (TVCs). TVCs are useful for modeling the effect of covariates for which values change over time and for which a current value is more important than the baseline value. Such covariates need to be collected or assessed longitudinally over the duration of a study (Therneau and Grambsch 2000).

Formally, let $j$=1,...,$p$ index $p$ covariates. Then $\mathbf{Z }(t)=\big (Z_{1}(t),\ldots ,Z_{p}(t)\big )'$ is the $(p \times 1)$ vector of covariates for a subject at time $t$. For any covariate $Z_{j}$ measured only at baseline, $Z_{j}(t)=Z_{j}$ and it is assumed that the baseline value is representative for the entire time period of observation. The PH model with TVCs is challenging from a number of perspectives. It requires consideration of missing covariate values, whether the TVC is internal or external to the failure mechanism, careful selection of the functional form of continuous covariates and consideration of the conceptual implications (Altman and de Stavola 1994; Andersen 1992; Kalbfleisch and Prentice 2002; Fisher and Lin 1999). However, expanding the PH model to include TVCs is simple in terms of notation. In the following we consider a model with one fixed binary covariate $Z_1$ and one binary TVC $Z_2$. In this case

$$\begin{aligned} \lambda (t|\mathbf{Z }(t))= \lambda _0(t)e^{ \beta _1 Z_1 + \beta _2 Z_2(t) }. \end{aligned}$$

The HR for the binary TVC is a single number, but the interpretation of $e^{\beta _2}$ is not independent of time. At time $t$, the hazard of an event for a patient who has $Z_2(t)=1$ is $e^{\beta _2}$ times the hazard of a patient who has $Z_2(t)=0$. Although $Z_2(t)$ can change over time, the HR is constant conditional on time $t$ (Hosmer et al. 2008, Sect. 7.3)

A crucial assumption of the PH model is that the effect of a covariate does not change over time (Cox 1972). In other words, ${\varvec{\beta }}$ are assumed to be constant for all $t$. This assumption applies even in the case of time-dependent covariates; though values may change, the effect of the covariate is assumed to be constant.

Formal testing of the PH assumption is often used in conjunction with graphical methods. One such example is plotting Schoenfeld residuals from the model (Schoenfeld 1980) or examining log-log survival plots. Many tests for PH have been proposed but few are suitable for use with TVCs, and even fewer are readily implemented. This paper considers the relative performance of the following tests, all of which are conceptually compatible with TVCs and available in standard statistical software packages or relatively easy to program.

• 1. Cox (1972) suggests adding a TVC to the model in the form of the product of the variable of interest and a function of time $g(t)$, and comparing the original and alternative models using a likelihood ratio test. The functions $g(t) = t$ and $g(t) = \ln (t)$ are popular choices.

• 2. Grambsch and Therneau (1994) propose a formal test analagous to plotting a function of time versus scaled Schoenfeld residuals and comparing the slope of a regression line to zero. Some choices for the function of time $g(t)$ are $t,\,\ln (t)$, the rank of the event times, and the Kaplan–Meier (KM) product-limit estimator.

• 3. Lin et al. (2006) propose a score test for PH comparing the standard PH model to a model containing an arbitrary smooth function of time. This test has one advantage over the tests discussed above: the function of time in the alternative hypothesis does not have to be defined, so departures from the PH assumption where the test could be expected to have adequate power are less limited. The test statistic is a function of the Schoenfeld residuals and observed information matrix under the null model.

For each test, a significant p-value implies that the variable of interest interacts with time and does not have a constant effect over the entire period of observation, i.e., the PH assumption is violated.

In the following, we assess the performance of these goodness-of-fit tests in terms of power under a number of different settings where the PH assumption is violated. In the next section, the settings for the simulations are described, followed by a summary of the simulation results (Sect. 3). Section 4 contains a data example using the well known Stanford Heart transplant data set. In the final section the results and in particular the limitations of the tests are discussed. Code for calculating the Lin et al. (2006) test in Stata is provided in the Appendix (Sect. 6).

2 Simulation methods

Our simulations focus on a simple case: a binary fixed covariate, a binary TVC that does not switch off after switching on, and a one-time jump in hazard occurring a specified amount of time after the TVC switches on. An example of such a binary TVC in the Stanford Heart Transplant data (Clark et al. 1971; Crowley and Hu 1977) is receiving a heart transplant after having been on a waiting list for some time. For the simulations, different settings are generated for time to change in the TVC, time to jump in hazard (violation of PH assumption), the effect size of the violation of PH, and the direction of the violation. Simulations are performed using Stata 10.1. Programs are validated by comparing results from simulations run in SAS and Stata with 100 replicates.

We generated time-to-failure data using an extension of the piecewise exponential method (Zhou 2001; Leemis et al. 1990). Let $Y_2$ be the failure time, and $Y_1$ the time when the TVC switches on. Let $t_0$ be the time after $Y_1$ where the jump in the HR occurs and the PH assumption is violated. Let $Z_1$ be a fixed covariate with coefficient $\beta _1$, and let $Z_2(t)$ be a TVC with coefficient $\beta _2$ prior to $Y_1 + t_0$ and coefficient $\beta _3$ after $Y_1 + t_0$. Zhou (2001) applied an arbitrary monotone increasing transformation $g(\cdot )$ to a piecewise exponential variable $W$ with two intervals and showed that $g(W)$ follows a Cox PH model with a binary TVC and baseline hazard $\frac{d}{dt}g^{-1}(t)$.

The addition of another interval facilitated the change in hazard occurring at time $Y_1 + t_0$. Thus we generated a piecewise exponential random variable $T$ with the following rate:

$$\begin{aligned} \lambda ={\left\{ \begin{array}{ll} r_0 = e^{\beta _1 Z_1} &{} \text {if}\,Y_2 < Y_1, \\ r_1(t) = e^{\beta _1 Z_1 + \beta _2 Z_2(t)} &{} \text {if}\,Y_1 \le Y_2 < t_0 + Y_1, \\ r_2(t) = e^{\beta _1 Z_1 + \beta _3 Z_2(t)} &{} \text {if}\, t_0 + Y_1 \le Y_2, \end{array}\right. } \end{aligned}$$

where the probability density function of $T$ is $f_T(t) = \lambda e^{- \lambda t}$. The function $g(t)$ is chosen such that $g(t)=t$, so $T$ follows the Cox PH model with baseline hazard 1. Subjects who failed before experiencing a change in the value of $Z_2(t)$ had $Y_2 < Y_1$. Subjects who failed after $Z_2(t)$ switched on but before the jump in hazard had $Y_1 \le Y_2 < t_0 + Y_1$. Subjects who failed after $Z_2(t)$ switched on and after PH was violated had $Y_2 \ge t_0 + Y_1$.

To create the piecewise exponential random variable $T$ (the observed time), we generated the random switching time as $Y_1 \sim$ Exp$(1)$ and the random failure time $Y_2 \sim$ Exp$(1)$ independently for each of $n$ subjects. We randomly generated values for the fixed covariate $Z_1$ such that 50 % had a value of one and 50 % had a value of zero and set $Z_2(t)=1$ for approximately 50 % of subjects. As an initial step we generated the observed time $T$ as

$$\begin{aligned} T ={\left\{ \begin{array}{ll} \frac{Y_1}{r_0} &{} \text {if}\,Y_2 < Y_1, \\ Y_1 + \frac{Y_2 - Y_1}{r_1(t)} &{} \text {if}\,Y_1 \le Y_2 < t_0 r_1(t) + Y_1, \\ Y_1 + t_0 + \frac{Y_2 - Y_1 - t_0 r_1(t)}{r_2(t)} &{} \text {if}\,Y_2 \ge t_0 r_1(t) + Y_1 \end{array}\right. } \end{aligned}$$

assuming all subjects failed on-study and created an event indicator. As a second step we created separate censoring times by multiplying the maximum follow-up time and random numbers from a Uniform$(0,1)$ distribution. To apply censoring we generated another random number from the Uniform$(0,1)$ distribution for each subject, sorted subjects by the random number, and applied censoring times to the specified proportion of subjects by replacing $T$ with the separately generated censoring times and updating the event indicator accordingly. As a third step we applied administrative censoring for subjects where the observed time $T$ is beyond the maximum follow-up time. Here administrative censoring is defined as right censoring of subjects due to the fact that a study ends based on administrative reasons (e.g. end of funding period) and subjects are no longer followed.

For the test proposed by Grambsch and Therneau (1994) the following functions $g(t)$ were used: $t,\,ln(t)$, rank, and KM survival estimate. P-values for the tests proposed by Cox (1972) were obtained by fitting models with and without the interaction terms and performing likelihood ratio tests. The interaction terms were defined by $\text{ TVC }\times \ln (t)$ and $\text{ TVC }\times t$. See Sect. 6 (Appendix) for a Stata Mata function to perform the test proposed by Lin et al. (2006).

To estimate power, the PH assumption was violated in one of three ways: the TVC effect disappeared, doubled, or reversed at time $Y_1 + t_0$. Time between change in TVC and jump in HR was varied for all three scenarios. We used a fixed value for $t_0$ as well as randomly generated values of $t_0$ from a Uniform$(0, 3 - Y_1)$ distribution. The impact of sample size and uniform censoring on power were investigated as well.

See Table 1 for simulation settings for the disappearing effect case $(\beta _3 = 0)$. Note that we considered a wide range of pre-jump TVC effects, including HRs as extreme as 20. Increasing $(\beta _3 = 2\beta _2)$ and reversing $(\beta _3=-\beta _2)$ effect cases included the same values of $\beta _2$ and $t_0$, but $n$ and censoring were fixed at 500 and 0 %, respectively. Note, if the coefficient $\beta _2$ is negative, an increasing effect means that $\beta _3$ is double in magnitude compared to $\beta _2$, but remains negative and thus represents a stronger negative effect. Finally, the null hypothesis of constant effect was investigated to assess test size with $n$ fixed at 500. For all simulations, the TVC switched on for 50 % of subjects and maximum follow-up time was set at 3 years.

Table 1 Simulation settings

3 Simulation results

Figure 1 summarizes power by various pre-jump TVC coefficients for increasing $(\beta _3 = 2\beta _2)$, disappearing $(\beta _3 = 0)$, and reversing $(\beta _3 = -\beta _2)$ effect scenarios with random time to violation of PH, $n=500$, and 0 % censoring. For all scenarios, power was lowest for pre-jump $\beta _2$ near zero (HR=1). In the increasing effect scenario, the power of all tests was 60 % or below for negative values of $\beta _2$, and below 15 % for positive values of $\beta _2$. In the disappearing effect scenario, all tests had high power for extreme values of $\beta _2$, but power was below 70 % for moderate HRs (between 0.4 and 2.7, $-1 \le \beta _2 \le 1$). Cox’s interaction with $t$ and $\ln (t)$, the Grambsch-Therneau test with $g(t)=t$, and the Lin–Zhang–Davidian had the highest power. In the reversing effect scenario, all tests had over 70 % power for $\beta _2 \ge 1.5$ and $\beta _2 \le -1.5$. The Grambsch–Therneau test with $g(t)=\ln (t)$ had the lowest power in the reversing effect scenario.

Fig. 1

Power in the scenarios of disappearing, increasing, and reversing effect, with random $t_0$

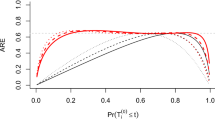
Figure 2 summarizes power by pre-jump TVC coefficient for differing values of $t_0$ in the disappearing effect scenario with $n=500$, and 0 % censoring. For the smallest time to violation of PH, power is very low for all tests when $\beta _2 < 0$ and increases with $\beta _2$ when $\beta _2 > 0$. At $t_0$ of 6 months all tests show the same pattern for positive $\beta _2$ with power peaking for $\beta _2$ between 1 and 1.75. For $t_0$ of 1 year, power is highest when $\beta _2$ is most negative. For negative $\beta _2$, when $t_0$ is lowest a large change in effect size for the TVC results in more powerful tests. Some tests, including Cox’s interaction with time, the Grambsch–Therneau test with $g(t) = t$, and the Lin–Zhang–Davidian test, had over 70 % power for log hazard ratios between 1 and 1.75 for $t_0$ of 6 months. The remaining tests have much lower power. When $t_0$ is 1 year, none of the tests perform well for positive $\beta _2$. However, when $\beta _2$ is negative, power increases as $t_0$ increases, and is highest for smallest values of $\beta _2$. All tests have over 70 % power at some point for $\beta _2 < 0$ and $t_0$ of 6 months or greater. Overall, power is below 70 % for moderate HRs between 0.4 and 2.7 $(-1 \le \beta _2 \le 1)$. Results from simulations investigating power for an increasing or decreasing effect had similar pattern, but power was in general lower for an increasing effect size (results not shown).

Fig. 2

Power in the scenarios of disappearing effect, by $t_0$

Higher censoring and smaller sample size resulted in lower power, as expected, but did not change the relationship between $\beta _2$ and power. Additionally, we assessed test sizes at the values of $\beta _2$ considered in previous simulations with 1,000 repetitions, $n=500$ and 0, 15, and 25 % uniform censoring. Neither censoring nor $\beta _2$ appeared to affect size. In particular, our assessment of the size of the Lin–Zhang–Davidian test did not differ from their results.

4 Example: stanford heart transplant program

4.1 Study background and interpretation

The Stanford heart transplant program began in 1967 and received considerable attention in the years that followed. The Stanford Hospital accepted end-stage heart disease patients who could not be helped by conventional medical and surgical interventions. Patients were required to have poor prognosis without a transplant and no other conditions which might impede post-transplant recovery. Participants moved to the San Francisco area and received the best possible therapy while waiting for a donor heart. During the waiting period, participants were monitored for improvement that would make a transplant unnecessary. After transplantation, patients received post-operative care and were followed as long as possible. (Clark et al. 1971)

Crowley and Hu (1977) used PH regression to estimate the effect of heart transplantation on survival for patients who were accepted into the program betwen November 1967 and March 1974. This public dataset contains date of program acceptance, transplant, and last follow-up, along with other patient information such as age and surgical history. Crowley and Hu fit a variety of Cox models based on survival time in days. Transplant status was included as a TVC, along with other covariates for adjustment purposes. The ultimate conclusion was that heart transplantation was beneficial, particularly for younger patients.

Aitkin et al. (1983) presented exploratory analyses describing the survival of participants in the Stanford program. Because there was little reason to expect that the effect of transplant status would remain constant over time, they modeled post-transplant survival using a variety of parametric and semi-parametric methods. Using a piecewise exponential model they estimated a post-transplant increase in hazard for 60 days followed by a decline in hazard. A similar pattern was estimated using a Weibull model, though the post-transplant hazard was found to increase for 90 days. Though the estimated hazards were imprecise, there was some evidence for nonproportionality of the effect of transplant status in these data. The long-term effect of heart transplantation was found to be a reduction in risk of death.

According to Kalbfleisch and Prentice (2002), selection bias may have resulted in an overstatement of the beneficial effect of transplantation on survival in the analysis by Crowley and Hu (1977). Though the causal interpretation of the HR associated with transplantation is certainly questionable, these data are ideal for our purposes and will be analyzed to illustrate the tests for goodness-of-fit described in Sect. 1.

4.2 Goodness-of-fit analysis

We focused the model adjusting for age at transplant presented by Crowley and Hu:

$$\begin{aligned} \lambda (t|\mathbf{Z }(t))= \lambda _0(t)e ^{ \beta _1 Z_1(t) + \beta _2 Z_2(t)}, \end{aligned}$$

where $Z_1(t)$ is age at transplant and $Z_2(t)$ is transplant status. The PH model was fit using Stata 10 with Breslow’s method for ties (Breslow 1974). The tests for the PH assumption proposed by Cox (1972), Grambsch and Therneau (1994), and Lin et al. (2006) were applied as described in Sect. 2.

We also used simulations to assess the power of goodness-of-fit tests under conditions similar to the Stanford study. The reversing effect scenario was closest to the post-transplant increase in risk described by Aitkin, Laird and Francis (1983). Immediate post-transplant log HRs between 0 and 3 were considered, and after 60 and 90 days the log HR was dropped to $-2.5$. We used a sample size of 100 with 25 % censoring and 1,000 replicates.

4.3 Results and discussion

Crowley and Hu (1977) present data for 103 patients. 69 patients (67 %) received a heart transplant, and 75 (73 %) died during follow-up. Crowley and Hu calculated estimates of $\hat{\beta _1} = 0.057$ and $\hat{\beta _2} = -2.67$ for the log HRs associated with age at transplant and transplant status. Our reanalysis of the data resulted in estimates of $\hat{\beta _1} = 0.054$ and $\hat{\beta _2}= -2.41$. See Table 2 for results from the tests for PH. None of the seven tests give evidence for a non-constant transplant effect.

Table 2 Tests for PH assumption in the Stanford heart transplant study

See Fig. 3 for simulation results. For both values of $t_0$, highest power was achieved when the pre-jump TVC coefficient was between 1 and 2. Power is lower for all tests when the jump in HR occurs after 3 months, and the difference in power between 2 and 3 months is most striking for the largest pre-jump log HRs. When the jump in HR occurs after 60 days, power is over 70 % for $1 \le \beta _2 \le 2.5$ for all tests except the Grambsch–Therneau test with $g(t) = \ln (t)$. When the jump in HR occurs after 90 days, power is over 70 % for $0.75 \le \beta _2 \le 2$ for Cox’s test of interaction with $t$ and $\ln (t)$, the Grambsch–Therneau test with $g(t) = t$, and the Lin–Zhang–Davidian test.

Fig. 3

Power simulations for the Stanford heart transplant study

Therefore tests for PH are actually quite powerful if post-transplant hazard of death declined after two months, and considerably less powerful if the decline in hazard occurred after three months. However, we do not have a precise estimate of the immediate post-transplant hazard of death and thus can not give a more specific estimate of power in the Stanford situation. If the post-transplant increase in hazard was small or extreme, or if the decline in hazard occurred after 90 days, tests for the violation of PH will be less powerful.

5 Discussion

In the disappearing TVC effect case, the power of tests for the PH assumption depends on the hazard prior to the change in HR and time to HR change. The pattern in power by difference in effect and time to effect change is intuitive. Since these data were generated using an exponential distribution, most events are expected to occur early on. When the HR for the TVC changes quickly, most patients experiencing a switch in the TVC will survive to experience a jump in TVC effect. If the HR is low, we will observe few events before the jump in effect occurs. If the HR is high, we expect to see many events immediately after the TVC switches on. As time between change in TVC and jump in HR increases, patients must survive longer in order for the TVC effect to change. Thus when the initial HR is high, subjects may not survive long enough to experience the jump in TVC effect. When the pre-change HR is low, power increases with time to effect change because the lower hazard causes slower accrual of events.

When the TVC effect doubles, all tests exhibit lower power regardless of how quickly the TVC effect changes. In this case the magnitude of change in effect was identical to that of the disappearing effect case. However, in the increasing effect case the relationship between the groups defined by the TVC changed in magnitude but not direction. The jump in effect simply made the HR more extreme. In the disappearing effect case, violation of the PH assumption eliminated any difference in risk between groups defined by the TVC. However, when the form of the violation of PH was a reversal of the TVC effect, all tests were more powerful than in the disappearing effect case. This was true regardless of the time to violation of PH. The reversing effect case can be seen as a more extreme extension of the disappearing effect case: in both cases the direction of the violation of PH was the same, but the magnitude of the change in log HR in the reversing effect case was twice as large. The pattern in power by pre-jump TVC log HR is similar between the two cases.

Thus we conclude that the power of tests for the violation of PH in the presence of TVCs depends on time to violation of PH, as well as magnitude and direction of the violation of PH. The hazard prior to violation of PH is also a factor. In order for goodness-of-fit tests to be powerful, events must be balanced around the time when the PH assumption is violated. A small number of events on either side results in lower power. Goodness-of-fit tests have more power when the PH assumption is violated quickly, the pre-violation HR is high, and the change in the HR is large. Tests are also powerful when time to PH violation, pre-violation HR, and the magnitude of violation are moderate. In both of these scenarios, power is high only when the relationship between groups defined by the TVC changes direction. This concept is best illustrated by comparing the cases of increasing and disappearing effect. Finally, tests are also powerful when the TVC HR is less than one and time to jump in the HR is high. In this case events accrue slowly so more time before change in HR is needed to detect a change in HR.

As time to change in the TVC effect increases in the cases of disappearing and reversing effect, the most powerful tests appear to be Cox’s test of the interaction between time and the TVC and the Lin–Zhang–Davidian test. The Grambsch–Therneau test of the interaction between time and the TVC also performs better than the remaining tests. The tests of interaction between the TVC and time may be most powerful because linear interaction with time is a better approximation of a one-time jump in hazard than interaction with $\ln (t)$. The Lin–Zhang–Davidian test does not require specification of the form of interaction with time, eliminating the possibility of misspecification.

The assumption of constant time to violation of PH is relevant in scenarios where a biological mechanism is the reason for the change in the HR. In the Stanford heart transplant study, the immediate post-transplant increase in hazard was thought to be due to the dangerous nature of the operation (Aitkin et al. 1983). In this case all patients underwent the same procedure and received the same pre- and post-transplant care, so fixed time to change in HR seems appropriate. However, in other scenarios more variability in time to violation of PH may be anticipated. For example, consider a randomized study assessing the effectiveness of pharmaceutical interventions in delaying progression to Alzheimer’s disease (Petersen et al. 2005). Patients with depression were excluded from enrollment, but particpants could develop depression at any time. If the investigators wished to control for depression it would be included as a TVC. However, the relationship between depression and Alzheimer’s disease may not be constant over time as depressed patients may go on medication or recover without intervention, reducing the impact of depression on cognition. In this case, time to change in the effect of depression is most likely not due to a particular mechanism so the assumption of random time to violation of PH is reasonable.

Finally, we turn to limitations of our simulation study. We considered only a one-time jump in hazard rather than more subtle violations of PH, such as interaction with a continuous function of time. Additionally, the PH model accomodates more complex TVCs, such as binary covariates which turn on and off as well as continuous covariates. We do not plan to investigate the power of goodness-of-fit tests in these cases because we do not anticipate that our conclusions would change in more complicated scenarios. In order to fit the model, TVC values must be known at every event time so an underlying model for change in the continuous covariate over time must be specified or assumed. Ng’andu (1997) found little difference in power between binary and continuous predictors when evaluating goodness-of-fit tests for the PH model with fixed covariates, and we expect the PH model with TVCs to behave similarly. Also, our exploration of the impact of censoring and sample size on power was brief. However, we do not expect a wider variety of censoring and sample size choices to alter our understanding of the relationship between power, time to violation of PH, and pre-violation HRs. At this time we do not intend to investigate censoring and sample size further.

The primary limitation of our simulation study is our use of the exponential distribution in generating failure times. In doing so we create a constant baseline hazard function and cause the majority of events to occur early in the study. The Weibull and Gompertz distributions are commonly used to allow non-constant baseline hazard functions (Bender et al. 2005). In the future we may use these distributions to generate survival data where the majority of the events occur toward the end of the study. The distribution of events, combined with assumptions about time to violation of PH, is likely to influence the power of tests for goodness-of-fit so use of a different baseline hazard function may result in different trends in power.

In conclusion, we expect application of goodness-of-fit tests to TVCs to be of limited usefulness. We considered a wide range of TVC effects in our simulation study, including HRs from 0.05 to 20, and power was over 70 % only for HRs of 2.7 and above or 0.4 and below. For the purposes of our study, HRs between 2.7 and 0.4 are relatively small; however, in real data, estimates of this magnitude would be far more common than more extreme HRs. Though our simulations showed that tests have adequate power in some cases, in an applied setting we would not be able to determine if goodness-of-fit tests could be expected to have high power. Returning to the Stanford heart transplant data analyzed by Crowley and Hu (1977), we would not have suspected a change in the transplant effect after 60 or 90 days without the additional analyses of Aitkin et al. (1983). Occasionally, as in the Alzheimer’s example (Petersen et al. 2005), we may have some idea about the characteristics of the TVC effect, but we rarely have enough information to judge the power of goodness-of-fit tests in practice. Thus we do not recommend using the goodness-of-fit tests examined here to assess the PH assumption for TVCs.

6 Appendix: Implementing the Lin–Zhang–Davidian test

This Stata code creates a Mata function to implement the test for PH proposed by Lin, Zhang, and Davidian when there are two covariates in the model, but only one is of interest. The function should be called after the Cox PH model has been run. It draws from a subset of the analysis dataset as defined by the indicator variable use, which should be set to one wherever Schoenfeld residuals are nonmissing (at event times). In addition to event times, calculations require the covariance matrix from fit of null model (Cov) and Schoenfeld residuals from the covariate of interest saved as sch2. The Mata function returns the test statistic as chilzd and degrees of freedom as dflzd. The notation in the Mata function is similar to that in the paper. $\gamma$ (g) is the coefficient for the covariate of interest and $\beta$ (b) is the coefficient for the other covariate.