What price semiparametric Cox regression?

Abstract

Cox’s proportional hazards regression model is the standard method for modelling censored life-time data with covariates. In its standard form, this method relies on a semiparametric proportional hazards structure, leaving the baseline unspecified. Naturally, specifying a parametric model also for the baseline hazard, leading to fully parametric Cox models, will be more efficient when the parametric model is correct, or close to correct. The aim of this paper is two-fold. (a) We compare parametric and semiparametric models in terms of their asymptotic relative efficiencies when estimating different quantities. We find that for some quantities the gain of restricting the model space is substantial, while it is negligible for others. (b) To deal with such selection in practice we develop certain focused and averaged focused information criteria (FIC and AFIC). These aim at selecting the most appropriate proportional hazards models for given purposes. Our methodology applies also to the simpler case without covariates, when comparing Kaplan–Meier and Nelson–Aalen estimators to parametric counterparts. Applications to real data are also provided, along with analyses of theoretical behavioural aspects of our methods.

1 Introduction and summary

For each individual $i=1,\ldots ,n$ with a q-dimensional covariate vector $X_i=x$, the semiparametric Cox model (Cox 1972) postulates a hazard rate function of the form

$$\begin{aligned} \alpha (s)\exp (x^\mathrm{t}\beta ), \end{aligned}$$

(1)

with the baseline hazard $\alpha (\cdot )$ left unspecified, and $\beta =(\beta _1,\ldots ,\beta _q)^\mathrm{t}$ the vector of regression coefficients. Maximising a partial likelihood leads to the Cox estimator ${{\widehat{\beta }}}_\mathrm{cox}$, accompanied when necessary by the Breslow estimator ${\widehat{A}}_\mathrm{cox}(\cdot )$ for the cumulative baseline hazard function $A(t)=\int _0^t\alpha (s)\,\mathrm{d}s$ (Breslow 1972). Easily interpretable output from standard software then yields inference statements pertaining to the influence of the specific covariates, survival curves for individuals with given covariates, etc.; see e.g. Aalen et al. (2008) for clear accounts of the relevant methodology and for numerous illustrations.

The semiparametric Cox regression method is a statistical success story, scoring high regarding ease, convenience, and communicability. This risks making statisticians unnecessarily lazy, however, when it comes to modelling the $\alpha (\cdot )$ part of the model. When the underlying hazard curve is inside or close to some parametric class, say $\alpha _{\mathrm{pm}}(s;\theta )$, then relying on the semiparametric machinery may lead to a loss in terms of precision of estimates and predictions. There is also a potential price to pay in terms of understanding less well the biostatistical or demographic phenomena under study. Thus, we advocate attempting fully parametric versions of (1), with analysis proceeding via fully parametric likelihood methods for $\theta$ and $\beta$ jointly. For instance, exponentially and Weibull distributed survival times correspond to, respectively, constant ($\alpha _{\text {exp}}(s;\theta )=\theta$) and monotone ($\alpha _{\text {wei}}(s;\theta ) = \theta _2 (\theta _1 s)^{\theta _2-1}\theta _1$) parametric hazards.

The title of our paper is notably reminiscent of the corresponding question ‘what price Kaplan–Meier?’, which is the title of Miller (1983). In the simpler case without covariates, Miller examined efficiency loss when using the nonparametric Kaplan–Meier ${\widehat{S}}_{\text {km}}(t)$ compared to a maximum likelihood (ML) based parametric alternative $S_\mathrm{pm}(t;{\widehat{\theta }})=\exp \{-A_\mathrm{pm}(t;{\widehat{\theta }})\}$, when the latter is true. Here $A_{\mathrm{pm}}(t;\theta )=\int _0^t \alpha _{\mathrm{pm}}(s;\theta )\,\mathrm{d}s$ is the cumulative hazard rate under the parametric model. Miller found that these losses might be sizeable, especially for very low and high t. Miller’s results were discussed and partly countered in the paper ‘the price of Kaplan–Meier’ (Meier et al. 2004), where the authors in particular argue that the results need not be as convincing for estimation of other quantities, or under model misspecification.

These studies motivate the current paper aiming at providing machinery for answering

• (a) the more general ‘what price semiparametric Cox regression?’ question, in terms of loss of efficiency when estimating different quantities when a certain parametric model holds; but also

• (b) the inevitable follow-up question; how we can meaningfully choose between the semiparametric and given parametric alternatives in practical situations.

Since the precise answers to the covariate-free analogue of (a) depend on the quantity under study, it is natural to answer these questions in terms of so-called focus parameters. A focus parameter $\mu$ is a population quantity having special importance and relevance for the analysis. Examples include the survival probability at a certain point, the increase in cumulative hazard between two time points, a life time quantile, the expected time spent in a restricted time interval (all possibly conditioned on certain covariate values), and the hazard rate ratio between two individuals associated with different covariates.

We shall restrict ourselves to focus parameters which may be written as $\mu =T(A(\cdot ),\beta )$ for some smooth functional T, i.e. to functionals of the cumulative baseline hazard $A(\cdot )$ and the regression coefficients $\beta$, in addition to one or more covariate values x (omitted in the notation). This covers almost all natural choices, including those mentioned above. For ${\widehat{A}}_\mathrm{cox}(\cdot ), {\widehat{\beta }}_\mathrm{cox}$ and ${\widehat{A}}_\mathrm{pm}(\cdot ), {\widehat{\beta }}_\mathrm{pm}$ being the semiparametric and fully ML-based parametric estimators of respectively $A(\cdot )$ and $\beta$, these focus parameters may be estimated either semiparametrically, by ${\widehat{\mu }}_\mathrm{cox}=T({\widehat{A}}_\mathrm{cox}(\cdot ), {\widehat{\beta }}_\mathrm{cox})$, or parametrically, by ${\widehat{\mu }}_\mathrm{pm}=T(A_\mathrm{pm}(\cdot ;{\widehat{\theta }}),{\widehat{\beta }}_\mathrm{pm})$.

Under certain regularity conditions, we shall later see that the two types of estimators fulfill

$$\begin{aligned} \sqrt{n}({\widehat{\mu }}_\mathrm{cox}- \mu _\mathrm{true}) {\mathop {\rightarrow }\limits ^{d}} \mathrm{N}(0,v_{\mathrm{cox}}) \quad \mathrm{and} \quad \sqrt{n}({\widehat{\mu }}_\mathrm{pm}- \mu _0) {\mathop {\rightarrow }\limits ^{d}} \mathrm{N}(0,v_{\mathrm{pm}}) \quad \text {as } n\rightarrow \infty , \end{aligned}$$

(2)

where $v_{\mathrm{cox}}$ and $v_{\mathrm{pm}}$ are limiting variances explicitly specified later. The $\mu _\mathrm{true}$ is the true unknown value of $\mu$, and $\mu _0$ is the so-called least false value of the focus parameter for the particular parametric class. When obtaining answers to (a) above, we work under the traditional efficiency comparison framework also used by Miller (1983) assuming that the parametric model is correct and $\mu _0=\mu _\mathrm{true}$. To measure the efficiency loss by relying on the semiparametric model when estimating $\mu$, we use the asymptotic relative efficiency $\text {ARE}=v_\mathrm{pm}/v_\mathrm{cox}$. It is well known that generally ARE $\le 1$, corresponding to the parametric model being more efficient. The scientifically interesting question here is rather in which situations the ARE is extremely low, and when it is so close to 1 that one should not risk restricting oneself to the parametric form. On the other hand, when the true model is not within that particular parametric class, $\mu _0$ is typically different from $\mu _\mathrm{true}$, reflecting a nonzero bias $b=\mu _0-\mu _\mathrm{true}$. In any case, (2) motivates the following approximations to the mean squared error for the estimators of $\mu$: $\mathrm{mse}_{\mathrm{np}}=0^2+n^{-1}v_{\mathrm{cox}}$ and $\mathrm{mse}_{\mathrm{pm}}=b^2+n^{-1}v_{\mathrm{pm}},$ which we utilise to present efficiency comparisons also outside model conditions.

There is a certain intention overlap of our take on question (a) with work by Efron (1977) and Oakes (1977). The former paper related to the efficiency of ${{\widehat{\beta }}}_\mathrm{cox}$, examined for certain classes of parametric families, and involves parametric and semiparametric information calculus. Efron also identified conditions giving full efficiency. The latter paper developed methods for estimating lack of efficiency for certain models, via functions of Hessian matrices. For further results along these lines, also with finite-sample efficiency discussion, see (Kalbfleisch and Prentice 2002, pp. 181–187). Yet further results along similar lines are provided in Jeong and Oakes (2003, 2005), with attention also to survival curve estimators. Some of our results are more general than in these papers, however, in that efficiency results are achieved also outside model conditions. Crucially, we also work with question (b), which we discuss now.

For the model selection task in (b) we develop focused and average focused information criteria (FIC and AFIC). The FIC concept involves estimating mses for a pre-chosen focus parameter $\mu$. As the form of $\mathrm{mse}_\mathrm{pm}$ is specified for a general parametric model, one may compare several parametric models simultaneously with the semiparametric alternative, and rank all of them according to their estimation performance for that particular focus parameter. The FIC is a flexible model selection approach, where one does not need to decide on an overall best model to be used for all of a study’s estimation and prediction tasks, but merely one tuned specifically for estimating $\mu$. Thus, this allows different models to be selected for estimating different focus parameters. The AFIC concept generalises that of the FIC, aiming at selecting the optimal model for a full set of focus parameters, possibly given different weights to reflect their relative importance.

Note also that we cannot turn to the more traditional model selection criteria here, such as the Akaike (AIC), the Bayesian (BIC) or the deviance (DIC) criteria, as these involve comparing parametric likelihoods, and there is no such for the semiparametric model in (1). Hjort and Claeskens (2006); Hjort (2008) have developed FIC methodology for hazard models, but these are restricted solely to covariate selection within a specific model (such as the semiparametric Cox model). Those are based on Claeskens and Hjort (2003), relying on a certain local misspecification framework, also requiring the candidate models to be parametrically nested. Thus, the earlier work on focused model selection is incompatible with selecting between the nonparametric and parametric alternatives for the baseline hazard. The current model selection problem therefore requires development of new methodology which deals with the aforementioned issues. We follow the principled procedure of Jullum and Hjort (2017) which establishes and works out FIC and AFIC procedures for comparing nonparametric and parametric candidate models in the i.i.d. case without censoring nor covariates. Their development does not rely on a local misspecification framework, and also allows for selection among non-nested candidate models.

We start the main part of the paper setting the stage by presenting basic asymptotic results for semiparametric and fully parametric estimators in Sect. 2, pointing also to the covariate free special case. In Sect. 3 we work out answers to various variants of the ‘what price’ question in (a). In Sect. 4 we offer constructive FIC and AFIC apparatuses for answering question (b), i.e. when one should rely on semiparametrics and when one should prefer parametrics in practice. Section 5 studies the asymptotic behaviour for the suggested FIC and AFIC procedures under model conditions, and also includes a minor simulation study. Section 6 contains applications of our FIC and AFIC procedures to a dataset related to survival with oropharynx carcinoma. Various concluding remarks are offered in Sect. 7. The Appendix gives technical formulae for consistent estimators of a list of necessary variances and covariances. The supplementary material accompanying this paper (Jullum and Hjort, this work) contains proofs of a few technical results presented in the paper, in addition to some lengthy algebraic derivations. ,R,-scripts are available on request from the authors.

2 Basic estimation theory for the two types of regression models

Consider survival data with covariates being realisations of random variables $(T_i,X_i,D_i)$ for individuals $i=1,\ldots ,n$ observed over a time window $[0,\tau ]$. Here $T_i$ is the possibly censored time to an identified event, $X_i$ is a covariate vector, and $D_i$ is the indicator of $T_i$ being equal to the uncensored life-time $T_{i}^{(0)}$.

To model these data we consider two types of models: The semiparametric Cox model which models the hazard rate by $\alpha (s)\exp (x^\mathrm{t}\beta )$, and a general fully parametric version which uses $\alpha _{\mathrm{pm}}(s;\theta )\exp (x^\mathrm{t}\beta )$.

When studying these two model types, both counting processes and martingale theory play an important role. Let $N_i(\cdot )$ and $Y_i(\cdot )$ be respectively the counting process and at-risk indicator at individual level, $N_i(s)=\mathbf {1}_{\{T_i \le s, D_i=1\}}$ and $Y_i(s)=\mathbf {1}_{\{T_i\ge s\}}$, where $\mathbf {1}_{\{ \cdot \}}$ denotes the indicator function. The individual risk quantities are $R^{(0)}_{(i)}(s;\beta )=Y_i(s)\exp (X_i^{\mathrm{t}}\beta )$, having first and second order derivatives with respect to $\beta$: $R^{(1)}_{(i)}(s;\beta )=Y_i(s)\exp (X_i^{\mathrm{t}}\beta )X_i$ and $R^{(2)}_{(i)}(s;\beta )=Y_i(s)\exp (X_i^{\mathrm{t}}\beta )X_iX_i^{\mathrm{t}}$. The corresponding total risks

$$\begin{aligned} R^{(k)}_n(s;\beta )=\sum _{i=1}^nR^{(k)}_{(i)}(s;\beta ) \quad \mathrm{for\ } k=0,1,2, \end{aligned}$$

will also be important in what follows.

Below we state the working conditions, which will be assumed throughout the paper. Note first of all that we shall restrict our attention to the case where the Cox model actually is correct, that is, individual i has hazard rate

$$\begin{aligned} \alpha _{\mathrm{true}}(s\,|\,X_i)=\alpha _\mathrm{true}(s)\exp (X_i^\mathrm{t}\beta _\mathrm{true}) \quad \mathrm{for\ }i=1,\ldots ,n , \end{aligned}$$

(3)

for a suitable q-dimensional coefficient vector $\beta _\mathrm{true}$, and a baseline hazard $\alpha _\mathrm{true}(\cdot )$ which is positive on $(0,\tau )$ and has at most a finite number of discontinuities. The $\alpha _\mathrm{true}$ also has cumulative $A_\mathrm{true}(t)=\int _0^{t} \alpha _{\mathrm{true}}(s)\,\mathrm{d}s$ which is finite on the observation window $[0,\tau ]$. We shall also assume that independent censoring is in force, allowing the censoring time to be random and covariate dependent, and implying that the counting processes $N_i(t)$ have intensity processes given by $\int _0^t Y_i(s)\alpha _{\mathrm{true}}(s\,|\,X_i)\,\mathrm{d}s$ for $i=1,\ldots ,n$; see also Aalen et al. (2008, Ch. 2.2.8). This has the consequence that the martingales $M_i$ associated with the counting process $N_i$ take the form $M_i(t)=N_i(t) - \int _0^t Y_i(s)\alpha _\mathrm{true}(s\,|\,X_i)\,\mathrm{d}s$ for $i=1,\ldots ,n$. For presentational simplicity, we also assume there are no tied events.¹

Although a part of this paper concerns the special case where the parametric model is indeed correct, we shall not in general assume that $\alpha _{\mathrm{true}}(s)$ is equal to $\alpha _{\mathrm{pm}}(s;\theta )$ for some $\theta$, as we shall also need results outside such model conditions. In assuming (3) above, we do however concentrate on parametric misspecification of the baseline hazard $\alpha _{\mathrm{true}}$, rather than potential misspecification of the relative risk function $\exp (\cdot )$ or the proportional hazards assumption (such misspecification may also occur in practice, but is outside the current scope). In addition, we shall put up conditions sufficient for ensuring limiting normality for both semiparametric and parametric estimators. These refer to the divergence measure in (13) and the matrices $J_\mathrm{cox}$, J, K given in (7), (14), (16) and (17). The conditions are:

• (A) There exists a neighbourhood $\mathcal {B}$ around $\beta _{\mathrm{true}}$ and a function $r^{(0)}(s;\beta )$ with first and second order $\beta$ derivatives $r^{(1)}(s;\beta )$ and $r^{(2)}(s;\beta )$, where $r^{(k)}, k=0, 1, 2$ are continuous functions of $\beta \in \mathcal {B}$ uniformly in $s\in [0,\tau ]$ and bounded on $\mathcal {B}\times [0,\tau ]$, such that for $k=0,1,2$, $n^{-1}R_n^{(k)}(s;\beta )$ converges uniformly over $\beta \in \mathcal {B}$ and $s \in [0,\tau ]$ to $r^{(k)}(s;\beta )$ in probability. In addition $r^{(0)}(\cdot ; \beta _{\mathrm{true}})$ is bounded away from zero on $[0,\tau ]$. The matrix $J_{\mathrm{cox}}$ defined in (7) below is also positive definite.

• (B) The triples $(T_i,X_i,D_i), i=1,\ldots ,n$ are i.i.d., and the covariates stem from a distribution C with bounded domain.

• (C) The parametric models have unique minimisers $(\theta _0,\beta _0)$ of the divergence function in (13) which are inner points in their parameter spaces; each $\alpha _{\mathrm{pm}}(s;\theta )$ is positive on $(0,\tau )$, has at most a finite number of discontinuities in s, and is three times differentiable with respect to $\theta$ in a neighbourhood $N(\theta _0)$ of $\theta _0$; the cumulatives $A_\mathrm{pm}(t;\theta )=\int _0^t \alpha _\mathrm{pm}(s;\theta ) \, \mathrm{d}s$ are finite on the observation window $[0,\tau ]$ and three times differentiable under the integral sign for all $\theta \in N(\theta _0)$; the third derivatives of $\log \alpha _\mathrm{pm}(s;\theta )$ and $A_\mathrm{pm}(s;\theta )$ (with respect to $\theta$) are bounded uniformly in $\theta \in N(\theta _0)$ for all $s\in [0,\tau ]$. The J and K in (14), (16) and (17) are finite and positive definite.

These conditions are to some extent similar to those used in Andersen et al. (1993, Ch. VII) (semiparametrics) and Hjort (1992, Section 6) (parametrics). Although condition (C) is slightly weakened, exploring the proofs in Hjort (1992) shows that the parametric results still go through. We shall thus re-use the results in the two references without proofs. Note however that the results stated there, and the new ones we shall provide, also hold under weaker conditions, with more complicated proofs. The i.i.d. assumption in (B) is only needed for deriving explicit expressions for some of the limiting quantities related to the parametric models. Similar results, with even more abstract limiting quantities, may be derived without this assumption. The bounded domain condition in (B) may typically be weakened to a Lindeberg type of condition (Andersen et al. 1993, Condition VII.2.2). Further technicalities should allow the covariates to be time-dependent as well. More technical conditions, generalising Borgan (1984, Conditions A–D) may also replace some of the conditions in (C). Yet other weaker sufficient conditions may be put up in the style of Hjort and Pollard (1993, Sections 6 and 7A).

2.1 The semiparametric Cox model

The classic semiparametric version relies on Cox’s partial likelihood or the log-partial likelihood

$$\begin{aligned} \ell _{n,\mathrm{cox}}(\beta )=\sum _{i=1}^n\int _0^\tau \{X_i^\mathrm{t}\beta -\log (R^{(0)}_n(s;\beta ))\}\,\mathrm{d}N_i(s), \end{aligned}$$

(4)

while leaving $\alpha ()$ unspecified. The maximiser of $\ell _{n,\mathrm{cox}}$ is the Cox estimator ${{\widehat{\beta }}}_\mathrm{cox}$. When the analysis requires more than solely $\beta$, the Breslow estimator (Breslow 1972)

$$\begin{aligned} {{\widehat{A}}}_{\mathrm{cox}}(t)=\int _0^t \frac{\sum _{i=1}^n\mathrm{d}N_i(s)}{R^{(0)}_n(s;{\widehat{\beta }}_{\mathrm{cox}})}, \end{aligned}$$

(5)

is typically used to estimate the cumulative hazard function $A_{\mathrm{true}}(t)=\int _0^t\alpha _\mathrm{true}(s)\,\mathrm{d}s$.

Under our working conditions, Andersen et al. (1993, Ch. VII) establishes asymptotic distribution results for $({\widehat{A}}_\mathrm{cox}(\cdot ),{\widehat{\beta }}_\mathrm{cox})$. The first key result is that

$$\begin{aligned} \sqrt{n}({{\widehat{\beta }}}_\mathrm{cox}-\beta _\mathrm{true}){\mathop {\rightarrow }\limits ^{d}} J_\mathrm{cox}^{-1}U_\mathrm{cox}\sim \mathrm{N}_q(0,J_\mathrm{cox}^{-1}), \end{aligned}$$

(6)

for a certain variable $U_\mathrm{cox}\sim \mathrm{N}_q(0,J_\mathrm{cox})$ and $J_\mathrm{cox}$ the $q\times q$-dimensional matrix

$$\begin{aligned} J_\mathrm{cox}&=\int _0^{\tau } \left\{ \frac{r^{(2)}(s;\beta _{\mathrm{true}})}{r^{(0)}(s;\beta _{\mathrm{true}})} - E(s;\beta _\mathrm{true})E(s;\beta _\mathrm{true})^{\mathrm{t}}\right\} r^{(0)} (s;\beta _{\mathrm{true}})\alpha _{\mathrm{true}}(s)\,\mathrm{d}s, \end{aligned}$$

(7)

where $E(s;\beta )=r^{(1)}(s;\beta )/r^{(0)}(s;\beta )$. The second result may be formulated as

$$\begin{aligned} \sqrt{n}\{{\widehat{A}}_\mathrm{cox}(\cdot )-A_\mathrm{true}(\cdot )\}{\mathop {\rightarrow }\limits ^{d}} W(\cdot ) - F(\cdot )^\mathrm{t}J_\mathrm{cox}^{-1}U_\mathrm{cox}, \end{aligned}$$

(8)

where $W(\cdot )=W_0(\sigma ^2(\cdot ))$ for $W_0$ a standard Wiener process independent of $U_\mathrm{cox}$; and,

$$\begin{aligned} \sigma ^2(t)=\int _0^t\frac{\alpha _\mathrm{true}(s)}{ r^{(0)}(s;\beta _\mathrm{true})}\,\mathrm{d}s, \qquad F(t)=\int _0^t E(s;\beta _\mathrm{true})\alpha _\mathrm{true}(s)\,\mathrm{d}s. \end{aligned}$$

(9)

The two limit results (6) and (8) settle the limit behaviour, not only for the covariates and the cumulative baseline hazard, but for most quantities that may be estimated from these data. Recall the focus parameter $\mu =T(A(\cdot ),\beta )$, with true value $\mu _\mathrm{true}=T(A_\mathrm{true}(\cdot ),\beta _\mathrm{true})$ and semiparametric estimator ${\widehat{\mu }}_\mathrm{cox}=T({\widehat{A}}_\mathrm{cox}(\cdot ),{\widehat{\beta }}_\mathrm{cox})$. Under a mild additional condition on T (being precisely stated in Sect. 4) we have that for some appropriate finite variance $v_\mathrm{cox}$

$$\begin{aligned} \sqrt{n}({\widehat{\mu }}_\mathrm{cox}-\mu _\mathrm{true}) {\mathop {\rightarrow }\limits ^{d}} \mathrm{N}(0,v_{\mathrm{cox}}). \end{aligned}$$

(10)

2.2 Parametric Cox regression models

The alternative parametric Cox regression models take the hazard rate to be of the generic form

$$\begin{aligned} \alpha _{\mathrm{pm}}(s;\theta ,\beta \,|\,X_i)=\alpha _{\mathrm{pm}}(s;\theta )\exp (X_i^\mathrm{t}\beta ) \quad \mathrm{for\ }i=1,\ldots ,n, \end{aligned}$$

with $\alpha _{\mathrm{pm}}(s;\theta )$ a suitable baseline hazard function with cumulative $A_\mathrm{pm}(s;\theta )$, involving a p-dimensional parameter $\theta$. For notational convenience we shall, where appropriate, write $\gamma$ for the pair $\theta ,\beta$, or more precisely $\gamma ^{\mathrm{t}}=(\theta ^{\mathrm{t}},\beta ^{\mathrm{t}})$ for the full $p+q$-dimensional parameter vector. Inference here is based on the log-likelihood function²

$$\begin{aligned} \ell _n(\gamma ) =\sum _{i=1}^n\int _0^\tau \left[ \{\log \alpha _{\mathrm{pm}}(s;\theta ) +X_i^\mathrm{t}\beta \}\,\mathrm{d}N_i(s) -Y_i(s)\alpha _{\mathrm{pm}}(s;\gamma \,|\,X_i)\,\mathrm{d}s\right] . \end{aligned}$$

(11)

Let ${\widehat{\gamma }}^\mathrm{t}=(\widehat{\theta }^\mathrm{t},{\widehat{\beta }}_\mathrm{pm}^\mathrm{t})$ be the maximum likelihood estimator which maximises (11), also being the zero of ${\bar{U}}_n(\gamma )=n^{-1}\partial \ell _n(\gamma )/\partial \gamma =n^{-1}\sum _{i=1}^nU_i(\gamma )$ where

$$\begin{aligned} U_i(\gamma )&=\int _0^\tau \begin{pmatrix} \psi (s;\theta ) \\ X_i \\ \end{pmatrix} \{\mathrm{d}N_i(s)-Y_i(s)\alpha _{\mathrm{pm}}(s;\gamma \,|\,X_i)\,\mathrm{d}s\}\nonumber \\&=\int _0^\tau \begin{pmatrix}\psi (s;\theta ) \\ X_i \\ \end{pmatrix} \left\{ Y_i(s)q(s;\gamma \,|\,X_i)\,\mathrm{d}s+\mathrm{d}M_i(s)\right\} ,\nonumber \end{aligned}$$

(12)

with $q(s;\gamma \,|\,x) =\alpha _{\mathrm{true}}(s\,|\,x)-\alpha _{\mathrm{pm}}(s;\gamma \,|\,x)$ and $\psi (s;\theta )=\partial \log \alpha _{\mathrm{pm}}(s;\theta )/\partial \theta$.

Working outside parametric model conditions, no true value of $\gamma$ exists. There is rather a least false parameter $\gamma _0^{\mathrm{t}}=(\theta _0^{\mathrm{t}} , \beta _0^{\mathrm{t}})$ which is defined as the minimiser of the following divergence function:

$$\begin{aligned}&d[\{\alpha _{\mathrm{true}}(\cdot ), \beta _{\mathrm{true}}\},\{\alpha _{\mathrm{pm}}(\cdot ;\theta ),\beta \}]\nonumber \\&\quad = \int \int _0^\tau y(s\,|\,x)\left[ \alpha _{\mathrm{true}}(s\,|\,x) \log \frac{\alpha _{\mathrm{true}}(s\,|\,x)}{\alpha _{\mathrm{pm}}(s;\gamma \,|\,x)}- q(s;\gamma \,|\,x)\right] \mathrm{d}s\,\mathrm{d}C(x), \end{aligned}$$

(13)

where $y(s\,|\,x)=\mathrm{E}\{Y_i(s)\,|\,X_i=x\}=\Pr (T_i \ge s|X_i=x)$. This specific divergence function takes the same role as the Kullback–Leibler divergence does for standard uncensored ML estimation, see e.g. Hjort (1992) for details. That is, from an outside-model-conditions perspective with random covariates, $\gamma _0$ is the unknown quantity which the maximum likelihood estimator ${\widehat{\gamma }}$ is aiming at. Hjort (1992) further shows that ${\widehat{\gamma }} \rightarrow _p \gamma _0$ as $n\rightarrow \infty$ and gives the asymptotic distribution of $\sqrt{n}({\widehat{\gamma }}-\gamma _0)$. Observe also that $\mathrm{E}\{U_i(\gamma _0)\}=0_{(p+q)\times 1}$. Letting $I_i(\gamma )=\partial U_i(\gamma )/\partial \gamma ^{\mathrm{t}}$, define

$$\begin{aligned} J= \begin{pmatrix} J_{11} &{} J_{12} \\ J_{21} &{} J_{22} \end{pmatrix}=-\mathrm{E}\{I_i(\gamma _0)\} \quad \mathrm{and} \quad K=\begin{pmatrix} K_{11} &{} K_{12} \\ K_{21} &{} K_{22} \end{pmatrix} = \mathrm{Var}\{U_i(\gamma _0)\}, \end{aligned}$$

(14)

where the expectation and variance are taken with respect to both the survival distribution and the covariate distribution C. Let us write

$$\begin{aligned} g^{(k)}(s;\beta )=\alpha _{\mathrm{true}}(s)r^{(k)}(s;\beta _\mathrm{true}+\beta )-\alpha _{\mathrm{pm}}(s;\theta _0)r^{(k)}(s;\beta _0+\beta ), \text { for }k=0,1,2, \end{aligned}$$

(15)

for the limit in probability of $n^{-1}\sum _{i=1}^nR_{(i)}^{(k)}(s;\beta )q(s;\gamma _0\,|\,X_i)$. The blocks of J and K are then given by

$$\begin{aligned} J_{11}&= \int _0^{\tau } \{\psi (s;\theta _{0})\psi (s;\theta _{0})^{\mathrm{t}} r^{(0)}(s;\beta _0)\alpha _{\mathrm{pm}}(s;\theta _0) - \psi ^\mathrm{d}(s;\theta _{0}) g^{(0)}(s;0) \} \, \mathrm{d}s, \nonumber \\ J_{12}&= J_{21}^{\mathrm{t}} = \int _0^{\tau } \psi (s;\theta _{0})r^{(1)}(s;\beta _0)^{\mathrm{t}} \alpha _{\mathrm{pm}}(s;\theta _0) \, \mathrm{d}s, \\ J_{22}&= \int _0^{\tau } r^{(2)}(s;\beta _0)\alpha _{\mathrm{pm}} (s;\theta _0) \, \mathrm{d}s, \nonumber \end{aligned}$$

(16)

$$\begin{aligned} K_{11}&=\int _0^{\tau } [\psi (s;\theta _0)\psi (s;\theta _0)^{\mathrm{t}} r^{(0)}(s;\beta _{\mathrm{true}})\alpha _{\mathrm{true}}(s) \nonumber \\&\quad -\{A^{\mathrm{d}}_\mathrm{pm}(s;\theta _0) \psi (s;\theta _0)^{\mathrm{t}} + \psi (s;\theta _0)A^{\mathrm{d}}_ \mathrm{pm}(s;\theta _0)^{\mathrm{t}}\}g^{(0)}(s;\beta _0)]\, \mathrm{d}s, \nonumber \\ K_{12}&=K_{21}^{\mathrm{t}}= \int _0^{\tau } [\psi (s;\theta _0) r^{(1)}(s;\beta _{\mathrm{true}})^{\mathrm{t}}\alpha _{\mathrm{true}}(s) - \{A^{\mathrm{d}}_\mathrm{pm}(s;\theta _0) \\&\quad + \psi (s;\theta _0) A_\mathrm{pm}(s;\theta _0)\}g^{(1)}(s;\beta _0)^{\mathrm{t}}]\,\mathrm{d}s, \nonumber \\ K_{22}&=\int _0^{\tau } [r^{(2)}(s;\beta _{\mathrm{true}}) \alpha _{\mathrm{true}}(s)-2g^{(2)}(s;\beta _0)A_\mathrm{pm}(s;\theta _0)]\,\mathrm{d}s,\nonumber \end{aligned}$$

(17)

where $\psi ^\mathrm{d}(s;\theta )=\partial \psi (s;\theta )/\partial \theta ^{\mathrm{t}}$ and $A^{\mathrm{d}}_\mathrm{pm}(s;\theta )=\partial A_{\mathrm{pm}}(s;\theta )/\partial \theta = \int _0^s \psi (u;\theta )\alpha _{\mathrm{pm}}(u;\theta )\,\mathrm{d}u$. The expressions in (16) are reformulated from Hjort (1992), while those in (17) are derived in the supplementary material. For $U\sim \mathrm{N}_{p+q}(0,K)$, the asymptotic distribution related to ${\widehat{\gamma }}$ is (by Hjort 1992, Theorem 6.1) given by

$$\begin{aligned} \sqrt{n}({\widehat{\gamma }}-\gamma _0) {\mathop {\rightarrow }\limits ^{d}} J^{-1}U \sim \mathrm{N}_{p+q}(0,J^{-1}KJ^{-1}). \end{aligned}$$

(18)

Analogous to (10) for the semiparametric Cox model, mild regularity conditions (again being specified in Sect. 4) allow extending (18) to parametric focus parameter estimators of the form ${\widehat{\mu }}_\mathrm{pm}=T(A_\mathrm{pm}(\cdot ; \widehat{\theta }),{\widehat{\beta }}_\mathrm{pm})$ aiming at the least false parameter value $\mu _0=T(A_\mathrm{pm}(\cdot ;\theta _0),\beta _0)$. For $v_\mathrm{pm}$ the appropriate parametric variance term, the generic limit result reads

$$\begin{aligned} \sqrt{n}({\widehat{\mu }}_\mathrm{pm}-\mu _0) {\mathop {\rightarrow }\limits ^{d}} \mathrm{N}(0,v_{\mathrm{pm}}). \end{aligned}$$

(19)

2.3 The covariate free special case

Consider now the case where there are no covariate information ($q=0$), and the hazard rate $\alpha _\mathrm{true}(s\,|\,x)=\alpha _\mathrm{true}(s)$ is common for all individuals. This is indeed a special case of the general regression model formulation of (1). Hence, the asymptotic results stated above still hold. This is seen by observing that the covariate free special case appears when defining ‘$0/\infty =0$’ and letting the covariate distribution C be degenerate at zero. The semiparametric case is now a nonparametric one, with $U_\mathrm{cox}$ degenerate at zero, and $R_n^{(0)}(s;\beta )=\sum _{i=1}^nY_i(s)$, such that the Breslow estimator in (5) reduces to the well-known Nelson–Aalen estimator ${{\widehat{A}}}_{\text {naa}}(t)=\int _0^t \{\sum _{i=1}^n\mathrm{d}N_i(s)\}/\{\sum _{i=1}^nY_i(s)\}$. Further, $r^{(0)}(s;\beta )=y(s)=\Pr (T_i \ge s)$, and $\sigma ^2(t)$ reduces to $\eta ^2(t)=\int _0^t \alpha _\mathrm{true}(s)/y(s)\,\mathrm{d}s$ such that (8) reduces to $\sqrt{n}\{{\widehat{A}}_\mathrm{{naa}}(\cdot )-A_\mathrm{true}(\cdot )\} \rightarrow _d W_0(\eta ^2(\cdot ))$.

For the parametrics, exclusion of the covariates implies that the log-likelihood in (11) with $\gamma =\theta$ reduces to $\sum _{i=1}^n\int _0^\tau \{\log \alpha _{\mathrm{pm}}(s;\theta )\,\mathrm{d}N_i(s) -Y_i(s)\alpha _{\mathrm{pm}}(s;\theta )\,\mathrm{d}s\}$, such that the divergence function in (13) reduces to $d(\alpha _{\mathrm{true}},\alpha _{\mathrm{pm}}) =\int _0^\tau y(s)\Big [\alpha _{\mathrm{true}}(s)\log (\alpha _{\mathrm{true}}(s)/ \alpha _{\mathrm{pm}}(s;\theta )) - \{\alpha _\mathrm{true}(s)-\alpha _{\mathrm{pm}}(s;\theta )\}\Big ]\, \mathrm{d}s.$ Since $q=0$, the matrices J and K of (14) first reduce to respectively $J_{11}$ and $K_{11}$. Second, since $r^{(0)}$ and $g^{(0)}$ are simplified, we get $\sqrt{n}(\widehat{\theta }-\theta _0) \rightarrow _d \mathrm{N}_p(0,J_0^{-1}K_0J_0^{-1})$, with $J_0$ and $K_0$ the two $p\times p$-dimensional matrices given by

$$\begin{aligned} J_0&=\int _0^{\tau } y(s)[\psi (s;\theta _0)\psi (s;\theta _0)^{\mathrm{t}} \alpha _{\mathrm{pm}}(s;\theta _0) - {\psi }^\mathrm{d}(s;\theta _0)\{\alpha _{\mathrm{true}}(s) -\alpha _{\mathrm{pm}}(s;\theta _0)\}]\,\mathrm{d}s, \\ K_0&=\int _0^{\tau } [\psi (s;\theta _0)\psi (s;\theta _0)^{\mathrm{t}} y(s)\alpha _{\mathrm{true}}(s) \\&\quad - \{A^{\mathrm{d}}_\mathrm{pm}(s;\theta _0) \psi (s;\theta _0)^{\mathrm{t}} + \psi (s;\theta _0)A^{\mathrm{d}}_\mathrm{pm}(s;\theta _0)^{\mathrm{t}}\} \{\alpha _{\mathrm{true}}(s)-\alpha _{\mathrm{pm}}(s;\theta _0)\}]\, \mathrm{d}s. \end{aligned}$$

As the Cox regression formulation in (1) covers both the case when covariates are present and not, we shall from here on out use the terminology and notation of semiparametric Cox regression independently of whether covariates are available or not.

3 What price?

The main reason for using the fully parametric options introduced above is that they lead to estimators and inference methods sharper than those of the semiparametric nature commonly employed. Thus, one may expect that for general focus parameters, the estimators based on parametric models have smaller variances than those based on the semiparametric strategy, i.e. $v_{\text {pm}}< v_{\text {cox}}$.

Below we study the asymptotic relative efficiency

$$\begin{aligned} \text {ARE}=\frac{v_\mathrm{pm}}{v_{\mathrm{cox}}} \end{aligned}$$

of the parametric and semiparametric models estimating different types of focus parameters $\mu =T(A(\cdot ),\beta )$. The smaller the ARE is, the more deficient is the semiparametric Cox model compared to the fully parametric option. It is not our intention to try to cover all of the possible $\mu$, models or special cases one could consider. Our aim is rather to exemplify that whether there is any point in considering a parametric model really depends on what is estimated (i.e. the focus parameter $\mu$) – and to pinpoint cases where there is a lot and essentially nothing to lose. Thus, we shall restrict ourselves to the case where (1) holds and the true baseline survival distribution and censoring distribution are exponentially distributed with rates respectively $\lambda$ and $\rho$. In the cases with covariates we shall assume that the covariates are univariate and Uniform(0, 1) distributed. Although the true survival distribution is exponential, we shall compute ARE both for the exponential and Weibull as the estimated parametric model. We consider the following quantities: The cumulative hazard without covariates A(t); the cumulative hazard conditional on some covariate x, $A(t\,|\,x)=A(t)\exp (x^{\mathrm{t}}\beta )$; and the regression coefficient $\beta$. As a consequence of model conditions and the delta method, any continuously differentiable function of an estimand has the same ARE as the estimand itself. Therefore the survival probability $S(t)=\exp \{-A(t)\}$, has the same ARE as the cumulative hazard A(t). As noted in Remark S1 of the supplementary material (Jullum and Hjort, this work), the u-quantile for which $u=1-S(t)$ also has the very same ARE. These equivalences also hold with covariates present. The ARE of hazard ratios between individuals with different covariates also have equivalences with ARE for $\beta$. Thus, our examples span quite broadly.

Since simple, interpretable closed form expressions for the ARE are only available for the simplest cases, we shall present the ARE by plots, typically relying on numerical integration. To restrict the time domain to practically reasonable values, all ARE-plots, except those for $\beta$, are presented as functions of the (conditional) ‘death probability’ $\Pr (T^{(0)}_i \le t)$ (and $\Pr (T^{(0)}_i \le t\,|\,x)$), rather than the time index itself. Thus, we may without loss of generality set $\lambda =1$ and scale $\rho$ to match different censoring proportions which we study.

3.1 What price Nelson–Aalen and Kaplan–Meier?

The ARE related to estimation of the cumulative hazard for the covariate free case was considered already by Miller (1983), but only for $\tau =\infty$. With notation as in Sect. 2.3 and with $\tau$ finite, we get that under these model conditions the nonparametric limit variance (using either Nelson–Aalen or a transformation of Kaplan–Meier) is

$$\begin{aligned} \eta ^2(t)=\frac{\lambda [\exp \{(\lambda +\rho ) t\}-1]}{\lambda +\rho }. \end{aligned}$$

The limit variance under the exponential model is moreover $A^\mathrm{d}_\mathrm{pm}(t;\theta _0)^\mathrm{t}J_0^{-1}A^\mathrm{d}_\mathrm{pm}(t;\theta _0)$, with $A^\mathrm{d}_\mathrm{pm}(t;\theta _0)=t$, and in full generality with $\theta _0=\lambda$, we have

$$\begin{aligned} J_0=\lambda ^{-1}\int _0^\tau \exp \{-(\lambda +\rho )s\}\, \mathrm{d}s= \frac{1-\exp \{-(\lambda +\rho )\tau \}}{\lambda (\lambda +\rho )}. \end{aligned}$$

Thus, the ARE of the cumulative hazard with the exponential model as reference becomes

$$\begin{aligned} \text {ARE}_{\text {exp}} = \frac{\exp \{(\lambda +\rho ) t\}-1}{\{(\lambda +\rho )t \}^2}[1-\exp \{-(\lambda +\rho )\tau \}], \end{aligned}$$

(20)

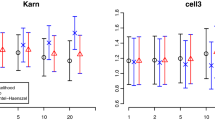
which can be dramatically small, especially for small and large t. Note that when $\tau \rightarrow \infty$, the factor in the brackets disappears, and leaves us with the less general formula given by Miller (1983) – which is only precise for very large observations windows $[0,\tau ]$. As noted also by Miller (1983), (20) has a global maximum point which independently of $\lambda$ and $\rho$ reaches approximately 0.65 as $\tau \rightarrow \infty$. Figure 1 presents the ARE for the exponential and the Weibull model (the former via (20)), with a few different censoring schemes, as $\tau \rightarrow \infty$. As noted above these ARE results also hold for S(t) and the u-quantile for which $u=1-S(t)$.

Fig. 1

ARE curves for cumulative hazards, survival probabilities and quantiles without covariates. Black (thin) and red (thick) lines correspond to, respectively, the exponential and Weibull models. Solid, dashed and dotted line type refer to censoring proportions of respectively $0\%, 20\%$ and $40\%$. The dotted grey line shows the mode of the ARE for the exponential model (Color figure online)

As seen from the figure, the ARE is dramatically small for very small and large time points. For the exponential model, the ARE is very small also for moderate t with little censoring. When t is large, the ARE generally become smaller when the censoring proportion increases, while it increases for small t.

3.2 What price semiparametric Cox regression? Conditional cumulative hazard and survival probability

The natural extension of the previous subsection is to ask what the ARE looks like when covariates are available and are being conditioned upon, i.e. when comparing semiparametric and parametric options of the form

$$\begin{aligned} {\widehat{A}}_\mathrm{cox}(t\mid x)={\widehat{A}}_\mathrm{cox}(t)\exp (x^{\mathrm{t}}{\widehat{\beta }}_\mathrm{cox})&\quad \mathrm{and} \quad {\widehat{A}}_\mathrm{pm}(t\,|\,x)=A_\mathrm{pm}(t;\widehat{\theta })\exp (x^{\mathrm{t}}{\widehat{\beta }}_\mathrm{pm}). \end{aligned}$$

(21)

Under model conditions this amounts to comparing the semiparametric asymptotic variance of the form

$$\begin{aligned} v_{\text {cox}} = \exp (2x^{\mathrm{t}}\beta _\mathrm{true})[\sigma ^2(t) + \{F(t)-A_\mathrm{true}(t)x\}^{\mathrm{t}}J_\mathrm{cox}^{-1}\{F(t)-A_\mathrm{true}(t)x\}], \end{aligned}$$

(22)

with parametric asymptotic variances of the general form

$$\begin{aligned} v_{\text {pm}} = \exp (2x^{\mathrm{t}}\beta _\mathrm{true})\begin{pmatrix} A^{\mathrm{d}}_\mathrm{pm}(t;\theta _\mathrm{true}) \\ A_\mathrm{pm}(t;\theta _\mathrm{true})x\end{pmatrix}^{\mathrm{t}} J^{-1}\begin{pmatrix} A^{\mathrm{d}}_\mathrm{pm}(t;\theta _\mathrm{true}) \\ A_\mathrm{pm}(t;\theta _\mathrm{true})x\end{pmatrix}. \end{aligned}$$

(23)

For this case, the ARE depends not only on t and the censoring proportion, but also on $\beta _\mathrm{true}$ and the chosen x. As noted above these ARE results also hold for $S(t\,|\,x)$ and the u-quantile for which $u=1-S(t\,|\,x)$.

A snapshot of this situation with a scalar covariate is shown in Fig. 2, where the ARE are presented for the four combinations of $x=0.5,0.8$ and $\beta _\mathrm{true}=1,2.5$, all with three different censoring proportions, when $\tau \rightarrow \infty$.

Fig. 2

ARE curves for conditional cumulative hazards, survival probabilities and quantiles for four situations described by the panel headings. Black (thin) and red (thick) lines correspond to, respectively, the exponential and Weibull models. Solid, dashed and dotted line type refer to censoring proportions of respectively $0\%, 20\%$ and $40\%$. The dotted grey line indicates (for comparison) the mode of the ARE for the exponential model in the covariate free case (Color figure online)

Similar results are found for negative $\beta$ of the same magnitudes. With small values of x, the ARE curves are similar to those presented for $x=0.8$. Note in particular the curves in the upper right panel, representing the efficiency when $\beta$ is large and x is average valued (i.e. around 0.5): The low mode of the exponential model (especially when there is no censoring) shows that there is quite a lot to gain by relying on a constant baseline hazard for all time points – significantly more than what was the case without covariates. As seen in the upper left panel, a smaller $\beta$ results in a smaller gain. In fact, when $\beta$ reaches zero for this case of $x=0.5$, the ARE curves are identical to those for the covariate free case in Fig. 1. On the other hand, as illustrated by the lower two panels, there is less to gain from relying on parametric models when the covariate values are far from the average, and moderately large time points are of interest.

3.3 What price semiparametric Cox regression? – Regression coefficient and hazard ratios

In some regression situations, interest is solely in the regression coefficients $\beta$ and hazard ratios $\exp (\Delta ^{\mathrm{t}}\beta )$ for individuals whose covariates differ by some vector $\Delta$. The latter here has the same ARE as $\Delta ^{\mathrm{t}}\beta$. Comparison of the semiparametric estimator ${\widehat{\beta }}_\mathrm{cox}$ with fully parametric ${\widehat{\beta }}_\mathrm{pm}$ amounts to comparing the diagonal of $J_\mathrm{cox}^{-1}$ with the diagonal of $[J^{-1}]_{22}=J_{22}-J_{21}J_{11}^{-1}J_{12}$, where $[J^{-1}]_{22}$ denotes the $q\times q$-dimensional lower right block matrix of $J^{-1}$. Figure 3 shows ARE curves as a function of $\beta _\mathrm{true}$ when $q=1$ for the exponential and Weibull models, once again with three different censoring proportions as $\tau \rightarrow \infty$. The figure suggests that when $\beta$ is close to zero, there is practically nothing to lose by using ${\widehat{\beta }}_\mathrm{cox}$ as opposed to ${\widehat{\beta }}_\mathrm{pm}$. If the effect of the covariate is large (i.e. $\,|\,\beta \,|\,$ is large), it is however significantly more efficient to use a parametric option, especially when the amount of censoring is small.

Fig. 3

ARE curves for $\beta$ and hazard ratios. Black (thin) and red (thick) lines correspond to, respectively, the exponential and Weibull models. Solid, dashed and dotted line type refer to censoring proportions of respectively $0\%, 20\%$ and $40\%$ (Color figure online)

Remark 1

One may suspect that the high ARE for $\beta$-estimation is caused by the simplicity of the linear baseline hazard. The results are however practically identical under a Weibull model with shape parameters both below and above 1. ARE curves not shown here for the ‘expected time lived in a restricted time interval’ $\int _0^t S(s\,|\,x)\, \mathrm{d}s$, which is further discussed in Sect. 4.1, also turn out similar to those in Fig.  2. In the efficiency results above, we have only included a single covariate. When there are several covariates present, the numerical procedures and algorithms required to compute the ARE grow quickly in complexity and become rather unwieldy. Finite sample based simulation are then more suitable. Rough results from some brief simulation tests (not shown here) are as follows: Increasing the number of covariates drags the ARE towards 1 for both the exponential and the Weibull model for estimation of $\beta$, i.e. the Cox model closes in even further on parametric models in terms of efficiency. This is also the case when estimating conditional cumulative hazards, survival probabilities and quantiles, as this increases the total effect of the covariates. When $x^{\mathrm{t}}\beta _\mathrm{true}$ is held constant when increasing q, however, the ARE decreases. Our results do not indicate that the correlation between variables affects this decrease.

3.4 Efficiency outside model conditions

The above illustrations showed what losses could be expected when using the semiparametric Cox model when a simpler parametric model is indeed correct. In practical situations, a parametric model is seldom 100% correct, so using it typically incurs a nonzero bias. The question is then whether this bias is small compared to the increase in variance induced by the asymptotically unbiased semiparametric Cox model.

In formalising this, the limit results in (10) and (19) motivate the following natural approximations to the mean squared errors of ${\widehat{\mu }}_\mathrm{cox}$ and ${{\widehat{\mu }}}_\mathrm{pm}$,

$$\begin{aligned} \mathrm{mse}_\mathrm{cox}= 0^2 + n^{-1}v_\mathrm{cox}\quad \mathrm{and} \quad \mathrm{mse}_\mathrm{pm}= b^2 + n^{-1}v_\mathrm{pm}, \end{aligned}$$

(24)

for a general focus parameter $\mu$. Here $b=\mu _0-\mu _\mathrm{true}$ is the asymptotic bias incurred by using the parametric model. Since typically $v_\mathrm{pm}<v_\mathrm{cox}$ also when the parametric model is incorrect, $\mathrm{mse}_\mathrm{pm}$ can be expected to be lower than $\mathrm{mse}_\mathrm{cox}$ if the b is not too large for the particular focus parameter. Note however that when increasing n, the squared bias term will eventually dominate, making $\mathrm{mse}_\mathrm{pm}$ the largest unless $b=0$.

Consider now the conditional cumulative hazard case in Sect. 3.2, but without assuming the parametric model is fully correct. In this case $v_\mathrm{cox}$ takes the same form as in (22), while $v_\mathrm{pm}$ generalises (23) and takes the form

$$\begin{aligned} v_\mathrm{pm}=\exp (2x^{\mathrm{t}}\beta _0)\begin{pmatrix} A^{\mathrm{d}}_\mathrm{pm}(t;\theta _0) \\ A_\mathrm{pm}(t;\theta _0)x\end{pmatrix}^{\mathrm{t}} J^{-1}KJ^{-1}\begin{pmatrix} A^{\mathrm{d}}_\mathrm{pm}(t;\theta _0) \\ A_\mathrm{pm}(t;\theta _0)x\end{pmatrix}. \end{aligned}$$

The bias incurred by the incorrect parametric bias is $b=A_0(t\,|\,x)-A_\mathrm{true}(t\,|\,x)$, where

$$\begin{aligned} A_\mathrm{true}(t\,|\,x)=A_\mathrm{true}(t)\exp (x^{\mathrm{t}}\beta _\mathrm{true}) \quad \mathrm{and} \quad A_0(t\,|\,x)=A_\mathrm{pm}(t;\theta _0)\exp (x^{\mathrm{t}}\beta _0). \end{aligned}$$

(25)

To illustrate the behaviour of the Cox model as opposed to a misspecified parametric model, we shall compare $\mathrm{mse}_\mathrm{cox}$ with $\mathrm{mse}_\mathrm{pm}$ when the exponential model is misspecified. We take the baseline survival distribution to be Weibull distributed with scale parameter $\lambda =1$ and shape parameter $d \ne 1$, i.e. having hazard rate $\alpha _{\text {wei}}(s;\lambda ,d) = d (\lambda s)^{d-1}\lambda$. The mse ratio $\mathrm{mse}_\mathrm{pm}/ \mathrm{mse}_\mathrm{cox}$ is the natural outside-model-conditions version of the ARE. Figure 4 displays such ratios for four combinations of shape parameters and sample sizes when estimating the conditional cumulative hazard. In all cases we take $\beta _\mathrm{true}=1$ and $x=0.5$. Unlike the case under model conditions, nonlinear functions of the cumulative hazard, such as survival probabilities, will have different efficiency results.

Fig. 4

Mse ratio curves for the exponential model vs. the semiparametric Cox model when estimating the conditional cumulative hazard under the Weibull$(\lambda =1,d)$ model, i.e. $A_\mathrm{true}(t\,|\,x)=t^d\exp (x\beta _{\mathrm{true}})$. Four combinations of the parameter d and the sample size n are displayed, all with $\beta _\mathrm{true}=1$ and $x=0.5$. Solid, dashed and dotted line type refer to censoring proportions of respectively $0\%, 20\%$ and $40\%$. The dashed horizontal grey line indicates the point where the models are equally efficient

As the plots show, even when moderately misspecified, the exponential model estimator is sometimes more efficient than that of the semiparametric Cox model. In particular this is the case for the smallest sample size at the time range boundaries and with considerable censoring proportions. In fact, for $d=0.9$ and $n=100$, the exponential model is uniformly more efficient in this sense. As n increases, the squared bias part dictate $\mathrm{mse}_\mathrm{pm}$ to a larger degree and thereby increases the mse ratio. When the amount of censoring increases, the mse ratio decreases for most of the data range as this in practice reduces the effective sample size. In particular, increasing censoring significantly reduces the loss of using the exponential model when the semiparametric is more efficient.

4 Focused and averaged focused information criteria

In the previous section we studied ARE under model conditions, in addition to some approximate mean squared error ratios, working also outside model conditions. We saw that there is sometimes quite a lot to gain from relying on a parametric model, not only if it is fully correct, but the gain or loss depends heavily on the exact quantity being estimated, i.e. the focus parameter. The ‘what price’ themes lead to answers to important and intriguing questions and may to some extent also be exploited by practitioners.

However, their dependence on the true unknown distribution makes them unusable as model selectors to choose among a set of different parametric models and the semiparametric Cox model in practice.

The ultimate goal of analysis is often to estimate some focus parameter $\mu$. The results in the previous section then motivate guiding practical model selection by estimating the mean squared error approximation in (24). We shall here construct a variant of the focused information criterion (FIC) (Claeskens and Hjort 2003; Jullum and Hjort 2017), aiming precisely at estimating these mean squared errors based on available data. The FIC selects the model/estimator with the smallest estimated mean squared error. We shall also present a more general average focused information criterion (AFIC), which may deal with situations where a single model ought to be chosen for estimating a full set of focus parameters.

4.1 Joint convergence

In order to estimate (24) we need estimates of both the variances and the square of the bias, b. While the bias itself may be estimated by ${\widehat{b}} = {\widehat{\mu }}_\mathrm{pm}- {\widehat{\mu }}_\mathrm{cox}$, its square, ${\widehat{b}}^2$, will typically have mean close to $b^2 + \mathrm{Var}\,{\widehat{b}} = b^2 + \mathrm{Var}\,{\widehat{\mu }}_\mathrm{pm}+ \mathrm{Var}\,{\widehat{\mu }}_\mathrm{cox}- 2\,\mathrm{Cov}({\widehat{\mu }}_\mathrm{pm},{\widehat{\mu }}_\mathrm{cox})$. Thus, to correct for the overshooting quantity, we need an estimate of the $\mathrm{Cov}({\widehat{\mu }}_\mathrm{pm},{\widehat{\mu }}_\mathrm{cox})$. See more on this in Sect. 4.2. This covariance cannot be estimated based on the limiting marginals of $\sqrt{n}({\widehat{\mu }}_\mathrm{cox}-\mu _\mathrm{true})$ and $\sqrt{n}({\widehat{\mu }}_\mathrm{pm}- \mu _0)$ alone (as was heuristically given in (10) and (19)), but requires an explicit form for their joint limiting distribution.

Before stating a theorem with the joint limiting distribution, we present some notation and a helpful lemma. Let us write ‘block(B, C)’ for the block diagonal matrix with B and C in, respectively, the upper left and lower right corner, and zeros elsewhere. Denote also the $q\times q$-dimensional identity matrix by ${\mathcal {I}}_q$. Let also the covariances $G=\mathrm{Cov}(U_\mathrm{cox},U^{\mathrm{t}})$ and $\nu (s)=\mathrm{Cov}(W(s),U^{\mathrm{t}})$ for $U_\mathrm{cox}$ as in (6), U as in (18), and W(s) as in (8) and (9), and recall that we write $A^{\mathrm{d}}_\mathrm{pm}(s;\theta )=\partial A_{\mathrm{pm}}(s;\theta )/\partial \theta = \int _0^s \psi (u;\theta )\alpha _{\mathrm{pm}}(u;\theta )\,\mathrm{d}u$.

Lemma 1

Under the working conditions in Sect. 2, the limit results in (6), (8) and (18) hold jointly, and in particular

$$\begin{aligned} \sqrt{n}\begin{pmatrix} {\widehat{A}}_{\mathrm{cox}}(\cdot )-A_\mathrm{true}(\cdot ) \\ {{\widehat{\beta }}}_{\mathrm{cox}} - \beta _{\mathrm{true}} \\ A_{\mathrm{pm}}(\cdot ;\widehat{\theta })-A_{0}(\cdot ) \\ {\widehat{\beta }}_\mathrm{pm}- \beta _0 \end{pmatrix} {\mathop {\rightarrow }\limits ^{d}} \begin{pmatrix} W(\cdot ) - F(\cdot )^{\mathrm{t}}J_\mathrm{cox}^{-1}U_\mathrm{cox}\\ J_{\mathrm{cox}}^{-1}U_\mathrm{cox}\\ \mathrm{{block}}(A^{\mathrm{d}}_\mathrm{pm}(\cdot ;\theta _0)^{\mathrm{t}},{\mathcal {I}}_q)J^{-1}U \end{pmatrix}= \begin{pmatrix} Z_{\mathrm{cox}}(\cdot ) \\ Z_{\mathrm{pm}}(\cdot ) \end{pmatrix},\nonumber \\ \end{aligned}$$

(26)

which is a $2(1+q)$-dimensional zero-mean Gaussian process with covariance function

$$\begin{aligned} \Sigma (s,t) = \begin{pmatrix} \Sigma _{11}(s,t) &{} \Sigma _{12}(s,t) \\ \Sigma _{21}(s,t) &{} \Sigma _{22}(s,t) \end{pmatrix}, \end{aligned}$$

where the $(1+q)\times (1+q)$-dimensional blocks $\Sigma _{ij}(s,t), i,j=1,2$ are given by

$$\begin{aligned} \begin{aligned} \Sigma _{11}(s,t)&= \begin{pmatrix} \sigma ^2(\min (s,t)) + F(s)^{\mathrm{t}}J_\mathrm{cox}^{-1}F(t) &{} -F(s)^{\mathrm{t}}J^{-1}_\mathrm{cox}\\ -J^{-1}_\mathrm{cox}F(t) &{} J^{-1}_{\mathrm{cox}} \end{pmatrix},\\ \Sigma _{12}(s,t)&= \Sigma _{21}(t,s)^{\mathrm{t}}= \begin{pmatrix} \{\nu (s)- F(s)^{\mathrm{t}}J_{\mathrm{cox}}^{-1}G\}J^{-1}\mathrm{{block}} (A^{\mathrm{d}}_\mathrm{pm}(t;\theta _0),{\mathcal {I}}_q) \\ J^{-1}_\mathrm{cox}GJ^{-1}\mathrm{{block}}(A^{\mathrm{d}}_\mathrm{pm}(t;\theta _0),{\mathcal {I}}_q) \end{pmatrix}, \\ \Sigma _{22}(s,t)&= \mathrm{{block}}(A^{\mathrm{d}}_\mathrm{pm}(s;\theta _0)^{\mathrm{t}},{\mathcal {I}}_q)J^{-1}KJ^{-1}\mathrm{{block}}(A^{\mathrm{d}}_\mathrm{pm}(t;\theta _0),{\mathcal {I}}_q). \end{aligned} \end{aligned}$$

(27)

The proof of the lemma is given in the supplementary material (Jullum and Hjort, this work). Recall also the $g^{(k)}(u;\beta )$ notation in (15). Under the conditions in the above lemma, G and $\nu (s)$ take the following explicit forms:

$$\begin{aligned} G&= \begin{pmatrix} 0_{p \times q} \\ J_{\mathrm{cox}} \end{pmatrix}^{\mathrm{t}} - \int _0^{\tau } \begin{pmatrix} \psi (u;\theta _0)\{A_\mathrm{true}(u)g^{(1)}(u;\beta _\mathrm{true})^{\mathrm{t}} - g^{(0)}(u;\beta _\mathrm{true})F(u)^{\mathrm{t}}\} \\ A_\mathrm{true}(u)g^{(2)} (u;\beta _\mathrm{true}) - g^{(1)}(u;\beta _\mathrm{true})F(u)^{\mathrm{t}} \end{pmatrix}^{\mathrm{t}} \mathrm{d}u,\end{aligned}$$

(28)

$$\begin{aligned} \nu (s)&=\begin{pmatrix} \int _0^s \psi (u;\theta _0) \alpha _\mathrm{true}(u)\, \mathrm{d}u \\ F(s) \end{pmatrix}^{\mathrm{t}} - \int _0^{\tau } \begin{pmatrix} g^{(0)}(u;\beta _\mathrm{true})\psi (u;\theta _0) \\ g^{(1)}(u;\beta _\mathrm{true}) \end{pmatrix}^{\mathrm{t}} \sigma ^2(\min (s,u)) \, \mathrm{d}u. \end{aligned}$$

(29)

Derivations of these expressions are given in the supplementary material (Jullum and Hjort, this work).

The above lemma motivates a theorem specifying that the limit results in (10) and (19) hold jointly, i.e. that $\sqrt{n}({\widehat{\mu }}_{\mathrm{cox}}-\mu _\mathrm{true})$ and $\sqrt{n}({\widehat{\mu }}_\mathrm{pm}- \mu _0)$ have a joint limit distribution. To give a full proof, the general notion of Hadamard differentiability is central. For general normed spaces $\mathbb {D}$ and $\mathbb {E}$, a map $T:\mathbb {D}_{T} \mapsto \mathbb {E}$, defined on a subset $\mathbb {D}_{T} \subseteq \mathbb {D}$ that contains $\phi$, is called Hadamard differentiable at $\phi$ if there exists a continuous, linear map $T'_{\phi }:\mathbb {D} \mapsto \mathbb {E}$ (called the derivative of T at $\phi$) such that $\Vert \{T(\phi +t h_t)-T(\phi )\}/t -T'_{\phi }(h) \Vert _{\mathbb {E}} \rightarrow 0$ as $t \searrow 0$ for every $h_t \rightarrow h$ such that $\phi +th_t$ is contained in $\mathbb {D}_{T}$.³ In our applications, the norm $\Vert \cdot \Vert _\mathbb {E}$ will be either the Euclidean norm $\Vert \cdot \Vert$, the uniform norm $\Vert f(\cdot )\Vert _\mathbb {E} =\sup _{a} \Vert f(a)\Vert$, or a combination of these. Recall the functional form of the focus parameter $\mu =T(A(\cdot ),\beta )$, and denote (in the Hadamard sense) the derivatives of T at $(A_\mathrm{true}(\cdot ),\beta _\mathrm{true})$ and $(A_{0}(\cdot ),\beta _0)$ by respectively $T'_{\mathrm{cox}}$ and $T'_{\mathrm{pm}}$.

Theorem 1

Assume that T is Hadamard differentiable with respect to the uniform norm at $(A_\mathrm{true}(\cdot ),\beta _\mathrm{true})$ and $(A_{0}(\cdot ),\beta _0)$, and that the conditions of Lemma 1 hold. Then, as $n\rightarrow \infty$

$$\begin{aligned} \sqrt{n}\begin{pmatrix} {{\widehat{\mu }}}_\mathrm{cox}-\mu _\mathrm{true}\\ {{\widehat{\mu }}}_\mathrm{pm}-\mu _0 \end{pmatrix} {\mathop {\rightarrow }\limits ^{d}} \begin{pmatrix} \Lambda _{\mathrm{cox}} \\ \Lambda _{\mathrm{pm}} \end{pmatrix} = \begin{pmatrix} T'_{\mathrm{cox}}(Z_\mathrm{cox}) \\ T'_{\mathrm{pm}}(Z_\mathrm{pm}) \end{pmatrix} \sim \mathrm{N}_2\left( \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \Sigma _\mu \right) , \end{aligned}$$

(30)

where $v_\mathrm{cox}=\mathrm{Var}\,(\Lambda _{\mathrm{cox}})$, $v_\mathrm{pm}=\mathrm{Var}\,(\Lambda _{\mathrm{pm}})$ and $v_c=\mathrm{Cov}\,(\Lambda _{\mathrm{cox}},\Lambda _{\mathrm{pm}})$ in

$$\begin{aligned} \Sigma _\mu = \begin{pmatrix} v_\mathrm{cox}&{} v_c \\ v_c &{} v_\mathrm{pm}\end{pmatrix}. \end{aligned}$$

(31)

The proof of the theorem is given in the supplementary material (Jullum and Hjort, this work). The generality of the above theorem, involving the functional derivative etc., has the possible downside that a fairly high level of theoretical expertise is required to actually compute the resulting covariance matrix $\Sigma _\mu$, which will be needed in our upcoming FIC and AFIC formulae. Below we therefore provide simplified formulae for the most natural classes of focus parameters. Some of the most common focus parameters depend on $A(\cdot )$ only at a finite number of time points, in addition to $\beta$. Consider the functional $\mu =T(A(\cdot ),\beta )=z(m_1(A(t_1),\beta ),\ldots ,m_k(A(t_k),\beta ))$, where $t_1,\ldots ,t_k$ are k time points, $m_1,\ldots ,m_k$ are smooth functions $m_j: \mathbb {R}^{1+q} \mapsto \mathbb {R}$, and z is a function $z:\mathbb {R}^k \mapsto \mathbb {R}$. Since T involves only a finite number of time points, the ordinary delta method applies, and $\Sigma _\mu$ is established by a series of matrix products. Let $m'_\mathrm{cox}$ and $m'_\mathrm{pm}$ be the $k\times (q+1)$-dimensional Jacobian matrices of $m(a)=(m_1(a_1), \ldots ,m_k(a_k))^{\mathrm{t}}$ evaluated at respectively $a_\mathrm{cox}=\{ a_{\mathrm{cox},j}\}_{j=1,\ldots ,k}$ and $a_\mathrm{pm}=\{ a_{\mathrm{pm},j}\}_{j=1,\ldots ,k}$, where $a_{\mathrm{cox},j}=(A_\mathrm{true}(t_j),\beta _\mathrm{true})$ and $a_{\mathrm{pm},j}=(A(t_j;\theta _0),\beta _0)$. Let similarly $z'_\mathrm{cox}$ and $z'_\mathrm{pm}$ be the $1\times k$-dimensional Jacobian matrices of z evaluated at respectively $m_\mathrm{cox}=m(a_\mathrm{cox})$ and $m_\mathrm{pm}=m(a_\mathrm{pm})$. Then

$$\begin{aligned} T'_{\mathrm{cox}}(Z_\mathrm{cox}) = z'_\mathrm{cox}m'_\mathrm{cox}\begin{pmatrix} Z_\mathrm{cox}(t_1) \\ \vdots \\ Z_\mathrm{cox}(t_k) \end{pmatrix} , \quad \mathrm{and} \quad T'_{\mathrm{pm}}(Z_\mathrm{pm}) = z'_\mathrm{pm}m'_\mathrm{pm}\begin{pmatrix} Z_\mathrm{cox}(t_1) \\ \vdots \\ Z_\mathrm{cox}(t_k) \end{pmatrix}, \end{aligned}$$

such that $\Sigma _\mu$ of (31) is specified by $v_\mathrm{cox}=z'_\mathrm{cox}m'_\mathrm{cox}\Sigma _{11}^* \{z'_\mathrm{cox}m'_\mathrm{cox}\}^{\mathrm{t}}$, in addition to

$$\begin{aligned} v_c= z'_\mathrm{cox}m'_\mathrm{cox}\Sigma _{12}^* \{z'_\mathrm{pm}m'_\mathrm{pm}\}^{\mathrm{t}} \quad \mathrm{and} \quad v_\mathrm{pm}=z'_\mathrm{pm}m'_\mathrm{pm}\Sigma _{22}^* \{z'_\mathrm{pm}m'_\mathrm{pm}\}^{\mathrm{t}} \end{aligned}$$

(32)

where each block $\Sigma _{lo}^*$ have elements $\{\Sigma _{lo}(t_i,t_j) \}_{i,j=1,\ldots ,k}$, $l,o=1,2$ as described in (27). This indeed covers simple conditional cumulative hazards via $m(A(t),\beta )=A(t\,|\,x)=A(t)\exp (x^{\mathrm{t}}\beta )$ and conditional survival probabilities $m(A(t),\beta )=S(t\,|\,x)=\exp \{-A(t|x)\}$, but also, say, the difference between the probabilities of observing an event in the interval $(t_1,t_2)$ for two different covariate values $x_a,x_b$: $\{S(t_1\,|\,x_a)-S(t_2\,|\,x_a)\}-\{S(t_1\,|\,x_b)-S(t_2\,|\,x_b)\}$.

Explicit expressions for the $\Sigma _\mu$ associated with focus parameters dependent on the complete cumulative baseline hazard function $A(\cdot )$ are more involved and perhaps easiest handled on a case by case basis. Such derivations for the life time quantile can be found in the supplementary material (Jullum and Hjort, this work). Here we shall consider the expected time lived in a restricted time interval [0, t] for an individual with covariate values corresponding to some x, given by $\mu =\xi _{t,x}=T(A(\cdot ),\beta ;t,x) = \int _0^t \exp \{-A(s)\exp (x^{\mathrm{t}}\beta )\}\,\mathrm{d}s =\int _0^t S(s\,|\,x)\,\mathrm{d}s.$ With $\widehat{S}_\mathrm{cox}(t\,|\,x) =\exp \{-{\widehat{A}}_\mathrm{cox}(t\,|\,x)\}$ and $\widehat{S}_\mathrm{pm}(t\,|\,x)=\exp \{-{\widehat{A}}_\mathrm{pm}(t\,|\,x)\}$, this focus parameter has semiparametric and fully parametric estimators given by respectively ${\widehat{\mu }}_\mathrm{cox}=\int _0^t \widehat{S}_\mathrm{cox}(s\,|\,x)\, \mathrm{d}s$ and ${\widehat{\mu }}_\mathrm{pm}=\int _0^t \widehat{S}_\mathrm{pm}(s\,|\,x)\, \mathrm{d}s$, consistent for respectively $\mu _\mathrm{true}=\int _0^t S_\mathrm{true}(s\,|\,x)\,\mathrm{d}s$ and $\mu _0=\int _0^t S_0(s\,|\,x)\,\mathrm{d}s$, where $S_\mathrm{true}(s\,|\,x)=\exp \{-A_\mathrm{true}(s\,|\,x)\}$ and $S_0(s\,|\,x)=\exp \{-A_0(s\,|\,x)\},$ having exponents as defined in (25). Application of the functional delta method (van der Vaart 2000, Theorem 20.8) gives

$$\begin{aligned} \sqrt{n}\begin{pmatrix} {\widehat{A}}_\mathrm{cox}(\cdot \,|\,x)- A_\mathrm{true}(\cdot \,|\,x) \\ {\widehat{A}}_\mathrm{pm}(\cdot \,|\,x)- A_{0}(\cdot \,|\,x) \\ \end{pmatrix}&{\mathop {\rightarrow }\limits ^{d}} \begin{pmatrix} Z_{A,\mathrm{cox}}(\cdot ) \\ Z_{A,\mathrm{pm}}(\cdot ) \end{pmatrix} = \begin{pmatrix} \zeta _\mathrm{cox}( \cdot )^{\mathrm{t}}Z_{\mathrm{cox}}(\cdot ) \\ \zeta _\mathrm{pm}(\cdot )^{\mathrm{t}}Z_{\mathrm{pm}}(\cdot ) \end{pmatrix}, \end{aligned}$$

(33)

with ${\widehat{A}}_\mathrm{cox}(\cdot \,|\,x), {\widehat{A}}_\mathrm{pm}(\cdot \,|\,x)$ and $A_\mathrm{true}(\cdot \,|\,x), A_0(\cdot \,|\,x)$ as defined in (21) and (25), and with slight abuse of notation (omitting the x index), $\zeta _\mathrm{cox}(\cdot )=(\exp (x^{\mathrm{t}}\beta _\mathrm{true}) , A_\mathrm{true}(\cdot )\exp (x^{\mathrm{t}}\beta _\mathrm{true})x^{\mathrm{t}})^{\mathrm{t}}$ and $\zeta _\mathrm{pm}(\cdot )=(\exp (x^{\mathrm{t}}\beta _0) , A_\mathrm{pm}(\cdot ;\theta _0)\exp (x^{\mathrm{t}}\beta _0)x^{\mathrm{t}})^{\mathrm{t}}$. In addition,

$$\begin{aligned} \sqrt{n}\begin{pmatrix} \widehat{S}_\mathrm{cox}(\cdot \,|\,x)- S_\mathrm{true}(\cdot \,|\,x) \\ \widehat{S}_\mathrm{pm}(\cdot \,|\,x)- S_0(\cdot \,|\,x) \\ \end{pmatrix}&{\mathop {\rightarrow }\limits ^{d}} \begin{pmatrix} Z_{S,\mathrm{cox}}(\cdot ) \\ Z_{S,\mathrm{pm}}(\cdot ) \end{pmatrix} = -\begin{pmatrix} S_\mathrm{true}(\cdot \,|\,x)Z_{A,\mathrm{cox}}(\cdot ) \\ S_0(\cdot \,|\,x)Z_{A,\mathrm{pm}}(\cdot ) \end{pmatrix}. \end{aligned}$$

Omitting once again the notational dependence on x, let $\xi _{t,\mathrm{true}}=\int _0^t S_\mathrm{true}(s\,|\,x)\,\mathrm{d}s$ and $\xi _{t,0}=\int _0^t S_0(s\,|\,x)\,\mathrm{d}s$, and also $V_{t,\mathrm{cox}}(s)=\xi _{t,\mathrm{true}}-\xi _{s,\mathrm{true}}$ and $V_{t,\mathrm{pm}}(s)=\xi _{t,0}- \xi _{s,0}$. By applying integration by substitution and by parts, it follows that

$$\begin{aligned} \sqrt{n}\begin{pmatrix} {{\widehat{\mu }}}_\mathrm{cox}-\mu _\mathrm{true}\\ {{\widehat{\mu }}}_\mathrm{pm}-\mu _0 \end{pmatrix}&= \int _0^{t} \sqrt{n}\begin{pmatrix} \widehat{S}_\mathrm{cox}(s\,|\,x)- S_\mathrm{true}(s\,|\,x) \\ \widehat{S}_\mathrm{pm}(s\,|\,x)- S_0(s\,|\,x) \\ \end{pmatrix} \mathrm{d}s \\&{\mathop {\rightarrow }\limits ^{d}} - \begin{pmatrix} \int _0^t S_\mathrm{true}(s\,|\,x)Z_{A,\mathrm{cox}}(s)\, \mathrm{d}s\\ \int _0^t S_0(s\,|\,x)Z_{A,\mathrm{pm}}(s)\, \mathrm{d}s \end{pmatrix} =\begin{pmatrix} \int _0^t Z_{A,\mathrm{cox}}(s)\, \mathrm{d}V_{t,\mathrm{cox}}(s)\\ \int _0^t Z_{A,\mathrm{pm}}(s)\, \mathrm{d}V_{t,\mathrm{pm}}(s) \end{pmatrix} \\&=- \begin{pmatrix} \int _0^t V_{t,\mathrm{cox}}(s)\, \mathrm{d}Z_{A,\mathrm{cox}}(s) \\ \int _0^t V_{t,\mathrm{pm}}(s)\, \mathrm{d}Z_{A,\mathrm{pm}}(s) \end{pmatrix}. \end{aligned}$$

Thus, for this focus parameter, $\Sigma _\mu$ of (31) has elements $v_\mathrm{cox}, v_c$ and $v_\mathrm{pm}$ given by

$$\begin{aligned} \begin{aligned} v_\mathrm{cox}&=\int _0^t V_{t,\mathrm{cox}}(s)^2 \, \mathrm{d}\{\zeta _\mathrm{cox}(s)^{\mathrm{t}}\Sigma _{11}(s,s)\zeta _\mathrm{cox}(s)\}, \\ v_\mathrm{pm}&=\int _0^t V_{t,\mathrm{pm}}(s)^2 \, \mathrm{d}\{\zeta _\mathrm{pm}(s)^{\mathrm{t}} \Sigma _{22}(s,s)\zeta _\mathrm{pm}(s)\}, \\ v_c&= \int _0^t V_{t,\mathrm{cox}}(s)V_{t,\mathrm{pm}}(s) \, \mathrm{d}\{\zeta _\mathrm{cox}(s)^{\mathrm{t}}\Sigma _{12}(s,s) \zeta _\mathrm{pm}(s)\}. \end{aligned} \end{aligned}$$

(34)

4.2 The focused information criterion

With the limit theorem (Theorem 1) and applicable formulae for $\Sigma _\mu$ available, we turn to the actual derivation of the FIC. As mentioned, this amounts to estimating $\mathrm{mse}_\mathrm{cox}=n^{-1}v_\mathrm{cox}$ and $\mathrm{mse}_\mathrm{pm}=b^2+n^{-1}v_\mathrm{pm}$, essentially requiring (consistent) estimates of the covariance matrix $\Sigma _\mu$ of (31) and the square of the parametric bias $b=\mu _\mathrm{true}-\mu _0$, for the chosen focus parameter $\mu$. The Appendix provides and discusses estimators ${\widehat{v}}_\mathrm{cox}, {\widehat{v}}_c$ and ${\widehat{v}}_\mathrm{pm}$ consistent for estimating, respectively, $v_\mathrm{cox}, v_c$ and $v_\mathrm{pm}$ for the above focus parameters.

With such estimators on board, the FIC score of the semiparametric Cox model is given by

$$\begin{aligned} \mathrm{FIC}_\mathrm{cox}=\widehat{\mathrm{mse}}_\mathrm{cox}=n^{-1}{\widehat{v}}_\mathrm{cox}. \end{aligned}$$

(35)

Estimating the variance part for the parametric case is similarly taken care of by inserting ${\widehat{v}}_\mathrm{pm}$ for $v_\mathrm{pm}$. Estimating the squared bias is however more demanding. Consider the bias estimator ${\widehat{b}}={{\widehat{\mu }}}_\mathrm{pm}-{{\widehat{\mu }}}_\mathrm{cox}$. From Theorem 1 it is immediate that

$$\begin{aligned} \sqrt{n}({\widehat{b}}-b) =\sqrt{n}({{\widehat{\mu }}}_\mathrm{pm}-\mu _0) -\sqrt{n}({{\widehat{\mu }}}_{\mathrm{cox}}-\mu _\mathrm{true}) {\mathop {\rightarrow }\limits ^{d}} \Lambda _\mathrm{pm}-\Lambda _\mathrm{cox}\sim \mathrm{N}(0,\kappa ), \end{aligned}$$

(36)

where $\kappa =v_\mathrm{pm}+v_\mathrm{cox}-2v_c$, also implying consistency of ${\widehat{b}}$. From this limit it is seen that although ${\widehat{b}}$ is approximately unbiased for b, its square ${{\widehat{b}}}^2$ has mean close to $b^2+\kappa /n$. It is therefore appropriate to adjust the square of the bias estimate ${\widehat{b}}^2$ by subtracting $\widehat{\kappa }/n=({\widehat{v}}_\mathrm{pm}+{\widehat{v}}_\mathrm{cox}-2{\widehat{v}}_c)/n$. To avoid ending up with unappealing negative squared bias estimates, an appropriate additional modification is to truncate negative squared bias estimates to zero. We thus arrive at

$$\begin{aligned} \mathrm{FIC}_\mathrm{pm}=\widehat{\mathrm{mse}}_\mathrm{pm}=\max ({\widehat{b}}^2-{\widehat{\kappa }}/n,0)+{\widehat{v}}_\mathrm{pm}/n. \end{aligned}$$

(37)

These are the FIC scores, which ranks the candidate models when being computed in practical situations. Note that the parametric FIC score typically ought to be computed for several different parametric options, with different estimates of squared bias and variance, resulting in a ranking of say four parametric options, in addition to the nonparametric.

4.3 The average focused information criterion

The FIC apparatus arrived at above works for ranking candidate models when the ultimate goal of analysis is to estimate a single given focus parameter $\mu$. In some situations one may wish one’s model to do well across a certain set of such focus parameters, like estimating all hazard rates across a certain time window, or for a stratum of individuals defined by a subset of the covariate space. For such problems we suggest the following average FIC strategy (AFIC).

Consider a collection or class of focus parameters $\mu (u)$, indexed by u, for which we contemplate using either ${{\widehat{\mu }}}_\mathrm{cox}(u)$, or one of the fully parametric estimators ${{\widehat{\mu }}}_\mathrm{pm}(u)$. Assume that Theorem 1 is applicable for each index u of the focus parameter $\mu (u)$, and that the loss of using ${{\widehat{\mu }}}(u)$ is $\int \{{{\widehat{\mu }}}(u)-\mu _\mathrm{true}(u)\}^2\,\mathrm{d}\omega (u)$ for a cumulative weight function or measure $\omega$, defined by the statistician to reflect the relative importance of the focus parameters.

This setup allows more importance to be assigned to estimating some $\mu (u)$ well compared to others. The integral can also be a finite sum over a list of focus parameters. Expressions for the risk, i.e. expected losses, or mean integrated squared errors, then follow from previous efforts:

$$\begin{aligned} \mathrm{mise}_\mathrm{cox}=\int n^{-1}v_\mathrm{cox}(u)\,\mathrm{d}\omega (u), \quad \mathrm{and} \quad \mathrm{mise}_\mathrm{pm}=\int \{b(u)^2+n^{-1}v_\mathrm{pm}(u)\}\,\mathrm{d}\omega (u). \end{aligned}$$

Here $b(u)=\mu _0(u)-\mu _\mathrm{true}(u)$ may be estimated via ${\widehat{b}}(u)={{\widehat{\mu }}}_\mathrm{pm}(u)-{{\widehat{\mu }}}_\mathrm{cox}(u)$, for which $\sqrt{n}\{{\widehat{b}}(u)-b(u)\}\rightarrow _d\mathrm{N}(0,\kappa (u))$, with $\kappa (u)=v_\mathrm{cox}(u)+v_\mathrm{pm}(u)-2v_c(u)$. In the final estimator for the integrated squared bias, one may choose either to truncate before or after integration. We here choose the latter as we are no longer seeking natural estimates for the individual mses, but for the new integrated risk function. This gives the following AFIC formulae

$$\begin{aligned} \begin{aligned} \mathrm{AFIC}_\mathrm{cox}&=0+n^{-1}\int {\widehat{v}}_\mathrm{cox}(u)\,\mathrm{d}\omega (u), \\ \mathrm{AFIC}_\mathrm{pm}&= \max \Bigl (0,\int \{{\widehat{b}}(u)^2-n^{-1}{\widehat{\kappa }}(u)\} \,\mathrm{d}\omega (u)\Bigr ) +n^{-1}\int {\widehat{v}}_\mathrm{pm}(u)\,\mathrm{d}\omega (u). \end{aligned} \end{aligned}$$

As for the FIC, these are then to be computed for the semiparametric Cox regression model and all the different parametric candidates under consideration, followed by ranking them all from smallest to largest. The model with the smallest AFIC score is selected and should be used for estimation of the whole set of focus parameters.

5 Performance of FIC and AFIC

5.1 Asymptotic behaviour and indirect goodness-of-fit testing

In terms of the ‘what price’ questions in Sect. 3, it is natural to ask how the FIC procedure selects under model conditions. Consider however first the case when a parametric candidate model is incorrect and has bias $b\ne 0$. From the structure of the FIC formulae in (35) and (37), and consistency of the estimators involved, it is seen that as n grows, the squared bias term will dominate. The semiparametric Cox model will therefore be the winning model with probability tending to 1 as $n\rightarrow \infty$. This may be seen as an insurance against model misspecification when using the FIC – i.e. any parametric model returning a biased estimator, will be selected with a probability tending to 0 as $n \rightarrow \infty$.

From (35) and (37) we see that a specific parametric model is selected over Cox whenever

$$\begin{aligned} \max ({\widehat{b}}^2-{\widehat{\kappa }}/n,0) + n^{-1}{\widehat{v}}_\mathrm{pm}\le n^{-1}{\widehat{v}}_\mathrm{cox}. \end{aligned}$$

As long as ${\widehat{v}}_\mathrm{cox}\ge {\widehat{v}}_\mathrm{pm}$ (which typically is the case and happens with probability tending to 1 under model condtions), this is seen to be equivalent to the inequality

$$\begin{aligned} Z_n = n{\widehat{b}}^2/({\widehat{v}}_\mathrm{cox}- {\widehat{v}}_c) \le 2, \end{aligned}$$

(38)

It turns out that under model conditions, we have $v_c=v_\mathrm{pm}$. This follows since in that case $J=K, G=(0_{q\times p},J_\mathrm{cox})$ and $\nu (s)=(A^{\mathrm{d}}_\mathrm{pm}(s;\theta _0)^{\mathrm{t}},F(s)^{\mathrm{t}})$, such that $\Sigma _{12}(s,t)=\Sigma _{22}(s,t)$. In addition, the ‘cox’ and ‘pm’ quantities in the $v_c$- and $v_\mathrm{pm}$-formulae in (32) and (34) are all identical. Since ${\widehat{v}}_\mathrm{cox}$ and ${\widehat{v}}_c$ are consistent, it further follows under these model conditions that ${\widehat{v}}_\mathrm{cox}- {\widehat{v}}_c \rightarrow _p v_\mathrm{cox}- v_c = v_\mathrm{cox}- v_\mathrm{pm}$. The limit distribution result of $\sqrt{n}({\widehat{b}} - b)$ in (36) then ensures that $Z_n \rightarrow _d \chi _1^2$, with $\chi ^2_1$ a chi-squared distributed variable with one degree of freedom. That is, the probability that the parametric model will be selected when it is indeed true is $\Pr (Z_n \le 2) \rightarrow \Pr (\chi _1^2 \le 2) \approx 0.843$. Thus, if exactly one of the parametric candidate models possesses the property that $b=0$ (and is correct), then that model and estimator will be selected with a probability tending to 84.3%, while the semiparametric Cox model will be selected the remaining 15.7% of the times.

Note that for the AFIC, no such general limit result exists. The reason for this is that the AFIC equivalent of (38) is $Z^*_n = n\int {\widehat{b}}(u)^2\mathrm{d}\omega (u) \le 2\int \{{\widehat{v}}_\mathrm{cox}(u) - {\widehat{v}}_c(u)\}\mathrm{d}\omega (u),$ which depends on the class of focus parameters under consideration, and how they are weighted.

The AFIC is a model selection criterion aimed at estimating all focus parameters $\mu (u)$ well. It may, however, also be viewed as an implied test of the hypothesis that a given parametric model is adequate, in the form of the subhypothesis $\mu _0(u)=\mu _\mathrm{true}(u)$ for each u. That subhypothesis is accepted, perhaps translated to the statement that the parametric model is adequate for the purpose, provided $\mathrm{AFIC}_\mathrm{pm}\le \mathrm{AFIC}_\mathrm{cox}$. If once again ${\widehat{v}}_\mathrm{cox}(u) \ge {\widehat{v}}_\mathrm{pm}(u)$ for every u with increasing cumulative weight $\omega$, or at least $\int {\widehat{v}}_\mathrm{cox}(u)\, \mathrm{d}\omega (u) \ge \int {\widehat{v}}_\mathrm{pm}(u)\, \mathrm{d}\omega (u)$, then the parametric model is accepted provided

$$\begin{aligned} n\int {\widehat{b}}(u)^2\,\mathrm{d}\omega (u)\le & {} \int \{{\widehat{v}}_\mathrm{cox}(u) -{\widehat{v}}_\mathrm{pm}(u) + {\widehat{\kappa }}(u)\}\,\mathrm{d}\omega (u)\\= & {} 2\int \{{\widehat{v}}_\mathrm{cox}(u)-{\widehat{v}}_c(u)\}\,\mathrm{d}\omega (u). \end{aligned}$$

An example could be $\mu (u)=A(u\,|\,x)$ for an interval of u, which leads to a goodness-of-fit test of the form

$$\begin{aligned} n\int \{{\widehat{A}}_{\mathrm{pm}}(u\,|\,x)-{{\widehat{A}}}_\mathrm{cox}(u\,|\,x)\}^2\,\mathrm{d}\omega (u) \le 2\int \{{\widehat{v}}_\mathrm{cox}(u)-{\widehat{v}}_c(u)\}\,\mathrm{d}\omega (u), \end{aligned}$$

see also Hjort (1990). A more elaborate form could average also over different covariate values x. Notably, as with the FIC, such a test comes as a byproduct of the AFIC apparatus, without the need to put up a specific significance level like e.g. 0.05.

5.2 Summary of simulation experiments

To properly validate that the use of the FIC estimates works as intended in practical finite sample situations, we have conducted a small simulation experiment. Using the same survival distribution as in Sect. 3.4, with $d=1.15$ and $20\%$ censoring, we measure the performance of the FIC as MSE estimators by comparing the average FIC scores in repeated samples with the empirical MSE of the resulting ${{\widehat{\mu }}}$. We consider two focus parameters: $\mu _1=S(1\,|\,0.5)$ and $\mu _2=\beta$, with sample sizes $n=100, 300, 600$. As both the accuracy and computational cost increases with n, we repeat the sampling $4.5\cdot 10^8/n^2$ times (i.e. respectively 45000, 5000 and 1250 times), requiring similar computation time for all sample sizes. Table 1 displays the results, indicating that on average the FIC estimates the intended quantities sufficiently well. The variability of the individual FIC scores is indicated through their standard deviation specified in the brackets. As expected, the variability decreases with the sample size, typically also relative to their mean. Note that the truncation of negative squared bias, occurring only for some of the samples, leads to a somewhat misleading increase in the standard deviation, and thereby also the reported variability of the FIC scores. Taking also sensitivity to the precise study setup into account, the results and associated variability measures should be read and interpreted with care.

Table 1 Results from finite sample simulation experiment with FIC using the two focus parameters $\mu _1=S(t=1|x=0.5)$ and $\mu _2=\beta$

6 Application: survival with oropharynx carcinoma

We illustrate the practical use of our criteria by applying them to a real data set with survival with oropharynx carcinoma. These data are discussed and analysed with different models and methods (Aalen and Gjessing (2001); Kalbfleisch and Prentice (2002, p. 378); Claeskens and Hjort (2008, Ch. 3.4)). There are $n=192$ individuals, and we shall restrict ourselves to the following two covariates: $X_1$, the so-called condition (1 for no disability, 2 for restricted work, 3 for requiring assistance with self-care, and 4 for confined to bed), and $X_2$, the T-stage (an index of size and infiltration of tumour, ranging from 1, a small tumour, to 4, a massive invasive tumour). Following the analysis in the above references, we include these variables in the models on the scale in which they were provided.

We compare the semiparametric Cox model with four parametric versions: From the simplest constant hazard model $\alpha _{\mathrm{pm},1}(s;\theta )=\theta$, to

$$\begin{aligned} \alpha _{\mathrm{pm},2}(s;\theta )= & {} \theta _2(\theta _1 s)^{\theta _2-1}\theta _1, \quad \alpha _{\mathrm{pm},3}(s;\theta )=\theta _1\exp (\theta _2 s), \hbox { and} \\ \alpha _{\mathrm{pm},4}(s;\theta )= & {} \theta _1\,\text {gam}(s;\theta _2,\theta _3). \end{aligned}$$

The second and third are the Weibull and Gompertz models for hazard rates, whereas the fourth is a three-parameter model with a multiplicative parameter times the gamma density gam$(s;\theta _2,\theta _3)$. We shall not list all the various parameter estimates here, but note that ${\widehat{\beta }}_\mathrm{cox}=(0.89,0.28)^{\mathrm{t}}$. It is then a question of whether the variability caused by estimating extra $\theta$ parameters from data, combined with a perhaps small modelling bias, makes any of the parametric models better than the semiparametric Cox model. The FIC provides answers to such questions.

6.1 Survival probabilities without covariates

In the spirit of Miller (1983) and Meier et al. (2004) we first look at the data ignoring the covariates. The top panel of Fig. 5 displays the survival probability curve for the four parametric models in addition to the nonparametric Kaplan–Meier estimator, while the bottom panel shows the root of the FIC scores corresponding to each time point. The bottom colour bar indicates which model has the smallest FIC score for each time point. As the figure indicates, each model wins in some time interval, with the parametric gamma density option being deemed the best most of the time. As expected, the Kaplan–Meier estimator does a fairly good job overall, but at most time points there is a better parametric option available.

Fig. 5

Estimates of survival probabilities for a range of time points and corresponding root-FIC scores for each model fitted to the oropharynx carcinoma survival data. The bottom colour bar shows which model is deemed best by the FIC, i.e. has smallest estimated risk (Color figure online)

6.2 Various focus parameters with covariates

We now include the two covariates and compare estimators from the five different models for each of four selected focus parameters: $\mu _1= \beta _1$; $\mu _2= \beta _2$: $\mu _3= S(5\,\text {months}\,|\,x_1)-S(5\,\text {months}\,|\,x_2)$, with $x_1=(1,1)^\mathrm{t}$ and $x_2=(4,4)^\mathrm{t}$; and $\mu _4= \text {median}(T_i^{(0)}\,|\,x=(3,3)^\mathrm{t})$. The $\mu _3$ corresponds to the difference in the survival probability after five months for individuals with respectively the ‘worst’ and ‘mildest’ conditions and T-stage indices, and $\mu _4$ is the median life time for an individual with the second worst condition and T-stage index. Figure 6 shows ‘FIC plots’ for the four different focus parameters, with the root of the FIC score, plotted against the five estimates of the focus parameter in question. Thus, the best models are furthest to the left in each plot. As the figure shows, different estimation tasks are, according to the FIC, best handled by different models and estimators. For instance, the gamma-density model does rather poorly for the three first focus parameters, while it is the winner for the fourth. On the other hand, the overall rather good Cox model, is significantly outperformed by three parametric models for the third focus, and seems to underestimate the survival probability difference.

Fig. 6

‘FIC plots’ for the four focus parameters $\mu _1,\mu _2,\mu _3,\mu _4$ when applied to five competing models for the oropharynx carcinoma survival data

6.3 Cumulative hazard over time

Finally, we turn to an application of the AFIC. We take the set of focus parameters to be the first year survival probabilities for an individual with covariates $X_1=2$ and $X_2=2$, i.e. $S(t\,|\,x=(2,2)^{\mathrm{t}})$ for $t\in (0,1)$. Deeming all probabilities equally important, we use a constant weight function i.e. uses $\omega (u)=u$. Table 2 summarises the AFIC application results, and shows that if one model should be used to estimate the full set of these survival probabilities, one should use the gamma density model, being deemed slightly better than the Cox model. The main reason for the success of the gamma density model here, is the tiny estimated integrated squared bias (represented by its root, $\widehat{\text {bias}}^*$), while achieving a reduced integrated variance (represented by its root $\widehat{\text {sd}}^*$) compared to the Cox model. These results are also in accordance with the visual impression from the top panel of Fig. 5.

Table 2 Results from an AFIC application to the oropharynx carcinoma data with equal weight on all cumulative hazards in the interval (0, 1) conditioned on covariates $X_1=2$ and $X_2=2$

7 Concluding remarks

A. Summary of the price of semiparametric Cox regression. Our efficiency checks in part 1 indicate that there may be drastic gains relying on a parametric model compared to the ‘safer’ choice of the Cox model. We found this behaviour when estimating conditional cumulative hazards, survival probabilities and quantiles, particularly for small and large time points. When estimation interest is solely in $\beta$, there is however not much to gain from parametric modelling, and one may as well rely on semiparametrics to avoid introducing a bias.

B. Covariate selection and time dependent covariates. The methods developed in Section 4 aim at comparing semiparametric with parametric proportional hazards regressions, with all the covariates on board, say $x_1,\ldots ,x_q$. One might wish to complement these FIC methods with those dealing also with all possible subsets of these q regressors. In the application given in Section 6, with five models and $p=2$ covariates, this would amount to an extended machinery with $5\times 2^{p}=20$ candidate models. This can indeed be carried out, but developing all the required limit results, with even more least false parameters and sandwich matrices, has proven beyond the scope of the present paper. The framework could also be generalised by allowing the covariates to be time-dependent. This would further increase the complexities of the variance and covariance formulae, and their estimators.

C. Non-random covariates. In this paper we have derived limit results when the covariates are considered random variables. An alternative, equally common and reasonable framework is to treat the covariate values as fixed. In such a situation, both the semiparametric and parametric estimators remain unchanged, along with the asymptotics for the semiparametrics. For the parametrics, however, the alternative framework gives rise to a different least false parameter, for which the maximum likelihood estimator ${\widehat{\gamma }}$ is aiming at. This new least false parameter $\gamma _{0,n}$ depends on the fixed covariates and is defined as the minimiser of (13), but now with the empirical distribution of the covariates $C_n$, inserted for C. This gives zero-mean Gaussian limits for $\sqrt{n}({\widehat{\gamma }}-\gamma _{0,n})$, which by the reduced randomness has a generally smaller variance. Under model conditions, however, the variances are identical. Thus, the ‘what price’ results and the behavioural results of the FIC formula are all unaffected by such a choice of framework, while the general limit results and the FIC/AFIC formulae in Section 4 would turn out somewhat differently.

D. Local neighbourhood models. As mentioned in the introduction, Hjort and Claeskens (2006) have constructed a somewhat different FIC apparatus, essentially restricted to covariate selection within the Cox model. In addition to their different aim (performing covariate selection, as opposed to considering fully parametric alternatives to the Cox model), their asymptotic machinery is different, involving the mathematics of local neighbourhood models (which we did not need). From our point of view, ‘what price’ questions and appropriate FIC formulae are more generally and naturally answered and derived without relying on a constructed local misspecification framework. See also Jullum and Hjort (2017) for an asymptotic comparison of the two FIC approaches.

E. Bootstrapping. Instead of computing estimated variances and covariances with recipes from the Appendix, we may estimate them by bootstrapping from the ‘biggest’ Cox model, see e.g. Hjort (1985).

F. Model averaging. Rather than relying solely on the model with the best FIC score in the end, one may use e.g. a weighted average ${{\widehat{\mu }}}^*=\sum _M {\widehat{w}}(M){{\widehat{\mu }}}_M$ of all model based estimators ${{\widehat{\mu }}}_M$, as the final estimator. In cases with small differences in the FIC scores, such an estimator would be less sensitive to the exact ranking of the models, and would therefore give a more stable estimator than that based only on the single best ranked model. Within the FIC framework, a natural construction emerges by taking ${\widehat{w}}(M)$ proportional to say $\exp (-\lambda \,\mathrm{FIC}_M)$ and summing to one. Here $\lambda$ is a tuning parameter, indicating the degree of smoothing among the best models, with a large $\lambda$ corresponding to only keeping the winner, whereas $\lambda =0$ means giving equal weight to all candidate models. For further material and discussion of similarly inspired model average estimators, see Hjort and Claeskens (2003) or Claeskens and Hjort (2008, Ch. 7).

Appendices

Appendix

Estimating variances and covariances

For FIC and AFIC applications we need not only the focus parameter estimators ${{\widehat{\mu }}}_\mathrm{cox}$ and ${{\widehat{\mu }}}_\mathrm{pm}$ themselves (yielding also ${\widehat{b}}={{\widehat{\mu }}}_\mathrm{pm}-{{\widehat{\mu }}}_\mathrm{cox}$), but also (consistent) recipes for estimating the quantities $v_\mathrm{cox}$, $v_c$, $v_\mathrm{pm}$, making up the covariance matrix $\Sigma _\mu$ in (31). The main ingredient in $\Sigma _\mu$ is indeed $\Sigma (s,t)$, with blocks as in (27), consisting of the quantities

$$\begin{aligned} \sigma ^2(t), \quad F(t), \quad J_\mathrm{cox}, \quad J, \quad K, \quad \nu (t),\quad \mathrm{and} \quad G. \end{aligned}$$

(39)

In this appendix we provide explicit consistent estimators for these quantities, in addition to a simple consistent estimation strategy for other quantities typically involved in $\Sigma _\mu$.

The principle we essentially follow is to insert the empirical analogues of all unknown quantities. This amounts firstly to estimating $\beta _\mathrm{true}$, $\beta _0$, $\theta _0$, $A_\mathrm{true}(\cdot )$, by respectively ${\widehat{\beta }}_\mathrm{cox}$, ${\widehat{\beta }}_\mathrm{pm}$, $\widehat{\theta }$, ${\widehat{A}}_\mathrm{cox}(\cdot )$. Secondly, $r^{(k)}(s;h(\beta _\mathrm{true},\beta _0))$ is estimated by $n^{-1}R^{(k)}_n(s;h({\widehat{\beta }}_\mathrm{cox},{\widehat{\beta }}_\mathrm{pm}))$ for $k=0,1,2$, and h some simple continuous function combining $\beta$ and $\beta _0$. For f some vector function involving unknown quantities, integrals of the form $\int _0^t f\alpha _\mathrm{true}\,\mathrm{d}s=\int _0^t f\, \mathrm{d}A_\mathrm{true}$ are then estimated by $\int _0^t {\widehat{f}}\,\mathrm{d}{\widehat{A}}_\mathrm{cox}= \sum _{T_i \le t} {\widehat{f}}(T_i)D_i/R^{(0)}_n(T_i;{\widehat{\beta }}_\mathrm{cox})$. Note also that integrals $\int _0^t f(s)r^{(k)}(s;h(\beta _\mathrm{true},\beta _0))\,\mathrm{d}s$ are estimated by $n^{-1}\int _0^t {\widehat{f}}(s) R_n^{(k)}(s;h({\widehat{\beta }}_\mathrm{cox},{\widehat{\beta }}_\mathrm{pm}))\, \mathrm{d}s$, which may be expressed as the sum

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\left\{ \int _0^{\min (T_i,t)}{\widehat{f}}(s)\,\mathrm{d}s\right\} R_{(i)}^{(k)}(h({\widehat{\beta }}_\mathrm{cox},{\widehat{\beta }}_\mathrm{pm})), \end{aligned}$$

(40)

where $R_{(i)}^{(k)}(h(\cdot ))=R_{(i)}^{(k)}(0;h(\cdot ))$ is equal to respectively $\exp \{X_i^{\mathrm{t}}h(\cdot )\},X_i \exp \{X_i^{\mathrm{t}}h(\cdot )\}$, and $X_i X_i^{\mathrm{t}}\exp \{X_i^{\mathrm{t}}h(\cdot )\}$ for $k=0,1,2$. Thus, estimators of the form $\int _0^t f(s)g^{(k)}(s;\beta )\, \mathrm{d}s$ may be expressed by

$$\begin{aligned}&\frac{1}{n}\sum _{T_i \le t} {\widehat{f}}(T_i)D_i\frac{R_n^{(k)}(T_i;{\widehat{\beta }}_\mathrm{cox}+ {\widehat{\beta }})}{R_n^{(0)}(T_i;{\widehat{\beta }}_\mathrm{cox})}\nonumber \\&\quad -\frac{1}{n}\sum _{i=1}^n\left\{ \int _0^{\min (T_i,t)}{\widehat{f}}(s)\alpha _{\mathrm{pm}} (s;\widehat{\theta })\,\mathrm{d}s\right\} R_{(i)}^{(k)}({\widehat{\beta }}_\mathrm{pm}+{\widehat{\beta }}), \end{aligned}$$

(41)

with ${\widehat{\beta }}$ inserted to estimate $\beta$. The f-function is sometimes partly estimated by a step-function, like when f(s) is equal to either $A(s)f_1(s), \sigma ^2(\min (s,t))f_1(s)$ or $F(s)f_1(s)$ for some function $f_1$. In such cases, integrals like $\int _0^{t} f(s)r^{(k)}(s;h(\beta ,\beta _0))\,\mathrm{d}s$ are decomposed even further. To see this, assume $f(s)=f_0(s)f_1(s)$ is estimated by ${\widehat{f}}(s)={\widehat{f}}_0(s){\widehat{f}}_1(s)$ where ${\widehat{f}}_0(s)$ is a step function of the form ${\widehat{f}}_0(s)=\sum _{j=1}^n \text {step}_{j} \mathbf {1}_{\{ T_j \le s \}}=\sum _{j:T_j\le s} \text {step}_j$. Then (40) decomposes further into the ‘triangle sum’

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\sum _{j:T_j< \min (T_i,t)} \text {step}_{j} \left\{ \int _{T_j}^{\min (T_i,t)}{\widehat{f}}_1(s)\,\mathrm{d}s \right\} R_{(i)}^{(k)}(h({\widehat{\beta }}_\mathrm{cox},{\widehat{\beta }}_\mathrm{pm})). \end{aligned}$$

As a consequence, also $\int _0^t f(s)g^{(k)}(s;\beta )\, \mathrm{d}s$ decomposes further, such that the subtrahend in (41) equals

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\sum _{j:T_j< \min (T_i,t)} \text {step}_{j} \left\{ \int _{T_j}^{\min (T_i,t)}{\widehat{f}}_1(s) \alpha _{\mathrm{pm}}(s;\widehat{\theta })\,\mathrm{d}s \right\} R_{(i)}^{(k)}({\widehat{\beta }}_\mathrm{pm}+{\widehat{\beta }}). \end{aligned}$$

Let us now turn to the actual estimation of the quantities in (39).

• [1] First, consider $\sigma ^2(t)$ as given in (9). The estimation strategy outlined above gives the estimator

  $$\begin{aligned} {\widehat{\sigma }}^2(t)=\int _0^t \frac{\mathrm{d}{{\widehat{A}}}_\mathrm{cox}(s)}{ n^{-1}R_n^{(0)}(s;{{\widehat{\beta }}}_\mathrm{cox})} =\sum _{T_i\le t}\frac{nD_i}{ \{R^{(0)}_n(T_i,{{\widehat{\beta }}}_\mathrm{cox})\}^2}. \end{aligned}$$

• [2] Next consider F(t) as given in (9). Writing $E_n(s;\beta )$ for $R_n^{(1)}(s;\beta )/R_n^{(0)}(s;\beta )$, this function is similarly estimated by

  $$\begin{aligned} {\widehat{F}}(t)=\int _0^t E_n(T_i;{\widehat{\beta }}_\mathrm{cox})\,\mathrm{d}{{\widehat{A}}}_\mathrm{cox}(s) =\sum _{T_i\le t} \frac{D_i E_n(T_i;{\widehat{\beta }}_\mathrm{cox})}{R_n^{(0)}(T_i;{\widehat{\beta }}_\mathrm{cox})}. \end{aligned}$$

• [3] Consider now $J_\mathrm{cox}$ as given in (7). Following the plug-in procedure, we get

  $$\begin{aligned} \widehat{J}_\mathrm{cox}=\frac{1}{n} \sum _{T_i \le \tau } \left\{ \frac{R^{(2)}_n(T_i;{\widehat{\beta }}_\mathrm{cox})}{R^{(0)}_n(T_i; {\widehat{\beta }}_\mathrm{cox})} - E_n(T_i;{\widehat{\beta }}_\mathrm{cox})E_n(T_i;{\widehat{\beta }}_\mathrm{cox})^{\mathrm{t}}\right\} D_i. \end{aligned}$$

  Alternatively, $J_\mathrm{cox}$ may be estimated by $n^{-1}$ times minus the Hessian matrix of log-partial likelihood in (4).

• [4] Consider J as given in (14) with blocks as in (16). Following the plug-in procedure, we estimate J by $\widehat{J}$ having blocks

  $$\begin{aligned} \widehat{J}_{11}&= \frac{1}{n}\sum _{i=1}^nR_{(i)}^{(0)}({\widehat{\beta }}_\mathrm{pm}) \int _0^{T_i} \{\psi (s;\widehat{\theta })\psi (s;\widehat{\theta })^{\mathrm{t}} +\psi ^\mathrm{d}(s;\widehat{\theta })\}\alpha _{\mathrm{pm}}(s;\widehat{\theta })\, \mathrm{d}s\\&\quad -\frac{1}{n} \sum _{i=1}^n\psi ^\mathrm{d}(T_i;\widehat{\theta })D_i , \\ \widehat{J}_{12}&= \widehat{J}_{21}^{\mathrm{t}} = \frac{1}{n}\sum _{i=1}^n\int _0^{T_i} \psi (s;\widehat{\theta })\alpha _{\mathrm{pm}}(s;\widehat{\theta }) \, \mathrm{d}s R_{(i)}^{(1)}({\widehat{\beta }}_\mathrm{pm})^{\mathrm{t}}\\&= \frac{1}{n}\sum _{i=1}^nA^{\mathrm{d}}_\mathrm{pm}(T_i;\widehat{\theta })R_{(i)}^{(1)} ({\widehat{\beta }}_\mathrm{pm})^{\mathrm{t}}, \\ \widehat{J}_{22}&= \frac{1}{n}\sum _{i=1}^nR_{(i)}^{(2)} ({\widehat{\beta }}_\mathrm{pm}) \int _0^{T_i} \alpha _{\mathrm{pm}} (s;\widehat{\theta }) \, \mathrm{d}s =\frac{1}{n}\sum _{i=1}^nR_{(i)}^{(2)} ({\widehat{\beta }}_\mathrm{pm}) A_{\mathrm{pm}}(T_i;\widehat{\theta }). \end{aligned}$$

  Similarly to $J_\mathrm{cox}$, J may be estimated by $n^{-1}$ times minus the Hessian of the parametric log-likelihood in (11).

• [5] We continue with K as given in (14). The plug-in procedure applied to the formulae in (17) results in K being estimated by $\widehat{K}$ having blocks

  $$\begin{aligned} \widehat{K}_{11}&= \frac{1}{n}\sum _{i=1}^n\bigg [ \psi (T_i;\widehat{\theta })\psi (T_i;\widehat{\theta })^{\mathrm{t}}\\&\quad - \{A^{\mathrm{d}}_\mathrm{pm}(T_i;\widehat{\theta })\psi (T_i;\widehat{\theta })^{\mathrm{t}} + \psi (T_i;\widehat{\theta })A^{\mathrm{d}}_\mathrm{pm}(T_i;\widehat{\theta })^{\mathrm{t}}\} \frac{R_n^{(0)}(T_i;{\widehat{\beta }}_\mathrm{cox}+{\widehat{\beta }}_\mathrm{pm})}{R_n^{(0)}(T_i;{\widehat{\beta }}_\mathrm{cox})}\bigg ]D_i\\&\quad + \frac{1}{n}\sum _{i=1}^nR_{(i)}^{(0)}(2{\widehat{\beta }}_\mathrm{pm}) \int _0^{T_i} [A^{\mathrm{d}}_\mathrm{pm}(s;\widehat{\theta })\psi (s;\widehat{\theta })^{\mathrm{t}}\\&\quad + \psi (s;\widehat{\theta })A^{\mathrm{d}}_\mathrm{pm}(s;\widehat{\theta })^{\mathrm{t}}] \alpha _{\mathrm{pm}}(s;\widehat{\theta })\, \mathrm{d}s,\\ \widehat{K}_{12}&=\widehat{K}_{21}^{\mathrm{t}}= \frac{1}{n}\sum _{i=1}^n\bigg [\psi (T_i;\widehat{\theta }) E_n(T_i;{\widehat{\beta }}_\mathrm{cox})^{\mathrm{t}}\\&\quad - \{A^{\mathrm{d}}_\mathrm{pm}(T_i;\widehat{\theta })+\psi (T_i;\widehat{\theta }) A_\mathrm{pm}(T_i;\widehat{\theta })\}\frac{R_n^{(1)}(T_i; {\widehat{\beta }}_\mathrm{cox}+{\widehat{\beta }}_\mathrm{pm})^{\mathrm{t}}}{R_n^{(0)} (T_i;{\widehat{\beta }}_\mathrm{cox})} \bigg ]D_i \\&\quad + \frac{1}{n}\sum _{i=1}^n\left[ \int _0^{T_i} \{A^{\mathrm{d}}_\mathrm{pm}(s;\widehat{\theta })+\psi (s; \widehat{\theta })A_\mathrm{pm}(s;\widehat{\theta })\} \alpha _{\mathrm{pm}} (s;\widehat{\theta })\, \mathrm{d}s \right] R_{(i)}^{(1)} (2{\widehat{\beta }}_\mathrm{pm})^{\mathrm{t}}, \\ \widehat{K}_{22}&=\frac{1}{n}\sum _{i=1}^n\frac{R_n^{(2)}(T_i; {\widehat{\beta }}_{\mathrm{cox}})-2R_n^{(2)}(T_i;{\widehat{\beta }}_\mathrm{cox}+{\widehat{\beta }}_\mathrm{pm})A_\mathrm{pm}(T_i;\widehat{\theta })}{R_n^{(0)}(T_i;{\widehat{\beta }}_{\mathrm{cox}})} D_i \\&+ \quad \frac{2}{n} \sum _{i=1}^nR_{(i)}^{(2)}(2{\widehat{\beta }}_\mathrm{pm}) \int _0^{T_i} \alpha _{\mathrm{pm}}(s;\widehat{\theta })A_\mathrm{pm}(s; \widehat{\theta })\, \mathrm{d}s. \end{aligned}$$

• [6] We go on to the covariance $\nu (t)=\mathrm{Cov}(W(t),U^{\mathrm{t}})$ as given in (29). This covariance formula may be estimated by

  $$\begin{aligned} \widehat{\nu }(t)&= \begin{pmatrix} \sum _{T_i \le t} D_i\psi (T_i;\widehat{\theta })/R_n^{(0)} (T_i;{\widehat{\beta }}_\mathrm{cox}) \\ \widehat{F}(t) \end{pmatrix}^{\mathrm{t}}\\&\quad - \frac{1}{n}\sum _{i=1}^n\frac{D_i \widehat{\sigma }^2(\min (T_i,t))}{R_n^{(0)}(T_i;{\widehat{\beta }}_\mathrm{cox})} \begin{pmatrix} R_n^{(0)}(T_i;2{\widehat{\beta }}_\mathrm{cox}) \psi (T_i;\widehat{\theta }) \\ R_n^{(1)}(T_i;2{\widehat{\beta }}_\mathrm{cox}) \end{pmatrix}^{\mathrm{t}} \\&\quad + \sum _{i=1}^n\sum _{j:T_j < \min (T_i,t)} \frac{D_j}{R^{(0)}_n(T_j;{\widehat{\beta }}_\mathrm{cox})^2} \begin{pmatrix} R_{(i)}^{(0)}({\widehat{\beta }}_\mathrm{pm}+{\widehat{\beta }}_\mathrm{cox}) \{A^{\mathrm{d}}_{\mathrm{pm}}(T_i;\widehat{\theta })-A^{\mathrm{d}}_\mathrm{pm}(T_j;\widehat{\theta })\} \\ R_{(i)}^{(1)}({\widehat{\beta }}_\mathrm{pm}+{\widehat{\beta }}_\mathrm{cox}) \{A_\mathrm{pm}(T_i;\widehat{\theta })-A_\mathrm{pm}(T_j;\widehat{\theta })\} \end{pmatrix}^{\mathrm{t}}. \end{aligned}$$

• [7] Finally, we estimate the covariance $G=\mathrm{Cov}(U_\mathrm{cox},U^{\mathrm{t}})$ as given in (28). We use

  $$\begin{aligned} \widehat{G}&= - \frac{1}{n}\sum _{i=1}^n\frac{D_i}{R^{(0)}_n(T_i;{\widehat{\beta }}_\mathrm{cox})} \begin{pmatrix} \psi (T_i;\widehat{\theta })\{{\widehat{A}}_\mathrm{cox}(T_i) R^{(1)}_n(T_i;2{\widehat{\beta }}_\mathrm{cox})^{\mathrm{t}} - R^{(0)}_n(T_i; 2{\widehat{\beta }}_\mathrm{cox})\widehat{F}(T_i)^{\mathrm{t}}\} \\ {\widehat{A}}_ \mathrm{cox}(T_i)R^{(2)}_n(T_i;2{\widehat{\beta }}_\mathrm{cox}) - R^{(1)}_n(T_i; 2{\widehat{\beta }}_\mathrm{cox})\widehat{F}(T_i)^{\mathrm{t}} \end{pmatrix}^{\mathrm{t}} \\&\quad - \frac{1}{n} \sum _{i=1}^n\sum _{j:T_j \le T_i} \frac{D_j E_n(T_j;{\widehat{\beta }}_\mathrm{cox})}{R_n^{(0)}(T_j;{\widehat{\beta }}_\mathrm{cox})} \begin{pmatrix} R^{(0)}_{(i)}({\widehat{\beta }}_\mathrm{cox}+{\widehat{\beta }}_\mathrm{pm}) \{A^{\mathrm{d}}_\mathrm{pm}(T_i;\widehat{\theta }) - A^{\mathrm{d}}_\mathrm{pm}(T_j;\widehat{\theta })\} \\ R^{(1)}_{(i)}({\widehat{\beta }}_\mathrm{cox}+{\widehat{\beta }}_\mathrm{pm}) \{A_\mathrm{pm}(T_i;\widehat{\theta })-A_\mathrm{pm}(T_j;\widehat{\theta })\} \end{pmatrix}^{\mathrm{t}} \\&\quad + \frac{1}{n} \sum _{i=1}^n\sum _{j:T_j \le T_i} \frac{D_j}{R^{(0)}_n(T_j;{\widehat{\beta }}_\mathrm{cox})} \begin{pmatrix} \{A^{\mathrm{d}}_\mathrm{pm}(T_i;\widehat{\theta }) - A^{\mathrm{d}}_\mathrm{pm}(T_j;\widehat{\theta })\} R^{(1)}_{(i)}({\widehat{\beta }}_\mathrm{cox}+{\widehat{\beta }}_\mathrm{pm})^{\mathrm{t}} \\ \{A_\mathrm{pm}(T_i;\widehat{\theta })-A_\mathrm{pm}(T_j;\widehat{\theta })\} R^{(2)}_{(i)}({\widehat{\beta }}_\mathrm{cox}+{\widehat{\beta }}_\mathrm{pm}) \end{pmatrix}^{\mathrm{t}} \\&\quad + \begin{pmatrix} 0_{p \times q} \\ \widehat{J}_{\mathrm{cox}} \end{pmatrix}^{\mathrm{t}}. \end{aligned}$$

Relying strictly on the plug-in principle has the beneficial property that all estimators are consistent. This follows from the continuous mapping theorem since the precise formulae for the quantities in (39) are all seen to be continuous in the quantities and functions (in their appropriate spaces) for which we employ the plug-in principle.

To arrive at consistent estimators for $v_\mathrm{cox}, v_c$ and $v_\mathrm{pm}$ for the classes of focus parameters we have investigated, one typically needs consistent estimators also for the quantities: $m'_\mathrm{pm}, m'_\mathrm{cox}, z'_\mathrm{pm}, z'_\mathrm{cox}$, $\zeta _\mathrm{pm}(\cdot )$, $\zeta _\mathrm{cox}(\cdot ), V_{t,\mathrm{pm}}(\cdot ), V_{t,\mathrm{cox}}(\cdot ),h_\mathrm{pm}(\phi _\mathrm{pm})$ and $h_\mathrm{cox}(\phi _\mathrm{cox})$, as described in Section 4.1. All except the last of these are continuous when viewed as functions of the unknown quantities $\theta _0, \beta _0, \beta _\mathrm{true}$ and $A_\mathrm{true}(\cdot )$. These are therefore estimated consistently by plugging in empirical analogues, like above. The last quantity $h_\mathrm{cox}(\phi _\mathrm{cox})=\alpha _\mathrm{true}(\phi _\mathrm{cox})\exp (x^{\mathrm{t}}\beta _\mathrm{true})$, with $\phi _\mathrm{cox}=A^{-1}_\mathrm{true}(-\log (1-u)/\exp (x^{\mathrm{t}}\beta _\mathrm{true}))$ involved in estimation of a quantile (see Sect. 3 in the supplementary material (Jullum and Hjort, this work)), is more delicate as we need the estimator to be smooth or at least nonzero. The troublesome part is estimation of $\alpha _\mathrm{true}$ at the unknown position $\phi _\mathrm{cox}$. This position is estimated by ${\widehat{\phi }}_\mathrm{cox}={\widehat{A}}^{-1}_\mathrm{cox}(-\log (1-u)/\exp (x^{\mathrm{t}}{\widehat{\beta }}_\mathrm{cox}))$, while a smooth estimate of $\alpha _\mathrm{true}$ is obtained e.g. via a kernel estimator ${\widehat{\alpha }}_\mathrm{cox}(t) = \int h^{-1} K^\circ ((t-s)/h) \, \mathrm{d}{\widehat{A}}_\mathrm{cox}(s)$ for some suitable kernel $K^\circ$ and bandwidth $h=h_n$, which then is evaluated in ${\widehat{\phi }}_\mathrm{cox}$. As long as the bandwidth has the property that $h_n \rightarrow 0$, $n h_n \rightarrow \infty$, and $\alpha _\mathrm{true}$ is positive and two times differentiable in a neighborhood of $\phi _\mathrm{cox}$, this strategy also yields a consistent estimator. Thus, replacing the quantities in the various forms of $v_\mathrm{cox}$, $v_c$, $v_\mathrm{pm}$ towards the end of Section 4.1, by the estimators presented in this appendix, yields consistent estimators ${\widehat{v}}_\mathrm{cox}$, ${\widehat{v}}_c$, ${\widehat{v}}_\mathrm{pm}$.