Significance of entropy generation and heat source: the case of peristaltic blood flow through a ciliated tube conveying Cu-Ag nanoparticles using Phan-Thien-Tanner model

Abstract

The present speculative investigation is concentrated to analyze the entropy generation and heat transfer phenomena in ciliary induced peristalsis of blood with the suspension of hybrid nanoparticles in a tube with heat source impact. The blood is assumed to contain copper (Cu) and silver (Ag) nanoparticles (NPs). The ciliary inner wall of the tube has been considered with small hair-like structures. The Phan-Thien-Tanner (PTT) fluid model is employed to describe the non-Newtonian rheological characteristics of blood. The conservative equations are normalized and simplified by utilizing scaling analysis with the assumption of low Reynolds number and large wavelength approximations. The analytical inspection exposes that the total entropy generation gets a decrement for mounting values of cilia length, while reversed impact is detected for an increment in heat source parameter. Hybrid nano-blood exhibits a greater total entropy number than mono nano-blood. This research study may be beneficial to medical experts and researchers in the field of embryology. Cysts in the ciliated fallopian tube, where embryos develop, are removed by using nanoparticles (nano-drug delivery).

1 Introduction

In the 21st century, the phenomenon of peristalsis has become very exigent in the study of physiological transport mechanisms and biomedical industries. This mechanism appears mainly in living organs and organisms. In the peristaltic transport mechanism, physiological fluids are driven through confined tubes/channels/ducts by rhythmic continuous contraction/expansion of the adjacent materials. This mechanical process has an imperative role in medical, physiological, industrial, and engineering processes, for example, cilia movement, food bolus movement in stomach, blood circulation via arteries/ vessels, urine transport through ureters, chyme movement in gastrointestinal tract, sperm transport from male reproductive tract, motion of ovum in fallopian tube, liver, small intestine, and earthworm locomotion, etc. The peristaltic flow principle is adapted in many biomedical devices, for example, blood pump machine, heart-lung machine, ventilator machine, dialysis machine, insulin delivery, roller and finger pumps, stethoscope, glucose-sensing, etc. (Husband et al. 2004; Tamada et al. 2002). Latham (1966) first time reported the mechanism of peristalsis. After his pioneer study, the transport phenomena via peristalsis have been massively researched by numerous scholars under various physiological and geometrical aspects. Vajravelu et al. (2007) highlighted the thermal feature of peristaltic transport of viscous fluid through a tube via long-wave assumption. Akbar and Nadeem (2012) presented the simulation of non-Newtonian nanofluid in a diverging tube due to peristalsis. A mathematical model for the peristaltic transportation of blood containing nanoparticles through an artery with deformable wall was elucidated by Abdelsalam and Vafai (2017). Some other relevant examinations in this domain are provided in Refs. (Reddy and Makinde 2016; Makinde et al. 2017; Reddy et al. 2017; Mehmood et al. 2020; Vaidya et al. 2021a, b; Rajashekhar et al. 2021).

In the current era, bionanotechnology has radically changed the biomedical and engineering sciences. Cooling issues and product quality control in the shortest amount of time are two major challenges confronting manufacturing industries as heat production continues to rise. In order to save energy and reduce process time, scientists have come to appreciate the distinct nature and thermal properties of some fluids formed by incorporating micrometer or millimeter sized solid particles (Song et al. 2021). Recently, various novel nanomaterials were successfully developed by scientific community to utilize in biomedical, biomechanics, and bioengineering processes. Nanoparticles are metallic or non-metallic tiny-sized particles (10-100 nm) with augmented thermo-physical characteristics. Nanofluid (NF) was invented by Choi (1995) and found that the thermal characteristics of the working host fluid can be enhanced by the impulsion of nanoparticles into it. Due to vast applications of nanofluids in electrical, electronics, medical and modern sciences, many researchers (Das et al. 2020; Abo-Dahab et al. 2021; Ali et al. 2021) have extensively investigated the nanofluid flow with various aspects. In the biomedical domain, nanofluids are being massively administrated in pharmaceutical processes, wound treatment, resonance imaging, vivo therapy, surgeries, cancer tumor remedy, and nano cryosurgery, etc. Among various nanoparticles, copper (Cu) and silver (Ag) nanoparticles seem to have attracted the fewest interests in terms of their potential applications. Copper is a key component and a catalyst for many enzymes and proteins in the human body, so it can control human health via multiple mechanisms. Based on the biological functions, copper nanoparticles show unique properties in protecting the cardiovascular system, promoting bone fracture healing and antibacterial effects, Positron Emission Tomography (PET) imaging, promoting cure, killing cancer cells, and radio-immunological tracing and cancer radiotherapy (Wang et al. 2021). On another side, Ag-nanoparticles have ensured a rapid adoption in medical practice due to their unique physicochemical properties. Silver nanoparticles play an important role in the inhibiting/killing of numerous pathogenic-microorganisms (antimicrobial), biosensors, anti-diabetic agents, anticancer therapy, vaccine adjuvant, promoting of wound repair and bone healing (Hayat et al. 2017; Xu et al. 2020).

Hybrid nanofluids (HNFs) are an advanced generation of nanofluids that convey dissimilar nanomaterials in a host base fluid (Sarkar et al. 2015). These types of nanofluids have higher proficiency to augment thermo-physical properties as contrast to mono nanofluids. This new emergent class of nanofluids has enormous applications in all fields of sciences. In hemodynamics, blood is taken as the host liquid and can be treated as a suspension of hybrid nanoparticles. Various theoretical and experimental examinations available in literature explored that the incredible enhancement in the thermo-physical properties by using hybrid nanofluids. Ijaz and Nadeem (2018) illustrated the transport of blood with the concentration of hybrid nanoparticles through a stenosed artery. Ijaz et al. (2018) developed a mathematical model for hybrid Cu-CuO nano-blood flow through an artery having stenosis. Sadaf et al. (2019) exposed the upshots of hybrid nanoparticles suspension in blood during the peristaltic pumping through an endoscope with wall properties. Their observation disclosed that the temperature in the blood flow is sharply dropped owing to the dispersion of hybrid nanoparticles in the blood. It is asserted in Sowmya et al. (2021) that increasing NPs volume fraction has a substantial impact on the thermal profile and streamlined of stagnant fluid flow. Significance of NPs volume fraction in nanofluid (Al$_2$O$_3$-water) flow over a uniformly thickened surface with heat source/sink, and Coriolis force has been presented by Oke et al. (2021). Their outcomes show that an increment in NPs volume fraction explores boosting behavior for local Nusselt number. Moreover, the adding of Al$_2$O$_3$ NPs can help to detect enhancements in hardness, strength and tensile strength of the Mg-matrix. Elnaqeeb et al. (2021) examined the insight into the flow dynamics of water-based nanofluids with three different nanoparticles of smaller and substantial large densities. They concluded that greater Nusselt numbers relative to heat transfer were detected in the case of water mixed with heavy densities nanomaterials (i.e., copper, copper oxide, and silver) at all expanding ratios and suction rates. In a research, Koriko et al. (2021) discovered that an increasing trend in buoyancy is reliable for increasing the velocity profiles for both fluids (Au-blood Carreau nanofluid and dusty fluid). Several significant studies on peristalsis dynamics of hybrid nanofluids are communicated in Refs. (Abdelsalam et al. 2020; Saleem et al. 2020; Ellahi et al. 2020; Shahzadi et al. 2020).

Rheological characteristics of the viscoelastic fluids like some condensed solute-solvent polymeric solutions and polymeric melts can be correctly predicted by the Phan-Thien-Tanner (PTT) model (Phan-Thien and Tanner 1977, 1978). Oliveira and Pinho (1999) analytically studied the viscoelastic fluids flow through channel/pipe via PPT fluid model and reported that the PPT model accomplishes lower shear stress compared to the upper-convective Maxwell (UCM) fluid/Newtonian fluid. In polymer processing industries, thermofluid characteristics of melted polymer flow in channel/pipes at high temperature are very important for efficient polymer processing equipment. Recently, the peristalsis flow of a Phan-Thien-Tanner fluid model has attracted the consciousness of researchers. El Naby (2009) examined the creeping PTT fluid flow through a peristaltic tube. Peristalsis flow of a PTT fluid inside a divergent tube has been explored by Akbar and Nadeem (2012). Some peristaltic flow models of PTT fluids through various flow regimes like a tube, channel, diverging/asymmetric tube/channel are reported in references (Hayat et al. 2012; Vajravelu et al. 2016, 2016).

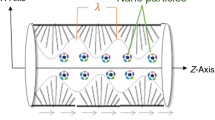
Cilia-induced flow is significant in the locomotion of the cells themselves or other substances past the cell surface. Cilia can be explained as very tiny hair-resembling structures that transpire throughout the surface of eukaryotic cells and biological vessels. They behave like oars, whipping back and forth in unison to generate a wave pattern traveling along the surface, such wave is called metachronal wave. Moving cilia in the respiratory tract (Bustamante-Marin and Ostrowski 2017; Knowles and Boucher 2002) is accountable for assisting fluid flow on the cell surface by their beating movement to remove mucus and dust to clean off airways. In the digesting tract Pablo et al. (2016), cilia assists food and its egestation movement. Ciliated female fallopian tubes (Ghazal et al. 2014; Eddy and Pauerstein 1980) carry the egg and sperm through the oviducts. Cilia blends sperms in male efferent ductules (Lehti and Sironen 2017) to prevent them from aggregating and blockading the tube so they can transfer to their final destination. They are also observed in kidneys, ears, eye retina, and brain. Cilia finds its diverse applications in biomedicine, bioengineering, and physiological disciplines (Mills et al. 2012; Drummond 2012; Agrawal and Anawaruddin, 1984). Cilia plays as a sensory-antenna in our kidneys. They perceive signals from the nearby urine and transmit a response to alert the cells about the flow of it. Qiu et al. (2014) presented an interesting observation dealing with the movement of micro-organisms in non-Newtonian fluid induced by cilia and flagella. The mobility of cells in a viscous fluid induced by harmonic waves was investigated by Brennen (1974). Wu et al. (2020) studied the transportation of Carreau fluid due to ciliary motion. Farooq and Siddiqui (2017) performed a study on cilia-induced flow of a couple-stress fluid. Farooq et al. (2019) illustrated the peristaltic pumping of a micropolar fluid due to cilia beating through a tube.

In physiological structures, spontaneous chemical reactions take place by a drop in free-energy. In living organisms, for example, metabolism involving various chemical reactions generates free-energy and is associated with significant production of entropy. Anti-entropic functions such as dynamical flow of substances (sweat, urination, sperms, and blood flow, etc.), muscle contractions, and biosynthesis are usually considered as compensating for entropy in physiological systems. In recent years, the assessment of entropy generation (EG) during the flow of physiological fluids is of main concerned and challenging research field (Makinde 2012; Adesanya and Makinde 2015; Chamkha and Selimefendigil 2018; Butt et al. 2013) due to its crucial role in physiology, medicine, bioengineering, and biomechanics. Motivated by the pioneer work of Bejan (Bejan 1979, 1982) in this domain, many researchers (Marzougui et al. 2021; Fares et al. 2021) have examined the entropy generation under various aspects. Souidi et al. (2009) assessed the entropy generation rate in the peristaltic flow of biological fluid. This work was elaborated by Akbar (2015) under the magnetic impact. Saleem (2018) and Munawar et al. (2016) have enquired about the entropy rate in peristaltic flow through symmetric/asymmetric channels with variable viscosity property. Later on, they (Saleem and Munawar 2020) researched entropy analysis in the ciliary flow of biomagnetic fluids. Abrar et al. (2020) analyzed the entropy generation in the flow of magneto-nanofluid through a ciliated tube with Joule heating. They concluded that the entropy production enhances due to larger concentration of nanoparticles. Recently, an analysis of entropy generation in cilia-induced peristaltic flow in the microchannel under the impact of magnetic field was elucidated by Munawar and Saleem (2020).

It is identified that no study is found in the literature, where the entropy generation and heat transport analysis in ciliary induced peristaltic motion of blood with non-Newtonian fluid model through a tube is deliberated under the concentration of hybrid nanoparticles. In view of this, our intention here to assess the entropy generation in the peristaltic transport of hybrid nano-blood (Cu-Ag/blood) with Phan-Thien-Tanner fluid model due to the metachronal beating of cilia through a tube. The constitutive equations are formulated in a cylindrical coordinate system and simplified by employing lubrication approximations. Exact solutions are achieved for the non-dimensional transformed equations. Numerical integration scheme is deployed to compute the pressure-rise per metachronal wavelength (MW) and frictional forces (FR) at the ciliated tube by using Mathematica built-in program. The physical impacts of various evolving parameters on the velocity profile, temperature profile, pressure gradient, pressure rise, heat transfer coefficient, streamlines, total entropy generation number, and Bejan number are illustrated graphically and interpreted in all physical aspects in the results and discussion section. The novelty of our current work is to explore a comprehensive insight into the peristaltic transport and thermal phenomena of non-Newtonian blood with the suspension of hybrid nanoparticles through a tube owing to metachronal wave-propulsion of the beating cilia. This examination will be more exposed by placing the following research questions:

• What is the role of entropy generation (EG) in hybrid nano-blood flow through ciliary tube?

• How heat source modify the entropy generation (EG) and temperature variation?

• What are the potential strategies for improving the thermal characteristics of a conventional fluid?

• What are the main drawbacks of mono nanofluids as a contrast to hybrid nanofluids?

• How the blood motion due to cilia beating is altered by the volumetric concentration of hybrid nanoparticles?

2 Mathematical formulation

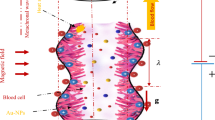
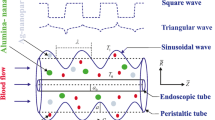
Consider the two-dimensional laminar incompressible flow of a non-Newtonian hybrid nano-blood with Phan-Thien-Tanner (PTT) fluid model in a ciliated tube of length L. The flow is induced by the cilia beating. Blood is simulated as a homogeneous suspension with dispersed dissimilar (hybrid) nanoparticles (Cu-Ag NPs). A cylindrical coordinate system $(\tilde{R},\tilde{\theta },\tilde{Z})$ is considered to formulate the modeled problem, where $\tilde{R}$ is radial coordinate, $\tilde{\theta }$ the azimuthal coordinate, and $\tilde{Z}$ the axial coordinate. There is no flow in the azimuthal ($\tilde{\theta }$) direction due to the assumption of an axisymmetric blood flow in the ciliated tube. The wall of the ciliated tube is sustained with the uniform temperature $T_0$. Phan-Thien-Tanner (PTT) fluid model is engaged to mimic the non-Newtonian characteristics of blood. The constitutive relation for PTT fluid is given by (Phan-Thien and Tanner 1977, 1978):

$$\begin{aligned} \tilde{f}(tr(\tilde{\tau })){\tilde{\tau }}+\Lambda \tilde{ \tau }^\Delta= & {} \mu _{hnf} (\nabla \mathbf{V}+(\nabla \mathbf{V})^T), \end{aligned}$$

(1)

where

$$\begin{aligned} \tilde{\tau }^\Delta= & {} \frac{\partial \tilde{ \tau }}{\partial t}+\mathbf{V}\cdot \nabla \tilde{\tau }-\tilde{ \tau }\cdot \nabla \mathbf{V} -(\nabla \mathbf{V})^T\cdot \tilde{\tau }, \end{aligned}$$

(2)

$$\begin{aligned} \tilde{f}(tr(\tilde{\tau }))= & {} 1+\frac{\varepsilon \Lambda }{\mu _{hnf}}tr(\tilde{\tau }), \end{aligned}$$

(3)

in which $\varepsilon$ is a free parameter related to the extensional properties of the fluid, $\Lambda$ the relaxation time, $\mu _{hnf}$ a constant viscosity coefficient, $\tilde{\tau }$ the extra stress tensor and $\tilde{\tau }^\Delta$ Oldroyd’s upper convected derivative (Akbar and Nadeem 2012). The extensional parameter $\varepsilon$ has a consequence on the shear properties as well as it imparts shear-thinning to the fluid provided that its value is not too small. The envelopes of the cilia tips can be expressed mathematically as (Blake 1971, 1972):

$$\tilde{R}= \tilde{H} =\tilde{F}(\tilde{Z},\tilde{t})=\tilde{a}+\delta \tilde{a} \cos \left(\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t})\right),$$

(4)

$$\tilde{Z}= \tilde{G}(\tilde{Z},\tilde{Z}_0,\tilde{t})=\tilde{a}+\delta \tilde{a} \alpha \sin \left(\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t})\right),$$

(5)

where $\tilde{a}$ designates the mean radius of the ciliated tube, $\delta$ the non-dimensional measure of the cilia length, $\lambda$ the metachronal wavelength, c metachronal wave speed, $\tilde{Z}_0$ the reference particle position, and $\alpha$ the eccentricity due to elliptical movement. Physically, large number of cilia merge and exhibit a beating pattern on the inner wall of the tube. This beating pattern generates a continuous chain of waves that acts like a peristaltic or sinusoidal wave at the wall of the tube. Eqs. (4–5) represent the geometry of cilia movement in the form of elliptical shape.

The velocity components of the blood flow induced by the cilia tips can be mathematically expressed as (Blake 1971, 1972) Fig. 1:

$$\begin{aligned} \tilde{W}= \left( \frac{\partial \tilde{Z}}{\partial \tilde{t}}\right) _{\tilde{Z}_0}=\frac{\partial \tilde{G}}{\partial \tilde{t}}+\frac{\partial \tilde{G}}{\partial \tilde{Z}}\frac{\partial \tilde{Z}}{\partial \tilde{t}}=\frac{\partial \tilde{G}}{\partial \tilde{t}}+\frac{\partial \tilde{G}}{\partial \tilde{Z}}\tilde{W} \end{aligned}$$

(6)

$$\begin{aligned} \tilde{U}= \left( \frac{\partial \tilde{R}}{\partial \tilde{t}}\right) _{\tilde{Z}_0}=\frac{\partial \tilde{F}}{\partial \tilde{t}}+\frac{\partial \tilde{F}}{\partial \tilde{Z}}\frac{\partial \tilde{Z}}{\partial \tilde{t}}=\frac{\partial \tilde{F}}{\partial \tilde{t}}+\frac{\partial \tilde{F}}{\partial \tilde{Z}}\tilde{W} \end{aligned}$$

(7)

In view of Eqs. (4–5), Eqs. (6–7) are rewritten as:

$$\begin{aligned} \tilde{W}= -\frac{\frac{2\pi }{\lambda }\delta \alpha \tilde{a} c \cos \left(\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t})\right)}{1-\frac{2\pi }{\lambda }\delta \alpha \tilde{a} \cos \left(\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t})\right)} \end{aligned}$$

(8)

$$\begin{aligned} \tilde{U}= \frac{\frac{2\pi }{\lambda }\delta \alpha \tilde{a} c \sin \left(\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t})\right)}{1-\frac{2\pi }{\lambda }\delta \alpha \tilde{a} \cos \left(\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t})\right)} \end{aligned}$$

(9)

Fig. 1

Physical model of the problem

The governing equations in the fixed frame (laboratory frame) for an incompressible viscoelastic PTT hybrid nano-blood flow are given by (Akbar and Nadeem 2012; Butt et al. 2020):

$$\begin{aligned} \frac{\partial \tilde{U}}{\partial \tilde{R}}+\frac{\tilde{U}}{\tilde{R}}+\frac{\partial \tilde{W}}{\partial \tilde{Z}}=0, \end{aligned}$$

(10)

$$\begin{aligned} \rho _{hnf}\left(\frac{\partial \tilde{U}}{\partial \tilde{t}}+\tilde{U}\frac{\partial \tilde{U}}{\partial \tilde{R}}+\tilde{W}\frac{\partial \tilde{U}}{\partial \tilde{Z}}\right)= -\frac{\partial \tilde{P}}{\partial \tilde{R}}-\frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}(\tilde{R}\tilde{\tau }_{\tilde{R}\tilde{R}})-\frac{\partial }{\partial \tilde{Z}}(\tilde{\tau }_{\tilde{R}\tilde{Z}})-\frac{\tilde{\tau }_{\tilde{\theta }\tilde{\theta }}}{\tilde{R}}, \end{aligned}$$

(11)

$$\begin{aligned} \rho _{hnf}\left(\frac{\partial \tilde{W}}{\partial \tilde{t}}+\tilde{U}\frac{\partial \tilde{W}}{\partial \tilde{R}}+\tilde{W}\frac{\partial \tilde{W}}{\partial \tilde{Z}}\right)= -\frac{\partial \tilde{P}}{\partial \tilde{Z}}+\frac{1}{\tilde{R}}\frac{\partial }{\partial \tilde{R}}(\tilde{R}\tilde{\tau }_{\tilde{R}\tilde{Z}})+\frac{\partial }{\partial \tilde{Z}}(\tilde{\tau }_{\tilde{Z}\tilde{Z}}), \end{aligned}$$

(12)

$$\begin{aligned} (\rho c_p)_{hnf}\left(\frac{\partial \tilde{T}}{\partial \tilde{t}}+\tilde{U}\frac{\partial \tilde{T}}{\partial \tilde{R}}+\tilde{W}\frac{\partial \tilde{T}}{\partial \tilde{Z}}\right)&= \tilde{\tau }_{\tilde{R}\tilde{R}}\frac{\partial \tilde{U}}{\partial \tilde{R}}+\tilde{\tau }_{\tilde{R}\tilde{Z}}\frac{\partial \tilde{W}}{\partial \tilde{R}}+\tilde{\tau }_{\tilde{Z}\tilde{R}}\frac{\partial \tilde{U}}{\partial \tilde{Z}}+\tilde{\tau }_{\tilde{Z}\tilde{Z}}\frac{\partial \tilde{W}}{\partial \tilde{Z}}\\ &\quad+ k_{hnf}\left(\frac{\partial ^2 \tilde{T}}{\partial \tilde{R}^2}+\frac{1}{\tilde{R}}\frac{\partial \tilde{T}}{\partial \tilde{R}}+\frac{\partial ^2 \tilde{T}}{\partial \tilde{Z}^2}\right)+Q_0, \end{aligned}$$

(13)

where $\tilde{P}$ is the pressure, $\tilde{U}$, $\tilde{W}$ the respective velocity components in the radial $\tilde{R}$ and axial $\tilde{Z}$ directions in the fixed frame, $\tilde{T}$ the temperature, $k_{hnf}$ the thermal conductivity of hybrid nanofluid, $\rho _{hnf}$ the density of hybrid nanofluid, $(c_p)_{hnf}$ the specific heat of hybrid nanofluid at constant pressure, and $Q_0$ the internal heat source coefficient.

In the fixed (laboratory) frame, the suitable boundary conditions for the flow configuration are proposed as (Hanasoge et al. 2017):

$$\begin{aligned}&\frac{\partial \tilde{W}}{\partial \tilde{R}}=0,\,\frac{\partial \tilde{T}}{\partial \tilde{R}}=0,\; \mathrm{at} \;\tilde{R}=0,\nonumber \\&\tilde{W}=-\frac{\frac{2\pi }{\lambda }\delta \alpha \tilde{a} c \cos (\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t}))}{1-\frac{2\pi }{\lambda }\delta \alpha \tilde{a} \cos (\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t}))},\,\tilde{T}=\tilde{T}_0\; \mathrm{at} \;\tilde{R}=\tilde{H}=\tilde{a}+\delta \tilde{a} \cos (\frac{2\pi }{\lambda }(\tilde{Z}-c\tilde{t})). \end{aligned}$$

(14)

In the fixed frame $(\tilde{R},\tilde{Z})$, the flow problem is unsteady. To convert the unsteady state in the fixed frame into the steady state in the wave frame $(\tilde{r},\tilde{z})$, moving with the same vave speed c, the following linear transformations are introduced as (Akbar and Nadeem 2012; Butt et al. 2020):

$$\begin{aligned}&\tilde{r}=\tilde{R},\, \tilde{z}=\tilde{Z}-c\tilde{t},\, \tilde{u}=\tilde{U},\, \tilde{w}=\tilde{W}-c,\, \tilde{h}(\tilde{z},\tilde{t})=\tilde{H}(\tilde{Z},\tilde{t}),\, \tilde{p}(\tilde{z},\tilde{r},\tilde{t})=\tilde{P}(\tilde{Z},\tilde{R},\tilde{t}),\nonumber \\&\tilde{T}(\tilde{z},\tilde{r},\tilde{t})=\tilde{T}(\tilde{Z},\tilde{R},\tilde{t}), \end{aligned}$$

(15)

We introduce non-dimensional variable:

$$\begin{aligned}&r=\frac{\tilde{r}}{\tilde{a}},\,z=\frac{\tilde{z}}{ \lambda },\,w=\frac{\tilde{w}}{c},\,u=\frac{\lambda \tilde{u}}{\tilde{a} c},\,p=\frac{\tilde{a}^2\tilde{p}}{c\lambda \mu _{f}},\,\theta =\frac{\tilde{T}-\tilde{T}_0}{\tilde{T}_0},\,t=\frac{c\tilde{t}}{\lambda },\,\beta =\frac{\tilde{a}}{\lambda },\,\nonumber \\&Re=\frac{c\tilde{a}\rho _f}{\mu _f},\,Br=\frac{c^2\mu _f}{(c_p)_f \tilde{T}_0},\,\tau _{ij}=\frac{\tilde{a}\tilde{\tau }_{ij}}{c\mu _f},\,We=\frac{\Lambda c}{\tilde{a}},\,h=\frac{\tilde{h}}{\tilde{a}},\, \gamma =\frac{Q_0\tilde{a}^2}{k_f\tilde{T}_0}, \end{aligned}$$

(16)

where Re is the Reynolds number which signifies the ratio of the inertial force to the viscous force, Br is the Brinkman number that is related to the heat transfer phenomena of the flow field, We is the Weissenberg number representing the ratio of relaxation time to the radius of the tube, and $\gamma$ is the internal heat source parameter.

In pursuance of Eqs. (1–3) and Eqs. (15–16), Eqs. (10–13) related to the blood flow model under the assumption of long wavelength can be put in the non-dimensional form as (Akbar and Nadeem 2012; Butt et al. 2020):

$$\begin{aligned}&\frac{\partial p}{\partial r}= 0, \end{aligned}$$

(17)

$$\begin{aligned}&\frac{\partial p}{\partial z}= \frac{1}{r}\frac{\partial }{\partial r}(r\tau _{rz}), \end{aligned}$$

(18)

$$\begin{aligned}&\frac{x_4}{r}\frac{\partial }{\partial r}\left(r\frac{\partial \theta }{\partial r}\right)+x_2 Br \frac{\partial w}{\partial r} \tau _{rz}+\gamma = 0, \end{aligned}$$

(19)

$$\begin{aligned}&f\tau _{zz}=2\, We\tau _{rz}\frac{\partial w}{\partial r}, \end{aligned}$$

(20)

$$\begin{aligned}&f\tau _{rz}=\frac{\partial w}{\partial r}+ We\tau _{rr}\frac{\partial u}{\partial r}, \end{aligned}$$

(21)

$$\begin{aligned}&f=1+\varepsilon We (\tau _{rr}+\tau _{\theta \theta }+\tau _{zz}), \end{aligned}$$

(22)

The dimensionless form of the physical boundary conditions become (Hanasoge et al. 2017):

$$\begin{aligned}&\frac{\partial w}{\partial r}=0,\,\frac{\partial \theta }{\partial r}=0,\; \mathrm{at} \;r=0,\nonumber \\&w=-1-\frac{2\pi \delta \alpha \beta \cos (2\pi z)}{1-2\pi \delta \alpha \beta \cos (2\pi z)},\,\theta =0\; \mathrm{at} \;r=h(z)=1+\delta \cos (2\pi z), \end{aligned}$$

(23)

where $\beta$ is the wave number.

The integration of the longitudinal momentum Eq.(18) subject to the boundary conditions $\tau _{rz}=0$ at the symmetry line $r = 0$ yields:

$$\begin{aligned} \tau _{rz}= & {} \frac{r}{2}\frac{d p}{d z}, \end{aligned}$$

(24)

By neglecting the wave number $\beta$, we get $\tau _{\theta \theta }=0$, and $\tau _{rr}=0$, and thus trace of stress tensor becomes $\tau _{rz}$. Eqs. (20) and (21) together imply:

$$\begin{aligned} \tau _{zz}= & {} 2 \,We\,\tau _{rz}^2, \end{aligned}$$

(25)

Inserting Eqs. (22) and (25) in Eq. (21), one has

$$\begin{aligned} \frac{\partial w}{\partial r}= & {} \tau _{rz}+2\varepsilon We^2 \tau _{rz}^3, \end{aligned}$$

(26)

Substituting Eq. (24) into Eq. (26), the velocity gradient takes the form:

$$\begin{aligned} \frac{\partial w}{\partial r}= & {} \frac{r}{2}\frac{d p}{d z}+2\varepsilon We^2 \left( \frac{r}{2}\frac{d p}{d z}\right) ^3, \end{aligned}$$

(27)

The type I and type II models for the thermo-physical properties suitable for studying the dynamics of hybrid nano-blood are given in Table 1.

Table 1 Models of nano-blood (Type I) and hybrid nano-blood (Type II) (Xu and Sun 2019; Shah et al. 2020)

where $\phi _1$ and $\phi _2$ designate the solid volume fractions of copper and silver nanoparticles, respectively. The suffices $s_1$, $s_2$, f, nf, hnf denote solid nanoparticles of copper (Cu), solid nanoparticles of silver (Ag), base fluid (blood), nano-blood, and hybrid nano-blood, respectively. The case $\phi _1=\phi _2 =0$ (without suspension of nanoparticles) corresponds to the pure-blood. Moreover, in the present study, it is assumed that the nanoparticles are in thermal equilibrium and no-slip occurs between them. The thermo-physical properties are given in Table 2.

Table 2 Thermo-physical properties of blood, copper nanoparticles (Cu), and silver nanoparticles (Ag)Saleem et al. (2020)

3 Exact solution

On integrating Eq.(27) and employing the boundary conditions (23), the exact solution for the velocity field is obtained as follows:

$$\begin{aligned} w(r,z)= & {} \frac{1}{16} We^2 \varepsilon \left( \frac{dp}{dz}\right) ^3 \left( r^4-h^4\right) +\frac{1}{4} \left( \frac{dp}{dz}\right) (r^2-h^2)-1-\frac{2\pi \delta \alpha \beta \cos (2\pi z)}{1-2\pi \delta \alpha \beta \cos (2\pi z)}, \end{aligned}$$

(28)

After using Eq.(28) in Eq.(19), and solving, we achieve the temperature distribution of the blood flow as:

$$\begin{aligned} \theta (r,z)= & {} \frac{1}{576\, x_4}\left[ 2\,\varepsilon \, x_2\, Br\, We^2 \left( \frac{dp}{dz}\right) ^4 \left( h^6-r^6\right) +9\, x_2 \,Br \, \left( \frac{dp}{dz}\right) ^2 \left( h^4-r^4\right) \right. \nonumber \\+ & {} \left. 144\, \gamma \, (h^2-r^2)\right] , \end{aligned}$$

(29)

3.1 Flow rate, stream function, and heat transfer

The volume flow rate Q can be calculated as

$$\begin{aligned} Q= & {} 2\int _{0}^{h}r\,w(z,r) dr, \end{aligned}$$

(30)

which gives the expression for the pressure gradient as

$$\begin{aligned} \frac{dp}{dz}=\frac{A}{h^6 We^2 \varepsilon }-\frac{h^4}{A}, \end{aligned}$$

(31)

where

$$\begin{aligned} A= & {} \left( 12 h^{12} We^4 \varepsilon ^2 B+\sqrt{h^{24} We^6 \varepsilon ^3 \left( h^6+144 We^2 \varepsilon B^2\right) }\right) ^{1/3},\; B=\left( h^2 X-Q\right) ,\nonumber \\X= & {} -\frac{2 \pi \alpha \beta \delta \cos (2 \pi z)}{1-2 \pi \alpha \beta \delta \cos (2 \pi z)}-1, \end{aligned}$$

(32)

The mean volume flow rate over one period of the peristaltic wave is defined as

$$\begin{aligned} F= & {} Q + \frac{1}{2} \left( \frac{\delta ^2}{2}+1\right) , \end{aligned}$$

(33)

The dimensionless pressure rise $\Delta p$ over one period of wavelength can be expressed as

$$\begin{aligned} \Delta p= & {} \int _{0}^{1} \frac{dp}{dz}\,dz, \end{aligned}$$

(34)

Due to the complication of the expression (34), the symbolic software Mathematica has been deployed to assess the numerical integration of the pressure-rise.

The velocity components are expressed in terms of the stream-function and are mathematically defined as

$$\begin{aligned}&u=-\frac{1}{r}\frac{\partial \psi }{\partial r},\;w=\frac{1}{r}\frac{\partial \psi }{\partial r}, \end{aligned}$$

(35)

To obtain the stream function $\psi$, we integrate $w=\frac{1}{r}\frac{\partial \psi }{\partial r}$ with $\psi =0$ at $r = 0$, and then the stream function is given by

$$\begin{aligned} \psi= & {} \frac{1}{48} r^2 \left[ We^2 \varepsilon \left( \frac{dp}{dz}\right) ^3 \left( r^4-3 h^4\right) +6 \frac{dp}{dz} \left( r^2-2 h^2\right) +48 X\right] , \end{aligned}$$

(36)

The stream function represents the volumetric flow rate through the cross section bounded by the ciliated tube wall.

The heat transfer coefficient at the wall of ciliated tube is computed as:

$$\begin{aligned} Z^*= & {} \frac{k_{hnf}}{k_f}\frac{dh}{dz}\left( \frac{\partial \theta }{\partial r}\right) _{r=h}\nonumber \\= & {} \frac{1}{24} \pi \delta h \sin (2 \pi z) \left[ Br \left( \frac{dp}{dz}\right) ^2 h^2 x_2 \left\{ \left( \frac{dp}{dz}\right) ^2 h^2 We^2 \varepsilon +3\right\} +24 \gamma \right] , \end{aligned}$$

(37)

3.2 Entropy generation

Non-equilibrium situation emerges as a result of the exchange of momentum, and temperature within the hybrid nano-blood and at the wall of the ciliated tube which causes a continuous entropy generation (EG). The volumetric entropy generation (EG) term $(E_G)$ can be calculated as follows:

$$\begin{aligned} E_G=\underbrace{\frac{k_{hnf}}{\tilde{\theta }_0^2}\left\{ \left( \frac{\partial \tilde{T}}{\partial \tilde{r}}\right) ^2+ \left( \frac{\partial \tilde{T}}{\partial \tilde{z}}\right) ^2\right\} }_{\text{ Thermal } \text{ irreversibility }} +\underbrace{\frac{1}{\tilde{\theta }_0}\tilde{\tau }_{\tilde{r}\tilde{z}}\frac{\partial \tilde{w}}{\partial \tilde{r}}}_{\text{ Fluid } \text{ friction } \text{ irreversibility }}, \end{aligned}$$

(38)

Utilizing non-dimensional variables in Eq.(16), the entropy generation number can be expressed as

$$\begin{aligned} E_G= & {} E_g\left[ x_4\left( \frac{\partial \theta }{\partial r}\right) ^2+x_2 Br \zeta \tau _{rz}\frac{\partial w}{\partial r}\right] , \end{aligned}$$

(39)

where $E_g=\frac{k_f\tilde{T}_0^2}{\tilde{\theta }_0^2\tilde{a}^2}$, and $\zeta =\frac{\tilde{\theta }_0}{\tilde{T}_0}$ are the characteristic entropy generation rate and the dimensionless temperature difference, respectively.

Entropy gives the degree of disorder of the system and its surroundings. The rate of dimensionless entropy formation is as follows

$$\begin{aligned} N_S= & {} \frac{E_G}{E_g},\nonumber \\= & {} \frac{r^2}{2304 x_4}\left[ Br \left( \frac{dp}{dz}\right) ^4 r^4 We^2 x_2 \varepsilon +3 Br \left( \frac{dp}{dz}\right) ^2 r^2 x_2+24 \gamma \right] ^2\nonumber \\ {}+ & {} \frac{1}{8} Br \left( \frac{dp}{dz}\right) ^2 \zeta r^2 x_2 \left[ \left( \frac{dp}{dz}\right) ^2 r^2 We^2 \varepsilon +2\right] , \end{aligned}$$

(40)

One more significant pertinent parameter is Bejan number Be, which is the ratio of heat and mass transfer and it is given by

$$\begin{aligned} Be= & {} \frac{r^2}{2304 x_4}\left[ Br \left( \frac{dp}{dz}\right) ^4 r^4 We^2 x_2 \varepsilon +3 Br \left( \frac{dp}{dz}\right) ^2 r^2 x_2+24 \gamma \right] ^2/\nonumber \\&\left\{ \frac{r^2}{2304 x_4}\left[ Br \left( \frac{dp}{dz}\right) ^4 r^4 We^2 x_2 \varepsilon +3 Br \left( \frac{dp}{dz}\right) ^2 r^2 x_2+24 \gamma \right] ^2\right. \nonumber \\ {}+ & {} \left. \frac{1}{8} Br \left( \frac{dp}{dz}\right) ^2 \zeta r^2 x_2 \left[ \left( \frac{dp}{dz}\right) ^2 r^2 We^2 \varepsilon +2\right] \right\} , \end{aligned}$$

(41)

4 Validation of results

In order to verify the validity of this research study, we have considered some particular cases. The results of Butt et al. (2020) are recovered by deputizing $\gamma =\phi _1=\phi _2=0$. Our results are in an excellent covenant with the Ref. Butt et al. (2020). Furthermore, we have attempted to check the correctness of the present results by comparing them to those previously recorded by Akbar and Butt (2014). The results of the present model and those of Akbar and Butt (2014) show a good deal of agreement via Fig. 2a–b. This graphical comparison asserts the authenticity about the perfection of the present study.

Fig. 2

Comparison of velocity and temperature profiles with $\phi _1=0.0$, $\phi _2=0.0$, $We=0$, $\varepsilon =0.1$, $\alpha =0.1$, $\beta =0.2$, $\delta =0.1$, $F=0.5$, $Br=0.2$, $z=0.75$, $\gamma =0.5$

5 Analysis and Discussion of Results

This segment is devoted to explore the significant flow characteristics, viz. the axial velocity profile, temperature profile, pressure gradient, pressure rise, heat transfer coefficient, entropy generation, Bejan number, and streamline structure under variation of emerging thermo-physical parameters/ constraints through the graphical expositions and physical interpretations. For graphical computation, the default estimations of non-dimensional quantities/parameters are selected based on Butt et al. (2020): $\phi _1=0.02$, $\phi _2=0.02$, $\varepsilon =0.1$, $\alpha =0.1$, $\beta =0.2$, $\delta =0.1$, $F=0.5$, $We=1$, $Br=0.2$, $z=0.75$, $\gamma =0.5$ and $\zeta =0.2$. In addition, $\phi _1=\phi _2=0$ corresponds to pure blood, $\phi _1=0.01$, $\phi _2=0$ for Cu-blood, and $\phi _1=0.01$, $\phi _2=0.02$ for Cu-Ag/blood. The graphical presentations are performed through computational software Mathematica.

5.1 Axial velocity profile

Figure 3a–d are exposed to analyze the effects of different increasing emerging dynamical parameters, viz. Weissenberg number We, mean flow rate F, Phan-Thien-Tanner (PTT) elongation parameter $\varepsilon$, and cilia length $\delta$ on the non-dimensional velocity field w(r, z). The dependency of velocity field on Weissenberg number We is demonstrated in Fig. 3a. The curves in this figure manifest that the velocity field diminishes for upsurging We and gets its maximum value at the center of the tube. The Weissenberg number is a proportion of relaxation time to the radius of the tube. Growing We increases the relaxation time of the blood particles, which enhances viscosity and generates resistance to the blood flow, resulting in a decrement in blood velocity. Furthermore, a reversal of the outcome is detected near the ciliated tube wall because the radius of the ciliated tube is inversely related to We. To disclose the variation of the velocity field for viscous dumping parameter F, Fig. 3b is designed. An increment in F exhibits an uplifting trend in the velocity field within the flow domain. For greater F, less resistive force is perceived within the ciliated tube and consequently, the velocity profile enhances. The consequence of PTT elongation parameter $\varepsilon$ on velocity field is sketched in Fig. 3c. Increasing $\varepsilon$ augments the velocity profile near the ciliated tube wall but lessens these curves at the central domain. These features are similar to the outcome of We, which is quite expected as $\varepsilon$ is proportional to We in Phan-Thien-Tanner (PTT) model. Fig. 3d divulges the variation of the velocity field for increasing cilia length parameter $\delta$. Boosted $\delta$ shows the declining feature on the velocity field throughout the flow domain. The larger $\delta$ produces more resistance in the flow region which causes a diminution in the velocity field.

Fig. 3

Variation of axial velocity profile w(r, z) for different physical parameters

5.2 Temperature profile

In this subsegment, Fig. 4a–g are sketched to demystify the effects of various emerging physical parameters like Weissenberg number We, Brinkman number Br, mean flow rate F, heat source parameter $\gamma$, Phan-Thien-Tanner (PTT) elongation parameter $\varepsilon$, cilia length $\delta$, and nanoparticle volume fractions ($\phi _1, \; \phi _2$) on the non-dimensional temperature field $\theta (r,z)$. The temperature field is the measure of the average kinetic energy of the blood cells, copper and silver nanoparticles present in the hybrid nano-blood (Cu-Ag/blood). Fig. 4a discloses the impact of increasing Weissenberg number We on the temperature field. It is detected from the pictorial representation that the temperature field is greatest at the central region of the ciliated tube and least nearby the ciliated walls. For larger We, the relaxation time of the hybrid nano-blood particles increases which generates resistance to flow particles and reduces the kinetic energy, as a result, the temperature field significantly declines. Influence of elevating Brinkman number Br on the temperature field is reflected in Fig. 4b. Incremented Br boosted up the temperature profile. Brinkman number is the proportion of viscous heat generation to heat transport due to molecular conduction. Hence greater estimation of Br slows down the heat conduction (i.e., the diffusion of thermal(heat) energy) which is suppressed by viscous dissipation and consequently, the average kinetic energy of hybrid nano-blood particles enhances and temperature profile gets an increment. Figure 4c demonstrates the variation of temperature field for increasing viscous dumping parameter F. An increment in F accomplishes an augmentation in the temperature field. The impact of the heat source parameter $\gamma$ on the temperature profile is reflected in Fig. 4d. This pictorial presentation clarifies that increasing $\gamma$ shows an ascending trend in the temperature profile. The temperature field earns its maximum value at the central line of the ciliated tube and gradually decreases toward the wall. It happens due to more heat generation within hybrid nano-blood which warms up the molecules or particles and enhances the average kinetic energy of the molecules or particles, when the internal heat source increases. The dependency of the PTT elongation parameter $\varepsilon$ on temperature field is graphed in Fig. 4e. Thriving $\varepsilon$ tends to a diminution in blood temperature. Fig. 4f demonstrates the upshot of increasing cilia length $\delta$ on the temperature field. Larger estimations of cilia length $\delta$ induce a remarkable declination in the blood temperature at the central region of the ciliated tube because an increment in cilia length generates resistance to the hybrid nano-blood particles movement which reduces average kinetic energy. The effectiveness of nanoparticle volume fractions $\phi _1$ and $\phi _2$ on the temperature profile is depicted in Fig. 4g. The blood temperature field declines considerably for evolving $\phi _1$ or $\phi _2$. For larger $\phi _1$ or $\phi _2$, the thermal conductivity improves and the nano-blood becomes more viscous which induces resistance to the flow field. Consequently, the average kinetic energy decreases, and temperature field gets an intensive decrement. From Fig. 4a–f, it can be perceived that the hybrid nano-blood (Cu- Ag/blood) accomplishes lower temperature compared to nano-blood (Cu-blood) because hybrid nano-blood possess more viscous nature than nano-blood. These results also demonstrate that the concentration of hybrid nanoparticles in the blood is preferable to the concentration of mono nanoparticles due to a significant improvement in the thermal properties of the blood flow. The physical reason for this activity is that as blood flows away from the ciliated tube wall, nanoparticles near the ciliated tube wall heat up, increasing blood flow away from the ciliated tube wall and decreasing the temperature gradient. Furthermore, Ag nanoparticles have a higher atomic number, which induces a significant decline in the temperature profile of blood. As a result, when compared to Cu nanoparticles, Ag nanoparticles have better thermal properties. Such a finding is extremely beneficial to the cancer care process (Ag nanoparticles as a drug carrier).

Fig. 4

Variation of temperature profile $\theta (r,z)$ for different physical parameters

Fig. 5

Variation of pressure gradient $\frac{dp}{dz}$ for different physical parameters

Fig. 6

Variation of pressure rise $\Delta P$ for different physical parameters

5.3 Pumping characteristics

5.3.1 Axial pressure gradient

Figure 5a–d presents the variation of the pressure gradient $\frac{dp}{dz}$ along the length of the ciliated tube under the impact of Weissenberg number We, mean flow rate F, Phan-Thien-Tanner (PTT) elongation parameter $\varepsilon$, and cilia length $\delta$. Figure 5a illustrates the physical consequence of Weissenberg number We on the pressure gradient. An augmented We tends to boost the pressure gradient. On the contrary, Fig. 5b explores the descending behavior of boosted mean flow rate F on the pressure gradient. The impression of the augmented PTT elongation parameter $\varepsilon$ on the pressure gradient is disclosed in Fig. 5c. It is witnessed from the pictorial illustration that the pressure gradient is directly related to the PTT elongation parameter. Meanwhile, the pressure gradient at the central line of the ciliated tube, as visualized in Fig. 5d, enhances and then starts to oscillate gradually to the wall with incrementing cilia length $\delta$.

5.3.2 Pressure rise per wavelength

The pressure rise $\Delta P$ (i.e., pressure difference across single wavelength) is a significant physical measure in the peristaltic pumping mechanism. The variation in the pressure rise $\Delta P$ with mean flow rate F under the respective influence of Weissenberg number We, Phan-Thien-Tanner (PTT) elongation parameter $\varepsilon$, and cilia length $\delta$ is depicted in Fig. 6a–c. Figure 6a demystifies a decrement in pressure rise by energized Weissenberg number We in the region $-2\le F\le -0.45$ while reversed behavior is detected when $-0.45\le F\le 2$. It can be witnessed from Fig. 6b that the pressure rise lessens with an increase in PTT elongation parameter $\varepsilon$ in the region ($\Delta P>0,\;F<-0.45$). However, a contrary trend is disclosed in the region ($\Delta P<0,\;F> -0.45$). Figure 6c clarifies that higher estimations of cilia length $\delta$ tend to boost the pressure rise in the pumping zone $-2\le F\le -0.32$ but expose a declination in the region $-0.32\le F\le 2$.

Fig. 7

Variation of heat transfer coefficient $Z^*$ for different physical parameters

5.4 Heat transfer coefficient

The variations of the heat transfer coefficient $Z^*$ at the wall of the ciliated tube for various values of We, Br, F, $\gamma$, $\delta$, $\varepsilon$, $\phi _1$, and $\phi _2$ against z are publicized via Fig. 7a–g. The absolute value of the heat transfer coefficient $\mid {Z^*}\mid$ declines with an increment in We, and $\varepsilon$, but a contrary behavior is witnessed for greater values of Br, F, $\gamma$, $\delta$, $\phi _1$ and $\phi _2$. A mounted Br boots the kinetic energy of nanoparticles which expedites $\mid {Z^*}\mid$. The minimum of $\mid {Z^*}\mid$ associates to a lower volume fraction of both nanoparticles in the blood. It is also notable that the feature of heat transport is oscillatory. This behavior is under the physical expectation due to metachronal waves traveling along the ciliated tube (stimulated by the power and recovery strokes of evenly distributed cilia lined in the tube wall). The heat transfer coefficient $\mid {Z^*}\mid$ for hybrid nano-blood (Cu-Ag/blood) is higher compared to nano-blood (Cu-blood).

5.5 Entropy generation and Bejan Number

In this subsegment, the variations of entropy generation Ns and Bejan number Be for mounted values of We, F, Br, $\gamma$, $\zeta$, $\delta$, $\phi _1$, and $\phi _2$ are illustrated via Fig. 8a–n. Figure 8a indicates the descending behavior of total entropy number near the ciliated tube wall but no effect at the center for increasing Weissenberg number We. It is also remarkable that maximum value of Ns is detected at the wall of the tube. Fig. 8b shows a decrement in the proximity of the tube wall but an opposite behavior at the center for Bejan number Be when We increases. An augmentation in the mean flow rate F tends to boost both Ns and Be near the tube wall as plotted in Fig. 8c–d. Further, at the center of the tube ($r=0$), the entropy number does not respond and the Bejan number reduces significantly for growing F. The variations of Brinkman number Br on total entropy number and Bejan number are reflected in Fig. 8e–f Increasing Br markedly upsurges the total entropy number and Bejan number near the ciliated tube wall. A diminution in Be at the center of the ciliated tube is observed due to enhancement in Br. The dependency of heat source $\gamma$ on total entropy number and Bejan number is disclosed via Fig. 8g–h. Both the quantities Ns and Be are upsurged for increasing heat source $\gamma$. For higher temperature difference parameter $\zeta$, as publicized in Fig. 8i–j, total entropy number Ns enhances except the center of the tube but Bejan number Be declines throughout the flow domain. Fig. 8k–l is designed to demonstrate the variation of the total entropy number and Bejan number for thriving cilia length $\delta$. It is noted from these curves that Ns decelerates with incrementing cilia length $\delta$. Moreover, as disclosed in Fig. 8l, Bejan number Be is found to upsurge owing to augmenting $\delta$ except the proximity of the ciliated tube wall. The effectiveness of volume fractions of suspended nanoparticles $\phi _1$ and $\phi _2$ on the total entropy number and Bejan number is graphed in Fig. 8m–n. By an increment in $\phi _1$ and $\phi _2$, total entropy number Ns expedites within the ciliated tube except for the center ($r=0$) but a contrary trend is detected for Bejan number Be. It is worth mentioning that the entropy generation number tends to zero at the center-line of the tube and gradually increases as it tends to the tube wall and attains its maximum at the wall. It is also witnessed that hybrid nano-blood exhibits a greater total entropy number than nano-blood. The contrary behavior is marked in the case of the Bejan number.

In Fig. 9a–b, 3D surface plots of total entropy generation number Ns and Bejan number Be are depicted. Figure 9a exposes that supremum estimation of Ns is noted at the narrow segment of the ciliated tube and in the wider segment it reaches its least value. This clarifies that the compressed segment of the tube is found to boost the entropy number. In Fig. 9b, the Bejan number is imprinted against r and z variables. It discloses that at the compressed part of the tube, the impact of heat transfer irreversibility is dominated, but, in the expanded segment of the tube, heat transfer irreversibility declines and the blood friction irreversibility gradually upsurges.

Fig. 8

Variation of entropy generation and Bejan number for different physical parameters

Fig. 9

Surface plot of entropy generation and Bejan number, when $\varepsilon =0.1$, $\alpha =0.1$, $\beta =0.2$, $\delta =0.1$, $z=0.75$, $Br=0.2$, $\zeta =0.2$, $F=0.5$, $We=0.1$, $\gamma = 0.5$, $\phi _1=0.01$ and $\phi _2=0.02$

5.6 Streamlines pattern

Trapping is an interesting manifestation of cilia-assisted pumping flow, which does not occur below the critical flow rate. It is the development of a bolus of blood confined by the closed and internally circulating streamlines and driven forward along with the metachronal wave. To disclose the trapping feature, streamlines pattern of the blood flow have been visualized for various values of We, F, $\beta$, and $\delta$ via Fig. 10a–h. Figure 10a–b are portrayed to disclose the streamlines pattern for increasing values of Weissenberg number We. It is watched that number and size of trapped bolus increase for an elevated We which indicates a higher flow rate. Physically, Weissenberg number is proportional to the relaxation time of fluid particles. An increment in Weissenberg number increases the relaxation time of the blood particles and viscoelastic properties of blood become more significant which generates a drag force to the blood particles so that number and size of trapped bolus enhance. The impression of mean flow rate F on streamlines is depicted in Fig. 10c–d. On contrary, the number of imprisoned bolus reduces with an increment in F. Moreover, for a higher mean flow rate, the size of the bolus lessens. The upshot of $\beta$ on streamlines is exposed in Fig. 10e–f. A mounted $\beta$ energizes the trapped bolus in size as well as in number. Fig. 10g–h explore that the trapped bolus size and number are significantly increased when the cilia length $\delta$ enlarges. This means that the trapping is augmented by the increment in cilia length due to more powerful and effective recovery stokes of cilia within the blood flow.

Fig. 10

Streamlines for different physical parameters

5.7 Conclusions

Analysis of entropy generation in ciliary induced peristaltic transport of blood with Phan-Thien-Tanner (PTT) non-Newtonian fluid model in a tube under the volumetric concentration of hybrid nanoparticles and internal heat source impacts has been performed in this study. The constituting equations describing the blood flow have been simplified under the postulates of lubrication theory. The resulting equations are solved analytically subject to the prescribed boundary conditions. The alternation in hemodynamic quantities for varying thermophysical parameters has been visualized and illustrated via graphs. Some key consequences of this analysis are pointed out as follows:

• The axial velocity is significantly reduced by boosting Weissenberg number, Phan-Thien-Tanner (PTT) elongation parameter, and cilia length.

• The blood temperature is remarkably augmented with escalating Brinkman number and heat source parameter.

• Impacts of increasing nanoparticle volume fractions have a declining behavior in blood temperature.

• The hybrid nano-blood (Cu- Ag/blood) accomplishes lower temperature via compared to nano-blood (Cu-blood).

• The absolute estimation of the heat transfer coefficient is markedly elevated with ascending Brinkman number, heat source parameter, and nanoparticle volume fractions.

• Larger length of cilia causes a deterioration in the entropy generation number in the blood flow due to cilia movement.

• Bejan number declines with the volumetric concentration of hybrid nanoparticles and it is significantly elevated by heat source.

• Hybrid nano-blood exhibits a greater total entropy number than nano-blood and a contrary behavior is marked in case of Bejan number.

• The trapping of bolus is augmented by the increment in cilia length due to more power and effective recovery stokes of cilia within blood flow.