Introduction

In recent years, the problem of fluid flow flanked by the rotating surfaces has drawn substantial attention of the researchers owing to its numerous applications in engineering and industrial fields; for example, in rotating machinery, thermal-power system, aeronautical systems, medical equipment, gas turbine rotors, storage devices in computers, air cleaning machines, crystal growth process and foodprocessing technology. Wu et al. [1] took up experimental investigation of the flow over grooved rotating disk. Rizwan et al. [2] simulated numerically magnetite nanoparticles considering water as base fluid between two parallel disks. Turkyilmazoglu [3,4,5] investigated fluid flow over rotating moving disk. Rashidi et al. [6, 7] reported MHD nanofluid flow considering porous rotating disk. Qayyum et al. [8] took up comparative scrutiny of fluid flow over a rotating disk by considering five nanoparticles. Pourmehran et al. [9] reported rheological characteristic of metal-based nanofluid flow between rotating disks. Attia [10] studied steady flow considering porous medium on a rotating disk. Mellor et al. [11] investigated flow amid rotating and stationary disks. Kavenuke et al. [12] modeled flow amid porous rotating disk and a fixed impermeable disk. Awati et al. [13] studied the flow amid porous rotating and fixed impermeable disk.

Constant advancement in the electronic equipment frequently faces the challenges pertaining to the thermal management from declining accessible to surface area for heat exclusion or from the improved phase of heat generation. These challenges could be conquered with modeling the cooling equipment with optimal geometry or by increasing heat transfer characteristics. Choi [14] suggested that nanofluid in this context will sort out all these issues. Sarafraz et al. [15] studied convective boiling heat transfer of CuO-water/ethylene glycol nanofluid. Salari et al. [16] studied thermal behavior of aqueous iron oxide nanofluid on a flat disk. Kamalgharibi et al. [17] took up experimental study on the stability of CuO nanoparticles dispersed in different base fluids. Sajid et al. [18] studied thermal conductivity of hybrid nanofluid. Imtiaz et al. [19] demonstrated convective flow between rotating stretchable disks considering carbon nanotubes and thermal radiation effects. Salari et al. [20] studied boiling thermal performance of TiO2 aqueous nanofluid on a disk copper block. Hayat et al. [21] reported induced magnetic field and melting heat transfer effects along with variable thickness on nanofluid flow along a rotating disk. Bachok et al. [22] portrayed flow and heat transport of nanofluid on a porous revolving disk. Ellahi et al. [23] carried out simulation of spherically shaped hydrogen bubbles with stenosis through a tube nozzle. Ellahi et al. [24] probed the impact of hybrid nanofluid flow with the slip effects. Nazari et al. [25] investigated mixed convective non-Newtonian nanofluid in a lid-driven square cavity. Maleki et al. [26, 27] investigated flow and heat transfer in nanofluid considering various parameters. Giwa et al. [28] addressed heat, flow and mass transfer considering hybrid nanofluid. Peng [29] investigated energy performance along a U-shaped evacuated solar tube via considering oxide nanoparticles. Ahmadi [30] took up machine learning approach to study dynamic viscosity of nanofluid. Yousefzadeh et al. [31] studied convection in nanofluid in a cavity. Arasteh et al. [32] explored heat and fluid flow of nanofluid in a double-layered sinusoidal heat sink. Sarafraz et al. [33] investigated on thermal analysis and thermo-hydraulic characteristics of zirconia-water nanofluid. Maleki et al. [34] addressed flow and heat transfer of pseudo-plastic nanofluid with viscous dissipation over a moving permeable plate. Thus, researchers [35,36,37,38,39,40,41,42,43,44] have observed anomalously that diffusion of nanometer-sized solid particles in the base fluid shows high effective thermal conductivity, longer suspension time, larger surface area, lower clogging and erosion, significant energy saving and lower operating cost. Thermal conductivity of nanofluid is enhanced with suspension of metallic or non-metallic particles. Hence, carbon materials such as graphite nanoparticles, carbon nanotubes, exfoliated graphite, diamond nanoparticles, nanofibers, carbon black and graphene have gained more importance due to low density and large intrinsic thermal conductivity compared to metal/metal oxides.

Recent studies reveal that graphene, a perfect two-dimensional lattice of carbon, has a very high thermal conductivity with many unique chemical, physical and mechanical properties. Hence, graphene material has emerged as a fascinating material of the carbon in the field of technology and science. Graphene can be offered in granular form, and hence it could be dispersed in organic solvents, water and polymers which are advantageous in super conductors, lithium ion batteries, gas censors, fabrication of transparent conductive films, solar cells, advanced electronics, etc. Keeping this into view, the authors [45,46,47,48,49] studied flow, heat and mass transfer with the inclusion of graphene nanoparticles on various flow configurations.

Constantly engineers and researchers are looking forward to scrutinize the fluids subjected to the thermal radiation as it has major influence in high-temperature processes, for instance, in nuclear power plants, gas turbines, satellites, power generation, combustion and polymer processing industry. Mamatha et al. [50,51,52,53] portrayed non-Newtonian flow and heat transform over different geometry considering deferment of dust particles and nanoparticles. Sharma et al. [54] investigated buoyancy effects on unsteady convection radiating fluid over a vertically moving porous plate. Santhosh et al. [55] studied radiated convective Carreau nanofluid flow with heat generation. Nayak et al. [56] investigated viscous dissipation and partial slip influence on the radiative nano-Tangent hyperbolic fluid over permeable Riga plate. Eid and Makinde [57] studied effects of solar radiation on a MHD nanofluid flow over a porous medium considering chemically reactive species.

The aim of the current theoretical model is to investigate the nonlinear convective flow between the stationary nonporous and porous rotating disks utilizing graphene nanoparticles in a water and ethylene glycol base fluid. Heat transfer distinctiveness is analyzed considering thermal radiation and heat absorption/generation. The governing fluid equations are computed using Runge–Kutta based shooting method. Characteristics of sundry variables are elaborated graphically and through the construction of Table.

Mathematical formulation

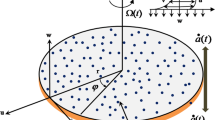
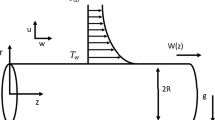
Steady nonlinear nanofluid flow (water and graphene, ethylene glycol and graphene) between the stationary and porous disks is considered in this study. Nanofluid motion is generated by the rotary motion of porous disk as well as suction/injection of nanofluid. Rotating and stationary disks are separated by the distance \(l\). Compared to the radii of the disk, the distance \(l\) is very small. Transverse magnetic field with strength \(B_{0}\) acts all along the \(z\) direction. The process of heat transfer occurs due to heat absorption/generation and thermal radiation. Path of fluid flow is indicated with arrows (see Fig. 1) heading towards the porous disk which is rotating with constant angular speed \(\Omega\) about the \(z\) axis with the rotation speed \(\Omega \varepsilon\), and \(\varepsilon\) is a regulator which controls rotation of the disk. When \(\varepsilon = 0\) no rotation takes place and \(\varepsilon \, > 0\) rotation exists and \(\left( {0 \le \varepsilon \, \le 1} \right)\). Here, the suction velocity \(W\) is assumed to be constant.

Fig. 1
figure 1

Geometry of flow model

Full size image

Considering the above said assumptions and following (Hayat et al. [17, 21] and Kavenuke et al. [12], the flow model is governed by the subsequent equations.

$$\left( \frac{1}{r} \right)\frac{\partial }{\partial r}\left( {ru} \right) + \frac{\partial w}{{\partial z}} = 0$$
(1)
$$u\frac{\partial u}{{\partial r}} + w\frac{\partial u}{{\partial z}} - \left( {\frac{{v^{2} }}{r}} \right) + \frac{1}{{\rho_{{{\text{nf}}}} }}\frac{\partial p}{{\partial r}} = \left( \begin{gathered} \upsilon_{{{\text{nf}}}} \left[ {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{\partial }{\partial r}\left( \frac{u}{r} \right) + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right] - \frac{{\sigma_{{\text{f}}} B_{0}^{2} u}}{{\rho_{{\text{f}}} }} + \hfill \\ \left( {\left( {\frac{1}{{\rho_{{\text{f}}} }}} \right)g\left[ {\left( {\rho \beta } \right)_{{{\text{nf}}}} \left( {T - T_{2} } \right) + \left( {\rho \beta_{1} } \right)_{{{\text{nf}}}} \left( {T - T_{2} } \right)^{2} } \right]} \right) \hfill \\ \end{gathered} \right)$$
(2)
$$\frac{u}{r}\frac{\partial }{\partial r}\left( {rv} \right) + w\frac{\partial v}{{\partial z}} = \upsilon_{{{\text{nf}}}} \left[ {\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{\partial }{\partial r}\left( \frac{v}{r} \right) + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right] - \frac{{\sigma_{{\text{f}}} B_{0}^{2} v}}{{\rho_{{\text{f}}} }}$$
(3)
$$u\frac{\partial w}{{\partial r}} + w\frac{\partial w}{{\partial z}} + \left( {\frac{1}{{\rho_{{{\text{nf}}}} }}} \right)\frac{\partial p}{{\partial z}} = \left( {\upsilon_{{{\text{nf}}}} } \right)\left[ {\left( \frac{1}{r} \right)\frac{\partial w}{{\partial r}} + \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right]$$
(4)
$$u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}} = \alpha_{{{\text{nf}}}} \left[ {\left( \frac{1}{r} \right)\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right] + \frac{Q}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} }}(T - T_{2} ) + \frac{16}{3}\frac{{\sigma^{*} }}{{k^{*} }}\frac{{T_{2}^{3} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} }}\left[ {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{{\partial r}} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right].$$
(5)

Boundary conditions (following Kavenuke et al. [12]) are given by

  • With reference to fixed impermeable disk at\(z = 0\)

    $$\begin{aligned} & u\left( {r,0} \right) = 0 \\ & v\left( {r,0} \right) = 0 \\ & w(r,0) = 0 \\ & T(r,0) = T_{1} \\ \end{aligned}$$
    (6)

  • With reference to porous disk at\(z = l\)

    $$\begin{aligned} & u\left( {r,l} \right) = 0 \\ & v\left( {r,l} \right) = r\Omega \\ & w(r,l) = \varepsilon W \\ & T(r,l) = T_{2} \\ \end{aligned}.$$
    (7)

Here, \(\left( {u,v,w} \right)\) specify the velocity components along the \(\left( {r,\phi ,z} \right)\) directions, \(T\) the temperature of the nanofluid, \(T_{1}\) the temperature at fixed impermeable disk, \(T_{2}\) the temperature at rotating porous disk, \(\upsilon_{{{\text{nf}}}}\) represents the nanofluid kinematic viscosity, \(p\) the pressure and \(\rho_{{{\text{nf}}}}\) the density of the nanofluid, \(\alpha_{{{\text{nf}}}}\) and \(\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}}\) signify the thermal diffusivity and effective heat capacity of nanofluid, \(Q\) the heat (generation, absorption), and Stefan–Boltzmann constant and coefficient of mean absorption are represented as \(\sigma^{*}\) and \(k^{*}\).

Following Bachok et al. [22]

$$\left. {\begin{array}{*{20}l} {\rho_{{{\text{nf}}}} = \phi \rho_{{\text{s}}} + \left( {1 - \phi } \right)\rho_{{\text{f}}} ,\,\,\mu_{{{\text{nf}}}} = \mu_{{\text{f}}} \left( {1 - \phi } \right)^{ - 2.5} ,\;\;\left( {\rho c_{{\text{p}}} } \right)_{{{\text{nf}}}} = \phi \left( {\rho c_{{\text{p}}} } \right)_{{\text{s}}} + \left( {1 - \phi } \right)\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} ,} \hfill \\ {\frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }} = \frac{{ - \phi \left( {n - 1} \right)\left( {k_{\rm{f}} - k_{{\text{s}}} } \right) + k_{{\text{s}}} + \left( {n - 1} \right)k_{{\text{f}}} }}{{k_{{\text{s}}} + \left( {n - 1} \right)k_{{\text{f}}} + \phi \left( {k_{{\text{f}}} - k_{{\text{s}}} } \right)}},\,\,\left( {\rho \beta } \right)_{{{\text{nf}}}} = \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{{\text{f}}} + \phi \left( {\rho \beta } \right)_{{\text{s}}} ,} \hfill \\ \end{array} } \right\}.$$
(8)

Here, \(\phi\) represents the solid volume fraction of the nanoparticles, \(\left( {\mu_{{{\text{nf}}}} ,\mu_{{\text{f}}} } \right)\) indicate the nanofluid effective and base fluid dynamic viscosity, \(\left( {\rho_{{{\text{nf}}}} ,\rho_{{\text{f}}} ,\rho_{{\text{s}}} } \right)\) signify the density of nanofluid, base fluid and density of the solid nanoparticles and \(\left( {k_{{{\text{nf}}}} ,k_{{\text{f}}} } \right)\) the thermal conductivity of nanofluid and base fluid, and \(\left( {\rho \beta } \right)_{{{\text{nf}}}}\) is volumetric thermal expansion coefficient.

We considered the following transformations following Awati et al. [13] and Mellor et al. [11]:

Velocity components in terms of stream function are considered as

$$u = \frac{1}{r}\,\frac{\partial \psi }{{\partial z}},\,\,\,\,w = - \frac{1}{r}\,\frac{\partial \psi }{{\partial r}}.$$
(9)

Similarity variable and physical stream function are

$$\zeta = \frac{z}{l} = \frac{\Omega z}{W}\;\;\;{\text{and}}\;\;\;\;\psi \left( {r,n} \right) = r^{2} f\left( \zeta \right)W.$$
(10)

Thus, from (9) and (10) radial and axial velocity components are

$$\frac{u}{r} = \Omega \,\left( {f^{\prime}\left( \zeta \right)} \right),\,\,\,\,\,\,\,\frac{w}{W} = - 2\left( {f\left( \zeta \right)} \right).$$
(11)

Tangential velocity and pressure variable are

$$v = r\Omega g\left( \zeta \right),\,\,\,\,p = \frac{1}{2}\rho r^{2} \Omega^{2} A + \rho W^{2} P\left( \zeta \right).$$
(12)

Non-dimensional temperature is given by

$$\theta \left( \zeta \right) = \frac{{T - T_{2} }}{{T_{1} - T_{2} }}.$$
(13)

Applying the transformation from Eqs. (11), (12) and (13) in Eqs. (1)–(7) and (8), one obtains

$$\begin{gathered} \left[ {\left( {\frac{1}{{\text{Re}}}} \right)\left( {\frac{1}{{\left( {1 - \phi } \right)^{2.5} \left( {\left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right)}}} \right)} \right]\frac{{{\text{d}}^{3} f}}{{{\text{d}}\zeta^{3} }} = \left( \begin{gathered} \left[ \begin{gathered} \left( {\frac{{{\text{d}}f}}{{{\text{d}}\zeta }}} \right)^{2} - 2f\left( \zeta \right)\frac{{{\text{d}}^{2} f}}{{{\text{d}}\zeta^{2} }} \hfill \\ - g^{2} \left( \zeta \right) - A \hfill \\ \end{gathered} \right] + \left( M \right)\frac{{{\text{d}}f}}{{{\text{d}}\zeta }} \hfill \\ - \theta \left( \zeta \right)\alpha_{1} \left[ \begin{gathered} \left( {\left( {1 - \phi } \right) + \left( {\frac{{\phi \left( {\rho \beta } \right)_{{\text{s}}} }}{{\left( {\rho \beta } \right)_{{\text{f}}} }}} \right)} \right) + \hfill \\ \beta_{t} \theta \left( \zeta \right)\left( {\left( {1 - \phi } \right) + \left( {\frac{{\phi \left( {\rho \beta } \right)_{{\text{s}}} }}{{\left( {\rho \beta } \right)_{{\text{f}}} }}} \right)} \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered} \right) \hfill \\ \hfill \\ \end{gathered}$$
(14)
$$\left[ {\left( {\frac{1}{{\text{Re}}}} \right)\left( {\frac{1}{{\left( {1 - \phi } \right)^{2.5} \left( {\left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right)}}} \right)} \right]\frac{{{\text{d}}^{2} g}}{{{\text{d}}\zeta^{2} }} = \left[ {2\frac{{{\text{d}}f}}{{{\text{d}}\zeta }}g\left( \zeta \right) - 2f\left( \zeta \right)\frac{{{\text{d}}g}}{{{\text{d}}\zeta }} + Mg\left( \zeta \right)} \right]$$
(15)
$$\left[ {\left( {\frac{2}{{\text{Re}}}} \right)\left( {\frac{1}{{\left( {1 - \phi } \right)^{2.5} \left( {\left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right)}}} \right)} \right]\frac{{{\text{d}}^{2} f}}{{{\text{d}}\zeta^{2} }} = \left[ { - P^{\prime}\left( \zeta \right) - 4f\left( \zeta \right)\frac{{{\text{d}}f}}{{{\text{d}}\zeta }}} \right]$$
(16)
$$\left[ {\frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} \left( {\left( {1 - \phi } \right) + \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}\phi } \right)}} + \frac{4}{3}R} \right]\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\zeta^{2} }} = \left( {\Pr } \right)\left( {\text{Re}} \right)\left[ {\left( {2f\left( \zeta \right)\frac{{{\text{d}}\theta }}{{{\text{d}}\zeta }}} \right) - \frac{\delta \theta \left( \zeta \right)}{{\left( {\left( {1 - \phi } \right) + \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}\phi } \right)}}} \right]$$
(17)
$$\,f\left( 0 \right) = 0,\,\theta \left( 0 \right) = 1,\,g\left( 0 \right) = 0,\,f^{\prime}\left( 0 \right) = 0$$
$$\theta \left( 1 \right) = 0,\,f^{\prime}\left( 1 \right) = 0,\,g\left( 1 \right) = 1,\,f\left( 1 \right) = - \left( {\frac{\varepsilon }{2}} \right).$$
(18)

Here, \({\text{Re}} = \frac{{W^{2} }}{{\Omega \upsilon_{{\text{f}}} }}\) signifies Reynolds number,\(M = \frac{{\sigma B_{0}^{2} }}{{\Omega \rho_{{\text{f}}} }}\) Hartman number, \(\alpha_{1} = \frac{{g\beta_{{\text{f}}} \left( {T_{1} - T_{2} } \right)}}{{r\Omega^{2} }}\) thermal buoyancy (or mixed convection) variable, A is the arbitrary constant,\(\beta_{{\text{t}}} = \frac{{\beta_{{1{\text{f}}}} \left( {T_{1} - T_{2} } \right)}}{{\beta_{{\text{f}}} }}\) nonlinear convection variable owing to temperature, \(\delta = \frac{Q}{{\Omega \left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}\) heat generation variable, \(\Pr = \frac{{\left( {\mu c_{{\text{p}}} } \right)_{{\text{f}}} }}{{k_{{\text{f}}} }}\) Prandtl number, and \(R = \frac{{16\sigma^{*} T_{2}^{3} }}{{3k^{*} k_{{\text{f}}} }}\) is the radiation parameter.

Expression of coefficient of skin friction (radial and tangential direction) and Nusselt number: Following Imtiaz et al. [19]

$$C_{{{\text{fr}}}} \left( {R_{{\text{e}}} } \right)^{\frac{1}{2}} = \frac{1}{{\left( {1 - \phi } \right)^{2.5} }}\frac{{{\text{d}}^{2} f\left( 0 \right)}}{{{\text{d}}\zeta^{2} }},\,\,\,C_{{{\text{f}}\phi }} \left( {R_{{\text{e}}} } \right)^{\frac{1}{2}} = \frac{1}{{\left( {1 - \phi } \right)^{2.5} }}\frac{{{\text{d}}g\left( 0 \right)}}{{{\text{d}}\zeta }},$$
$$Nu\left( {R_{{\text{e}}} } \right)^{{ - \frac{1}{2}}} = - \frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }}\left( {1 + \frac{4}{3}R} \right)\frac{{{\text{d}}\theta \left( 0 \right)}}{{{\text{d}}\zeta }}.$$
(19)

Method of Numerical solution

The nonlinear differential conditions (14)–(17) subject to conditions (18) originate from the third solicitation in f and the second solicitation in g and θ. These conditions can be seen numerically utilizing a fourth solicitation Runge–Kutta technique that consolidates a terminating framework and Newton–Raphson innovation. We portray here \((\xi = \zeta )\)

$$\begin{aligned} & f = Y_{1} ,\,\,\frac{\partial f}{{\partial \xi }} = Y_{2} ,\,\,\frac{{\partial^{2} f}}{{\partial \xi^{2} }} = Y_{3} ,\,\,g = Y_{4} ,\,\,\frac{\partial g}{{\partial \xi }} = Y_{5} ,\,\,\theta = Y_{6} ,\,\,\frac{\partial \theta }{{\partial \xi }} = Y_{7} \\ & \left( {1 - \phi } \right)^{2.5} \left( {\left( {1 - \phi } \right) + \phi \frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right) = A_{1} ,\left( {\left( {1 - \phi } \right) + \left( {\frac{{\phi \left( {\rho \beta } \right)_{{\text{s}}} }}{{\left( {\rho \beta } \right)_{{\text{f}}} }}} \right)} \right) = B_{1} ,\left( {\left( {1 - \phi } \right) + \frac{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{s}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{f}}} }}\phi } \right) = C_{1} \\ \end{aligned}.$$
(20)

We also define the following:

$$f = F_{1} ,\frac{{\partial f}}{{\partial \xi }} = F_{2} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \frac{{\partial ^{2} f}}{{\partial \xi ^{2} }} = F_{3} ,{\mkern 1mu} {\mkern 1mu} g = F_{4} ,{\mkern 1mu} {\mkern 1mu} \frac{{\partial g}}{{\partial \xi }} = F_{5} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \frac{{\partial \theta }}{{\partial \xi }} = F_{7} .$$
(21)

Substituting conditions (20) and (21) by conditions (18) transformed to an arrangement of nine synchronous conditions of the principal request as follows:

$$F_{1} = Y_{2} ,$$
(22)
$$F_{2} = Y_{3} ,$$
(23)
$$F_{3} = \left( {\left[ {\left( {F_{2} } \right)^{2} - 2F_{1} F_{3} - F_{4}^{2} - A} \right] + \left( M \right)F_{2} - F_{6} \alpha_{1} \left[ {B_{1} + \beta_{{\text{t}}} F_{5} } \right]} \right).$$
(24)

In a similar way we have converted other two equations with higher derivatives (\(F_{5} ^{\prime},F_{7} ^{\prime}\)) into initial value problem as mentioned above and the boundary conditions are given as follows:

$$F_{1} (0) = 0,\,\,\,F_{2} (0) = 0,\,\,\,Y_{4} (0) = 0,\,\;\;Y_{6} (0) = 1,\;\;\;Y_{2} (1) = 1,\,\;\;\;Y_{4} (1) = 1,\,\;\;\;Y_{2} (1) = 1 \ldots \ldots$$
(25)

Here, \(\xi_{\infty }\) is selected as \(\xi_{\infty } = 1\). The unclear introductory conditions are taken as \(Y_{3} (0) = s,\,\,Y_{5} (0) = t\) and \(Y_{7} (0) = p\). We utilize the Newton–Raphson technique to discover \(s,\,\,t\) and \(q\) with the goal that the arrangements of the conditions (25) fulfill as far as possible conditions (18). Right now, start with the underlying evaluations \((p(0),\,\,t(0),\,\,s(0))\) through the trigger strategy. The Newton–Raphson calculation is stretched out to incorporate the halfway subordinates of the components of every factor. This will create the subordinates of \(F(F_{1} ,\,\,F_{2} ,\,\,.\,\,.\,\,.,\,\,F_{5} )\) on \(p,\,\,t\) and \(s\) as follows:

$$F_{\text{p}} (F_{6} ,\,\,F_{7} ,\,\,.\,\,.\,\,.\,\,F_{10} ),\,\,\,\,F_{\text{t}} (F_{11} ,\,\,F_{12} ,\,\,.\,\,.\,\,.\,\,F_{15} ),\,\,F_{\text{s}} (F_{16} ,\,\,F_{17} ,\,\,.\,\,.\,\,.\,\,F_{20} ).$$
(26)

Thus, we need to find \(F_{{\text{p}}} = 0,\,\,F_{\rm{t}} = 0,\,\,F_{\rm{s}} = 0,\) simultaneously. Following Cebeci and Keller, these yield a system of algebraic equations which satisfy the boundary conditions when \(\upxi =0.\)

$$f^{\prime}_{\upzeta } p + f^{\prime}_{\text{t}} t + f^{\prime}_{\text{s}} s + f^{\prime} = 0,\,\,\,g_{\upzeta } p + g_{\text{t}} t + g^{\prime}_{\text{s}} s + \theta = 0,\,\,\,\theta_{\text{p}} p + \theta_{\text{t}} t + \theta ^{\prime}_{\text{s}} s + \theta = 0.$$
(27)

Revamping the framework in condition (27) yields a grid condition AX = B:

$$\left[ {\begin{array}{*{20}c} {f^{\prime}_{\upzeta } } & {f^{\prime}_{\rm{t}} } & {f^{\prime}_{\rm{s}} } \\ {g_{\upzeta } } & {g_{\rm{t}} } & {g_{\rm{s}} } \\ {\theta_{\upzeta } } & {\theta_{\rm{t}} } & {\theta_{\rm{s}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} p \\ t \\ s \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - f^{\prime}} \\ { - g} \\ { - \theta } \\ \end{array} } \right].$$
(28)

This lattice condition can be found by Cramer's standard. The following estimation of \(p,\,\,t\) and can be computed by using the following formula:

$$p^{{({\text{new}})}} = p^{{({\text{old}})}} + \frac{{\det \left( {A_{{\text{B}}} (I,J)} \right)}}{\det (A)},\,\,\,\,t^{{({\text{new}})}} = t^{{({\text{old}})}} + \frac{{\det \left( {A_{{\text{B}}} (I,J)} \right)}}{\det (A)},\,\,\,\,s^{{({\text{new}})}} = s^{{({\text{old}})}} + \frac{{\det \left( {A_{{\text{B}}} (I,J)} \right)}}{\det (A)}.$$
(29)

When the estimations of \(p,\,\,t\) and \(s\) are known, we utilized the Runge–Kutta strategy to tackle the main request of common differential conditions F1, F2,...,F20. For arrangement, the most extreme supreme relative difference between two methods is employed inside a pre-doled out resilience \(\varepsilon < 10^{ - 6}\). In the process, the distinction meets the grouping criteria, the arrangement is projected to have amalgamated and the iterative procedure is ended.

Validation of the numerical procedure

To check the numerical program, the outcomes were contrasted with those recently announced in the writing. We thought about the particular qualities of the stream parameters with the investigation consequences of existing writing. These examinations are contrasted in Tables 4 and 5. It is discovered that the examination is satisfactory and reliable with the current outcomes.

Results and discussion

The influence of relevant variables \({\text{Re}} = 0.051,\;\;\phi = 0.02,\;\;R = 0.5,\;\;\;\delta = 0.1,\;\;A = 0.4,\;\;M = 0.5,\) \(\beta_{{\text{t}}} = 0.2,\;\;\;\alpha_{1} = 0.2\) on velocities (axial \(f\left( \zeta \right)\), tangential \(g\left( \zeta \right)\) and radial \(f^{\prime}\left( \zeta \right)\)), temperature \(\theta \left( \zeta \right)\), skin friction \(\left( {c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}} ,c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}} } \right)\) and Nusselt number \(\left( - Nu\left( {\text{Re}} \right)^{ - {\frac{1}{2}} } \right)\) for Graphene + \(H_{2} O\) and Graphene + \(EG\) nanofluid are discussed in this section. Thermophysical features of water, ethylene glycol and graphene are illustrated in Table 1. The coefficient of skin friction (radial and tangential direction), and Nusselt number for Graphene + \(H_{2} O\) and Graphene + \(EG\) nanofluid are portrayed in Tables 2 and 3. In Tables 4 and 5, comparison of obtained results with the published results of Stewartson [31] and Imtiaz et al. [19] for various values of \(\Omega\) is tabulated and excellent agreement is observed with the published results.

Table 1 Thermophysical features of base fluid (EG), water and nanoparticles (graphene) (Mamatha et al. [53])
Full size table
Table 2 Coefficient of skin friction \(\left( {c_{{\text{f}}}/{\text{Re}}^{\frac{1}{2}} ,c_{{\text{g}}} /{\text{Re}}^{\frac{1}{2}} } \right)\) and Nusselt number \(\left( - Nu/{\text{Re}} ^{-{\frac{1}{2}}}\right)\) for Graphene + \(H_{2} O\) nanofluid
Full size table
Table 3 Coefficient of skin friction \(\left( {c_{{\text{f}}}/{\text{Re}}^{\frac{1}{2}} ,c_{{\text{g}}}/{\text{Re}}^{\frac{1}{2}} } \right)\) and Nusselt number \(\left( - Nu/{\text{Re}}^{-{\frac{1}{2}}}\right)\) for Graphene + \(EG\) nanofluid
Full size table
Table 4 Comparison of \(\frac{{{\text{d}}^{2} f\left( 0 \right)}}{{{\text{d}}\zeta^{2} }}\) for various values of \(\Omega\) when \(M = \alpha_{1} = \delta = \Upsilon_{1} = \Upsilon_{2} = \phi = 0,\) and \({\text{Re}} = 1\)
Full size table
Table 5 Comparison of \(\left( { - \frac{\rm{d}g\left( 0 \right)}{{\rm{d}\zeta }}} \right)\) for various values of \(\Omega\) when \(M = \alpha_{1} = \delta = \Upsilon_{1} = \Upsilon_{2} = \phi = 0,\) and \({\text{Re}} = 1\)
Full size table

Figures 2–5 expose the influence of Reynolds number \(\left( {\text{Re}} \right)\) on axial \(f\left( \zeta \right)\), radial \(f^{\prime}\left( \zeta \right)\) tangential \(g\left( \zeta \right)\) velocity and temperature \(\theta \left( \zeta \right)\). It is observed that intensification in \({\text{Re}}\) ensures decrement in \(f\left( \zeta \right)\),\(g\left( \zeta \right)\) and \(\theta \left( \zeta \right),\) whereas \(f^{\prime}\left( \zeta \right)\) improves. Physically, higher \({\text{Re}}\) ensures decay in the viscous nature of the fluid and thus less resistance is required for the fluid motion. Graphene + water based nanofluid shows higher boundary layer compared with Graphene + Ethylene glycol-based nanofluid. This nature may be because viscosity of water is less compared with ethylene glycol. Figures 6 and 7 portray the authority of radiation parameter \(\left( R \right)\) on axial \(f\left( \zeta \right)\) velocity and temperature \(\theta \left( \zeta \right)\) profile. It is pragmatic that increment in \(R\) improves the \(f\left( \zeta \right)\) velocity and reduces the \(\theta \left( \zeta \right)\) profile in both Graphene + Ethylene glycol and Graphene + water nanofluid. It may be due to rotation of the disk. It is also evident that Graphene + water based nanofluid shows higher temperature distribution compared to Graphene + Ethylene glycol based nanofluid. Figures 8–10 illustrate the influence of larger values of Hartman number \(\left( M \right)\) on \(f\left( \zeta \right),f^{\prime}\left( \zeta \right),g(\zeta )\) velocity profiles. Existence of the Lorentz force decreases tangential and radial velocity distributions. Because of the rotation, larger value of \(M\) has no greater influence on axial velocity and thus velocity increases in this direction. Magnitude of velocity distribution is higher for Graphene + water based nanofluid in case of axial direction, whereas in tangential and radial direction magnitude of velocity distribution is higher for Graphene + Ethylene glycol based nanofluid. Figures 11 and 12 depict the influence of increasing values of nonlinear convection variable due to temperature \(\left( {\beta_{{\text{t}}} } \right)\) on \(f\left( \zeta \right)\) and \(f^{\prime}\left( \zeta \right)\) profiles. Improvement in \(\beta_{t}\) increases \(f^{\prime}\left( \zeta \right)\) profiles and decreases \(f\left( \zeta \right)\) profiles. In \(f\left( \zeta \right)\) case Graphene + water profiles shows higher distribution in velocity, whereas in \(f^{\prime}\left( \zeta \right)\) case Graphene + Ethylene glycol mixture shows higher distribution in velocity. In Figs. 13–15, the results due to the improvement in heat generation variable \(\left( \delta \right)\) can be observed. Improvement in \(\delta\) lessens \(f\left( \zeta \right)\) velocity profiles and improves \(f^{\prime}\left( \zeta \right)\) and \(\theta \left( \zeta \right)\) profiles. Graphene + water nanofluid shows higher velocity distribution in case of \(f\left( \zeta \right)\) similar to temperature distribution \(\theta \left( \zeta \right)\) profiles. However, Graphene + Ethylene glycol based nanofluid depicts higher distribution in velocity in case of \(f^{\prime}\left( \zeta \right)\).

Fig. 2
figure 2

Behavior of nanofluid axial velocity for various \({\text{Re}}\)

Full size image
Fig. 3
figure 3

Behavior of nanofluid radial velocity for various \({\text{Re}}\)

Full size image
Fig. 4
figure 4

Behavior of nanofluid tangential velocity for various \({\text{Re}}\)

Full size image
Fig. 5
figure 5

Behavior of nanofluid temperature for various \({\text{Re}}\)

Full size image
Fig. 6
figure 6

Behavior of nanofluid axial velocity for various \(R\)

Full size image
Fig. 7
figure 7

Behavior of nanofluid temperature for various \(R\)

Full size image
Fig. 8
figure 8

Behavior of nanofluid axial velocity for various \(M\)

Full size image
Fig. 9
figure 9

Behavior of nanofluid tangential velocity for various \(M\)

Full size image
Fig. 10
figure 10

Behavior of nanofluid radial velocity for various \(M\)

Full size image
Fig. 11
figure 11

Behavior of nanofluid axial velocity for various \(\beta_{{\text{t}}}\)

Full size image
Fig. 12
figure 12

Behavior of nanofluid radial velocity for various \(\beta_{{\text{t}}}\)

Full size image
Fig. 13
figure 13

Behavior of nanofluid axial velocity for various \(\delta\)

Full size image
Fig. 14
figure 14

Behavior of nanofluid radial velocity for various \(\delta\)

Full size image
Fig. 15
figure 15

Behavior of nanofluid temperature for various \(\delta\)

Full size image

The coefficient of skin friction (radial and tangential direction, \(\left( {c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}} ,c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}} } \right)\)) and Nusselt number \(\left( - Nu\left( {\text{Re}} \right)^{ -{\frac{1}{2}} } \right)\) for Graphene + \({\text{H}}_{2} {\text{O}}\) and Graphene + \(EG\) nanofluid are portrayed in Tables 2 and 3. It is observed that improvement in Reynolds number \(\left( {\text{Re}} \right)\) improves \(c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) and the \(- Nu \left( {\text{Re}} \right)^{\frac{(-1)}{2}}\) but decreases \(c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) for both nanofluid Graphene + water and Graphene + Ethylene glycol. Increasing radiation parameter \(\left( {\text{R}} \right)\) diminishes \(c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) and elevates \(c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) and \(- Nu \left( {\text{Re}} \right)^{\frac{(-1)}{2}}\) in both the nanofluid Graphene + water and Graphene + Ethylene glycol. Improvement in Hartman number \(\left( M \right)\) decreases \(c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) and \(c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) and the \(- Nu \left( {\text{Re}} \right)^{\frac{(-1)}{2}}\) in case of Graphene + water and Graphene + Ethylene glycol nanofluid. Improvement in nonlinear convection variable due to temperature \(\left( {\beta_{{\text{t}}} } \right)\) and heat generation variable \(\left( \delta \right)\) elevates \(c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) and \(- Nu \left( {\text{Re}} \right)^{\frac{(-1)}{2}}\) but decreases \(c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) in both the nanofluid Graphene + water and Graphene + Ethylene glycol. Ethylene glycol-based graphene nanofluid takes less time for execution as compared to water based nanofluid.

Conclusions

Flow and heat transfer of graphene nanoparticles in water- and ethylene glycol based nonlinear convective flow between porous rotating disk and fixed impermeable are studied. The main results are as follows:

  • Intensification in \({\text{Re}}\) ensures decrement in \(f\left( \zeta \right),g\left( \zeta \right),\theta \left( \zeta \right)\) profiles, whereas \(f^{\prime}\left( \zeta \right)\) profile improves.

  • Increment in \(R\) reduces the \(\theta \left( \zeta \right)\) profile in graphene and water mixture and graphene and ethylene glycol mixture.

  • Existence of Lorentz force decreases tangential and radial velocity distribution.

  • Ethylene glycol based graphene nanoparticles take less time for execution compared to water base.

  • Improvement in \(\beta_{{\text{t}}}\) increases \(f^{\prime}\left( \zeta \right)\) profiles and decreases \(f\left( \zeta \right)\) profiles.

  • Improvement in \(\delta\) lessens \(f\left( \zeta \right)\) velocity profiles and improves \(f^{\prime}\left( \zeta \right)\) and \(\theta \left( \zeta \right)\) profiles.

  • Improvement in \(M\) decreases skin friction \(\left( {c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}} ,c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}} } \right)\) along with \(- Nu \left( {\text{Re}} \right)^{\frac{(-1)}{2}}\) in both the nanofluid graphene and ethylene glycol and graphene and water.

  • Improvement in \(\beta_{{\text{t}}}\) and \(\delta\) elevates \(c_{{\text{f}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) and Nusselt number but decreases \(c_{{\text{g}}} \left( {\text{Re}} \right)^{\frac{1}{2}}\) in both the nanofluid graphene and water and graphene and ethylene glycol.