1 Introduction

Polymeric flows are generally non-Newtonian in nature. In coating applications, fluid mechanics and heat transfer play a key role in determining the constitution of manufactured polymers [1]. In dip coating processes, for example, the surface to be coated is first immersed in a polymer and then steadily withdrawn [2]. Since polymers have high viscosity levels, industrial chemical/manufacturing flow processes exploiting such fluids are generally laminar in nature [3]. The rheological nature of polymers also necessitates more sophisticated mathematical models for describing shear stress–strain relationships [4]. Important characteristics include relaxation, retardation, viscoelasticity and elongational viscosity. A number of theoretical and computational studies have been communicated on transport phenomena from cylindrical bodies, which frequently arise in polymer processing systems. These Newtonian studies were focused more on heat transfer aspects and include Eswara and Nath [5], Rotte and Beek [6] and the pioneering analysis of Sakiadis [7]. Further, more recent studies examining multi-physical and chemical transport from cylindrical bodies include Zueco et al. [8, 9]. An early investigation of rheological boundary layer heat transfer from a horizontal cylinder was presented by Chen and Leonard [10] who considered the power-law model and demonstrated that the transverse curvature has a strong effect on skin friction at moderate and large distances from the leading edge of the boundary layer. Lin and Chen [11] also studied axisymmetric laminar boundary layer convection flow of a power-law non-Newtonian fluid over both a circular cylinder and a spherical body using the Merk-Chao series solution method. Pop et al. [12] simulated numerically the steady laminar forced convection boundary layer of power-law non-Newtonian fluids on a continuously moving cylinder with the surface maintained at a uniform temperature or uniform heat flux. Further, non-Newtonian models employed in analyzing convection flows from cylinders include micropolar liquids [13], viscoelastic materials [14, 15], micropolar nanofluids [16] and Casson fluids [17]. One subclass of non-Newtonian fluids known as the Jeffreys fluid [18] is particularly useful owing to its simplicity. This fluid model is capable of describing the characteristics of relaxation and retardation times which arise in complex polymeric flows. Furthermore, the Jeffrey type model utilizes time derivatives rather than convected derivatives, which make it more amenable for numerical simulations. Recently, the Jeffreys model has received considerable attention. Interesting studies employing this model include peristaltic magnetohydrodynamic non-Newtonian flow [19], variable-viscosity peristaltic flow [20], convective-radiative flow in porous media [21] and stretching sheet flows [22, 23].

Heat and mass transfer in porous media arise in an extensive array of applications in modern nuclear engineering, mineral and chemical process engineering. These include transport of nuclear waste in geomaterial repositories [24–26], petroleum product filtration [27] and insulation systems [21]. The non-Newtonian nature of waste products has been identified by various studies [28]. Simulations of non-Newtonian transport in porous media have, therefore, employed a diverse range of rheological models including Bingham plastic models [29], capillary hybrid viscoelastic models incorporating a viscous mode and an elongational mode [30], viscoplastic Schwedoff-Bingham fluids [31], Maxwell fluids [32], power-law fluids [33] and pseudoplastic fluids [34], Stokesian couple stress fluids [35] and Reiner-Rivlin third-grade differential liquids [36]. These studies have adopted a variety of simulation approaches for porous media including percolation theory [31], volume-averaging [32] and network modeling [34]. They have generally employed the Darcy model which is valid for viscous-dominated low Reynolds number transport. Kadet and Polonski [31], however, also considered inertial (Forchheimer) losses for higher Reynolds numbers. Non-Darcian flows may involve Forchheimer effects and also Brinkman vorticity diffusion effects, channeling, tortuosity and other phenomena. Vafai [37] presented a seminal theoretical and experimental study of the influence of variable porosity and also inertial forces (Forchheimer drag) on thermal convection flow in porous media, with the channeling effect being studied in detail. He elucidated the qualitative aspects of variable porosity in generating the channeling effect with an asymptotic analysis. A number of investigations have subsequently addressed rheological flows in non-Darcian porous media. Bég et al. [38] used a finite element method to simulate micropolar heat and mass transfer in Darcy–Forchheimer porous media with cross-diffusion effects. Kairi and Murthy [39] analyzed the influence of melting and Soret diffusion on mixed convection heat and mass transfer from vertical surface adjacent to an Ostwald–de Waele power law fluid-saturated non-Darcy porous medium. Bég et al. [40] used an electrical thermal network solver code (PSPICE) to simulate the magnetohydrodynamic heat transfer in Walter-B viscoelastic flow in Darcy–Forchheimer porous media. Prasad et al. [41] studied the non-Darcy effects on thermal convection boundary layer flow of a second-order Reiner-Rivlin fluid in a porous medium. Rashidi et al. [42] used a differential transform numerical solver to study Forchheimer drag and buoyancy effects on magneto-micropolar thermal convection in a vertical porous medium conduit.

The objective of the present paper is to investigate the laminar boundary layer flow, heat and mass transfer of a Jeffreys non-Newtonian fluid from a horizontal isothermal cylinder in a non-Darcy porous medium. The non-dimensional transport equations with associated dimensionless boundary conditions constitute a highly non-linear, coupled two-point boundary value problem. Keller’s implicit finite difference “box” scheme is implemented to solve the problem. The effects of the emerging thermo-physical parameters, namely Prandtl number (Pr), Deborah number (De), ratio of relaxation to retardation times (λ), Forchheimer inertial parameter (Λ), Darcy number (Da) and transpiration (wall suction or injection) on the velocity, temperature, concentration, local skin friction, heat transfer rate (local Nusselt number) and mass transfer rate (local Sherwood number) characteristics are studied. The present problem has to the authors’ knowledge not appeared thus far in the scientific literature and is relevant to polymeric manufacturing processes.

2 Non-Newtonian constitutive Jeffrey fluid model

In the present study, a subclass of non-Newtonian viscoelastic fluids known as the Jeffreys fluid [20–23] is employed owing to its simplicity. This fluid model is capable of describing the characteristics of relaxation and retardation times which arise in complex polymeric flows. Furthermore, the Jeffrey type model utilizes time derivatives rather than convected derivatives, which greatly facilitates numerical simulations. The Cauchy stress tensor, T, of a Jeffreys non-Newtonian fluid [43] takes the form:

$$\begin{gathered} {\mathbf{T}} = - p{\mathbf{I}} + {\mathbf{S}},\,\, \hfill \\ \tau + \lambda_{1} \frac{\partial \tau }{\partial t}\, = \,\mu \left( {\mathop \gamma \limits^{.} \, + \,\lambda_{2} \,\frac{{\partial \mathop \gamma \limits^{.} }}{\partial t}} \right)\, \hfill \\ \end{gathered}$$
(1)

where S is the extra stress tensor, p is the pressure, I is the identity tensor, This is a linear model proposed as an extension to the Maxwell model by including a time derivative of the strain rate, that is where is the retardation time that accounts for the corrections of this model and can be seen as a measure of the time the material needs to respond to deformation. The Jeffreys model has three constants: a viscous parameter μ, and two elastic parameters λ 1 and λ 2. The Jeffreys model provides an elegant formulation for simulating elastic effects arising in non-Newtonian flows. The shear stress rate and gradient of shear stress rate are further defined in terms of velocity vector, V, as:

$$D \, = \nabla {\text{V}} + \, (\nabla {\text{V}})^{\text{T}}$$
(2)
$$\mathop D\limits^{.} = \frac{\text{d}}{{{\text{d}}t}}(D) = \frac{\partial }{\partial t}\left( D \right) + \left( {V.\nabla } \right)D.$$
(3)

The introduction of the appropriate terms into the flow model is considered next. The resulting boundary value problem is found to be well posed and permits an excellent mechanism for the assessment of rheological characteristics on the flow behavior.

3 Mathematical model

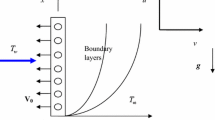
Laminar incompressible boundary layer flow, heat and mass transfer under thermal buoyancy force from a horizontal isothermal cylinder in a non-Darcy porous medium to a Jeffreys rheological fluid is examined, as illustrated in Fig. 1. Both cylinder and Jeffreys fluid are maintained initially at the same temperature and concentration. Instantaneously they are raised to a temperature T w  > T ∞ and the concentration C w  > C ∞, where the latter (ambient) temperature and concentration of the fluid are sustained constant. The x-coordinate (tangential) is orientated along the circumference of the horizontal cylinder from the lowest point and the y-coordinate (radial) is directed perpendicular to the surface, with a denoting the radius of the horizontal cylinder. Φ = x/a represents the angle of the y-axis with respect to the vertical (0 ≤ Φ ≤ π). The gravitational acceleration g, acts vertically downwards. The Boussinesq approximation holds, i.e., density variation is only experienced in the buoyancy term in the momentum equation.

Fig. 1
figure 1

Physical model and coordinate system

Full size image

The Jeffreys model provides an elegant formulation for simulating retardation and relaxation effects arising in polymer flows. Introducing the boundary layer approximations, and incorporating the stress tensor for a Jeffreys fluid in the momentum equation (in differential form), the conservations equations take the form:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$
(4)
$$\begin{gathered} u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \frac{\nu }{1 + \lambda }\left( {\frac{{\partial^{2} u}}{{\partial y^{2} }} + \lambda_{1} \left( {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} - \frac{\partial u}{\partial x}\,\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\partial u}{\partial y}\frac{{\partial^{2} u}}{\partial x\partial y} + v\frac{{\partial^{3} u}}{{\partial y^{3} }}} \right)} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\; + g\beta \left( {T - T_{\infty } } \right)\sin \left( \frac{x}{a} \right) + g\beta^{*} \left( {C - C_{\infty } } \right)\sin \left( \frac{x}{a} \right) - \frac{\nu }{K}u - \varGamma u^{2} \hfill \\ \end{gathered}$$
(5)
$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }}$$
(6)
$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{m}} \frac{{\partial^{2} C}}{{\partial y^{2} }}.$$
(7)

The Jeffreys fluid model, therefore, introduces a number of mixed derivatives into the momentum boundary layer Eqs. (3, 5) and in particular two-third order derivatives, making the system an order higher than the classical Navier–Stokes (Newtonian) viscous flow model. The non-Newtonian effects feature in the shear terms only of Eqs. (3, 5) and not the convective (acceleration) terms. The second term on the right hand side of Eqs. (3, 5) represents the thermal buoyancy force and couples the velocity field with the temperature field Eq. (6). The third term on right hand side of Eqs. (3, 5) represents the species buoyancy effect (mass transfer) and couples Eqs. (3, 5) to the species diffusion Eq. (7). The fourth and fifth terms on the right hand side of Eqs. (3, 5) denote the Darcian linear drag and Forchheimer second-order drag, respectively. Viscous dissipation effects are neglected in the model. In Eqs. (2)–(7), u and v designate velocity components in the x- and y-directions, respectively, ν = μ/ρ, kinematic viscosity of the Jeffreys fluid; β, coefficient of thermal expansion; β *, coefficient of concentration expansion; K, permeability (hydraulic conductivity) of the porous medium; Γ, Forchheimer inertial drag coefficient of the porous medium; α, thermal diffusivity; T, temperature; C, concentration; ρ, density of the Jeffreys fluid; D m, mass (species) diffusivity, and all other parameters have been defined earlier. The appropriate boundary conditions are imposed at the cylinder surface and in the free stream (edge of the boundary layer) and take the form:

$$\begin{gathered} {\text{At}}\,\,\,\,\,y = 0,\quad u = 0,\quad v = - V_{w} ,\,\quad T = T_{w} ,\quad C = C_{w} \hfill \\ {\text{As}}\,\quad y \to \infty ,\,\quad u \to 0,\quad v \to 0,\quad T \to T_{\infty } ,\quad C \to C_{\infty } \hfill \\ \end{gathered}$$
(8)

V w denotes the uniform transpiration (blowing or suction) velocity at the surface of the permeable cylinder, T ∞ the free stream temperature, C ∞ the free stream concentration. To transform the boundary value problem to a dimensionless one, we introduce a stream function ψ defined by the Cauchy–Riemann equations, \(u = \frac{\partial \psi }{\partial y}\) and \(v = - \frac{\partial \psi }{\partial x}\), and therefore, the mass conservation Eqs. (2, 4) is automatically satisfied. Furthermore, the following dimensionless variables are introduced into Eqs. (3)–(7) and (8):

$$\begin{gathered} \xi = \frac{x}{a},\quad \eta = \frac{y}{a}\sqrt[4]{Gr},\quad f\left( {\xi ,\eta } \right) = \frac{\psi }{{\nu \xi \sqrt[4]{Gr}}},\quad \theta \left( {\xi ,\eta } \right) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\quad \varphi \left( {\xi ,\eta } \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }} \hfill \\ Pr = \frac{\nu }{\alpha },\quad Sc = \,\frac{\nu }{{D_{m} }}\,,\,\quad f_{w} = - \frac{{V_{w} a}}{{\nu^{4} \sqrt {Gr} }},\quad Gr = \frac{{g\beta \left( {T_{w} - T_{\infty } } \right)a^{3} }}{{\nu^{2} }},\,\quad De = \frac{{\lambda_{1} \nu \sqrt {Gr} }}{{a^{2} }} \hfill \\ \end{gathered}$$
(9)

where ξ is the non-dimensional tangential coordinate, η the non-dimensional radial coordinate, f the dimensionless stream function, Pr the Prandtl number, f w the wall transpiration parameter (f w  > 0 for suction and f w  < 0 for injection, the case of an impermeable cylinder is retrieved for f w  = 0), Gr the Grashof number and De the Deborah number. The resulting momentum, energy and concentration boundary layer equations take the form:

$$\begin{gathered} \frac{1}{1 + \lambda }f^{\prime \prime \prime} \, + ff^{\prime \prime} + \frac{De}{1 + \lambda }\left( {f^{\prime \prime ^{2}} - ff^{\text{iv}} } \right) - (1 + \varLambda \xi )\left( {f^{\prime} } \right)^{2} + \frac{\sin \xi }{\xi }(\theta + N\phi ) - \frac{1}{Da}f^{\prime} \hfill \\ \,\quad \, = \,\xi \left( {f^{\prime} \frac{\partial f^{\prime} }{\partial \xi } - f^{\prime \prime} \frac{\partial f}{\partial \xi } - \frac{De}{1 + \lambda }\left( {f^{\prime} \frac{\partial f^{\prime \prime \prime} }{\partial \xi } - f^{\prime \prime \prime} \frac{\partial f^{\prime} }{\partial \xi } + f^{\prime \prime} \frac{\partial f^{\prime \prime} }{\partial \xi } - f^{\text{iv}} \frac{\partial f}{\partial \xi }} \right)} \right) \hfill \\ \end{gathered}$$
(10)
$$\frac{\theta^{\prime \prime}}{Pr} + f\theta^{\prime} = \xi \left( {f^{\prime} \frac{\partial \theta }{\partial \xi } - \theta^{\prime} \frac{\partial f}{\partial \xi }} \right)$$
(11)
$$\frac{\phi^{ \prime \prime} }{Sc} + f\phi^{ \prime} = \xi \left( {f^{\prime} \frac{\partial \phi }{\partial \xi } - \phi^{ \prime} \frac{\partial f}{\partial \xi }} \right).$$
(12)

The location, ξ ~ 0, corresponds to the vicinity of the lower stagnation point on the cylinder, an aspect discussed in more detail subsequently. The corresponding non-dimensional boundary conditions for the collectively sixth-order, multi-degree partial differential equation system defined by Eqs. (10)–(12) assume the form:

$$\begin{gathered} {\text{At}}\quad \eta = 0,\quad f = f_{w} ,\quad f^{\prime} = 0,\quad \theta = 1,\quad \phi = 1 \hfill \\ {\text{As}}\quad \eta \to \infty ,\quad f^{\prime} \to 0,\quad f^{\prime \prime} \to 0,\quad \theta \to 0,\quad \phi \to 0 \hfill \\ \end{gathered}$$
(13)

Here, primes denote the differentiation with respect to η. Λ = Γa, local inertia coefficient (Forchheimer parameter); \(N = \frac{{\beta^{*} \left( {C_{w} - C_{\infty } } \right)}}{{\beta \left( {T_{w} - T_{\infty } } \right)}}\), the concentration to thermal buoyancy ratio parameter; \(Da = \frac{{K\sqrt {Gr} }}{{a^{2} }}\), the Darcy parameter; β *(C w  − C ∞), Schmidt number; \(f_{w} = - \frac{{V_{w} a}}{{\nu \sqrt[4]{Gr}}}\), blowing/suction parameter. The skin friction coefficient (shear stress at the cylinder surface), Nusselt number (heat transfer rate at the cylinder surface) and Sherwood number (mass transfer rate at the cylinder surface) can be defined using the transformations described above with the following expressions:

$$\frac{1}{2}C_{\text{f}} Gr^{{3/4}} = \xi f\prime \prime \left( {\xi ,0} \right)$$
(14)
$$\frac{Nu}{{\sqrt[4]{Gr}}} = - \theta^{ \prime} \left( {\xi ,0} \right)$$
(15)
$$\frac{Sh}{{^{4} \sqrt {Gr} }} = - \varphi^{\prime}(\xi ,0)$$
(16)

4 Computational finite differences solution

Purely analytical solutions for the boundary value problem defined by Eqs. (10)–(12) and conditions (13) are extremely difficult, if not intractable. A computational solution is, therefore, developed using a versatile and stable finite difference algorithm based on Keller’s box method [44]. This implicit method has been implemented extensively in non-Newtonian fluid mechanics simulations for a variety of different rheological models. Hossain et al. [45] used a power-law model and Keller’s scheme to study free convection boundary layers from a slotted vertical plate. Javed et al. [46] employed the Eyring–Powell rheological model and the Keller box method to simulate stretching sheet boundary layer flow. Bég et al. [47] used Keller’s box algorithm to study magneto-viscoelastic natural convection from a wedge in porous media. Further, non-linear thermal convection studies using Keller’s box method include Vajravelu et al. [48, 49], Bég et al. [50] and Vasu et al. [51]. The present code has received extensive validation in previous studies, as described in [52–55] and therefore, confidence is high in the accuracy of computations. The fundamental steps of the Keller Box Scheme are as follows:

  1. 1.

    Reduction of the Nth order partial differential equation system to N first order equations

  2. 2.

    Finite Difference Discretization

  3. 3.

    Quasilinearization of Non-Linear Keller Algebraic Equations

  4. 4.

    Block-tridiagonal Elimination of Linear Keller Algebraic Equations

5 Results and discussion

Comprehensive solutions have been obtained and are presented in Tables 1, 2, 3, 4 and 5 and Figs. 2, 3, 4, 5, 6, 7, 8 and 9. The numerical problem comprises two independent variables (ξ, η), three dependent fluid dynamic variables (f, θ, ϕ) and nine thermo-physical and body force control parameters, namely, De, λ, Da, Λ, Pr, Sc, N, f w . The following default parameter values, i.e., De = 0.1, λ = 0.2, Da = 0.1, Λ = 0.1, Pr = 0.71, Sc = 0.6, N = 0.5, f w  = 0.5 are prescribed (unless otherwise stated).

Table 1 Values of the local heat transfer coefficient (Nu) for various values of ξ with De = 0.0, λ = 0.0, Da → ∞, Λ = 0, Pr = 0.71, N = 0, f w  = 0, Sc = 0.6
Full size table
Table 2 Values of f ′′(ξ, 0), −θ ′(ξ, 0) and −ϕ ′(ξ, 0) for different De, Sc and ξ (λ = 0.2, Pr = 0.71, N = 0.5, Da = 0.1, f w  = 0.5, Λ = 0.1)
Full size table
Table 3 Values of f″(ξ, 0), −θ′(ξ, 0) and −ϕ′(ξ, 0) for different values of De, Sc and ξ (\(\lambda = 0.2,\;Pr = 0.71,\;N = 0.5,\;Gr = 1.0,\;Da = 0.1,\;f_{w} = 0.5,\;\varLambda = 0.1\))
Full size table
Table 4 Values of f ′′(ξ, 0), −θ ′(ξ, 0) and −ϕ ′(ξ, 0) for different λ, Pr and ξ \(\left( {De = 0.1, \, N{ = 0} . 5 , { }Sc = 0.6,\;f_{w} { = 0} . 5 , { }Da{ = 0} . 1 , { }\varLambda { = 0} . 1} \right)\)
Full size table
Table 5 Values of f ′′(ξ, 0), −θ ′(ξ, 0) and −ϕ ′(ξ, 0) for different λ, Pr and ξ \(\left( {De = 0.1, \, N{ = 0} . 5 , { }Sc = 0.6,\;f_{w} { = 0} . 5 , { }Da{ = 0} . 1 , { }\varLambda { = 0} . 1} \right)\)
Full size table
Fig. 2
figure 2

a Influence of De on velocity profiles, b influence of De on temperature profiles, c influence of De on concentration profiles

Full size image
Fig. 3
figure 3

a Influence of λ on velocity profiles, b influence of λ on temperature profiles, c influence of λ on concentration profiles

Full size image
Fig. 4
figure 4

a Influence of Λ on velocity profiles, b influence of Λ on temperature profiles, c influence of Λ on concentration profiles

Full size image
Fig. 5
figure 5

a Influence of Da on velocity profiles, b influence of Da on temperature profiles, c influence of Da on concentration profiles

Full size image
Fig. 6
figure 6

a Influence of ξ on velocity profiles, b influence of ξ on temperature profiles, c influence of ξ on concentration profiles

Full size image
Fig. 7
figure 7

a Influence of f w on velocity profiles, b influence of f w on temperature profiles, c influence of f w on concentration profiles

Full size image
Fig. 8
figure 8

a Influence of De on local skin friction number, b influence of De on Nusselt number, c influence of De on local Sherwood number

Full size image
Fig. 9
figure 9

a Influence of λ local skin friction number, b influence of λ on Nusselt number, c influence of λ on local Sherwood number

Full size image

Table 1 presents the values of local heat transfer coefficient (Nu) for different values of ξ and is compared with those of Merkin [59] and Yih [60]. Excellent correlation with previous studies is demonstrated testifying to the validity of the present code.

Tables 2 and 3 presents the influence of increasing Prandtl number (Pr) on skin friction, heat transfer rate and mass transfer rate, along with a variation in the parameter (λ), ratio of relaxation and retardation times and transverse coordinate (ξ). With increasing Prandtl number, the skin friction is generally decreased, whereas heat transfer rate is markedly enhanced. Heat transfer rate is maximized at the lower stagnation point (ξ = 0), for any value of Prandtl number or rheological parameter (λ). And an increase in Prandtl number decreases the mass transfer rate. With an increase in λ, all the three i.e., the skin friction, heat transfer rate and mass transfer rate are increased. This implies that as the relaxation time is reduced (and the retardation time increased) the polymer flows faster and also transfers heat more efficiently from the cylinder surface. This appears consistent with other studies [21, 22]. In Table 2, f w is positive corresponding to wall suction.

Tables 4 and 5 presents the influence of increasing Deborah number parameter, De on skin friction, heat transfer rate and mass transfer rate, along with a variation in the Schmidt number (Sc) and transverse coordinate, ξ. With increasing Deborah number, the skin friction is generally decreased, and heat transfer rate and mass transfer rates are also decreased. This trend is sustained for all values of transverse coordinate. An increase in Schmidt number reduces skin friction and heat transfer rates at higher values of the transverse coordinate, for any value of Deborah number. But the mass transfer rate is markedly enhanced with increasing Schmidt number. In the vicinity of the lower stagnation point, ξ → 0 and the boundary layer equations Eqs. (10) to (12) contract to a system of ordinary differential equations:

$$\frac{1}{1 + \lambda }f^{\prime \prime \prime} + ff^{\prime \prime} - \frac{De}{1 + \lambda }ff^{iv} + \frac{De}{1 + \lambda }f^{\prime \prime 2} - f^{\prime 2} + (\theta + N\varphi ) - \frac{1}{Da}f^{\prime} = 0$$
(17)
$$\frac{1}{Pr}\left( {1 + \frac{4}{3F}} \right)\theta^{ \prime} + f\theta^{ \prime} + \varDelta \theta = 0$$
(18)
$$\frac{{\phi^{\prime \prime } }}{Sc} + f\phi^{ \prime} = 0$$
(19)

Since \(\frac{\sin \xi }{\xi } \to \frac{0}{0}\) i.e. 1, so that \(\frac{\sin \xi }{\xi }\theta \to \theta\). At the upper stagnation point, ξ ~ π.

In Figs. 2a–c, the evolution of velocity (f′), temperature (θ) and concentration (ϕ) functions with a variation in Deborah number, De, is depicted. Dimensionless velocity component (Fig. 2a) is considerably reduced with increasing De near the cylinder surface and for some distance into the boundary layer. De clearly arises in connection with some high order derivatives in the momentum boundary layer equation, (10) i.e. \(\frac{De}{1 + \lambda }[f^{\prime \prime 2} - ff^{\text{iv}} ]\) and also \(\xi \left( { - \frac{De}{1 + \lambda }\left[ {f\prime \frac{{\partial f^{\prime \prime \prime } }}{\partial \xi } - f\prime \prime \prime \frac{{\partial f^{\prime } }}{\partial \xi } + f^{\prime \prime } \frac{{\partial f^{\prime \prime } }}{\partial \xi } - f^{\text{iv}} \frac{\partial f}{\partial \xi }} \right]} \right)\). It, therefore, is intimately associated with the shearing characteristics of the polymer flow. Further, from the cylinder surface, we observe that there is a slight increase in velocity, i.e., the flow is accelerated with increasing Deborah number. With greater distance from the solid boundary, the polymer is, therefore, assisted in flowing even with higher elastic effects. Clearly the responses in the near-wall region and far-field region are very different. In Fig. 2b, an increase in Deborah number is seen to considerably enhance temperatures throughout the boundary layer regime. This has also been observed by Hayat et al. [21]. Although, De does not arise in the thermal boundary layer Eq. (11), there is a strong coupling of this equation with the momentum field via the convective terms \(\xi \left[ {f^{\prime}\frac{\partial \theta }{\partial \xi }} \right]\) and \(\xi \left[ { - \theta^{\prime}\frac{\partial f}{\partial \xi }} \right]\). Furthermore, the thermal buoyancy force term, \(+ \frac{\sin \xi }{\xi }\theta\), in the momentum Eq. (10) strongly couples the momentum flow field to the temperature field. With greater elastic effects, it is anticipated that thermal conduction plays a greater role in heat transfer in the polymer. Thermal boundary layer thickness is also elevated with increasing Deborah number. Figure 2c shows a slight increase in concentration is achieved with increasing De values.

Figure 3a–c illustrates the effect of the ratio of relaxation to retardation times, i.e., λ on the velocity(f′), temperature (θ) and concentration (ϕ) distributions through the boundary layer regime. Velocity is significantly increased with increasing λ, in particular close to the cylinder surface. The polymer flow is, therefore ,considerably decelerated with an increase in relaxation time (or decrease in retardation time). Conversely temperature and concentration are depressed slightly with increasing values of λ. The mathematical model reduces to the Newtonian viscous flow model as λ → 0 and De → 0, since this negates relaxation, retardation and elasticity effects. The momentum boundary layer equation in this cases contracts to the familiar equation for Newtonian mixed convection from a cylinder:

$$f^{\prime \prime \prime } + ff^{\prime \prime} - f^{\prime{2}} + \frac{\sin \xi }{\xi }\theta = \xi \left( {f^\prime \frac{\partial f^\prime }{\partial \xi } - f^{\prime \prime} \frac{\partial f}{\partial \xi }} \right)$$
(20)

The thermal boundary layer equation and the concentration Eqs. (11–12) remain unchanged. Effectively with greater relaxation time of the polymer the thermal boundary layer thickness is reduced. However with greater relaxation times, the momentum boundary layer thickness is only decreased near the cylinder surface; whereas further away it is enhanced since the flow is strongly accelerated there.

Figure 4a–c presents typical profiles for velocity (f′), temperature (θ) and concentration (ϕ) for various values of Forchheimer inertial parameter Λ. This parameter is associated with the second-order Forchheimer resistance term, −ξΛ(f′)2 in the momentum Eq. (10). Forchheimer drag is directly proportional to the parameter, Λ. An increase in Λ markedly decelerates the flow as illustrated in Fig. 4a, for some considerable distance into the in the boundary layer, transverse to the cylinder surface. Inertial quadratic drag has a stronger effect closer to the wall. Kaviany [56] has indicated that Forchheimer effects are associated with higher velocities in porous media transport. Forchheimer drag, however, is second order and the increase in this “form” drag effectively swamps the momentum development, thereby decelerating the flow, in particular near the cylinder surface. The term “non-Darcian” does not allude to a different regime of flow, but to the amplified effects of Forchheimer drag at higher velocities, as elaborated also in Bég et al. [40] and Prasad et al. [52]. With a dramatic increase in Λ, there is also a slight elevation in temperatures (Fig. 4b) in the regime. The deceleration in the flow generates a decrease in momentum boundary layer thickness which aids in energy diffusion and a thickening in the thermal boundary layer. The influence on the concentration (species diffusion) field (Fig. 4c) is similar to that of the temperature field. However, with the same increment in Forchheimer parameter, greater disparity in concentration profiles is caused. Concentration (ϕ) is markedly increased, in particular at some distance from the cylinder surface, with an increase in Forchheimer parameter, Λ. As with temperature response, the concentration profiles exhibit a monotonic decay from the cylinder surface to the edge of the boundary layer regime.

Figure 5a–c depict the velocity (f′), temperature (θ) and concentration (ϕ) distributions for various values of Darcy parameter, Da. Velocity is clearly enhanced considerably with increasing Darcy number as shown in Fig. 5a, since greater permeability of the regime corresponds to a decrease in Darcian drag force. The velocity peaks close to the cylinder surface are also found to be displaced further from the wall with increasing Darcy number. A very strong decrease in temperature (θ) and concentration (ϕ), as shown in Fig. 5b, c, respectively, occurs with increasing Da values. The progressive reduction in solid fibers in the porous medium with large Da values serves to decrease thermal conduction heat transfer in the regime. This inhibits the diffusion of thermal energy from the cylinder surface to the regime and cools the boundary layer also decreasing thermal boundary layer thickness. Concentration boundary layer thickness will also be decreased with a rise in Darcy number.

Figure 6a–c depict the velocity (f′), temperature (θ) and concentration (ϕ) distributions with radial coordinate, for various transverse (stream wise) coordinate values, ξ. Generally velocity is noticeably lowered with increasing migration from the leading edge, i.e., larger ξ values (Fig. 6a). The maximum velocity is computed at the lower stagnation point (ξ ~ 0) for low values of radial coordinate (η). The transverse coordinate clearly exerts a significant influence on momentum development. A very strong increase in temperature (θ), as observed in Fig. 6b, is generated throughout the boundary layer with increasing ξ values. The temperature field decays monotonically. Temperature is maximized at the cylinder surface (η = 0) and minimized in the free stream (η = 25). Although the behavior at the upper stagnation point (ξ ~ π) is not computed, the pattern in Fig. 6b suggests that temperature will continue to progressively grow here compared with previous locations on the cylinder surface (lower values of ξ). Similar behavior has been observed with respect to the concentration as that of temperature.

Figure 7a–c present typical profiles for velocity (f′), temperature (θ) and concentration (ϕ) for various values of the transpiration parameter, f w . As in all other graphs, only the case of wall suction is studied (f w  > 0). It is observed that an increase in the suction parameter significantly decelerates the flow for all values of radial coordinate. The boundary layer thickness is reduced and suction causes the boundary layer to adhere closer to the wall. Similarly increasing wall suction is found to lower temperatures and concentration in the boundary layer regime and strongly decreases thermal boundary layer thickness. Although boundary layer separation has not been identified in the present regime, suction has been shown to delay this effect in certain viscoelastic cylinder flow problems [14].

Figure 8a–c show the influence of Deborah number, De on dimensionless skin friction coefficient (ξf″(ξ, 0)), heat transfer rate (θ′(ξ, 0)) and mass transfer rate (ϕ′(ξ, 0)) at the cylinder surface. It is observed that the dimensionless skin friction is decreased with the increase in the De, i.e., the boundary layer flow is decelerated. Likewise, on the other hand, the heat transfer rate is also substantially decreased with increasing De values. There is also a progressive decay in heat transfer rate (local Nusselt number) with increasing tangential coordinate, i.e., ξ-value. A decrease in heat transfer rate at the wall will imply less heat is convected from the fluid regime to the cylinder, thereby heating the boundary layer. The mass transfer rate (local Sherwood number) is also found to be suppressed with increasing values of De and furthermore plummets with further distance from the lower stagnation point (i.e. higher ξ values).

Figure 9a–c illustrates the response to the parameter ratio of relaxation and retardation times, λ, on the dimensionless skin friction coefficient (ξf″(ξ, 0)), heat transfer rate (θ′(ξ, 0)) and mass transfer rate (ϕ′(ξ, 0)) at the cylinder surface. The skin friction at the cylinder surface is accentuated with increasing λ. Also there is a strong elevation in shear stress (skin friction coefficient) with increasing value of the tangential coordinate, ξ. The flow is, therefore, strongly accelerated along the cylinder surface away from the lower stagnation point. Heat (local Nusselt number) and mass transfer (local Sherwood number) rates are increased with increasing, λ, although not as profoundly as the skin friction. With increasing values of the tangential coordinate, ξ; however, both local Nusselt number and local Sherwood number are depressed. As elaborated earlier, these characteristics are only maximized at the lower stagnation point.

6 Conclusions

A mathematical model has been developed for boundary layer mixed convection flow of a Jeffreys non-Newtonian fluid from a horizontal cylinder, with wall transpiration. The transformed conservation equations have been solved with prescribed boundary conditions using the implicit Keller box finite difference method. The present simulations have shown that:

  1. 1.

    Increasing the viscoelasticity parameter, i.e., Deborah number (De), reduces the velocity, skin friction, heat transfer rate and mass transfer rates; whereas it enhances temperature and concentration boundary layer thickness.

  2. 2.

    Increasing the parameter ratio of relaxation and retardation times (λ), increases velocity, skin friction coefficient, heat transfer rate and mass transfer rates; whereas it reduces temperature and concentration for all values of radial coordinate.

  3. 3.

    Increasing Forchheimer parameter, Λ, decelerates the flow; whereas it elevates both temperature and concentration magnitudes.

  4. 4.

    Increasing transverse coordinate (ξ) generally decelerates the flow near the cylinder surface and reduces momentum boundary layer thickness; whereas it enhances temperature and concentration. Heat transfer rate is also maximized at the lower stagnation point (ξ = 0).

  5. 5.

    Increasing suction at the cylinder surface (f w  > 0) decelerates the flow and also strongly depresses temperature and concentration.

Generally, very stable and accurate solutions are obtained with the present finite difference code and it is envisaged that other non-Newtonian flows will be studied using this methodology in the future including Maxwell upper convected fluids [27], Walters-B liquids [57] and couple stress fluids [58].