Introduction

Convection heat transfer is one of the most important and most widely used industrial topics which has always been studied by the energy due to the optimization of energy efficiency. On the other hand, the global development of research on microelectromechanical (MEMS) and nanoelectromechanical (NEMS) systems suggests the growth of investment and the use of this technology in a variety of areas, including the automotive industry, medicine, and electronic applications in telecommunication and defense systems. The abundant capabilities of this field have accelerated innovation and increased patents in the field of microprocessors. Therefore, the use of lattice Boltzmann method which is appropriate for flow simulation in microscopic dimensions is increasing [1].

So far various numerical methods have been introduced for analyzing and simulating heat transfer. Generally, the fluid flow can be in two ways. The first method involves fluid continuum in which macroscopic equations are presented. The classic Navier–Stokes (NS) equations [2] contain the same method. The second method consists of particle-based methods the performance of which is based on the action and reaction between fluid particles [3]. This method has a large volume and is not suitable for use in macroscopic dimensions. The lattice Boltzmann method (LBM) is one of the particle-based methods with lower computational cost than other particle-based methods such as the molecular dynamics (MD) method and direct simulation of Monte Carlo (DSMC) [4,5,6]. Therefore, many researchers have used this method [7, 8]. The lattice Boltzmann method is a new way for simulating compressible viscose flows and has the most application range in a variety of fluid flow regimes. This method can well be used to simulate convective flow and heat transfer in multi-phase, liquid–gas systems in microscopic dimensions [9,10,11]. In LBM by averaging the microscopic particles’ properties, it is possible to gain macroscopic quantities of the flow and provide the mass and momentum survival equations [12,13,14,15]. The performance of this method involves the steps of collision at a location and diffusion within the range of fluid flow [16]. The BGK operator [17] is used o express the particles’ collision where the Boltzmann equation has a proper accuracy and has a good convergence in the thermal lattice Boltzmann which is also based on internal energy of the fluid [18,19,20,21].

The desirability of this method has led to its increasing use in the studies conducted by the engineers and has made it more versatile in fluid flow simulations by providing different models [22,23,24]. Microstructure simulation using LBM and Langmuir slip model adoption by Chen et al. [25] is an example of it. He introduced the developed Langmuir slip model instead of Maxwell slip model that had a brighter physical image. Also, the relationship between the molecular slip coefficient and the macroscopic slip length in a Newtonian fluid proposed using LBM by Oldrich and Jan [26] is an alternative method for calculating the local shear rate for calculating the macroscopic slip length. Due to the wide application of LBM and the presentation of varied models, modified relationships are proposed to be applied in solving various problems including the introduction of a modified Richardson number by Monfared et al. [27]. They used LBM to determine the thermal flux in a successive square cylinder with the constant thermal flux boundary condition in 2D mode. The results of their work showed that using the buoyancy force term in hydrodynamic and thermal equations creates a vortex phenomenon in the fluid flow and the amount of buoyancy force has a great effect on the start of the vortex and the lift and drag force. The LBM has a good accuracy in simulating irregular geometries and complicated boundary conditions [28, 29], and it has an optimal performance in the analysis of channels with curved walls [30]. Also, the simulation of the displacement of the fluid inside the chamber and the obstructed channels by LBM has been reported in many studies [31,32,33,34].

In recent years, various simulations have been performed in various conditions [35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88]. Also the analysis of the Couette and Poiseuille flow within a microchannel has been studied by LBM under various conditions using [39,40,41]. Gas flow analysis within microchannels is very important in engineering fields due to its diverse applications. Shu et al. [42] studied the gas flow inside the microchannel with the aid of the diffuse scattering boundary condition (DSBC) using LBM. In adapting his results, he was able to provide an acceptable mathematical model for simulating the flow of microchannels. Liu and colleagues studied the gas flow in a long microchannel using the LBM. He showed that LBM equation can describe the flow behavior of the fluid in the transient region. Then Yun and Rahman [44] studied the gas flow in the microchannel by means of LBM for a range of different Knudsen numbers with several comfort times. They examined the effect of the Knudsen layer on the gas flow rate for different Knudsen numbers.

The present study simulates the effect of buoyancy force on the flow components in the microchannel using LBM and simulates the effect of varying slip flow parameters such as Grashof number and slip coefficient on the hydrodynamic and thermal properties of the fluid flow.

Statement of the problem

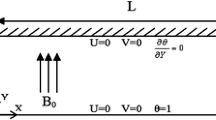
In the present work, the mixed convection of heat transfer is investigated in microscopic dimensions. Here the water/functionalized multi-wall carbon nanotube (FMWCNT) nanofluid mixed convection is studied in a long 2-D microchannel under fixed wall temperature in slip flow regime and by using LBM. The force of mass as an external force influences the collision between fluid particles and the fluid flow causes mixed convection movements within the microchannel. The cold air flows into the microchannel and leaves it after cooling the walls, Tw = 2Tc. In parallel with this flow, gravity also changes the velocity components in the direction of perpendicular to the flow and by creating a vertical temperature gradient creates free convection. Since the Reynolds number is small in the microchannel, the presumed value for Reynolds is equal to Re = 0.01 and Pr = 4.42 which represents the mass fraction of 0.0025 of FMWCNT in water [45].

The effect of gravity on the formation of mixed convection is investigated on different flow parameters for B = 0.1, 0.01 and 0.001 and Gr = 1, 10 and 100. The flow is in a two-dimensional microchannel with an aspect ratio of AR = 30 and hot walls. Because of the length of the microchannel after the input, the conditions are fully developed for velocity and temperature (See Fig. 1).

Fig. 1
figure 1

Microchannel formation

Full size image

Assumptions

The microflows are classified based on Knudsen number and have a certain limit for different flow regimes. λ is the mean molecular free path and Dh is the hydraulic diameter (characteristic length):

$$Kn = \frac{\lambda }{{D_{\text{H}} }}$$
(1)
$$Kn = \sqrt {\frac{\varPi k}{2}} \frac{Ma}{Re}$$
(2)

The sound speed is Cs = (kRT)0.5 and Reynolds and Mach numbers are Re = UL/ν and Ma = U/Cs. k also represents the specific heat ratio (k = cP/cν). A computer code is developed in FORTRAN language to simulate the fluid flow and heat transfer. To have appropriate convergence through the solvation process, the compressibility error of LBM should be small. The compressibility error of density variation is proportional to Ma2. Hence it will be negligible for the low value of Mach number which is chosen as 0.1 through the present using code.

Moreover, the hydrodynamic and thermal relaxation times are considered as \(\tau_{\text{f}} = \sqrt {6/(\pi k)} D_{\text{H}} Kn\) and \(\tau_{\text{g}} = \tau_{\text{f}} /Pr\), respectively [22]. It should mentioned that the expression of Knudsen number is not usually applied for the liquid microflows. As a result, the dimensionless slip coefficient of “B = (Slip coefficient)/(Characteristic length) = 0.1, 0.01 and 0.001” is used instead of “Kn = 0.1, 0.01 and 0.001” in the following parts of the present work which represents the same theoretical and physical concepts [52].

Equations

Boltzmann equation

The lattice Boltzmann equation obtained by Lattice Gas Automata developed by Frisch et al. The performance of this model consists of the collision processes in one place and diffusion in the fluid range in a time step. If the diffusion function f denotes the statistical description of the probability of the presence of particles in the place and time x and t, at a particle velocity (microscopic) of c, the macroscopic quantities of density, velocity vector, internal energy, and heat flux can be calculated:

$$\rho (x,t) = \int {f(\varvec{x},\varvec{c},t){\text{d}}\varvec{c}}$$
(3)
$$\rho \varvec{u}(x,t) = \int {\varvec{c}f(\varvec{x},\varvec{c},t){\text{d}}\varvec{c}}$$
(4)
$$\rho e(\varvec{x},t) = \int {\varvec{c}_{\text{o}}^{2} f(\varvec{x},\varvec{c},t){\text{d}}\varvec{c}}$$
(5)
$$\varvec{q}(x,t) = \frac{1}{2}\int {\varvec{c}_{\text{o}} (\varvec{c}_{\text{o}} \cdot \varvec{c}_{\text{o}} )f(\varvec{x},\varvec{c},t){\text{d}}\varvec{c}}$$
(6)

An external force F on the unit gas molecule mass leads to a change in the particle velocity and its displacement. In this case the distribution function f for particles at time t, in the space interval x, has a velocity between c and c + dc. Thus the Boltzmann equation is written as follows:

$$f(x + c{\text{d}}t,c + F{\text{d}}t,t + {\text{d}}t){\text{d}}x{\text{d}}c - f(x,c,t){\text{d}}x{\text{d}}c = 0$$
(7)

By introducing an appropriate operator for the collision term, it is possible to achieve the distribution of particles after the collision and diffuse the effect of new alignment on the entire flow range.

$$f(x + c{\text{d}}t,\;c + F{\text{d}}t,\;t + {\text{d}}t)\,{\text{d}}x{\text{d}}c - f(x,c,t) = \varOmega (f){\text{d}}x{\text{d}}c{\text{d}}t$$
(8)

Thus

$$\frac{\partial f}{\partial t} + \frac{\partial f}{\partial x} \cdot c + \frac{F}{m} \cdot \frac{\partial f}{\partial c} = \varOmega$$
(9)

If the external force is ignored, the Boltzmann equation is written as follows:

$$\frac{\partial f}{\partial t} + c_{\text{o}} \nabla f = \varOmega$$
(10)

BGK approximation

The collision operator represents the rate of change in the distribution function. These changes occur between the initial and final modes of the distribution function due to collision between particles. Because of the complexity of Boltzmann equation solution, so far various models have presented to solve it; a simple and popular model that is introduced for the collision operator is the BGK model:

$$\varOmega = - \,\omega \,(f^{\text{eq}} - f)$$
(11)

feq is the local equilibrium distribution function; \(\omega\) is the collision frequency and \(\tau\) is the coefficient of comfort that are inversely correlated \(\left( {\omega = \frac{1}{\tau }} \right)\) By introducing the BGK approximation, the Boltzmann equation is expressed as follows:

$$\frac{\partial f}{\partial t} + c_{\text{i}} \frac{\partial f}{\partial x} + \frac{{F_{\text{i}} }}{m} \cdot \frac{\partial f}{{\partial c_{\text{i}} }} = \omega \left( {f^{\text{eq}} - f} \right)$$
(12)

Boltzmann equation with BGK approximation without the external force F is rewritten as follows:

$$\frac{\partial f}{\partial t} + c_{\text{i}} \frac{\partial f}{{\partial x_{\text{i}} }} = \omega \left( {f^{\text{eq}} - f} \right)$$
(13)

Hydrodynamic lattice Boltzmann relations

The analytic solution of Boltzmann equation is difficult even with the BGK collision operator which is a simple and suitable model. Therefore, this equation must be discretized and solve approximately. To facilitate solution, discretization is done on the velocity domain using a symmetric network at certain velocities.

In this case, the distribution function is discretized that α represents the direction of the discretization rate on the lattice and, as mentioned, the macroscopic properties are obtained by summing up the microscopic properties and the laws of conservation of mass, momentum and energy are calculated as follows:

$$\begin{aligned} \rho = & \sum\limits_{\alpha = 0}^{b} {f_{\upalpha} } \\ \rho u = & \sum\limits_{\alpha = 1}^{b} {e_{\upalpha} f_{\upalpha} } \\ \rho e = & \sum\limits_{\alpha = 1}^{b} {c_{{{\text{o}}\upalpha}}^{2} f_{\upalpha} } \\ \end{aligned}$$
(14)

Finally, using Eq. (12) and applying the Boussinesq approximation (all fluid characteristics except density are constant in the buoyancy force term) and considering the effects of the mass force on the fluid flow, the Boltzmann discrete motion equation is written as follows:

$$\begin{aligned} & f_{\upalpha} (x + e_{\upalpha} \Delta t,t + \Delta t) - f_{\upalpha} (x,t) \\ & \quad = \frac{ - \,\Delta t}{{\tau_{\text{f}} + 0.5\Delta t}}\left[ {f_{\upalpha} (x,t) - f_{{_{\upalpha} }}^{\text{eq}} (x,t)} \right] + \left( {\frac{{\Delta t\tau_{\text{f}} }}{{\tau_{\text{f}} + 0.5\Delta t}}\frac{{3G(e_{{\upalpha{\text{y}}}} - V)}}{{C^{2} }}f^{\text{eq}} } \right) \\ \end{aligned}$$
(15)

where β coefficient of volumetric expansion and G is the buoyancy force per unit of mass defined as \(G = \beta g\left( {T - \bar{T}} \right)\) that g is the force of gravity. In this relation, the last right term denotes the collision of particles under the influence of the gravitational buoyancy force.

Equilibrium distribution in the BGK model

The BGK approximation represents the density distribution function in terms of the equilibrium distribution function and no macroscopic velocity exists in the equilibrium distribution function because it is considered constant. Therefore, the values of motion equilibrium distribution function values are calculated as follows:

$$f_{\upalpha}^{\text{eq}} = \omega_{\upalpha} \rho \left[ {1 + \frac{{3(e_{\upalpha} \cdot u)}}{{c^{2} }} + \frac{{9(e_{\upalpha} \cdot u)}}{{2c^{4} }} - \frac{{3u^{2} }}{{2c^{2} }}} \right]$$
(16)

In the D2Q9 model (Fig. 2), the microscopic velocity vectors of the lattice particles are calculated as follows. Mass functions are also in the form of \(\omega_{{\upalpha = 0}} = \frac{4}{9},\;\omega_{\upalpha} = \frac{1}{9}\;{\text{for}}\;\alpha = 1,\;2,\;3,\;4\) and \(\omega_{\upalpha} = \frac{1}{36}\;{\text{for}}\;\alpha = 5,\;6,\;7,\;8\).

Fig. 2
figure 2

D2Q9 lattice

Full size image
$$\begin{aligned} e_{\upalpha} &= \left( {\cos \frac{\alpha - 1}{2}\pi ,\;\sin \frac{\alpha - 1}{2}\pi } \right)c,\quad \alpha = 1,\,2,\,3,\,4 \\ e_{\upalpha} & = \sqrt 2 \left( {\cos \left[ {\frac{\alpha - 5}{2}\pi + \frac{\pi }{4}} \right],\;\sin \left[ {\frac{\alpha - 5}{2}\pi + \frac{\pi }{4}} \right]} \right)c,\quad \alpha = 5,\,6,\,7,\,8 \\ e_{0} & = (0,\,0) \\ \end{aligned}$$
(17)

As already mentioned, the flow range can be calculated by macroscopic quantities. The laws of conservation of mass, momentum and energy are as follows:

$$\rho = \sum\limits_{\alpha } {f_{\upalpha} }$$
(18)
$$u = (1/\rho )\sum\limits_{\alpha } {f_{\upalpha} e_{\upalpha} x}$$
(19)
$$v = (1/\rho )\sum\limits_{\alpha } {f_{\upalpha} e_{\upalpha} y + \frac{\Delta t}{2}G}$$
(20)

The discretized distribution function in the presence of buoyancy force is as follows:

$$f_{\upalpha} = \frac{{\tau_{\text{f}} f_{\upalpha} + 0.5\Delta tf_{\upalpha}^{\text{eq}} }}{{\tau_{\text{f}} + 0.5\Delta t}} + \left( {\frac{{0.5\Delta t\tau_{\text{f}} }}{{\tau_{\text{f}} + 0.5\Delta t}}\frac{{3G\left( {e_{{\upalpha{\text{y}}}} - V} \right)}}{{c^{2} }}f_{\upalpha}^{\text{eq}} } \right)$$
(21)

Thermal lattice Boltzmann relations

The optimal performance of lattice Boltzmann in solving the mixed convection problems and its proper application in simulating multi-phase flows and different geometries lead to its increased application.

In the hydraulic analysis of the flow through the lattice Boltzmann, the second-order accuracy is used to satisfy the laws of conservation and the equilibrium function versus velocity will be of the second order. Thus the thermal energy distributed function model by He et al. [18] is used in the simulation of heat transfer in the LBM where a separate distribution function, g, is used to simulate the temperature field. This model is applicable to complex geometries and boundary conditions.

The BGK thermal lattice Boltzmann model based on internal energy is described as follows over a process similar to discretization of hydrodynamic lattice Boltzmann with BGK approximation. Thermal lattice Boltzmann equation which includes the collision and diffusion:

$$\begin{aligned} \tilde{g}_{\upalpha} \left( {x + e_{\upalpha} \Delta t,\;t + \Delta t} \right) - \tilde{g}_{\text{e}} (x,\;t) = & - \,\frac{\Delta t}{{\tau_{\text{g}} + 0.5\Delta t}}\left[ {\tilde{g}_{\upalpha} (x,t) - g_{\upalpha}^{\text{eq}} (x,t)} \right] \\ & \; - \,\frac{{_{{\tau_{\text{g}} \Delta t}} }}{{\tau_{\text{g}} + 0.5\Delta t}}f_{\upalpha} (x,\,t)Z_{\upalpha} (x,t) \\ \end{aligned}$$
(22)

That

$$\tilde{g}_{\upalpha} = g_{\upalpha} - \frac{\Delta t}{{2\tau_{\text{g}} }}\left( {g_{\upalpha} - g_{\upalpha}^{\text{eq}} } \right) + \frac{\Delta t}{2}f_{\upalpha} Z_{\upalpha}$$
(23)

The heat loss due to viscosity and condensation in the equation above are as follows:

$$Z_{\upalpha} = \left[ {e_{\upalpha} - u(x,\,t)} \right] \cdot \left[ {u(x \cdot e_{\upalpha} \Delta t,\;t + \Delta t) - u(x,\,t)} \right]/\Delta t$$
(24)

Discretized lattice Boltzmann equation:

$$\begin{aligned} g_{0}^{\text{eq}} = & - \,\frac{4}{9}\left[ {\frac{3\rho e}{2}\frac{{u^{2} + v^{2} }}{{c^{2} }}} \right] \\ g_{\upalpha}^{\text{eq}} = & \frac{1}{9}\rho e\left[ {1.5 + 1.5\frac{{e_{\upalpha} \cdot u}}{{c^{2} }} + 4.5\frac{{(e_{\upalpha} \cdot u)^{2} }}{{c^{4} }} - 1.5\frac{{u^{2} + v^{2} }}{{c^{2} }}} \right],\quad \alpha = 1,\;2,\;3,\;4 \\ g_{\upalpha}^{\text{eq}} = & \frac{1}{9}\rho e\left[ {3 + 6\frac{{e_{\upalpha} \cdot u}}{{c^{2} }} + 4.5\frac{{(e_{\upalpha} \cdot u)^{2} }}{{c^{4} }} - 1.5\frac{{u^{2} + v^{2} }}{{c^{2} }}} \right],\quad \alpha = 5,\;6,\;7,\;8 \\ \end{aligned}$$
(25)
$$\begin{aligned} \rho e = & \sum\limits_{\alpha } {\tilde{g}_{\upalpha} - \frac{\Delta t}{2}\sum\limits_{\alpha } {f_{\upalpha} } } Z_{\upalpha} \\ q = & \left( {\sum\limits_{\alpha } {e_{\upalpha} \tilde{g}_{\upalpha} - \rho eu} - \frac{\Delta t}{2}\sum\limits_{\alpha } {e_{\upalpha} f_{\upalpha} Z_{\upalpha} } } \right)\frac{{\tau_{\text{g}} }}{{\tau_{\text{g}} + 0.5\Delta t}} \\ \end{aligned}$$
(26)

Boundary conditions

The application of boundary conditions in the LBM is very different from the methods of the Navier–Stokes equations and has a more complex process due to the use of the distribution function variable. In this method, boundary conditions affect the distribution functions and these effects are applied to the hydrodynamic and thermal properties of the flow indirectly. In lattice Boltzmann, the domain of the solution must be divided into lattices that distribution function particles are on each lattice. Some of these particles flow along the specified directions to the adjacent nodes.

Hydrodynamic boundary conditions

In the fluid flow in the microscopic dimensions, the fluid slips on the channel walls with a limited tangential velocity which causes the slip boundary condition on the walls to be applied. The directions of the velocities thrown by the fluid domain to the boundaries are considered as known quantities, and it is not necessary to calculate them on the boundary and their values are obtained from the previous stages of the collision and the previous diffusion of the fluid range. Here, the unknown distribution functions can be obtained using unbalanced return boundary condition [46]. In this model, the collision is performed on a node on the solid–fluid boundary and the distribution functions colliding with the wall are returned in a direction that is in line with equilibrium conditions. The left wall with distribution functions related to directions α = 1, 5 and 8 is the missing quantities:

$$\begin{aligned} f_{1} & = f_{3} + \frac{2}{3}\rho_{\text{in}} u_{\text{in}} \\ f_{5} & = f_{7} + \frac{{f_{4} - f_{2} }}{2} + \frac{1}{6}\rho_{\text{in}} u_{\text{in}} + \frac{1}{2}\rho_{\text{in}} V_{\text{in}} - \frac{\Delta t}{4}\rho_{\text{in}} G \\ f_{8} &= f_{6} - \frac{{f_{4} - f_{2} }}{2} + \frac{1}{6}\rho_{\text{in}} u_{\text{w}} - \frac{1}{2}\rho_{\text{in}} V_{\text{in}} + \frac{\Delta t}{4}\rho_{\text{in}} G \\ \end{aligned}$$
(27)
$$\begin{aligned} \tilde{f}_{3} & = \tilde{f}_{1} - \frac{2}{3}\rho_{\text{out}} u_{\text{out}} \\ \tilde{f}_{7} & = \tilde{f}_{5} - \frac{1}{2}\left( {\tilde{f}_{4} - \tilde{f}_{2} } \right) - \frac{1}{6}\rho_{\text{out}} u_{\text{out}} - \frac{1}{2}\rho_{\text{out}} v_{\text{out}} + \frac{1}{4}\Delta t\rho_{\text{out}} G \\ \tilde{f}_{6} & = \tilde{f}_{8} - \frac{1}{2}\left( {\tilde{f}_{4} - \tilde{f}_{2} } \right) - \frac{1}{6}\rho_{\text{out}} u_{\text{out}} + \frac{1}{2}\rho_{\text{out}} v_{\text{out}} - \frac{1}{4}\Delta t\rho_{\text{out}} G \\ \end{aligned}$$
(28)

The upper and lower walls have different boundary condition because of the slip in the walls and here the Knudsen number is important. In this situation, fluid molecules located on the wall surface slip on it and cause a slip boundary condition in hydrodynamic problems. Slip velocity condition:

$$\Delta u_{\text{wall}} = u_{{{\text{fluid}}\,({\text{y}} \to {\text{wall}})}} - u_{\text{wall}} = \ell_{\text{S}} \frac{{\partial u_{\text{fluid}} }}{{\partial_{\text{y}} }}{\text{wall}}$$
(29)

Maxwell completes the above relation by introducing the tangential momentum accommodation coefficient

$$\begin{aligned} & u_{\text{slip}} = u_{\text{s}} - u_{\text{wall}} = \left. {\frac{2 - \sigma }{\sigma }\lambda \frac{{\partial u_{\text{S}} }}{\partial n}} \right|_{\text{w}} + \left. {\frac{3}{4}\frac{\eta }{PT}\frac{\partial T}{\partial S}} \right|_{\text{w}} \\ & {\text{In}}\;{\text{dimensionless}}\;{\text{form}}: \, U_{\text{slip}} = \left. {B\frac{\partial U}{\partial n}} \right|_{\text{w}} \\ \end{aligned}$$
(30)

where B represent the dimensionless slip coefficient. Slip velocity boundary condition in lattice model [47]:

$$\begin{aligned} \tilde{f}_{4} & = \tilde{f}_{2} \\ \tilde{f}_{7} & = r\tilde{f}_{5} + (1 - r)\tilde{f}_{6} \\ \tilde{f}_{8} & = r\tilde{f}_{6} + (1 - r)\tilde{f}_{5} \\ \end{aligned}$$
(31)
$$\begin{aligned} \tilde{f}_{2} &= \tilde{f}_{4} \\ \tilde{f}_{5} & = r\tilde{f}_{7} + (1 - r)\tilde{f}_{8} \\ \tilde{f}_{6} & = r\tilde{f}_{8} + (1 - r)\tilde{f}_{7} \\ \end{aligned}$$
(32)

where r = 0.7 is chosen as the matching coefficient.

Thermal boundary conditions

As mentioned before in a fluid flow in microscopic dimensions, the fluid slips on a channel wall with limited tangential velocity causing thermal jumps to occur in thermal problems. Here, the thermal boundary condition is applied using the model provided by He et al. [18] which has a proper function. In their model, the non-equilibrium return boundary condition by Zhu and He functions is used [48]. In the present study, the thermal boundary condition is constant temperature and insulated wall. D’Orazio et al. [49] applied He’s model and complete it by GPTBC model. In this model, the unknown thermal distribution functions are equalized with equilibrium distribution functions with reverse slip thermal energy:

$$\begin{aligned} \tilde{g}_{5} = & \frac{1}{12}\left[ {1.5\Delta t\sum\limits_{\alpha = 1}^{8} {e_{{{\alpha x}}} f_{\upalpha} Z_{\upalpha} + 3\left( {\tilde{g}_{3} + \tilde{g}_{6} + \tilde{g}_{7} } \right)} } \right] \\ \tilde{g}_{1} = & \frac{1}{6}\left[ {1.5\Delta t\sum\limits_{\alpha = 1}^{8} {e_{{{\alpha x}}} f_{\upalpha} Z_{\upalpha} + 3\left( {\tilde{g}_{3} + \tilde{g}_{6} + \tilde{g}_{7} } \right)} } \right] \\ \tilde{g}_{8} = & \frac{1}{12}\left[ {1.5\Delta t\sum\limits_{\alpha = 1}^{8} {e_{{{\alpha x}}} f_{\upalpha} Z_{\upalpha} + 3\left( {\tilde{g}_{3} + \tilde{g}_{6} + \tilde{g}_{7} } \right)} } \right] \\ \end{aligned}$$
(33)
$$\begin{aligned} \tilde{g}_{6} = & \frac{1}{12}\left[ { - \,1.5\Delta t\sum\limits_{\alpha = 1}^{8} {e_{{{\alpha x}}} f_{\upalpha} Z_{\upalpha} + 3\left( {\tilde{g}_{1} + \tilde{g}_{5} + \tilde{g}_{8} } \right)} } \right] \\ \tilde{g}_{3} = & \frac{1}{6}\left[ { - \,1.5\Delta t\sum\limits_{\alpha = 1}^{8} {e_{{{\alpha x}}} f_{\upalpha} Z_{\upalpha} + 3\left( {\tilde{g}_{1} + \tilde{g}_{5} + \tilde{g}_{8} } \right)} } \right] \\ \tilde{g}_{8} = & \frac{1}{12}\left[ { - \,1.5\Delta t\sum\limits_{\alpha = 1}^{8} {e_{{{\alpha x}}} f_{\upalpha} Z_{\upalpha} + 3\left( {\tilde{g}_{1} + \tilde{g}_{5} + \tilde{g}_{8} } \right)} } \right] \\ \end{aligned}$$
(34)

The unknown distribution functions of g on the lower and upper walls are as follows to simulate the temperature jump boundary condition:

$$\begin{aligned} \tilde{g}_{2} = & \frac{3}{\rho e}g_{2}^{\text{eq}} \left( {\rho_{\text{w}} ,u_{\text{w}} ,e_{\text{w}} } \right)\left( {g_{7} + g_{4} + g_{8} } \right) \\ \tilde{g}_{5} = & \frac{3}{\rho e}g_{5}^{\text{eq}} \left( {\rho_{\text{w}} ,u_{\text{w}} ,e_{\text{w}} } \right)\left( {g_{7} + g_{4} + g_{8} } \right) \\ \tilde{g}_{6} = & \frac{3}{\rho e}g_{6}^{\text{eq}} \left( {\rho_{\text{w}} ,u_{\text{w}} ,e_{\text{w}} } \right)\left( {g_{7} + g_{4} + g_{8} } \right) \\ \end{aligned}$$
(35)
$$\begin{aligned} \tilde{g}_{4} = & \frac{3}{\rho e}g_{2}^{\text{eq}} \left( {\rho_{\text{w}} ,u_{\text{w}} ,e_{\text{w}} } \right)\left( {g_{2} + g_{5} + g_{6} } \right) \\ \tilde{g}_{7} = & \frac{3}{\rho e}g_{7}^{\text{eq}} \left( {\rho_{\text{w}} ,u_{\text{w}} ,e_{\text{w}} } \right)\left( {g_{2} + g_{5} + g_{6} } \right) \\ \tilde{g}_{8} = & \frac{3}{\rho e}g_{8}^{\text{eq}} \left( {\rho_{\text{w}} ,u_{\text{w}} ,e_{\text{w}} } \right)\left( {g_{2} + g_{5} + g_{6} } \right) \\ \end{aligned}$$
(36)

The velocity and temperature values are also calculated as dimensionless as follows:

$$U = u/u_{\text{i}}$$
(37)
$$\theta = T/T_{\text{c}}$$
(38)

The dimensional quantities of spatial coordinates x and y also become dimensionless as follows:

$$X = x/H$$
(39)
$$Y = y/H$$
(40)

It should be noted that L/H = 30. Therefore, for the dimensionless quantities of X and Y used in plotting the output charts and figures: 0 < Y < 1 and 0 < X < 30. The following equation is used for the Nusselt number [52].

$$Nu = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\frac{{D_{\text{H}} \left. {\frac{\partial T}{\partial y}} \right)_{\text{w}} }}{{T_{\text{w}} - T_{\text{bulk}} }}$$
(41)

Validation

For implementation of the numerical solution of the problem algorithm, a computer code written in FORTRAN language is used. To verify the independence of the solution process to the number of point in the lattice, it is examined according to Table 1. The mean value of the Nusselt number, as well as the dimensionless values of the horizontal velocity U, the vertical velocity W, and the dimensionless temperature θ at X = 1.5 for three lattices 35 × 350, 40 × 400 and 450 × 450 are shown. Due to the small difference between the lattices’ results, 40 × 400 lattice is applied for further calculations.

Table 1 Checking the independence of the lattice in terms of the flow in the microchannel for B = 0.01 and Re = 0.01
Full size table

In order to verify the performance validity of the code and the applied relations, the flow of fluid inside the microchannel is studied in the slip flow regime and then compressible fluid flow in the microchannel under different boundary conditions. In the first problem the results of the present study are compared with the results of Zhang et al. [15] in Fig. 3 for validating numerical solution for fluid flow properties. Using the LBM, they simulated gas flow in the slip flow regime within the microchannel. According to the above-mentioned figure, the dimensionless velocity profile of Zhang et al. for Kn = 0.05 and 0.1 shows a good consistency with the present work.

Fig. 3
figure 3

Dimensionless velocity profiles (lines) with those of Zhang et al. [15] (symbols)

Full size image

To evaluate the accuracy of the numerical solution in the heat transfer problems in microscopic dimensions, the results were compared with the results of Kavehpour et al. [23]. They modeled the compressible fluid flow in a microchannel under the boundary conditions of temperature and constant thermal flux using LBM. Figure 4 shows the comparison between dimensionless temperature profiles in the fluid flow for Re = 0.01 and Kn = 0.01 (similar to the present work). The results of comparison show an acceptable match.

Fig. 4
figure 4

Dimensionless temperature profiles of θ = T/Ti at various cross sections of microchannel for Kn = 0.01 (lines) with Kavehpour et al. [23] (symbols)

Full size image

In Table 2 the coefficient of friction amounts, CfRe, and Knudsen number, Kn, are compared with those of Kavehpour et al. [23]. The accuracy of the performed simulation by comparing the results with past valid research indicates the high accuracy of the written computer code.

Table 2 Validation of the coefficient of friction amounts and Knudsen number in the developed current in the microchannel with Ref. [23] for Re = 0.01
Full size table

Results and discussion

The laminar flow of cold nanofluid in a microchannel at a constant heat flux for cooling the walls is examined in a two-dimensional mode using the LBM. The effect of gravity on the flow and mixed convection heat transfer in a microchannel for different values of B = 0.001, 0.01 and 0.1 are investigated. It should be noted that the Reynolds number is Re = 0.01. The effect of buoyancy force on free motion is applied by Boussinesq approximation. The water/functionalized multi-wall carbon nanotubes nanofluid (see Table 3) is considered as the working fluid with different Grashof numbers as Gr = 1, 10 and 100. The Grashof number indicates the buoyancy to viscosity forces ratio and using \(Gr = g\beta D_{\text{H}}^{3} \left( {T_{\text{h}} - T_{\text{c}} } \right)/\upsilon^{2}\) and constant values for viscosity are assumed at β = 1/T and g = 9.8 ms−2. In Fig. 5, the flow after the microchannel input tends to development. The maximum velocity Umax occurs in the horizontal axis.

Table 3 Thermo-physical properties of FMWCNT/water [45]
Full size table
Fig. 5
figure 5

U profiles at different sections of the microchannel for B = 0.001 and Gr = 1

Full size image

In Fig. 6, the velocity profile is displayed for different Gr in different sections. In the rule of forced convective heat transfer (Gr = 1), the presence of the slip velocity at Y = 0 and Y = 1 is well seen in this figure and its maximum value is at the microchannel input which decreases with movement along it and eventually reaches a constant value. Reducing the slip velocity along the microchannel is observed for different values of X. By increasing the Grashof number and generating buoyancy force, the flow moves toward the mixed convection heat transfer. At Gr = 10 the effect of gravity on mixed convection causes a change in the velocity profile and a negative slip velocity. The velocity changes are increased at the microchannel input and more movement along the microchannel is needed to reach the developed flow. At Gr = 10, the shape of the velocity profile at X = 0.06 L and X = 0.1 L return flow and the resulting recirculating cell in the range of Y > 0.5. The buoyancy force is diminished increasing X by moving ahead of the input and the velocity profile approaches the development and symmetrical shape. The reason for the presence of a strong buoyancy force at the microchannel input is the difference in temperature between the input fluid and the walls especially in the input. As the fluid moves along the path and the temperature difference between the fluid and the walls is reduced, the free movement force is reduced and the velocity profile develops. This powerful buoyancy force on the upper wall leads to a negative slip velocity resulting from a return flow in the area. This phenomenon is only due to gravity and the negative value of the velocity profile at Y > 0.75. At Gr = 100, it can be seen that with the increase in the Grashof number and the stronger buoyancy force, the velocity profile has a higher negative slip rate which can affect the velocity profile at points far from the flow input section. Comparison of Figs. 5 and 6 shows that in the rule of forced convective heat transfer (Gr = 1), it is observed that the buoyancy force is diminished by increasing the slip coefficient (B) and separating nanoparticles from each other. Also more B leads to higher value of slip velocity.

Fig. 6
figure 6

U profiles at different sections of the microchannel for B = 0.1 and Gr = 1, 10 and 100

Full size image

Figure 7 shows velocity profile for different values of slip coefficient. In this figure, it is clearly seen that the higher slip coefficient leads to an increase in slip velocity on the walls. Also, by increasing the amount of slip velocity on the walls the maximum velocity decreases in the horizontal axis of the microchannel. Figure 8 shows the dimensionless temperature profile θ = T/Tin at different sections of the flow. The increase in fluid temperature due to heat exchange with hot walls is evident; therefore the temperature gradient is high at the microchannel input. As the fluid moves along the path and the nanofluid temperature increases, the flow will be convective and this convection is evident at X = 0.4 L.

Fig. 7
figure 7

U Profiles at section X = 0.1 L for different values of slip coefficient

Full size image
Fig. 8
figure 8

Profiles of θ at different sections of the microchannel for B = 0.1 and Gr = 1

Full size image

It can be seen from Figs. 6 and 8 that the slip velocity has led to temperature jump which has dropped along the microchannel. Figure 9 shows the dimensionless temperature profile θ = T/Tin for different values of slip coefficient at X = 0.1 L. This figure clearly indicates an increase in the amount of temperature jump due to the increase in the slip coefficient. Figure 10a–c presents the streamlines and isotherms for different values of Grashof number in the range of one-sixth of the input from the microchannel length for the sake of clarity. In Fig. 10a, in the flow lines at Gr = 1 the flow is developed and exits on the right side after entering the microchannel without changing. In this figure the flow lines are completely parallel and there is no trace of the buoyancy force and the recirculating cell. In Fig. 10b, in Gr = 10 by increasing the buoyancy force and creating buoyancy motions, the flow after entering microchannel is dragged down under the influence of gravity and then its temperature is increased through the exchange of heat with the hot walls and, as a result, the buoyancy force pushes it up and creates a weak cell in the input region. Figure 10c shows that the same cell is formed in Gr = 100 but due to the strong buoyancy forces a recirculating cell is created in the opposite direction of the input fluid. Since the circulation direction is counterclockwise, it leads to a negative slip velocity in the input area.

Fig. 9
figure 9

Profiles of θ at different slip coefficient at X = 0.1 L and Gr = 1

Full size image
Fig. 10
figure 10

Streamlines and dimensionless isotherms in the microchannel in aGr = 1, bGr = 10, cGr = 100

Full size image

Figure 11 shows the variations in the slip velocity Us along the microchannel for different values of slip coefficient. In the rule of forced flow convection Gr = 1, due to the flow lines and the parallelism of the flow lines, the slip velocities in the upper and lower walls match. Also it is seen that slip velocity has its greatest value at inlet, and then it decreases mildly along the microchannel wall to approach a constant value. For Gr = 10, the slip velocity of the input area is obvious in the upper and lower walls which is affected by buoyancy motions. At distances away from the input section the nanofluid temperature tends to the wall temperature and the buoyancy motions due to free movement are weak. It is observed that as the nanofluid moves along the path, the slip velocity decreases and eventually reaches a constant value. The phenomenon of negative slip velocity is evident along the wall for Gr = 10 which its amount will be increased with B. In the lower wall for Gr = 100 the positive slip velocity increases and then reaches a constant value.

Fig. 11
figure 11

Changes in Us for different values of slip coefficient and Gr = 1, 10

Full size image

In Fig. 12, the temperature jump (θS) changes along the upper wall of the microchannel are shown for different values of slip coefficient. In this figure temperature jump is increased by slip coefficient. For a specific Gr, the temperature jump decreases along the microchannel path so that it reaches the constant value of zero. At Gr = 100 where there is a strong buoyancy force, this constant value is slightly greater than zero for B = 0.1. Figure 13 shows the variations of Nusselt number along the microchannel walls for nanofluid (FMWCNT in water with mass fraction of 0.0025) versus pure water. The positive effect of adding CNTs to increase Nu of the base fluid can be seen clearly in this figure.

Fig. 12
figure 12

θS along microchannel for different values of slip coefficient in Gr = 1, 10 and 100

Full size image
Fig. 13
figure 13

The variations of Nusselt number along the microchannel walls for nanofluid (FMWCNT in water with mass fraction of 0.0025) versus pure water

Full size image

Conclusions

In the present study mixed convection of water/functionalized multi-wall carbon nanotubes (FMWCNT) nanofluid flow is simulated in a microchannel with hot walls by the lattice Boltzmann method. Given the gravity in this research and the emergence of buoyancy force the flow velocity components changed and therefore the relationships used to compute macroscopic properties were corrected to include these changes. By increasing the slip coefficient, the slip velocity and temperature jumps also increase. The maximum of these parameters occurred in the input region, and afterward, their amount had a decreasing trend to reach a corresponding constant value along its path. Including the gravity term in Boltzmann equation as an external force changed motion properties and increases the length of the hydrodynamic input length of the flow. Gravity creates powerful buoyancy motions at the input area. Therefore, in the input range where the temperature gradient between the nanofluid and the wall is high, the required distance for flow development increases. For Gr = 1 the rule of forced convective heat transfer the buoyancy is negligible and for higher values of Grashof number Gr = 100 the buoyancy force creates buoyancy motions in the input region. So that in Gr = 100 the vortex power increases and the gravitational buoyancy force changes the hydrodynamic properties of the flow such as the slip velocity and coefficient of friction. These changes lead to the formation of a counterclockwise vortex along the flow direction.