Keywords

1 Introduction

Natural double diffusive convection is the phenomenon where the flow is simultaneously induced by the thermally driven buoyant and the solutally driven buoyant forces, such kind of flow occurs in many applications such as in drying technique, chemical process, crystal growth, solidification, and food processing, etc. Some reviews on this matter are reported in [1, 2] to highlight different features of this type of flow. In [3,4,5,6,7], one can find the scrutiny of the double diffusive natural or mixed convection inside different configurations.

The interest of using high performant heat transfer fluids rose by suspending nanoscale particles with high thermal conductivity in conventional fluids, namely water and oil, which led to a developed type of fluids called nanofluid. Previous experimental studies showed that the addition of a small concentration of Cupper nanoparticles in EG resulted in a 40% growth in the thermal conductivity [8]. Such enhancement made nanofluids be adopted in some engineering utilizations, for instance cooling of electronic equipment [9]. Therefore, researchers became enthusiastic to investigate experimentally and numerically the advantage of using nanofluids in mixed or natural convection in different enclosures and using different nanofluids and models [10].

Recently, the lattice Boltzmann method turned out to be more popular over the traditional CFD methods for its advantages such as easy implementation for complex geometries, parallelism computation and simple adoption of the method. This method is based on the Boltzmann’s equation that describes the fluid as a package of microscopic particles moving with random motions; an interesting review about this method is presented in [11].

Framed in this background, the main goal of this paper is to examine the double diffusive convection of Al2O3 water based nanofluid enclosed by a square cavity using the lattice Boltzmann method and to obtain a fundamental knowledge on the effects of governing parameters, for example, the buoyancy ration and the Lewis number in addition to the volume fraction of nanoparticles using variable models of thermal conductivity and viscosity.

2 Problem and Governing Equations

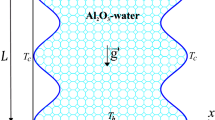
The geometry under investigation is depicted in Fig. 1. It is a square cavity containing Al2O3/water nanofluid. The horizontal boundaries are adiabatic and impermeable, while the right and left walls are, respectively, maintained at low and high temperature and concentration.

Fig. 1.
figure 1

Sketch of the geometry and coordinates system.

Full size image

The flow is considered laminar, incompressible and both nanoparticles and the base fluid are kept in thermal equilibrium. The density of the nanofluid in the buoyancy force conforms the Boussinesq approximation, \(\rho_{{{\text{nf}}}} \left( {T,\,S} \right)\, = \,\rho_{{{\text{nf0}}}} \left( {1\, - \,\beta_{{{\text{Tnf}}}} \left( {T\, - \, T_{0} } \right)\, - \,\beta_{{{\text{Snf}}}} \left( {S\, - \,S_{0} } \right)} \right),\) while the thermal conductivity and the viscosity of the nanofluid are calculated according to more sophisticated models. The thermophysical properties of water and Al2O3 are tabulated in Table 1.

The dimensionless steady-state equations governing the conservation of mass, momentum, energy and concentration can be written as follows:

$$ {\varvec{\nabla}} \,.\,{\mathbf{u}}\, = \,0 $$
(1)
$$ \left( {{\mathbf{u}}\,.\,{\varvec{\nabla}} } \right){\mathbf{u}}\, = \, - \, \frac{1}{{\rho_{r} }}{\varvec{\nabla}} P\, + \,\Pr \varvec{\nabla} \,.\, \left( {\vartheta_{r} {\varvec{\nabla}} {\mathbf{u}}} \right)\, - \,{\text{RaPr}}\beta_{r} \left( {T\, + \,{\text{NS}}} \right)\frac{{\varvec{g}}}{{\left| {\varvec{g}} \right|}} $$
(2)
$$ \left( {{\mathbf{u}}\,.\,{\varvec{\nabla}} } \right)T\, = \,{\varvec{\nabla}} \,.\,\left( {\alpha_{r} {\varvec{\nabla}} T} \right) $$
(3)
$$ \left( {{\mathbf{u}}\,.\,{\varvec{\nabla}} } \right)S\, = \,\frac{1}{Le}{\varvec{\nabla}} \,.\,\left( {{\varvec{\nabla}} S} \right) $$
(4)
Table 1. Thermophysical properties of the nanoparticles and water.
Full size table

The velocity, pressure, temperature and concentration are respectively scaled by \({{\alpha_{f,\,0} } \mathord{\left/ {\vphantom {{\alpha_{f,\,0} } L}} \right. \kern-0pt} L},\,{{\left( {\rho \alpha^{2} } \right)_{f,\,0} } \mathord{\left/ {\vphantom {{\left( {\rho \alpha^{2} } \right)_{f,\,0} } {L^{2} }}} \right. \kern-0pt} {L^{2} }},\,\Delta T\, = \,T_{h} \, - \,T_{l} \,{\text{and}}\,\Delta S\, = \,S_{h} \, - \,S_{l} .\) And the relative thermal diffusivity is \(\alpha_{r} \, = \,{{k_{r} } \mathord{\left/ {\vphantom {{k_{r} } {\left( {\rho c_{p} } \right)}}} \right. \kern-0pt} {\left( {\rho c_{p} } \right)}}.\) Pr is the Prandtl number, RaT is the thermal Rayleigh number, Le is the Lewis number, and N is the buoyancy ratio whose expressions are:

$$ \begin{gathered} {\text{Ra}}_{T} \, = \,\frac{{g\beta_{Tf} L^{3} \Delta T}}{{\vartheta_{f} \alpha_{f} }}; \hfill \\ {\text{Pr}}\, = \,\frac{{\vartheta_{f} }}{{\alpha_{f} }}; \hfill \\ {\text{Le}}\, = \,\frac{{\alpha_{f} }}{{D_{{{\text{nf}}}} }}; \hfill \\ N\, = \, \frac{{\beta_{{{\text{Snf}}}} \Delta T}}{{\beta_{{{\text{Tnf}}}} \Delta S}} \hfill \\ \end{gathered} $$
(5)

The associated dimensionless boundary conditions are as follows: on all the walls u = 0, on the left wall Th = Sh = 1, on the right wall \(T_{l} \, = \,S_{l} \, = \,0,\) and on the horizontal walls \( {{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial y}}} \right. \kern-0pt} {\partial y}}\, = \,{{\partial S} \mathord{\left/ {\vphantom {{\partial S} {\partial y}}} \right. \kern-0pt} {\partial y}}\, = \,0. \)

The local heat and mass transfer rates on the hot wall based on the base fluid are defined respectively by the local Nusselt and Sherwood numbers as:

$$ \begin{gathered} {\text{Nu}}\left( y \right)\, = \, - \, k_{r} \left. {\frac{\partial T}{{\partial x}}} \right|_{x\, = \,0} ; \hfill \\ {\text{Sh}}\left( y \right)\, = \, - \, \left. {\frac{\partial S}{{\partial x}}} \right|_{x\, = \,0} \hfill \\ \end{gathered} $$
(6)

The average Nusselt and Sherwood numbers are evaluated respectively as:

$$ \begin{gathered} \overline{{{\text{Nu}}}} \, = \,\mathop \smallint \limits_{0}^{1} {\text{Nu}}\left( y \right)dy; \hfill \\ \overline{{{\text{Sh}}}} \, = \,\mathop \smallint \limits_{0}^{1} {\text{Sh}}\left( y \right)dy \hfill \\ \end{gathered} $$
(7)

3 Nanofluid Model

There exist plenty of experimental and theoretical models that can be adopted to approximate the thermophysical properties of nanofluids, especially for thermal conductivity and viscosity whose behaviors depend on many parameters such as nanofluid temperature, nanoparticles size, Brownian motion in addition to the nanoparticles volume fraction and the proprieties of both the base fluid and nanoparticles. The effective density [12], heat capacitance [13], and thermal expansion coefficient [12] are modeled as:

$$ \rho_{{{\text{nf}}}} \, = \,\varphi \rho_{{{\text{np}}}} \, + \,\left( {1\, - \,\varphi } \right)\rho_{f} $$
(8)
$$ \left( {\rho c_{p} } \right)_{{{\text{nf}}}} \, = \,\varphi \left( {\rho c_{p} } \right)_{{{\text{np}}}} \, + \,\left( {1\, - \,\varphi } \right)\left( {\rho c_{p} } \right)_{f} $$
(9)
$$ \left( {\rho \beta } \right)_{{{\text{nf}}}} \, = \,\varphi \left( {\rho \beta } \right)_{{{\text{np}}}} \, + \,\left( {1\, - \,\varphi } \right)\left( {\rho \beta } \right)_{f} $$
(10)

The relative thermal conductivity is approximated by Chon’s model [14]:

$$ k_{r} \, = \,1\, + \,64.7\varphi^{0.746} \left( {\frac{{d_{f} }}{{d_{p} }}} \right)^{0.369} \left( {\frac{{k_{p} }}{{k_{f} }}} \right)^{0.7476} {\text{Pr}}_{T}^{0.9955} {\text{Re}}_{T}^{1.2321} $$
(11)
$$ \begin{gathered} {\text{Re}}_{T} \, = \,\frac{{\rho_{f} k_{b} \left( {T\, + \,273.15} \right)}}{{3\pi l_{f} \mu_{f}^{2} }}; \hfill \\ {\text{Pr}}_{T} \, = \,\frac{{\mu_{f} }}{{\rho_{f} \alpha_{f} }}; \hfill \\ \mu_{f} \, = \,10^{{\frac{247.8}{{\left( {T\, + \,273.15} \right)\, - \,140}}}} 2.414\, \times \,10^{ - \,5} \hfill \\ \end{gathered} $$
(12)

kb = 1.3807 × 10−23 J/K and lf = 0.17 nm.

The relative kinematic viscosity is calculated using experimental data of Nguyen [15] and the expression of [10]:

$$ \vartheta_{r} \, = \,\frac{{{\text{exp}}\left( {3.003\, - \,0.04203T\, - \,0.5445\varphi \left( \% \right)\, + \,0.0002553T^{2} \, + \,0.0524\varphi \left( \% \right)^{2} \, - \,1.622\varphi \left( \% \right)^{ - \,1} } \right)}}{{\rho_{r} \mu_{f,\,0} }}10^{ - \,3} $$
(13)

4 Numerical Procedure

The main variable of the lattice Boltzmann method is the general distribution function, \(\Gamma_{i} \left( {{\varvec{r}},\,t} \right)\), which represents the probability of detecting fluid particles moving with the velocities, \({\varvec{c}}_{i}\), at a certain time, t, and position, r. The implemented LBM adopting a uniform lattice with the BGK collision operator uses three distribution functions f, g and h for density, temperature and concentration fields, respectively, whose equations are as follows:

$$ \Gamma_{i} \left( {{\varvec{r}} \, + \,{\varvec{c}}_{i} \Delta t,\,t\, + \,\Delta t} \right)\, - \,\Gamma_{i} \left( {{\varvec{r}},\,t} \right)\, = \,\frac{1}{{\tau_{\Gamma } \left( {\varvec{r}} \right)}}\left( {\Gamma_{i} \left( {{\varvec{r}},\,t} \right)\, - \,\Gamma_{i}^{{{\text{eq}}}} \left( {{\varvec{r}},\,t} \right)} \right)\, + \,\Delta t\Lambda_{i} \left( {\varvec{r}} \right) $$
(14)

The identification of the functions \(\Gamma_{i} ,\,\tau_{\Gamma } \,{\text{and}}\,\Lambda_{i}\) for each distribution is given in Table 2. Where the kinematic viscosity, thermal and solutal diffusivities, and thermal and solutal expansion coefficients in lattice Boltzmann are implemented as follows:

$$ \begin{gathered} \vartheta^{{{\text{lbm}}}} \, = \,3{\text{M}}\,{\text{Ma}}\sqrt {\frac{{\beta_{r} }}{{\alpha_{r}^{2} }}\frac{{{\text{Pr}}}}{{{\text{Ra}}}}} ; \hfill \\ \alpha^{{{\text{lbm}}}} \, = \,\frac{{\alpha_{r} }}{{\vartheta_{r} }}\frac{{\vartheta^{{{\text{lbm}}}} }}{{{\text{Pr}}}}; \hfill \\ D^{{{\text{lbm}}}} \, = \,\frac{1}{{\alpha_{r} }}\frac{{\alpha^{{{\text{lbm}}}} }}{{{\text{Le}}}}; \hfill \\ \beta_{T}^{{{\text{lbm}}}} \, = \,\frac{{\beta_{r} }}{{\left( {\vartheta_{r} \alpha_{r} } \right)}}\vartheta^{{{\text{lbm}}}} \alpha^{{{\text{lbm}}}} \frac{{{\text{Ra}}}}{{\sqrt {M^{3} } }} \hfill \\ {\text{and}} \hfill \\ \beta_{S}^{{{\text{lbm}}}} \, = \,\beta_{T}^{{{\text{lbm}}}} N\frac{\Delta T}{{\Delta S}}. \hfill \\ \end{gathered} $$
Table 2. Identification of the functions in (14).
Full size table

The D2Q9 model is used and the assigned values of the weighting factors, wi, and the discrete velocities, ci, are w0 = 4/9 and c0 = (0,0), for i = 1–4: wi = 1/9 and \({\varvec{c}}_{{\varvec{i}}} \, = \,c\left( {{\text{cos}}\left[ {\left( {i\, - \,1} \right){\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2} } \right],\,{\text{sin}}\left[ {\left( {i\, - \, 1} \right){\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}} \right]} \right),\) for i = 5–8: wi = 1/36 and \({\varvec{c}}_{{\varvec{i}}} \, = \,\sqrt 2 c\left( {{\text{cos}}\left[ {\left( {2i\, - \, 9} \right){\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}} \right],\,{\text{sin}}\left[ {\left( {2i\, - \,9} \right){\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}} \right]} \right),\) and c is the termed lattice speed given by \(c\, = \,{{\Delta x} \mathord{\left/ {\vphantom {{\Delta x} {\Delta t}}} \right. \kern-0pt} {\Delta t}}\, = \,{{\Delta y} \mathord{\left/ {\vphantom {{\Delta y} {\Delta t}}} \right. \kern-0pt} {\Delta t}}\) in which \(\Delta x,\,\Delta y\,{\text{and}}\,\Delta t\) are the grid spacings in x and y directions, and the discrete time step, respectively, which are all equal to 1. The equilibrium density, temperature and concentration distribution functions are expressed as:

$$ \begin{gathered} f_{i}^{{{\text{eq}}}} \, = \,{\text{w}}_{i} \rho \left[ {1\, + \,3\frac{{{\varvec{c}}_{{\varvec{i}}} \,.\,{\mathbf{u}}}}{{c^{2} }}\, + \,\frac{9}{2}\frac{{\left( {{\varvec{c}}_{{\varvec{i}}} \,.\,{\mathbf{u}}} \right)^{2} }}{{c^{4} }}\, - \,\frac{3}{2}\frac{{{\mathbf{u}}\,.\,{\mathbf{u}}}}{{c^{2} }}} \right]; \hfill \\ g_{i}^{{{\text{eq}}}} \, = \,{\text{w}}_{i} T\left[ {1\, + \,3\frac{{{\varvec{c}}_{{\varvec{i}}} \,.\,{\mathbf{u}}}}{{c^{2} }}} \right]; \hfill \\ h_{i}^{{{\text{eq}}}} \, = \,{\text{w}}_{i} S\left[ {1\, + \,3\frac{{{\varvec{c}}_{{\varvec{i}}} \,.\,{\mathbf{u}}}}{{c^{2} }}} \right] \hfill \\ \end{gathered} $$
(15)

Finally, the macroscopic variables, ρ, u, T and S are respectively calculated as the following:

$$ \begin{gathered} \rho \, = \,\mathop \sum \limits_{i} f_{i} ;\,{\mathbf{u}}\, = \,\frac{1}{\rho }\mathop \sum \limits_{i}\varvec{c}_{\varvec{i}} f_{i} ; \hfill \\ T\, = \,\mathop \sum \limits_{i} g_{i} ;\,S\, = \,\mathop \sum \limits_{i} h_{i} \hfill \\ \end{gathered} $$
(16)

Concerning the boundary conditions, the bounce-back method is applied on all the boundaries of the enclosure, which implies that the outgoing distribution functions from the domain are recognized by the streaming step and the ingoing ones are calculated as in [16].

5 Results and Discussion

5.1 Grid Independency and Validation

To ensure a grid independency on the solution and to find a better compromise between the solution accuracy and the computational time, a considerable mesh testing procedure was performed for the case of Pr = 6.5; N = 1; Le = 5; RaT = 5.104 and φ = 0.05. Table 3 presents the effect of the grid lattices on the average heat and mass transfer rates, \(\overline{{{\text{Nu}}}}\) and \(\overline{{{\text{Sh}}}} ,\) it was found that a grid lattice of 80 × 80 ensures all the requirements in a way that the difference with the highest grid doesn’t reach 1%.

Furthermore, our numerical solution was compared with different previous studies developed by [5, 17, 18] in order to build confidence of the present results in this study. It is evident that the outcomes of the previous studies and the present code are in excellent agreement as reflected in Table 4.

Table 3. Grid independence examination.
Full size table
Table 4. Validation of our numerical code with previous studies.
Full size table

Thus, the investigations on the effect of the pertinent parameters on the double diffusive natural convection in a square enclosure filled with Al2O3/water nanofluid is presented and discussed. In this study, the thermal Rayleigh number is kept constant at, RaT = 5.104, the Prandtl number, Pr = 6.5, the temperature of the right wall is fixed at the reference temperature 22℃, while the difference between the cold and the hot walls is set to 20℃. To make sure that the present code treats an incompressible regime, the Mach number is equal to 0.1, this leaves the pertinent parameters, the Lewis number, Le, the nanoparticles volume fraction, φ, and the buoyancy ratio, N.

5.2 Effect of the Buoyancy Ratio, the Lewis Number and the Nanoparticles Volume Fraction on the Stream Lines, Isotherms and Isoconcentrations

Figure 2 depicts the effect of nanoparticles volume fraction and the buoyancy ratio on the streamlines, isotherms and isoconcentrations for two cases; the dominating thermal convection (low Le) case and the dominating solutal convection (high Le) case. The solid lines represent the case of clear water φ = 0.0 and the dashed lines present the case where the nanoparticles volume fraction in water is φ = 0.05. The flow consists of a unicellular clockwise rotating cell. The intensity of this cell decreases significantly with increasing the volume fraction of nanoparticles when the thermal convection is predominant. However, when the solutal convection predominates, the intensity of the maximum stream function |ψmax| increases sightly with φ as can be seen from Table 5. The isotherms of the nanofluids are further from the hot wall than the ones of the clear water which is an indication of the increase in the thickness of the thermal boundary layer with φ. The same behavior was observed for the isoconcentrations, except for the case of small values of Le where φ has no effect on the isoconcentrations.

The transition from the predominant thermal to solutal convections affects seriously the contours of the stream function, temperature and concentration. The stream function moves from the rounded to the square shaped form and its value reduces as Le increases for Le ≤ 5 but it increases lightly beyond that interval. The isotherms are nearly vertical at the left-bottom and right-top corners while they are shaped in a spiral form (flat) in the core of the cavity for low (high) Le values, this is due to the fact that increasing Le means increasing the thermal diffusion and weaking the convictive mode where the thermal boundary layer gets thicker with increasing Le. On the other hand, the isoconcentrations are vertical in the whole enclosure for low values of Le indicating that the mass transfer is governed by the diffusion mode, whereas they get condensed in the vicinity of the vertical walls for high Le.

Comparing both the right and left columns of Fig. 2 demonstrates that the contours of the stream function, temperature and concentration show, in general, no significant change in their form when N increases from 1 to 2 for either the dominating thermal convection or the dominating solutal one. But the only change was observed in the maximum stream function where it was doubled when N goes from 1 to 2 when φ = 0.05 because the velocity increases with this parameter since it contributes in the source term of the momentum, Eq. (2).

Table 5. Maximum stream function |ψmax|.
Full size table
Fig. 2.
figure 2

Streamlines (top), isotherms (middle) isoconcentrations (bottom) for N = 1 (left 2 columns) and 2 (right 2 columns), Le = 0.001 (left) and Le = 10 (right), \(\varphi \, = \,0.05\) (dashed lines) \(\varphi \, = \,0.0\) (solid lines)

Full size image

5.3 Effect of the Buoyancy Ratio, the Lewis Number and the Nanoparticles Volume Fraction on the Average Nusselt and Sherwood Numbers

Figure 3 illustrates the variations of the average Nusselt, \(\overline{{{\text{Nu}}}}\), and Sherwood, \(\overline{{{\text{Sh}}}}\), numbers with the Lewis number, Le, for φ = 0.0 and φ = 0.05 when N = 1 (top) and N = 2 (bottom). As the buoyancy ration increases both heat and mass transfer rates increase, but slightly.

For low values of the Lewis number both \(\overline{{{\text{Nu}}}}\) and \(\overline{{{\text{Sh}}}}\) show a stable variation where \(\overline{{{\text{Sh}}}}\) is equal to unity (no mass transfer by convection) and \(\overline{{{\text{Nu}}}}\) is in its higher values. As Le rises both \(\overline{{{\text{Nu}}}}\) and \(\overline{{{\text{Sh}}}}\) are characterized by a weak slope, where \(\overline{{{\text{Nu}}}}\) decreases and \(\overline{{{\text{Sh}}}}\) increases, this slope takes importance with higher Le. The addition of nanoparticles into water enhances heat transfer but it deteriorates mass transfer. This enhancement (deterioration) gets smaller (bigger), respectively for high values of Le. It must be noted that even though the thermal boundary layer becomes thicker with increasing the nanoparticles volume fraction, which means smaller thermal gradients, the heat transfer rate rises as a consequence of the improvement of the thermal conductivity ratio which enhances explicitly \(\overline{{{\text{Nu}}}}\) unlike \(\overline{{{\text{Sh}}}}\). This thermal enhancement is important when the buoyancy ratio, N, is higher.

Fig. 3.
figure 3

Average Nusselt (left) and Sherwood (right) for N = 1 (top) and 2 (bottom)

Full size image

6 Conclusion

In the present study, the double diffusive natural convection in a square cavity filled with Al2O3/water nanofluid is studied numerically using the lattice Boltzmann method. The effective thermal conductivity and viscosity are considered to be thermally dependent adopting Chon’s model and the experimental data of Nguyen. The pertinent parameters are the Lewis number, 10−3 ≤ Le ≤ 10, the buoyancy ratio, N = 1, 2, and the nanoparticles volume fraction, φ = 0.0, 0.05.

The outcomes of the lattice Boltzmann method are in an accordance with the previous studies. Therefore, some important points that can be concluded are as the following:

  • Varying the Lewis number in the considered interval, results in a significant change in the isotherms, isoconcentrations and streamlines.

  • Enhancing the Lewis number from 10−3 to 10−2 has no effect on heat and mass transfer rates, but an increase beyond that leads to lower heat transfer rate and higher mass transfer rate.

  • The rise in the buoyancy ratio results in a moderate rise in the average Nusselt and Sherwood numbers and in an important growth in the maximum stream function.

  • The addition of the alumina nanoparticles into water enhances the heat transfer but reduces the mass transfer for all values of the Lewis number and the buoyancy ratio.