Second-order slip, cross-diffusion and chemical reaction effects on magneto-convection of Oldroyd-B liquid using Cattaneo–Christov heat flux with convective heating

Abstract

The present article investigates the effect of second-order slip, chemical reaction and Soret and Dufour effects on MHD convective flow of an Oldroyd-B liquid toward a stretchy surface. Analysis of thermal relaxation time is made by using Cattaneo–Christov heat flux model. The effects of radiation and convective heating are also taken into account. The ordinary differential equations are retrieved by the help of suitable transformations of governing equations. The analytical solutions are observed by homotopy progress. The velocity, concentration and temperature field are analyzed for various pertinent parameters involved in the study. The graphical results of physical quantities of interest such as skin friction, local Nusselt number and local Sherwood number are presented. A comparative study with existing result indicates excellent agreement.

Introduction

The flow of non-Newtonian fluids past a stretchy surface has attracted many scientists by interest of its engineering-related applications. These fluids did not satisfy the “Newton’s law of viscosity”, that is, these fluids change their flow behavior with respect to stress. Also, it cannot be interpreted the aspects of non-Newtonian fluids as a single constitutive relationship. Many investigators developed the different models of such fluids. Fourier heat statement yields parabolic energy equation which presents that the total system is immediately affected by the initial disturbance. To taken this issue, Cattaneo [1] altered Fourier’s law of heat conduction in appearance of thermal relaxation. The hyperbolic-type energy equation exists in the presence of Cattaneo’s statement. Christov [2] upgraded the analysis of Cattaneo [1] by involving thermal relaxation time with Oldroyd’s upper-convected derivatives to attain the material invariant formulation. The Oldroyd-B liquid model is one of the non-Newtonian fluid models, which describes the retardation and relaxation effects. Hayat et al. [3] investigated about 2D MHD steady flow of an Oldroyd-B liquid with Cattaneo–Christov model. Li et al. [4] depicted the slip effects of MHD flow of viscoelastic fluid bounded by a vertical stretching sheet with Cattaneo–Christov heat flux model. Imtiaz et al. [5] provided the 2D third-grade liquid flow over a linear stretchy sheet with chemical reaction. Mixed convection flow of an Oldroyd-B liquid with cross-diffusion effects was analyzed by Ashraf et al. [6]. Effect of various non-Newtonian nanofluids over a cone was done by Reddy et al. [7]. Rashidi et al. [8] examined the second-order slip flow and heat transfer of a nanofluid toward a stretchy surface. Zhu et al. [9] studied the magneto-hydrodynamic flow and heat transfer with effects of the second-order velocity slip and temperature-jump boundary conditions. Vishnu Ganesh et al. [10] performed the magneto-hydrodynamic axisymmetric slip flow along a vertical stretching cylinder with convective heating.

In recent years, quite a large number of studies dealing with Dufour–Soret effects on mass and heat transfer of viscoelastic fluids have been appeared. Dufour and Soret effects combined with radiation and chemical reaction on Oldroyd-B liquid flow upon a stretchy surface with Cattaneo–Christov heat flux were analyzed by Loganathan et al. [11]. By using Lie group analysis, Bhuvaneswari et al. [12] explored the double-diffusive convective flow of an incompressible fluid past an inclined semi-infinite surface with first-order homogeneous chemical reaction. Siddiqa et al. [13] studied about Casson particulate suspension flow past a complex isothermal wavy surface with thermal radiation. Freidoonimehr et al. [14] obtained an analytical solution of heat and mass transfer for MHD three-dimensional flow toward a bidirectional stretching sheet with velocity slip conditions. The approximate analytical method of homotopy analysis is widely used in the flow and heat transfer problems to solve the highly nonlinear equations. This homotopy analysis method has been extensively used/studied in Refs. [15,16,17,18,19].

We attempt this study to explore the effects of second-order slip flow of an Oldroyd-B fluid toward a stretching surface in the appearance of radiation, convective heating, chemical reaction and cross-diffusion effects using Cattaneo–Christov heat flux model.

Flow analysis

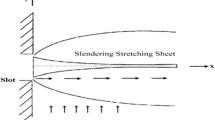
Consider the two-dimensional MHD convective flow of an incompressible Oldroyd-B liquid over a linear stretchy sheet (Fig. 1). The velocity distributions (u, v) are taken in the (x, y)-directions, respectively. The velocity of sheet is assumed as $u_{\mathrm{w}}=ax$, where $a>0$ is the stretching rate. The two temperatures on and apart from the surface are expressed by $T_{\mathrm{w}}$ and $T_\infty$ with $T_{\mathrm{w}}>T_\infty$. Heat flux ($q_{1}$) in view of Cattaneo–Christov theory is expressed

$$\begin{aligned} q_{1} + \lambda \left[ \frac{\partial q_{1}}{\partial t} + V. \nabla q_{1}-q_{1}. \nabla V+(\nabla .V)q_{1} \right] =-\,k_0 \nabla T \end{aligned}$$

(1)

in which $\lambda$ is the thermal relaxation, V is the velocity and k is the fluid thermal conductivity. Equation (1) reduces to the classical Fourier’s law when $\lambda = 0$. Finally, Eq. (1) for incompressible fluid case reduces to the following expression:

$$\begin{aligned} q_{1}+\lambda \left( \frac{\partial q_{1}}{\partial t}+V. \nabla q_{1}-q_{1}. \nabla V \right) =-\,k \nabla T \end{aligned}$$

(2)

The magnetic field of strength $B_0$ is applied upright to the stretchy surface. The electric and induced magnetic fields are neglected. The governing equations of the flow are taken as, see Hayat et al. [3]

Fig. 1

Schematic diagram

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0, \end{aligned}$$

(3)

$$\begin{aligned}&u \frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+A_1 \left( u^2\frac{\partial ^2 u}{\partial x^2}+v^2 \frac{\partial ^2 u}{\partial y^2}+2uv \frac{\partial ^2 u}{\partial x \partial y} \right) = \nu \frac{\partial ^2 u}{\partial y^2} \nonumber \\&\quad -\nu A_2 \bigg (u \frac{\partial ^3 u}{\partial x \partial y^2} +v \frac{\partial ^3 u}{\partial y^3}-\frac{\partial u}{\partial x}\frac{\partial ^2 u}{\partial y^2}-\frac{\partial u}{\partial y}\frac{\partial ^2 v}{\partial y^2} \bigg )-\frac{\sigma B^2_{0}}{\rho } \bigg (u+A_1 v \frac{\partial u}{\partial y} \bigg ), \nonumber \\ \end{aligned}$$

(4)

$$\begin{aligned}&u \frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\frac{k}{\rho c_{\mathrm{p}}}\frac{\partial ^2 T}{\partial y^2}-\frac{1}{\rho c_{\mathrm{p}}}\frac{\partial q_{\mathrm{r}}}{\partial y}+\frac{D_{\mathrm{m}} k_{\mathrm{T}}}{c_{\mathrm{s}} c_{\mathrm{p}}}\frac{\partial ^2 C}{\partial y^2} \end{aligned}$$

(5)

$$\begin{aligned}&u \frac{\partial C}{\partial x}+v \frac{\partial C}{\partial y} =D_{\mathrm{m}} \frac{\partial ^2 C}{\partial y^2}-k_{\mathrm{m}}(C-C_\infty )+\frac{D_{\mathrm{m}} k_{\mathrm{T}}}{T_{\mathrm{m}}}\frac{\partial ^2 T}{\partial y^2} \end{aligned}$$

(6)

The corresponding boundary conditions are

$$\begin{aligned}&u=u_{\mathrm{w}}+u_{\mathrm{slip}}=ax+\lambda _1 \frac{\partial u}{\partial y}+\lambda _2 \frac{\partial ^2 u}{\partial y^2}, \quad v=0, \nonumber \\&\quad -\,k\frac{\partial T}{\partial y}=h_{\mathrm{f}}(T_{\mathrm{w}}-T_\infty ), \quad T=T_{\mathrm{w}}\quad C=C_{\mathrm{w}} \quad {\mathrm{at}} \; y=0, \nonumber \\&\quad u \rightarrow 0, \quad v \rightarrow 0, \quad T \rightarrow T_{\infty },\quad C \rightarrow C_{\infty } \quad {\mathrm{as}}\; y\rightarrow \infty , \end{aligned}$$

(7)

where $\nu$, $\rho$, $A_1$ & $A_2$, c, $c_{\mathrm{p}}$, $\sigma$, $D_{\mathrm{m}}$, $k_{\mathrm{T}}$, $\lambda _1$ & $\lambda _2$ are the kinematic viscosity, density, relaxation time and retardation time, concentration, specific heat, electrical conductivity, diffusion coefficient, first-order chemical reaction parameter and first- and second-order slip velocity factors, respectively. Using Cattaneo–Christov heat flux theory, we obtain the following energy equation

$$\begin{aligned}&u \frac{\partial T}{\partial x}+v \frac{\partial T}{\partial y} + \lambda \Bigg ( u^2 \frac{\partial ^2 T}{\partial x^2}+ v^2 \frac{\partial ^2 T}{\partial y^2} +\left( u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y} \right) \frac{\partial T}{\partial x} + 2uv \frac{\partial T^2}{\partial x \partial y}\nonumber \\&\quad +\left( u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y} \right) \frac{\partial T}{\partial y}\Bigg )=\frac{k}{\rho c_{\mathrm{p}}}\frac{\partial ^2 T}{\partial y^2}-\frac{1}{\rho c_{\mathrm{p}}}\frac{\partial q_{\mathrm{r}}}{\partial y}+\frac{D_{\mathrm{m}} k_{\mathrm{T}}}{c_{\mathrm{s}} c_{\mathrm{p}}}\frac{\partial ^2 C }{\partial y^2} \end{aligned}$$

(8)

The radiative heat flux is taken as

$$\begin{aligned}&q_{\mathrm{r}}=-\frac{4\sigma _0}{3k^*}\frac{\partial T^4}{\partial y} \end{aligned}$$

(9)

Consider the following similarity transformations

$$\begin{aligned} \psi&= \sqrt{a\nu }xf(\eta ),\quad u=\frac{\partial \psi }{\partial y},\quad v=-\frac{\partial \psi }{\partial x}, \quad \eta =\sqrt{\frac{a}{\nu }}y\nonumber \\ v&= -\sqrt{a\nu }f(\eta ), \ \ u= axf^{\prime}(\eta ), \ \ \theta (\eta )=\frac{T-T_{\infty }}{T_{\mathrm{w}}-T_{\infty }}, \ \ \phi (\eta )=\frac{C-C_{\infty }}{C_{\mathrm{w}}-C_{\infty }} \end{aligned}$$

(10)

Substituting Eq. (10) in Eqs. (4), (6) and (8), we have

$$\begin{aligned}&f^{{\prime}{\prime}{\prime}}+\beta \left( f^{{\prime}{\prime}{2}}-f f^{\mathrm{iv}}\right) +\alpha \left( 2ff^{{\prime}}f^{{\prime}{\prime}}-f^{2}f^{{\prime}{\prime}{\prime}} \right) \nonumber \\&\quad +ff^{{\prime}{\prime}}-f^{{\prime}{2}} -M\left( f^{{\prime}}-\alpha ff^{{\prime}{\prime}} \right) =0 \end{aligned}$$

(11)

$$\begin{aligned}&\frac{1}{Pr}\left( 1+\frac{4}{3}R_{\mathrm{d}}\right) \theta^{{\prime}{\prime}}+f \theta^{{\prime}} -\gamma \left( f^{2}\theta^{{\prime}{\prime}}+ff^{{\prime}}\theta^{{\prime}} \right) +D_{\mathrm{f}}\phi^{{\prime}{\prime}}=0 \end{aligned}$$

(12)

$$\begin{aligned}&\frac{1}{Sc}\phi^{{\prime}{\prime}}+f \phi^{{\prime}}-Cr\phi +Sr\theta^{{\prime}{\prime}}=0 \end{aligned}$$

(13)

with boundary conditions

$$\begin{aligned}&f(0)=0, \ f^{{\prime}}(0)=1+\epsilon_1 f^{{\prime}{\prime}}(0)+\epsilon _2 f^{{\prime}{\prime}{\prime}}(0), \ \ \theta^{{\prime}}(0)=-\,Bi(1-\theta (0)),\ \ \phi (0)=1 \nonumber \\&\quad f^{{\prime}}(\infty )=0, \ \ \theta (\infty )=0, \ \ \phi (\infty )=0, \end{aligned}$$

(14)

Here we declare the dimensionless variables as follows: $\epsilon _1=\lambda _1 \sqrt{a/\nu }$ & $\epsilon _2=\lambda _2 \frac{a}{\nu }$ are the first- and second-order slip velocity constants, $\frac{h_{\mathrm{f}}}{k} \sqrt{\nu /a}$ is the Biot number, $\alpha =A_1 a$ and $\beta =A_2 a$ are the dimensionless relaxation and retardation time constants, respectively, $M = \frac{\sigma B_{0}^2}{\rho a}$ the Hartmann number, $Pr=\frac{\rho \nu C_{\mathrm{p}}}{k}$ the Prandtl number, $R_{\mathrm{d}}=\frac{4 \sigma ^* T_{\infty }^3}{kk^*}$ the thermal radiation parameter, $\gamma =\lambda a$, the non-dimensional thermal relaxation time, $D_{\mathrm{f}}=\frac{D_{\mathrm{m}} k_{\mathrm{T}}}{\nu c_{\mathrm{s}} c_{\mathrm{p}}}\frac{c_{\mathrm{w}}-c_\infty }{T_{\mathrm{w}}-T_\infty }$, the Dufour number, $Cr=\frac{k_{\mathrm{m}}}{ a}$ the chemical reaction constant, $Sc=\frac{\nu }{D_{\mathrm{m}}}$ the Schmidt number, $Sr=\frac{D_{\mathrm{m}} k_{\mathrm{T}}}{\nu T_{\mathrm{m}}} \frac{T_{\mathrm{w}}-T_\infty }{c_{\mathrm{w}}-c_\infty }$ the Soret number.

The dimensionless forms of local skin friction ($Re^\frac{1}{2}Cf_{\mathrm{x}}$), heat $(Re^{-\frac{1}{2}}Nu_{\mathrm{x}})$ and mass $(Re^{-\frac{1}{2}}Sh_{\mathrm{x}})$ transfer rates are represented below

$$\begin{aligned} Re^\frac{1}{2}Cf_{\mathrm{x}}&= \frac{1+\alpha }{1+\beta }f^{{\prime}{\prime}}(0) \\ Re^{-\frac{1}{2}}Nu_{\mathrm{x}}&= -\,\left( 1+\frac{4}{3}R_{\mathrm{d}}\right) \theta^{{\prime}}(0) \\ Re^{-\frac{1}{2}}Sh_{\mathrm{x}}&= -\,\phi^{{\prime}}(0) \end{aligned}$$

Solution methodology

We incorporated the homotopy analysis method in order to get the convergent solution of the system of equations. The initial approximations and complementary linear operators can be put in the form

$$\begin{aligned}&f_{0}=\eta {e^{-\upeta }}+\frac{3\epsilon _2-2\epsilon _1}{\epsilon _2-1-\epsilon _1}*e^{-\upeta }-\frac{3\epsilon _2-2\epsilon _1}{\epsilon _2-1-\epsilon _1}, \ \ \ \ \theta _{0}=\frac{Bi*e^{-\upeta }}{1+Bi}, \ \ \ \ \phi _{0}=e^{-\upeta }. \\&\quad L_{\mathrm{f}}=f^{{\prime}{\prime}{\prime}}-f^{{\prime}}, \ \ \ \ L_{\uptheta }=\theta^{{\prime}{\prime}}-\theta , \ \ \ \ L_{\upphi }=\phi^{{\prime}{\prime}}-\phi \end{aligned}$$

which satisfies the property

$$\begin{aligned} L_{\mathrm{f}}\left[ D_1+D_2 e^{\upeta }+D_3 e^{-\upeta }\right] =0, \quad L_{\uptheta }\left[ D_4e^{\upeta }+D_5 e^{-\upeta }\right] =0, \quad L_{\upphi }\left[ D_6e^{\upeta }+D_7 e^{-\upeta }\right] =0, \end{aligned}$$

where $D_{\mathrm{k}} (k=1-7)$ are constants. The zeroth-order deformation equation is constructed as

$$\begin{aligned} \left( 1-p\right) L_{\mathrm{f}}\left[ \widehat{f}\left( \eta ;p\right) -f_{0}\left( \eta \right) \right]&= p H_{\mathrm{f}} h_{\mathrm{f}} N_{\mathrm{f}} \left[ \widehat{f}\left( \eta ;p\right) \right] \end{aligned}$$

(15)

$$\begin{aligned} \left( 1-p\right) L_{\uptheta }\left[ \widehat{\theta }\left( \eta ;p\right) -\theta _{0}\left( \eta \right) \right]&= p H_{\uptheta } h_{\uptheta } N_{\uptheta } \left[ \widehat{\theta }\left( \eta ;p\right) ,\ \widehat{f}\left( \eta ;p\right) , \widehat{\phi }\left( \eta ;p\right) \right] \end{aligned}$$

(16)

$$\begin{aligned} \left( 1-p\right) L_{\upphi }\left[ \widehat{\phi }\left( \eta ;p\right) -\phi _{0}\left( \eta \right) \right]&= p H_{\upphi } h_{\upphi } N_{\upphi } \left[ \widehat{\phi }\left( \eta ;p\right) ,\ \widehat{f}\left( \eta ;p\right) , \ \widehat{\theta }\left( \eta ;p\right) \right] . \end{aligned}$$

(17)

where the system of nonlinear operators in HAM for the present problem is

$$\begin{aligned}&N_{\mathrm{f}} \left[ \widehat{f}\left( \eta ;p\right) \right] = \frac{\partial ^{3} \widehat{f}\left( \eta ;p\right) }{\partial \eta ^{3}} - \left( \frac{\partial \widehat{f}\left( \eta ;p\right) }{\partial \eta }\right) ^{2}+ \widehat{f}\left( \eta ;p\right) \frac{\partial ^{2} \widehat{f}\left( \eta ;p\right) }{\partial \eta ^{2}} \nonumber \\&\quad +\alpha \left( 2\widehat{f}\left( \eta ;p\right) \frac{\partial \widehat{f}\left( \eta ;p\right) }{\partial \eta } \frac{\partial ^{2} \widehat{f}\left( \eta ;p\right) }{\partial \eta ^{2}}-\left( \widehat{f}\left( \eta ;p\right) \right)^{2} \frac{\partial ^{3} \widehat{f}\left( \eta ;p\right) }{\partial \eta ^{3}} \right) \nonumber \\&\quad +\beta \left( \left( \frac{\partial ^{2} \widehat{f}\left( \eta ;p\right) }{\partial \eta ^{2}} \right) ^{2}-\widehat{f}\left( \eta ;p\right) \frac{\partial ^{4} \widehat{f}\left( \eta ;p\right) }{\partial \eta ^{4}} \right) \nonumber \\&\quad -M\left( \frac{\partial \widehat{f}\left( \eta ;p\right) }{\partial \eta }-\alpha \widehat{f}\left( \eta ;p\right) \frac{\partial ^{2} \widehat{f}\left( \eta ;p\right) }{\partial \eta ^{2}}\right) \end{aligned}$$

(18)

$$\begin{aligned}&N_{\uptheta } \left[ \widehat{f}\left( \eta ;p\right) ,\ \widehat{\theta }\left( \eta ;p\right) , \ \widehat{\phi }\left( \eta ;p\right) \right] = \left( 1 + \frac{4}{3} R_{\mathrm{d}}\right) \frac{\partial ^{2} \widehat{\theta }\left( \eta ;p\right) }{\partial \eta ^{2}}+Pr\widehat{f}\left( \eta ;p\right) \frac{\partial \widehat{\theta }\left( \eta ;p\right) }{\partial \eta }\nonumber \\&\quad -Pr \gamma \left( \widehat{f}\left( \eta ;p\right) \frac{\partial \widehat{f}\left( \eta ;p\right) }{\partial \eta }\frac{\partial \widehat{\theta }\left( \eta ;p\right) }{\partial \eta }+\left( \widehat{f}\left( \eta ;p\right) \right)^{2} \frac{\partial^{2} \widehat{\theta }\left( \eta ;p\right) }{\partial \eta ^{2}}\right) \nonumber \\&\quad + Pr D_{\mathrm{f}}\left( \frac{\partial ^{2} \widehat{\phi }\left( \eta ;p\right) }{\partial \eta ^{2}}\right) \end{aligned}$$

(19)

$$\begin{aligned}&N_{\upphi } \left[ \widehat{f}\left( \eta ;p\right) ,\ \widehat{\theta }\left( \eta ;p\right) , \widehat{\phi }\left( \eta ;p\right) \right] = \frac{\partial ^{2} \widehat{\phi }\left( \eta ;p\right) }{\partial \eta ^{2}} + Sc \widehat{f}\left( \eta ;p\right) \frac{\partial \widehat{\phi }\left( \eta ;p\right) }{\partial \eta } \nonumber \\&\quad -Sc \ Cr \ \widehat{\phi }\left( \eta ;p\right) +ScSr\left( \frac{\partial ^{2} \widehat{\theta }\left( \eta ;p\right) }{\partial \eta ^{2}}\right) \end{aligned}$$

(20)

The boundary conditions are

$$\begin{aligned} \widehat{f}\left( 0;p\right)&= 0, \widehat{f}^{{\prime}}\left( 0;p\right) = 1 + \epsilon _1 \widehat{f}^{{\prime}{\prime}}\left( 0;p\right) +\epsilon _2 \widehat{f}^{{\prime}{\prime}{\prime}}\left( 0;p\right) , \widehat{f}^{{\prime}}\left( \infty ;p\right) = 0, \nonumber \\ \widehat{\theta}^{{\prime}}\left( 0;p\right)&= -\,Bi \left( 1-\widehat{\theta }\left( 0;p\right) \right) , \widehat{\theta }\left( \infty ;p\right) = 0, \nonumber \\ \widehat{\phi }\left( 0;p\right)&= \left( 1;p\right) , \widehat{\phi }\left( \infty ;p\right) = 0. \end{aligned}$$

(21)

The $m{\mathrm{th}}$-order deformation equations are

$$\begin{aligned} {L}_{\mathrm{f}}\left( f_{\mathrm{m}}\left( \eta \right) - \chi _{\mathrm{m}} f_{{\mathrm{m}}-1}\left( \eta \right) \right)&= h_{\mathrm{f}} R_{\mathrm{m}}^{\mathrm{f}}\left( \eta \right) \end{aligned}$$

(22)

$$\begin{aligned} {L}_{\uptheta }\left( \theta _{\mathrm{m}}\left( \eta \right) - \chi _{\mathrm{m}} \theta _{{\mathrm{m}}-1}\left( \eta \right) \right)&= h_{\uptheta } R_{\mathrm{m}}^{\uptheta }\left( \eta \right) \end{aligned}$$

(23)

$$\begin{aligned} {L}_{\upphi }\left( \phi _{\mathrm{m}}\left( \eta \right) - \chi _{\mathrm{m}} \phi _{{\mathrm{m}}-1}\left( \eta \right) \right)&= h_{\upphi } R_{\mathrm{m}}^{\upphi }\left( \eta \right) \end{aligned}$$

(24)

subject to the boundary conditions

$$\begin{aligned} f_{\mathrm{m}}\left( 0\right)&= 0, \ f^{{\prime}}_{\mathrm{m}}\left( 0\right) - \epsilon _1 f^{{\prime}{\prime}}_{\mathrm{m}}\left( 0\right) -\epsilon _2 f^{{\prime}{\prime}{\prime}}_{\mathrm{m}}\left( 0\right) = 0 \ {\text{and}} \ f^{{\prime}}_{\mathrm{m}}\left( \eta \right) \rightarrow 0 \ {\text{when }} \ \eta \rightarrow \infty \nonumber \\&\quad \theta^{{\prime}}_{\mathrm{m}}\left( 0\right) - Bi \theta _{\mathrm{m}}\left( 0\right) = 0 \ {\text{ and }} \ \theta _{\mathrm{m}}\left( \eta \right) \rightarrow 0 \ {\text{ when }} \ \eta \rightarrow \infty \nonumber \\ \phi^{{\prime}}_{\mathrm{m}}\left( 0\right)&= 0 \ {\hbox {and}} \ \phi _{\mathrm{m}}\left( \eta \right) \rightarrow 0 \ {\hbox {when}} \ \eta \rightarrow \infty \end{aligned}$$

(25)

$$\begin{aligned} {R}_{\mathrm{m}}^{\mathrm{f}}\left( \eta \right)&= f^{{\prime}{\prime}{\prime}}_{{\mathrm{m}}-1} + \Sigma ^{{\mathrm{m}}-1}_{{\mathrm{k}}=0} \left[ f_{{\mathrm{m}}-1-{\mathrm{k}}} f^{{\prime}{\prime}}_{\mathrm{k}} - f^{{\prime}}_{{\mathrm{m}}-1-{\mathrm{k}}} f^{{\prime}}_{\mathrm{k}} \right] \nonumber \\&\quad +\alpha \Sigma ^{{\mathrm{m}}-1}_{{\mathrm{l}}=0}f_{{\mathrm{m}}-1-{\mathrm{l}}}\left( 2\Sigma ^{\mathrm{l}}_{{\mathrm{j}}=0}f^{{\prime}}_{{\mathrm{l}}-{\mathrm{j}}}f^{{\prime}{\prime}}_{\mathrm{j}}+\Sigma ^{\mathrm{l}}_{{\mathrm{j}}=0}f_{{\mathrm{l}}-{\mathrm{j}}}f^{{\prime}{\prime}{\prime}}_{\mathrm{j}}\right) \nonumber \\&\quad +\beta \Sigma ^{{\mathrm{m}}-1}_{{\mathrm{k}}=0}\left[ f^{{\prime}{\prime}}_{{\mathrm{m}}-1-{\mathrm{k}}}f^{{\prime}{\prime}}_{\mathrm{k}}-f_{{\mathrm{m}}-1-{\mathrm{k}}}f_{\mathrm{k}}^{\mathrm{iv}}\right] \nonumber \\&\quad -M \left( f_{{\mathrm{m}}-1}-\alpha \Sigma ^{{\mathrm{m}}-1}_{{\mathrm{k}}=0}f_{{\mathrm{m}}-1-{\mathrm{k}}} f^{{\prime}{\prime}}_{\mathrm{k}}\right) \end{aligned}$$

(26)

$$\begin{aligned} {R}_{\mathrm{m}}^{\uptheta }\left( \eta \right)&= \left( 1 + \frac{4}{3} R_{\mathrm{d}}\right) \theta^{{\prime}{\prime}}_{{\mathrm{m}}-1}+Pr\Sigma ^{{\mathrm{m}}-1}_{{\mathrm{l}}=0}\left[ \theta^{{\prime}}_{{\mathrm{m}}-1-{\mathrm{l}}}f_{\mathrm{l}}\right] \nonumber \\&\quad -Pr \gamma \left( f_{{\mathrm{m}}-1-{\mathrm{l}}}\Sigma ^{\mathrm{l}}_{{\mathrm{j}}=0}f^{{\prime}}_{{\mathrm{l}}-{\mathrm{j}}}\theta^{{\prime}}_{\mathrm{j}}+f_{{\mathrm{m}}-1-{\mathrm{l}}}\theta^{{\prime}{\prime}}_{\mathrm{l}}\right) +Pr D_{\mathrm{f}}\Sigma ^{{\mathrm{m}}-1}_{{\mathrm{k}}=0}\phi^{{\prime}{\prime}}_{{\mathrm{m}}-1} \end{aligned}$$

(27)

$$\begin{aligned} {R}_{\mathrm{m}}^{\upphi }\left( \eta \right)&= \frac{1}{Sc}\phi^{{\prime}{\prime}}_{{\mathrm{m}}-1} + \ \Sigma ^{{\mathrm{m}}-1}_{{\mathrm{k}}=0} f_{{\mathrm{m}}-1-{\mathrm{k}}} \phi^{{\prime}}_{\mathrm{k}} -Cr \phi _{{\mathrm{m}}-1} +Sr\Sigma ^{{\mathrm{m}}-1}_{{\mathrm{k}}=0}\theta^{{\prime}{\prime}}_{{\mathrm{m}}-1} \end{aligned}$$

(28)

where $\chi _{\mathrm{m}} = \left\{ {\mathop {1,\ \ m \ge 1.}\limits ^{\displaystyle 0, \ \ m \le 1,}}\right.$

After solving ${m}{\mathrm{th}}$ -order HAM equations, we get the followings

$$\begin{aligned} f_{\mathrm{m}}(\eta )&= f^{*}_{\mathrm{m}}(\eta )+D_{1}+D_{2}e^{\upeta} +D_{3}e^{-\upeta } \\ \theta _{\mathrm{m}}(\eta )&= \theta ^{*}_{\mathrm{m}}(\eta )+D_{4}e^{\upeta }+D_{5}e^{-\upeta } \\ \phi _{\mathrm{m}}(\eta )&= \phi ^{*}_{\mathrm{m}}(\eta )+D_{6}e^{\upeta }+D_{7}e^{-\upeta } \end{aligned}$$

Fig. 2

h-curves for $h_{\mathrm{f}}, h_{\uptheta} , h_{\upphi}$

Table 1 Order of approximations

The $f^{*}_{\mathrm{m}}(\eta )$, $\theta ^{*}_{\mathrm{m}}(\eta )$ and $\phi ^{*}_{\mathrm{m}}(\eta )$ are the special solutions of the equations. The complementary constants $h_{\mathrm{f}}$, $h_{\uptheta}$ and $h_{\upphi}$ perform a key role and the fields are drawn at fifteenth order of approximation to accomplish the valid range of constants (see Fig. 2). The acceptable values of $h_{\mathrm{f}}$, $h_{\uptheta}$ and $h_{\upphi}$ are $-\,1.7 \le h_{\mathrm{f}} \le -\,0.6, -\,1.2 \le h_{\uptheta} \le -\,0.6 , -\,1.2 \le h_{\upphi} \le -\,0.3$, respectively. Table 1 shows the order of approximation for HAM. Table 2 depicts $f^{{\prime}{\prime}}(0)$ in the absence of MHD and retardation time parameter. It is observed that all obtained values of $f^{{\prime}{\prime}}(0)$ are in an excellent agreement with the values found in Sadghey et al. [20], Mukhopadhyay [21] and Abbasi et al. [22]. A comparison of $-\,f^{{\prime}{\prime}}(0)$ and $-\,\theta^{{\prime}}(0)$ has been made between the results of the HAM solution and the results in Ref. [3] in Table 3.

Table 2 Comparison with $f^{{\prime}{\prime}}(0)$ obtained by Sadghey et al. [20], Mukhopadhyay [21] and Abbasi et al. [22] in the limiting case for different $\alpha$ by fixing $\beta =M=0$

Table 3 Comparison with $-\,f^{{\prime}{\prime}}(0)$ and $-\,\theta^{{\prime}}(0)$ obtained by Hayat et al. [3], when $\epsilon _1=\epsilon _2=R_{\mathrm{d}}=D_{\mathrm{f}}=Bi=0$

Results and discussion

The numerical values of velocity, concentration and temperature distributions are computed through various combination of parameters involved in this study with the fixed values of $\epsilon _1=0.2$, $\epsilon _2=0.3$, $M=0.5$, $\alpha =0.1$, $\beta =0.1$, $\gamma =0.5$, $R_{\mathrm{d}}=0.3$, $Pr=1.0$, $D_{\mathrm{f}}=0.5$, $Sc=0.9$, $Bi=0.5$, $Cr=1.0$, $Sr=0.3$.

Effect on velocity

It is surveyed from Fig. 3 that the velocity diminishes while increasing the values of relaxation time constant. This is due to increasing the stretching rate of the sheet which reduces the flow speed. Figure 4 demonstrates that the velocity decreases near boundary and rises after some distance when raising the values of retardation time constant. Increasing stretching rate affects retardation time parameter which provides this peculiar result. The velocity profile slowly diminishes on increasing the values of first-order slip constant, which is plotted in Fig. 5. Figure 6 indicates that the velocity enhances when the second-order slip constant rises. Here viscosity of the fluid reduces on increasing $\epsilon _2$. When comparing Figs. 5 and 6, the effect of first-order slip constant on velocity is more pronounced than the second-order slip constant.

Fig. 3

Velocity variations for different ranges of relaxation time parameter ($\alpha$)

Fig. 4

Velocity variations for different ranges of retardation time parameter ($\beta$)

Fig. 5

Velocity variations for different ranges of first-order velocity slip parameter ($\epsilon _1$)

Fig. 6

Velocity variations for different ranges of second-order velocity slip parameter ($\epsilon _2$)

Effect on temperature

The influence of thermal relaxation time for heat flux $\gamma$ on the temperature profile is analyzed in Fig. 7. It can be archived that the temperature in Cattaneo–Christov heat flux model is less than the Fourier’s model. Figure 8 displays the impact of radiation parameter on temperature. By raising the values of radiation parameter, the thermal boundary layer thickness develops. Raising the radiation parameter enhances the thermal conductivity of the medium and it results in the growth of thermal boundary layer. It is seen from Figs. 9 and 10 that first- and second-order slip constants showed the opposing tendency on temperature profile. Figure 11 shows the effect of Biot number on temperature profile. It shows that temperature is growing function of Bi near the surface because the Biot number affects much the temperature near the surface. Rising values of Bi are due to higher heat transfer resistance inside a body as compared to surface. The impact of Dufour number on temperature is sketched in Fig. 12. It is concluded that the thermal boundary layer thickness boosted up on raising the values of Dufour number.

Fig. 7

Temperature variations for different ranges of thermal relaxation time parameter ($\gamma$)

Fig. 8

Temperature variations for different ranges of radiation parameter ($R_{\mathrm{d}}$)

Fig. 9

Temperature variations for different ranges of first-order velocity slip parameter ($\epsilon _1$)

Fig. 10

Temperature variations for different ranges of second-order velocity slip parameter ($\epsilon _2$)

Fig. 11

Temperature variations for different ranges of Biot number (Bi)

Fig. 12

Temperature variations for different ranges of Dufour number ($D_{\mathrm{f}}$)

Effect on concentration

Figure 13 demonstrates the effect of chemical reaction on concentration profile. It shows that concentration reduces on higher values of chemical reaction parameter. It is inspected from Fig. 14 that a rise in Soret number initially gives less effect on concentration, while the tremendous trend occurs when $\eta >1$. That is, concentration rises with Soret number after $\eta >1$.

Fig. 13

Concentration variations for different range of Chemical reaction parameter (Cr)

Fig. 14

Concentration variations for different range of Soret number (Sr)

Local skin friction, Nusselt number and Sherwood number

The effects of $\epsilon _1$, $\epsilon _2$ with $\alpha$ on skin friction are investigated through Figs. 15 and 16. Apparently, first- and second-order slip constants with relaxation time have opposite effects on skin friction. Figure 17 presents the effects of both the first-order slip constant $\epsilon _1$ and the magnetic field constant M on the local Nusselt number. The graph represented that the heat transfer rate decreases when $\epsilon _1$ increases. Figure 18 depicts the influence of both the second-order slip constant $\epsilon _2$ and the magnetic field constant M on the local Nusselt number. From the figure, we can observe that the heat transfer rate on the surface enhances when the second-order slip constant $\epsilon _2$ increases. Figures 19 and 20 explore the variation of the local Sherwood number. It is clear that the local mass transfer rate diminishes with the growth of $\alpha$ and Cr, and it decreases on raising the value of M and Cr. Comparing these figures, it is concluded that the first- and second-order slip constants provide opposite tendency on physical quantities.

Conclusions

The present study reports the second-order slip and chemical reaction on steady two-dimensional flow of an incompressible Oldroyd-B liquid over a stretching sheet with convective heating. The following observations are found.

• 1. The skin friction enhances with first-order velocity slip, and it diminishes with second-order velocity slip.

• 2. The chemical reaction boosted up the mass transfer rate. Similar behavior on mass transfer rate with magnetic field is observed.

• 3. The first-order velocity slip provides much effect on heat transfer rate comparing second-order velocity slip while increasing Hartmann number.

Fig. 15

Local skin friction for various values of $\epsilon _1$ versus $\alpha$

Fig. 16

Local skin friction for various values of $\epsilon _2$ versus $\alpha$

Fig. 17

Local Nusselt number for various values of $\epsilon _1$ versus M

Fig. 18

Local Nusselt number for various values of $\epsilon _2$ versus M

Fig. 19

Local Sherwood number for various values of $\alpha$ versus Cr

Fig. 20

Local Sherwood number for various values of M versus Cr