1 Introduction

The non-Newtonian fluids reflect the physiological properties. These fluids are utilized to analyze the physiological materials, like peristaltic transport, swallowing food, the motion of small blood vessels, chyme motion, etc. The Carreau fluid is one of the physiological fluid models, and it represents both shear-thickening and shear-thinning characteristics based on power law index. This model was firstly investigated by Pierre Carreau. It is a four-parameter model and has effective properties of a truncated power law model which did not have a discontinuous first derivative. Cross [1] reported the rheological nature of non-Newtonian materials and proposed the new relationship of pseudo-plastic materials. Later on, Perktold et al. [4] described the pulsatile phenomenon of non-Newtonian blood material with different bifurcation angles. They proposed the hemodynamic phenomenon which is important in atherogenesis. Joshua et al. [5] analyzed the Carreau-Yasuda and Casson non-Newtonian models. Nadeem et al. [4] investigated the time-dependent peristaltic Carreau material flow through eccentric cylinders. They addressed that the presence of Weissenberg factor declines the pressure rise in peristaltic pumping process. Khan et al. [5] described the shear-thinning and shear-thickening behavior of Carreau model. They reported that the temperature for shear-thinning case is reversed to shear-thickening situation for the influence of Weissenberg number. Some more remarkable contributions on Carreau model are reported in Refs. [7,8,9, 9, 12,13,14,15, 15, 16].

Study of velocity slip is the most challenging and has noteworthy role in myriad applications. One of the archetypal benefits of slippage is the deduction of flow resistance in micro-channels. The velocity slip instantly occurs in complex fluids such as colloids, polymeric solutions, suspensions and foams. The materials which reflect the boundary slip have remarkable technological implications include the artificial heart and internal cavities polishing. In early nineteenth century, Navier [16] firstly described the concept of slip condition. The boundary-driven slip momentum flow was reported by Khader and Megahed [17]. They noticed that the local factors of skin friction reduced with the incrementing slip velocity values. Bhargava and Goyal [18] presented the hydro-magneto nanofluid flow under momentum slip and revealed that the velocity declines for stronger slip and the opposite phenomenon founded in temperature and concentration fields. Mutlag et al. [31] analyzed the momentum slip condition on the power-law material flow through radiation. They reported that the momentum slip factor reduces the rate of energy transport and skin friction. Khan et al. [34] presented the slip conditions on the flow of Phan-Thien–Tanner fluid over double-layered optical fibers. Raisi et al. [21] analyzed the micro-channels flow under slip and no-slip circumstances. They addressed that the rate of energy transportation is not affected by slip condition at low Reynolds number. Georgiou [22] considered the slip at the wall on extradite-swell and Poiseuille flow of Carreau fluid.

The viscous dissipation is also important in the analysis of heat transfer problems, and it has various applications like cooling of turbine blades and controlling the heat transfer in machines. Gebhart [23] described the influence of viscous heating in naturally convected viscous material flow. Gireesha et al. [24] evaluated the Joule and Ohmic dissipation consequences on the nonlinear Carreau–Casson fluids under magnetic force with heterogeneous and homogeneous reactions. In this research, they executed that the Eckert number improves the thermal layer and liquid temperature. The Joule and Ohmic dissipation nature on the unsteady radiated flow with the transverse magnetic field is considered by Jana et al. [25]. They stated that the temperature and velocity distributions raise with Eckert number. Cookey et al. [26] and Das et al. [27] addressed the viscous dissipation influence on free-convected time-dependent fluid flow. Recently, some more investigations on viscous dissipation for different kinds of fluid flows with momentum slip conditions are presented in [28,29,30,31,32,33,34]. Sheremet et al. [35] illustrated the combined effect of variable viscosity and thermal conductivity on mixed convection flow of viscous fluid over a vertical channel by considering the chemical reaction effect. The impact of chemical reaction over a vertical duct with convection condition was discussed by Sheremet et al. [36]. Jabeen et al. [37] thermal radiations and mass transfer analysis of the 3D magnetite Carreau fluid flow past a horizontal surface of paraboloid of revolution. Ullah et al. [38] analyzed the nonlinear thermal radiations and mass transfer analysis of the magnetite Carreau fluid flowing past a Permeable stretching or shrinking surface under cross-diffusion and Hall effects.

To the best of author’s knowledge, the three-dimensional flow of magnetized Carreau material by the bidirectional stretched surface immersed in porous space is not available in the literature. Hence, the present article is focused to describe the different effects on the three-dimensional flow of magnetized Carreau material by the bidirectional stretched surface immersed in porous space. The set of transformed ordinary system of expressions is tackled numerically. The impression of distinct flow constraints on the practically important quantities for both shear-thickening and shear-thinning models are described and interpreted.

2 Problem formulation

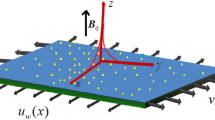
The laminar three-dimensional (3D) Carreau non-Newtonian material flow induced by the bidirectional movement of surface in porous surface is considered.

  • The slip condition mechanisms are taken into consideration.

  • The constant magnetic force having strength \(B_{0}\) is performed in the normal direction of sheet.

  • The viscous heating and radiation phenomenon is retained.

  • The first-order chemically reaction term is accounted.

  • The electric and induced magnetic forces are removed due to account of small magnetic Reynolds number.

  • The Hall current and Joule dissipative effects are ignored.

The coordinate system and physical configuration of the present investigation with the above assumptions are pictured in Fig. 1.

Fig. 1
figure 1

Physical model and co-ordinate system

Full size image

2.1 Rheological model

Steady-state generalized non-Newtonian material that fulfills the rheological nature of Carreau model is considered in this analysis. The Cauchy stress tensor expression for Carreau non-Newtonian fluid is considered as [39]:

$$\tau = - pI + \mu (\dot{\gamma }){\rm A}_{1}$$
(1)

with

$$\mu (\dot{\gamma }) = \mu_{\infty } + (\mu_{0} - \mu_{\infty } )[1 + (\Gamma \dot{\gamma })^{2} ]^{{\frac{n - 1}{2}}} ,$$
(2)

where \(\frac{{\mu - \mu_{\infty } }}{{\mu_{0} - \mu_{\infty } }}\) defines the slope in the region of power-law, \(A_{1} = (\nabla V)^{T} + \nabla V\) the first Rivlin–Erickson tensor and \(\dot{\gamma } = \sqrt {\frac{1}{2}tr(A_{1} )^{2} }\) is the shear rate.

In most practical cases, \(\mu_{0} > > \mu_{\infty }\) and \(\mu_{\infty }\) tends to be zero. Consequently, Eqs. (1) and (2) reduced to the following expression:

$$\tau = - pI + \mu_{0} [1 + (\Gamma \dot{\gamma })^{2} ]^{{\frac{n - 1}{2}}} A_{1} .$$
(3)

Carreau fluid model can be grouped into two types namely pseudo-plastic or shear-thinning fluids for \(0 < n < 1\) and dilatants or shear-thickening when \(n > 1\). For \(n = 1\) or \(\Gamma = 0,\) this model converted to Newtonian model.

From the above assumptions, the governing equations are taken as [5, 24, 28]:

$$\frac{\partial u}{{\partial x}} + \frac{\partial w}{{\partial z}} + \frac{\partial v}{{\partial y}} = 0,$$
(4)
$$\rho \left( {u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + w\frac{\partial u}{{\partial z}}} \right) = \mu \frac{\partial }{\partial z}\left[ {\frac{\partial u}{{\partial z}} + \Gamma^{2} \left( {\frac{\partial u}{{\partial z}}} \right)^{3} \frac{(n - 1)}{2}} \right] - \left( {\sigma B_{0}^{2} + \frac{\mu }{kp}} \right)u,$$
(5)
$$\rho \left( {u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} + w\frac{\partial v}{{\partial z}}} \right) = \mu \frac{\partial }{\partial z}\left[ {\frac{\partial v}{{\partial z}} + \Gamma^{2} \left( {\frac{\partial v}{{\partial z}}} \right)^{3} \frac{(n - 1)}{2}} \right] - \left( {\sigma B_{0}^{2} + \frac{\mu }{kp}} \right)v,$$
(6)
$$\rho C_{P} \left( {u\frac{\partial T}{{\partial x}} + w\frac{\partial T}{{\partial z}} + v\frac{\partial T}{{\partial y}}} \right) = \left[ {\alpha \rho C_{P} + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}} \right]\left( {\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + \mu \left[ {\left( {\frac{\partial u}{{\partial z}}} \right)^{2} + \left( {\frac{\partial v}{{\partial z}}} \right)^{2} } \right],$$
(7)
$$u\frac{\partial C}{{\partial x}} + w\frac{\partial C}{{\partial z}} + v\frac{\partial C}{{\partial y}} = D\frac{{\partial^{2} C}}{{\partial z^{2} }} + k_{1} (C_{\infty } - C).$$
(8)

The related conditions for the problem are as follows:

$$\begin{aligned} & u = B_{1}^{ * } \frac{\partial u}{{\partial z}} + U_{\text{w}} ,\quad \,v = B_{2}^{ * } \frac{\partial v}{{\partial z}} + V_{\text{w}} ,\,\quad w = 0,\,\quad C = C_{\text{w}} ,\,\quad T = T_{\text{w}} \quad {\text{at}}\quad z = 0, \\ & u \to 0,\quad v \to 0,\quad \,T \to T_{\infty } ,\,\quad C \to C_{\infty } \quad {\text{as}}\quad z \to \infty . \\ \end{aligned}$$
(9)

2.2 Solution of problem

The following similarities variables are considered [5, 31]:

$$\begin{aligned} & u = axf^{\prime}(\eta ),\,\quad w = - \sqrt {a\vartheta } [f(\eta ) + g(\eta )],\quad v = ayg^{\prime}(\eta ),\, \\ & \eta = \sqrt {\frac{a}{\vartheta }} z,\quad \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\quad \,\phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{\text{w}} - C_{\infty } }}. \\ \end{aligned}$$
(10)

Equation (4) is directly satisfied. Equations (5)–(8) and boundary conditions (9) are reduced to the following forms:

$$f^{\prime\prime\prime}\left[ {\frac{3(n - 1)}{2}{\text{We}}_{1}^{2} f^{{\prime\prime}{2}} + 1} \right] - f^{{\prime}{2}} + (f + g)f^{\prime\prime} - (K + M^{2} )f^{\prime} = 0,$$
(11)
$$g^{\prime\prime\prime}\left[ {\frac{3(n - 1)}{2}{\text{We}}_{2}^{2} g^{{\prime\prime}{2}} + 1} \right] - g^{{\prime}{2}} + (f + g)g^{\prime\prime} - (K + M^{2} )g^{\prime} = 0,$$
(12)
$$(1 + R)\theta^{\prime\prime} + \Pr \theta^{\prime}(f + g) + \Pr {\text{Ec}}_{x} f^{{\prime\prime}{2}} + \Pr {\text{Ec}}_{y} g^{{\prime\prime}{2}} = 0,$$
(13)
$$\phi^{\prime\prime} + {\text{Sc}}\phi^{\prime}(f + g) - {\text{KrSc}}\phi = 0.$$
(14)

Transformed non-dimensional boundary conditions are:

$$\begin{aligned} & f(0) = g(0) = 0,\quad f^{\prime}(0) = 1 + B_{1} f^{\prime\prime}(0),\,\quad \,g^{\prime}(0) = S + B_{2} g^{\prime\prime}(0),\quad \theta (0) = \phi (0) = 1, \\ & f^{\prime}(\infty ) \to 0,\,\quad g^{\prime}(\infty ) \to 0,\,\quad \theta (\infty ) \to 0,\quad \,\phi (\infty ) \to 0. \\ \end{aligned}$$
(15)

The non-dimensional constraints are defined as follows:

$$\begin{gathered} \text{We}_{1} = \sqrt {\frac{{\Gamma^{2} a^{3} x^{2} }}{\vartheta }} ,\,\quad \text{We}_{2} = \sqrt {\frac{{\Gamma^{2} a^{3} y^{2} }}{\vartheta }} ,\quad M^{2} = \frac{{\sigma B_{0}^{2} }}{a\rho },\,\quad K = \frac{\vartheta }{aKp},\quad \Pr = \frac{{\mu C_{P} }}{k},\,\quad S = \frac{b}{a},\,\quad \text{Kr} = \frac{{k_{1} }}{a}, \hfill \\ R = \frac{{16\sigma T_{\infty }^{3} }}{{kk^{ * } }},\,\quad \text{Ec}_{x} = \frac{{a^{2} x^{2} }}{{C_{P} (T_{\text{w}} - T_{\infty } )}},\,\quad \text{Ec}_{y} = \frac{{a^{2} y^{2} }}{{C_{P} (T_{\text{w}} - T_{\infty } )}}Sc = \frac{\vartheta }{D},\quad B_{1} = B_{1}^{ * } \sqrt {\frac{a}{\vartheta }} ,\quad B_{2} = B_{2}^{ * } \sqrt {\frac{a}{\vartheta }} . \hfill \\ \end{gathered}$$

2.3 Quantities of interest

The quantities from practical point of view are skin-friction factors along \(Y\) and \(X\) directions, the local Nusselt and Sherwood numbers which are defined below:

$$Cf_{y} = \frac{{\tau_{yz} }}{{\rho V_{\text{w}}^{2} }},\quad Cf_{x} = \frac{{\tau_{xz} }}{{\rho U_{\text{w}}^{2} }},\quad Nu_{x} = \frac{{xq_{\text{w}} }}{{k(T_{\text{w}} - T_{\infty } )}},\quad \,Sh_{x} = \frac{{xj_{\text{w}} }}{{D(C_{\text{w}} - C_{\infty } )}}.$$
(16)

The stresses at wall along \(Y\) and \(X\) directions are given by

$$\tau_{xz} = \mu \left[ {\frac{\partial u}{{\partial z}} + \frac{(n - 1)}{2}\Gamma^{2} \left( {\frac{\partial u}{{\partial z}}} \right)^{3} } \right]_{z = 0} ,\tau_{yz} = \mu \left[ {\frac{\partial v}{{\partial z}} + \frac{(n - 1)}{2}\Gamma^{2} \left( {\frac{\partial v}{{\partial z}}} \right)^{3} } \right]_{z = 0} .$$
(17)

Energy and mass species fluxes at the surface are:

$$q_{w} = - \left[ {k + \frac{{16\sigma T_{\infty }^{3} }}{{3k^{ * } }}} \right]\left( {\frac{\partial T}{{\partial z}}} \right)_{z = 0} ,\quad j_{w} = - D\left( {\frac{\partial C}{{\partial z}}} \right)_{z = 0}.$$
(18)

The above equations are reduced to following non-dimensional form by using similarity transformations:

$${\text{Re}}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} Cf_{x} = f^{\prime\prime}(0) + \frac{(n - 1)}{2}\text{We}_{1}^{2} f^{{\prime\prime}{3}} (0),$$
(19)
$${\text{Re}}_{y}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}} Cf_{y} = g^{\prime\prime}(0) + \frac{(n - 1)}{2}\text{We}_{2}^{2} g^{{\prime\prime}{3}} (0),$$
(20)
$${\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} Nu_{x} = - (1 + R)\theta^{\prime}(0),$$
(21)
$${\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}} Sh_{x} = - \phi^{\prime}(0).$$
(22)

Here, \({\text{Re}}_{y} = \frac{{V_{\text{w}} y}}{\vartheta }\) and \({\text{Re}}_{x} = \frac{{U_{\text{w}} x}}{\vartheta }\) are the local Reynolds numbers.

3 Results and discussions

The structured mathematical problem in Eqs. (11)–(15) is described numerically by the help of bvp4c scheme in MATLAB. Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19 interpret the trends of distinct emerging constraints on non-Newtonian fluid velocity, energy field and mass species for shear-thinning \((n < 1)\) and shear-thickening \((n > 1)\) cases.

Fig. 2
figure 2

Axial velocity profiles for different values of \(\text{We}_{1}\)

Full size image

Figures 2, 3, 4 and 5 are the descriptions of local Weissenberg numbers \(\text{We}_{1}\) and \(\text{We}_{2}\) on axial and transverse velocity distributions. Figures 2 and 3 reveal the velocity distributions for rising values of \(\text{We}_{1}\). From these figures, we observed that the axial velocity distribution increases for shear-thickening case \((n = 1.5)\) and decreases for shear-thinning case \((n = 0.5).\) However, the transverse velocity profiles improve for shear-thickening materials and augmented in the case of shear-thinning. The opposite phenomenon occurred in Figs. 4 and 5 for incrementing trend of \(\text{We}_{2} .\) Here, the transverse velocity risen for shear-thickening and declines for shear-thinning materials. On contrary, axial velocity decreases in shear-thickening case and enhances for shear-thinning situation. Practically, the Weissenberg number is inverse to liquid viscosity and directly related to the factor of relaxation time. Also, the larger Weissenberg number corresponds to stronger thickness of momentum layer for shear-thinning fluids and weaker for shear-thickening materials. Figure 6 explains the trends of magnetic constraint \(M\) on velocity distributions for both shear-thickening and shear-thinning materials cases. Generally, the Lorentz force is arisen by the enforcing of stronger magnetic force. Such forces create resistance in the material velocity. Hence, the fluid velocities are suppressed with the incrementing \(M.\) The larger porosity parameter \(K\) values decrease the velocity distributions (see Fig. 7). The presence of porous medium causes to high restriction to the fluid flow and then slow-down its motion. Therefore, with an enhancement in porosity parameter, the resistance to the fluid flow rises which suppress the velocity of the fluid.

Fig. 3
figure 3

Transverse velocity profiles for different values of \(\text{We}_{1}\)

Full size image
Fig. 4
figure 4

Axial velocity profiles for different values of \(\text{We}_{2}\)

Full size image
Fig. 5
figure 5

Transverse velocity profiles for different values of \(\text{We}_{2}\)

Full size image
Fig. 6
figure 6

Velocity profiles for different values of \(M\)

Full size image
Fig. 7
figure 7

Velocity profiles for different values of \(K\)

Full size image

Figures 8 and 9 reflect that the improving \(S\) reduces the velocity curves in axial direction and opposite tendency occurs in transverse direction. Practically, the stretching ratio \(S\) is the relation of movement in the \(X\)-direction to movement of sheet in the \(Y\)-direction. Hence, the increasing \(S\) demonstrates that the velocity in transverse direction dominates the velocity in axial direction due to which the velocity in transverse direction raises while declines the velocity in the axial direction. Figures 10, 11, 12 and 13 demonstrate the momentum slip parameters \(B_{1}\) and \(B_{2}\) on velocity fields. It is seen that the enhancing value of \(B_{1}\) causes the reduction in axial velocity. For higher values of velocity slip parameter, the momentum boundary layer thickness is reduced and the stretching velocity is partially changed to fluid and thus the velocity decreases. The increasing trend is noticed in transverse velocity. The quite opposite behavior is observed for \(B_{2}\) (see Figs. 12 and 13). The improving value of radiation \(R\) accelerates the temperature curves shown in Fig. 14. Physically, thermal radiation exerts more heat in the fluid that resulted in the incrementing temperature field. Figure 15 reveals the impact of \(\Pr\) on temperature. Generally, the thermal conductivity is enhanced at low Prandtl number. Hence, the larger \(\Pr\) declines the temperature curves.

Fig. 8
figure 8

Axial velocity profiles for different values of \(S\)

Full size image
Fig. 9
figure 9

Transverse velocity profiles for different values of \(S\)

Full size image
Fig. 10
figure 10

Axial velocity profiles for different values of \(B_{1}\)

Full size image
Fig. 11
figure 11

Transverse velocity profiles for different values of \(B_{1}\)

Full size image
Fig. 12
figure 12

Axial velocity profiles for different values of \(B_{2}\)

Full size image
Fig. 13
figure 13

Transverse velocity profiles for different values of \(B_{2}\)

Full size image
Fig. 14
figure 14

Temperature profiles for different values of \(R\)

Full size image
Fig. 15
figure 15

Temperature profiles for different values of \(\Pr\)

Full size image

Figures 16 and 17 reflect the nature of Eckert number along \(Y\) and \(X\) directions for both shear-thinning and shear-thickening materials temperatures. It is achieved that the temperature is increased in both shear-thinning and shear-thickening cases along with local Eckert numbers \(\text{Ec}_{x}\) and \(\text{Ec}_{y}\). Generally, frictional heating is improved for larger Eckert numbers that resulted the higher temperature curves. Figure 18 depicts the features of Sc on the concentration field \(\phi (\eta )\) for shear-thickening and shear-thinning phenomenon. The species concentration is reduced for rising Schmidt number. The species concentration is decreased with increasing chemical reactive parameter \(\text{Kr}\) (see Fig. 19).

Fig. 16
figure 16

Temperature profiles for different values of \(\text{Ec}_{x}\)

Full size image
Fig. 17
figure 17

Temperature profiles for different values of \(\text{Ec}_{y}\)

Full size image
Fig. 18
figure 18

Concentration profiles for different values of Sc

Full size image
Fig. 19
figure 19

Concentration profiles for different values of \(\text{Kr}\)

Full size image

We verified the present methodology with the Khan et al. [5] and Ariel [40] in Table 1. The remarkable agreement between the present and previous solutions is achieved under limiting cases (\(n = 3,\,\,M = K = \text{We}_{1} = \text{We}_{2} = 0\)). Additionally, Tables 2 and 3 describe the numeric results of local friction factors, Nusselt and Sherwood numbers. Complete discussion is based on the following physical parameters \(\text{Kr} = R = S = M = K = B_{1} = B_{2} = \text{We}_{1} = \text{We}_{2} = 0.5,\Pr = 3,Sc = 0.6,\)\(\text{Ec}_{x} = \text{Ec}_{y} = 0.05\) as long as there is no special mention. In this study, \(n = 1.5\) represents shear-thickening fluids and dotted line at \(n = 0.5\) represents the shear-thinning fluids.

Table 1 Comparison results of \(- f^{\prime\prime}(0)\) and \(- g^{\prime\prime}(0)\) for different values of \(S\) with \(n = 3,\,\,M = K = \text{We}_{1} = \text{We}_{2} = 0.\)
Full size table
Table 2 Local skin friction coefficients in shear-thinning and shear-thickening cases
Full size table
Table 3 Nusselt number and Sherwood number in shear-thinning and shear-thickening cases
Full size table

The numeric values of friction factor coefficients \(Cf_{x} {\text{Re}}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) and \(Cf_{y} {\text{Re}}_{y}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) at the surface in \(X\) and \(Y\)-directions for distinct physical parametric values of shear-thinning and shear-thickening cases are given in Table 2. The values of \(Cf_{x} {\text{Re}}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) and \(Cf_{y} {\text{Re}}_{y}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) are augmented with the increasing values of porosity parameter and magnetic field parameter. This is due to involvement of porosity and magnetic field at the surface. The velocities and momentum thickness are reduced in both cases. The values of \(Cf_{x} {\text{Re}}_{x}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) and \(Cf_{y} {\text{Re}}_{y}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) are decreased with the increasing values of velocity slips \(B_{1}\) and \(B_{2}\). With the increasing values of local Weissenberg numbers \(\text{We}_{1}\) and \(\text{We}_{2}\), local friction factors are decreased in shear-thinning and opposite tendency is noticed in shear-thickening fluids. The Weissenberg number is inversely proportional to the viscosity of the fluid due to which such trends are shown in Table 2. Also, the local friction factor coefficients are increased with an increase in the stretching parameter \(S\). Table 3 illustrates the \(Nu_{x} {\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}}\) and \(Sh_{x} {\text{Re}}_{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) values for different parameters. With the increasing values of magnetic and porosity parameters, the values of \(Nu_{x} {\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}}\) and \(Sh_{x} {\text{Re}}_{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) are falling down. The progressive values of local Weissenberg numbers decline the \(Nu_{x} {\text{Re}}_{x}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}}\) and \(Sh_{x} {\text{Re}}_{x}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}}\) in thinning fluids and opposite phenomenon occurred for thickening fluids. The Nusselt number is decreased by raising the values of local Eckert numbers. Nusselt number is increased with incrementing radiation parameter.

4 Conclusions

The three-dimensional hydromagnetic slip flow of Carreau non-Newtonian material under viscous heating, radiation and first-order destructive chemical reactions is investigated. Both shear-thickening \((n > 1)\) and shear-thinning \((n < 1)\) cases are reported. The key outcomes of the present investigation are summarized here:

  • The velocities \(f^{\prime}(\eta )\) and \(g^{\prime}(\eta )\) are opposite in both shear-thinning and shear-thickening cases for incrementing ratio parameter.

  • The magnetic and porous medium effects are acted as drag forces in velocity fields.

  • The local friction factor coefficients are decreased as the velocity slip increases.

  • Temperature profile is extended with peaked values of thermal radiation and local Eckert numbers.

  • The influence of local Weissenberg numbers on Sherwood and Nusselt numbers for shear-thinning fluids is reversed to shear-thickening fluids.