Introduction

Recent advances in miniaturization of electrical, chemical and mechanical processes have opened new horizons in design, development and practical applications of micro- and nanoelectromechanical systems (MEMS/NEMS) in various industries such as electronics, medical and biological sciences, energy harvesting and instruments such as micropumps, accelerometers and microsensors [1, 2]. The prevalent and ever increasing use of microchannels in these applications necessitates the development of purpose-specific numerical methods capable of modeling and optimizing the working conditions. In other words, arriving at the desired performance making these devices economically viable requires simulation techniques to precisely predict the physiochemical behaviors and control the fluid flow and heat transfer for reduced pumping power demand and improved cooling efficiency.

One practical approach to enhancing heat transfer efficiency in microchannels [3] is to increase the fluid thermal conductivity by suspending solid nanoparticles (such as TiO2, Cu, AL2O3) [4] or carbon nanotubes (CNT) in a base fluid to make a mixture coolant referred to as nanofluid [5, 6]. Carbon nanotubes are widely used as suspending nanoparticles in nanofluids due to their high mechanical, electrical and thermal properties [7]. For this purpose, CNTs are generally used in forms of single-wall (SWCNT), multi-wall (MWCNT) or double-wall (DWCNT) [8]; however, to intensify their dispersibility and solubility, multi-wall CNTs may be functionalized (FMWCNT) by adding a surfactant in the base (carrier) fluid [9, 10]. Transverse magnetic field can enhance the heat transfer by affecting via Lorentz force [11] on Newtonian [12] and non-Newtonian [13] as it flows through the microchannel. Sawada et al. [14] experimentally showed that the flow resistance coefficient in a parallel plate channel is directly proportional to the length and strength of applied magnetic field.

Duwairi and Abdullah [15] analytically and numerically studied the transient fully developed fluid flow and heat transfer in a magnetohydrodynamic micropump. They found that controlling the flow and the temperature can be achieved by controlling the magnetic flux, the potential difference and electrical conductivity. Aminossadati et al. [16] numerically investigated the effect of magnetic field on water–Al2O3 nanofluid in a partially heated microchannel using finite volume method (FVM). In addition to an increase in average Nusselt number (\(\overline{Nu}\)) with increasing volume fraction (φ) of nanoparticles, they reported a multi-fold increase in \(\overline{Nu}\) versus φ at higher Reynolds and Hartmann numbers.

Besides improved heat transfer by using nanofluids under the influence of transverse magnetic field, the undesirable consequence of their usage in microchannels is the significant increase in wall shear stress that demands higher pumping power. A practical solution is to utilize hydrophobic material at the microchannel surfaces to reduce the wall shear stress. This method works effectively even in the absence of the magnetic field and nanofluids, i.e., with pure water only. Tretheway and Meinhart [17] experimentally studied water flow through a 3D rectangular microchannel coated with 2.3-nm-thick monolayer of hydrophobic material and observed velocity slip at the walls. Actually, this significant slippage seen is due to air bubbles trapper in the surface asperities, the so-called superhydrophobic surfaces. Hence, liquid flow in a microchannel with superhydrophobic walls results in slip flow regime knowing that Knudsen number may represent a continuum medium, Kn < 0.001.

Surface phenomena inherent in microscale flows at the fluid–solid interface such as velocity and temperature slippage violate the classic boundary conditions and thus require dedicated simulation treatments. Afrand et al. [18] used FVM to numerically study the effects of velocity slip (without temperature jump) and transverse magnetic field on the fluid flow and heat transfer of FMWCNT–water nanofluid in a parallel plate microchannel at constant-temperature boundary condition. They found that higher volume fraction of nanoparticles, Reynolds (Re) and Hartmann (Ha) numbers each promote the heat transfer rate. Karimipour et al. [19] used FVM to perform a relatively similar study to Afrand et al. [18], but with constant heat flux at the wall boundaries. By considering a velocity slippage without temperature jump at walls, they concluded that imposing a transverse magnetic field is very effective on heat transfer efficiency in the thermally developing region and is insignificant in thermally fully developed region. Karimipour and Afrand [20] studied the forced convection of Cu–water nanofluid in a two-dimensional microchannel using FVM and confirmed that heat transfer rate is directly related with Re, Ha and φ; however, the effects of Ha and φ are more significant at higher Re. Using FVM, Karimipour et al. [21] also studied the effects of different nanoparticles of Al2O3 and Ag on the MHD nanofluid flow and heat transfer in a microchannel with considering both velocity slip and temperature jump at constant-temperature boundary condition. They reported that increasing slip coefficient decreases Nusselt number specially at higher Hartmann numbers.

Lattice Boltzmann method (LBM) as a mesoscale method like dissipative particle dynamics (DPD) [22] has been proved to be a suitable approach to numerical study of different topic in thermos-fluid such as particle-laden flows [23], mixed and natural convection heat transfer [24, 25], multi-phase flow [26]. Because of its intrinsically mesoscopic kinetic nature, it is reported to be more capable for simulation of microscale slip and transitional regimes. LBM is advantageous as an explicit method because of simpler programming and easier parallel processing which make it more computationally efficient over computational fluid dynamics [27]. Also, lattice Boltzmann method with BGK model for collision operator is linear equation, unlike traditional CFD based on Navier–Stokes equations. Nonlinear terms of convection in the latter cause instability in explicit solution of these equations. In addition, implicit or semi-implicit algorithm such as SIMPLE or SIMPLE C should be used in CFD and so a set of equations should be solved unlike LBM. Finally, in LBM there is no need to satisfy the equation of pressure correction and Laplace equation.

LBM simulations of MHD effects on fluid flow and heat transfer in cavities and enclosures are widely studied in the past [28]. Agarwal [29] showed a reasonable agreement between analytic solution and LBM results when studying the effects of magnetic field on the microchannel velocity and pressure fields of a conductive gas in slip flow regime. Kalteh and Abedinzadeh [30] investigated the effects of MHD forced convection on Al2O3–water nanofluid flow and heat transfer in a microchannel with constant-temperature boundary condition. They found that although magnetic field does not significantly affect the heat transfer coefficient, it increases the friction factor of up to 86%. Along with popularity of LBM in modeling nanofluid MHD flows [31, 32], different approaches have been taken so far to whether consider velocity slip and temperature jump at the liquid–solid interface. Despite many works ignoring both treatments for boundary condition such as [33], some studies have considered velocity slip only [34], while other works implemented temperature jump as well [35]. Disregarding the temperature jump at the boundaries as a result of slippage causes inaccurate temperature profile in the vicinity of the walls that leads to overestimation of Nusselt number and heat transfer rate.

To the best of our knowledge, there is no numerical simulation study, Navier–Stokes-based CFD or LBM, of microchannel flow and heat transfer of nanofluid in the presence of concurrent application of transverse magnetic field and constant heat flux when both velocity slip and temperature jump boundary conditions are considered. Besides, it will be shown that the accuracy of standard LBM is inadequate for a uniform magnetic field partially applied on a microchannel. Hence, for the first time we have utilized incompressible preconditioned lattice Boltzmann method (IPLBM) for solving MHD forced convection problem in a superhydrophobic microchannel with slip flow regime, to demonstrate that this method is capable of correctly simulating such physics.

In this work, upon validation of our IPLBM model against analytic solutions, numerical models and an experimental study, effects of magnetic field intensity, wall hydrophobicity level, and volume fraction of nanoparticles on flow hydrodynamics and heat transfer are comprehensively studied. Flow behavior, flow resistance and heat transfer rate are rigorously quantified by analyzing velocity and temperature profiles, wall shear stress, slip velocity and temperature jump, as well as local and total heat transfer rates.

Problem statement

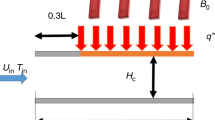
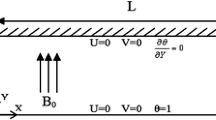
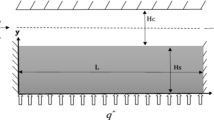
Figure 1 shows the 2D microchannel (Hc = 50 µm and L = 30 Hc) with 70% trailing segment of the upper wall to be under the influence of a uniform and transverse magnetic field as well as a uniform heat flux. Slip flow regime applies because of using superhydrophobic coating on the walls which necessitates considering both velocity slip and temperature jump. FMWCNT–water nanofluid, assumed to be incompressible and Newtonian, flows with Re = 100 for all laminar cases studied and enters the microchannel with uniform velocity uin and uniform temperature Tin = 303 K. Lower wall of microchannel is fully isolated, while the upper wall is insulated only for the 30% leading segment, referred to as entrance length (x = 0.3 L) where hydrodynamic fully developed condition is reached. A magnetic field with the strength of B0 as well as a uniform heat flux of q″ is applied on the 70% trailing segment of the upper wall (0.3 L < x < L).

Fig. 1
figure 1

Geometry of the 2D microchannel with partially insulated walls and applied magnetic field and heat flux

Full size image

To increase the accuracy of modeling, the thermo-physical properties of FMWCNT–water nanofluid obtained from experimental data of Amrollahi and Rashidi [36] as per Table 1 are used [18, 19]. Here, ρ and µ are the nanofluid density and dynamic viscosity, k is the thermal conductivity coefficient, and Cp is the heat capacity at constant pressure.

Table 1 Thermo-physical properties of FMWCNT–water nanofluid [36]
Full size table

Mathematical formulations

Preconditioned LBM was initially proposed by Gue et al. [37] in order to increase convergence rate in conventional LBM. Incompressible version of LBM was also introduced earlier by He and Luo [38] to reduce the errors caused by spurious compressibility effects inherent in conventional LBM. To get benefit from both mentioned improvements of LBM in solving velocity fields in MHD forced convection, for the first time, preconditioned incompressible lattice Boltzmann method based on D2Q9 single relaxation time approach with a source term is used. The discretized form of hydrodynamic Boltzmann equation is as follows and to be solved in two steps of collision and streaming [39]:

$$f_{\text{k}} \left( {\vec{r} + \Delta \vec{r},t + \Delta t} \right) - f_{\text{k}} \left( {\vec{r},t} \right) = - \frac{\Delta t}{{\tau_{\text{f}} }}\left[ {f_{\text{k}} \left( {\vec{r},t} \right) - f_{\text{k}}^{\text{eq}} \left( {\vec{r},t} \right)} \right] + \Delta t F_{\text{k}}$$
(1)

where f is the density distribution function at mesoscopic scale, k subscript is the direction for lattice links, \(\vec{r} = x \vec{i} + y\overrightarrow { j}\) is the position vector whereby \(\Delta \vec{r}\) is defined as the product of discrete lattice velocity (\(c_{\text{k}}\)) and time step ∆t, and τf is the relaxation time for density distribution function which is related to fluid kinematic viscosity (\(\upsilon\)) as follows [37]:

$$\upsilon = \gamma C_{\text{s}}^{2} \left( {\frac{{\tau_{\text{f}} }}{\Delta t} - 0.5} \right)\Delta t$$
(2)

In this relation and forthcoming ones, 0 < γ ≤ 1 is an adjustable parameter chosen arbitrarily to increase the convergence rate [37] and \(c_{\text{s}} = \Delta x/(\sqrt 3 \Delta t)\) is the speed of sound. In Eq. 1, feq is the equilibrium distribution function defined as below [40]:

$$f_{\text{k}}^{\text{eq}} = w_{\text{k}} \left[ {\rho + \rho_{0} \left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }} + \frac{1}{2\gamma }\left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }}} \right)^{2} - \frac{{\vec{V} \cdot \vec{V}}}{{2\gamma c_{\text{s}}^{2} }}} \right)} \right]$$
(3)

Here, \(\rho\) is the fluid density, \(\rho_{0}\) is the constant initial density, \({\vec{\text{V}}}\) is the macroscopic velocity, and \(\overrightarrow {{{\text{c}}_{\text{k}} }}\) is the microscopic lattice velocity vector which is defined as follows in D2Q9 lattice with uniform grid:

$$\overrightarrow {{c_{\text{k}} }} = \left\{ {\begin{array}{*{20}l} {\left( {0,0} \right)} \hfill & {k = 0} \hfill \\ {\left( {\cos \frac{{\pi \left( {k - 1} \right)}}{2},\sin \frac{{\pi \left( {k - 1} \right)}}{2}} \right)\frac{\Delta x}{\Delta t}} \hfill & {k = 1 - 4} \hfill \\ {\sqrt 2 \left( {\cos \frac{{\pi \left( {2k - 1} \right)}}{4},\sin \frac{{\pi \left( {2k - 1} \right)}}{4}} \right)\frac{\Delta x}{\Delta t}} \hfill & {k = 5 - 8} \hfill \\ \end{array} } \right.$$
(4)

Also, \(w_{\text{k}}\) is the weight function along various directions of lattice links (\(k\)) given by:

$$w_{\text{k}} = \left\{ {\begin{array}{*{20}l} {\frac{1}{4}} \hfill & {k = 0} \hfill \\ {\frac{1}{9}} \hfill & {k = 1 - 4} \hfill \\ {\frac{1}{36}} \hfill & {k = 5 - 8} \hfill \\ \end{array} } \right\}$$
(5)

The source term Fk from Eq. 1 is also defined in the direction of lattice links based on Gue et al. method [39] and has to be scaled by γ as follows:

$$F_{\text{k}} = \frac{1}{{\gamma^{2} }}w_{\text{k}} \left( {1 - \frac{\Delta t}{{2\tau_{\text{f}} }}} \right)\left[ {\frac{{\overrightarrow {{c_{\text{k}} }} - \vec{V}}}{{c_{\text{s}}^{2} }} + \left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{4} }}} \right)\overrightarrow {{c_{\text{k}} }} } \right] \cdot \rho_{0} \vec{a}$$
(6)

Here, \(\vec{a}\) is the acceleration vector for transverse magnetic field given by [19]:

$$\vec{a} = a_{\text{x}} \vec{i} + a_{\text{y}} \overrightarrow { j} = - \frac{{B_{0}^{2} \sigma_{\text{nf}} }}{{\rho_{0} }}u \vec{i} + 0 \overrightarrow {j} = \frac{{Ha^{2} \mu_{\text{nf}} }}{{\rho_{0} H_{\text{c}}^{2} }} u \vec{i}$$
(7)

where \(\sigma_{\text{nf}}\) is the electrical conductivity of nanofluid, Ha is the non-dimensional Hartmann number, and \(\mu_{\text{nf}}\) is the dynamic viscosity of nanofluid.

Figure 2 shows D2Q9 lattice based upon which macroscopic nanofluid density and velocity are obtained via [39, 40]:

$$\rho = \mathop \sum \limits_{k = 0}^{8} f_{\text{k}}$$
(8)
$$\rho_{0} \vec{V} = \mathop \sum \limits_{k = 0}^{8} \overrightarrow {{C_{\text{k}} }} .f_{\text{k}} + \frac{\Delta t}{2}\rho_{0} \vec{a}$$
(9)
Fig. 2
figure 2

Lattice links between nodes in D2Q9 lattice model

Full size image

Temperature field is solved using standard LBM based on passive scalar approach with D2Q9 lattice via the discretized Boltzmann equation in following form [41]:

$$g_{\text{k}} \left( {\vec{r} + \overrightarrow {\Delta r} ,t + \Delta t} \right) - g_{\text{k}} \left( {\vec{r},t} \right) = - \frac{\Delta t}{{\tau_{\text{g}} }}\left[ {g_{\text{k}} \left( {\vec{r},t} \right) - g_{\text{k}}^{\text{eq}} \left( {\vec{r},t} \right)} \right]$$
(10)

where g and geq are, respectively, the distribution function and equilibrium distribution function of dimensionless temperature field. Also, τg is the relaxation time for dimensionless temperature distribution function which relates the thermal diffusion coefficient (\(\alpha\)) to speed of sound as follows [41]:

$$\alpha = C_{\text{s}}^{2} \left( {\frac{{\tau_{\text{g}} }}{\Delta t} - 0.5} \right)\Delta t$$
(11)

Moreover, geq along the various directions of lattice links (\({\text{k}}\)) is given by [41]:

$$g_{\text{k}}^{\text{eq}} = w_{\text{k}} \theta \left[ {1 + \left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }} + \frac{1}{2}\left( {\frac{{\overrightarrow {{c_{\text{k}} }} \cdot \vec{V}}}{{c_{\text{s}}^{2} }}} \right)^{2} - \frac{{\vec{V} \cdot \vec{V}}}{{2c_{\text{s}}^{2} }}} \right)} \right]$$
(12)

Also, dimensionless temperature is calculated as follows:

$$\theta = \mathop \sum \limits_{k = 0}^{8} g_{\text{k}}$$
(13)

Dimensionless parameters in this study are defined as follows:

$$X^{*} = \frac{x}{Hc}\quad Y^{*} = \frac{y}{Hc}\quad u^{*} = \frac{u}{{u_{\text{in}} }}\quad v^{*} = \frac{v}{{u_{\text{in}} }}\quad \theta = \frac{{T - T_{\text{in}} }}{{\frac{{q{\prime \prime } Hc}}{{k_{\text{f}} }}}}$$
(14)

where \(k_{\text{f}}\) is the thermal conductivity coefficient of pure (base) fluid.

Hydrodynamic boundary conditions

Using Eqs. (8) and (9) at the channel inlet, a counter-slip approach with second-order accuracy similar to standard LBM [42,43,44] is applied for incompressible preconditioned LBM with a magnetic field. This approach assumes that unknown distribution function is equal to equilibrium distribution function with a different density as follows.

$$\rho_{\text{in}} = U_{\text{in}} \rho_{0} + f_{0} + f_{2} + f_{4} + 2(f_{3} + f_{6} + f_{7} ) - \frac{\Delta t}{2}\rho_{0} a_{\text{x}} U_{\text{in}}$$
(15)
$$\left\{ {\begin{array}{*{20}c} {f_{1} = \frac{{w_{1 } }}{{\left( {w_{1} + w_{5} + w_{8} } \right)}}\left[ {\rho_{\text{in}} - \left( {f_{0} + f_{2} + f_{3} + f_{4} + f_{6} + f_{7} } \right)} \right]} \\ {f_{5} = \frac{{w_{5 } }}{{\left( {w_{1} + w_{5} + w_{8} } \right)}}\left[ {\rho_{\text{in}} - \left( {f_{0} + f_{2} + f_{3} + f_{4} + f_{6} + f_{7} } \right)} \right]} \\ {f_{8} = \frac{{w_{8 } }}{{\left( {w_{1} + w_{5} + w_{8} } \right)}}\left[ {\rho_{\text{in}} - \left( {f_{0} + f_{2} + f_{3} + f_{4} + f_{6} + f_{7} } \right)} \right]} \\ \end{array} } \right.$$
(16)

At channel outlet, second-order extrapolation scheme is used to calculate unknown distribution function [44]:

$$\left\{ {\begin{array}{*{20}c} {f_{{3,{\text{m}}}} = 2f_{{3,{\text{m}} - 1}} - f_{{3,{\text{m}} - 2}} } \\ {f_{{6,{\text{m}}}} = 2f_{{6,{\text{m}} - 1}} - f_{{6,{\text{m}} - 2}} } \\ {f_{{7,{\text{m}}}} = 2f_{{7,{\text{m}} - 1}} - f_{{7,{\text{m}} - 2}} } \\ \end{array} } \right.$$
(17)

where m subscript denotes the last lattice node in horizontal direction.

Due to geometric and therefore hydrodynamic symmetries about channel centerline, only lower half of the channel is hydrodynamically solved and the upper half domain is duplicated by symmetry boundary condition at the centerline according to [44]:

$$\left\{ {\begin{array}{*{20}c} {f_{4} = f_{2} } \\ {f_{7} = f_{6} } \\ {f_{8} = f_{5} } \\ \end{array} } \right.$$
(18)

At the lower wall of the channel, Navier formula is used [17, 21] to consider both no-slip and slip boundary conditions:

$$u = B\frac{\partial u}{{\partial Y^{*} }}|_{{Y^{*} = 0}}$$
(19)

where \(B = \frac{\beta }{Hc}\) is the dimensionless slip coefficient and β is the slip coefficient. By second-order forward derivative discretization, Eq. (17) reforms to:

$$u_{0} = \frac{B}{{2\Delta Y^{*} + 3B}}(4u_{1} - u_{2} )$$
(20)

where \(u_{0}\), \(u_{1}\) and \(u_{2}\) are horizontal velocity, respectively, on the wall boundary, and at first and second nodes above the lower wall. By using Eqs. (8) and (9) in conjunction with auxiliary equation of non-equilibrium bounce-back for the unknown distributive function [45], unknown distribution functions at the lower wall boundary are determined as:

$$\rho_{\text{w}} = f_{0} + f_{1} + f_{3} + 2\left( {f_{4} + f_{7} + f_{8} } \right)$$
(21)
$$\left\{ {\begin{array}{*{20}l} {f_{2} = f_{4} } \hfill \\ {f_{5} = \frac{{\left( {\rho_{\text{w}} + \rho_{0} u_{0} } \right) - \left( {f_{0} + f_{2} + f_{4} } \right) - 0.5 \rho_{0} a_{\text{x}} u_{0} }}{2} - \left( {f_{1} + f_{8} } \right)} \hfill \\ {f_{6} = \frac{{\left( {\rho_{\text{w}} - \rho_{0} u_{0} } \right) - \left( {f_{0} + f_{2} + f_{4} } \right) + 0.5 \rho_{0} a_{\text{x}} u_{0} }}{2} - \left( {f_{3} + f_{7} } \right)} \hfill \\ \end{array} } \right.$$
(22)

where \(\rho_{\text{w}}\) is the density of fluid (nanofluid) adjacent to the wall.

Thermal boundary conditions

Similar to hydrodynamic boundary condition, counter-slip approach is used at the inlet:

$$\left\{ {\begin{array}{*{20}c} {g_{1} = \frac{{w_{1 } }}{{\left( {w_{1} + w_{5} + w_{8} } \right)}}\left[ {\theta_{\text{in}} - \left( {g_{0} + g_{2} + g_{3} + g_{4} + g_{6} + g_{7} } \right)} \right]} \\ {g_{5} = \frac{{w_{5 } }}{{\left( {w_{1} + w_{5} + w_{8} } \right)}}\left[ {\theta_{\text{in}} - \left( {g_{0} + g_{2} + g_{3} + g_{4} + g_{6} + g_{7} } \right)} \right]} \\ {g_{8} = \frac{{w_{8 } }}{{\left( {w_{1} + w_{5} + w_{8} } \right)}}\left[ {\theta_{\text{in}} - \left( {g_{0} + g_{2} + g_{3} + g_{4} + g_{6} + g_{7} } \right)} \right]} \\ \end{array} } \right.$$
(23)

where \(\theta_{\text{in}}\) is zero as per Eq. (13). Boundary treatment for channel outlet is similar to Eq. (17) with second-order extrapolation to calculate unknown distribution functions. Insulated boundary condition is imposed on the full length of lower wall of microchannel and partial length of upper wall up to x = 0.3 L as follows [44]:

$$\left\{ {\begin{array}{*{20}c} {g_{2,0} = g_{2,1} } \\ {g_{5,0} = g_{5,1} } \\ {g_{6,0} = g_{6,1} } \\ \end{array} } \right.$$
(24)

Energy balance on the walls in dimensionless form is given by:

$$\left. {\frac{\partial \theta }{{\partial Y^{*} }}} \right|_{{Y^{*} = 1}} = - 1$$
(25)

By discretizing this equation with second-order backward derivative, dimensionless temperature of fluid on the wall (θn) is developed. Using counter-slip approach, unknown distribution functions are given as follows:

$$\left\{ {\begin{array}{*{20}l} {g_{4} = \frac{{w_{4} }}{{\left( {w_{4} + w_{7} + w_{8} } \right)}}\left[ {\theta_{\text{n}} - \left( {g_{0} + g_{1} + g_{3} + g_{2} + g_{5} + g_{6} } \right)} \right] \times \left[ {1 - \frac{1}{{2c_{\text{s}}^{2} }}u_{\text{n}}^{2} } \right]} \hfill \\ {g_{7} = \frac{{w_{7} }}{{\left( {w_{4} + w_{7} + w_{8} } \right)}}\left[ {\theta_{\text{n}} - \left( {g_{0} + g_{1} + g_{3} + g_{2} + g_{5} + g_{6} } \right)} \right] \times \left[ {1 - \frac{1}{{c_{\text{s}}^{2} }}u_{\text{n}} + \left( {\frac{1}{{2c_{\text{s}}^{4} }} - \frac{1}{{2c_{\text{s}}^{2} }}} \right)u_{\text{n}}^{2} } \right]} \hfill \\ {g_{8} = \frac{{w_{8} }}{{\left( {w_{4} + w_{7} + w_{8} } \right)}}\left[ {\theta_{\text{n}} - \left( {g_{0} + g_{1} + g_{3} + g_{2} + g_{5} + g_{6} } \right)} \right] \times \left[ {1 + \frac{1}{{c_{\text{s}}^{2} }}u_{\text{n}} + \left( {\frac{1}{{2c_{\text{s}}^{4} }} - \frac{1}{{2c_{\text{s}}^{2} }}} \right)u_{\text{n}}^{2} } \right]} \hfill \\ \end{array} } \right.$$
(26)

where n denotes the last (outermost) node on the upper wall when marching away from the lower wall in vertical direction.

Temperature jump occurs on the upper wall for 0.3L < x ≤ L, where microchannel is not insulated, which is numerically applied by [21]:

$$T_{\text{nf}} = T_{\text{w}} + \zeta^{*} \frac{\partial T}{{\partial y^{*} }}_{{\left| {y^{*} = 1} \right.}}$$
(27)

where \(\zeta^{*} = \frac{\zeta }{Hc} = \frac{B 2\varGamma }{\Pr (\varGamma + 1)}\) is the dimensionless temperature jump coefficient, Pr is the Prandtl number, and Γ is the ratio of specific heat capacity at constant pressure to that at constant volume which is equal to 1 for liquids. Also, \(T_{\text{nf}}\) is the nanofluid temperature adjacent to upper wall whose temperature is referred to as \(T_{\text{w}}\). Dimensionless temperature jump is then defined by:

$$\theta_{\text{jump}} = \frac{{T_{\text{nf}} - T_{\text{w}} }}{{\frac{{q{\prime \prime }Hc}}{{k_{\text{f}} }}}}$$
(28)

Moreover, the average wall shear stress and friction factor, as well as the local and average Nusselt numbers [18], are, respectively, defined by:

$$\overline{{\tau_{\text{w}} }} = \frac{{\mathop \smallint \nolimits_{0}^{L} \mu_{\text{nf}} \frac{\partial u}{\partial y}|_{y = 0} {\text{d}}x}}{L}$$
(29)
$$\overline{{c_{\text{f}} }} = \frac{{2\overline{{\tau_{\text{w}} }} }}{{\rho u_{\text{in}}^{2} }}$$
(30)
$$Nu = \frac{{\left. { - k_{\text{nf}} \frac{\partial T}{\partial y}} \right|_{y = Hc} }}{{T_{\text{w}} - T_{\text{in}} }} \frac{Hc}{{k_{\text{f}} }}$$
(31)
$$\overline{Nu} = \frac{{\mathop \smallint \nolimits_{0.3L}^{L} Nu {\text{d}}x}}{0.7L}$$
(32)

Also, the dimensionless average velocity is defined as bellow:

$$V_{\text{avg}}^{*} = \frac{{\mathop {\iint }\nolimits \rho \vec{V} \cdot \vec{n}{\text{d}}A}}{{\rho A U_{\text{in}} }} = \frac{{\mathop \smallint \nolimits_{0}^{Hc} \vec{V} \cdot \vec{n}{\text{d}}y}}{{Hc U_{\text{in}} }} = \frac{{\mathop \smallint \nolimits_{0}^{Hc} (u \vec{i} + v \vec{j}) \cdot \vec{i}{\text{d}}y}}{{Hc U_{\text{in}} }} = \frac{{\mathop \smallint \nolimits_{0}^{Hc} u{\text{d}}y}}{{Hc U_{\text{in}} }} = \frac{{u_{\text{avg}} }}{{U_{\text{in}} }} = u_{\text{avg}}^{*}$$
(33)

where \(k_{\text{nf}}\) is the thermal conductivity coefficient of nanofluid.

Numerical modeling

Incompressible preconditioned LBM

Compressibility effects are negligible for continuum flow of liquid nanofluids in microchannel; therefore, flow rate and average velocity along the microchannel have to remain constant. Lattice Boltzmann method by nature considers a virtual compressibility for LBM fluid allowing density variations along the stream [37]. For incompressible flows, this virtue could be somewhat mitigated by measures such as keeping the Mach number as low as possible which causes an compressibility error in the order of \({\mathcal{O}}\)(Ma2) [38]. Although this is not problematic in the absence or presence of a transverse magnetic field applied over the full length of a microchannel, it causes a considerable compressibility error when a partial magnetic field is in place. The augmented compressibility error results in making the solution not only deviate from but also inconsistent with analytic solutions and physical expectations. IPLBM has the advantage to reduce the inherent compressibility error in standard LBM to the order \({\mathcal{O}}\)(Ma3) [38] and therefore conserves the flow rate and average velocity along the microchannel in the presence of partial magnetic field.

In this section, we challenge the numerical fidelity of standard LBM versus incompressible preconditioned LBM (\(\gamma = 0.7\)) from various aspects in the context of partial magnetic field using a similar case study in Fig. 1. Dimensionless average velocity along the microchannel is compared between two methods in Fig. 3 at Ha = 0 and 30. In the absence of magnetic field (Ha = 0), average velocity for both methods all along the channel remains almost constant, while, in the presence of partial magnetic field (Ha = 30) applied on microchannel from X* = 9, a significant deviation from constant average velocity (\(u_{\text{avg}}^{*} = 1\)) is observed with standard LBM.

Fig. 3
figure 3

Comparison of dimensionless average velocity between incompressible PLBM and standard LBM at Ha = 0 and 30

Full size image

Figure 4 cross-compares the convergence quality of dimensionless average velocity at the microchannel outlet between standard LBM and incompressible LBM, at Ha = 0 and 30, B = 0.1, grids resolution of (70 × 2100), zero initial velocity \(u^{*} = V^{*} = 0\) and total time steps of 280,000. It is shown that solution convergence occurs quicker and more stable at Ha = 0 using incompressible LBM. In the presence of partial magnetic field (Ha = 30), velocity no longer fluctuates under both methods; however, only IPLBM can converge to dimensionless velocity of unity (\(u_{\text{avg}}^{*} = 1\)). Convergence of velocity field is guaranteed by simultaneously meeting the following criteria:

$${\text{Residual}} = \sqrt[2]{{\frac{{\mathop \sum \nolimits_{\text{x,y}} \left[ {u\left( {x,y,t + \Delta t} \right) - u\left( {x,y,t} \right)} \right]^{2} + \left[ {v\left( {x,y,t + \Delta t} \right) - v\left( {x,y,t} \right)} \right]^{2} }}{{\mathop \sum \nolimits_{\text{x,y}} \left[ {u\left( {x,y,t} \right)^{2} + v\left( {x,y,t} \right)^{2} } \right]}}}} < 6 \times 10^{ - 6}$$
(34)
$${\text{Error}} = \hbox{max} \left( {\frac{{u_{\text{ave}}^{*} \left( x \right) - u_{\text{inlet}}^{*} }}{{u_{\text{inlet}}^{*} }}} \right) < 0.01$$
(35)

where the second condition continues the solution until the dimensionless average velocity at all sections along the microchannel falls within the range of \(0.99 < u_{\text{avg}}^{*} < 1.01\). Upon convergence of the velocity field, temperature field is solved by meeting the criterion below:

$${\text{Residual}} = \sqrt[2]{{\frac{{\mathop \sum \nolimits_{\text{x,y}} \left\{ {\left[ {\theta \left( {x,y,t + \Delta t} \right) - \theta \left( {x,y,t} \right)} \right]^{2} } \right\}}}{{\mathop \sum \nolimits_{\text{x,y}} \left\{ {\theta \left( {x,y,t} \right)^{2} } \right\}}}}} < 10^{ - 6}$$
Fig. 4
figure 4

Comparison of convergence history of dimensionless average velocity at the microchannel outlet between standard LBM and incompressible LBM at Ha = 0 and 30

Full size image

Residuals of numerical solution of velocity and temperature fields at Ha = 30 and B = 0.1 are plotted in Fig. 5.

Fig. 5
figure 5

Solution residuals of velocity and temperature fields, at Ha = 0 and 30 and in slip coefficient of 0.1 (B = 0.1)

Full size image

Grid independency study

An in-house FORTRAN code was developed for numerical solution of governing equations. To ensure a grid-independent solution, the average wall friction factor and Nusselt number at Ha = 30 and B = 0.1, for nanofluid with volume fraction of 0.2%, were calculated over a range of grid resolutions and are shown in Table 2. According to results, values for \(\overline{{c_{\text{f}} }}\) and \(\overline{Nu}\) did not significantly change for two consecutive grid resolutions as (70 × 2100) and (80 × 2400); hence, (70 × 2100) grid resolution was chosen for this study.

Table 2 Grid independency study at Ha = 30 and B = 0.1, for φ = 0.2%
Full size table

Validation

Accuracy of numerical setup and the applied slip velocity and temperature jump boundary conditions were validated separately in the absence and presence of magnetic field with analytical, numerical and experimental benchmarks. Analytical solutions for fully developed velocity and temperature profiles with slippage in the absence of magnetic field [46] were evaluated in a similar microchannel geometry (see Fig. 1). Figures 6 and 7, respectively, compare the fully developed dimensionless velocity and temperature profiles obtained from our LBM simulation with the analytic solution at dimensionless slip coefficients of B = 0, B = 0.05 and B = 0.1. Figure 8 evaluates another analytic solution [47] in the presence of a range of magnetic fields (Ha = 0, 10, 30) and compares them with numerical results for fully developed dimensionless velocity profile. An acceptable agreement is observed between numerical and analytical solutions for prediction of velocity and temperature profiles as well as the amount of slippage next to the wall such that maximum error is less than 1%.

Fig. 6
figure 6

Fully developed dimensionless velocity profile compared between analytical solution [46] and numerical results in the absence of magnetic field (Ha = 0) for air with Pr = 0.7 at B = 0, 0.05, 0.1

Full size image
Fig. 7
figure 7

Fully developed dimensionless temperature profile (\(\theta_{\text{FD}} = \frac{T - Tw}{{\frac{q\prime \prime Hc}{2kf}}}\)) compared between analytical solution [46] and numerical results in the absence of magnetic field (Ha = 0) for air with Pr = 0.7 at B = 0, 0.05, 0.1

Full size image
Fig. 8
figure 8

Fully developed dimensionless velocity profile compared between analytical solution [47] and numerical results in the presence of magnetic field at Ha = 0, 10, 30 for air with Pr = 0.7 and zero slip B = 0

Full size image

In the presence of a uniform magnetic field (Ha = 0, 20), heat transfer rate quantified by local Nusselt number along the microchannel was also benchmarked with numerical results of Aminossadati et al. [16] in Fig. 9 where a reasonable agreement is observed. Further validation is performed via comparing the present model results with the experimental results of Manay and Sahin [48] in three cross sections of the microchannel. The microchannel in their work has the height of 200 μm, and its length is 250 times its height (Table 3).

Fig. 9
figure 9

Comparison of local Nusselt number at Ha = 0 and 20 for nanofluid with volume fraction of 2% between current study and numerical results of Aminossadati et al. [16]

Full size image
Table 3 Comparison of Nusselt number between the present study and experimental work [48] at three horizontal sections for pure water and TiO2–water nanofluid with volume fraction of 2%, and mass flow rate of 37.7 kg h−1
Full size table

Results and discussion

Hydrodynamics and heat transfer of FMWCNT–water nanofluid flow in the hydrophobic microchannel are comprehensively studied for a range of magnetic field intensities (Ha = 0, 15, 30), dimensionless slip coefficients 0 ≤ B ≤ 0.1 and suspension volume fractions (φ = 0, 0.1%, 0.2%) at a fix Reynolds number (Re = 100) and a uniform external heat flux q″. The adjustable parameter of \(\gamma\) is appropriately selected in the range of 0.5 to 0.8.

Hydrodynamic Analysis

Figure 10 compares the effects of magnetic field between Ha = 0 and Ha = 30 on flow streamlines for nanofluid with φ = 0.2% and B = 0.1. In the absence of magnetic field, streamlines reach fully developed condition near the entrance around x* = 6 (or 0.2L) where they remain parallel up to the end of microchannel. The presence of a transverse magnetic field (Ha = 30) starting from x* = 9 disrupts the flow locally, causes a second fully developed region at x* = 10 due to an applied force in opposite direction of fluid flow, and then widens the streamlines as a sign of decreased velocity in form of a plug flow.

Fig. 10
figure 10

Effects of partial magnetic field on flow streamlines for nanofluid at φ = 0.2% and B = 0.1, Ha = 0 (Top) and Ha = 30 (Bottom)

Full size image

Given that two separate fully developed regions coexist in the presence of magnetic field, dimensionless velocity profiles at x = 0.2L and at the channel outlet (x = L) are plotted in Fig. 11 with Ha = 15 and 30. No-slip (B = 0) and velocity slip (B = 0.1) boundary conditions are used to model both hydrophilic and hydrophobic microchannel walls. Regardless of fluid slippage, obvious effect of magnetic field at x = L is a flow deceleration in the middle of microchannel compensated by an accelerated flow in the vicinity of the walls. This causes a plug flow followed by a reduced mixing and intra-layer diffusion of nanofluid particles. Also, slip velocity increases from 0.6 to 0.75 when Hartmann number changes from 15 to 30.

Fig. 11
figure 11

Effects of magnetic field on dimensionless velocity profile for nanofluid with φ = 0.2% at B = 0 and 0.1. Profiles are plotted at two fully developed regions, x = 0.2L and x = L, Ha = 15 (Top) and Ha = 30 (Bottom)

Full size image

Comparing the fully developed profiles at x = L and B = 0 between Ha = 15 and 30 reveals a direct relationship between Hartmann number and velocity gradient near walls. In contrast, comparing fully developed profiles at x = L between B = 0 and 0.1 under both magnetic fields confirms an indirect relationship between slip coefficient and velocity gradient near walls. As expected, no significant change is observed with velocity profiles in the leading segment of microchannel where no magnetic field is in place (x = 0.2L) such that slip velocity and peak velocity of parabolic profile remain unchanged.

In addition to slip coefficient which adjusts the degree of surface hydrophobicity in this study, intensity of magnetic field also affects the amount of slip velocity. Figure 12 shows the spatial changes of dimensionless slip velocity on the microchannel wall at B = 0.05 and B = 0.1 across Hartmann numbers of Ha = 0, 15 and 30. For all cases, slip velocity significantly declines from the channel entrance within developing flow region and then reaches a constant value of Us = 0.23 and 0.38, respectively, at B = 0.05 and B = 0.1 when flow becomes fully developed.

Fig. 12
figure 12

Local velocity slip along the microchannel wall in dimensionless form plotted at Ha = 0, 15, 30 and at B = 0.05 (Top) and B = 0.1 (Bottom) for nanofluid with φ = 0.2%

Full size image

When magnetic field is absent, no further change in Us is seen; however, as the transverse magnetic field begins at x* = 9, velocity slippage dramatically increases for both levels of wall hydrophobicity. For B = 0.05, velocity increases from Us = 0.23 to 0.44 and 0.58, respectively, at Ha = 15 and Ha = 30, while for B = 0.1 it increases from Us = 0.38 to 0.61 and 0.73 as Hartmann number intensifies. This shows that stronger magnetic field could potentially have same effect as using more degree of hydrophobicity; therefore, both are effective and direct mechanisms to control liquid slippage on the surface. A twofold increase in Hartmann number from Ha = 15 to Ha = 30 results in 32% and 19% increase in slip velocity, respectively, for B = 0.05 and B = 0.1. In contrast, a twofold increase in slip coefficient from B = 0.05 to B = 0.1 leads to 65% rise in slip velocity in the absence of magnetic field. Elevated slip velocity at x* = 9 remains constant further along the microchannel due to the uniform intensity of applied magnetic field.

Wall shear stress analysis

Wall shear stress is known as an important hydrodynamic factor to quantify the extent of friction between moving fluid and conduits, such that in the context of microchannel it is an indirect measure of the pumping power required. Figure 13 shows the distribution of local wall shear stress (WSS) for pure water and nanofluid with volume fraction of 0.2%, each at four different conditions generated by Ha = 0, 30 and B = 0, 0.1. Common behavior between all cases is the sudden decline of WSS in flow developing region (x* < 9), confirming that growth of boundary layers within entrance length causes a reduction in velocity gradient near wall regardless of hydrophobicity.

Fig. 13
figure 13

Distribution of local wall shear stress (log scale) along the microchannel at Ha = 0, 30 and dimensionless slip coefficients of B = 0 and 0.1, compared between pure water and nanofluid with φ = 0.2%

Full size image

For Ha = 0 in the fully developed region, WSS remains constant along the microchannel such that superhydrophobic surface (B = 0.1) decreases the velocity gradient as well as wall shear stress. In contrast, adding FMWCNT suspending particles to water increases the WSS in similar cases. Transverse magnetic field abruptly raises the WSS and near-wall velocity gradient by reducing and flattening the velocity profile in the microchannel center. It is worth noting that WSS is indirectly proportional to slip coefficient, while a direct relationship between WSS and Hartmann number is evident. Hence, the sudden increase in WSS due to magnetic field is almost doubled with hydrophilic wall (B = 0) compared to superhydrophobic wall (B = 0.1).

Conclusively, for fully developed region, velocity gradient and WSS are directly proportional to Hartmann number while they have an indirect relationship with slip coefficient (compare Figs. 11, 13). In contrast, slip velocity is directly proportional to both Hartmann number and slip coefficient (see Fig. 10).

Wall shear stress was averaged on the microchannel walls under various magnetic field intensities (Ha = 0, 15, 30) and plotted across a range of dimensionless slip coefficients (0 ≤ B ≤ 0.1) for pure water and nanofluid with φ = 0.2%, as shown in Fig. 14. Confirming the results above, average WSS significantly increases with Hartmann number, but decreases with surface hydrophobicity level. On the other hands, increasing dimensionless slip coefficient from 0 to 0.1 decreases the average WSS due to reduced near-wall velocity gradient, such that this descending trend is more significant at higher Hartmann numbers. Superhydrophobic walls can reduce the WSS at B = 0.1 of up to 38.4, 58.5 and 70%, respectively, for Ha = 0, 15 and 30. Using FMWCNT–water nanofluid at all Hartmann numbers and slip coefficients results in a slight increase in wall shear stress due to increased fluid viscosity and inlet velocity.

Fig. 14
figure 14

Average wall shear stress versus a range of dimensionless slip coefficients (0 ≤ B ≤ 0.1) at Ha = 0, 15 and 30, compared between pure water and nanofluid with φ = 0.2%

Full size image

Heat transfer analysis

Figure 15 shows the dimensionless temperature contours in the absence and presence of magnetic field (Ha = 0, 30) and at slip coefficients B = 0 and 0.1 compared between pure water and FMWCNT–water nanofluid with φ = 0.2%. It is evident that cooling efficiency associated with heat transfer rate from the heated upper wall is enhanced when magnetic field is applied. Similar enhancement is also seen when hydrophobicity increases. Comparing Fig. 15 (a) with (b) reveals that nanofluid with suspending FMWCNT improves the fluid conductivity and heat transfer.

Fig. 15
figure 15

Dimensionless temperature contours in microchannel at B = 0, 0.1 and Ha = 0, 30, compared between a pure water and b nanofluid with φ = 0.2%

Full size image

Dimensionless temperature jump along the microchannel wall is shown in Fig. 16 across 0 < Ha < 30 and B = 0.05, 0.1 for pure water and two nanofluids with φ = 0.1 and 0.2%. Due to constant heat flux boundary condition for x* > 9, temperature jump along the microchannel wall remains constant for all cases with no dependence on Hartmann number.

Fig. 16
figure 16

Dimensionless temperature jump along the upper wall of microchannel, for B = 0.05 and 0.1, at Ha = 0, 15 and 30, compared between pure water and nanofluid with volume fractions of 0.1% and 0.2%

Full size image

Due to the constant heat flux applied to the wall, the temperature gradient is only a function of the nanofluid thermal conductivity coefficient. Thus, in a constant volume fraction of nanoparticles, the temperature gradient and the Prandtl number are constant, and as a result, the temperature jump is merely a function of the slip coefficient (see Eq. 27 and following paragraph). This causes two times higher temperature jump as the slip coefficient doubles.

Also, an increment of volumetric concentration of carbon nanoparticles slightly decreases temperature jump due to a decrease in temperature gradient at the wall.

Figure 17 shows the distribution of local Nusselt number along the upper wall with superhydrophobic surface (B = 0.1) at Ha = 0 and 30 plotted for pure water and nanofluid with volume fraction of 0.2%. Heat transfer rate dramatically declines within non-insulated length (x* > 9) confirming the behavior of temperature contours in Fig. 13. The slope of such descending trend is an indicative of declining cooling capacity of microchannel to remove the constant heat flux imposed. Nusselt number locally increases in the presence of magnetic field, because of a flattened velocity profile in the central region and therefore steeper velocity gradient adjacent to wall that causes stronger convection, while a milder increase of Nu is observed when switching from pure water to FMWCNT–water nanofluid with higher thermal conductivity.

Fig. 17
figure 17

Local Nusselt number along the microchannel upper wall with hydrophobic surface B = 0.1 at Ha = 0, 30 compared between pure water and nanofluid with φ = 0.2%

Full size image

Averaged Nusselt number on the upper wall as a quantifier of overall heat transfer in microchannel is shown in Fig. 18 across a range of dimensionless slip coefficients (0 ≤ B ≤ 0.1) and magnetic fields (Ha = 0, 15, 30) for pure water and nanofluid with volume fractions of 0.1% and 0.2%. Dashed and solid lines, respectively, represent data with and without considering temperature jump while slip velocity is still in place, in order to show the real heat transfer under the influence of temperature jump.

Fig. 18
figure 18

Averaged Nusselt number across a range of dimensionless slip coefficients (0 ≤ B ≤ 0.1) at Ha = 0, 15 and 30, compared between pure water and nanofluid with φ = 0.1% and 0.2%. Effects of inclusion of temperature jump are also compared

Full size image

Total heat transfer commonly increases in all cases as the hydrophobicity of microchannel wall enhances, except for cases with temperature jump where \(\overline{Nu}\) reaches a peak in between B = 0.025 and 0.075 followed by a decline. For cases with temperature jump, heat transfer peaks at lower B values when stronger magnetic field is applied (at B = 0.075, 0.05, 0.025, respectively, for Ha = 0, 15, 30) and consequently declines sharper as slip coefficient (B) increases. This phenomenon is due to the confrontation of velocity slip (that augments the convection mechanism) and temperature jump (which acts as a fluid insulator reducing the heat transfer rate). In other words, ignoring the temperature jump leads to overestimating the Nusselt number with an error that culminates at B = 0.1 and φ = 0.2% to 19.6, 22.7 and 25%, respectively, for Ha = 0, 15 and 30. This also reveals that in reality where temperature jump takes place with superhydrophobic walls, surface material should be chosen properly to avoid inevitable and uncontrolled reduction in heat transfer, especially when transverse magnetic field is utilized for enhanced heat transfer. At all Hartmann numbers and slip coefficients, higher volume fraction of carbon nanotubes increases the Nusselt number. In the presence of temperature jump, maximum Nusselt number occurs at B = 0.025 and Ha = 30 at which about 9% increase in heat transfer takes place when volume fraction increases from 0 to 0.2%. For the studied microchannel, the highest heat transfer in reality takes place with temperature jump at the strongest magnetic field used (Ha = 30) and the highest volume fraction of nanoparticles (φ = 0.2%) but at a relatively low hydrophobicity of the microchannel walls (B = 0.025).

Our future studies will shed light on the effects of non-uniform distributions of magnetic field on the hydrodynamics, shear stress, velocity and temperature profiles, amount of slippage and heat transfer.

Conclusions

In this study, FMWCNT–water nanofluid flow and heat transfer under the influence of uniform magnetic field and heat flux partially applied on the microchannel with variable hydrophobicity were investigated considering velocity and temperature slippage. Velocity field was resolved using incompressible preconditioned lattice Boltzmann method (IPLBM), while standard LBM based on passive scaler approach was utilized to solve temperature field. At a constant Reynolds number (Re = 100), various volume fractions of nanoparticles (0 ≤ φ ≤ 0.2%), Hartmann numbers (0 ≤ Ha ≤ 30), and slip coefficients (0 ≤ B ≤ 0.1) were studied with considering velocity and temperature slippage. Significant findings are concluded as follows:

  • Standard LBM causes a considerable compressibility error when a partial magnetic field is applied on the microchannel, and therefore poorly performs to maintain conservation of flow rate in an incompressible flow setting. In contrast, incompressible preconditioned LBM significantly reduces the inherent compressibility error and successfully conserves the flow rate and average velocity along the microchannel.

  • Upon an abrupt decline of slip velocity in developing region, it reaches a constant value in the absence of magnetic field. However, at B = 0.05 the presence of magnetic field causes a sudden increase in slip velocity for 91% and 152%, respectively, at Ha = 15 and Ha = 30. In contrast, at B = 0.1 these numbers reduce to 61% and 92% showing that higher hydrophobicity attenuates the direct effect of magnetic field on velocity slip, although it solely increases US when Ha = 0. Hence, slip velocity has a direct relationship with both magnetic field and slip coefficient.

  • Wall shear stress shows an indirect relation with surface degree of hydrophobicity, as well as a direct relationship with magnetic field intensity and volume concentration of FMWCNT nanoparticles. An abrupt increase in WSS due to magnetic field is almost doubled with hydrophilic wall (B = 0) compared to superhydrophobic wall (B = 0.1). Superhydrophobic walls can reduce the WSS at B = 0.1 of up to 38.4, 58.5 and 70%, respectively, for Ha = 0, 15 and 30.

  • Inclusion of temperature jump in simulation avoids inaccurate and non-stop increase in total heat transfer versus hydrophobicity (or slip coefficient) such that averaged Nusselt number \(\overline{Nu}\) reaches a peak in between B = 0.025 and 0.075 followed by a decline. Ignoring the temperature jump in modeling overestimates the Nusselt number with an error that culminates at B = 0.1 and φ = 0.2% to 19.6, 22.7 and 25%, respectively, for Ha = 0, 15 and 30.

  • For the cases studied, maximum heat transfer rate is obtained at the strongest magnetic field (Ha = 30) and the highest volume fraction of nanoparticles (φ = 0.2%) but at a relatively low hydrophobicity of the microchannel walls (B = 0.025).