1 Introduction

Advancements in the electrical and mechanical sciences have resulted in smaller devices and improved their efficiency and also reduced their energy consumption. Because of higher heat transfer area, the microchannel’s ability in heat dissipation is more than the conventional devices. Tullius et al. (2011) comprehensively reviewed the studies on the heat transfer performance of microchannels for various designs and fluids.

By introducing the nanofluids and demonstrating their ability for heat transferring better than the conventional fluids (Choi 1995), the application of these new fluids has increased in microscale systems. Several studies have been conducted on the application of nanofluids in microchannels. Raisi et al. (2011) numerically investigated forced convection of nanofluid in a microchannel with both slip and no-slip boundary conditions. They concluded that using the nanofluid improves the microchannel heat transfer performance.

Akbarinia et al. (2011) investigated the heat transfer of water–alumina nanofluid in a two-dimensional microchannel at low Reynolds number by using FVM. They concluded that at a fixed Reynolds number, the main reason for increasing the Nusselt number is not because of adding the nanoparticles, but it is because of increasing the fluid velocity in order to maintain the constant Reynolds number. Mohammed et al. (2011) examined laminar flow and heat transfer of a nanofluid in a three-dimensional microchannel heat sink with a trapezoidal cross section for different wall materials. They used the FVM and concluded that using the glycerin-based nanofluid achieves the best heat transfer performance. They (Mohammed et al. 2011) also performed a similar study on a microchannel heat sink with triangular cross section and various water-based nanofluids. They showed that water–diamond and water–alumina have the highest and lowest heat transfer coefficients, respectively. Also, the highest and lowest pressure drop in the microchannel belongs to water–SiO2 and water–Ag nanofluids, respectively.

Hung et al. (2012) numerically studied the heat transfer of different nanofluids in a three-dimensional microchannel heat sink. They concluded that the heat transfer performance of water–alumina and water–diamond nanofluid is 21.6% higher than pure water. Kalteh et al. (2012) investigated the heat transfer of the water–alumina nanofluid in a microchannel heat sink by using numerical and experimental methods. The results of their study showed that the Nusselt number increases at higher values of the Reynolds number and the nanoparticles volume fraction and also by reducing the size of nanoparticles. Kalteh (2013) also numerically investigated the heat transfer and the pressure drop of various nanofluids in a microchannel with constant wall temperature. He observed that water–diamond and water–SiO2 nanofluids have maximum and minimum heat transfer coefficients, respectively. Sheikholeslami et al. (2015) studied Cu–water nanofluid flow and heat transfer characteristics of a stretching permeable cylinder. They considered the effect of thermal radiation term in the energy equation and solved the governing partial differential equations numerically by the fourth-order Runge–Kutta integration scheme. They concluded that skin friction coefficient increases with increase in Reynolds number and suction parameter but decreases with increase in nanoparticle volume fraction. Also, Nusselt number is an increasing function of nanoparticle volume fraction, Reynolds number and suction parameter, but it is a decreasing function of radiation parameter.

The motion of an electrically conductive fluid in a magnetic field is called magnetohydrodynamics or MHD. This phenomenon is used in various industrial equipments and processes such as flow meters, MHD pumps and accelerators. Because of the magnetic field effect on the fluid flow and heat transfer mechanism, researchers were interested in analyzing and understanding the behavior of fluids in a magnetic field. Back (1968) studied heat transfer of a laminar electrically conductive fluid flow in a channel with parallel plates. The results showed that the hydrodynamic entrance length of the channel is proportional to the Reynolds and the Prandtl numbers.

Makinde and Chinyoka (2010) investigated MHD unsteady flow and heat transfer of a dusty fluid with variable viscosity and heat conductivity between two parallel plates with slip boundary condition and constant wall temperature. They concluded that slip boundary condition can increase the flow velocity but has no effect on the temperature profile. Also, increasing the Hartmann number reduced the flow velocity. Aminossadati et al. (2011) investigated the MHD flow and heat transfer of water–alumina nanofluid in a microchannel with constant heat flux boundary condition by using finite volume method. They concluded that increasing the nanoparticles volume fraction and magnetic field improves the heat transfer in the microchannel. Bandyopadhyay and Layek (2012) studied MHD pulsatile flow in a constricted channel and concluded that increasing the magnetic field intensity increases the shear stress at the channel’s wall and decreases the flow velocity.

Aminfar et al. (2012) investigated fluid flow and heat transfer of an electrically conductive ferrofluid in the presence of a magnetic field. They used two-phase mixture model and FVM for their simulation and investigated different magnetic field conditions. They concluded that both uniform and non-uniform transverse magnetic fields with negative slope increase the Nusselt number. Sheikholeslami et al. (2013) analytically investigated MHD nanofluid flow in a semi-porous channel. They concluded that the thickness of the velocity boundary layer decreases at higher values of the Reynolds and the Hartmann numbers. Aminfar et al. (2013) numerically investigated the ferrofluid flow and heat transfer through a rectangular duct in the presence of a non-uniform transverse magnetic field. They concluded that the applied magnetic field increases the Nusselt number and the friction factor and prevents the sedimentation of nanoparticles. Deepa and Murali (2014) investigated the effects of variable chemical reaction, thermophoresis, temperature-dependent viscosity and thermal radiation on an unsteady MHD free convective heat and mass transfer flow of a viscous, incompressible and electrically conducting fluid past an impulsively started infinite inclined porous plate. The governing nonlinear partial differential equations are solved numerically by using implicit finite difference scheme with shooting method. The results show that variable viscosity significantly increases viscous drag and rate of heat transfer. The results also show that higher-order chemical reaction induces the concentration of the particles for a destructive reaction and reduces for a generative reaction.

In lattice Boltzmann method, fluid is considered as distinct small particles. These particles move on predetermined paths on the lattice and collide with each other according to the Boltzmann equation. The LBM with BGK model (Bhatnagar et al. 1954) is used extensively due to its simplicity in programming, computational efficiency and also its ability to expand it to multicomponent flows.

Some researchers have used lattice Boltzmann method to simulate fluid flow in microchannel. Yang and Lai (2011) investigated forced convection of water–alumina nanofluid in a microchannel by using LBM. They concluded that increasing the nanoparticles volume fraction improves the heat transfer in microchannel, but it has no effect on the dimensionless velocity profile. Li et al. (2011) investigated transition flow regime of a rarefied gas in microchannel by using the lattice Boltzmann method. They showed that at different Knudsen numbers, numerical results are in good agreement with the experimental results and the direct simulation Monte Carlo ones. Chatterjee and Amiroudine (2011) used lattice Boltzmann method to study the flow and heat transfer inside a rectangular DC MHD micropump. They investigated effects of various parameters such as the channel geometry and the electric field intensity on fluid flow and heat transfer and observed that with increasing the Hartmann number, fluid velocity and heat transfer is reduced.

The purpose of this study is to investigate the flow and heat transfer of water–Al2O3 nanofluid inside a microchannel that is under the influence of a uniform magnetic field by using LBM. Also, the effect of various parameters such as the Reynolds number, the Hartmann number and the nanoparticles volume fraction on the flow and heat transfer is studied.

In the next section, the geometry of the problem, governing boundary conditions, non-dimensional parameters and the relevant models for nanofluid thermophysical properties are presented. In Sect. 3, the governing equations for LBM solution and the boundary conditions are discussed. In Sect. 4, the grid independency study and validation results are presented, and finally, in Sect. 5, the obtained results for different Re, Ha and nanoparticles volume concentration are presented.

2 Problem Statement

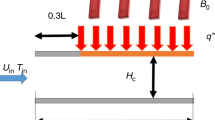
Figure 1 shows the geometry of this study that consists of a microchannel with parallel plates. The microchannel height is 200 μm, and its length is 10 times longer (L/H = 10). Laminar flow of water–alumina nanofluid with uniform velocity and temperature enters the microchannel. The inlet fluid temperature is 293 K, and fully developed conditions for the velocity and temperature fields are considered at the microchannel outlet. The upper wall is insulated, and the bottom wall is kept at constant temperature of 303 K. A uniform transverse magnetic field with strength B 0 is applied perpendicular to the fluid.

Fig. 1
figure 1

A schematic diagram of the physical model

Full size image

Nanofluid is assumed Newtonian fluid, and alumina nanoparticles are identical in shape and size. It is assumed that the nanofluid flow in microchannel is laminar, steady and incompressible. The Reynolds number is considered 5–25 because in microchannels the flow velocity is low. Also, the nanoparticles volume fraction and the Hartmann number vary from 0 to 4% and 0 to 10, respectively. Further increasing the nanoparticles volume fraction causes deposition of the nanoparticles in the microchannels. No-slip boundary condition at the microchannel walls is considered. The thermophysical properties of pure water and the alumina nanoparticles are presented in Table 1.

Table 1 Thermophysical properties of water and alumina
Full size table

The following non-dimensional parameters are used:

$$\begin{aligned} X & = \frac{x}{H},\;Y = \frac{y}{H},\;U = \frac{u}{{u_{\text{in}} }},\;V = \frac{v}{{u_{\text{in}} }} \\ \theta & = \frac{{T - T_{\text{in}} }}{{T_{\text{w}} - T_{\text{in}} }},\;Re = \frac{{u_{\text{in}} H}}{{\upsilon_{\text{nf}} }},\;Ha = B_{\text{o}} H\sqrt {\frac{{\sigma_{\text{nf}} }}{{\mu_{\text{nf}} }}} ,\;Pr = \frac{{\nu_{\text{nf}} }}{{\alpha_{\text{nf}} }} \\ \end{aligned}$$
(1)

The properties of the nanofluid can be defined based on the properties of water and alumina:

$$\rho_{\text{nf}} = (1 - \varphi )\rho_{\text{f}} + \varphi \rho_{\text{s}}$$
(2)
$$\left( {\rho c_{\text{p}} } \right)_{\text{nf}} = (1 - \varphi )(\rho c_{\text{p}} )_{\text{f}} + \varphi (\rho c_{\text{p}} )_{\text{s}}$$
(3)

where φ represents the volume fraction of nanoparticles.

Nanofluid viscosity is calculated by using Batchelor theoretical model in which Brownian motion is also considered (Nguyen et al. 2008):

$$\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} = 1 + 2.5\varphi + 6.5\varphi^{2}$$
(4)

The thermal conductivity of nanofluid is approximated by using Patel model (Patel et al. 2005). In this model, the Brownian motion of nanoparticles, the diameter and the volume fraction of nanoparticles and the nanofluid temperature is considered:

$$\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \left[ {1 + \frac{{k_{\text{s}} A_{\text{s}} }}{{k_{\text{f}} A_{\text{f}} }} + ck_{\text{s}} Pe\frac{{A_{\text{s}} }}{{k_{\text{f}} A_{\text{f}} }}} \right] \,$$
(5)

where

$$\frac{{A_{\text{s}} }}{{A_{\text{f}} }} = \frac{{d_{\text{f}} }}{{d_{\text{s}} }}\frac{\varphi }{1 - \varphi }$$
(6)
$$Pe = \frac{{u_{\text{s}} d_{\text{s}} }}{{\alpha_{\text{f}} }} \,$$
(7)

and the Brownian motion velocity of the particles is calculated as follows:

$$u_{s} = \frac{{2k_{\text{b}} T}}{{\pi \mu_{\text{f}} d_{\text{s}}^{2} }}$$
(8)

Appropriate value of ‘c’ has been calculated by matching the experimental result, and it is equal to 25,000 for a wide range of experimental data (Patel et al. 2005). k b is the Boltzmann constant (\(k_{\text{b}} = 1.3807 \times 10^{ - 23} \,J/K\)). The diameter of the nanoparticles is d s = 40 nm, and the molecular diameter of the base fluid is d f = 2 Å.

The local Nusselt number at the lower wall of the microchannel is calculated as follows:

$$Nu_{x} = - \frac{{\left. {\frac{\partial T}{\partial y}} \right|_{y = 0} }}{{T_{\text{w}} - T_{\text{m}} }}H$$
(9)

and the local friction coefficient is defined as follows:

$$C_{\text{f}} = \frac{{2\mu_{\text{nf}} \left. {\frac{\partial u}{\partial y}} \right|_{y = 0} }}{{\rho_{\text{nf}} u_{m}^{2} }}$$
(10)

3 Lattice Boltzmann Method

The thermal lattice Boltzmann method calculates the fluid velocity and temperature fields by using two distribution functions f and g, which represent the fluid density distribution function and energy distribution function, respectively. The TLBM equations with external force and without considering viscous dissipation by using BGK collision model are as follows (Zhang 2011; Karimipour et al. 2012):

$$f_{\alpha } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \Delta t,t + \Delta t) - f_{\alpha } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} ,t) = - \frac{\Delta t}{{\tau_{\text{f}} + 0.5\Delta t}}\left[ {f_{\alpha } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} ,t) - f_{\alpha }^{eq} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} ,t)} \right] + \frac{{\tau_{\text{f}} \Delta tF_{\alpha } }}{{\tau_{\text{f}} + 0.5\Delta t}}$$
(11)
$$g_{\alpha } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \Delta t,t + \Delta t) - g_{\alpha } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} ,t) = - \frac{\Delta t}{{\tau_{\text{g}} + 0.5\Delta t}}[g_{\alpha } (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} ,t) - g_{\alpha }^{\text{eq}} (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {x} ,t)]$$
(12)

where \(\Delta t\) represents the lattice time step and \(e_{\alpha }\) is microscopic velocity vector in α direction where for D2Q9 the model is defined as follows:

$$\begin{aligned} e_{\alpha = 0} & = C(0,0) \, \\ e_{\alpha = 1 - 4} & = C\left( {\cos \frac{\pi (\alpha - 1)}{2},\sin \frac{\pi (\alpha - 1)}{2}} \right) \, \\ e_{\alpha = 5 - 8} & = \sqrt 2 C\left( {\cos \frac{\pi (2\alpha - 9)}{4},\sin \frac{\pi (2\alpha - 9)}{4}} \right) \\ \end{aligned}$$
(13)

\(C = {\raise0.7ex\hbox{${\Delta x}$} \!\mathord{\left/ {\vphantom {{\Delta x} {\Delta t}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\Delta t}$}} = {\raise0.7ex\hbox{${\Delta y}$} \!\mathord{\left/ {\vphantom {{\Delta y} {\Delta t}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\Delta t}$}}\) is lattice microscopic velocity. \(\Delta x\) and \(\Delta y\) are the lattice step in the directions of x and y, respectively. τ f and τ g are the relaxation time that controls the rate of reaching the equilibrium state. The relationship between kinematic viscosity (\(\upsilon\)), thermal diffusivity (χ) and relaxation time is:

$$\nu = \tau_{\text{f}} C_{\text{s}}^{2} \Delta t$$
(14)
$$\chi = 2\tau_{\text{g}} C_{\text{s}}^{2} \Delta t$$
(15)

\(C_{\text{s}} = \sqrt {\text{RT}} = {C \mathord{\left/ {\vphantom {C {\sqrt 3 }}} \right. \kern-0pt} {\sqrt 3 }}\) is lattice sound speed. To consider the effect of the magnetic field, the force term in Eq. (11) is calculated as follows (Karimipour et al. 2012; Sheikholeslami et al. 2013):

$$F_{\alpha } = \frac{{3G(e_{\alpha x} - u)}}{{C^{2} }}f_{\alpha }^{\text{eq}}$$
(16)
$$G = - Au$$
(17)

where \(A = {{{\text{Ha}}^{2} \nu_{\text{nf}} } \mathord{\left/ {\vphantom {{{\text{Ha}}^{2} \nu_{\text{nf}} } {L^{2} }}} \right. \kern-0pt} {L^{2} }}\).

The equilibrium density distribution function and the equilibrium internal energy distribution function are defined as follows:

$$f_{\alpha = 0 - 8}^{\text{eq}} = \omega_{\alpha } \rho \left[ {1 + \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} }}{{C_{\text{s}}^{2} }} + \frac{1}{2}\frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} )^{2} }}{{C_{\text{s}}^{4} }} - \frac{1}{2}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}^{2} }}{{C_{\text{s}}^{2} }}} \right]$$
(18)
$$\begin{aligned} g_{\alpha = 0}^{\text{eq}} & = \omega_{\alpha } \rho \varepsilon \left[ { - \frac{1}{2}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}^{2} }}{{C_{\text{s}}^{2} }}} \right] \\ g_{\alpha = 1 - 4}^{\text{eq}} & = \omega_{\alpha } \rho \varepsilon \left[ {\frac{3}{2} + \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} }}{{2C_{\text{s}}^{2} }} + \frac{1}{2}\frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} )^{2} }}{{C_{\text{s}}^{4} }} - \frac{1}{2}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}^{2} }}{{C_{\text{s}}^{2} }}} \right] \\ g_{\alpha = 5 - 8}^{\text{eq}} & = \omega_{\alpha } \rho \varepsilon \left[ {3 + \frac{{2\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} }}{{C_{\text{s}}^{2} }} + \frac{1}{2}\frac{{(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} )^{2} }}{{C_{\text{s}}^{4} }} - \frac{1}{2}\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}^{2} }}{{C_{\text{s}}^{2} }}} \right] \\ \end{aligned}$$
(19)

In the above, the velocity is \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} = \left( {u,v} \right)\), the thermal energy density is \(\rho \varepsilon = \rho {\text{RT}}\) (in 2D) and ω is the weight factor where for D2Q9, the model is calculated as (D’Orazio and Succi 2004):

$$\omega_{\alpha = 0} = \frac{4}{9},\;\omega_{\alpha = 1 - 4} = \frac{1}{9},\;\omega_{\alpha = 5 - 8} = \frac{1}{36}$$
(20)

Finally, macroscopic variables including density, velocity, internal energy per unit mass and heat fluxes are calculated by using the following equations:

$$\rho = \sum\limits_{\alpha } {f_{\alpha } }$$
(21)
$$\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} = \sum\limits_{\alpha } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } f_{\alpha } } + \frac{{\rho \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {G} \Delta t}}{2}$$
(22)
$$\rho \varepsilon = \sum\limits_{\alpha } {g_{\alpha } }$$
(23)
$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {q} = \left( {\sum\limits_{\alpha } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {e}_{\alpha } g_{\alpha } } - \rho \varepsilon \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} } \right)\frac{{\tau_{\text{g}} }}{{\tau_{\text{g}} + 0.5\Delta t}}$$
(24)

3.1 Boundary Conditions

Figure 2 shows the D2Q9 lattice model used in the present study. In lattice Boltzmann method, values of the distribution functions on the boundaries that enter the computational domain are unknown and must be determined, while the distribution functions that exit the solution area are known from streaming step (Fig. 3). Based on the work done by Zou and He (1997), the fluid density at the microchannel inlet is calculated from the following equation:

$$\rho_{\text{in}} = \frac{{2\left( {f_{0} + f_{2} + f_{4} + 2\left( {f_{3} + f_{6} + f_{7} } \right)} \right)}}{{G\Delta t + 2(1 - u_{\text{in}} )}}$$
(25)
Fig. 2
figure 2

D2Q9 model

Full size image
Fig. 3
figure 3

Distribution functions on the boundaries of the microchannel

Full size image

By using the above equation, the unknown input distribution functions are derived as follows:

$$\begin{aligned} f_{1} & = f_{3} + \frac{2}{3}\rho_{\text{in}} u_{\text{in}} \\ f_{5} & = f_{7} + \frac{1}{2}(f_{4} - f_{2} ) + \frac{1}{6}\rho_{\text{in}} u_{\text{in}} + \frac{1}{6}\rho_{\text{in}} v_{\text{in}} - \frac{\Delta t}{4}\rho_{\text{in}} G \\ f_{8} & = f_{6} - \frac{1}{2}(f_{4} - f_{2} ) + \frac{1}{6}\rho_{\text{in}} u_{\text{in}} - \frac{1}{6}\rho_{\text{in}} v_{\text{in}} - \frac{\Delta t}{4}\rho_{\text{in}} G \\ \end{aligned}$$
(26)

The above equations are obtained by using Eqs. (21) and (22) and bounce-back rule for non-equilibrium density distribution function perpendicular to the microchannel inlet (i.e., \(f_{1} - f_{1}^{\text{eq}} = f_{3} - f_{3}^{\text{eq}}\)).

Because of fully developed condition for the velocity field at the microchannel outlet, the second-order linear extrapolation is used to determine the unknown distribution functions f 3, f 6 and f 7:

$$\begin{aligned} f_{3} (Nx,t) & = 2f_{3} (Nx - 1,t) - f_{3} (Nx - 2,t) \\ f_{6} (Nx,t) & = 2f_{6} (Nx - 1,t) - f_{6} (Nx - 2,t) \\ f_{7} (Nx,t) & = 2f_{7} (Nx - 1,t) - f_{7} (Nx - 2,t) \\ \end{aligned}$$
(27)

At the upper and lower walls where there is no-slip condition, the bounce-back rule is used to determine the unknown distribution functions.

To determine the thermal boundary conditions, the method proposed by D’Orazio and Succi (2004) is used. The microchannel inlet fluid temperature is known, and thus, the unknown internal energy distribution functions g1, g5, g8, are determined as:

$$\begin{aligned} g_{1} & = \frac{1}{9}[1.5 + 1.5u_{\text{in}} + 3u_{\text{in}}^{2} ]\frac{{6\rho_{\text{in}} \varepsilon_{\text{in}} - 6(g_{0} + g_{2} + g_{3} + g_{4} + g_{6} + g_{7} )}}{{2 + 3u_{\text{in}} + 3u_{\text{in}}^{2} }} \\ g_{5} & = \frac{1}{36}[3 + 6u_{\text{in}} + 3u_{\text{in}}^{2} ]\frac{{6\rho_{\text{in}} \varepsilon_{\text{in}} - 6(g_{0} + g_{2} + g_{3} + g_{4} + g_{6} + g_{7} )}}{{2 + 3u_{\text{in}} + 3u_{\text{in}}^{2} }} \\ g_{8} & = \frac{1}{36}[3 + 6u_{\text{in}} + 3u_{\text{in}}^{2} ]\frac{{6\rho_{\text{in}} \varepsilon_{\text{in}} - 6(g_{0} + g_{2} + g_{3} + g_{4} + g_{6} + g_{7} )}}{{2 + 3u_{\text{in}} + 3u_{\text{in}}^{2} }} \\ \end{aligned}$$
(28)

Assuming thermally fully developed flow in the microchannel outlet, second-order linear extrapolation is used to determine the unknown distribution functions g 3, g 6, g 7:

$$\begin{aligned} g_{3} (Nx,t) & = 2g_{3} (Nx - 1,t) - g_{3} (Nx - 2,t) \\ g_{6} (Nx,t) & = 2g_{6} (Nx - 1,t) - g_{6} (Nx - 2,t) \\ g_{7} (Nx,t) & = 2g_{7} (Nx - 1,t) - g_{7} (Nx - 2,t) \\ \end{aligned}$$
(29)

The unknown internal energy distribution functions at upper insulated wall and lower constant temperature wall can be calculated, respectively, as follows:

$$\begin{aligned} g_{4} & = \frac{{g_{2} + g_{5} + g_{6} }}{2} \\ g_{7} & = \frac{{g_{2} + g_{5} + g_{6} }}{4} \\ g_{8} & = \frac{{g_{2} + g_{5} + g_{6} }}{4} \\ \end{aligned}$$
(30)
$$\begin{aligned} g_{2} = \frac{{3\rho_{\text{w}} \varepsilon_{\text{w}} - 3\left( {g_{0} + g_{1} + g_{3} + g_{4} + g_{7} + g_{8} } \right)}}{6} \hfill \\ g_{5} = \frac{{3\rho_{\text{w}} \varepsilon_{\text{w}} - 3\left( {g_{0} + g_{1} + g_{3} + g_{4} + g_{7} + g_{8} } \right)}}{12} \hfill \\ g_{6} = \frac{{3\rho_{\text{w}} \varepsilon_{\text{w}} - 3\left( {g_{0} + g_{1} + g_{3} + g_{4} + g_{7} + g_{8} } \right)}}{12} \hfill \\ \end{aligned}$$
(31)

4 Code Validation and Grid Independence Study

In this study, to solve the governing equations, a computer code in FORTRAN is developed. The following criteria are used to ensure the steady-state solution:

$$\begin{aligned} \frac{{\sum {\left| {u(x,t + \Delta t) - u(x,t)} \right|} }}{{\sum {\left| {u(x,t)} \right|} }} & \le 1.0 \times 10^{ - 6} \\ \frac{{\sum {\left| {T(x,t + \Delta t) - T(x,t)} \right|} }}{{\sum {\left| {T(x,t)} \right|} }} & \le 1.0 \times 10^{ - 6} \\ \end{aligned}$$
(32)

After solving the governing equations and obtaining the velocity and temperature fields, other useful quantities such as Nusselt number and friction factor are calculated. For grid independence study, the Nusselt number on the microchannel bottom wall is calculated for various lattice numbers, and the result is given in Table 2. Also, Fig. 4 shows a portion of the dimensionless velocity profile for different grid numbers. According to Table 2 and Fig. 4, 80 × 800 lattice numbers are chosen as the final lattice numbers in the present study.

Table 2 Grid independence study for Re = 25, Ha = 0 and φ = 0
Full size table
Fig. 4
figure 4

Dimensionless developed velocity profile in the cross section of the microchannel (Re = 25, Ha = 0, φ = 0)

Full size image

To validate the present code, the numerical results are compared with previous works. In Fig. 5, the ratio of the bulk temperature to the inlet temperature for three Reynolds numbers (5, 10, and 20) is compared with the work done by Gokaltun and Dulikravich (2010) for pure water. Also, in Fig. 6 dimensionless temperature variation for Re = 10 and volume fraction 0% and 3% for water–Cu nanofluid are compared with the work done by Raisi et al. (2011). In addition, the velocity profile for fully developed laminar MHD flow in a channel is compared with the analytical model offered by Back (1968):

$$U = \left( {\frac{Ha}{2}} \right)\frac{{\left[ {\cosh \left( {Ha/2} \right) - \cosh \left( {\left( {Ha/2)(2Y - 1} \right)} \right)} \right]}}{{\left[ {\left( {Ha/2} \right)\cosh \left( {Ha/2} \right) - \sinh \left( {Ha/2} \right)} \right]}}$$
(33)
Fig. 5
figure 5

Comparing the present results with Gokaltun and Dulikravich (2010) for pure water

Full size image
Fig. 6
figure 6

Comparing the present results with Raisi et al. (2011). Dimensionless temperature profile in the center of the microchannel for water–Cu nanofluid (Re = 10)

Full size image

The fully developed velocity profile for three different Hartmann numbers is shown in Fig. 7.

Fig. 7
figure 7

Comparing the present results with the analytical solution (Back 1968). Dimensionless developed velocity profiles for MHD flow between two parallel plates

Full size image

5 Results

In this study, flow and heat transfer of water–alumina nanofluid in a two-dimensional microchannel under the influence of the magnetic field is investigated. The lattice Boltzmann method with BGK model is used to obtain the velocity and temperature distribution in the microchannel. In this section, the effects of the Reynolds number (Re = 5–25), the Hartmann number (Ha = 0–10) and the nanoparticles volume fraction (φ = 0–4%) on the flow and temperature field as well as the Nusselt number and friction factor are investigated.

In Figs. 8 and 9, isotherms and streamlines are shown for Reynolds numbers 5 and 25, and Hartmann numbers 0 and 10 at φ = 2%. At Ha = 0, the streamlines indicate that the flow develops rapidly after entering the microchannel. But at Ha = 10 due to Lorentz force caused by the external magnetic field, it is observed that the streamlines are almost parallel at the entrance of the microchannel. This indicates that the magnetic field causes the flow to be developed much earlier than the previous case. Isotherms also change with the Reynolds and the Hartmann numbers. By increasing the Reynolds number, the temperature gradient at the lower wall increases and this caused higher heat transfer rate. Also, for higher Reynolds number, the nanofluid leaves the microchannel with lower temperature.

Fig. 8
figure 8

Isotherms and streamlines. Solid line represents Ha = 0, and dashes represents Ha = 10 (Re = 5, φ = 2%)

Full size image
Fig. 9
figure 9

Isotherms and streamlines. Solid line represents Ha = 0, and dashes represent Ha = 10. (Re = 25, φ = 2%)

Full size image

Figure 10a, b shows the dimensionless velocity and temperature profiles along the microchannel centerline for different Reynolds numbers and Ha = 0. Figure 10a shows that the dimensionless velocity along the microchannel centerline is developed shortly after entering and reaches its maximum value (i.e., 1.5 times the inlet velocity) that is in agreement with the results of the analytical solution for the developed flow in a channel. It is also observed that by increasing the Reynolds number, the velocity field is developed later. Figure 10b shows the dimensionless temperature variations at the microchannel centerline. At low Reynolds number, the nanofluid has more time to exchange heat with microchannel wall and that increases the nanofluid temperature more.

Fig. 10
figure 10

a Dimensionless velocity variations along the center line of the microchannel (Ha = 0, φ = 2%). b Dimensionless temperature variations along the center line of the microchannel (Ha = 0, φ = 2%)

Full size image

Figure 11 shows the variations of dimensionless developed velocity profile at the microchannel middle section for different Hartmann numbers. In the absence of a magnetic field, developed velocity profile is parabolic and the maximum velocity occurs at the microchannel centerline. But with the addition of the magnetic field, the fluid velocity increases near the walls and decreases in the channel centerline which develops a flatter shape for velocity profile.

Fig. 11
figure 11

Variations of dimensionless developed velocity profile at the microchannel cross section with Hartman number (Re = 25, φ = 2%)

Full size image

Figure 12a, b shows the effect of the Reynolds and the Hartmann numbers on the local Nusselt number along the microchannel lower wall. Figure 12a shows that higher values of the Reynolds number increase the local Nusselt number at fixed Hartmann number (Ha = 0). This can be explained due to increasing the convective effects by increasing the Reynolds number. Also, Figure 12b shows that increasing the Hartmann number has little effect on the Nusselt number. This little increase in the heat transfer is due to the velocity increase near the walls because of the magnetic field effect (as observed in Fig. 11).

Fig. 12
figure 12

a The local Nusselt number variation with the Reynolds number in microchannel (Ha = 0, φ = 2%). b The local Nusselt number variation with the Hartmann number in microchannel (Re = 25, φ = 2%)

Full size image

Figure 13 shows the average Nusselt number changes in microchannel with the Reynolds and the Hartmann numbers at the fixed volume fraction (φ = 2%). These results show that at a constant Hartmann number, the average Nusselt number increases at a constant rate with increasing the Reynolds number due to the increased velocity near the wall. Also, it can be seen that higher values of the Hartmann number increase the average Nusselt number slightly at a constant Reynolds number. For example, at Re = 25 the average Nusselt number increases 3% with increasing the Hartmann number from 0 to 10.

Fig. 13
figure 13

Variation of the average Nusselt number with the Reynolds and the Hartmann numbers (φ = 2%)

Full size image

In Fig. 14a, b, variation of the C f Re along the microchannel lower wall by changing the Reynolds and the Hartmann numbers is shown. In Fig. 14a, it is observed that due to the high velocity gradient, the friction factor has its maximum value at the beginning of the microchannel and decreases to a constant value at the fully developed region. It is also observed that with increasing the Reynolds number the friction factor in the developing zone has increased. Figure 14b shows the friction factor variations with the Hartmann number at a fixed Reynolds number. It is observed that by increasing the Hartmann number, the friction factor along the microchannel is increased. As mentioned earlier, Lorentz force caused by the effect of external magnetic field changes the velocity field distribution near the wall and increases the friction coefficient.

Fig. 14
figure 14

a Variations of C f Re along the microchannel for different values of Reynolds numbers. (Ha = 0, φ = 2%). b Variations of C f Re along the microchannel for different values of Hartmann numbers. (Re = 25, φ = 2%)

Full size image

The dimensionless average heat transfer coefficient is used to investigate the effect of nanoparticles volume fraction on the heat transfer in microchannel. It is defined as ratio of the average heat transfer coefficient of nanofluid to average heat transfer coefficient of pure water:

$$\hat{h} = \frac{{h_{\text{ave}} }}{{h_{{{\text{ave}} . {\text{f}}}} }}$$
(34)

Figure 15 shows the dimensionless average heat transfer coefficient at different values of the nanoparticles concentrations and various Reynolds numbers for constant Hartmann number. From this figure, it is observed that for all values of the Reynolds number, by increasing the nanoparticles volume fraction, the average heat transfer coefficient increases. Adding the nanoparticles increases the thermal conductivity of the fluid that in turn enhances the heat transfer. In addition, it is observed that the effect of nanoparticles in improving the heat transfer reduces by increasing the Reynolds number. This can be explained by the fact that by increasing the Reynolds number, there is less time for heat exchange between the fluid and microchannel wall that makes the addition of nanoparticles less effective for heat transfer enhancement. Figure 16 represents the dimensionless heat transfer coefficient variations with the nanoparticles volume fraction and the Hartmann number at constant Reynolds number. It is observed that the Hartmann number has small effect on \(\hat{h}\).

Fig. 15
figure 15

Variation of the dimensionless average heat transfer coefficient with the volume fraction and the Reynolds number. (Ha = 5)

Full size image
Fig. 16
figure 16

Variation of the dimensionless average heat transfer coefficient with the volume fraction and the Hartmann number. (Re = 25)

Full size image

6 Conclusions

In this study, Lattice Boltzmann method is used to study the flow and heat transfer of water–Al2O3 nanofluid in a two-dimensional microchannel under the influence of an external magnetic field. The temperature of the lower wall is kept constant, and the upper wall is insulated. An external magnetic field perpendicular to the flow direction with constant intensity is applied to the microchannel. The lattice Boltzmann method results are compared with the results of the work done with other methods, and good agreement is observed. Also, the effects of relevant parameters such as the Reynolds number, the Hartmann number and the nanoparticles volume fraction on the heat transfer and the friction coefficient are examined. The results of the numerical solution can be summarized as follows:

  • Isotherms and streamlines are affected by the magnetic field. By increasing the Reynolds number, the hydrodynamic entrance length is increased. While increasing the Hartmann number reduces the hydrodynamic entrance length.

  • Local and average Nusselt number increases by increasing the Reynolds and the Hartmann numbers. The effect of Reynolds number on increasing the Nusselt number is more than the effect of the Hartmann number. At Re = 25, the average Nusselt number increased 3% with increasing the Hartmann number from 0 to 10, while it increased 19% with increasing the Reynolds number from 5 to 25 at Ha = 5.

  • Friction factor increased by increasing the Reynolds and Hartmann numbers. The effect of Hartmann number on increasing the friction factor is more than the effect of increasing the Reynolds number.

  • Increasing the nanoparticles volume fraction at all values of the Reynolds and the Hartmann numbers improved the heat transfer coefficient. Also, the effect of increasing the nanoparticles volume fraction on the heat transfer coefficient decreased by increasing the Reynolds and the Hartmann numbers.